Дисперсионный анализ

С помощью дисперсионного анализа исследуют влияние одной или нескольких независимых переменных на одну зависимую переменную (одномерный анализ) или на несколько зависимых переменных (многомерный анализ). В обычном случае независимые переменные принимают только дискретные значения (и относятся к номинальной или порядковой шкале); в этой ситуации также говорят о факторном анализе. Если же независимые переменные принадлежат к интервальной шкале или к шкале отношений, то их называют ковариациями, а соответствующий анализ — ковариационным.

В рамках дисперсионного анализа SPSS предлагает множество возможностей, в которых, однако, не всегда легко разобраться, в особенности для новичка. Даже учебники по SPSS напрямую не способствуют облегчению освоения имеющихся возможностей. Во-первых, нужно отметить, что в принципе дисперсионный анализ может выполняться в рамках двух подходов:

•  при помощи традиционного "классического" метода по Фишеру (Fisher) и

•  при помощи нового метода "обобщенной линейной модели".

Первый подход сводится к разложению по методу наименьших квадратов (МНК); в однофакторном случае совокупная дисперсия всех наблюдаемых значений раскладывается на дисперсию внутри отдельных групп и дисперсию между группами. В основе обобщенной линейной модели напротив, лежит, корреляционный или регрессионный анализ.

До 6 версии SPSS обобщенная линейная модель была реализована на основе процедуры MANOVA, управление которой могло происходить как через диалоговое окно, так и при помощи командного синтаксиса. В 7-ой версии эта процедура была заменена на процедуру GLM; при этом процедура MANOVA осталась, как и прежде, доступной через командный синтаксис.

Главным отличием между GLM и MANOVA является то, что в MANOVA используется, так называемая, "full rank linear model" (линейная модель полного ранга), а в GLM, так называемая, "поп full rank linear model" (линейная модель неполного ранга). Более подробную информацию по этому вопросу можно найти в специальной литературе, к примеру, в книге Р. Е. Кирка (R. E. Kirk) (см. список литературы). В GLM предлагаются ещё и дополнительные расширения, самым важным из которых, конечно же, является тест для сравнения средних значений отдельных слоев (подпопуляций), который выполняется после проведения дисперсионного анализа. Слои или подпопуляций определяются различными уровнями величины фактора, положенного в основу классификации. В то же время, MANOVA включает ряд дополнительных видов анализа (регрессионный анализ, дискриминантный анализ, канонический анализ, анализ главных компонентов и т.д.), которых нет в GLM.

В дальнейшем мы ограничимся рассмотрением только наиболее часто употребительных видов дисперсионного анализа. При этом будет проведено различие между, одномерными и многомерным дисперсионным анализом (в зависимости от количества зависимых переменных), а также выделен случай, когда факторы (независимые переменные) включают повторные измерения.

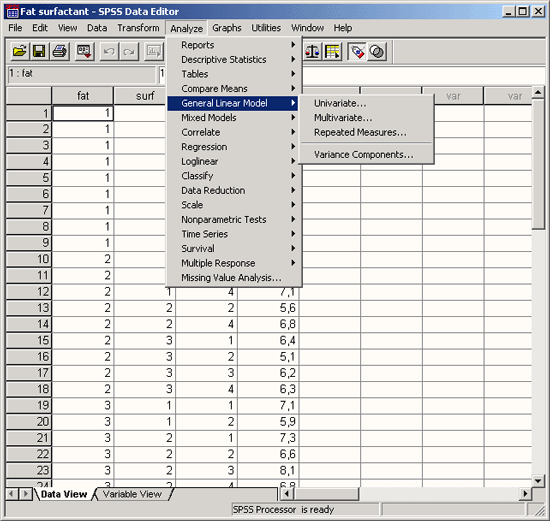
После открытия соответствующего файла (к примеру, varana.sav), дисперсионный анализ может быть вызван посредством выбора меню Analyze (Анализ) General Linear Model (Общая линейная модель)

Откроется вспомогательное меню (см. рис. 17.1)

Все без исключения возможности, предлагаемые в диалоговом окне, предполагают проведение расчётов на основе общей линейной модели. Если перечислять по очереди, то с помощью данного меню можно провести одномерный дисперсионный анализ (Univariate...), многомерный дисперсионный анализ (Multivariate...), многомерный дисперсионный анализ с учетом повторных измерений (Repeated Measures...). И, наконец, в данном меню имеется один пункт для расчёта компонентов дисперсии (Variance Components...) (см. гл. 17.4).

Возможно также проведение дисперсионного анализа по традиционному "классическому" методу Фишера. Однако такой анализ выполним только за счёт использования программного синтаксиса (процедура ANOVA). Этому методу посвящен отдельный раздел (см. гл. 17.1.2).

Рис. 17.1: Вспомогательное меню General Linear Model (Общая линейная модель)

В рамках данной книги нет возможности полностью рассмотреть все, что предлагается пользователю SPSS для проведения дисперсионного анализа, поэтому с помо-:лью нескольких примеров мы попытаемся сделать общий обзор и изложить вводные замечания для основных ситуаций. К основным ситуациям относятся:

•  одномерный анализ,

•  ковариационный анализ и

•  многомерный анализ.

Для одномерного анализа будут рассмотрены варианты без повторных измерений и с повторными измерениями. Последний раздел главы посвящен расчёту компонентов дисперсии.

17.1 Одномерный дисперсионный анализ

Однофакторный дисперсионный анализ (без и с повторными измерениями) уже рассматривался в главе 13, поэтому мы сразу обратимся к многофакторному дисперсионному анализу.

Так как дисперсионный анализ очень часто находит применение в области психологии, то первым примером и будет пример из этой области. В четыре различных момента времени 27 испытуемых были подвергнуты тесту на внимательность. Причём для каждого испытуемого регистрировался пол и возраст. Собранные значения представлены в следующей сводной таблице.

С	А	M1	М2	М3	М4	С	А	М1	М2	МЗ	М4
1	1	16	18	21	20	1	3	8	11	12	12
1	1	17	19	18	22	2	1	17	18	20	21
1	1	15	15	17	18	2	1	15	15	18	17
1	1	16	17	18	19	2	1	16	17	17	18
1	2	15	16	20	18	2	2	15	18	19	21
1	2	16	19	18	20	2	2	17	20	21	22
1	2	13	14	16	17	2	2	14	16	17	20
1	2	14	14	15	17	2	2	14	14	16	18
1	2	15	16	16	18	2	3	12	11	14	15
1	3	13	14	15	16	2	3	10	12	13	14
1	3	14	17	16	19	2	2	10	10	11	13
1	3	13	13	15	16	2	3	9	10	12	11
1	3	10	11	11	11	2	3	10	9	12	13
1	3	9	10	10	13

Полу (G) соответствуют коды: 1 для мужского и 2 для женского; возраст (А) представлен тремя возрастными группами. Испытуемым в возрасте до 30 лет соответствует код 1, испытуемым в возрасте от 31 до 50 лет — код 2 и испытуемым в возрасте свыше 50 лет — код 3. Четыре показателя внимательности соответствуют переменным М1-М4.

При помощи этого примера мы рассмотрим, во-первых, одномерный дисперсионный анализ без повторных измерений и, во-вторых, одномерный дисперсионный анализ с повторными измерениями. Одномерный дисперсионный анализ без повторных измерений может быть проведен как при помощи общей линейной модели, так и при помощи классического метода Фишера.

17.1.1 Одномерный дисперсионный анализ (общий многофакторный)

Исследуем влияние пола и возраста на результирующую величину показателя внимательности (M1). Здесь мы имеем дело с двумя факторами, из которых один (пол) разделён на две категории, а второй (возраст) на три. Комбинации этих двух факторов образуют в общей сложности шесть групп испытуемых (называемых также ячейками). Число наблюдений, относящихся к отдельным ячейкам является не одинаковым, а наоборот различным.

•  Откройте файл varana.sav.

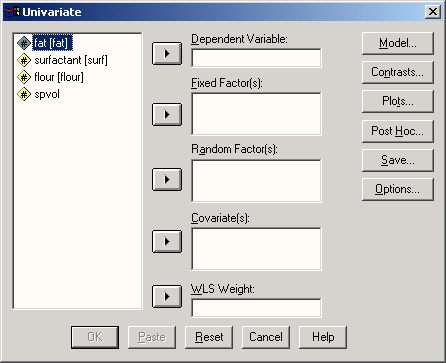
•  Выберите в меню Analyze (Анализ) General Linear Model (Общая линейная модель) Univariate... (Одномерная) Откроется диалоговое окно Univariate (Одномерная) (см. рис. 17.2).

•  Перенесите переменную ml в поле зависимых переменных, а переменные geschl (пол) и alter (возраст) в поле фиксированных факторов.

Понятия "фиксированные" и "случайные" факторы требуют дополнительного объяснения. Фиксированными факторами или факторами с фиксированными эффектами называются такие факторы, которые охватывают все возможные классификационные слои одной независимой переменной, к примеру, пол мужской — женский или образование начальное — среднее — высшее. Однако, если слои (подпопуляции) фактора выбирается случайным образом из бесконечного множества возможных подпопуляции факторов, называемого генеральной популяцией, то говорят о факторах со случайными эффектами. В этом случае является уместным компонентный анализ, то есть расчёт так называемых компонентов дисперсии (см. гл. 17.4).

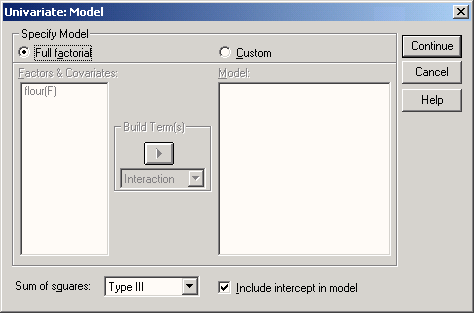
•  Щёлкните по кнопке Model... (Модель)

Откроется диалоговое окно Univariate: Model (Одномерная: Модель) (см. рис. 17.3).

Рис. 17.2: Диалоговое окно Univariate (Одномерная)

Рис. 17.3: Диалоговое окно Univariate: Model (Одномерная: Модель)

Модель дисперсионного анализа — это математическое соотношение, в котором каждая переменная представлена в виде суммы среднего значения и ошибки. Что касается выбора конкретной формы модели, то по умолчанию установлена полнофакторная модель Full factorial). В этой модели среднее значение каждого наблюдения представлено в виде генерального среднего и суммы вклада всех главных "эффектов" (факторов влияния), помимо которых производится также расчёт всех взаимодействий между факторами. Альтернативой является возможность выбора отдельных взаимодействий факторов влияния, которая осуществляется посредством активирования опции Custom (Пользовательский режим). Таким же образом должны быть отобраны и взаимодействия с ковариациями.

Для формирования сумм квадратов для МНК существует четыре различных подхода (четыре типа, обозначенных с помощью римских чисел I, II, III и IV), по умолчанию установлен тип III.

•  Оставьте в этом окне все установки по умолчанию и покиньте диалоговое окно нажатием кнопки Continue (Далее).

•  Щёлкните на выключателе Options... (Опции)

Откроется диалоговое окно Univariate: Options (Одномерная: Опции) (см. рис. 17.4)

•  Перенесите OVERALL (В целом) и обе переменные geschl (пол) и alter (возраст) в поле Display means for (Показать средние значения для); в этом случае в качестве результатов будут выведены средние значения и стандартная ошибка для совокупной выборки (OVERALL) и для всех слоев по обоим факторам. Средние значения для комбинаций взаимодействия на этом этапе рассчитываются только для неполнофакторных моделей.

•  Затем активируйте Descriptive Statistics (Дескриптивные статистики); благодаря выбору этой опции выводятся среднее значение, стандартные отклонения и количество наблюдений во всех ячейках.

•  Активируйте затем опцию Homogeneity tests (Тесты на однородность). Таким образом активируется проверка однородности дисперсии. Покиньте диалоговое окно нажатием Continue (Далее).

•  При помощи выключателя Plots... (Диаграммы) откройте диалоговое окно Univariate: Profile Plots (Одномерная: Профильные диаграммы) (см. рис. 17.5).

Рис. 17.4: Диалоговое окно Univariate: Options (Одномерная: Опции)

Рис. 17.5: Диалоговое окно Univariate: Profile Plots (Одномерная: Профильные диаграммы)

В случае профильных диаграмм речь идёт о графическом представлении средних значений слоев выбранных факторов в виде линейчатых диаграмм. При этом слои второго фактора соответственно могут быть использованы для отображения второй линии. Таким образом можно наглядно изобразить взаимодействия между двумя факторами.

•  Поместите переменную alter (возраст) в поле Horizontal Axis (Горизонтальная ось), а переменную geschl (пол) в поле Separate Lines (Отдельные линии). В принципе можно указывать дополнительную переменную и в поле Separate Plots (Отдельные графики); тогда для отдельных слоев этой переменной будут построены отдельные диаграммы.

•  Щёлкните на выключателе Add (Добавить) и покиньте диалоговое окно нажатием Continue (Далее).

•  В заключение щёлкните на выключателе Post Hoc... (Дополнительный тест). Откроется диалоговое окно Univariate: Post Hoc Multiple Comparisons for Observed Means (Одномерная: Дополнительно — множественные сравнения для наблюдаемых средних значений).

У Вас появится возможность выбрать один или несколько из восемнадцати тестов, необходимых для проведения дополнительного сравнения отдельных слоев выбранных факторов. Конечно же, это имеет смысл только для факторов с более чем двумя слоями.

•  Поместите переменную alter (возраст) в поле Post Hoc Tests for (Дополнительные тесты для).

•  Активируйте тест Шеффе (Scheffe). Теперь диалоговое окно выглядит так, как изображено на рисунке 17.6.

•  Покиньте диалоговое окно нажатием Continue (Далее).

•  Далее Вы имеете возможность определить контрасты и для каждого наблюдения сохранить некоторые статистические характеристики, как новые переменные. Мы от этого откажемся. Начните расчёт нажатием ОК.

В окне сначала появляется сводная таблица, озаглавленная "Межсубъектные факторы". Затем следует вывод средних значений, стандартных отклонений и количества наблюдений для отдельных ячеек, а также результаты теста на однородность.

Рис. 17.6: Диалоговое окно Univariate: Post Hoc Multiple Comparisons for Observed Means (Одномерная: Дополнительно — многократные сравнения для наблюдаемых средних значений)

Between-Subjects Factors (Межсубъектные факторы)

Value Label (Метка значения)	N
GESCHL (Пол)	1	maennlich (Мужской)	15
	2	weiblich (Женский)	12
ALTER (Возраст)	1	bis 30 Jahre (До 30 лет)	7
	2	31 - 50 Jahre (31 - 50 лет)	9
	3	ueber 50 Jahre (Свыше 50 лет)	11

Descriptive Statistics (Дескриптивные статистики)

Dependent Variable: М1 (Зависимая переменная: М1)
GESCHL ' (Пол)	ALTER (Возраст)	Mean (Среднее значение)	Std. Deviation (Стандартное отклонение)	N
maennlich (Мужской)	bis 30 Jahre (До 30 лет)	16,00	,82	4
	31 - 50 Jahre (31 - 50 лет)	14,60	1,14	5
	ueber 50 Jahre (Свыше 50 лет)	11,7	2,48	6
	Total (Сумма)	13,60	2,69	15
weiblich (Женский)	bis 30 Jahre (До 30 лет)	16,00	1,00	3
	31 - 50 Jahre (31 - 50 лет)	15,00	1,41	4
	ueber 50 Jahre (Свыше 50 лет)	10,20	1,10	5
	Total (Сумма)	13,25	2,93	12
Total (Сумма)	bis 30 Jahre (До 30 лет)	16,00	,82	7
	31 - 50 Jahre (31 - 50 лет)	14,78	1,20	9
	ueber 50 Jahre (Свыше 50 лет)	10,73	1,95	11

Levene's Test of Equality of Error Variances a (Тест Левене на равенство дисперсии ошибок)

Dependent Variable: М1 (Зависимая переменная: М1)

F	df1	df2	Sig(Значимость)
4,177	5	21	,009

Tests the null hypothesis that the error variance of the dependent variable is equal across groups (Проверяет нулевую гипотезу о том, что дисперсия ошибок зависимых переменных одинакова для всех групп).

a. Design: Intercept+GESCHL+ALTER+GESCHL * ALTER (Компоновка: Отрезок + Пол + Возраст + Пол*Возраст)

К сожалению, тест Левене на равенство дисперсий показывает, значимый результат со значением вероятности ошибки р = 0,009. Это означает, что отсутствует однородность дисперсий между группами, которая наряду с нормальным распределением значений выборки, является основной предпосылкой для возможности проведения дисперсионного анализа.

Традиционная схема дисперсионного анализа (еще раз отметим: проводимого на основе общей линейной модели) показывает незначимое влияние пола (р = 0,761), очень значимое влияние возраста (р = 0,001) и незначимое взаимодействие между обоими переменными (р = 0,611).

Tests of Between-Subjects Effects (Тест межсубъектных эффектов)

Dependent Variable: M1 (Зависимая переменная: М1)

Source (Источник)	Type III Sum of Squares (Сумма квадратов III типа)	Df	Mean Square (Среднее значение квадрата)	F	Sig. (Значи-мость)
Corrected Model (Подпра- вленная модель)	145,833a	5	29,167	12,049	,000
Intercept (Отрезок)	4916,763	1	4916,763	2031,187	,000
GESCHLJOonl	,229	1	,229	,095	,761
ALTER (Возраст)	144,273	2	72,137	29,801	,000
GESCHL * ALTER (Пол'Возраст)	2,446	2	1,223	,505	,611
Error (Ошибка)	50,833	21	2,421
Total (Сумма)	5077,000	27
Corrected Total	196,667	26

a R Squared = ,742 (Adjusted R Squared = ,680) (R-квадрат = 0,742 (смещённый R-квадрат = 0,680))

В случае отсутствия однородности дисперсии границу значимости рекомендуется устанавливать равной не р = 0,05, а р =0,01. Значимое влияние возраста проявляется в любом случае.

Если вы сравните эти результаты с результатами, полученными при методе Фишера (Fisher) (см. гл. 17.1.2), то заметите незначительное отклонение значения р для фактора влияния пол (geschlecht). Далее следует вывод дескриптивных статистик для совокупной выборки и для отдельных слоев факторов.

1. Grand Mean (Общее среднее значение)

Dependent Variable: М1 (Зависимая переменная: М1)
Mean (Среднее значение)	Std. Error (Стандартная ошибка)	95% Confidence Interval (95 % доверительный интервал)
		Lower Bound (Нижний предел)	Upper Bound (Верхний предел)
13,828	,307	13,190	14,466

2. GESCHL (Пол)

Dependent Variable: М1 (Зависимая переменная: М1)
GESCHL (Пол)	Mean (Среднее значение)	Std. Error (Стандартная ошибка)	95% Confidence Interval (95 % доверительный интервал)
			Lower Bound (Нижний предел)	Upper Bound (Верхний предел)
maennlich (Мужской)	13,922	,407	13,075	14,769
weiblich (Женский)	13,733	,459	12,779	14,688

3. ALTER (Возраст)

Dependent Variable: М1 (Зависимая переменная: М1)
ALTER (Возраст)	Mean (Среднее значение)	Std. Error (Стандартная ошибка)	95% Confidence Interval (95 % доверительный интервал)
			Lower Bound (Нижний предел)	Upper Bound (Верхний предел)
bis 30 Jahre (До 30 лет}	16,000	,594	14,764	17,236
31 - 50 Jahre (31 - 50 лет)	14,800	,522	13,715	15,885
ueber 50 Jahre (Свыше 50 лет)	10,683	,471	9,704	11,663

Затем следует вывод результатов теста Шеффе по сравнению отдельных возрастных групп. На основании частично дублированных результатов, можно сделать вывод, что самая старшая возрастная группа очень значимо отличается от двух других:

Multiple Comparisons (Множественные сравнения)

Dependent Variable: M1 (Зависимая переменная: М1) Scheffe (Шеффе)
(I) ALTER (Возраст)	(J) ALTER (Возраст)	Mean Difference (I-J) (Средняя разность)	Std. Error (Стандар -тная ошибка)	Sig. (Значи-мость)	95% Confidence Interval (95 % доверительный интервал)
					Lower Bound (Нижний предел)	Upper Bound (Верхний предел)
bis 30 Jahre (До 30 лет)	31 -50 Jahre (31 -50 лет)	1,22	,784	,317	-.84	3,29
	ueber 50 Jahre (Свыше 50 лет)	5,27*	,752	,000	3,29	7,25
31 -50 Jahre (31 -50 лет)	bis 30 Jahre (До 30 лет)	-1,22	,784	,317	-3,29	,84
	ueber 50 Jahre (Свыше 50 лет)	4,05*	,699	,000	2,21	5,89
ueber 50 Jahre (Свыше 50 лет)	bis 30 Jahre (До 30 лет)	-5,27*	,752	,000	-7,25	-3,29
	31 -50 Jahre (31 -50 лет)	-4,05*	,699	,000	-5,89	-2,21

Based on observed means (Основываясь на наблюдаемых средних значениях). * The mean difference is significant at the ,05 level (Усреднённая разность является значимой на уровне 0,05).

Этот факт подтверждается ещё раз при выводе результатов для рассматриваемых "однородных подгрупп" в другой форме.

М1

Scheffe аbс (Шеффе)
ALTER	N	Subset (Подгруппа)
		1	2
ueber 50 Jahre (Свыше 50 лет)	11	10,73
31 - 50 Jahre (31 - 50 лет)	9	14,78
bis 30 Jahre (До 30 лет)	7	16,00
Sig. (Значимость)	1,000	,283

Means for groups in homogeneous subsets are displayed (Выводятся средние значения для групп в однородных подгруппах).

Based on Type III Sum of Squares (На основе суммы квадратов III типа).

The error term is Mean Square(Error) = 2,421 (Слагаемое ошибки равно среднему значению квадрата (ошибки) = 2,421).

a. Uses Harmonic Mean Sample Size = 8,699 (Используя среднегармонический размер выборок = 8,699).

b. The group sizes are unequal (Размеры групп не одинаковы). The harmonic mean of the group sizes is used (Используется среднее гармоническое размера групп). Туре I error levels are not guaranteed (Уровень ошибки для I типа не гарантируется).

с. Alpha = ,05

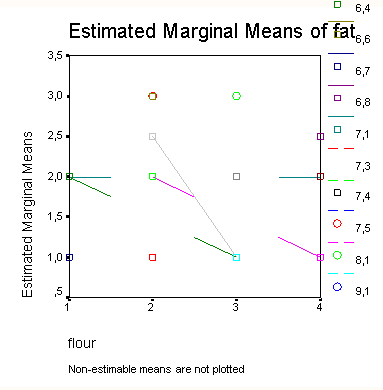
Завершает вывод результатов профильная диаграмма, в которой представлена линейчатая диаграмма возраста отдельно для каждого пола:

Вид графиков для обоих полов почти одинаков, что свидетельствует о незначимом взаимодействии между двумя факторами. Кроме того, наглядно проявляется незначимость различия между двумя полами.

17.1.2 Одномерный дисперсионный анализ по методу Фишера (Fisher)

Проанализируем теперь пример, приведенный в разделе 17.1.1, при помощи традиционного "классического" метода Фишера. Так как, начиная с 8.0 версии программы, этот вид анализа уже не выводится в диалоговое окно, то нам придётся воспользоваться программным синтаксисом (процедура AN OVA).

•  Откройте файл varana.sav.

•  Выберите в меню File (Файл) New (Новый) Syntax (Синтаксис) Наберите следующую команду в поле редактора синтаксиса:

 ANOVA VARIABLES=ml  BY  geschl  (1,2)  alter  (1,3) 

    /STATISTICS  MCA  MEAN  

  /METHOD   EXPERIM. 

SPSS предлагает три метода для разложения квадратов отклонения в МНК для случая, когда объемы отдельных ячеек (количества наблюдений, относящихся к данной ячейке) не равны. При такой "несбалансированной компоновке", которая часто появляется при "непланируемых" (не экспериментальных) исследованиях, без дальнейшей обработки нельзя к общей сумме прибавлять суммы квадратов отдельных эффектов. Вы можете выбрать один из следующих методов обработки:

•  UNIQUE: Вклад каждого из факторов влияния рассматривается одновременно; каждый из них рассчитывается при условии сохранения постоянного значения всех остальных. Так как в этом случае можно сделать неявное предположение о возможном существовании причинной связи между факторами, то этот вариант следует выбирать тогда, когда не должно проводиться весовое сравнение значения отдельных факторов. Этот метод устанавливается по умолчанию.

•  HIERARCHICAL: Очерёдность расчёта эффектов определяется очерёдностью выбранных факторов. Этот метод следует применять тогда, когда можно заранее предположить иерархическую упорядоченность факторов.

•  EXPERIMENTAL: Эффекты обрабатываются в следующей последовательности: эффекты ковариаций, главные эффекты, взаимодействия в порядке возрастания. При расчёте одного эффекта производится вычисление всех предшествующих эффектов и эффектов, находящихся на том же уровне.

При одинаковых объемах ячеек ("ортогональная компоновка") все три метода дают одинаковые результаты.

При помощи вспомогательной команды STATISTICS можно организовать вывод следующих данных:

•  Mean: Выводятся средние значения и количество наблюдений для совокупной популяции, отдельных слоев фактора и каждой ячейки. Удивительно, но если вы выбираете метод UNIQUE для разложения суммы квадратов в МНК, то эта опция становится недоступной.

•  MCA (Множественный классификационный анализ): С помощью специальных коэффициентов (называемых т) (Eta) и Р (Beta)) отображается сила связи между отдельным фактором и зависимой переменной. Это является уместным, если не наблюдается ни каких значимых взаимодействий. Вывод результатов МСА недоступен при выборе метода UNIQUE.

•  Запустите команду ANOVA на исполнение щелчком на знаке Run Current (Запустить синтаксис).

После обычной сводной таблицы обрабатываемых наблюдений, сначала выводятся средние значения и частоты (соответствующие результаты вывода здесь не приводятся). Затем следует сводка дисперсионного анализа с суммами квадратов, степенями свободы, средними значениями сумм квадратов и т.д.:

ANOVA a
			Experimental Method (Экспериментальный метод)
			Sum of Squares (Сумма квадра-тов)	df (Степень свободы)	Mean Square (Среднее значение квадрата)	F	Sig. (Значи-мость)
М1	Main Effects (Главные эффекты)	(Combined) (Объеди-нённо)	143,388	3	47,796	19,745	,000
		GESCHL (Пол)	,458	1	,458	,189	,668
		ALTER (Возраст)	142,571	2	71,285	29,449	,000
	2-Way Interacti-ons (2-сторонние взаимо-действия)	GESCHL * ALTER (Пол' Возраст)	2,446	2	1,223	,505	,611
	Model (Модель)		145,833	5	29,167	12,049	,000
	Residual (Остатки)		50,883	21	2,421
	Total (Сумма)		196,667	26	7,564

а М1 by GESCHL, ALTER (М1/по полу, возрасту)

Вероятность ошибки р, соответствующая тестовому значению F-критерия, выводится в правой колонке под заголовком "Sig." ("Значимость"). Ее величина свидетельствует о глобальной значимости для главных эффектов (р < 0,001). Данное значение основано только на факторе Alter (Возраст) (р < 0,001), но не на факторе Geschlecht (Пол) (р = 0,668). Взаимодействия в данном случае не наблюдаются (р = 0,611). Результаты очень близки к результатам расчёта при помощи общей линейной модели (см. гл. 17.1.1).

Результаты МСА выглядят следующим образом:

MCA a (Множественный классификационный анализ)
			N	Predicted Mean (Прогнозируемое среднее значение)		Deviation (Отклонение)
				Unadjusted (Несме-щенное)	Adjusted for Factors (Смещенное по факторам)	Unad-justed (Несме-щенное)	Adjusted for Factors (Смещенное по факторам)
М1	GESCHL (Пол)	maennlich (Мужской)	15	13,60	13,56	,16	,12
		weiblich (Женский)	12	13,25	13,30	-,19	-.15
	ALTER (Возраст)	bis 30 Jahre (До 30 лет)	7	16,00	16,00	2,56	2,55
		31 - 50 Jahre (31 -50 лет)	9	14,78	14,78	1,33	1,33
		ueber 50 Jahre (Свыше 50 лет)	11	10,73	10,73	-2,72	-2,71

a Ml by GESCHL, ALTER (M1/no полу, возрасту)

 

Factor Summary a (сводные данные для факторов)
Eta (Эта)	Beta (Бета)
	Adjusted for Factors (Смещено по факторам)
М1 GESCHL (Пол)	,064	,048
ALTER (Возраст)	,853	,852
а М1 by GESCHL, ALTER (М1/по полу, возрасту)

Model Goodness of Fit (Критерий согласия для модели)

R	R Squared (R-квадрат)
М1 by GESCHL, ALTER (М1/по полу, возрасту)	,854	,729

Оба коэффициента n (Eta) являются мерой силы связи (корреляции) между соответствующим фактором и зависимыми переменными, относящейся сюда же коэффициент (i (Beta) имеет частную природу и характеризует силу связи при отсутствии влияний со стороны других факторов. Значительное отличие коэффициентов Eta и Beta друг от друга (которое в данном случае не наблюдается) указывает на наличие взаимосвязи между факторами. И, наконец, величина "R Squared" ("R-квадрат") указывает на ту степень отклонения от совокупной дисперсии, которая может быть объяснена главными эффектами.

17.1.3 Одномерный дисперсионный анализ с повторным измерением

Исследуем вопрос следующего характера: наблюдаются ли в течение четырёх моментов времени значимые изменения показаний теста на внимательность. При этом необходимо учесть влияние двух факторов: пола и возраста.

В общем, в нашем распоряжении имеется три фактора: пол с двумя категориями, возраст с тремя категориями и время с четырьмя категориями. Это приводит к необходимости выполнения трёхфакторного дисперсионного анализа, в котором третий фактор (время) является фактором с повторным измерением. Этот фактор будет представлен не при помощи отдельных групп испытуемых, а при помощи значений переменных ml-m4.

•  Откройте файл varana.sav.

•  Выберите в меню Analyze (Анализ) General Linear Model (Общая линейная модель) Repeated Measures... (Повторные измерения)

•  Как уже было изложено в главе 13.4, отроется диалоговое окно Repeated Measures Define Factors(s) (Повторные измерения: Определение фактора(ов)).

•  Вместо установленного по умолчанию имени фактора factorl введите новое имя: zeit (время).

•  В поле Number of Levels (Количество слоев) введите значение 4. Щёлкните на Add (Добавить), и, если больше цет никаких факторов с повторными измерениями, покиньте диалоговое окно посредством нажатия кнопки Define (Определить).

Появится диалоговое окно Repeated Measures (Повторные измерения) (см. рис. 17.7).

•  Здесь, в первую очередь, последовательно перенесите четыре переменные повторных измерений ml-m4 в поле для внутрисубъектных переменных (Within-Subjects Variables).

•  Затем, переменные geschl (пол) и alter (возраст) перенесите в поле для межсубъектных факторов (Between-Subjects Factor(s)).

•  В диалоговом окне Options (Опции) активируйте вывод средних для трёх факторов: geschl (пол), alter (возраст) и zeit (время), в поле отображаемых результатов (Display) активируйте вывод дескриптивных статистик и, помимо этого, сделайте запрос на тест однородности.

Рис. 17.7: Диалоговое окно Repeated Measures (Повторные измерения)

•  Начните расчёт нажатием ОК.

На экране появятся довольно обширные результаты расчёта. Их расшифровка может оказаться довольно проблематичной для новичка. Поэтому ниже будет рассмотрена только та часть результатов, которая является важной для поиска ответа на вопрос: какой из трёх факторов — пол, возраст или время, оказывает значимое влияние и какие взаимодействия между этими факторами являются значимыми.

Сначала даётся сводная таблица для внутрисубъектных (время) и межсубъектных (пол и возраст) факторов. Затем выводятся дескриптивные статистики (среднее значение, стандартное отклонение, количество наблюдений) для отдельных ячеек, то есть характеристики переменных ml-m4 отдельно для пола и возрастных групп. Вывод этих показателей в книге не приводится.

Далее следуют результаты расчёта для фактора "Zeit" ("Время") и для взаимодействий с этим фактором, в основу которых положен метод общей линейной модели. Для этого были определены различные тестовые величины, которые выводятся под наименованиями: "Pillai's Trace" (След Пиллая), "Wilks' Lambda" (Лямбда Уилкса), "Hotelling's Trace" (След Хоттелинга) и "Roy's Largest Root" (Максимальный характеристический корень по методу Роя). С помощью надлежащих преобразований по этим тестовым величинам восстанавливается рампределения значение F, по которому затем определяется значение р, приводимое в колонке "Значимость" (Sig). Следует отметить, что след Пиллая ("Pillai's Trace") является наиболее сильным и устойчивым (робастным) тестом.

Результаты первых трёх тестов являются практически идентичными. Обнаружено очень значимое влияние временного фактора, а вот взаимодействия других факторов со временем, напротив, оказались не значимыми.

Одни и те же расчёты, то есть проверка временного фактора и взаимодействий со временем, производятся также при помощи традиционного "классического" метода Фишера. Соответствующие результаты можно взять из строки "Предполагается сферичность" во второй из нижеследующих таблиц, которая наряду с ними содержит ещё три варианта проверок.

Multivariate Tests ^c (Многомерные тесты)

Effect (Эффект)		Value (Значе-ние)	F	Hypothesis df (Гипотеза df)	Error df (Ошибка df)	Sig. (Зна-чимость)
ZEIT (Время)	Pillai's Trace (След Лиллая)	,955]	133,367"	3,000	19,000	,000
	Wilks' Lambda (Лямбда Уилкса)	,045	133,367"	3,000	19,000	,000
	Hotelling's Trace (След Хоттелинга)	21,058	133,367а	3,000	19,000	,000
	Roy's Largest Root (Макси-мальный характе-ристический корень по методу Роя)	21,058	133,367е	3,000	19,000	,000
ZEIT*GESCHL (Время'Пол)	Pillai's Trace (След Пиллая)	,106	,752"	3,000	19,000	,535
	Wilks1 Lambda (Лямбда Уилкса)	,894	,752а	3,000	19,000	,535
	Hotelling's Trace (След Хоттелинга)	,119	,752а	3,000	19,000	,535
	Roy's Largest Root (Макси-мальный характе-ристический корень по методу Роя)	,119	,752"	3,000	19,000	,535
ZEIT * ALTER (Время* Возраст)	Pillai's Trace (След Пиллая	,293	1,145	6,000	40,000	,355
	Лямбда Уилкса)	,710	1,183а	6,000	38,000	,336
	Hotelling's Trace (След Хоттелинга)	,404	1,213	6,000	36,000	,322
	Roy's Largest Root (Макси-мальный характе-ристический корень по методу Роя)	,394	2,625"	3,000	20,000	,079
ZEIT * GESCHL * ALTER (Время'Пол* Возраст)	Pillai's Trace (След Пиллая)	,406	1,699	6,000	40,000	,146
	Wilks1 Lambda (Лямбда Уилкса)	,622	1,699а	6,000	38,000	,148
	Hotelling's Trace (След Хоттелинга)	,564	1,691	6,000	36,000	,151
	Roy's Largest Root (Макси-мальный характе-ристический корень по методу Роя)	,468	3,118Ь	3,000	20,000	,049
a, b, с — см. след. стр.

Tests of Within-Subjects Effects (Тест внутрисубъектных эффектов)

Measure: MEASURE_1 (Мера: MEASURE_1 )

Source Источник)		Type III Sum of Squares (Сумма квадратов III типа)	df	Чеап Square (Среднее значение квадрата)	F	Sig. (Значи-мость)
ZEIT Время)	Sphericity Assumed (Предполагается сферичность)	185,661	3	61,887	83,028	,000
	Greenhouse-Geisser (Гринхауз-"айссер)	185,661	2,577	72,055	83,028	,000
	Huynh-Feldt (Гин-Фельд)	185,661	3,000	61,887	83,028	,000
	Lower-bound (Нижний предел)	185,661	1,000	185,661	83,028	,000
ZEIT* GESCHL Время * Пол)	Sphericity Assumed (Предполагается сферичность)	1,520	3	,507	,680	,568
	Greenhouse-Geisser (Гринхауз-"айссер)	1,520	2,577	,590	,680	,547
	Huynh-Feldt (Гин-Фельд1	1,520	3,000	,507	,680	,568
	.ower-bound (Нижний предел)	1,520	1,000	1,520	,680	,419
ZEIT* ALTER (Время * Возраст)	Sphericity Assumed ^Предполагается сферичность)	4,190	6	,698	,937	,475
	Greenhouse-Geisser (Гринхауз-Гайссер)	4,190	5,153	,813	,937	,467
	Huynh-Feldt (Гин-Фельд)	4,190	6,000	,698	,937	,475
	Lower-bound (Нижний предел)	4,190	2,000	2,095	,937	,408
ZEIT* GESCHL* ALTER Время * Пол* Зозраст)	Sphericity Assumed (Предполагается сферичность)	6,557	6	1,093	1,466	,204
	Greenhouse-Geisser (Гринхауз-Гайссер^	6,557	5,153	1,272	1,466	,215
	Huynh-Feldt (Гин-Фельд)	6,557	6,000	1,093	1,466	,204
	Lower-bound (Нижний предел)	6,557	2.00C	3,278	1,466	,254
Error (ZEIT) (Ошибка (Время))	Sphericity Assumed (Предполагается сферичность)	46,958	63	,745
	Greenhouse-Geisser (Гринхауз-Гайссер)	46,958	54,110	,868
	Huynh-Feldt (Гин-Фельд)	46,95f	63,000	,745
	Lower-bound (Нижний предел)	46,958	21.00C	2,236

a Exact statistic (Точная статистика)

b The statistic is an upper bound on F that yields a lower bound on the significance level (Статистической характеристикой является верхний придел значения Е-распределе-ния, который указывает на нижний предел уровня значимости).

c Design: Intercept+GESCHL+ALTER+GESCHL * ALTER (Компоновка: Отрезок + Пол + Возраст + Пол * Возраст )

Within Subjects Design: ZEIT (Компоновка внутри субъектов: Время)

Полученные результаты близки к результатам расчётов по общей линейной модели. Тест Левене на равенство дисперсий демонстрирует однородность дисперсии для моментов времени со второго по четвёртый и неоднородность дисперсии (р = 0,009) для первого момента (см. гл. 17.1.1).

Levene's Test of Equality of Error Variances a (Тест Левене на равенство дисперсии ошибок)

F	df1	df2	Sig. (Значимость)
М1	4,177	5	21	,009
М2	,878	5	21	,513
МЗ	1,751	5	21	,167
М4	2,022	5	21	,117

Tests the null hypothesis that the error variance of the dependent variable is equal across groups (Проверяется нулевая гипотеза о том, что дисперсия ошибки независимых переменных остаётся постоянной для всех групп). a. Design: Intercept+GESCHL+ALTER+GESCHL * ALTER (Компоновка: Отрезок + Пол + Возраст + Пол * Возраст ) Within Subjects Design: ZEIT (Компоновка внутри субъектов: Время)

Далее идут расчёты для обоих факторов (пол и возраст), для которых не производятся повторные измерения, а также для их взаимодействия.

Tests of Between-Subjects Effects (Тест межсубъектных эффектов)

Measure: MEASURE_1 (Мера: MEASURE_1)

Transformed Variable: Average (Трансформированная переменная: Среднее значение)

Source (Источник)	Type III Sum of Squares (Сумма квадратов III типа)	Df	Mean Square (Среднее значение квадрата)	F	Sig. (Значимость)
Intercept (Отрезок)	25080,367	1	25080,367	2029,299	,000
GESCHL (Пол)	,738	1	,738	,060	,809
ALTER (Возраст)	667,147	2	333,573	26,990	,000
GESCHL * ALTER (Пол * Возраст)	33,571	2	16,785	1,358	,279
Error (Ошибка)	259,542	21	12,359

Получается незначимое влияние пола (р = 0,809), очень значимое влияние возраста (р < 0,001) и незначимое взаимодействие (р = 0,279). Под заголовком "Оцененные пределы средних" (Estimated Marginal Means) выводится информация о средних значениях и стандартных отклонениях для отдельных слоев факторов:

1. GESCHL (Пол)

Measure: MEASURE_1 (Мера: MEASURE_1)
GESCHL (Пол)	Mean (Среднее значение)	Std. Error (Стандартная ошибка)	95% Confidence Interval (95 % доверительный интервал)
			Lower Bound (Нижний предел)	Upper Bound (Верхний предел)
maennlich (Мужской)	15,700	,460	14,743	16,657
weiblich (Женский)	15,531	,519	14,452	16,609

2. ALTER (Возраст)

Measure: MEASURE 1 (Мера: MEASURE 1)
ALTER (Возраст)	Mean (Среднее значение)	Std. Error (Стандартная ошибка)	95% Confidence Interval (95 % доверительный интервал)
			Lower Bound (Нижний предел)	Upper Bound (Верхний предел)
bis 30 Jahre (До 30 лет)	17,646	,671	16,250	19,042
31 - 50 Jahre (31 - 50 nejr)	16,988	,590	15,761	18,214
ueber 50 Jahre (Свыше 50 лет)	12,213	,532	11,106	13,319

3. ZEIT (Время)

Measure: MEASURE_1 (Мера: MEASURE_1)
ZEIT (Время)	Mean (Среднее значение	Std. Error (Стандартная ошибка;	95% Confidence Interval (95 % доверительный интервал)
			Lower Bound (Нижний предел)	Upper Bound (Верхний предел)
1	13,828	,307	13,190	14,466
2	14,964	,405	14,121	15,807
3	16,275	,386	15,472	17,078
4	17,394	,400	16,562	18,227

Для факторов, для которых не производятся повторные измерения (межсубъектные эффекты), можно вновь провести дополнительные тесты (Post Hoc), но, к сожалению, их нельзя применить для факторов, для которых производятся повторные измерения.

17.2 Ковариационный анализ

Если в дисперсионном анализе используется независимая переменная, относящаяся к интервальной шкале или к шкале отношений (метрической), то говорят не о факторе, а о ковариации. Поясним значение такой "контрольной переменной" на следующем примере.

Двадцать испытуемых с избыточным весом (11 мужчин и 9 женщин) изъявили желание похудеть и для этого взялись следовать определённой диете. Одиннадцать испытуемых дополнительно вступили в некоторое общество для желающих похудеть, в котором процесс похудения подстегивается при помощи специальных стимулирующих лекций и других мотивирующих методов. Для всех тестируемых были сняты показатели роста (в см) и веса (в кг) до и после прохождения курса. Далее при помощи расчета индекса Брока (Вгоса) фактический вес был отнесен к нормальному весу, где нормальный вес в килограммах мы можем получить, если от роста, взятого в сантиметрах, отнимем 100:

Так индекс Брока, равный 100 процентам означает нормальный вес, превышающий 100 процентов — избыточный вес.

•  Откройте файл gewicht.sav.

Переменная beh указывает на группу (1 = диета, 2 = диета + общество для желающих похудеть), а переменная g указывает на пол (1 = мужской, 2 = женский). К остальным переменным, участвующими в расчётах, относятся: gr (Рост), gew (Вес до лечения), gewl (Вес в конце лечения), ЬгосаО (Индекс Брока до лечения), brocaab (Уменьшение индекса Брока). Последняя переменная должна служить мерой эффективности диеты.

Мы хотим провести двухфакторный дисперсионный анализ с использованием переменных beh и g в качестве независимых переменных (факторов) и переменной brocaab в качестве зависимой переменной.

•  Выберите в меню Analyze (Анализ) General Linear Model (Общая линейная модель) Univariate... (Одномерная)

•  В появившемся диалоговом окне переменной brocaab присвойте статус зависимой переменной, а переменным beh и g — статус постоянных факторов.

•  После прохождения кнопки Options... (Опции) активируйте вывод оценки пределов средних для факторов beh и g.

•  Начните расчёт нажатием ОК.

Для группы, члены которой дополнительно вступили в общество для желающих похудеть, средний показатель снижения индекса Брока равен 11,558, в то время как для группы, члены которой худеют только при помощи одной диеты, снижение в среднем составляет 5,178. Дисперсионный анализ дает следующие результаты:

Tests of Between-Subjects Effects (Тесты межсубъектных эффектов)

 Dependent Variable: BROCAAB (Зависимая переменная: BROCAAB)

Source (Источник)	Type III Sum of Squares (Сумма квадратов III типа)	Df	Mean Square (Средний квадрат)	F	Sig. (Значи-мость)
Corrected Model (Подправленная модель)	209,636"	3	69,879	12,836	,000
Intercept (Отрезок)	1371,877	1	1371,877	252,002	,000
ВЕН	199,414	1	199,414	36,631	,000
G	1.998E-03	1	1.998E-03	,000	,985
BEH*G	3,026	1	3,026	,556	,467
Error (Ошибка)	87,103	16	5,444
Total (Сумма)	1805,668	20
Corrected Total (Подправленная суммарная вариация)	296,738	19

a R Squared = ,706 (Adjusted R Squared = ,651) (R - квадрат = ,706 (смещённый R-квадрат = ,651))

Получается очень значимая разница между двумя группами (р < 0,001): то есть, членство в обществе оказывает очень значимое воздействие на процесс снижения веса.

Если рассмотреть результаты поподробнее, то можно заметить, что начальное значения индекса Брока для группы, дополнительно входящей в общество похудения, значительно выше (132,0 против 113,1). Таким образом, шансы потери веса в этой группе с самого начала выше, чем в другой. Поэтому было бы уместно включить в анализ начальное значение индекса Брока (переменную brоса0) в качестве контрольной переменной, то есть ковариации.

•  Откройте вновь диалоговое окно Univariate (Одномерная) и поместите дополнительно переменную brоса0 в поле ковариации.

•  Начните расчёт нажатием ОХ.

Результат ковариационного анализа будет выглядеть следующим образом:

Tests of Between-Subjects Effects (Тесты межсубъектных эффектов)

Dependent Variable: BROCAAB (Зависимая переменная: BROCAAB)

Source (Источник)	Type III Sum of Squares (Сумма квадратов III типа)	df	Mean Square (Средний квадрат)	F	Sig. (Значи-мость)
Corrected ModelПодправленная модель)	231,170a	4	57,842	13,273	,000
Intercept (Отрезок)	8.568	1	8,568	1,966	,181
BRACAO	21,734	1	21,734	4,987	,041
ВЕН	11.077	1	11,077	2, 542	,132
G	3.830	1	3,830	,879	,363
ВЕН *G	4.644	1	4,644	1,066	,318
Error (Ошибка)	65.368	15	4,358
Total (Сумма)	1805,668	20
Corrected Total (Подправленная суммарная вариация)	296,738	19

a R Squared = ,780 (Adjusted R Squared = ,721) (R - квадрат = ,780 (смещённый R-квадрат = ,721))

В результате, как и ожидалось, обнаружилось сильное влияние ковариации brоса0 (р = 0,041). Это ведёт к тому, что в обеих группах пропадает значимый эффект (р = 0,132). Из-за сильно отличающихся исходных показателей, доказательство значимого воздействия дополнительного членства в обществе для желающих похудеть является невозможным.

17.3 Многомерный дисперсионный анализ

Многомерный дисперсионный анализ применяется тогда, когда в одном дисперсионном анализе необходимо одновременно исследовать влияние факторов и возможных ковариации (независимых переменных) на несколько зависимых переменных. Такой многомерный дисперсионный анализ следует предпочесть одномерному тогда (и только тогда), когда зависимые переменные не являются независимыми друг от друга, а наоборот коррелируют между собой.

Если Вы откроете данные из исследования гипертонии (файл hyper.sav) и рассчитаете корреляции между исходными значениями систолического и диастолического давлений, уровнями холестерина и сахара в крови (переменные rrs0, rrd0, cho10 и bz0), то вы заметите, что эти переменные, хотя и не сильно, но всегда значимо коррелируют между собой.

Если Вы хотите узнать, значимо ли отличаются перечисленные переменные для четырёх заданных возрастных групп (переменная ak), то вместо четырёх отдельных одномерных однофакторных дисперсионных анализов Вы должны провести один многомерный однофакторный анализ.

•  Откройте файл hyper.sav.

•  Выберите в меню Analyze (Анализ) General Linear Model (Общая линейная модель) Multivariate... (Многомерная)

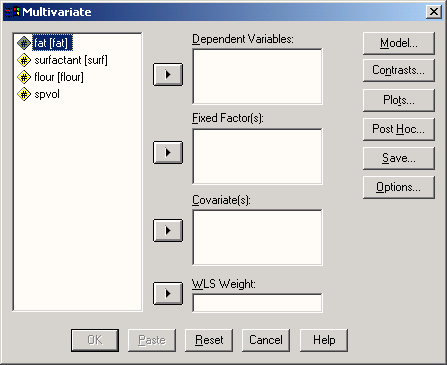
Откроется диалоговое окно Multivariate (Многомерная) (см. рис. 17.8).

Поместите переменные rs0, rrd0, cho10, и bz0 в поле. предусмотренное для зависимых переменных, а переменной ak присвойте статус постоянного фактора.

Под выключателями Contrasts... (Контрасты), Model... (Модель) и Options... (Опции) Вы найдёте множество разнообразных возможностей для задания контрастов, выбора различных вариантов моделей или организации вывода всевозможных дополнительных результатов расчёта; к примеру, здесь можно активировать тесты проверки дисперсии на однородность.

Уже было указано на невозможность в рамках этой книги представить все имеющиеся возможности по отдельности. Чтобы рассмотреть все эти возможности Вам придётся обратиться к оригинальному учебнику по SPSS; опытному же пользователю для понимания будет достаточно просто посмотреть на пункты, имеющиеся в диалоговом окне. В крайнем случае, можно воспользоваться справкой.

•  Оставьте все установки по умолчанию и начните расчёт нажатием ОК.

Рис. 17.8: Диалоговое окно Multivariate (Многомерная)

Появятся довольно обширные результаты расчёта. Важным для нас является в первую очередь глобальный многомерный тест на предмет выявления значимых различий "где-нибудь" между возрастными группами:

Multivariate Tests c (Многомерные тесты)

Effect (Эффект )		Value (Зна-чение)	F	Hypo-thesis df (Гипо-теза df)	Error df (Ошибка df)	Sig. (Значи-мость)
Inte-rcept Отре-зок)	Pillai's Trace (След Пиллая)	,996	9252, 061а	4,000	167,000	,000
	Wilks' Lambda (Лямбда Уилкса)	,004	9252,061 а	4,000	167,000	,000
	Hotelling's Trace (След Хоттелинга)	221,606	9252, 061а	4,000	167,000	,000
	Roy's Largest Root 'Макси-мальный характе-ристический корень по методу Роя)	221,606	9252,061 а	4,000	167,000	,000
АК	Dillai's Trace (След Пиллая)	,178	2,661	12,00ol	507,00o'	,002
	Wilks' Lambda (Лямбда Уилкса)	,827	2,740	12,000	442,132	,001
	Hotelling's Trace (След Хоттелинга)	,203	,805	12,000	197,000	,001
	Roy's Largest Root (Макси-мальный характе-ристический корень по методу Роя)	,169	7,159Ь	4,000	167,000	,000

a. Exact statistic (Точная статистика)

b. The statistic is an upper bound on F that yields a lower bound on the significance level (Статистической характеристикой является верхний придел значения F-распределе-ния, который указывает на нижний предел уровня значимости).

с Design: Intercept+AK (Компоновка: Отрезок + АК)

Здесь производится расчёт величин, традиционных для общей линейной модели. Они уже представлены в главе 17.1.3. Основываясь на критерии "След Пиллая" ("Pillai's Trace"), следует отклонить нулевую гипотезу о том, что между четырьмя возрастными группами не наблюдается различий ни для одной из зависимых переменных (значение р = 0,002).

Для проверки, какие из четырёх зависимых переменных в чем-то различаются между собой, были проведены одномерные тесты. Результаты этих тестов полностью соответствуют результатам отдельного одномерного дисперсионного анализа для каждой зависимой переменной.

Мы здесь воздержимся от подробной расшифровки довольно большой таблицы "Тесты межсубъектных эффектов". Отметим только, что для систолического и диастолического давлений, уровней холестерина и сахара в крови получаются следующие значения вероятности ошибки р: 0,153, 0,002, 0,267 и 0,688 соответственно. Причиной суммарной значимости, поучающейся в результате многомерного теста, являются прежде всего значимые различия для диастолического давления.

Для опытных статистиков, хорошо знакомых с тонкостями многомерных методов, SPSS может предложить избыточное количество разнообразных возможностей в области дисперсионного анализа. В первую очередь можно использовать разнообразные возможности процедуры MANOVA, доступной отныне только через командный синтаксис. Эта процедура позволяет проводить простой и множественный регрессионный анализ, дискриминантный анализ, канонический анализ, анализ главных компонентов и др. Однако сложность работы с заданием параметров может составить некоторые затруднения для менее опытных пользователей. Поэтому в данной книге мы ограничились рассмотрением наиболее часто применяемых компоновок дисперсионного анализа.

17.4 Компоненты дисперсии

Расчёт компонентов дисперсии в общей линейной модели производится при наличии факторов со случайными эффектами. Факторами со случайными эффектами являются те факторы, слои которых были случайно выбраны из популяции (совокупности) многих возможных слоев факторов.

Проанализируем длину листьев растений растущих на одной клумбе. Для этого вырвем произвольно три растения, листья которых мы и будем измерять.

Растения	Длина листьев (см)	Растения	Длина листьев (см)
1	9,5	2	9,0
1	9,8	2	9,5
1	8,7	3	8,0
1	8,8	3	7,8
1	8,9	3	9,0
1	10,0	3	8,7
2	11,0	3	8,9
2	10,5

Так как из большого количества растений мы произвольно взяли для исследований только три, то здесь можно говорить о факторе со случайными эффектами. Это следует учитывать, если при помощи некоего метода дисперсионного анализа нужно будет установить, зависит ли длина листьев от конкретного растения или насколько велика та часть дисперсии, причиной которой является неоднородность растений. Эти вопросы можно прояснить при помощи расчёта компонентов дисперсии.

•  Откройте файл pflanze.sav.

•  Выберите в меню Analyze (Анализ) General Linear Model (Общая линейная модель) Variance Components... (Компоненты дисперсии)

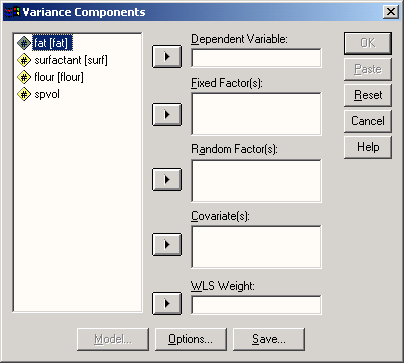
Откроется диалоговое окно Variance Components (Компоненты дисперсии).

•  Поместите laenge (длина) в поле для зависимой переменной, a pflanze (растение) в поле для случайных факторов.

•  Пройдя через кнопку Model... (Модель) вы можете выбрать, будете ли вы рассчитывать полнофакторную модель (установка по умолчанию) или включите в расчёт только некоторые факторы. При наличии только одного фактора, как в приведенном примере, можно говорить, конечно же, только о полнофакторной модели.

•  Выключатель Options... (Опции) предоставляет возможность выбора между четырьмя методами оценки компонентов дисперсии. Лучшим методом считается метод MINQUE (Minimum norm quadratic unbiased estimator) (Минимум нормы квадратической несмещённой оценки); поэтому он и установлен по умолчанию.

•  При помощи выключателя Save... (Сохранить) вы можете сохранить некоторые результаты в файле.

•  Оставьте это окно без изменений и начните расчёт нажатием ОК.

Рис. 17.9: Диалоговое окно Variance Components (Компоненты дисперсии)

В окне просмотра появятся оценки компонентов дисперсии.

Factor Level Information (Информация о слоях фактора)

N
PFLANZE (Растение)	1,00	6
	2,00	4
	3,00	5

Dependent Variable: LAENGE (Зависимая переменная: Длина) 

Variance Estimates (Оценки дисперсии)

Component (Компоненты)	Estimate (Оценка)
Var(PFLANZE) (Переменная (Растение))	,471
Var(Error) (Переменная (Ошибка))	,438

Dependent Variable: LAENGE (Зависимая переменная: Длина) Method: Minimum Norm Quadratic Unbiased Estimation (Weight = 1 for Random Effects and Residual) (Метод: Минимум нормы квадратичной несмещённой оценки (Вес = 1 для случайных эффектов и остатков))

На основе этих результатов можно найти процентную долю дисперсии, получающуюся из-за наличия разных растений:

0,471/(0,471+0,438)=51,8%

Приведём ещё один несколько усложненный пример из учебника SPSS. На некоторой фирме, работающей в области электроники, в 36 различных печах при различных температурах (550 и 600 градусов по Фаренгейту) измеряют выносливость (в минутах) определенных радиоэлектронных комплектующих. Один инженер предполагает, что не все печи создают одинаковые условия для тестирования комплектующих. Чтобы это проверить, он случайно выбирает три печи и для каждой печи делает по три измерения выносливости комплектующих для каждой из температур.

Данные находятся в файле ofen.sav в переменных of en (печь), temp (температура) и zeit (время). Переменная ofen (печь) соответствует фактору со случайными эффектами, так как из 36 печей три были выбраны случайно. Температура также является фактором со случайными эффектами, так как температуры 550 и 600 градусов были выбраны из бесконечного множества возможных температур.

Так как вполне возможно, что в разных печах действуют различные температурные режимы, предположим, что температурный фактор является вложенным в фактор печей — т.н. ("гнездовая компоновка'").

•  Откройте файл ofen.sav.

•  Откройте так, как было изложено ранее, диалоговое окно Variance Components (Компоненты дисперсии).

•  Переменную zeit (время) поместите в поле зависимых переменных, а переменные ofen (печь) и temp (температура) в поле случайных факторов.

Мы должны здесь также учесть и вложенность фактора temp (температура) в фактор ofen (печь). Это можно осуществить только при помощи программного синтаксиса.

•  Щёлкните по выключателю Paste (Внести) для того, чтобы перенести синтаксис данной команды в редактор синтаксиса.

В редакторе будет показан следующий синтаксис: 

VARCOMP 

 zeit BY ofen temp 

 /RANDOM = ofen temp 

 /METHOD = MINQUE (1) 

 /DESIGN 

 /INTERCEPT = INCLUDE .

•  Дополните вспомогательную команду DESIGN следующим образом:

VARCOMP 

 zeit BY ofen temp  

 /RANDOM = ofen temp 

  /METHOD = MINQUE (1) 

  /DESIGN = ofen temp(ofen) 

  /INTERCEPT = INCLUDE .

•  Запустите команду на исполнение при помощи кнопки Run Current. В окне просмотра появятся следующие оценки дисперсии:

Variance Estimates (Оценки дисперсии)

Component (Компонент)	Estimate (Оценка)
Var(OFEN) (Переменная (Печь))	29,287
Var(TEMP(OFEN)) (Переменная Температура (Печь))	1525,889
Var(Error) (Переменная (Ошибка))	69,778

Dependent Variable: ZEIT (Зависимая переменная: Время) Method: Minimum Norm Quadratic Unbiased Estimation (Weight = 1 for Random Effects and Residual) (Метод: Минимум нормы квадратичной несмещённой оценки (Вес = 1 для случайных эффектов и остатков))

Из таблицы можно узнать, что доля дисперсии объясняемая наличием разных печей очень незначительна:

[29, 287/(29,287 + 1525,889 + 69,778)]*100 = 1,8% 

До этого момента мы рассматривали только модели со случайными эффектами. Модели, содержащие как случайные, так и постоянные эффекты, получили название "смешанных" моделей.

И, наконец, следует указать на то, что методы MINQUE и ANOVA иногда могут выдавать негативные оценки компонентов дисперсии, что собственно противоречит самому определению дисперсии. Это может происходить потому, что количество наблюдений слишком мало, некоторые значения отсутствуют или выбран неподходящий метод оценки.