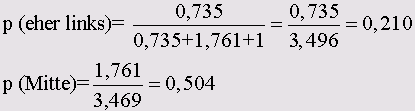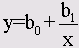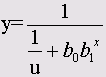Глава 16. Регрессионный анализ
Глава 16. Регрессионный анализ
1. Регрессионный анализ
Регрессионный анализ
Если расчёт корреляции характеризует силу связи между двумя переменными, то регрессионный анализ служит для определения вида этой связи и дает возможность для прогнозирования значения одной (зависимой) переменной отталкиваясь от значения другой (независимой) переменной.
-
Чтобы вызвать регрессионный анализ в SPSS, выберите в меню Analyze... (Анализ) Regression... (Регрессия)
Откроется соответствующее подменю.
Разделы этой главы соответствуют опциям вспомогательного меню. Причём при изучении линейного регрессионного анализа снова будут проведено различие между простым анализом (одна независимая переменная) и множественным анализом (несколько независимых переменных). Собственно говоря, никаких принципиальных отличий между этими видами регрессии нет, однако простая линейная регрессия является простейшей и применяется чаще всех остальных видов.
Рис. 16.1: Вспомогательное меню Regression (Регрессия)
Для проведения линейного регрессионного анализа зависимая переменная должна иметь интервальную (или порядковую) шкалу. В то же время, бинарная логистическая регрессия выявляет зависимость дихотомической переменной от некой другой переменной, относящейся к любой шкале. Те же условия применения справедливы и для пробит-анализа. Если зависимая переменная является категориальной, но имеет более двух категорий, то здесь подходящим методом будет мультиномиальная логистическая регрессия. Новшеством в 10 версии SPSS является порядковая регрессия, которую можно использовать, когда зависимые переменные относятся к порядковой шкале. И, наконец, можно анализировать и нелинейные связи между переменными, которые относятся к интервальной шкале. Для этого предназначен метод нелинейной регрессии.
Методы криволинейного приближения, весовые оценки и 2-ступенчатые наименьшие квадраты исследуют соответственно приближённость пути прохождения кривых при помощи компенсационных кривых, регрессионный анализ для изменяющейся дисперсии и проблемы из области эконометрии.
1.gif

16.1 Простая линейная регрессия
16.1 Простая линейная регрессия
Этот вид регрессии лучше всего подходит для того, чтобы продемонстрировать основополагающие принципы регрессионного анализа. Рассмотрим для этого диаграмму рассеяния из главы 15.1, которая иллюстрирует зависимость показателя холестерина спустя один месяц после начала лечения от исходного показателя, полученную при исследовании гипертонии. Можно легко заметить очевидную связь: обе переменные развиваются в одном направлении и множество точек, соответствующих наблюдаемым значениям показателей, явно концентрируется (за некоторыми исключениями) вблизи прямой (прямой регрессии). В таком случае говорят о линейной связи.
у=b*х + а
где b — регрессионные коэффициенты, a — смещение по оси ординат.
Смещение по оси ординат соответствует точке на оси у (вертикальной оси), где прямая регрессии пересекает эту ось. Коэффициент регрессии b через соотношение
b = tg(a) указывает на угол наклона прямой.
При проведении простой линейной регрессии основной задачей является определение параметров b и а. Оптимальным решением этой задачи является такая прямая, для которой сумма квадратов вертикальных расстояний до отдельных точек данных является минимальной.
Если мы рассмотрим показатель холестерина через один месяц (переменная chol1) как зависимую переменную (у), а исходную величину как независимую переменную (х), то тогда для проведения регрессионного анализа нужно будет определить параметры соотношения
chol1 = b-chol0 + a
После определения этих параметров, зная исходный показатель холестерина, можно спрогнозировать показатель, который будет через один месяц.
16.1.1 Расчёт уравнения регрессии
16.1.1 Расчёт уравнения регрессии
Откройте файл hyper.sav.
-
Выберите в меню Analyze... (Анализ) Regression...(Регрессия) Linear... (Линейная) Появится диалоговое окно Linear Regression (Линейная регрессия).
-
Перенесите переменную chol1 в поле для зависимых переменных и присвойте переменной chol0 статус независимой переменной.
-
Ничего больше не меняя, начните расчёт нажатием ОК.
Вывод основных результатов выглядит следующим образом:
Model Summary (Сводная таблица по модели)
Model (Модель) | R | R Square (R-квадрат) | Adjusted R Square (Смещенный R-квадрат) | Std. Error of the Estimate (Стандартная ошибка оценки) |
1 | ,861а | ,741 | ,740 | 25,26 |
а. Predictors: (Constant), Cholesterin, Ausgangswert (Влияющие переменные: (константы), холестерин, исходная величина)
ANOVA b
Model (Модель) | Sum of Squares (Сумма Квадратов) | df | Mean Square (Сред-нее значе- ние квадра- та) | F | Sig. (Значи-мость) | |
1 | Regre- ssion (Регре- ссия) | 314337,948 | 1 | 314337,9 | 492,722 | ,000a |
Residual (Остатки) | 109729,408 | 172 | 637,962 | |||
Total (Сумма) | 424067,356 | 173 |
a. Predictors: (Constant), Cholesterin, Ausgangswert (Влияющие переменные: (константа), холестерин, исходная величина)
b. Dependent Variable: Cholesterin, nach 1 Monat (Зависимая переменная холестерин через 1 месяц)
Рис.16.2: Диалоговое окно Линейная регрессия
Coefficients (Коэффициенты) а
Model (Модель) | Unstan- dardized Coefficients (Не стандарти-зированные коэф-фициенты) | Standa-rdized Coef- ficients (Стандарти-зированные коэф- фициенты) | Т | Sig. (Значи-мость) | |||
|
| В | Std: Error (Стандар-тная ошибка) | ß (Beta) | |||
1 | (Constant) (Конста- нта) | 34,546 | 9,416 | 3,669 | ,000 | ||
Choles- terin, Ausga- ngswert (холес- терин, исходная величина) | ,863 | ,039 | ,861 | 22,197 | ,000 | ||
a. Dependent Variable (Зависимая переменная)
Рассмотрим сначала нижнюю часть результатов расчётов. Здесь выводятся коэффициент регрессии b и смещение по оси ординат а под именем "константа". То есть, уравнение регрессии выглядит следующим образом:
chol1 = 0,863-chol0 + 34,546
Если значение исходного показателя холестерина составляет, к примеру, 280, то через один месяц можно ожидать показатель равный 276.
Частные рассчитанных коэффициентов и их стандартная ошибка дают контрольную величину Т; соответственный уровень значимости относится к существованию ненулевых коэффициентов регрессии. Значение коэффициента (3 будет рассмотрено при изучении многомерного анализа.
Средняя часть расчётов отражает два источника дисперсии: дисперсию, которая описывается уравнением регрессии (сумма квадратов, обусловленная регрессией) и дисперсию, которая не учитывается при записи уравнения (остаточная сумма квадратов). Частное от суммы квадратов, обусловленных регрессией и остаточной суммы квадратов называется "коэфициентом детерминации". В таблице результатов это частное выводится под именем "R-квадрат". В нашем примере мера определённости равна
314337,948/ 424067,356 =0,741
Эта величина характеризует качество регрессионной прямой, то есть степень соответствия между регрессионной моделью и исходными данными. Мера определённости всегда лежит в диапазоне от 0 до 1. Существование ненулевых коэффициентов регрессии проверяется посредством вычисления контрольной величины F, к которой относится соответствующий уровень значимости.
В простом линейном регрессионном анализе квадратный корень из коэфициента детерминации, обозначаемый "R", равен корреляционному коэффициенту Пирсона. При множественном анализе эта величина менее наглядна, нежели сам коэфициент детерминации. Величина "смещенный R-квадрат" всегда меньше, чем несмещенный. При наличии большого количества независимых переменных, мера определённости корректируется в сторону уменьшения. Принципиальный вопрос о том, может ли вообще имеющаяся связь между переменными рассматриваться как линейная, проще и нагляднее всего решать, глядя на соответствующую диаграмму рассеяния. Кроме того, в пользу гипотезы о линейной связи говорит также высокий уровень дисперсии, описываемой уравнением регрессии. О том, как регрессионную прямую можно встроить в диаграмму рассеяния, будет рассказано в разделе 16.1.3.
И, наконец, стандартизированные прогнозируемые значения и стандартизированные остатки можно предоставить в виде графика. Вы получите этот график, если через кнопку Plots...(Графики) зайдёте в соответствующее диалоговое окно и зададите в нём параметры *ZRESID и *ZPRED в качестве переменных, отображаемых по осям у и х соответственно. В случае линейной регрессии остатки распределяются случайно по обе стороны от горизонтальной нулевой линии.
2.gif

16.1.2 Сохранение новых переменных
16.1.2 Сохранение новых переменных
Многочисленные вспомогательные значения, рассчитываемые в ходе построения уравнения регрессии, можно сохранить как переменные и использовать в дальнейших расчётах.
-
Для этого в диалоговом окне Linear Regression (Линейная регрессия) щёлкните на кнопке Save (Сохранить).
Откроется диалоговое окно Linear Regression: Save (Линейная регрессия: Сохранение) как изображено на рисунке 16.3.
В 10 версии SPSS появилась новая возможность сохранять информацию о модели в так называемом XML-файле. В дальнейшем он может использоваться некоторыми дополнительными SPSS-продуктами (к примеру, Whatlf?).
Интересными здесь представляются опции Standardized (Стандартизированные значения) и Unstandardized (Нестандартизированные значения), которые находятся под рубрикой Predicted values (Прогнозируемые величины опции). При выборе опции Не стандартизированные значения будут рассчитывается значения у, которое соответствуют уравнению регрессии. При выборе опции Стандартизированные значения прогнозируемая величина нормализуется. SPSS автоматически присваивает новое имя каждой новообразованной переменной, независимо от того, рассчитываете ли Вы прогнозируемые значения, расстояния, прогнозируемые интервалы, остатки или какие-либо другие важные статистические характеристики. Нестандартизированным значениям SPSS присваивает имена pre_1 (predicted value), pre_2 и т.д., а стандартизированным zpr_l.
Рис. 16.3: Диалоговое окно Линейная регрессия: Сохранение
-
Щёлкните в диалоговом окне Linear Regression: Save (Линейная регрессия: Сохранение) в поле Predicted values (Прогнозируемые значения) на опции Unstandardized (Нестандартизированные значения).
-
Подтвердите нажатием Continue (Далее) и в заключение ОК.
Вы увидите, что в редакторе данных была образована новая переменная под именем рrе_1 и добавлена в конец списка переменных в файле. Для объяснения значений, находящихся в переменной рrе_1, возьмём случай 5. Для случая 5 переменная рrе_1 содержит нестандартизированное прогнозируемое значение 263,11289. Это прогнозируемое значение слегка отличается в сторону увеличения от реального показателя содержания холестерина, взятого через один месяц (chol1) и равного 260. Нестандартизированное прогнозируемое значение для переменной chol1, так же как и другие значения переменной рге_1, было вычислено исходя из соответствующего уравнения регрессии.
Если мы в уравнение регрессии
chol1 = 0,863 • chol0 + 34,546
подставим исходное значение для chol0 (265), то получим chol1 = 0,863 -265 + 34,546 =263,241
Небольшое отклонение от значения, хранящегося в переменной рге_1 объясняется тем, что SPSS использует в расчётах более точные значения, чем те, которые выводятся в окне просмотра результатов. На этом этапе мы ещё раз проиллюстрируем возможность использования регрессии в качестве прогноза.
-
Добавьте для этого в конец файла hyper.sav, ещё два случая, используя фиктивные значения для переменной chol0. Пусть к примеру, это будут значения 282 и 314.
Мы исходим из того, что нам не известны значения показателя холестерина через месяц после начала лечения, и мы хотим спрогнозировать значение переменной chol1.
-
Оставьте предыдущие установки без изменений и проведите новый расчёт уравнения регрессии.
В конце списка переменных добавится переменная рге_2. Для нового добавленного случая (№175) для переменной chol1 будет предсказано значение 277,77567, а для случая №176 — значение 305,37620.
3.gif

16.1.3 Построение регрессионной прямой
16.1.3 Построение регрессионной прямой
Чтобы на диаграмме рассеяния изобразить регрессионную прямую, поступите следующим образом:
-
Выберите в меню следующие опции Graphs ... (Графики) Scatter plots... Диаграммы рассеяния
Откроется диалоговое окно Scatter plots... (Диаграмма рассеяния) как изображено на рисунке 16.4.
-
В диалоговом окне Scatter plots...(Диаграмма рассеяния) оставьте предварительную установку Simple (Простая) и щёлкните на кнопке Define (Определить).
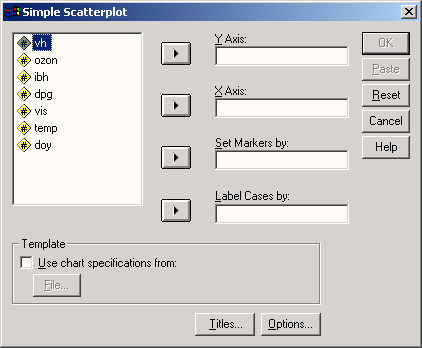
Откроется диалоговое окно Simple Scatter plot (Простая диаграмма рассеяния) (см. рис. 16.5).
Рис. 16.4: Диалоговое окно Scatter plots... (Диаграмма рассеяния)
Рис. 16.5: Диалоговое окно Simple Scatterplot (Простая диаграмма рассеяния).
-
Перенесите переменную chol1 в поле оси Y, а переменную chol0 в поле оси X.
-
Подтвердите щелчком на ОК.
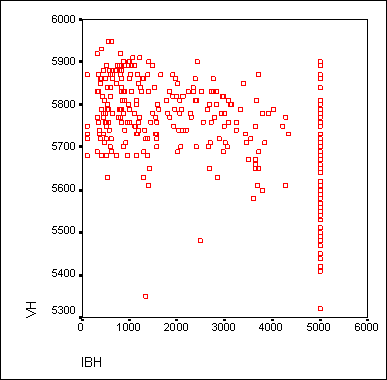
В окне просмотра результатов появится диаграмма рассеяния (см. рис. 16.6).
-
Щёлкните дважды на этом графике, чтобы перенести его в редактор диаграмм.
-
Выберите в редакторе диаграмм меню Chart... (Диаграмма) Options... (Опции)
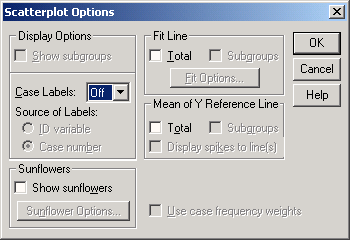
Откроется диалоговое окно Scatterplot Options (Опции для диаграммы рассеяния) (см. рис. 16.7).
-
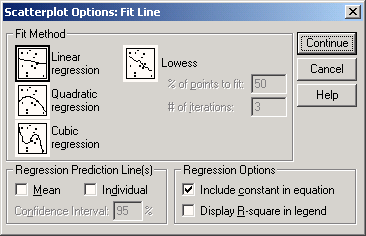
В рубрике Fit Line (Приближенная кривая) поставьте флажок напротив опции Total (Целиком для всего файла данных) и щёлкните на кнопке Fit Options (Опции для приближения). Откроется диалоговое окно Scatterplot Options: Fit Line (Опции для диаграммы рассеяния: приближенная кривая) (см. рис. 16.8).
-
Подтвердите предварительную установку Linear Regression (Линейная регрессия) щелчком Continue (Далее) и затем на ОК.
-
Закройте редактор диаграмм и щёлкните один раз где-нибудь вне графика.
Рис. 16.6: Диаграмма рассеяния в окне просмотра
Рис. 16.7: Диалоговое окно Scatterplot Options (Опции для диаграммы рассеяния)
Рис. 16.8: Диалоговое окно Scatterplot Options: Fit Line (Опции для диаграммы рассеяния:
Теперь в диаграмме рассеяния отображается регрессионная прямая (см. рис. 16.9).
4.gif

5.gif
6.gif
7.gif
8.gif
16.1.4 Выбор осей
16.1.4 Выбор осей
Для диаграмм рассеяния часто оказывается необходимой дополнительная корректировка осей. Продемонстрируем такую коррекцию при помощи одного примера. В файле raucher.sav находятся десять фиктивных наборов данных. Переменная konsum указывает на количество сигарет, которые выкуривает один человек в день, а переменная puls на количество времени, необходимое каждому испытуемому для восстановления пульса до нормальной частоты после двадцати приседаний. Как было показано ранее, постройте диаграмму рассеяния с внедрённой регрессионной прямой.
-
В диалоговом окне Simple Scatterplot (Простая диаграмма рассеяния) перенесите переменную puls в поле оси Y, а переменную konsum — в поле оси X.
Рис. 16.9: Диаграмма рассеяния с регрессионной прямой
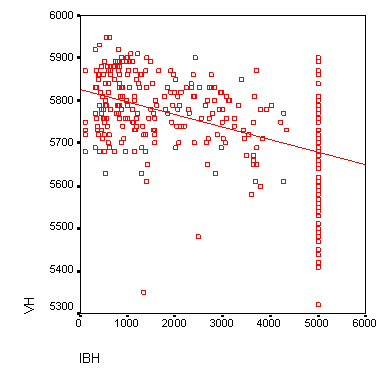
После соответствующей обработки данных в окне просмотра появится диаграмма рассеяния, изображённая на рисунке 16.10.
Рис. 16.10: Диаграмма рассеяния с регрессионной прямой до коррекции осей
Так как никто не выкуривает минус 10 сигарет в день, точка начала отсчёта оси X является не совсем корректной. Поэтому попробуем эту ось откорректировать.
-
Дважды щёлкните на графике и в меню редактора диаграмм вберите опции Chart... (Диаграмма) Axis... (Оси) Откроется диалоговое окно Axis Selection (Выбор оси) (см. рис. 16.11).
-
Подтвердите предварительный выбор оси X нажатием кнопки ОК.
Откроется диалоговое окно X-Scale Axis (Ось X) (см. рис. 16.12).
-
В редактируемом поле Displayed (Отображаемый) в рубрике Range (Диапазон) измените минимальное значение на 0.
-
Подтвердите нажатием на ОК.
Рис. 16.11: Диалоговое окно Axis Selection (Выбор оси)
Рис. 16.12: Диалоговое окно X-Scale Axis (Ось X)
-
Выберите вновь в меню редактора диаграмм опции Chart... (Диаграмма* Axis... (Оси)
-
Активируйте в диалоговом окне Axis Selection (Выбор оси) опцию Y Scale (Ось Y). Откроется диалоговое окно Y-Scale Axis (Ось Y).
-
И здесь в рубрике Range (Диапазон) в редактируемом поле Displayed (Отображаемый) измените минимальное значение на "0".
-
Подтвердите нажатием на ОК.
В окне просмотра Вы увидите откорректированную диаграмму рассеяния (см. рис. 16.13).
На откорректированной диаграмме рассеяния теперь стало проще распознать начальную точку на оси Y, которая образуется при пересечении с регрессионной прямой. Значение этой точки примерно равно 2,9. Сравним это значение с уравнением регрессии для переменных puls (зависимая переменная) и konsum (независимая переменная). В результате расчёта уравнения регрессии в окне отображения результатов появятся следующие значения:
Coefficients (Коэффициенты)а
Model (Модель) | Unstandardized Coefficients (He стандартизированные коэф- фициенты) | Standar- dized Coefficients (Стандарти- зированные коэф- фициенты) | Т | Sig. (Значи- мость) | |||
| В | Std. Error (Стандар- тная ошибка) | ß (Beta) | ||||
1 | (Constant) (Константа) | 2,871 | ,639 | 4,492 | ,002 | ||
tgl. Zigaretten-konsum (Коли- чество сигарет в день) | ,145 | ,038 | ,804 | 3,829 | ,005 | ||
a. Dependent Variable: Pulsfrequenz unter 80 (Зависимая переменная: частота пульса ниже 80)
Рис. 16.13: Диаграмма рассеяния с регрессионной прямой после корректировки осей
Что дает следующее уравнение регрессии:
pids = 0,145-konsum + 2,871
Мы видим, что константа в вышеприведенном уравнении регрессии (2,871) соответствует точке на оси Y, которая образуется в точке пересечения с регрессионной прямой.
9.gif
10.gif

11.gif
12.gif

13.gif
16.10 Двухступенчатый метод наименьших квадратов
16.10 Двухступенчатый метод наименьших квадратов
При помощи этого метода, используемого в эконометрии, производится анализ переменных, представленных в виде временных рядов. Примером может здесь послужить классическая эконометрическая модель, в которой спрос на некоторый продукт зависит от его цены, уровня обеспеченности (достатка) потенциальных покупателей и других неизвестных факторов:
Спрос = ß0 + ß1 • Цена + ß2 • Достаток + Ошибка
Наряду с независимыми переменными (называемыми также объявленными переменными) в этом уравнении должно быть указано, по меньшей мере, такое же количество так называемых инструментальных переменных. Они могут оказывать влияние на независимые переменные, при этом сами независимые переменные оказывать влияния на них не могут. Если речь идёт о сельскохозяйственном продукте, то такими переменными могут быть климатические переменные. Инструментальные переменные должны иметь сильную корреляцию с независимыми переменными, но совсем не иметь корреляции со слагаемыми ошибки.
В диалоговом окне для этого метода выводится запрос по поводу зависимых, объявленных и инструментальных переменных. На данном этапе рассмотрение конкретного примера мы опустим.
16.2 Множественная линейная регрессия
16.2 Множественная линейная регрессия
В общем случае в регрессионный анализ вовлекаются несколько независимых переменных. Это, конечно же, наносит ущерб наглядности получаемых результатов, так как подобные множественные связи в конце концов становится невозможно представить графически.
В случае множественного регрессионного анализа речь идёт необходимо оценить коэффициенты уравнения
у = b1-х1+b2-х2+... + bn-хn+а,
где n — количество независимых переменных, обозначенных как х1 и хn, а — некоторая константа.
Переменные, объявленные независимыми, могут сами коррелировать между собой; этот факт необходимо обязательно учитывать при определении коэффициентов уравнения регрессии для того, чтобы избежать ложных корреляций.
В качестве примера рассмотрим стоматологическое обследование 1130 человек, в котором исследуется вопрос необходимости лечения зубного ряда, измеряемой при помощи так называемого показателя CPITN, в зависимости от набора различных переменных.
При этом зубной ряд был разделён на секстанты, для которых и происходило определение показателя CPITN. Этот показатель может принимать значения от 0 до 4, где 0 соответствует здоровому состоянию, а 4 наибольшей степени развития заболевания. Затем значения показателя CPITN для всех секстант были усреднены.
Файл zahn.sav содержит следующие переменные:
Имя переменной | Расшифровка |
cpitn | Усредненное значение CPITN |
alter | Возраст |
g | Пол (1 = мужской, 2 = женский) |
s | Образование (1 = специальное школьное, 2 = неполное школьное, 3 = среднее, 4 = аттестат зрелости, 5 = высшее образование) |
pu | Периодичность чистки зубов (1 = меньше одного раза в день, 2 = один раз в день, 3 = два раза в день, 4 = долее двух раз в день) |
zb | Смена зубной щётки (1 = каждый месяц, 2 = каждые три месяца, 3 = раз в полгода, 4 = ещё реже) |
beruf (профессия) | Профессия (1 = государственный служащий/служащий, 2 = рабочий/профессиональный рабочий, 3 = занятость в области медицины, 4 = военный) |
Переменные cpitn и alter принадлежат к интервальной шкале, а переменные s, pu и zb при более подробном рассмотрении можно отнести к порядковой шкале, так что они могут быть подвергнуты регрессионному анализу. Переменная g относится к номинальной шкале, но в то же время является дихотомической. Поэтому если при оценке результатов обратить внимание на полярность, то и эта переменная так же может быть вовлечена в регрессионный анализ. Однако, переменная beruf относится к номинальной шкале и имеет более двух (а именно четыре) категории. Поэтому, без дополнительной обработки ее нельзя применять в дальнейших расчётах.
В данном случае можно прибегнуть к специальному трюку: разложить переменную beruf на четыре, так называемых, фиктивных переменных, с кодировками отвечающими О (действительно) и 1 (ложно). В файл добавляются четыре новые переменные: berufl-beruf4, которые поочередно соответствуют четырём различным кодировкам переменной beruf. Так, к примеру, переменная berafl указывает на то, является ли данный респондент государственным служащим/работником (кодировка 1) или нет (кодировка 0).
-
Откройте файл zahn.sav.
-
Выберите в меню Analyze... (Анализ) Regression...(Регрессия) Linear... (Линейная)
-
Поместите переменную cpitn в поле для зависимых переменных, объявите переменные: alter, berafl, bеrа0, beru0, beruf4, g, pu, S.H zb независимыми.
Для множественного анализа с несколькими независимыми переменными не рекомендуется оставлять метод включения всех переменных, установленный по умолчанию. Этот метод соответствует одновременной обработке всех независимых переменных, выбранных для анализа, и поэтому он может рекомендоваться для использования только в случае простого анализа с одной независимой переменной. Для множественного анализа следует выбрать один из пошаговых методов. При прямом методе независимые переменные, которые имеют наибольшие коэффициенты частичной корреляции с зависимой переменной пошагово увязываются в регрессионное уравнение. При обратном методе начинают с результата, содержащего все независимые переменные и затем исключают независимые переменные с наименьшими частичными корреляционными коэффициентами, пока соответствующий регрессионный коэффициент не оказывается незначимым (в данном случае уровень значимости равен 0,1).
Наиболее распространенным является пошаговый метод, который устроен так же, как и прямой метод, однако после каждого шага переменные, используемые в данный момент, исследуются по обратному методу. При пошаговом методе могут задаваться блоки независимых переменных; в этом случае заданные блоки на одном шаге обрабатываются совместно.
-
Выберите пошаговый метод, но воздержитесь от блочной формы ввода данных, не задавайте больше ни каких дополнительных расчётов и начните вычисление нажатием ОК.
Model Summary (Сводная таблица модели)
Model (Модель) | R | R Square (Коэф- фициент детерми- нации) | Adjusted R Square (Скорректи- рованный R-квадрат) | Std. Error of the Estimate (Станда- ртная ошибка оценки) |
1 2 3 4 5 | ,452а ,564b ,599с ,609d ,613е | ,204 ,318 ,359 ,371 ,375 | ,203 ,317 ,358 ,369 ,373 | ,8316 ,7698 ,7467 ,7402 ,7380 |
a. Predictors: (Constant), Alter (Влияющие переменные: (константа), возраст)
b. Predictors: (Constant), Alter, Putzhaeufigkeit (Влияющие переменные: (константа), возраст, периодичность чистки)
c Predictors: (Constant), Alter, Putzhaeufigkeit, Zahnbuerstenwechsel (Влияющие переменные: (константа), возраст, периодичность чистки, смена зубной щётки)
d Predictors: (Constant), Alter, Putzhaeufigkeit, Zahnbuerstenwechsel, Schulbildung (Влияющие переменные: (константа), возраст, периодичность чистки, смена зубной щётки, образование)
е. Predictors: (Constant), Alter, Putzhaeufigkeit, Zahnbuerstenwechsel, Schulbildung, Arbeiter/Facharbeiter (Влияющие переменные: (константа), возраст, периодичность чистки, смена зубной щётки, образование, рабочий/профессиональный работник) .
Из первой таблице следует, что вовлечение переменных в расчет производилось за пять шагов, то есть переменные возраст, периодичность чистки, смена зубной щётки, образование, рабочий/профессиональный работник поочерёдно внедрялись в уравнение регрессии. Для каждого шага происходит вывод коэффициентов множественной регрессии, меры определённости, смещенной меры определённости и стандартной ошибки.
К указанным результатам пошагово присоединяются результаты расчёта дисперсии (см. гл. 16.1.1), которые здесь не приводятся. Также, пошаговым образом, производится вывод соответствующих коэффициентов регрессии и значимость их отличия от нуля.
Coefficients (Коэффициенты) a
| Model (Модель) | UnStan- dardized Coefficients (He стандарти-зированные коэф- фициенты) | Standa- rdized Coefficients (Стандарти-зированные коэф-фициенты) | Т | Sig. (Значи мость) | ||
| В | Std. Error (Станда- ртная ошибка) | ß (Beta) | ||||
| (Constant) (Константа) Alter (Возраст) | 1,295 3,31 Е-02 | ,071
,002 |
,452 | 18,220 17,006 | ,000 ,000 | |
| 2 | (Константа) Возраст Перио- дичность чистки | 3,024 3.20Е-02 -,604 | ,142
,002 ,044 |
,437
-,339 |
21,317 17,765 -13,756 | ,000 ,000 ,000 |
| 3 | (Константа) Возраст Перио- дичность чистки Смена зубной щётки | 1,903 3.25Е-02 -,439 ,253 | ,191
,002 ,047 ,030 |
,443
-,246 ,222 |
9,976 18,555 -9,376 8,473 | ,000 ,000,
,000 ,000 |
| 4 | (Константа) Возраст Перио- дичность чистки Смена зубной щётки Образование | 2,188 3,31 Е-02 -,391 ,226 -,115 | ,199
,002 ,048 ,030 ,025 |
,451
-,220 ,199 -,116 |
10,992 19,011 -8,235 7,498 -4,580 | ,000 ,000
,000 ,000 ,000 |
| 5 | (Константа) Возраст Перио- дичность чистки Смена зубной щётки Образование Рабочий/ Профес- сиональный работник |
2,022 3.20Е-02 -,379 ,229 -8.3Е-02 ,143
|
,208 ,002 ,048 ,030 ,028 ,052
|
,437 -,213 ,201 -,084 ,075
|
9,743 18,041 -7,964 7,613 -2,983
2,757 |
,000 ,000 ,000 ,000 ,003
,006 |
а. Dереnаdеnt variable: Mittlerer CPITN-Wert (Зависимая переменная: усреднённое значение CPITN)
Вдобавок ко всему для каждого шага анализируются исключённые переменные. В вышеприведенной таблице в объяснениях нуждаются лишь коэффициенты ß. Это — регрессионные коэффициенты, стандартизованные соответствующей области значений, они указывают на важность независимых переменных, вовлечённых в регрессионное уравнение.
Уравнение регрессии для прогнозирования значения CPITN выглядит следующим образом:
cpitn = 0,032•alter - 0.379•рu + 0,229•zb - 0,083•s + 0,143- benif 2 + 2,022
Для 40-летнего рабочего с неполным школьным образованием, который ежедневно чистит зубы один раз в день и меняет щётку раз в полгода, с учётом соответствующих кодировок, получается следующее уравнение:
cpitn = 0,032•40-0,379•2 + 0,229•3- 0,083•2 + 0,143•1 + 2,022 = 3,208
При помощи соответствующих опций можно организовать вывод большого числа дополнительных статистических характеристик и графиков, на которых мы здесь останавливаться не будем. Можно также создать много дополнительных переменных и добавить их в исходный файл данных.
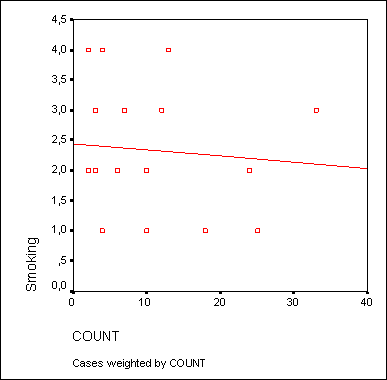
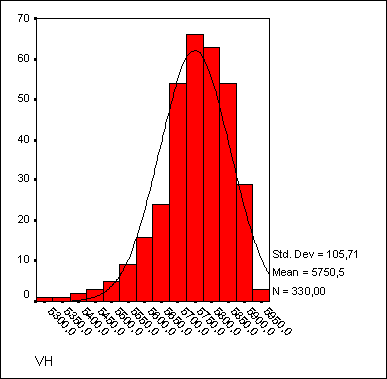
Важным моментом является анализ остатков, то есть отклонений наблюдаемых значений от теоретически ожидаемых. Остатки должны появляться случайно (то есть не систематически) и подчиняться нормальному распределению. Это можно проверить, если с помощью кнопки Charts... (Диаграммы) построить гистограмму остатков. В приведенном примере наблюдается довольно хорошее согласование гистограммы остатков с нормальным распределением.
Проверка на наличие систематических связей между остатками соседних случаев (что, однако, является уместным только при наличии так называемых данных с продольным сечением), может быть произведена при помощи теста Дарбина-Ватсона (Durbin-Watson) на автокорреляцию. Этот тест вычисляет коэффициент, лежащий в диапазоне от 0 до 4. Если значение этого коэффициента находится вблизи 2, то это означает, что автокорреляция отсутствует. Тест Дарбина-Ватсона можно активировать через кнопку Statistics (Статистические характеристики). В данном примере тест дает удовлетворительное значение коэффициента, равное 1,776.
Ещё одной дополнительной возможностью является задание переменной отбора в диалоговом окне Linear Regression (Линейная регрессия). Здесь, с помощью кнопки Rule... (Правило) в диалоговом окне Linear Regression: Define Selection Rule (Линейная регрессия: ввод условия отбора), Вы получаете возможность при помощи избирательного признака сформулировать условие, которое будет ограничивать количество случаев, вовлеченных в анализ.
Рис. 16.14: Гистограмма остатков
14.gif
16.3 Нелинейная регрессия
16.3 Нелинейная регрессия
Многие связи по своей природе, то есть в реальной жизни, либо являются строго линейными, либо их можно привести к линейному виду. Один пример линейной связи из области медицины был приведен в главе 16.1; ещё одним, уже знакомым нам примером является линейная связь между весом и ростом. При условии наличия лопаточного количества респондентов, на основании измеренных пар значений можно вывести уравнение регрессионной прямой, к которой более или менее приближается '.тожество точек, соответствующие парам значений.
Существуют также линейные связи, следующие непосредственно из физических закономерностей. Так путь s, пройденный, при постоянной скорости с за промежуток времени : рассчитывается по формуле:
s=c•t
Стало быть, путь является линейной функцией времени. А если мы рассмотрим закон свободного падения, то в этом случае расстояние s. которое проходили падающее тело увеличивается пропорционально квадрату времени:

где g — ускорение свободного падения.
Если Вы захотите проверить это экспериментально, то Вам надлежит сделать серию опытов, в которых будет необходимо бросать некоторый предмет, например, камень, с различной высоты (лучше всего, конечно же, в разряжённом, безвоздушном пространстве) и засекать время падения. Предположим, у Вас получились следующие результаты:
s (см) | t (сек) |
5 | 1,0 |
9 | 1,4 |
16 | 1,8 |
26 | 2,3 |
40 | 2,8 |
65 | 3,6 |
98 | 4,5 |
Хотя связь между 5 и с и не является линейной, её можно перевести в линейную модель, если взять квадратный корень из обоих сторон закона свободного падения:

С помощью преобразования данных, мы разрешаем компьютеру создать новую переменную, содержащую значения квадратного корня из величины s и рассматривать её как зависимую переменную, а время / как независимую переменную. Рассчитаем коэффициент регрессии b так, как это было изложено в разделе 16.1.
Используя этот коэффициент, можно теперь рассчитать искомое ускорение свободного падения:
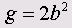
Если Вы выполните эти вычисления, то получите b = 0,2224 и g = 9,88.
При помощи соответствующих трансформаций в линейную модель можно перевести и другие исходно нелинейные связи. К примеру, очень часто встречающуюся экспоненциальную связь
у = а•еbx
можно преобразовать в линейную при помощи вычисления логарифма от обеих сторон уравнения
ln (у) = ln(a) + b•x
То есть в данном случае до проведения линейного регрессионного анализа необходимо прологарифмировать независимые переменные.
Связи, которые при помощи соответствующих трансформаций могут быть переведены в линейную связь, называются линейными по существу (Intrinsically Linear Model). Возможность перевода в линейную модель нужно использовать всегда, так как в этом случае параметры регресии вычисляются непосредственно, а не определяются с помощью итераций.
В качестве примера нелинейной по существу связи (Intrinsically Nonlinear Model) можно привести динамику роста населения США (этот пример взят из Справочника по SPSS):
Год | Лекала | Население |
1790 | 0 | 3,895 |
1800 | 1 | 5,267 |
1810 | 2 | 7,182 |
1820 | 3 | 9,566 |
1830 | 4 | 12,834 |
1840 | 5 | 1 6,985 |
1850 | 6 | 23,069 |
1860 | 7 | 31,278 |
1870 | 8 | 38,416 |
1880 | 9 | 49,924 |
1890 | 10 | 62,692 |
1900 | 11 | 75,734 |
1910 | 12 | 91,812 |
1920 | 13 | 109,806 |
1930 | 14 | 122,775 |
1940 | 15 | 131,669 |
1950 | 16 | 150,697 |
1960 | 17 | 178,464 |
В таблице приведена численность населения в миллионах и дополнительно количество декад (десятилетий), прошедших с 1790 года.
Зависимость численности населения (переменная pop) от времени t (выраженного здесь в декадах) часто описывается при помощи следующей формулы:
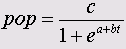
Эту связь нельзя перевести в линейную форму. Она включает три параметра: а, b и с, которые должны быть определены при помощи подходящего метода. Для этого необходимо задать начальные значения этих параметров.
Общего универсального метода определения параметров подобной нелинейной связи, к сожалению, не существует, поэтому описанная ниже последовательность действий может служить только примером.
В рассматриваемом примере параметр с является амплитудой, так что начальное значение может быть задано немного большим, чем максимум значения pop, то есть приблизительно с = 200.
При помощи значения параметра pop при t = 0 и начального значения параметра с можно получить начальную оценку параметра а:
3,895 = 200/(1+e2)
и следовательно
а = ln((200/3,895-1)) = 3,9
Исходя из значения параметра pop для первой декады, можно вычислить начальное значение параметра b:
5,267=200/(1+e3,9+b)
и следовательно
b=ln(5,267-1)-3,9 = -0,3
Определим теперь более точные значения параметров а, b и с с помощью итераций.
-
Откройте файл usa.sav.
-
Выберите в меню Analyze... (Анализ) Regression... (Регрессия) Nonlinear... (Нелинейная)
-
В диалоговом окне Nonlinear Regression (Нелинейная регрессия) перенесите переменную pop в поле для зависимых переменных.
-
Щёлкните на поле Model Expression (Модельное выражение) и внесите в него следующую формулу:
c/(l+exp(a+b*dekade))
При вводе формулы можно использовать клавиатуру, находящуюся в диалоговом окне. Диалоговое окно будет выглядеть так, как изображено на рисунке 16.15. Нам осталось только задать начальные значения параметров.
-
Щёлкните на кнопке Parameter... (Параметр)
Вы получите диалоговое окно, в котором сможете задавать начальные значения.
-
Укажите в поле имён имя первого параметра, то есть, к примеру, а, затем щёлкните в поле Starting value (Начальное значение), введите значение 3,9 и щёлкните на Add (Добавить).
Рис. 16.15: Диалоговое окно Nonlinear Regression (Нелинейная регрессия).
-
Поступите таким же образом с двумя другими параметрами бис (начальные значения —0,3 и 200 соответственно).
-
Покиньте диалоговое окно нажатием Далее.
-
Щёлкните на кнопке Save (Сохранить). Отметьте в диалоговом окне Nonlinear Regression: Save New Variables (Нелинейная регрессия: Сохранить новые переменные) параметры: Predicted Values (Прогнозируемые значения) и Residuals (Остатки). Таким образом, Вы создадите две новые переменные (с именами: pred_ и resid), которые содержат вычисленные значения и остатки для каждого года.
-
Начните расчёт нажатием ОК.
На экране появятся результаты, причём Вы можете заметить, что вывод происходит не в виде привычных современных таблиц. Сначала протоколируется процесс итерации; в рассматриваемом примере для достижения заданного уровня точности понадобилось 10 итерационных шагов. Дополнительно выводятся следующие статистические характеристики:
Nonlinear Regression | Summary Statistics Dependent Variable POP | ||
Source | DF | Sum of Squares | Mean Square |
Regression | 3 | 123048 ,61437 | 41016,20479 |
Residual | 15 | 186,50337 | 12,43356 |
Uncorrected Total | 18 | 123235,11774 |
|
(Corrected Total) | 17 | 53291,50763 |
|
R squared = 1Residual SS / CorrectedSS = ,99650 | |||
Здесь интерес может представлять только член, обозначенный R squared; его следует понимать как часть суммарной дисперсии, которая обусловлена построенной моделью. Вычисленное значение этого параметра, 0.9965, указывает на очень хорошую степень приближения. После этого вывода следует распечатка конечных значений всех трех параметров вместе с соответствующей стандартной ошибкой и доверительным интервалом:
Asymptotic 95 % Asymptotic Confidence Interval | ||||
Parameter Estimate | Std. Error | Lower Upper | ||
A | 3,888771432 , | 093688592 | 3,6890789254 ,088463938 | |
В | -,278834486, | 015593535 | -,312071318 - ,245597654 | |
С | 244,01372955 | 17,974966354 | 205, 70099568 282 | ,32646341 |
Завершает список выводимых результатов корреляционная матрица оценок параметров:
Asymptotic | Correlation А | Matrix of В | the | Parameter Estimates С |
А В С | 1,0000 -,7243 -,3759 | -,724: 1,000 ,904 | 3 '0 3 | -,3759 ,9043 1,0000 |
Очень высокие абсолютные значения корреляций указывают на то, что модель содержит неоправданно большое количество параметров. В рассматриваемом примере и модель с меньшим количеством параметров даст столь же хорошее приближение.
-
Если Вы хотите визуально сравнить рассчитанные значения с наблюдаемыми, то можете посредством меню Graph... (Графики) Scatter plots... (Диаграммы рассеяния)
построить многослойную диаграмму рассеяния (Staggered), на которой Вы можете представить переменные pop и pred_ в зависимости от переменной jahr. Также можно поступить и с остатками (переменная rcsid).
Согласно предварительным установкам при расчете нелинейной регрессии происходит минимизация суммы квадратов остатков. При помощи кнопки Loss...(Остаток) можно задать какую-либо другую минимизирующую функцию. Далее при помощи кнопки Constraints...(ограничения) может быть открыто окно, в котором можно задать ограничения для определяемых параметров нелинейной регрессии.
16.gif

19.gif

16.4 Бинарная логистическая регрессия
16.4 Бинарная логистическая регрессия
С помощью метода бинарной логистической регрессии можно исследовать зависимость дихотомических переменных от независимых переменных, имеющих любой вид шкалы.
Как правило, в случае с дихотомическими переменными речь идёт о некотором событии, которое может произойти или не произойти; бинарная логистическая регрессия в таком случае рассчитывает вероятность наступления события в зависимости от значений независимых переменных.
Вероятность наступления события для некоторого случая рассчитывается по формуле
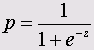
где z= b1*X1 + b2хХ2+ ...+ bnxXn+ a ,
X1 — значения независимых переменных, b1 — коэффициенты, расчёт которых является задачей бинарной логистической регрессии, а — некоторая константа.
Если для р получится значение меньшее 0,5, то можно предположить, что событие не наступит; в противном случае предполагается наступление события.
В качестве примера рассмотрим два диагностических теста из области медицины на предмет обнаружения карциномы (злокачественной опухоли) мочевого пузыря: подсчет количества (типизация) Т-клеток и тест LAI. Результатами первого теста являются значения, принадлежащие к интервальной шкале, а тест LAI дает дихотомический результат: "положительно" или "отрицательно".
Оба теста были проведены со здоровыми людьми и заведомо больными пациентами. Результаты представлены в следующей таблице:
Коллектив | Типизация t-клеток | LAI | Коллектив | Типизация t-клеток | LAI |
болен | 48.5 | положи-тельно | болен | 73.5 | положи-тельно |
болен | 55.5 | положи-тельно | здоров | 61.1 | положи-тельно |
болен | 57.5 | положи-тельно | здоров | 62.5 | отрица-тельно |
болен | 58.5 | положи-тельно | здоров | 63.5 | отрица-тельно |
болен | 61.0 | положи-тельно | здоров | 64.5 | положи-тельно |
болен | 61.5 | положи-тельно | здоров | 69.5 | положи-тельно |
болен | 61.5 | положи-тельно | здоров | 70.0 | отрица-тельно |
болен | 6,2.0 | положи-тельно | здоров | 70.0 | отрица-тельно |
болен | 62.0 | положи-тельно | здоров | 71.0 | положи-тельно |
болен | 62,0 | положи-тельно | здоров | 71,5 | положи-тельно |
болен | 62.5 | положи-тельно | здоров | 71.5 | отрица-тельно |
болен | 63.0 | положи-тельно | здоров | 72.0 | отрица-тельно |
болен | 63.5 | положи-тельно | здоров | 73.0 | отрица-тельно |
болен | 65.0 | положи-тельно | здоров | 76.0 | отрица-тельно |
болен | 65.0 | отрица-тельно | здоров | 72.5 | отрица-тельно |
болен | 66.5 | отрица-тельно | здоров | 73.0 | отрица-тельно |
болен | 66.5 | отрица-тельно | здоров | 73.5 | отрица-тельно |
болен | 66.5 | положи-тельно | здоров | 74.0 | отрица-тельно |
болен | 68.5 | положи-тельно | здоров | 75.0 | отрица-тельно |
болен | 69.0 | отрица-тельно | здоров | 77.0 | отрица-тельно |
болен | 71.0 | положи-тельно | здоров | 77.0 | отрица-тельно |
болен | 71.0 | положи-тельно | здоров | 78.5 | отрица-тельно |
болен | 71.0 | положи-тельно |
|
|
|
Если сначала посмотреть на результаты типизации Т-клеток, то можно заметить, что здесь для здоровых людей значения в среднем выше, чем для больных. Следовательно, исходя из значений, получившихся при типизации Т-клеток, можно попытаться, вывести вероятность наличия карциномы мочевого пузыря.
Приведенные в таблице данные находятся в файле hkarz.sav. Больным присвоена кодировка 1, а здоровым 2; для теста LA1 кодировка 0 соответствует положительному результату, а 1 отрицательному.
-
Откройте файл hkarz.sav.
-
Выберите в меню Analyze... (Анализ) Regression... (Регрессия) Binary logistic... (Бинарная логистическая)
Открывается диалоговое окно Logistic Regression (Логистическая регрессия).
-
Поместите переменную gruppe (группа), содержащую информацию о принадлежности к одному или второму коллективу (больным или здоровым), в поле для зависимых переменных, а переменную tzell — в поле ковариат. Результаты теста LAI сначала мы не будем использовать в расчёте.
Рис. 16.16: Диалоговое окно -Ogistic Regression (Логистическая регрессия).
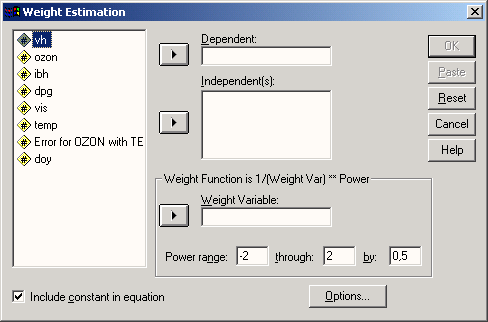
В качестве метода использования переменных в вычислениях предварительно установлен метод Enter (Вложение), при котором в расчёт одновременно вовлекаются :-:е переменные объявленные ковариатами. Альтернативой здесь являются прогрессивная и обратная селекции. В случае наличия лишь одной ковариаты, как в указаном примере, для расчёта подходит только предварительно установленный метод.
Кнопка Select» (Выбрать) предоставляет возможность отбора определённых случаев для дальнейшего анализа.
Используя кнопку Categorical... (Категориальные) Вы можете подготовить для расчета категориальные переменные (то есть переменные, принадлежащие к номинальной шкале). На этом мы остановимся более подробно, рассматривая второй пример.
При помощи кнопки Save... (Сохранить) Вы можете добавить в файл дополнительные переменные; активируйте к примеру в разделе Predicted Values (Спрогнозированные значения) предварительные установки Probabilities (Вероятности) и Принадлежность к группе.
Нажав на кнопку Options... (Опции), Вы сможете организовать вывод дополнительных статистических характеристик, различных диаграмм и произвести некоторые дополнительные установки. В данном расчёте мы этого делать не будем.
-
Начните расчёт нажатием ОК.
Наиболее важные результаты приведены в нижеследующей таблице, причём в 10 версии SPSS они уже выводятся в новой табличной форме.
Omnibus Tests of Model Coefficients (Универсальный критерий коэффициентов модели)
Chi-square (Хи-квадрат) | Df | Sig. (Значимость) | ||
Step 1 (ШаМ) 1 | Step (Шаг) | 18,789 | 1 | ,000 |
Block (Блок) | 18,789 | 1 | ,000 | |
Model (Модель) | 18,789 | 1 | ,000 |
Model Summary (Сводная таблица модели)
Step (Шаг) | -2 Log likelihood (-2 логарифмическое правдоподобие) | Сох & Snell R Square (R-квадрат Кокса и Шнела) | R Square Nadelkerkes (R-квадрат Наделькеркеса) |
1 | 43,394 | ,341 | ,456 |
Качество приближения регрессионной модели оценивается при помощи функции подобия. Мерой правдоподобия служит отрицательное удвоенное значение логарифма этой функции (-2LL). В качестве начального значения для -2LL применяется значение, которое получается для регрессионной модели, содержащей только константы. После добавления переменной влияния tzell значение -2LL равно 43,394; это значение на 18,789 меньше, чем начальное. Подобное снижение величины означает улучшение; разность обозначается как величина хи-квадрат и является очень значимой.
Это означает, что начальная модель после добавления переменной tzell претерпела значительное улучшение. Если при наличии некоторого количества независимых переменных анализ производится не при помощи метода вложения, а пошаговым образом, то получающиеся изменения отображаются в разделах "Блок" и "Шаг". При этом, если Вы производили ввод переменных в блочной форме, то показатель в разделе "Блок" приобретает особое значение.
Два других выведенных показателя, названные именами Кокса & Шела и Наделькеркеса, являются мерами определённости. Они также как и при линейной регрессии указывают на ту часть дисперсии, которую можно объяснить с помощью логистической регрессии. Мера определённости по Коксу и Шелу имеет тот недостаток, что значение равное 1 является теоретически не достижимым; этот недостаток устранен благодаря модификации данной меры по методу Наделькеркеса. Часть дисперсии, объяснимой с помощью логистической регрессии, в данном примере составляет 45,6 %.
Далее приводится классификационная таблица, в которой наблюдаемые показатели принадлежности к группе (1 = болен, 2 = здоров) противопоставляются предсказанным на основе рассчитанной модели.
Classification Table (Классификационная таблица) а
Observed (Наблюдаемый показатель) | Predicted (Спрогнозировано) | ||||
GRUPPE (Группа) | Percentage Correct (Процентный показатель верных показателей) | ||||
Krank (болен) | Gesund (здоров) | ||||
Шаг 1 | GRUPPE (Группа) | Krank (болен) | 18 | 6 | 75,0 |
| Gesund (здоров) | 4 | 17 | 81,0 | ||
| Overall Percentage (Суммарный процентный показатель) |
| 77,8 | |||
a. The cut value is ,500 (Разделительное значение равно ,500)
Из таблицы можно сделать вывод о том, что из общего числа больных, равного 24, тестом были признаны таковыми только 18 (в медицинской диагностике в таких случаях говорят о "строго положительных" результатах). Остальных 6 называют "ложно отрицательными"; они были признаны тестом здоровыми, хотя и являются больными. Из общего числа здоровых, равного 21, тестом были признаны таковыми только 17 ("строго отрицательные"), 4 признаны больными, хотя они и являются здоровыми ("ложно положительные"). В общем, правильно были распознаны 35 случаев из 45, это составляет 77,8 %.
В заключении выводятся результаты о рассчитанных коэффициентах и проверке их значимости:
Variables in the Equation (Переменные в уравнении)
|
| В (Коэф-фициент регрессии В) | S.E. (Стандарт- ная ошибка) | Wald (Вальд) | df | Sig. (Значи-мость) | Ехр (В) |
Step 1 (Шаг 1)а | TZELL | ,278 | ,082 | 11,599 | 1 | ,001 | 1,321 |
| Constant (Константа) | -19,005 | 5,587 | 11,571 | 1 | ,001 | ,000 |
a. Variable(s) entered on step 1: TZELL (Переменные, введенные на шаге 1: TZELL)
Проверка значимости отличия коэффициентов от нуля, проводится при помощи статистики Вальда, использующей распределение хи-квадрат, которая представляет собой квадрат отношения соответствующего коэффициента к его стандартной ошибке.
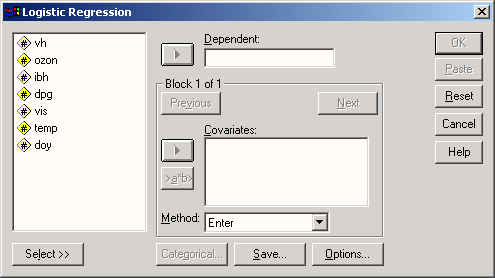
В приведенном примере получились сверх значимые коэффициенты а = -19,005 bt = 0,278. При помощи этих двух значений коэффициентов мы можем для каждого значения Т-типизации рассчитать вероятность р. К примеру, для некоего обследуемого со значением Т-типизации 72 получим
z= - 19,005+ 0,278x72= 1,018
и таким образом
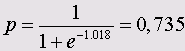
Рассчитанная вероятность р всегда указывает на исполнение предсказании, которое соответствует большей из двух кодировок зависимых переменных, в данном случае — на исполнение предсказания "здоров". Следовательно, рассматриваемый человек является здоровым с вероятностью 0,735.
Рассчитанная вероятность для всех случаев и связанная с ней принадлежность к группе кодировка 1 для болен и 2 для здоров) добавлены к файлу под именами рге_1 и pgr_l.
Теперь подключим к нашему анализу тест LAI. Дополнительно к переменной tzell теперь в поле ковариат поместите и переменную lai.
Расчёт выдаст сначала заметно снизившееся значение -2LL (хи-квадрат = 25,668) и следующую классификационную таблицу. Доля правильно спрогнозированных диагнозов незначительно выросла (с 77,8 % до 80,0 %).
Classification Table (Классификационная таблица)а
|
Observed (Наблюдаемый показатель) |
Predicted (Спрогнозировано) |
||||
|
Группа |
Percentage Correct (Процентный показатель верных показателей) |
||||
| Krank (болен) | Gesund (здоров) | ||||
|
Шаг 1 |
GRUPPE (Группа) | Krank (болен) |
20 |
4 |
83,3 |
| Gesund (здоров) |
5 |
16 |
76,2 |
||
| Overall Percentage (Суммарный процентный показатель) |
80,0 |
||||
а. The cut value is ,500 (Разделительное значение равно ,500)
Количество ложно отрицательных диагнозов снизилось на 2, а количество ложно положительных повысилось на 1. Для коэффициентов получим:
Variables in the Equation (Переменные в уравнении)
|
| В (Коэф0 фициент регрессии В) | S.E. Стандартная ошибка) | Wald (Вальд) | df | Sig. (Значи0 мость) | Ехр (В) |
Stepl (UJarlf | TZELL | ,201 | ,094 | 4,574 | 1 | 0,32 | 1,222 |
LAI | 2,205 | ,877 | 6,324 | 1 | ,012 | 9,074 | |
Constant (Константа) | -14,645 | 6,328 | 5,356 | 1 | ,021 | ,000 |
a. Variable(s) entered on step 1: TZELL, LAI. (Переменные, вводимые на шаге 1: TZELL, LAI)
Для обследуемого с типизированным числом Т-клеток равным 72 получилась вероятность оказаться здоровым р = 0,735. Если в дополнении к этому и тест LAI отрицателен (кодировка 1), то эта же вероятность рассчитывается следующим образом:

Вероятность, оказаться здоровым, при наличии данных уже двух диагностических методов значительно возросла.
Ещё один пример из области медицины, теперь уже с большим количеством независимых переменных, должен помочь нам разобраться в пошаговом методе анализа. Кроме того, в состав независимых переменных будет включена категориальная переменная.
Для данного примера в некоторой клинике со специальными автоматизированными методиками лечения были накоплены данные о пациентах с тяжёлыми (или даже смертельными) повреждениями лёгких. Из большого количества переменных были выбраны следующие:
Имя переменной | Расшифровка |
out | Исход (0 = скончался, 1 = выздоровел) |
alter (возраст) | Возраст |
bzeit | Время проведения искусственного дыхания в часах |
kob | Концентрация кислорода в воздушной массе для искусственного |
дыхания | |
адд | Интенсивность искусственного дыхания |
gesch (пол) | Пол (1 = мужской, 2 = женский) |
gr | Рост |
ursache (причина) | Причина повреждения лёгких (1 = несчастный случай, 2 = воспаление лёгких, 3 = прочее) |
Наряду с переменной out (исход), имеются переменные, при первом же взгляде на которые можно понять, что они с ней связаны. Причина повреждения лёгких является категориальной переменной, которая перед проведением анализа должна быть преобразована в несколько дихотомических переменных (к примеру, несчастный случай: да — нет).
Вопрос, на который нам предстоит найти ответ, звучит так: какое влияние на вероятность выздоровления оказывают отобранные переменные.
-
Откройте файл lunge.sav.
-
После выбора соответствующего меню в диалоговом окне Logistic Regression (Логистическая регрессия) переменной out присвойте статус независимой переменной, а всем остальным (кроме пг) присвойте статус ковариат. Здесь, как и при множественной линейной регрессии, ввод ковариат Вы можете производить по блокам.
Из-за вовлечения в анализ большого количества переменных компьютер должен решить, какие из них в конечном случае будут отобраны для использовании в уравнении вероятности. Поэтому здесь должен быть выбран не метод вложения, который включает в расчёт все переменные, а один из пошаговых методов.
Метод прямой селекции начинается с использования одних лишь констант на стартовом этапе , а затем последовательно подключаются переменные, которые демонстрируют сильную корреляцию с зависимыми переменными. Далее опять следует проверка того, какие переменные должны быть исключены, причём в качестве критерия проверки выбирается либо статистика Вальдовского (Wald), либо функция правдоподобия, либо один из вариантов, называемых "условной статистикой" (которые, однако, не рекомендуются). Метод обратной селекции сначала берёт в расчёт все переменные, а затем в обратном порядке происходит исключение малозначимых переменных.
-
Выберите в качестве метода Forward: LR (Прямой:LR) и щёлкните на кнопке Categorical... (Категориальные), чтобы поместить переменную ursache в поле, предусмотренное для категориальных ковариат.
Количество образовываемых "фиктивных" дихотомических переменных должно быть всегда на 1 меньше, чем число количество заданных категорий. Категория, оказавшаяся лишней, называется эталонной категорией и, в соответствии с предварительными установками, является последней категорией. При помощи поля контрастов Contrast) Вы можете управлять особенностями вовлечения в анализ образованных Фиктивных переменных; при контрасте равном Deviation (Отклонение) все категории кроме эталонной будут проверяются относительно суммарного эффекта.
-
Установите контраст Deviation (Отклонение) и при помощи щелчка на Continue (Далее) вернитесь в исходное диалоговое окно.
-
Начните расчёт нажатием ОК.
Вы можете проследить, какие переменные вовлекаются в анализ и как улучшается вероятность прогноза после вовлечения каждой новой переменной. На завершающей стати анализа присутствуют четыре переменные, а именно: возраст, время проведения искусственного дыхания, рост и концентрация кислорода в воздушной массе для искусственного дыхания.
Точность исполнения прогноза, которая достигается при использовании этих четыpex переменных, составляет 71,0 %; её можно увидеть в нижеследующей классификанионной таблице на стр 25.
Classification Table (Классификационная таблица)а
| Observed (Наблюдаемый показатель) | Predicted (Спрогнозировано) | ||||
| Outcome (Исход) | Percentage Correct (Процентный показатель верных прогнозов) | ||||
| gestorben (скончался) | ueberlebt (выздоровел) | ||||
|
Step 1 (Шаг)
|
Outcome (Исход) | gestorben (сконча-лся) | 29 | 34 | 46,0 |
| ueberlebt (выздоро- вел) | 14 | 54 | 79,4 | ||
| 63,4 | |||||
| Overall Percentage (Суммарный процентный показатель) | |||||
|
Step 2 Шаг 2)
|
Outcome (Исход) | gestorben (сконча- лся) | 32 | 31 | 50,8 |
| ueberlebt (выздоро- вел) | 16 | 52 | 76,5 | ||
| 64,1 | |||||
| Overall Percentage (Суммарный процентный показатель) | |||||
| StepS (Шаг 3) | Outcome (Исход) | gestorben (сконча- лся) | 33 | 30 | 52,4 |
| ueberlebt (выздоро- вел) | 19 | 49 | 72,1 | ||
| Overall Percentage (Суммарный процентный показатель) | 62,6 | ||||
| Step 4 (Шаг 4) | Outcome (Исход) | gestorben (сконча-лся) | 37 | 26 | 58,7 |
| ueberlebt (выздоро- вел) | 12 | 56 | 82,4 | ||
| 71,0 | |||||
| Overall Percentage (Суммарный процентный показатель) | |||||
a. The cut value is ,500 (Разделительное значение равно ,500)
Прогноз оправдался для 58,7 % умерших пациентов и для 82,4 % выздоровевших. Значения коэффициента Ь. и константы а для расчёта вероятности (выздоровления) находятся в следующей таблице:
Variables in the Equation (Переменные в уравнении)
В Коэф-фициент регрессии В) | S.E. (Стандар-тная ошибка) | Wald (Валь-довский) | df | Sig. (Значи- мость) | Ехр (В) | ||
Шаг 1а | BZEIT | -,081 | ,028 | 8,482 | 1 | ' ,004 | ,922 |
Конста- нта | 1,104 | ,385 | 8,205 | 1 | ,004 | 3,017 | |
Шаг 2b | GR | ,038 | ,017 | 5,109 | 1 | ,024 | 1,039 |
BZEIT | -,073 | ,028 | L 6,688 | 1 | ,010 | ,930 | |
Конста- нта | -5,460 | 2,924 | L 3,487 | 1 | ,062 | ,004 | |
Шаг 3c | КОВ | -2,678 | 1,264 | 4,489 | 1 | ,034 | ,069 |
GR | ,037 | ,017 | 4,622 | 1 | ,032 | 1,038 | |
BZEIT | -,077 | ,029 | 6,866 | 1 | ,009 | ,926 | |
Конста- нта | -2,995 | 3,192 | ,880 | 1 | ,348 | ,050 | |
Шаг 4d | ALTER (возраст) | -.037 | ,017 | 4,653 | 1 | ,031 | ,963 |
КОВ | -3,028 | 1,302 | 5,410 | 1 | ,020 | ,048 | |
GR | ,044 | ,017 | 6,650 | 1 | ,010 | 1,045 | |
BZEIT | -,062 | ,029 | 4,639 | 1 | ,031 | ,940 | |
Конста- нта | -2,884 | 3,079 | ,877 | 1 | ,349 | ,056 |
a. Variable(s) entered on step 1: BZEIT. (Переменные, вводимые на шаге 1: BZEIT.)
b. Variable(s) entered on step 2: GR. (Переменные, вводимые на шаге 2: GR.)
с. Variable(s) entered on step 3: КОВ. (Переменные, вводимые на шаге 3: КОВ.)
d. Variable(s) entered on step 4: ALTER. (Переменные, вводимые на шаге 4: ALTER.)
Если мы рассмотрим случай с 30-тилешим пациентом, с ростом 180 см, которому делали искусственное дыхание в течении 10 часов при концентрации кислорода в смеси равной 0,7, то исходя из соотношения
z= - 2,884- 0,037x30- 0,062x10+ 0,044x180- 3,028x0,7= 1,12В получим вероятность выздоровления
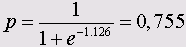
следовательно, вероятность выздоровления пациента равна 0,755
21.gif
22.gif
23.gif

16.5 Мультиномиальная логистическая регрессия
16.5 Мультиномиальная логистическая регрессия
Этот метод является вариантом логистической регрессии, при которой зависимая переменная не является дихотомической, как при бинарной логистической регрессии, а имеет больше двух категорий. В то время как, при бинарной логистической регрессии независимая переменная может иметь интервальную шкалу, то мультиномиальная логистическая регрессия пригодна только для категориальных независимых переменных, причём имеет значение, относятся ли они к шкале наименований или к порядковой шкале. Конечно же, не исключается возможность задания в качестве ковариат переменных, имеющих интервальную шкалу.
Начиная с 10 версии SPSS для независимых переменных, относящихся к порядковой шкале предусмотрен метод порядковой регрессии (см. гл. 16.6), который в данном случае является предпочтительным.
Для представления метода мольтиномиальной логистической регрессии был сначала взят простой пример с одной независимой переменной. Данные для этого примера "ыли взяты из ALLBUS (общий социологический опрос населения) 1998 года.
-
Откройте файл polein.sav, и при помощи выбора меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты)
достройте частотные таблицы для четырёх переменных, находящихся в этом файле:
Alter (Возраст)
| Frequency (Частота) | Percent (Процент) | Valid Percent (Действи- тельный процент) | Cumulative Percent (Совокупный процент) | |
Valid (Действи- тельное значение) | bis 45 Jahre (До 45 лет) | 1306 | 50,1 | 50,1 | 50,1 |
ueber 45 Jahre (Свыше 45 лет) | 1301 | 49,9 | 49,9 | 100,0 | |
Total (Сумма) | 2607 | 100,0 | 100,0 |
| |
Politische Links-Rechts-Einschaetzung (Политическая принадлежность к левым или правым)
| Frequency (Частота) | Percent (Процент) | Valid Percent (Действи- тельный процент) | Cumulative Percent (Совокупный процент) | |
Valid (Действи- тельное значение) | eher links (Скорее левый) | 740 | 28,4 | 28,4 | 28,4 |
Mitte (Центрист) | 1212 | 46,5 | 46,5 | 74,9 | |
eher rechts (Скорее правый) | 655 | 25,1 | 25,1 | 100,0 | |
Total (Сумма) | 2607 | 100,0 | 100,0 |
| |
Schicht (Прослойка)
Frequency (Частота) | Percent (Процент) | Valid Percent (Действи- тельный процент) | Cumulative Percent (Совокупный процент) | ||
Valid (Действи- тельное | Unterschicht (Нижняя прослойка) | 879 | 33,7 | 33,7 | 33,7 |
значение) | Mittelschicht (Средняя прослойка) | 1477 | 56,7 | 56,7 | 90,4 |
| Oberschicht (Верхняя прослойка) | 251 | 9,6 | 9,6 | 100,0 |
| Total (Сумма) | 2607 | 100,0 | 100,0 |
|
Schulbildung (Школьное образование)
Frequency (Частота) | Percent (Процент) | Valid Percent (Действи- тельный процент) | Cumulative Percent (Совокупный процент) | ||
Valid (Действи- тельное значение) | Hauptschule (Неполное среднее) | 1499 | 57,5 | 57,5 | 57,5 |
Mittlere Reife (Среднее) | 610 | 23,4 | 23,4 | 80,9 | |
Abitur (Атестат зрелости) | 498 | 19,1 | 19,1 | 100,0 | |
Total (Сумма) | 2607 | 100,0 | 100,0 |
| |
Мы хотим рассмотреть переменную polire (Политическая принадлежность к левым или правым) как зависимую переменную, а три остальные — как независимые переменные (факторы). В первом примере в качестве независимой переменной мы возьмем только переменную "Alter" (Возраст). Прежде всего построим таблицу сопряженности для этих двух переменных.
-
Выберите в меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
Переменной alter присвойте статус строчной переменной, a polire — столбцовой переменной, и через выключатель Cells... (Ячейки) активируйте вывод процентных показателей для ячеек.
Alter * Politische Links-Rechts-Einschfltzung Crosstabulation
(Возраст * Политическая принадлежность к левым или правым - таблица сопряженности)
| Politische Links-Rechts-Einschfltzung (Политическая принадлежность к левым или правым) | Total (Сумма) | ||||
eher links (Скорее левый) | Mitte (Цент- рист) | eher rechts (Скорее правый) | ||||
Alter (Воз-раст) | bis 45 Jahre (До 45 лет) | Count (Коли- чество) | 446 | 615 | 245 | 1306 |
| % of Total (% от возраста) | 34,2% | 47,1% | 18,8% | 100,0% | ||
ueber 45 Jahre (Свыше 45 лет) | Count % of Total (Коли- чество) | 294 | 597 | 410 | 1301 | |
| (% от возраста) | 22,6% | 45,9% | 31,5% | 100,0% | ||
Total (Сум- ма) | Count (Коли- чество) | 740 | 1212 | 655 | 2607 | |
| % of Total (% от возраста) | 28,4% | 46,5% | 25,1% | 100,0% | ||
Для младшей возрастной категории политическое самоопределение имеет тенденцию склонения симпатий к левым партиям, а для старшей — скорее к правым. Рассмотрим простую мультиномиальную логистическую модель, которая отражает взаимосвязь между политическим самоопределением и возрастом.
Так как политическое самоопределение, как зависимая переменная, включает три категории, то для определения вероятностей отнесения респондентов к этим трем категориям можно сформировать два недублированных логита, причём последняя категория "eher rechts" (скорее правый) будет использоваться как эталонная:
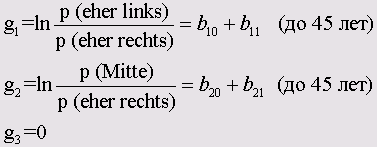
Нахождение коэффициентов b10, b11, b20 и b21 (называемых параметрическими оценками) и является основной задачей мультиномиальной логистической регрессии. Первая цифра индекса указывает на номер логита, а вторая на порядковый номер коэффициента в данном логите, причём цифра 0 на второй позиции индекса означает константу, за которой далее следует ровно столько коэффициентов, сколько независимых переменных (факторов) взято в рассмотрение. Коэффициентам последней (эталонной) категории присваивается значение 0.
Переменная Alter (Возраст), как единственная независимая переменная, имеет две категории, одна из которых рассматривается как эталонная, ее коэффициенты принимаются равными 0.
-
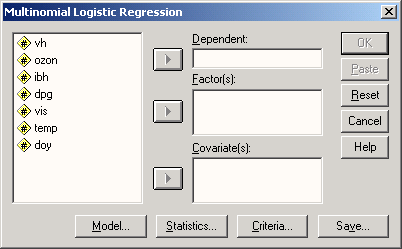
Выберите в меню Analyze (Анализ) Regression ...(Регрессия) Multinomial Logistic... (Мультиномиальная логистическая)
Откроется диалоговое окно Multinomial Logistic Regression (Мультиномиальная логистическая регрессия).
-
Переменную polire поместите в поле для зависимых переменных, а переменную alter (возраст) в поле для факторов и нажмите выключатель Statistics (Статистики).
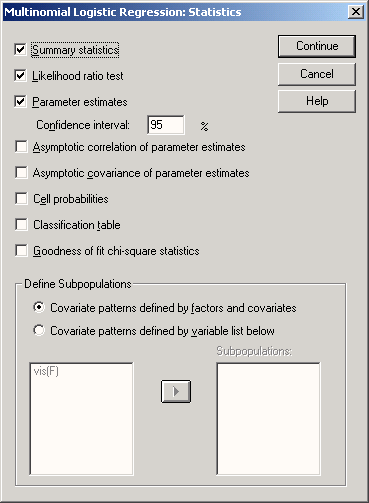
Откроется диалоговое окно Multinomial Logistic Regression: Statistics (Мультиномиальная логистическая регрессия: Статистики)
-
Оставьте активированным вывод параметрических оценок с доверительным интервалом соответствующим 95 % и покиньте это диалоговое окно нажатием Далее и ОК.
Рис. 16.17: Диалоговое окно Multinomial Logistic Regression (Множественная логистическая регрессия)
Рис. 16.18: Диалоговое окно Multinomial Logistic Regression: Statistics (Множественная логистическая регрессия: Статистики)
Содержание таблицы результатов расчёта, выглядит следующим образом. Для не дублирующих категорий она содержит параметрические оценки, стандартную ошибку, проверку значимости при помощи статистики Вальда, значение экспоненциальной функции от параметрической оценки и его доверительный интервал.
Parameter Estimates (Оценки параметров)
Politische Links-Rechts-Einschaetzung (Политическая принадлежность к левым или правым) | В | Std. Error (Станда- ртная ошибка) | Wald (Вальд) | df (Сте-пень сво- боды) | Sig. (Значи- мость) | Ехр(В) | 95% Confidence Interval for Ехр(В) (95 % довери- тельный интервал для Ехр(В)) | ||
Lower Bound (Нижний предел) | Upper Bound (Верхний предел) | ||||||||
eher links (Скорее левый) | Intercept (Постоян- ное слага- емое) | -,333 | ,076 | 18,938 | 1 | ,000 |
|
|
|
[ALTER= 1,00] | ,932 | ,110 | 71,353 | 1 | ,000 | 2,539 | 2,045 | 3,151 | |
[ALTER= 2,00] | Оа | 0 |
| 0 |
| , |
|
| |
Mitte (Цен-трист) | Intercept (Постоян- ное слага-емое) | ,376 | ,064 | 34,320 | 1 | ,000 |
|
|
|
[ALTER= 1,00] | ,545 | ,099 | 30,198 | 1 | ,000 | 1,724 | 1,420 | 2,094 | |
rALTER= 2,00] | 0" | 0 |
| 0 |
|
|
|
| |
a. This parameter is set to zero because it is redundant (Данный параметр обнуляется, т.к. он является дублирующим)
Из таблицы можно взять следующие значения для b-коэффициентов:
b10 =-0,333
b11 (до 45 лет) = 0,932
b20 = 0,376
b21 (до 45 лет) = 0,545 1
Таким образом, для возрастной группы до 45 лет получим
g1 = -0,333 + 0,932 = 0,599
g2 = -0,376 + 0,545 = 0,921
и следовательно
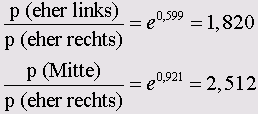
Для дублирующего логита по правилам вычисления логарифма справедливо
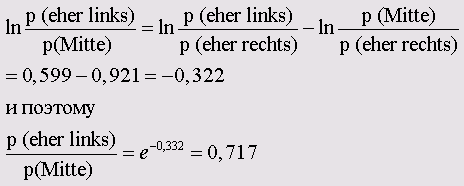
К примеру, в возрастной категории до 45 лет вероятность быть более склонным к тевым течениям в 1,820 раз выше вероятности склонности к правым течениям. Такой же расчёт можно произвести и для другой возрастной категории; в данном случае будут отсутствовать коэффициенты b11 и b21, т.к. они приравниваются к нулю.
Следует отметить, что прямое определение вероятности для трёх категорий политической самооценки, интересней, чем соотношение этих вероятностей между собой. Для каждой i-ой категории зависимых переменных эта вероятность может быть вычислена по следующей формуле:
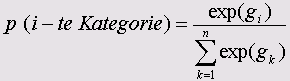
Здесь для большей удобочитаемости экспоненциальная функция обозначена как ехр. n указывает на число категорий (здесь n=3).
Для возрастной группы до 45 лет для трёх категорий политической самооценки получатся следующие вероятности:
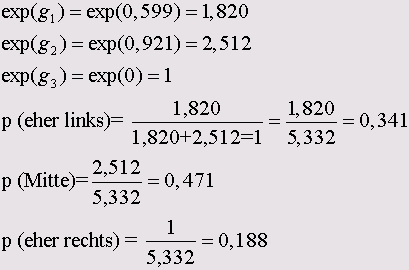
Стало быть, для отдельного человека, принадлежащего к возрастной группе до 45 лет вероятность склонения политической самооценки в сторону левых составляет, 0,341 или 34,1 %, в сторону центристов 47,1 % и в сторону правых 18,8 %. Внимательный читатель может заметить, что эти числа соответствуют процентным показателям таблицы сопряженности для возраста и политической самооценки. Таким образом, в случае наличия лишь одной независимой переменной легко удостовериться в правдоподобности расчётов, производимых при мультиномиальной логистической регрессии.
Для возрастной группы свыше 45 лет расчёты будут выглядеть следующим образом:
g1 = - 0,333 + 0 = - 0,333
g2 = 0,376 + 0 = 0,376
gз=0
ехр (g1) - ехр (-0,333) = 0,717
ехр (g2). ехр (0,376) = 1,456
ехр (g3) = ехр (0) = 1
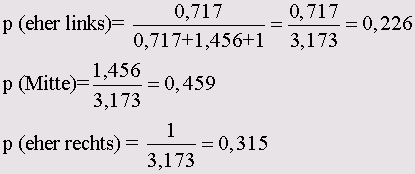
Если выразить полученные показатели в процентах, то и здесь так же наблюдается полное согласование с соответствующими процентными показателями таблицы сопряженности.
Следует отметить, что только в случае наличия лишь одной независимой переменной, как в приведённом примере, проведение расчёта с применением столь громоздкого метода, как многозначная логистическая регрессия, является достаточно бессмысленным — все соотношения могут быть выяснены проще, при помощи таблиц сопряженности. Поэтому мы введем в рассмотрение ещё одну дополнительную переменную — переменную schule (образование).
-
В диалоговом окне Multinomial Logistic Regression (Мультиномиальная логистическая регрессия) поместите переменную schule вместе с переменной alter в поле факторов.
-
В диалоговом окне Multinomial Logistic Regression: Statistics (Мультиномиальная логистическая регрессия: Статистики) активируйте дополнительные опции Cell probabilities (Вероятность по ячейкам) и Likelihood ratio test (Тест отношения правдоподобия) и начните расчёт вновь.
Таблица теста коэффициентов правдоподобия содержит изменения функции правдоподобия для случая, когда исключается соответствующий главный действующий фактор; эти изменения выражаются через соответствующие значения теста %2 (хи-квадрат). Выдаваемый уровень значимости р < 0,001 указывает на то, что оба фактора (возраст и школьное образование) оказывают очень значимое влияние на зависимую переменную (политическая самооценка).
Model Fitting Information (Информация о приближении, обеспечиваемой моделью)
Model (Модель) | -2 Log likelihood (-2 логарифми- ческое правдопо- добие) | Chi-square (Хи-квадрат) | df (степень свободы) | Sig. (Значи- мость) |
Intercept Only (Только постоянное слагаемое) | 252,208 | |||
Final (Оконча- тельно) | 93,429 | 158,779 | 6 | ,000 |
Likelihood Ratio Tests (Тест отношения правдоподобия)
(Результат) | -2 Log Likelihood of Reduced Model (-2 логарифми-ческое правдоподобие для сокращённой модели) | Chi-square (Хи-квадрат) | df (Степень свободы) | Sig. (Значи- мость) |
Intercept (Постоянное слагаемое) | 93,429 | ,000 | 0 | • |
ALTER (Возраст) | 171,496 | 78,067 | 2 | ,000 |
SCHULE (Образо- вание) | 178,489 | 85,060 | 4 | ,000 |
The chi-square statistic is the difference in -2 tog-likelihoods between the final model :-~d a reduced model. The reduced model is formed by omitting an effect from the final model. The null hypothesis is that all parameters of that effect are 0 (Статистика хи-квадрат отображает различие -2 логарифмического правдоподобия между окончательной моделью и усеченной моделью. Суть расчёта усеченной модели сводится к тому, что из окончательной модели исключается один фактор влияния.
Нулевая гипотеза соответствует обнулению всех параметров параметрических оценок данного фактора влияния).
Таблица (b — коэффициентов) выглядит следующим образом.
Parameter Estimates (Оценки параметров) | |||||||||
Politische Links-Rechts-Einschaetzung Политическая принадлежность к левым пли правым) | В | Std. Error (Стан- дартная ошибка) | Wald (Вальд) | df (Сте-пень сво-боды) | Sig. (Значи- мость) | Exp (В) | 95% Confidence Interval for Exp(B) (95 % довери- тельный интервал для Ехр(В)) | ||
Lower Bound (Ниж-ний пре-дел) | Upper Bound (Верх-ний пре-дел) | ||||||||
eher links (Ско- рее левый) | (Посто-янное слага-емое) | -,129 | ,137 | ,8feO | 1 | ,345 |
|
|
|
[ALTER= 1,00] | ,952 | ,117 | 66,600 | 1 | ,000 | 2,591 | 2,061 | 3,256 | |
ALTER= 2,00] | Oa | 0 |
| 0 |
| , | , |
| |
SCHULE= 1,00] | -,179 | ,142 | ,592 | 1 | ,207 | ,836 | ,632 | 1,104 | |
SHULE= 2,00] | -,480 | ,158 | 9,249 | 1 | ,002 | ,619 | ,454 | ,843 | |
[SHULE= 3,00] | 0" | 0 | l | 0 |
| , | , |
| |
Mine (Цент-рист) | (Постоян-ное слага-емое) | -,236 | ,137 | 2,982 | 1 | ,084 |
|
|
|
[ALTER= 1,00] | ,766 | ,106 | 52,174 | 1 | ,000 | 2,152 | 1,748 | 2,939 | |
[ALTER= 2,00] | Oa | 0 |
| 0 | , |
|
|
| |
[SCHULE= 1,00] | ,802 | ,141 | 32,539 | 1 | ,000 | 2,231 | 1,693 | 2,939 | |
[SHULE= 2,00] | ,149 | ,155 | ,922 | 1 | ,337 | 1,161 | ,856 | 1,574 | |
[SHULE= 3,00] | Oa | 0 | , | 0 | , | , | , | , | |
a. This parameter is set to zero because it is redundant (Данный параметр обнуляется, так как он является дублирующим)
В качестве примера определим вероятности для политической самооценки отдельного человека, принадлежащего к возрастной группе свыше 45 лет с неполным средним образованием. Для этого по аналогии с предыдущим примером произведём следующие вычисления:
g1 = - 0,129 + 0 - 0,179= - 0,308
g2 = - 0,236 + 0 + 0,802 = 0,566
gз= 0
exp (g1) = 0,735
exp (g2) = 1,761
exp (g3) - 1
Если перевести данные результаты в процентные показатели, то они будут означать, что среди граждан в возрасте свыше 45 лет с неполным средним образованием 21,0 % симпатизируют левым политическим течениям, 28,6 % правым, а 50,4 % остаются по центру.
Нет необходимости вычислять процентные показатели вероятностей самостоятельно. Вы можете взять их из следующей таблицы, отображающей наблюдаемые и прогнозируемые частоты:
Observed and Predicted Frequencies (Наблюдаемые и прогнозируемые частоты) | |||||||
Schulb-ildung (Образо- вание) | Alter (Возраст) | Politische Links-Rechts-Einschfltzung (Политическая левая или правая принадлежность) | Frequency (Частота) | Percentage (Процент) | |||
Observed (Наблю-даемая) | Predicted (Прогно-зируемая) | Pearson Residual (Остаток Пирсона) | Observed (Набл-юдаемый) | Predicted (Прогно-зируемый) | |||
Haupt- schule (Непол-ное среднее) | bis 45 Jahre (До 45 лет) | eher links (Скорее левый) | 143 | 157,488 | -1,365 | 25,8% | 28,4% |
Mitte (Центрист) | 312 | 313,760 | -,151 | 56,3% | 56,6% | ||
eher rechts (Скорее правый) | 99 | 82,752 | 1,937 | 17,9% | 14,9% | ||
ueber 45 Jahre(Свыше 45 лет) | eher links (Скорее левый) | 213 | 198,512 | 1,157 | 22,5% | 21,0% | |
Mitte (Центрист) | 478 | 476,240 | ,115 | 50,6% | 50,4% | ||
eher rechts (Скорее правый) | 254 | 270,248 | -1,170 | 26,9% | 28,6% | ||
Mifflere Reife (Сред-нее) | bis 45 Jahre (до 45 лет) | eher links (Скорее левый) | 129 | 131,561 | -,271 | 31,5% | 32,2% |
Mitte (Центрист) | 192 | 184,113 | ,784 | 46,9% | 45,0% | ||
eher rechts (Скорее правый) | 88 | 99,326 | -,628 | 21,5% | 22.8% | ||
ueber 45 Jahre(Свыше 45 лет) | eher links (Скорее левый) | 47 | 44,439 | ,435 | 23,4% | 22.1% | |
Mitte (Центрист) | 67 | 74,887 | -1,151 | 33,3% | 37,3% | ||
eher rechts (Скорее правый) | 87 | 81,674 | ,765 | 43,3% | 40,6% | ||
Abitur (Аттестат зрелости) | bis 45 Jahre (до 45 лет) | eher links (Скорее левый) | 174 | 156,952 | 1,848 | 50,7% | 45,8% |
Mitte (Центрист) | 111 | 117,127 | -,698 | 32,4% | 34,1% | ||
eher rechts (Скорее правый) | 58 | 68,922 | -1,472 | 16,9% | 20,1% | ||
ueber 45 Jahre(Свыше 45 лет) | eher links (Скорее левый) | 34 | 51,048 | -2,914 | 21,9% | 32,9% | |
Mitte (Центрист) | 52 | 45,873 | 1,078 | 33,5% | 29,6% | ||
eher rechts (Скорее правый) | 69 | 58,078 | 1,812 | 44,5% | 37,5% | ||
The percentages are based on total observed frequencies in each subpopulation (Процентные показатели основываются на наблюдаемых суммарных частотах для каждой частичной совокупности).
Теперь вы можете видеть, что наблюдаемые и прогнозированные значения оказались рассогласованными. Это произошло потому, что теперь в модель входят только главные факторы влияния, а не взаимодействия.
-
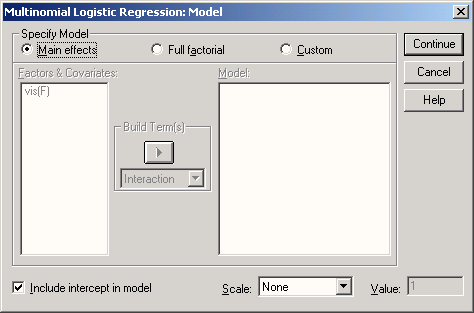
Чтобы это изменить, в диалоговом окне Multinomial Logistic Regression (Мультиномиальная логистическая регрессия) задействуйте выключатель Model (Модель).
Откроется диалоговое окно Multinomial Logistic Regression: Model (Мультиномиальная логистическая регрессия: Модель).
Вы можете включить в расчёт все главные факторы влияния и взаимодействия, если вместо предварительно установленной по умолчанию опции Main effects (Основные эффекты) активируете опцию Full factorial (Полнофакторная модель). При помощи опции Custom (Пользовательский режим), Вы можете отобрать включаемые в расчёт факторы влияния.
-
Активируйте опцию Full factorial (Полнофакторная модель) и начните расчёт вновь.
В таблице оценки параметра теперь находятся и взаимодействия. Если Вы обратите внимание на наблюдаемые и ожидаемые частоты, то заметите, что теперь они совпадают.
Рис. 16.19: Диалоговое окно Multinomial Logistic Regression: Model (Множественная логистическая регрессия: Модель)
-
Постройте самостоятельно ещё одну логистическую регрессию, в которой Вы можете взять .переменную schicht (Принадлежность к прослойке) в качестве третьего фактора.
25.gif
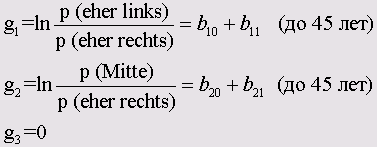
26.gif
27.gif
28.gif
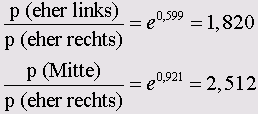
29.gif
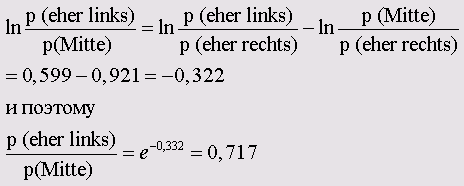
30.gif
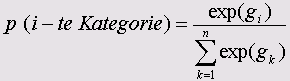
31.gif
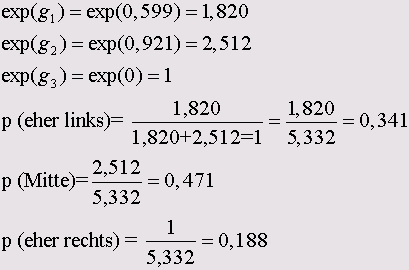
32.gif
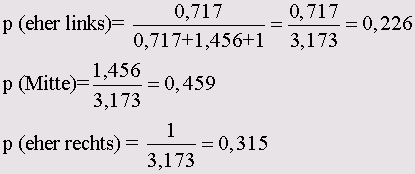
33.gif
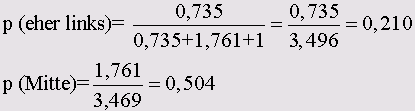
35.gif
16.6 Порядковая регрессия
16.6 Порядковая регрессия
В то время как, мультиномиальная регрессия, представленная в разделе 16.5, предназначена для зависимой переменной, относящейся к номинальной шкале, то порядковая регрессия предназначена для целевой переменной, принадлежащей к порядковой шкале. Независимые переменные и здесь должны быть категориальными (то есть иметь номинальную или порядковую шкалу), однако в качестве ковариат допускается применение переменных с интервальной шкалой.
Мы изучим данный метод при помощи примера из области психологии. В главе 19.3 будет рассматриваться "Анкета о специфике лечения психических заболеваний в больнице Фрайбурга", которая дает представление о работе с пациентами на основании 35 отдельных пунктов. К примеру, восприимчивость пациента к целенаправленным лечебным действиям выясняется при помощи пункта "Разработать план и затем приступить к его воплощению", причём ответ даётся в соответствии с пятибалльной шкалой: от "абсолютно не верно" (кодировка 1) до "абсолютно верно" (кодировка 5).
Эта типичная порядковая переменная должна быть исследована в зависимости от возраста, пола, продолжительности болезни и образования. Значения приведенных переменных были собраны в отношении 85 пациентов и находятся в файле plan.sav.
-
Откройте файл plan.sav.
-
Выберите в меню Analyze... (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты) и постройте частотные таблицы для всех переменных.
Alter (Возраст)
Freq-uency (Часто-та) | Percent (Про-цент) | valid Percent (Действи- тельный процент) | uumuiative percent (Совокупный процент) | ||
Valid (Действи-тельное значение) | bis 40 Jahrejflo 45 лет) | 29 | 34,1 | 34,1 | 34,1 |
41-55 Jahre (41-55 лет) | 29 | 34,1 | 34,1 | 68,2 | |
ueber 55 Jahre (Свыше 55 лет) | 27 | 31,8 | 31,8 | 100,0 | |
Total (Сумма) | 85 | 100,0 | 100,0 | |||
Geschlecht (Пол)
Frequ-ency (Часто-та) | Percent (Про-цент) | Valid Percent (Действи- тельный процент) | Cumulative Percent (Совокупный процент | ||
Valid (Действи-тельное значение) | maennlich (Мужской) | 44 | 51,8 | 51,8 | 51,8 |
weiblich (Женский) | 41 | 48,2 | 48,2 | 100,0 | |
Total (Сумма) | 85 | 100,0 | 100,0 |
Krankheitsdauer (Продолжительность болезни)
Frequ-ency (Часто-та) | Percent (Про-цент) | Valid Percent (Действи- тельный процент) | Cumu-lative Percent (Сово-купный процент) | ||
Valid | bis 5 Jahre {До 5 лет) | 24 | 28,2 | 28,2 | 28,2 |
(Действи- | 6-10 Jahre (6-1 Олег) | 16 | 18,8 | 18,8 | 47,1 |
тельное | 11-20 Jahre (11-20 лет) | 32 | 37,6 | 37,6 | 84,7 |
значение) | ueber 20 Jahre (Свыше 20 лет) | 13 | 15,3 | 15,3 | 100,0 |
Total (Сумма) | 85 | 100,0 | 100,0 |
Schulbildung (Образование)
Freq-uency (Часто- та) | Percent (Про-цент) | Valid Percent (Действи- тельный процент) | Cumu-lative Percent (Сово-купный процент) | ||
Valid (Действи-тельное значение) | Haupt-schule (неполное среднее) | 53 | 62,4 | 62,4 | 62,4 |
Mittlere Reife (среднее) | 18 | 21,2 | 21,2 | 83,5 | |
Abitur (аттестат зрелости) | 14 | 16,5 | 16,5 | 100,0 | |
Total (Сумма) | 85 | 100,0 | 100,0 |
Einen Plan machen und danach handeln (Разработать план и затем приступить к его воплощению)
Freq-uency (Часто-та) | Percent (Про-цент) | Valid Percent (Действи-тельный процент) | Cumu-lative Percent (Сово-купный процент) | ||
Valid (Действи-тельное значе- ние) | gar nicht (абсолютно не верно) | 24 | 28,2 | 28,2 | 28,2 |
Wenig (слабо) | 18 | 21,2 | 21,2 | 49,4 | |
mittelmaessig (посред- ственно) | 18 | 21,2 | 21,2 | 70,6 | |
ziemlich(достаточно) | 16 | 18,8 | 18,8 | 89,4 | |
sehr stark (абсолютно верно) | 9 | 10,6 | 10,6 | 100,0 | |
(Сумма) | 85 | 100,0 | 100,0 |
-
Если Вы с помощью меню Analyze...(Анализ) Correlate (Корреляция) Bivariate... (Парная)
произведёте расчёт ранговой корреляции по Спирману между пунктом "Составить план и затем приступить к его воплощению" и другими переменными (с использованием синтаксических приемов, описанных в главе 26.3), то получите следующий результат:
Correlations (Корреляции)
Einen Plan machen und danach handeln (Разработать план и затем приступить к его воплощению) | |||
Spearman's rho (p Спирмана) | Alter (Возраст) | Correlation Coefficient (Корре-ляционный коэффициент) | -,376** |
Sig. (2-tailed) (Значимость (2-сторонняя)) | ,000 | ||
N | 85 | ||
Geschlecht (Пол) | Correlation Coefficient (Корре-ляционный коэффициент) | ,298" | |
Sig. (2-tailed) (Значимость (2-сторонняя)) | ,006 | ||
N | 85 | ||
Krankheitsda uer (Продолжи- тельность болезни) | Correlation Coefficient (Корре-ляционный коэффициент) | -,260* | |
Sig. (2-tailed) (Значимость (2-сторонняя)) | ,016 | ||
N | 85 | ||
Schulbildung (Образование) | Correlation Coefficient (Корре-ляционный коэффициент) | ,314** | |
Sig. (2-tailed) (Значимость (2-сторонняя)) | ,003 | ||
N | 85 |
**. Correlation is significant at the .01 level (2-tailed) (Корреляция является значимой на уровне 0,01 (2 - сторонняя)).
*. Correlation is significant at the .05 level (2-tailed) (Корреляция является значимой на уровне 0,01 (2 - сторонняя)).
Стало быть, существует значимая, хоть и не очень большая корреляция. Если учесть принятое кодирование переменных, то можно заметить, что женщины более склонны сначала составить план действий, а затем приступать к лечению, чем мужчины. Кроме того, более молодые пациенты, пациенты с непродолжительным периодом болезни и пациенты, имеющие высшее образование, более активно занимаются своим лечением.
Попытаемся теперь изучить одновременное влияние возраста, пола, продолжительности болезни и образования на целевую переменную "Разработать план и затем приступить к его воплощению". Подходящим методом для этого является порядковая регрессия.
-
Выберите в меню Analyze (Анализ) Regression (Регрессия) Ordinal... (Порядковая)
Откроется диалоговое окно Ordinal Regression (Порядковая регрессия).
Рис. 16.20: Диалоговое окно Ordinal Regression (Порядковая регрессия)
-
Переменной plan (план) присвойте статус зависимой переменной, а переменным alter (возраст), g, kdauer (продолжительность болезни) и schule (образование) — статус факторов.
-
В поле Covariate(s) (Ковариаты) вы можете внести ковариаты, относящиеся к интервальной шкале. Однако, в нашем примере таковые отсутствуют.
-
Нажмите кнопку Options... (Опции).
Наряду с параметрами, которые управляют итерационным процессом (предварительные установки для них мы оставляем без изменения), можно выбрать одну из пяти связующих функций, смысл которых будет пояснен далее. Функцией, установленной по умолчанию, является Logit (Логит); эта связь, как правило, оказывается лучшей.
-
Щёлкните на кнопке Output... (Вывод). Откроется диалоговое окно Ordinal Regression:Output (Порядковая регрессия: Вывод).
Здесь Вы получаете возможность управлять данными, выводимыми в окне просмотра и создавать новые переменные.
-
В разделе Display (Показать) оставьте предварительные установки Goodness of Jit statistics (Статистика критерия согласия), Summary statistics (Отчётная статистика) и Parameter estimates (Параметрические оценки). В разделе Saved variables (Сохранённые переменные) активируйте опции Estimated response probabilities (Оценочные вероятности отклика), Predicted category (Прогнозируемая категория) и Predicted category probability (Вероятность прогнозируемой категории).
-
Теперь нажмите кнопку Location... (Положение)
Здесь у Вас появляется возможность выбора между моделью, которая содержит только главные факторы влияния и, в случае необходимости, — ковариаты, а также моделью, которую Вы можете подобрать самостоятельно (Custom). В последнем случае у Вас появляется возможность учесть также все мыслимые взаимодействия. В данном случае, сначала мы хотим учесть только главные эффекты, что соответствует предварительной установке.
-
Посредством кнопки Scale... (Шкала) можно ввести, так называемые, компоненты шкалы. Как правило, это не является необходимым, и мы от них откажемся.
-
Начните расчёт нажатием ОК.
Рис. 16.21. Диалоговое окно Ordinal Regression: Output (Порядковая регрессия: Вывод)
Отображение результатов в окне просмотра начинается с вывода предостережения. В 66,2% всех ячеек, которые образовываются из комбинаций факторов и зависимых переменных, частота равна нулю. При этом не учитываются те комбинации факторов, которые повторяются. Вы можете включить в список выдачи наблюдаемые и ожидаемые частоты, а также их остатки, если после нажатия кнопки Output... (Вывод) активируете опцию Cell infonnation (Информация по ячейкам).
Warnings (Предостережения)

Далее следует таблица, содержащая абсолютные и выраженные в процентах частоты различных категорий зависимых переменных и факторов.
Case Processing Summary (Сводная таблица обработки наблюдений)
N (Коли-чество) | Marginal Percentage (Предельный процент) | ||
Einen Plan machen und danach handeln (Разработать план и затем приступать к лечению) | gar nicht (Абсолютно не верно) | 24 | 28,2% |
wenig (Слабо) | 18 | 21,2% | |
mittelmaessig (Посредственно) | 18 | 21,2% | |
ziemlich (Достаточно) | 16 | 18,8% | |
sehr stark (Абсолютно верно) | 9 | 10,6% | |
Alter (Возраст) | bis 40 Jahre (До 45 лет) | 29 | 34,1% |
41-55 Jahre (41-55 лет) | 29 | 34,1% | |
ueber 55 Jahre (Свыше 55 лет) | 27 | 31,8% | |
Geschlecht (Пол) | maennlich (Мужской) | 44 | 51,8% |
weiblich (Женский) | 41 | 48,2% | |
Krankheitsdauer (Продолжительность болезни) | bis 5 Jahre (До 5 лет) | 24 | 28,2% |
6-10 Jahre (6-10 лет) | 16 | 18,8% | |
(6-10 лет) | 32 | 37,6% | |
11-20 Jahre (11 -20 лет) | 13 | 15,3% | |
Schulbildung (Образование) | Hauptschule (Неполное среднее) | 53 | 62,4% |
Mittlere Reife (Среднее) | 18 | 21,2% | |
Abitur (Аттестат зрелости) | 14 | 16,5% | |
Valid (Действительное значение) | 85 | 100,0% | |
Missing (Пропущенное значение) | 0 | ||
Tola (Сумма) | 85 | ||
В качестве оценки значимости вклада отдельных независимых переменных в улучшение прогнозов, получаемых с помощью модели также, как и при бинарной логистической регрессии, служит отрицательное значение 2LL (Удвоенное значение логарифма функции правдоподобия). Разность между начальным значением ("Только постоянное слагаемое") и конечным значением ("Окончательно") указывается в виде значения теста хи-квадрат. которому соотнесен соответствующий уровень значимости. В приведенном примере наблюдается очень значимое улучшение (р < 0,001).
Model Fitting Information (Информация о приближении модели)
Model (Модель) | -2 Log likelihood (-2 логарифми-ческое правдоподобие) | Chi-Square (Хи-квадрат) | df (Степень свободы) | Sig. (Значи-мость) |
Intercept Only (Только постоянное слагаемое) | 207,180 | |||
Final (Окончательно) | 170,408 | 36,772 | 8 | ,000 |
Link function: Logit (Связывающая функция: Логит). | ||||
Для проверки, будут ли наблюдаемые частоты по ячейкам значимо отличаться от ожидаемых частот, рассчитанных на основе модели, выполняется хи-квадрат тест по Пирсону. Его результатом, для данного примера, является не значимая разность значений (р = 0,190), что говорит о достижении высокой степени приближения. Однако, следует обратить внимание на то, что из-за большого количества пустых ячеек применение теста хи-квадрат становится проблематичным.
Goodness of fit (Критерий согласия)
Chi-Square (Хи-квадрат) | df (Степень свободы) | Sig. (Значимость) | |
Pearson (Пирсон) | 158,733 | 144 | ,190 |
Deviance (Отклонение) | 127,454 | 144 | ,835 |
Link function: Logit (Связывающая функция: Логит).
Из трёх мер согласия приведенных ниже, мера, вычисленная по методу Нагелькерке (Nagelkerke) является мерой определённости, которая указывает на процентную долю дисперсии, объяснимой при помощи порядковой регрессии, (см. разд. 16.4). В приведенном примере оценка дисперсии составляет 36,7 %.
Pseudo R-Square (Псевдо R-квадрат)
Сох and Snell (Кокс и Шелл) | ,351 |
Nagelkerke (Нагелькерке) | ,367 |
McFadden (МакФадден) | ,138 |
Linkfunction: Logit (Связывающая функция: Логит).
Результатом анализа являются оценки параметров регрессии приведенные в нижеследующей таблице.
Parameter Estimates (Оценки параметров регрессии) | ||||||||
| Esti-mate (Оце-нка) | Std. Error (Стандар-тная ошибка) | Wald (Валь-дов-ский) | df (Сте-пень сво-боды) | Sig. (Значи-мость) | 95% Confidence Interval (95 % довери- тельный интервал) | ||
Lower Bound | Upper Bound | |||||||
Threshold (Порог) | [PLAN = 1] | -,220 | ,968 | ,052 | 1 | ,820 | -2,118 | 1,677 |
[PLAN = 2] | ,981 | ,988 | ,986 | 1 | ,321 | -,955 | 2,918 | |
[PLAN = 3] | 2,253 | 1,013 | 4,949 | 1 | ,026 | ,268 | 4,238 | |
[PLAN = 4] | 3,907 | 1,048 | 13,905 | 1 | ,000 | 1,853 | 5,960 | |
Location (Поло-жение) | [G=1] | 2,145 | ,540 | 15,787 | 1 | ,000 | 1,087 | 3,204 |
[G=2] | 1,357 | ,529 | 6,574 | 1 | ,010 | ,320 | 2,394 | |
[ALTER =1] | Oa | , | , | 0 | , | f | ( | |
[ALTER =2] | -1,091 | ,433 | 6,355 | 1 | ,012 | -1,939 | -,243 | |
[ALTER =3] | Oa | , | , | 0 | , | f | j | |
[KDAUER =1] | 1,811 | ,740 | 5,990 | 1 | ,014 | ,361 | 3,261 | |
JKDAUER =2] | 1,486 | ,782 | 3,606 | 1 | ,058 | -4.772E-02 | 3,019 | |
IKDAUER =3] | 1,340 | ,678 | 1 3,905 | 1 | ,048 | 1.101E-02 | 2,669 | |
[KDAUER =4] | Oa | , | , | 0 | , | ( | , | |
[SCHULE =1] | -1,183 | ,618 | 3,665 | 1 | ,056 | -2,394 | 2.807E-02 | |
[SCHULE =2] | -,659 | ,700 | ,886 | 1 | ,347 | -2,031 | ,713 | |
rSCHULE =31 | Oa |
|
| 0 |
|
|
| |
Link function: Logit (Связывающая функция: Логит).
a. This parameter is set to zero because it is redundant (Этот параметр приравнен к нулю, так как является дублирующим). !
Каждой категории зависимых переменных и каждой категории факторов сопоставлена оценка параметра регрессии, причём оценки для соответствующих категорий высших порядков являются дублирующими и поэтому приравнены к нулю. Оценки параметров регрессии для зависимой переменной являются пороговыми оценками, которые для факторов называются оценками положения.
Оценки положения дают возможность толковать влияние факторов и указывают на степень этого влияния. Поэтому, прежде чем будет продемонстрирована точная математическая связь между факторами влияния и зависимой переменной, можно констатировать следующее:
-
Из таблицы можно узнать, какие из факторов вообще оказывают значимое влияние на зависимую переменную. Такими факторами являются возраст, пол и продолжительность болезни, в то время как образование находится на самой границы значимости, до перехода этой границы осталось совсем не много.
-
Положительные оценки означают, что соответствующая категория действует в качестве высшей категории зависимой переменной; отрицательные оценки указывают на действие в качестве низших категорий зависимых переменных.
Принадлежность к младшим возрастным группам является причиной более единодушного одобрения предложения: "Разработать план лечения и затем приступать к его воплощению", все мужчины менее склонны к такому предложению, небольшая продолжительность болезни, а также высокое или низкое образование ведут к снижению степени одобрения. Это соответствует результатам корреляционного анализа.
Математическое значение оценок параметров регрессии заключается в том, что на них основе могут быть вычислены кумулятивные (суммарные) вероятности для категорий независимых переменных. Покажем это на конкретном примере.
Для этого возьмем в редакторе данных первого пациента и рассчитаем совокупную вероятность для случая, когда он отмечает одну из первых двух категорий ("gar nicht" (абсолютно не верно) или "wenig" (слабо)) для зависимой переменной.
Первый пациент является мужчиной средней возрастной группы с большой продолжительностью болезни и неполным средним образованием. Учитывая все эти сведения, можно ожидать высокую вероятность того, что больной проявит слабую готовность планомерно лечить свою болезнь.
На первом шаге расчёта мы должны сложить оценки положения, соответствующие отдельным категориям:
alter = 2 | 1,347 |
g = 1 | -1,091 |
Kdauer = 4 | 0,000 |
Schule = 1 | -1,183 |
Сумма | -0,917 |
Эту сумму нам теперь нужно отнять от пороговой величины второй категории зависимой переменной (plan = 2):
0,981 - (-0,917) = 0,981 + 0,917 = 1,898
Как можно заметить по значению, которое превосходит единицу, этот показатель пока ещё не является искомой совокупной вероятностью того, что больной отметит одну из первых двух категорий. Значение этого показателя соответствует связующей функции, приведенной к этой вероятности. В нашем примере мы выбрали в качестве связующей логит-функцию, установленную по умолчанию, так что для искомой вероятности справедливо следующее выражение:
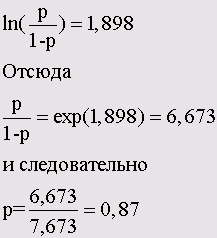
Таким образом, вероятность того, что первый пациент отметит одну из первых двух категорий, составляет р = 0,87 или 87 %. Фактически пациент отметил категорию 1.
Чтобы успокоить пользователей программы, следует сказать, что Вы можете избежать этих сложных расчётов. В диалоговом окне Ordinal Regression:Output (Порядковая регрессия: Вывод) мы активировали опцию сохранения некоторых переменных, которые теперь можем просмотреть.
Пять переменных est1_1-est5_1 соответствуют вероятностям для пяти категорий зависимой переменной. Если мы возьмем первого пациента, то достаточно сложить вероятности для первых двух категорий:
0,67 + 0,20 = 0,87
Это соответствует тому значению, которое мы рассчитали для совокупной вероятности второй категории. В переменной рге_1 сохранен номер категории, которой соответствует самая высокая вероятность, названная "прогнозируемой категорией". Переменная рср_1 ещё раз дает вероятность выбора этой категории.
Связующая логит-функция выбранная нами для этого примера, принадлежит к набору из пяти функций, приведенных ниже.
Функция | Форма | Применение |
Logit (Логит) | In (р/(1-р)) | Равномерно распределённые категории |
Complementary log-log (Сопряженный двойной логарифм) | ln(-ln(1-p)) | Высшие категории представлены сильнее |
Negative log-log (Отрицательный двойной логарифм) | -ln(-ln(p)) | Низшие категории представлены сильнее |
Probit (Пробит) | Инверсия стандартного комулятивного нормального распределения | Нормально распределённые частоты |
Cauchit (Коши) | tan(7t(p-0.5)) | Появление пиковых значений |
В качестве меры качества прогнозирования можно использовать ранговую корреляцию по Спирману между фактически наблюдаемой категорией (переменная plan) и прогнозируемой категорией (переменная рге_1). Для приведенного примера (связующая функция — логит) получим г = 0,611; для других связующих функций получаются более низкие значения.
Лучшую модель можно получить, если в диалоговом окне Ordinal Regression: Location (Порядковая регрессия: Положение) наряду с главными эффектами включить и взаимодействия. После активирования опции Custom (Пользовательский режим) в вашем распоряжении появляется вспомогательное меню, при помощи которого вместе с главным эффектом Вы сможете включить в модель и различные виды взаимодействия.
-
Активируйте опцию Custom (Пользовательский режим) и сперва выберите в появившемся списке Main effects (Главные эффекты).
-
При помоши транспортной кнопки перенесите все факторы в поле Location model: (Определение положения для модели).
-
Затем отметьте в разворачивающемся меню Interaction (Взаимодействие) и повторно перенесите все факторы в поле Location model: (Определение положения для модели). Будет выбрано взаимодействие четвёртого уровня. При помоши опции All 2-way (Все дважды) Вы можете задать взаимодействие второго уровня, при помощи опции АН З-way (Все трижды) — взаимодействие третьего уровня и т.д.
Теперь прогноз будет лучше; в случае применения для данного примера взаимодействия четвёртого уровня ранговая корреляция между наблюдаемой и прогнозируемой категориями возрастает с 0,611 до 0,739. При этом, конечно же, возрастает и количество параметрических оценок.
36.gif
37.gif
38.gif

39.gif
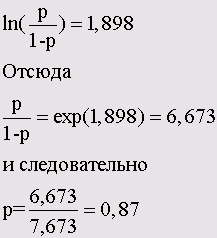
16.7 Пробит-анализ
16.7 Пробит-анализ
Этот метод известен также под именем "Дозаторный анализ кривых воздействия" и находит применение преимущественно в области токсикологии. В большинстве случаев речь идёт о том, как на заданное количество индивидуумов воздействуют различные дозировки некоторого вещества (к примеру, некоторого токсичного вещества).
Классический пример, который вошёл и в справочник по SPSS, исследует действие средства, предназначенного для уничтожения насекомых. При этом производится подсчёт, сколько насекомых из заранее известного количества погибли при воздействии определённых доз вещества. Особенный интерес в данном случае представляет дозировка, при которой уничтожается половина имеющихся насекомых.
Оставим животных в покое и обратимся, в виде исключения, к одному специально придуманному примеру. Шеф секретной службы некоторой вымышленной страны пожелал узнать, сколько денег он должен предложить гражданам соседнего государства, чтобы они доставляли ему некоторую тайную информацию. Для этой цели через своего посредника он предлагает первой группе 1000 долларов и отмечает, сколько человек соглашаются на его предложение вести шпионскую деятельность. Второй группе он предлагает 2000 долларов и вновь отмечает себе количество попаданий в цель. Он продолжает предлагать деньги и дальше, действуя таким пошаговым образом и доходит до суммы 10000 долларов. При этом исследованиям подвергаются две различные категории людей. К первой категории относятся люди, которые недовольны своим материальным положением, ко второй — люди, удовлетворенные своим материальным положением.
Для обеих категорий шеф секретной службы желает выяснить, сколько он должен предложить денег, чтобы достичь желаемой доли положительных ответов. К примеру, его интересует сумма, которую он должен заплатить, чтобы на его предложение согласилась половина опрашиваемой группы.
Для обеих категорий удовлетворенности материальным положением (доволен — недоволен) в нижеследующей таблице представлены долларовые суммы в порядке возрастания, количество вовлечённых в эксперимент людей (nges) и количество фактически завербованных шпионов (п).
группа | доллар | количество вовлечённых в эксперимент людей | количество фактически завербованных шпионов |
недоволен | 1000 | 59 | 8 |
недоволен | 2000 | 56 | 22 |
недоволен | 3000 | 53 | 28 |
недоволен | 4000 | 49 | 30 |
недоволен | 5000 | 51 | 35 |
недоволен | 6000 | 43 | 34 |
недоволен | 7000 | 40 | 36 |
недоволен | 8000 | 45 | 41 |
недоволен | 9000 | 40 | 38 |
недоволен | 10000 | 35 | 34 |
доволен | 1000 | 61 | 1 |
доволен | 2000 | 45 | 13 |
доволен | 3000 | 52 | 21 |
доволен | 4000 | 45 | 22 |
доволен | 5000 | 46 | 26 |
доволен | 6000 | 38 | 27 |
доволен | 7000 | 45 | 35 |
доволен | 8000 | 42 | 33 |
доволен | 9000 | 37 | 32 |
доволен | 10000 | 36 | 33 |
Эта информация построчно хранится в файле dollar.sav (переменные: gruppe, dollar, nges, n).
-
Откройте файл dollar.sav.
-
Выберите в меню Analyze (Анализ) Regression (Регрессия) Pmbit... (Пробит)
Откроется диалоговое окно Probit Analysis (Пробит-анализ).
Рис. 16.22: Диалоговое окно Probit Analysis (Пробит-анализ)
-
Поочерёдно перенесите переменные п в поле частоты отклика, переменную nges в поле наблюдаемого общего количества, переменную gruppe в поле факторов и переменную dollar в поле ковариат.
-
При помощи соответствующей кнопки для факторной переменной необходимо определить область принадлежности; для нашего примера она равна целым числам: 1 и 2.
-
Стандартным подходом при проведении пробит-анализа стало логарифмическое преобразование значений ковариат (при помощи десятичного логарифма); задайте и Вы это преобразование.
-
Оставьте установку обычной пробит-модели и щёлкните на кнопке опций. Дополнительно к установленным статистикам активируйте тест параллельности, который является уместным при анализе разнообразных групп.
-
Начните расчёт нажатием ОК.
Результирующие данные выводятся в старой табличной форме и являются довольно обширными. На одном из первых шагов определяются так называемые "пробиты". Они представляют собой стандартные значения, которые отвечают площади под частью кривой стандартной нормального распределения, соответствующей отношению частоты положительных ответов к общей частоте. Так, в первой группе, которой предлагалось по 1000 долларов, это предложение приняли 8 человек из 59, что соответствует относительной доле, равной
р=8/59= 0,1356
Это значение интерпретируется как часть площади под кривой стандартного нормального распределения (которая, как известно, суммарно нормирована к 1). По соответствующей статистической таблице можно установить, что стандартное значение равно -1,10. Это значение является пробитом к дозировке 1000 долларов.
Упомянутые пробиты для обеих групп в зависимости от логарифма дозировки представлены на одной диаграмме, которую вы можете увидеть в окне просмотра:
Для обеих групп график является практически линейным, что является предпосылкой для дальнейших рассуждений. В противном случае дополнительно следовало было бы рассматривать ход процесса воздействия на основе исходных значений (то есть без логарифмического преобразования).
Рис. 16.23: Отклики, трансформированные пробитом
Для обеих кривых определяется уравнение регрессионных прямых, причём для обеих прямых вычисляется общий угол наклона:
Regression Coeff. | Standard Error | Coeff./S.E. | ||||
DOLLAR | 2,78749 | ,17640 | 15,80205 | |||
Intercept | Standard Error | Intercept/S.E. | GRUPPE | |||
| -9 ,59552 | ,63415 | -15, 13130 | 1 | |||
| 2 | ||||||
| -9 ,99490 | ,64731 | -15,44060 | ||||
| Pearson Goodness -of -Fit Chi Square=10,043 DF = 17 P = ,902 | ||||||
Parallelism Test Chi Square = ,164 DF = 1 P = ,686 | ||||||
При тесте на качество согласия большое значение р (как в рассматриваемом примере) указывает на лучшее приближение. Второй тест по критерию хи-квадрат проясняет вопрос, действительно ли обе прямые могут рассматриваться как параллельные. Параллельности прямых соответствует незначимый результат теста (как в рассматриваемом случае).
Если мы рассмотрим уравнение регрессии для первой группы, то получим следующее уравнение, прогнозирующее значение пробита:
Probit= 2,78749xlog(Dollar)- 9,59552
Для значения 1000 долларов получим
Probit= 2,78749x3- 9,59552= - 1,2331
Если мы вновь обратимся к статистической таблице, содержащей значения стандартной кривой нормального распределения, то полученному стандартизированному значению в данном случае соответствует площадь 0,10878. Это значение используется для того, чтобы определить ожидаемую частоту отклика:
59x0,10878= 6,418
Полученные результаты сведены в следующую таблицу:
Number of Observed Expected | |||||||||||
GRUPPE | DOLLAR | Subjects Responses Responses Residual | Prob | ||||||||
1 | 3 | , 00 | 59 | ,0 | 8 | ,0 | 6,418 | 1 | ,582 | ,10878 | |
1 | 3 | ,30 | 56 | ,0 | 22, | 0 | 19 | ,422 | 2 | ,578 | ,34681 |
1 | 3 | ,48 | 53 | ,0 | 28, | 0 | 28 | ,546 | - | ,546 | ,53860 |
1 | 3 | , 60 | 49 | ,0 | 30, | 0 | 32 | , 923 | - | 2, 923 | , 67191 |
1 | 3 | ,70 | 51 | ,0 | 35, | 0 | 38 | , 902 | - | 3, 902 | ,76279 |
1 | 3 | ,78 | 43 | ,0 | 34, | 0 | 35 | ,491 | - | 1,491 | ,82537 |
1 | 3 | , 85 | 40 | ,0 | 36, | 0 | 34 | ,768 | 1 | ,232 | ,86921 |
1 | 3 | , 90 | 45 | ,0 | 41, | 0 | 40 | ,522 | , | 478 | , 90048 |
1 | 3 | , 95 | 40 | ,0 | 38, | 0 | 36 | ,928 | 1 | ,072 | , 92319 |
1 | 4 | ,00 | 35 | ,0 | 34, | 0 | 32 | ,899 | 1 | ,101 | , 93996 |
2 | 3 | ,00 | 61 | ,0 | 1, | 0 | 3, | 129 | - | 2,129 | ,05129 |
2 | 3 | ,30 | 45 | ,0 | 13, | 0 | 9, | 621 | 3 | ,379 | ,21380 |
2 | 3 | ,48 | 52 | ,0 | 21, | 0 | 19 | ,820 | 1 | ,180 | ,38115 |
2 | 3 | ,60 | 45 | ,0 | 22, | 0 | 23 | ,322 | - | 1,322 | ,51826 |
2 | 3 | ,70 | 46 | ,0 | 26, | 0 | 28 | ,703 | - | 2,703 | ,62397 |
2 | 3 | ,78 | 38 | ,0 | 27, | 0 | 26 | ,761 | , | 239 | ,70425 |
2 | 3 | ,85 | 45 | ,0 | 35, | 0 | 34 | ,436 | , | 564 | ,76524 |
2 | 3 | ,90 | 42 | ,0 | 33, | 0 | 34 | ,100 | - | 1,100 | ,81190 |
2 | 3 | ,95 | 37 | ,0 | 32, | 0 | 31 | ,373 | f | 627 | ,84791 |
2 | 4 | ,00 | 36 | /o | 33, | 0 | 31 | ,535 | 1 | ,465 | ,87597 |
Сразу же после этой таблицы для заданных вероятностей ( вероятности здесь следует понимать, как отношение частоты желательного отклика к общему числу испытуемых) выводятся значения необходимых дозировок (в нашем случае: денежная сумма в долларах) и их 95%-ый доверительный интервал. Ниже приводится таблица значений для первой группы:
95% Confidence Limits | |||
Prob | DOLLAR | Lower | Upper |
,01 | 405,30868 | 289,59056 | 529,15509 |
,02 | 507,66784 | 373,66257 | 647,93485 |
,03 | 585,63448 | 439,14578 | 736,94514 |
, 04 | 652,08194 | 495,79196 | 811,99633 |
,05 | 711,65439 | 547,15681 | 878,74346 |
,06 | 766,62851 | 594,99562 | 939,94335 |
, 07 | 818,31336 | 640,32303 | 997,17444 |
,08 | 867,54082 | 683,78664 | 1051,43643 |
,09 | 914,87813 | 725,82978 | 1103,40905 |
,10 | 960,73191 | 766,77131 | 1153,57841 |
, 15 | 1176,35221 | 961,74200 | 1387,62679 |
,20 | 1381,73708 | 1150,43739 | 1608,52696 |
,25 | 1586,29202 | 1340,43221 | 1827,40833 |
,30 | 1795,67203 | 1536,35222 | 2050,97344 |
,35 | 2014,28728 | 1741,83765 | 2284,49983 |
,40 | 2246,29254 | 1960,31730 | 2533,03836 |
,45 | 2496,16365 | 2195,45599 | 2802,13038 |
,50 | 2769,19498 | 2451,53866 | 3098,44683 |
,55 | 3072,09057 | 2733,92871 | 3430,56245 |
, 60 | 3413,82108 | 3049,73874 | 3810,08632 |
,65 | 3807,02441 | 3408,93562 | 4253,51516 |
, 70 | 4270,51303 | 3826,32195 | 4785,56534 |
,75 | 4834,19240 | 4325,40532 | 5445,75782 |
,80 | 5549,85527 | 4946,81830 | 6303,01441 |
,85 | 6518,83063 | 5769, 66817 | 7493,47901 |
, 90 | 7981,87380 | 6980,17468 | 9345,15098 |
, 91 | 8381,92608 | 7305,70121 | 9861,25890 |
,92 | 8839,28528 | 7675,37386 | 10455, 92397 |
, 93 | 9371,03216 | 8102,08907 | 11153,16983 |
,94 | 10002,81198 | 8605,11895 | 11989,28434 |
,95 | 10775,51263 | 9215,02568 | 13022,52271 |
, 96 | 11759, 93430 | 9984,40147 | 14354,56418 |
, 97 | 13094,24400 | 11015,11467 | 16185,74513 |
,98 | 15105,23259 | 12545,80989 | 18995,72850 |
, 99 | 18920,00171 | 15388,14261 | 24468,76250 |
Для того, чтобы переманить на свою сторону половину группы граждан чужой страны, недовольных своим финансовым положением (Prob = 0,5), начальник секретной службы должен предложить каждому по 2769 долларов, причём с 95%-ой вероятностью эта сумма колеблется от 2452 до 3098 долларов. Для группы довольных финансовым положением (для которой распечатка данных здесь не приведена) придётся заплатить больше: 3852 доллара, с 95%-ым доверительным интервалом эта сумма колеблется от 3437 до 4296 долларов.
Отношение этих двух значений медиан составит:
2769/3852= 0,719
Это соотношение отображается в небольшой статистической сводке:
Estimates of Relative Median Potency | |||
95% | Confidence | Limits | |
GRUPPE 1 VS. 2 | Estimate ,7190 | Lower ,60280 | Upper ,84419 |
Если Вы в диалоговом окне выберите не пробит, а логит-модель, то отношение частоты положительных откликов к общему количеству опрашиваемых р заменяется выражением
40.gif
41.gif
42.gif

16.8 Приближение с помощью кривых
16.8 Приближение с помощью кривых
При помощи этого пункта меню можно строить графики реального течения наблюдаемых процессов и приближать их при помощи аппроксимационных кривых. Для этого в ваше распоряжение предоставляется, в общей сложности, одиннадцать различных типов кривых. В большинстве случаев речь здесь будет идти о временных рядах.
В качестве примера рассмотрим изменение зарплаты в Федеративной республике Германии с 1950 года по 1988, описываемое так называемым индексом действительной зарплаты. Его можно получить при помощи соотнесения текущего годового уровня зарплаты к уровню к 1980 году, для которого значение индекса принимается равным 100.
Год | Индекс действительной зарплаты |
1950 | 28,6 |
1960 | 46,9 |
1965 | 63,0 |
1970 | 80,4 |
1975 | 87,9 |
1980 | 100,0 |
1981 | 98,2 |
1982 | 96,5 |
1983 | 96,0 |
1984 | 96,9 |
1985 | 98,0 |
1986 | 101,2 |
1987 | 104,5 |
1988 | 107,6 |
Эти данные находятся в файле lohasav. В файле также находится и ещё одна, третья, переменная, которая отражает разность между текущим значением года и 1949 годом. Эта переменная принимает значения от 1 до 39 и указывает на количество лет, прошедших с 1949 года.
-
Откройте файл lohn.sav.
-
Выберите в меню Analyze (Анализ) Regression (Регрессия) Curve Estimation...(Подгонка кривых)
Рис. 16.24: Диалоговое окно Curve Estimation (Подгонка кривых)
Откроется диалоговое окно Curve Estimation (Подгонка кривых), в котором можно выбрать одну из одиннадцати различных моделей.
Предлагаемым моделям соответствуют следующие формулы:
| Молель | Формула |
Линейная |
у= b0+ b1хX |
Логарифмическая | у= b0+ b1х ln(х) |
Обратная | |
Квадратичная | у= b0+ b1хX + b2хX2 |
Кубическая | у= b0+ b1хХ + b2хX2 + b3хX3 |
Степенная | y= b0хXb1 |
Показательная (комбинированная) | y= b0 * b1 |
S | у= е^(b0+b1xX) |
Логистическая | |
Рост | у= е^(b0+b1xX) |
Экспоненциальная | y=b0 х е^(b1xt) |
Для логистической модели необходимо предварительно задать параметр и, который задается непосредственно в диалоговом окне Curve Estimation (Подгонка кривых) в качестве верхнего предела. Задачей программы является определение коэффициентов b0, b1, b2 и b3.
В поле для меток наблюдений (Case labels) можете указать некоторую переменную для описания данного наблюдения, которая затем будет появляться в режиме выбора точек (см. гл. 22.8.1) на построенном графике (см. рис. 16.25).
-
Перенесите переменную lohn в поле для зависимых переменных, а переменную anz в поле для независимых переменных.
-
Произведём оценку при помощи квадратичной функции; деактивируйте линейную модель и отметьте вместо неё квадратичную модель.
Активирование опции Time (Время) имеет смысл только тогда, когда анализируемые переменные представлены в виде временных рядов с одинаковыми интервалами.
-
Затем щёлкните на кнопке Save (Сохранение) и в появившемся диалоговом окне выберите опцию, с помощью которой прогнозируемые значения переменной будут сохранены в исходном файле данных.
-
Вернувшись в первое диалоговое окно, начните расчёт нажатием ОК.
Вывод результатов производится в старой табличной форме. Самыми важными показателями являются:
Independent: ANZ
Dependent Mth Rsq d.f. F Sigf b0 b1 b2
LOHN QUA ,979 11 251,10 ,000 22,5918 3,0615 -,0242
Эта таблица содержит значения коэффициентов а, b1, и b2. К данным исходного файла была добавлена переменная fit_1, которая содержит прогнозируемые значения, найденные на основе рассчитанных коэффициентов. Далее в окне просмотра появляется график, на котором отображаются кривые, соответствующие изменению наблюдаемых и спрогнозированных значений.
Приближение с помощью выбранной кривой, как кажется, удалось довольно не плохо. В противном случае можно было бы применить и другие модели, для использования которых, конечно же, не помешал бы некоторый опыт в области подобных криволинейных приближений.
Рис 16.25: Наблюдаемая и оценочная кривая
43.gif

45.gif
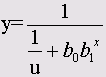
46.gif

16.9 Взвешенное оценивание (оценка с весами)
16.9 Взвешенное оценивание (оценка с весами)
В линейном регрессионном анализе, рассмотренном до настоящего времени, все наблюдения входят в модель равнозначно. При этом, исходной предпосылкой является тот факт, что все наблюдения должны иметь одинаковую дисперсию.
Если это условие не выполняется и дисперсия увеличивается с ростом значения независимой переменной, то отдельные точки можно взвесить так, чтобы наблюдения с большой дисперсией имели меньшее влияние.
В качестве примера рассмотрим тест, проверяющий знания детей в области географии. Дети в возрасте от 3 до 14 лет должны были в течение двух минут назвать как можно больше городов Германии. Результаты теста сведены в нижеследующей таблице, причём количество детей в каждой возрастной группе варьируется от двух до пяти:
Возраст | Количество названных городов |
3 | 2, 1, 0, 4 |
4 | 4, 2, 6 |
5 | 3, 8, 4, 7 |
6 | 3, 8, 9, 5 |
7 | 6, 10 |
8 | 7, 14, 10 |
9 | 9, 16, 10 |
10 | 9, 16, 15, 9 |
11 | 18, 12 |
12 | 22, 11, 14, 16 |
13 | 14, 21 |
14 | 20, 15, 23, 14, 26 |
Эти данные для сорока детей в общей сложности хранятся в переменных alter (возраст) и staedte (города), которые содержатся в файле snamen.sav.
-
Откройте файл snamen.sav.
-
Выберите в меню Graphs (Графики) Scatterplot... (Диаграмма рассеяния)
Рис. 16.26: Диаграмма рассеяния
-
Отметьте и постройте простую диаграмму рассеяния с переменной alter по оси абсцисс и переменной staedte пo оси ординат.
Вы увидите, что с ростом возраста растёт не только количество названных городов, но и рассеяние, то есть дисперсия, становится больше.
-
В соответствии с описанием из главы 16.1 проведите линейный регрессионный анализ, причём переменной staedte присвойте статус зависимой переменной, а переменной alter — независимой переменной.
-
Вы получите следующие результаты:
Model Summary (Сводная таблица по модели)
Model (Модель) | R | R Square (R-квадрат) | Adjusted R Square (Смещенный R-квадрат) | Std. Error of the Estimate (Стандартная ошибка оценки) |
1
| ,879а | ,772 | ,766 | 3,1623 |
a. Predictors: (Conslant), Alter (Bлияющие переменные: (Константа), возраст)
Coefficients (Коэффициенты) а | ||||||
Model (Модель) | Unstandardized Coefficients (He стандарти-зированные коэф-фициенты) | Standardized Coefficients (Стандарти-зированные коэф-фициенты) | Т | Sig. (Значи-мость) | ||
В | Std. Error (Станда-ртная ошибка) | /3 (Beta) | ||||
1 a. Dep | (Constant) (Koнстанта) | -2,722 | 1,273 |
| -2,138 | ,039 |
Alter (Возраст) endent Variable | 1,569 (Зависим | ,138 ая перемен-ная) | ,879 | 11,357 | ,000 | |
Коэффициент корреляции равен 0,879, а мера определённости 0,772.
В данном примере мы имеем дело с группами случаев, разделёнными по годам возраста, для которых независимая переменная имеет всегда одно и то же значение. Исходя из значений зависимой переменной сопоставленных каждому случаю, можно определить дисперсию; обратное значение этой дисперсии применяется обычно в качестве весового фактора для соответствующего случая.
Если подобной группировки данных нет, то пытаются выявить такую связь между дисперсией и переменной, чтобы степень дисперсии была пропорциональна значению данной переменной. При поиске так называемых весовых переменных речь идет о независимой переменной или, если их много, — об одной из независимых переменных. В приведенном примере такой переменной, очевидно, является независимая переменная alter, по которой и можно проследить изменение дисперсии.
Целью анализа сначала является определение наилучшей возможной степени р. а затем подсчёт веса для каждого случая, причём вес для значения переменной х определяется как
1/хp
-
Выберите в меню Analyze (Анализ) Regression.. .(Регрессия) Weight Estimation... (Взвешенное оценивание)
Откроется диалоговое окно Weight Estimation (Взвешенное оценивание).
Рис. 16.27: Диалоговое окно Weight Estimation (Весовая цепка)
-
Перенесите переменную staedte в поле зависимых переменных, а переменную alter в поля для независимых и для весовых переменных. Согласно с установками по умолчанию оптимальная степень вычисляется в пределе от —2 до 2 с шагом 0,5; измените шаг на 0,2.
-
Щёлкните на кнопке опций и в появившемся диалоговом окне активируйте опцию Save best weight as new variable (Сохранить лучший вес, как новую переменную).
Результаты расчёта, вывод которых производится в старой табличной форме, выглядят следующим образом:
Source variable | . . ALTER | Dependent variable. . STAEDTE | |
Log- likelihood | Function =-116,950816 | POWERvalue= -2,000 | |
log- likelihood | Function =-115,170919 | POWERvalue=-1,800 | |
Log- likelihood | Function =-113,434617 | POWERvalue=-1,600 | |
Log- likelihood | Function =-111,746484 | POWERvalue=-1,400 | |
Log- likelihood | Function =-110,111706 | POWERvalue=-1,200 | |
Log- likelihood | Function =-108,536154 | POWERvalue=-1,000 | |
Log- likelihood | Function =-107,026465 | POWERvalue=-,800 | |
Log- likelihood | Function =-105,590111 | POWERvalue=-,600 | |
Log- likelihood | Function =-104,235463 | POWERvalue=-,400 | |
Log- likelihood | Function =-102,971835 | POWERvalue=-,200 | |
Log- likelihood | Function =-101,809499 | POWERvalue=,000 | |
Log- likelihood | Function =-100,759655 | POWERvalue=,200 | |
Log- likelihood | Function =-99,834344 | POWERvalue=,400 | |
Log- likelihood | Function =-99,046284 | POWERvalue=,600 | |
Log- likelihood | Function =-98,408623 | POWERvalue=,800 | |
Log- likelihood | Function =-97,934594 | POWERvalue=1,000 | |
Log- likelihood | Function =-97,637078 | POWERvalue=1,200 | |
Log- likelihood | Function =-97,528092 | POWERvalue=1,400 | |
Log- likelihood | Function =-97,618231 | POWERvalue=1,600 | |
Log- likelihood | Function =-97,916114 | POWERvalue=1,800 | |
Log- likelihood | Function =-98,427890 | POWERvalue=2,000 | |
The Value ofPOWER MaximizingLog-likelihood Function =1,400 | |||
Source variable | ALTER | POWERvalue=:1,400 | |
Dependent variable. . STAEDTE | |||
Multiple R, 90081 | |||
R Square,81146 | |||
Adjusted R Square ,80650 | |||
Standard Error ,68669 | |||
| Analysis of Variance : |
|
|
| DF Sum of Squares | Mean Square |
|
Regression Residuals | 1 77,121477 38 17,918483 | 77,121477 ,471539 |
|
P = 163,55269 | Signif F = ,0000 |
|
|
------- | - — — Variables in the Equation — | - - - - - | - - - |
Variable | В SE В Beta | Т | Sig Т |
ALTER (Constant) | 1,569996 ,122764 ,900813 -2,728584 ,840793 | 12,789 -3,245 | ,0000 ,0025 |
Log-likelihood | Function = -97,528092 |
|
|
The following | new variables are being created: |
|
|
Name | Label |
|
|
WGT_1 | Weight for STAEDTE from WLS, MOD_ | 1 ALTER** | -1,400 |
Оптимальная степень оценивается при помощи логарифма функции правдоподобия; в данном случае максимальное значение получается при значении степени равном 1,4. Это значение используется для определения веса для каждого случая. К примеру, для трёхлетнего ребёнка вес равен
1/(31,4)=0,2148
Весовые показатели были добавлены в исходный файл под переменной с именем wgt_1. Затем повторно был выполнен расчёт регрессии. Корреляционный коэффициент при этом возрос до 0,90081, а мера определённости до 0,81146. Хотя эти изменения, а также изменение рассчитанных коэффициентов регрессии и констант незначительны, зато стала намного меньше соответствующая им стандартная ошибка.
47.gif
48.gif