Сравнение средних

Сравнение средних значений различных выборок относится к наиболее часто применяемым методам статистического анализа. При этом всегда должен быть выяснен вопрос, можно ли объяснить имеющееся различие средних значений статистическими колебаниями или нет. В последнем случае говорят о значимом различии.

При сравнении средних значений выборок предполагается, что обе выборки подчиняются нормальному распределению. Если это не так, то вычисляются медианы и для сравнения выборок используется непараметрический тест.

При сравнении средних значений выборок выделяют четыре различные тестовые ситуации:

•  сравнение двух независимых выборок

•  сравнение двух зависимых (спаренных) выборок

•  сравнение более двух независимых выборок

•  сравнение более двух зависимых выборок

В этих ситуациях соответственно применяются следующие статистические тесты:

•  t-тест для независимых выборок (тест Стьюдента)

•  t-тест для зависимых выборок

•  однофакторный дисперсионный анализ

•  однофакторный дисперсионный анализ с повторными измерениями

 Первые три из этих тестов вызываются с помощью меню Analyze (Анализ) Compare Means (Сравнение средних)

Чтобы провести однофакторный дисперсионный анализ с повторными измерениями (очень часто встречающаяся тестовая ситуация) надо вызвать команду меню Analyze (Анализ) General Linear Model (Общая линейная модель) Repeated Measures... (Повторные измерения)

Сначала мы рассмотрим тесты, вызов которых происходит посредством пункта меню Compare Means. Для примера мы возьмем данные исследования гипертонии в файле hyper.sav (см. главу 9).

•  Загрузите файл hyper.sav.

•  Выберите в меню команды Analyze (Анализ) Compare Means (Сравнение средних)

В подменю содержатся, в частности, t-тест для независимых выборок (Independent-Samples Т Test), t-тест для парных выборок (Paired-Samples Т Test) и однофакторный дисперсионный анализ (ANOVA) для сравнения нескольких независимых выборок ( One-Way ANOVA).

Еще один тест, включенный в данное подменю, это t-тест случайной выборки, используемый для сравнения с заданным значением (One-Sample T Test), рассматривается в разделе 13.5. В подпункте меню Means... (Средние) вычисляются средние значения раздельно по категориям группирующей переменной; здесь также можно проверить существование значимого различия при помощи однофакторного дисперсионного анализа. В этом отношении данный подпункт предоставляет меньше возможностей, чем подпункт One-Way ANOVA..., и поэтому здесь не рассматривается.

13.1 Сравнение двух независимых выборок

Мы хотим проверить, значительно ли различается действие двух групп медикаментов на людей в зависимости от их возраста. Такое различие было бы, конечно, нежелательным, так как в этом случае разницу в действии лекарств можно было бы объяснить разным возрастным составом пациентов.

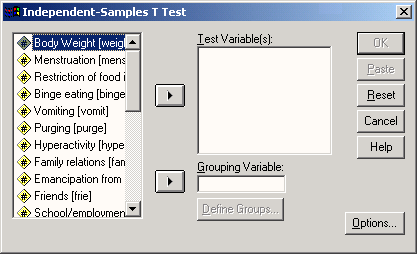
•  Выберите в подменю команду Independent-Samples T Test... (t-тест для независимых выборок)

Откроется диалоговое окно Independent-Samples T Test (см. рис. 13.1).

•  В списке исходных переменных щелкните на переменной а и щелчком на кнопке с треугольником перенесите ее в список тестируемых переменных (Test Variable(s)).

•  Таким же способом перенесите переменную med в поле Grouping Variable (Группирующая переменная).

•  Щелчком на кнопке Define Groups... (Определить группы) открывается окно, в котором можно ввести значения двух категорий для группирующей переменной. Мы будем сравнивать две группы, удовлетворяющие условиям соответственно med = 1 и med = 2. Поэтому внесите в поле Group 1 (Группа 1) значение 1, а в поле Group2 — значение 2.

•  Щелчком на кнопке Continue вернитесь в основное диалоговое окно.

•  Теперь следует выяснить, какие параметры установлены по умолчанию. Щелкните для этого на кнопке Options... (Параметры). Не изменяя настроек, щелкните на кнопке Continue и вернитесь в основное диалоговое окно.

Рис. 13.1: Диалоговое окно Independent-Samples T Test

•  Запустите t-тест, щелкнув на ОК. В окне просмотра появятся следующие результаты:

Group Statistics (Статистика групп)

Лекарство	N	Mean (Среднее)	Std. Deviation (Стандартное отклонение)	Std. Error Mean (Стандартная ошибка среднего)
Возраст	Альфасан	87	62,24	11,19	1,20
	Бетасан	87	61,98	11,96	1,28

Independent Samples Test (Тест для независимых выборок)

		Levene's Test for Equality of Variancies (Тест Левена на равенство дисперсий)		t-test for Equality of Means (Тест Стьюдента на равенство средних)
		F	Sig. (Значи-мость)	Т	df	Sig. (2-tailed) (Значимость (двусто- ронняя))	Mean Diffe-rence (Разность средних)	Std. Error Differe-псе (Станда- ртная ошибка разницы)	95 % Confidence Interval of the Difference (Довери-тельный интервал разницы)
Lower (Нижняя граница)	Upper (Верхняя граница)
Возраст	Equal variances assumed (Дис-персии равны)	,54	,462	,151	172	,880	,26	1,76	-3,20	3,73
	Equal variances not assumed (Ди- сперсии не равны)			,15'	171,249	,880	,26	1,76	-3,20	3,73

Выведенные результаты содержат:

•  количество наблюдений, средние значения, стандартные отклонения и стандартные ошибки средних в обеих группах,

•  результаты теста Левена на равенство дисперсий.

Как правило, гипотеза о равенстве (гомогенности) дисперсий не принимается, если тест Левена дает значение р < 0,05 (гетерогенность дисперсий). Для случаев как гомогенности (равенства), так и гетерогенности (неравенства) выводятся следующие характеристики:

•  результаты t-теста: значение распределения t, количество степеней свободы df, вероятность ошибки р (под обозначением "Значимость (2-сторонняя)"), а также

•  разница средних значений, ее стандартная ошибка и доверительный интервал.

В данном примере мы не получаем значимого различия воздействия двух группами лекарств по возрасту (р = 0,880).

В следующем t-тесте мы проверим, различается ли действие двух групп лекарств по так называемому индексу Брока. Этот индекс, разработанный одним парижским хирургом, предусматривает, что нормальный вес человека можно определить из следующего уравнения:

Нормальный вес (кг) = Рост (см) — 100

Если взять отношение фактического веса человека к нормальному весу по этой рормуле, то мы получим процентный показатель, который у людей с нормальным весом равен 100, у людей с избытком веса > 100 и т.д.

Индекс Брака =((Вес в кг)/(Рост в см - 100)) • 100

•   Определим на основе существующих переменных новую переменную, для чего выберем команды меню Transform (Преобразовать) Compute... (Вычислить)

•  В поле выходной переменной (Target Variable) задайте новое имя "broca", а в поле численного выражения (Numeric Expression) введите выражение gew I (gr- 100) * 100

•  Щелкните на кнопке ОК. Теперь можно командами меню Analyze (Анализ) Compare Means (Сравнение средних) Independent Samples T Test... (t-тест для независимых выборок) описанным выше способом провести t-тест для новой переменной broca.

И этот тест показывает, что между двумя труппами лекарств не наблюдается значимого различия по индексу Брока (р = 0,233).

13.2. Сравнение двух зависимых выборок

Сейчас мы выясним, значимо ли изменяется содержание холестерина через месяц : осле начала приема лекарств. Для этого мы сравним переменные cho10 и cho11 при помощи t-теста для зависимых выборок. В этом тесте будут участвовать данные всех пациентов, независимо от группы принимаемых лекарств.

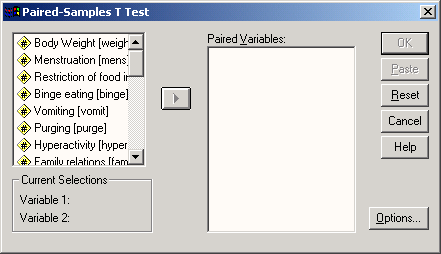
•  Выберите в соответствующем подменю команду Paired-Samples Т Test... (t-тсст для парных выборок) 

Откроется диалоговое окно Paired-Samples T Test.

Рис. 13.2: Диалоговое окно Paired-Samples T Test

•  Перенесите переменные cholO и choll из списка исходных переменных в поле парных переменных (Paired Variables).

•  Щелкните на ОК, чтобы начать вычисления. В окне просмотра появятся следующие результаты:

Paired Samples Statistics (Статистика для парных выборок)

Mean	N	Std. Deviation	Std. Error Mean
Pair (Пары)	Холестерин, исходный	237,27	174	49,42	3,75
	Холестерин, через 1 мес.	239,20	174	49,51	3,75

Paired Samples Correlations (Корреляции для парных выборок)

N	Correlation (Корреляция)	Sig. (Значимость)
Pair (Пары)	Холестерин, исходный & Холестерин, через 1 мес.	174	,861	,000

Paired Samples Test (Тест для парных выборок)

Paired Differences (Парные разницы)					Т	df	Sig. (2-tailed)
Mean	Std. Devi-ation	Std. Error Mean	95% Confi-dence Interval of the Diffe-rence
					Lower	Upper
Pair (Пары)	Холе- стерин, исходный -Холе- стерин, через 1 мес.	-1,93	26,09	1,98	-5,83	1,98	-,974	173	,332

Результаты, выведенные в окне просмотра, содержат:

•  средние значения, количество наблюдений, стандартные отклонения и стандартные ошибки средних для обеих переменных,

•  коэффициент корреляции (момент произведений Пирсона) между переменными и значимость его отклонения от нуля,

•  среднее значение, количество наблюдений, стандартное отклонение и стандартная ошибка разницы,

•  результаты t-теста: тестовая величина, полученная из распределения Стьюден-та, количество степеней свободы df, вероятность ошибки р, обозначенная "Sig. (2-tailed)").

Значимого изменения содержания холестерина за один месяц после начала приема лекарств не наблюдается (р = 0,332).

Повторим вычисления, но теперь только для пациентов, принимавших альфасан (переменная med имеет значение 1; условие med = 1).

•  Выберите в меню команды Data (Данные) Select Cases... (Выбрать наблюдения)

•  Выберите опцию If condition is satisfied... (Если выполняется условие). Щелчком на кнопке If... (Если) откройте диалоговое окно, в котором можно сформулировать условие. Введите в соответствующем поле условие "med = 1".

•  Щелкните на кнопке Continue, а в основном диалоге — на кнопке ОК.

•  Снова запустите t-тест. Теперь он будет выполнен только для наблюдений (N = 87), относящихся к первой группе лекарств. Мы снова получим незначимый результат (р = 0,666).

•  Чтобы последующий анализ снова можно было проводить с использованием всех наблюдений, откройте диалоговое окно Select Cases и выберите в нем опцию All cases (Все наблюдения).

13.3 Сравнение более двух независимых выборок

Далее мы исследуем, существует ли значимое различие веса (переменная gr) между четырьмя разными возрастными группами (переменная ak).

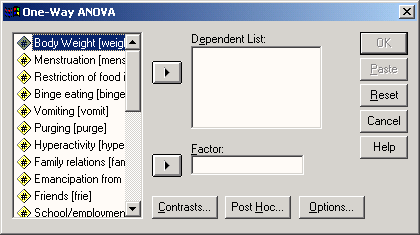
•  Выберите в подменю команду One-Way ANOVA... (Однофакторный дисперсионный анализ)

Подобная возможность есть и в первом пункте подменю (Means...), но она дает значительно более ограниченные возможности для анализа, и поэтому мы ее не рассматриваем. Появится диалоговое окно One-Way AN OVA.

•  Перенесите переменную gr в список зависимых переменных (Dependent List), a переменную ak — в поле Factor (Фактор).

•  Посмотрите, какие параметры можно задать для этого теста (кнопка Options...). Задайте вывод описательной статистики (флажок Descriptive) и проверку на гомогенность дисперсий (флажок Homogeneity-of-variance).

•  Чтобы выполнить апостериорный тест, вернувшись в основное диалоговое окно, щелкните на кнопке Post Нос... Откроется диалоговое окно One-Way ANOVA: Post Hoc Multiple Comparisons (Однофакторный дисперсионный анализ: апостериорные множественные сравнения) рис. 13.4.

•  Выберите тест Дункана (флажок Duncan). При значимом результате дисперсионного анализа этот тест показывает, какие именно возрастные группы значимо отличаются друг от друга. По умолчанию установлен уровень значимости 0,05; можно выбрать и другое значение.

•  Запустите тест, щелкнув на ОК.

Рис. 13.3: Диалоговое окно One-Way ANOVA

Рис. 13.4: Диалоговое окно One-Way AN OVA: Post Hoc Multiple Comparisons

В окне просмотра появятся следующие результаты:

Descriptives (Описательная статистика)

Рост
N	Mean	Std. Devi-ation	Std. Error	95 % Confidence Interval for Mean (95 % доверительный интервал среднего).		Mini-mum	Maxi-mum
				Lower Bound	Upper Bound
до 55 лет	52	169,10	8,21	1,14	166,81	171,38	150	185
56ч 65 лет	51	164,82	7,62	1,07	162,68	166,97	146	185
66ч75 лет	47	162,47	7,22	1,05	160,35	164,59	145	175
>75 лет	24	162,67	7,38	1,51	159,55	165,78	150	178
Total	174	165,17	8,08	61	16396	166,38	145	185

Test of Homogeneity of Variances (Тест гомогенности дисперсий)

Рост
Levene Statistic (Статистика Левена)	dfl	df2	Sig.
,639	3	170	591

ANOVA (Дисперсионный анализ)

Рост
Sum of Squares (Сумма квадратов)	Df	Mean Square (Средний квадрат)	F	Sig. (Значимость)
Between Groups (Между группами)	1301,200	3	433,733	7,380	,000
Within Groups (В группах)	9990,966	170	58,770
Total	111292,167	173

Апостериорные тесты Гомогенные подгруппы

Рост

Dunean"
Возрастной класс	N	Subset for alpha = ,05 (Подгруппа для альфа = ,05).
		1	2
66-75 лет	47	162.47
>75 лет	24	162,67
56-65 лет	51	164,82
до 55 лет	52	169,10
Sig. (Значимость)	,201	1,000

Means for groups in homogeneous subsets are displayed (Показаны средние значения для групп внутри гомогенных подгрупп).

a. Uses Harmonic Mean Sample Size = 39,300 (Используется гармоническое среднее для размера выборки = 39,300).

b. The group sizes are unequal. The harmonic mean of the group sizes is used. Type I error levels are not guaranteed. (Размеры групп неодинаковы. Используется гармоническое среднее размеров групп. Уровни ошибок типа I не гарантируются).

Выведенные результаты содержат:

•  количество наблюдений, средние значения, стандартные отклонения и стандартные ошибки средних, 95 % доверительные интервалы, минимумы и максимумы для всех слоев фактора,

•  результаты теста Левена на гомогенность дисперсий,

•  типовую схему дисперсионного анализа, включая вероятность ошибки р (значимость) для оценки общей значимости,

•  результаты многорангового теста Дункана.

В этом примере дисперсионный анализ дает максимально значимый результат (р < 0,001). Тест Дункана выделяет две гомогенные подгруппы (со стандартным значением р = 0,05), одна из которых включает возрастной класс до 55 лет, а другая — три остальных класса. Это означает, что возрастной класс до 55 лет значимо отличается от трех других возрастных классов, которые, в свою очередь, не обнаруживают значимого различия между собой.

Уменьшение роста с увеличением возраста может быть связано с тем, что в старших возрастных классах преобладают женщины, рост которых мал по сравнению с мужчинами, что и вызывает данный эффект. Повторим этот анализ для категорий пола. Окажется, что у мужчин факт уменьшения роста с увеличением возраста подтверждается, а для женщин — нет.

Далее мы подробно рассмотрим имеющиеся в диалоговом окне AN OVA кнопки Contrasts (Контрасты), Post Hoc... и Options..., а также возможности, которые они предоставляют.

13.3.1 Разложение на составляющие тренда

Сумму квадратов между группами можно разложить на линейные или полиномиальные (до 5 степени включительно) составляющие тренда.

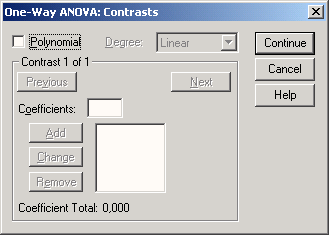
•  В диалоговом окне ANOVA щелкните на кнопке Contrasts... Появится диалоговое окно One-Way ANOVA: Contrasts (Однофакторный дисперсионный анализ: Контрасты).

Рис. 13.5: Диалоговое окно One-Way AN OVA: Contrasts

• Установите флажок Polynomial (Многочлен); после этого в списке Degree (Степень) можно будет выбрать порядок многочлена (линейный, квадратный, кубический, биквадратный или 5-й степени).

13.3.2 Априорные контрасты

Различия средних значений зависимых переменных, получаемые на базе априорных контрастов, можно подвергнуть t-тесту. Эта процедура называется априорным множественным сравнением. Контрасты определяются как последовательность (линейная комбинация) коэффициентов, каждый из которых соответствует отдельной категории независимой переменной.

Для коэффициентов, используемых при определении контрастов, можно задавать положительные, отрицательные, целые и дробные значения. Категории независимой переменной, соответствующие отрицательным коэффициентам, комбинируются, эти комбинации сопоставляются с комбинациями категорий, которые соответствуют положительным коэффициентам. Категории, которым соответствуют нулевые коэффициенты, не учитываются. Сумма всех коэффициентов должна равняться нулю.

В нашем примере сравнивались четыре возрастных класса (категории 1 -4) по переменной роста. Допустим, нам требуется сопоставить первую возрастную группу и комбинацию из трех остальных групп; для этого мы выберем нижеследующие априорные коэффициенты:

-3 1 1 1

Если же требуется сравнить комбинацию первых двух групп с последней группой, следует выбрать такие коэффициенты:

-1-1 0 2

Для определения описанных контрастов по вышеописанной процедуре множественного сравнения откроем в диалоге AN OVA вспомогательное диалоговое окно Contrasts. В поле Coefficients этого диалогового окна введем первый коэффициент и щелкнем на кнопке Add. Таким же образом вводятся остальные коэффициенты.

Когда все коэффициенты задачи введены, можно кнопкой Next (Следующий) перейти ко вводу следующей комбинации коэффициентов. После задания коэффициентов для всех требуемых контрастов кнопкой Continue закройте это диалоговое окно. Можно задать до десяти контрастов, каждый из которых содержит до пятидесяти коэффициентов.

13.3.3 Апостериорные тесты

Чтобы провести апостериорные тесты множественного сравнения средних, щелкните в диалоговом окне ANOVA на кнопке Post Hoc... В появившемся окне можно выбрать 'Мин или несколько из восемнадцати тестов, которые производят такие сравнения для всех групп:

•  Наименьшая значимая разность (многократный t-тест без альфа-коррекции) —LSD

•  Тест Бонферрони (многократный t-тест с альфа-коррекцией) — Bonferroni

•  t-тест Сидака (Sidak)

•  Тест Шеффе (Scheffe)

•  Процедура Райана-Эйно-Габриеля-Уэлша, или F-тест (R-E-G-W-F)

•  Процедура Райана-Эйно-Габриеля-Уэлша, или определение стьюдентизированного критерия размаха выборки (R-E-G-W-Q)

•  Тест Стьюдента-Иьюмена-Кейлса (S-N-K)

•  Тест Тьюки (Tukey) 

• b Тьюки (Tukey's b)

•  Тест Дункана (Duncari)

•  GT2 Хохберга (Hochberg's GT2)

•  Тест Габриеля (Gabriel)

•  Тест Уоллера-Дункана (Waller-Duncan)

•  t-тест Даннета, одно- и двусторонний (Dunnetf)

•  Т2 Тэмхена (Tamehane 's T2)

•  ТЗ Даннета (Dunnett's ТЗ)

•  Тест Геймса-Ховелла (Games-Howell)

•  С Даннета (Dunnett's С).

Средние значения групп выводятся в порядке возрастания.

13.3.4 Другие параметры

В диалоговом окне ANOVA: Options, кроме способа обработки пропущенных значений, можно дополнительно задать вывод описательной статистики по группам (средних значений, стандартных отклонений, стандартных ошибок, минимумов, максимумов, 95 % доверительных интервалов и количеств наблюдений), а также проверку на гомогенность дисперсий посредством теста Левена. Можно также задать вывод линейчатых графиков средних значений.

13.4. Сравнение более чем двух зависимых выборок

На основе данных по гипертонии исследуем, значимо ли изменяется содержание холестерина в течение четырёх промежутков времени (такое сравнение для первых двух промежутков времени мы уже провели в параграфе 13.2).

Для достижения этой цели подходит однофакторный дисперсионный анализ с повторными измерениями. Пользователи SPSS, работавшие с этим пакетом на больших компьютерах, знают, что выполнить эту весьма распространенную операцию можно было только с помощью процедуры MANOVA (многомерный дисперсионный анализ). Ясно, что эта процедура предназначена для разнообразных методов многомерного анализа, но может быть использована при одномерном дисперсионном анализе с повторными измерениями.

Начиная с версии 7 SPSS процедура MANOVA была заменена процедурой GLM (General Linear Model). Однако и в текущей версии процедура MANOVA по прежнему остается доступной при использовании программного синтаксиса.

Разнообразные возможности анализа, предоставляемые этими процедурами (GLM и MANOVA), обеспечиваются ценой уже практически необозримого количества команд, спецификаций, параметров и ключевых слов. Даже при решении такой простой задачи, как рассматриваемая, надо уметь ориентироваться в этом многообразии. Несколько подробнее процедура GLM рассматривается в главе 17; однако в рамках этой книги невозможно охватить всю широту диапазона возможностей, предоставляемых этой процедурой.  Теперь перейдем к решению нашей задачи при помощи однофакторного дисперсионного анализа с повторными измерениями.

•  Загрузите файл hyper, sav.

•  Выберите в меню команды Analyze (Анализ) General Linear Model (Общая линейная модель) Repeated Measures... (Повторные измерения)

Откроется диалоговое окно Repeated Measures Define Factors) (Определить фактор(ы) для повторных измерений).

В данном примере мы подвергнем анализу четыре переменных: cho10, cho11, cho16 и chol12; следовательно, фактор повторных измерений будет задаваться четырьмя уровнями (слоями).

•  Введите число 4 в поле Number of Levels (Количество уровней). По умолчанию принимается имя фактора faktorl; при желании можно задать для него любое другое i имя (например, "время").

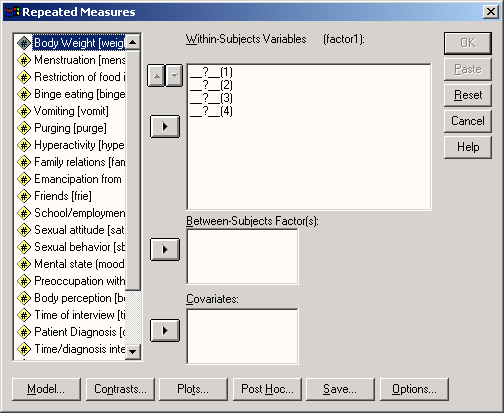
•  Щелкните на кнопке Add. Других факторов повторных измерений у нас нет, поэтому можно сразу закрыть этот диалог кнопкой Define (Определить). Появится диалоговое окно Repeated Measures (Повторные измерения) (см. рис. 13.7).

•  Перенесите переменные cho10, choll, cho16 и chol12 в список Within-Subject Variables (Переменные внутри субъекта); далее кнопками, которые находятся внизу диалогового окна, можно установить дополнительные параметры но мы не будем их рассматривать.

•  Запустите вычисления, щелкнув на ОК.

Рис. 13.6: Диалоговое окно Repeated Measures Define Factor(s)

Рис. 13.7: Диалоговое окно Repeated Measures

•  Проанализируйте результаты, появившиеся в окне просмотра.

Вы убедитесь, что для неподготовленного пользователя толкование полученных результатов расчёта может составить большие трудности. Подробнее о них мы поговорим в главе 17. Теперь же мы ограничимся указанием, что результаты обычного дисперсионного анализа содержатся в строке "Sphericity assumed" (Предположение о сферичности) таблицы вывода, приведенной ниже:

Tests of Within-Subjects Effects (Тест эффектов внутри субъекта)

Measure: MEASURE_1
Source (Источник)		Type III Sum of Squares (Сумма квадратов типа III)	df	Mean Square (Среднее квадратов)	F	Sig. (Значи-мость)
FACTOR1	Sphericity Assumed (Прини- мается гипотеза о сферич- ности)	3381,822	3	1127,274	2,653	,048
	Greenhouse- Geisser	3381,822	2,509	1347,779	2,653	,058
	Huynh-Feldt	3381 ,822	2,549	1326,675	2,653	,058
	Lower Bound	3381,822	1,000	3381,822	2,653	,105
Error (FACTOR1)	Sphericity Assumed (Прини- мается гипотеза о сферич- ности)	220504,678	519	424,865
	Greenhouse- Geisser	220504,678	434,088	507,972
	Huynh-Feldt	220504,678	440,994	500,018
	Lower Bound	220504,678	173,000	1274,594

Вероятность ошибки р составляет 0,048, что указывает на значимое различие между отдельными моментами времени. К сожалению, даже в 10-й версии SPSS отсутствует возможность провести апостериорный тест для повторных измерений, чтобы выяснить, какие именно промежутки времени значимо отличаются друг от друга. В случае, если выявлены значимые отличия, как в рассмотренном примере, пользователю не остается ничего другого, кроме выполнения парного t-теста.

13.5 Мест одной выборки

Этот тест позволяет выяснить, отличается ли среднее значение, полученное на основе данной выборки, от предварительно заданного контрольного значения.

Мы проверим, отличается ли средний показатель холестерина, полученный при исследовании гипертонии, от значения 229, которое могло быть определено в каком-либо другом исследовании.

•  Загрузите файл hyper.sav.

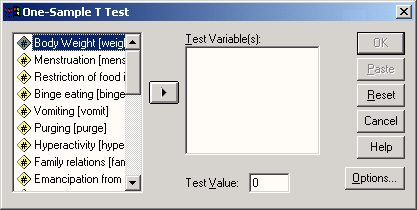
•  Выберите в меню команды Analyze (Анализ) Compare Means (Сравнение средних) One-Sample T Test... (t-тест для одной выборки) Откроется диалоговое окно One-Sample T Test (см. рис. 13.8).

•  Перенесите переменную cho10 в поле Test Variable(s) и введите в поле Test Value (Контрольное значение) значение 229.

•  Запустите вычисления, щелкнув на ОК.

Результаты, показанные в окне просмотра, свидетельствуют о том, что в данном исследовании средний исходный уровень холестерина составляет 237,27, что значимо (р = 0,029) отличается от контрольного значения 229.

Рис. 13.8: Диалоговое окно One-Sample T Test

One-Sample Statistics (Статистика одной выборки)

N	Mean	Std. Deviation	Std. Error Mean
Холестерин, исходный	174	237,27	49,42	3,75

One-Sample Test (Тест пои одной выборке)

Test Value = 229
T	df	Sig. (2-tailed)	Mean Difference	95 % Confidence Interval of the Difference
				Upper	Lower
Холестерин, исходный	2,207	173	,029	8,27	,88	15,66

Кнопкой Options... (Параметры) можно задать вместо 95 % любой другой доверительный интервал. Значение доверительного интервала может принимать значения в промежутке от 1 до 99%.