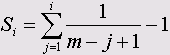Глава 8. Модификация данных
Глава 8. Модификация данных
1. Модификация данных
Модификация данных
Для проведения анализа часто бывает необходимо выполнить преобразование данных. На основе первоначально собранных данных можно создать новые переменные и изменить кодирование. Подобные преобразования называются модификацией данных.
В SPSS существует много возможностей для модификации данных. К важнейшим из них относятся:
-
Вычисление новых переменных путем использования различных арифметических выражений (математических формул)
-
Подсчет частоты появлений определенных значений
-
Перекодирование значений
-
Вычисление новых переменных при выполнении определенного условия
-
Агрегирование данных
-
Ранговые преобразования
-
Вычисление весов наблюдений
Разделы этой главы посвящены всем перечисленным возможностям модификации данных.
8.1 Вычисление новых переменных
8.1 Вычисление новых переменных
Путем вычислений в SPSS можно образовать новые переменные и добавить их в файл данных. Так, например, в медицинском исследовании (см. главу 9, файл hyper.sav) в два момента времени (до и после приема лекарства) проводились измерения систолического кровяного давления, которые фиксировались в переменных rrs0 и rrsl.
Если нас интересует изменение давления между двумя этими моментами, было бы глупо каждый раз вычислять разницу двух значений и вручную вводить ее в новую переменную. Эту работу можно переложить на компьютер, который сделает ее быстро и, главное, без ошибок. Для этого поступите следующим образом:
-
Загрузите файл hyper.sav в редактор данных.
-
Выберите в меню команды Transform (Преобразовать) Compute... (Вычислить) Откроется диалоговое окно Compute Variable (Вычислить переменную).
Рис. 8.1: Диалоговое окно Compute Variable
В поле Target Variable (Выходная переменная) указывается имя переменной, которой присваивается вычисленное значение. В качестве выходной переменной может служить уже существующая или новая переменная. В поле Numeric Expression (Численное выражение) вводится выражение, применяемое для определения значения выходной переменной. 3 этом выражении могут использоваться имена существующих переменных, константы, арифметические операторы и функции.
-
Введите в поле Target Variable имя rrsdiff, а в поле Numeric Expression формулу rrs0— rrsl. Зту формулу можно ввести либо вручную, либо используя список переменных и клавиатуру диалогового окна. Кнопка с треугольником позволяет копировать в поле формулы имена переменных, а кнопки клавиатуры — вставлять цифры и знаки.
-
Щелкните на кнопке Type&Label... (Тип и метка).
Откроется диалоговое окно Compute Variable: Type and Label (Вычислить переменную: Тип и метка).
Здесь можно задать метку для новой переменной rrsdiff. В поле Label введите текст Изменение сист. кровяного давления и щелкните на кнопке Continue.
-
В диалоговом окне Compute Variable щелкните на кнопке ОК.
Рис. 8.2: Диалоговое окно Compute Variable: Type and Label
Примечание: Выбранные опции соответствуют следующему командному синтаксису:
COMPOTE rrsdiff = rrs0 - rrsl.
VARIABLE LABELS rrsdiff = "Изменение сист. кровяного давления".
EXECUTE.
Общий формат команды COMPUTE имеет следующий вид:
COMPUTE целевая_переменная = арифметическое_выражение.
Команда EXECUTE считывает данные и выполняет предшествующие команды преобразования. В файл данных добавляется новая переменная rrsdiff. Теперь ее, как и прочие переменные, можно применять для вычислений. Для SPSS нет разницы, введены ли значения переменных через редактор данных или вычислены по формуле.
Вместо слова формула мы будем использовать в дальнейшем понятие численное выражение. При формулировке таких численных выражений нужно соблюдать определенные правила, которые представлены в следующем разделе.
1.gif

2.gif

8.1.1 Формулировка численных выражений
8.1.1 Формулировка численных выражений
Для построения численных выражений можно применять следующие арифметические операторы:
Арифметические операторы
+ | Сложение |
- | Вычитание |
* | Умножение |
/ | Деление |
** | Возведение в степень |
С помощью арифметических операторов в численных (арифметических) выражениях можно задавать такие основные действия, как сложение и вычитание.
Так как структура выражений может быть сложной, следует учитывать следующие приоритеты арифметических операторов:
Приоритет | Оператор | Значение |
1 | () | Оператор скобок |
2 | ** | Возведение в степень |
3 | * | Умножение |
/ | Деление | |
4 | + | Сложение |
— | Вычитание |
Операции более высокого приоритета выполняются раньше операций с более низким приоритетом; приоритет 1 наивысший, а 4 — самый низкий. Далее на нескольких типичных примерах показано, на что следует обращать внимание при записи численных выражений. Если вы хотите выразить только что вычисленное изменение кровяного давления в процентах от исходного значения, надо составить следующую команду:
COMPUTE rrsdiff = (rrsl - rrsO) / rrs0 * 100 .
В этой формуле выполняются операции трех разных видов, имеющие разные приоритеты. Так, умножение и деление выполняются всегда перед сложением и вычитанием, если только, как в данном примере, скобки не определяют другую последовательность выполнения.
Если рост (в см) записан в переменной gr, и вы хотите определить на его основе нормальный вес, который обычно равен росту в см минус 100, команда, которая создает для этой величины новую переменную, будет следующей:
COMPUTE ng = gг - 100 .
Если же требуется вычислить избыточный вес как разницу фактического веса, который хранится в переменной gew, и этой новой величины, для этого служит команда
COMPUTE uegew = gew — ng .
Отрицательное значение uegew указывает на недостаточный вес. Оба выражения можно объединить:
COMPUTE uegew = gew — (gr — 100) .
Это можно также записать в виде
COMPUTE uegew = gew — gr + 100 .
Формула для определения избыточного веса в процентах к нормальному:
COMPUTE puegew = (gew — ng) / ng * 100 .
Без использования вспомогательной переменной ng эта формула имеет вид
COMPUTE puegew = (gew - (gr - 100)) / (gr - 100) * 100 .
Эта запись выглядит уже довольно сложной и имеет тот недостаток, что выражение gr — 100 должно быть вычислено дважды. Разумеется, при высокой производительности компьютера это не так важно.
Мы уже видели, что в арифметических выражениях могут участвовать переменные и константы. Сейчас мы рассмотрим применение и них функций, которые встроены в SPSS. Если нас интересует не само изменение кровяного давления, а только его абсолютная ветчина, в этом случае можно применить функцию ABS:
COMPUTE rrsd = ABS(rrsl - rrs0)
Чтобы вычислить десятичный логарифм переменной х, применяется функция LG10:
COMPUTE у = LG10(x)
Мы также можем вычислить гипотенузу по теореме Пифагора, использовав функцию SQRT для извлечения квадратного корня и оператор возведения в степень:
COMPUTE с = SQRTfa ** 2 + b ** 2) .
Аргументы функций сами могут быть арифметическими выражениями: Если вы не хо-:ите работать с командами синтаксиса SPSS, можно, как показано в начале главы, применить диалоговое окно Compute Variable. В этом случае в редакторе условий достаточно вместо
COMPUTE rrsd = rrs1 - rrs0 .
ввести просто
rrsd = rrsl - rrs0 для достижения той же цели — вычисления изменения кровяного давления rrsd.
8.1.2 Функции
8.1.2 Функции
Из числа функций, которые отображаются в диалоговом окне Select Cases: If, мы рассмотрели только логические и строковые функции. Остальные функции можно разделить на следующие классы:
-
арифметические функции
-
статистические функции
-
функции даты и времени
-
функции обработки отсутствующих значений
-
функции извлечения значений наблюдений
-
статистические функции распределения
-
функции генерации случайных чисел.
Параметрами функций могут быть переменные, константы или выражения. Параметры заключаются в круглые скобки; несколько параметров отделяются друг от друга запятыми, например, SUM (5, 8, 10). Функция SUM вычисляет сумму трех параметров. SUM (5, 8, 10) возвращает значение 23.
Арифметические функции
-
ABS (numexpr): Функция ABS возвращает абсолютное значение. Если переменная celsius имеет значение -6,5, ABS (celsius) возвращает 6,5, a ABS (celsius + 3) — значение 3,5.
-
RND (numexpr): Функция RND округляет до ближайшего целого числа. Если переменная celsius имеет значение 3,6, RND (celsius) возвращает 4, a RND (celsius + 6) — значение 10.
-
TRUNC (numexpr): Функция отбрасывает дробную часть значения; округления не происходит. Если переменная celsius имеет значение 3,9, TRUNC (celsius) возвращает 3, a TRUNC (celsius + 4) — значение 7.
-
MOD (numexpr, modulus): Функция MOD возвращает остаток от деления первого аргумента (numexpr) на второй (modulus). Если переменная jaehr имеет значение 1994, MOD (jaehr, 100) возвращает 94.
-
SQRT (numexpr): Функция SQRT возвращает квадратный корень. Если переменная zahll имеет значение 9, SQRT (zahll) возвращает значение 3.
-
ЕХР (numexpr): Показательная функция.
-
LG10 (numexpr): Десятичный логарифм.
-
LN (numexpr): Натуральный логарифм.
-
ARSIN (numexpr): Арксинус.
-
ARTAN (numexpr): Арктангенс.
-
SIN (numexpr): Синус.
-
COS (numexpr): Косинус.
В тригонометрических функциях аргументы задаются в радианах.
Статистические функции
Статистические функции могут иметь любое количество параметров.
-
SUM (numexpr, numexpr,...): Функция SUM возвращает сумму значений допустимых аргументов. SUM (zahll, zahll, zah!3) возвращает сумму значений трех переменных.
-
MEAN (numexpr, numexpr,...): Функция MEAN возвращает среднее арифметическое допустимых аргументов. MEAN (42, 19, 29) возвращает значение 30.
-
SD (numexpr, numexpr,...): Функция SD возвращает стандартное отклонение значений допустимых аргументов.
-
VARIANCE (numexpr, numexpr,...): Функция VARIANCE возвращает дисперсию значений допустимых аргументов.
-
CFVAR (numexpr, numexpr,...): Функция CFVAR возвращает коэффициент вариации значений допустимых аргументов.
-
MIN (numexpr, numexpr,...): Функция MIN возвращает наименьшее из значений допустимых аргументов.
-
MAX (numexpr, numexpr,...): Функция МАХ возвращает набольшее из значений допустимых аргументов.
Функциям SUM, MEAN, MIN и МАХ требуется хотя бы один допустимый аргумент, функциям SD, VARIANCE и CFVAR — два. Остальные аргументы могут содержать отсуттвуюшие значения. Если это свойство, принятое по умолчанию, требуется деактивировать, то к имени функции через точку прибавляют количество необходимых аргументов, например, MEAN. 10. В этом случае значение функции вычисляется только тогда, когда существует хотя бы указанное количество аргументов (в данном примере 10).
Функции даты и времени
В SPSS очень часто в различных целях используются дата и время. Для ввода данных гтого типа в редакторе данных SPSS предоставляет ряд различных форматов, описанных в разделе 3.4.1. Существующие форматы можно просмотреть в диалоговом окне Variable Tуре (Тип переменной).
Мы рекомендует использовать общепринятый формат даты: указание числа месяца двумя цифрами, месяца — также двумя цифрами и года — четырьмя цифрами через течку: dd.mm.yyyy.
Экономии места за счет отбрасывания двух первых цифр года в последнее время, как известно, уделяется много внимания. При указании года двумя цифрами в качестве столетнего диапазона в SPSS принят срок с 1931 по 2030 г., следовательно, год 28 интерпретируется как 2028, а 32 — как 1932. В меню Edit (Правка) Options... (Параметры...) на вкладке Data (Данные) пользователь может самостоятельно задать столетний диапазон..
Если число или месяц можно записать одной цифрой, их не нужно дополнять спереди нулями. Таким образом, указание даты в следующих форматах будет допустимым:
20.6.1998
13.12.1887
1.10.2003
5.2.1997
Компьютер замечает противоречивое указание даты при вводе. Например, если попытаться ввести дату 29.2.1997, это значение не записано принято в ячейку.
Для времени мы рекомендуем формат hh:mm:ss, т.е. одна или две цифры для часов, минут и секунд через двоеточие. При отсутствии секунд можно также применять формат hh:mm. Примеры:
23:34:55
8:5:12
12:17:5
12:47 8:12
Дату и время, введенные в любом виде, SPSS преобразует во внутренний формат. Для даты это количество секунд, прошедших с 0 часов 15.10.1582 г. (момента введения григорианского календаря) до 0 часов заданного дня; для времени — количество секунд с 0 часов до заданного момента времени.
В принципе можно также хранить число, месяц, год, часы, минуты и секунды в отдельных переменных и определять дату или время во внутреннем формате при помощи соответствующих функций.
Всего в SPSS имеется 25 различных функций для работы с датой и временем. Важнейшие из них представлены ниже.
XDATE.MDAY(arg) | Выделяет из даты число |
XDATE.MONTH(arg) | Выделяет из даты месяц |
XDATE.YEAR(arg) | Выделяет из даты год |
XDATE.WKDAY(arg) | Номер дня недели (1 =' воскресенье, ,..., 7 = суббота) |
XDATE.JDAY(arg) | Номер дня в году |
XDATE.QUARTER(arg) | Номер квартала в году |
XDATE.WEEK(arg) | Номер недели в году |
XDATE.TDAY(arg) | Количество дней начиная с 15.10.1582 |
XDATE.DATE(arg) | Количество секунд начиная с 15.10.1582 |
DATE.DMY(d,m,y) | Преобразует данные числа месяца, месяца и года во внутреннюю дату |
DATE.MOYR(m.y) | Преобразует данные месяца и года во внутреннюю дату |
YRMODA(y,m,d) | Преобразует данные года, месяца и числа месяца (строго в приведенной последовательности) в количество дней начиная с 15.10.1582 |
XDATE.TIME(arg) | Количество секунд начиная с 0 часов |
TIME.HMS(h,m,s) | Преобразует данные часов, минут и секунд в секунды |
Функции даты и времени применяются чаще всего в ситуациях, когда требуется вычислить промежуток между двумя датами или моментами времени. Например, если имеется две даты, записанные в переменных datum 1 и datum2, длительность промежутка между ними в днях можно рассчитать по следующей формуле:
COMPUTE tage=XDATE.TDAY(datum2) - XDATE.TDAY(datural). EXECUTE.
Пример использования функции YRMODA приводится в разделе 8.8. Функции обработки пропущенных значений
-
VALUE (variable): Функция VALUE объявляет недействительным пользовательское пропущенное значение.
-
MISSING (variable): Функция MISSING возвращает значение 1 (или true), если переменная содержит пользовательское или системное пропущенное значение.
-
SYSMIS (variable): Функция SYSMIS возвращает значение 1 (или true), если переменная содержит системное пропущенное значение.
-
NMISS (variable,variable,...): Функция NMISS возвращает количество пропушен-нных значений в списке переменных.
-
NVALID (variable,variable,...): Функция NMISS возвращает количество допустимых значений в списке переменных.
Функции извлечения значений наблюдений
-
LAG (variable,n): Функция LAG возвращает значение соответствующей переменной за я наблюдений до текущего. Так, например, LAG( variable, I) позволяет получить значение переменной в предыдущем случае (см. первый пример в разделе 8.8).
Статистические функции распределения
В SPSS реализовано в совокупности 20 статистических функций распределения. Эти функций вычисляют значение вероятности для следующих распределений: ß-распределения, распределения Коши, хи-квадрат, экспоненциального распределения, Г-распределения, F-распределения, распределения Лапласа, логистического, логарифмически нормального. нормального распределений, распределения Парето, распределения Стьюдента, равномерного распределения, распределения Вейбулла (непрерывные функции), а также распределения Бернулли, биномиального, геометрического, гипергеометрического, негативно-биномиального распределений и распределения Пуассона (дискретные функции). Для 14 непрерывных функций распределения существуют соответствующие обратные функции.
Так, например, функция CDF.T(t,df) возвращает вероятность ошибки р для заданного значения функции распределения Стьюдента, t и числа степеней свободы df, функция IDF. T(p,df) возвращает значение t для заданных вероятности ошибки р и числа степеней свободы df.
Функции генерации случайных чисел
В SPSS реализовано в совокупности 24 функции генерации случайных чисел, в том теле для 20 встроенных статистических функций распределения; например функция RV.T(df) возвращает случайные числа, подчиняющиеся распределению Стьюдента при df степенях свободы. Функция UNIFORM (numexpr) генерирует равномерно распределенные случайные величины, находящиеся в интервале от 0 до 1, а ее аргумент задает начальное значение для генератора случайных чисел.
8.2 Подсчет частоты появлений определенных значений
8.2 Подсчет частоты появлений определенных значений
В SPSS есть возможность подсчитать количество появления одного и того же значения или значений для определенной переменной. Например, членам Дортмундского спортивного клуба задавались следующие вопросы:
Вопрос1: Вопрос 2: Вопрос3: | Укажите Ваш пол ... |
Укажите Ваш возраст ... | |
Какими из следующих видов спорта Вы активно занимаетесь: 3_1 : Плаванием: да/нет? 3_2: Гимнастикой: да/нет? 3_3: Легкой атлетикой: да/нет? 3_4: Волейболом: да/нет? 3_5: Теннисом: да/нет? 3 6: Велосипедным спортом: да/нет? 3_7: Футболом: да/нет? 3_8: Гандболом: да/нет? 3_9: Баскетболом: да/нет? |
Если во всех наблюдениях этого примера подсчитать число появлений значения 1 (= да) для переменных 3_1—3_9, то для каждого респондента мы получим количество видов спорта, которыми он активно занимается.
Для этого поступите следующим образом:
-
Загрузите файл sport.sav в редактор данных.
-
Выберите в меню команды Transform (Преобразовать) Count... (Подсчитать)
Откроется диалоговое окно Count Occurences of Values within Cases (Подсчитать количество значений в наблюдениях).
Рис. 8.3: Диалоговое окно Count Occurences of Values wirhin Cases
Это диалоговое окно разделено на следующие части:
-
Target variable (Выходная переменная): В поле Target variable указывается имя переменной, в которой будут содержаться подсчитанные значения.
-
Target Label (Метка): В поле Target Label указывается метка для выходной переменной.
-
Variables (Переменные): Этот список содержит переменные, выбранные из списка исходных переменных, хранящихся в файле данных, для которых нужно подсчитать определенные значения. Список не может одновременно содержать численные и строковые переменные.
-
Выделите в списке исходных переменных переменные v3_l—v3_9. Перенесите их в список переменных.
-
Присвойте выходной переменной имя sports и метку: «Количество разных видов спорта».
-
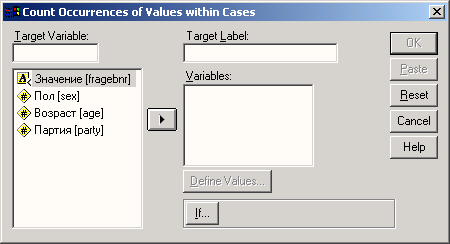
Щелкните на кнопке Define values... (Определить значения). Откроется диалоговое окно Count Values within Cases: Values to Count (Подсчитать значения в наблюдениях: какие значения?). (См. рис. 8.4.)
Рис. 8.4: Диалоговое окно Count Values within Cases:values to Count
Это диалоговое окно служит для определения подсчитываемых значений. Можно задать отдельное значение, диапазон или сочетание того и другого. В группе Value (Значение) можно выбрать один из следующих вариантов:
-
Value: Вводится отдельное значение, частоту которого необходимо подсчитать.
-
System missing (Системное пропущенное): Подсчитывается количество появлений системного пропущенного значения. В списке Values to count (Подсчитываемые значения) оно отображается как SYSMIS. Для строковых переменных этот вариант неприменим.
-
System- or user-missing (Пользовательские или системные пропущенные): Если выбрать этот вариант, будет подсчитано количество появлений всех пропущенных значений, как системных, так и пользовательских. В списке Values to count эти значения отображаются как MISSING.
-
Range through (Дипазон): Подсчитывается количество значений, находящихся в определенном диапазоне. Этот вариант также неприменим для строковых переменных.
-
Range: Lowest through (Диапазон: от наименьшего до): Подсчитывается количество значений, находящихся в диапазоне от наименьшего наблюдаемого до указанного. Этот вариант неприменим для строковых переменных.
-
Range: through highest (Диапазон: до наибольшего): Подсчитывается количество значений, находящихся в диапазоне от указанного до наибольшего наблюдаемого. Этот вариант неприменим для строковых переменных.
Если требуется подсчитать повторяемость нескольких значений, щелкните после выбора опции на кнопке Add (Добавить). В этом случае будет подсчитана частота повторений каждого значения, присутствующего в списке Values to count.
-
Задайте отдельное значение 1 и щелкните на кнопке Add.
-
Подтвердите ввод кнопкой Continue, а затем — ОК. В файл данных будет добавлена переменная sports, содержащая количество видов спорта, которыми занимается респондент.
3.gif
4.gif
8.3 Перекодирование значений
8.3 Перекодирование значений
Первоначально собранные данные можно перекодировать с помощью средств SPSS. Перекодирование численных данных необходимо, например, тогда, когда первоначальное разнообразие исходных данных не нужно для последующего анализа. В этом случае перекодирование означает уменьшение объема обрабатываемой информации. Перекодирование данных можно выполнить вручную или автоматически. Мы рассмотрим оба этих метода.
8.3.1 Ручное перекодирование
8.3.1 Ручное перекодирование
Для примера мы проанализируем результаты воскресного опроса (файл wahl.sav). Нас интересует процентное распределение опрашиваемых в классическом политическом спектре правые-левые. В этом случае переменную partei следует перекодировать и создать новую переменную lire (левые-правые). Новые значения будут определены следующим образом:
Левые:
СПДГ
Зеленые/Союз 90
ПДС
Правые:
ХДС/ХСС
СДП
Республиканцы
не определено:
нет данных
Прочие
Сравним значения переменной partei со значениями переменной lire:
Переменная partei Значения | Метки значений | Переменная lire Значения | Метки значений |
0 | нет данных | 0 | не определено |
1 | ХДС/ХСС | 2 | правые |
2 | СДП | 2 | правые |
3 | СДПГ | 1 | левые |
4 | Зеленые/Союз 90 | 1 | левые |
5 | ПДС | 1 | левые |
6 | Республиканцы | 2 | правые |
7 | Прочие | 0 | не определено |
Значение 1 (ХДС/ХСС) переменной partei соответствует значению 2 (правые) переменной lire, значение 2 (СДП) — значению 2 (правые), значение 3 (СДПГ) — значению 1 (левые) и т.д. Значение 0 переменной lire объявляется как отсутствующее.
Перекодирование производится следующим образом:
-
Загрузите файл wahl.sav в редактор данных.
-
Выберите в меню команды Transform (Преобразовать) Recede (Перекодировать)
Можно хранить перекодированные значения в той же переменной или перенести их в другую переменную. Если мы проведем перекодировку в прежней переменной, все ее старые значения будут стерты.
-
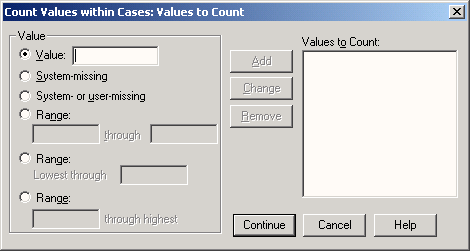
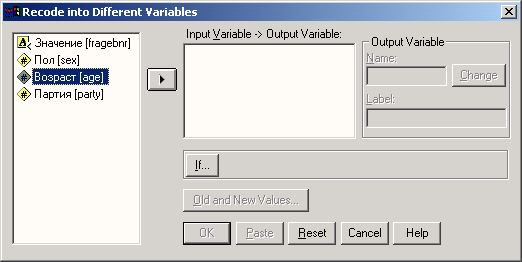
Выберите в подменю пункт Into Different Variables... (В другие переменные). Откроется диалоговое окно Recede into Different Variables (Перекодировать в другие переменные).
Рис. 8.5: Диалоговое окно Recede into Different Variables
Список исходных переменных содержит переменные файла данных. Здесь можно выбрать одну или несколько переменных для перекодирования. Если выбираются несколько переменных, все они должны быть одного типа.
-
Перенесите переменную partei (партия) в поле Input Variable -> Output Variable (Входная переменная > Выходная переменная). Вопросительный знак, добавленный в поле, говорит о том, что надо задать имя выходной переменной.
-
Введите в поле Name (Имя) текст lire. Щелкните на кнопке Change (Изменить). Вопросительный знак в поле Input Variable -> Output Variable будет заменен на lire.
-
Введите в поле Label обозначение: «Политический спектр». Подтвердите ввод, щелкнув на Change.
-
Чтобы установить значения, которые следует перекодировать, щелкните на кнопке Old and New Values... (Старые и новые значения). Откроется диалоговое окно Recede into Different Variables: Old and New Values.
Для осуществления каждого перекодирования надо указать значение или диапазон входной переменной и соответствующее значение выходной переменной. Перекодирование завершается щелчком на кнопке Add.
Это диалоговое окно разделено на следующие части. В группе Old Value (Старое значение) можно выбрать один из следующих вариантов:
Рис. 8.6: Диалоговое окно Recede into Different Variables: Old and New Values
-
Value: Вводится отдельное значение.
-
System missing (Системное пропущенное): С помощью этой опции значение входной переменной обозначается, как системное пропущенное. Это значение обозначается в списке значений переменных как SYSMIS. Такой вариант неприменим для строковых переменных.
-
System- or user-missing (Пользовательские или системные пропущенные): Эта опция служит для обозначения всех пользовательских или системных пропущенных значений. В списке значений переменных пользовательские пропущенные значения отображаются как MISSING.
-
Range through (Дипазон): Здесь можно задать замкнутый интервал значений. Этот вариант неприменим для строковых переменных.
-
Range: Lowest through (Диапазон: от наименьшего до): В этом случае будут перекодированы все значения от наименьшего наблюдаемого до указанного. Этот вариант неприменим для строковых переменных.
-
Range: through highest (Диапазон: до наибольшего): В этом случае будут перекодированы все значения от указанного до наибольшего наблюдаемого. Этот вариант неприменим для строковых переменных.
-
All other values (Все остальные значения): Эта опция касается всех еще не указанных значений. В списке значений переменных они отображаются как ELSE.
В группе New Value (Новое значение) можно выбрать один из следующих вариантов:
-
Value: Здесь вводится новое значение.
-
System missing (Системное отсутствующее): Эта опция служит для обозначения значения выходной переменной как системного отсутствующего значения. Значение появляется в списке значений переменных в виде SYSM1S. Этот вариант неприменим для строковых переменных.
-
Copy old value(s) (Копировать старые значения): Значения входной переменной сохранятся без изменений.
Если новые выходные переменные являются строковыми, следует установить флажок Output variables are strings (Выходные переменные являются строками). Теперь выполните следующие действия:
-
Введите старые и новые значения согласно следующей таблице:
1->22->23->14->15->16->2ELSE -> 0.
-
При этом старое значение вводите в поле Value в группе Old Value, новое значение — в поле Value в группе New Value и щелкайте на кнопке Add.
-
Чтобы перекодировать старые значения 0 и 7, выберите опцию All other values. Введите 0 в поле Value в группе New Value и щелкните на кнопке Add.
-
Щелкните на кнопке Continue, а затем на ОК. Новая переменная lire будет добавлена в файл wahl.sav.
Примечание: Выбранные опции соответствуют следующему командному синтаксису:
RECODE partei
(1=2) (2=2) (3=1) (4=1) (5=1) (6=2) (ELSE=0)
INTO lire . VARIABLE LABELS
lire "Политический спектр" EXECUTE .
-
В редакторе данных дважды щелкните на lire, чтобы перейти в редактор вида переменных.
-
Установите следующие параметры: тип переменной — численный, ширина — 1, десятичные разряды — 0. Укажите следующие метки значений:
0 = не определено
1 = левые
2 = правые.
-
Объявите нуль как пропущенное значение.
-
В заключение выполните частотный анализ переменной lire. Вы получите следующий результат:
Политический спектр
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | левые | 13 | 43,3 | 48,1 | 48,1 |
правые | 14 | 46,7 | 51,9 | 100,0 | |
Total | 27 | 90,0 | 100,0 | ||
Missing | не определено | 3 | 10,0 | ||
Total | 30 | 100,0 |
Из 30 респондентов 46,7% выбрали партии правого направления, а 43,3% — партии левого направления. Трое опрашиваемых (10%) не дали никакого ответа на вопрос: «За кого бы вы голосовали, если бы в воскресенье были выборы в бундестаг?».
5.gif
6.gif

8.3.2 Автоматическое перекодирование
8.3.2 Автоматическое перекодирование
Если категории не были закодированы непрерывно начиная с 1, то это может приводить к негативным последствиям при решении многих задач в SPSS. Поэтому для преобразования значений численных или строковых переменных в непрерывную последовательность целых чисел в SPSS реализована возможность автоматического перекодирования. В качестве примера рассмотрим автоматическое перекодирование строковой переменной в численную.
-
Загрузите файл string.sav.
В редакторе данных отобразятся значения строковой переменной beschw (недуги), соответствующие характеру жалоб пациентов. Они состоят не более чем из двадцати символов.
-
Выберите в меню команды Transform (Преобразовать) Automatic Recode... (Автоматическое перекодирование)
Откроется диалоговое окно Automatic Recede (см. рис. 8.7).
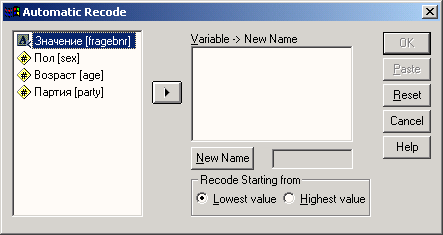
Рис. 8.7: Диалоговое окно Automatic Recede
-
Перенесите строковую переменную в поле Variable -> New Name (Переменная > Новое имя). В текстовое поле под ним введите новое имя, например, beschwn, и щелкните на кнопке New Name (Новое имя).
-
Щелкните на кнопке ОК.
В окне просмотра будет отображена таблица соответствия, отрывок из которой приводится ниже:
BESCHW Old Value | BESCHWN New Value | Жалобы Value Label |
Абсцесс | 1 | Абсцесс |
Аллергия | 2 | Аллергия |
Стенокардия | 3 | Стенокардия |
Одышка | 4 | Одышка |
Бактерии в моче | 5 | Бактерии в моче |
Боли в позвоночнике | 6 | Боли в позвоночнике |
Боли в животе | 7 | Боли в животе |
Затруднения | 8 | Затруднения |
Метеоризм | 9 | Метеоризм |
Гипертония | 10 | Гипертония |
Жжение | 11 | Жжение |
Бронхит | 12 | Бронхит |
Воспаление кишечника | 13 | Bocпаление кишечника |
Диабет | 14 | Диабет |
Диализ | 15 | Диализ |
Нарушения кровообр . | 1б | Нарушения кровообращения |
Понос | 17 | Понос |
Воспаления | 18 | Воспаления |
Лихорадка | 19 | Лихорадка |
Различным значениям строковой переменной beschw, выстроенным в алфавитном порядке, поставлена в соответствие непрерывная последовательность натуральных чисел от 1 до 58; эти численные значения сохраняются в переменной beschwn. Прежние строковые значения стали метками значений этой переменной.
7.gif
8.4 Вычисление новых переменных в соответствии с определенными условиями
8.4 Вычисление новых переменных в соответствии с определенными условиями
Вычисление новых переменных может быть поставлено в зависимость от определенных условий, как показано в разделе 8.4.1. Во втором разделе этого параграфа приводится практический пример использования условного вычисления — создание индекса.
8.4.1 Формулировка условий
8.4.1 Формулировка условий
В файле studium.sav (психологическое состояние и социальное положение студентов), в частности, содержатся переменные alter (возраст), fach (специальность), semester (количество семестров) и sex (пол).
Допустим, нам требуется образовать из переменных alter и semester новую переменную, которая будет показывать возраст студента в начале обучения. Кроме того, это значение следует вычислять только для старших курсов (semester>6).
-
Загрузите файл Studium.sav и выберите команды меню Transform (Преобразовать) Compute... (Вычислить)
-
В открывшемся диалоговом окне в поле выходной переменной (см. раздел 8.1) задайте, например, studbeg, а для численного выражения — alter — semester /2.
-
Щелкните на кнопке If... (Если). Откроется диалоговое окно Compute Variable: If Cases (Вычислить переменную: Если выполняется условие). Измените начальную настройку Include all cases (Включить все наблюдения) на Include if case satisfies condition (Включить, если для наблюдения выполняется условие). В поле под этой опцией введите условие: semester>6.
-
Закройте это диалоговое окно, щелкнув на кнопке Continue, и диалог Compute Variable кнопкой ОК.
Теперь в файле данных появилась переменная studbeg, которая в случаях, когда заданное условие не выполняется, содержит системное отсутствующее значение.
Примечание: Выбранные опции соответствуют следующему командному синтаксису:
IF (semester > 6) studbeg = alter - semester /2 .
EXECUTE .
Ниже приведен другой типичный пример условного вычисления новых переменных.
Если, к примеру, требуется определить, значительно ли отличаются юристы (fach = 1) от гуманитариев (fach = 3) по количеству семестров, которые прозанимались эти студенты, можно использовать переменную fach как группирующую и сравнить результаты U-теста по Манну и Уитни для переменной semester при значениях fach=l и fach=3 (см. раздел 14.1). Если же требуется сравнить юристов-мужчин с гуманитариями-мужчинами, то оба набора значений надо дополнительно ограничить условием sex = 2 (см. раздел 7. 1).
Однако, когда надо сравнить, например, юристов-мужчин со студентками-гуманитариями, возникает проблема — в этом случае появляются две группирующих переменных. В подобных ситуациях помогает создание вспомогательной переменной. Этой переменной присваивается значение 1, когда наблюдение соответствует студенту-юристу, и 2 — когда студентке гуманитарной специальности. Затем вспомогательная переменная используется как группирующая при проведении теста по Манну и Уитни.
-
Чтобы построить такую переменную, выберите в меню команды Transform (Преобразовать) Compute... (Вычислить)
-
Задайте выходную переменную, например, gruppe, а в поле численного выражения введите значение 1. В диалоговом окне If... укажите условие fach=l and sex=2.
-
Закройте диалоги кнопками Continue и ОК.
-
Повторите процесс; снова задайте выходную переменную gruppe, но численное выражение 2. В диалоге If... сформулируйте условие fach=3 and sex=l. На вопрос Change existing variables?, который появляется после закрытия диалогов, ответьте утвердительно (ОК).
В редакторе данных появится новая переменная gruppe, которая в наблюдениях, соответствующих сформулированным условиям, имеет значения ] или 2, Эту операцию можно выполнить быстрее при помощи командного синтаксиса SPSS.
-
Для этого командами меню File (Файл) New (Создать) Syntax (Синтаксис) откройте редактор синтаксиса и введите следующие команды:
IF (fach = 1 and sex = 2) gruppe = 1.
IF (fach = 3 and sex = 1) gruppe = 2. EXECUTE.
-
После выделения всех строк командами меню Edit (Правка) Select All (Выделить все) и щелчка на значке запуска (Run) в открытый файл данных будет добавлена новая переменная со значениями 1 (мужчины-юристы) и 2 (женщины-гуманитарии), которая может служить группирующей переменной, например, при U-тесте Манна и Уитни.
8.4.2 Создание индекса
8.4.2 Создание индекса
Индексом называют объединение нескольких отдельных вопросов (элементов) в едином показателе, который характеризует сложные, многоплановые состояния — например, показатель уровня жизни или уровня интеллекта. Создание такого индекса мы рассмотрим на примере теоремы об изменении ценностей американского политолога Рональда Инглхарта (Inglehart).
В своей работе «Культурный сдвиг. Смена ценностей в западном мире» (см. список литературы) Инглхарт выдвинул положение о том, что представления о ценностях в западном обществе претерпели значительное изменение. Ранее на первом месте стояли материальное благополучие и физическая безопасность, тогда как сегодня больше значения придается качеству жизни. Таким образом, ценностные приоритеты сместились от материализма к постматериализму. Это смещение Инглхарт объясняет, в частности, тем, что после второй мировой войны, прежде всего в западноевропейских странах и США, люди ощутили большую экономическую и физическую безопасность чем когда-либо до сих пор. Более молодые поколения, годы формирования которых пришлись на период безопасности и стабильности, будут постепенно отдаляться от традиционных норм и представлений о ценностях, свойственных старшим поколениям. Основываясь на факте достижения высокой экономической безопасности и стабильности, Инглхарт делает вывод о смене ценностей между поколениями, которая влечет за собой значительные социальные последствия.
Далее мы построим индекс, который будет указывать, придерживается ли респондент материалистических или же постматериалистических ценностей, согласно Рональду Ингчарту. Этот индекс будет построен на основе опроса ALLBUS, проведенного в 1991 г. В опpoce ALLBUS фигурировало четыре вопроса, касающиеся теоремы Инглхарта об изменении ценностей. В частности, респондента спрашивали, какое значение он придает ценностям «Спокойствие и порядок в стране» (переменная v108), «Увеличение степени частая народа в решениях власти» (переменная v109), «Борьба с ростом цен» (переменная v110) и «Право на свободное выражение мнения» (переменная v111). Респондент, :гавнивая эти четыре ценности между собой, мог указать для каждой из них один из четырех приоритетов: первостепенное значение, второстепенное значение, значение третье степени и значение четвертой степени. Данные находятся в файле ingle.sav.
-
Загрузите файл ingle.sav.
-
Чтобы получить первоначальное представление, проведите частотный анализ переменных v108, v109, v110 и v111. В окне просмотра вы увидите следующие результаты:
ВАЖНОСТЬ СПОКОЙСТВИЯ И ПОРЯДКА
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | первостепенная важность | 1313 | 42,9 | 42,9 | 42,9 |
второстепенная | 691 | 22,6 | 22,6 | 65,5 | |
важность третьей степени | 597 | 19,5 | 19,5 | 85,1 | |
важность четвертой степени | 395 | 12,9 | 12,9 | 98,0 | |
не знаю | 30 | 1,0 | 1,0 | 99,0 | |
нет данных | 32 | 1,0 | 1,0 | 100,0 | |
total | 3058 | 100,0 | 100,0 |
ВАЖНОСТЬ ВЛИЯНИЯ ГРАЖДАН НА ВЛАСТЬ
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | первостепенная важность | 976 | 31,9 | 31,9 | 31,9 |
второстепенная важность | 790 | 25,8 | 25,8 | 57,8 | |
важность третьей степени | 736 | 24,1 | 24,1 | 81,8 | |
важность четвертой степени | 477 | 15,6 | 15,6 | 97,4 | |
не знаю | 44 | 1,4 | 1.4 | 98,9 | |
нет данных | 35 | 1,1 | 1,1 | 100,0 | |
total | 3058 | 100,0 | 100,0 |
ВАЖНОСТЬ БОРЬБЫ С ИНФЛЯЦИЕЙ
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | первостепенная важность | 248 | 8,1 | 8,1 | 8,1 |
второстепенная важность | 696 | 22.8 | 22,8 | 30,9 | |
важность третьей степени | 879 | 28,7 | 28.7 | 59,6 | |
важность четвертой степени | 1142 | 37,3 | 37,3 | 97,0 | |
не знаю | 48 | 1.6 | 1.6 | 98,5 | |
нет данных | 45 | 1,5 | 1,5 | 100,0 | |
total | 3058 | 100,0 | 100,0 |
ВАЖНОСТЬ СВОБОДНОГО ВЫРАЖЕНИЯ МНЕНИЙ
Частота | Проценты | Допустимые | Накопленные проценты | ||
Valid | первосте- пенная важность | 488 | 16,0 | 16,0 | 16,0 |
второсте- пенная важность | 839 | 27,4 | 27,4 | 43,4 | |
важность третьей степени | 762 | 24,9 | 24,9 | 68,3 | |
важность четвертой степени | 880 | 28,8 | 28,8 | 97,1 | |
не знаю | 49 | 1,6 | 1,6 | 98,7 | |
нет данных | 40 | 1,3 | 1,3 | 100,0 | |
total | 3058 | 100,0 | 100,0 |
Элементы vl08 (Спокойствие и порядок) и v110 (Борьба с ростом цен/инфляцией) соответствуют материалистическим ценностям, а элементы v!09 (Влияние граждан на власть) и vl11 (Свободное выражение мнений) — постматериалистическим. Таким образом, за каждым материалистическим элементом следует постматериалистический элемент. Именно так эти четыре классических элемента были расположены в исследовании Инглхарта Это. В своих многочисленных работах, которые выходили с начала 70-х гг., Рональд Инглхарт объединял эти четыре элемента в шкалу из четырех степеней, или индекс. При этом элементы v!08 (Спокойствие и порядок) и v110 (Борьба с ростом цен/ инфляцией) служили для выделения материалистов, а элементы v!09 (Влияние граждан на власть) и v111 (Свободное выражение мнений) — для выделения постматериалистов. В зависимости от сочетания ответов Инглхарт классифицировал опрашиваемого как
-
чистого материалиста
-
чистого постматериалиста
-
материалистический смешанный тип
-
постматериалистический смешанный тип.
Сочетание ответов v108/v110 соответствует чистому материалисту, а сочетание v109/ v111 — чистому постматериалисту. При оставшихся сочетаниях ответов, в зависимости от того, был ли главной целью респондента материалистический или постматериалистический элемент, опрашиваемый классифицируется как материалистический или постматериалистический смешанный тип. Таким образом, мы получаем следующие варианты сочетаний для создаваемого индекса:
Индекс Инглхарта
Цель первостепенной важности | Цель второстепенной важности | Инлекс Инглхарта |
v108 | v110 | чистый материалист |
v110 | v108 | чистый материалист |
v109 | v111 | чистый постматериалист |
v111 | v109 | чистый постматериалист |
v108 | v109 | материалистический смешанный тип |
v108 | v111 | материалистический смешанный тип |
v110 | v109 | материалистический смешанный тип |
v110 | v111 | материалистический смешанный тип |
v109 | v108 | постматериалистический смешанный тип |
v109 | v110 | постматериалистический смешанный тип |
v111 | v108 | постматериалистический смешанный тип |
V111 | v110 | постматериалистический смешанный тип |
Рассмотрим теперь нижеследующую программу SPSS, которая строит индекс в соответствии с вышеприведенной таблицей.
/* Создание индекса */
.'* на примере теоремы Рональда
Инглхарта об изменении ценностей */
/* чистые материалисты */
if (v!08 = 1 and vl10 = 2)
ingl_ind = 4 . if (vl10 = 1
and vl08 = 2) ingl_ind = 4 .
/* чистые постматериалисты */
if (v!09 = 1 and vlll = 2)
ingl_ind = 1 .
if (vl11 = 1 and vl09 = 2)
ingl_ind = 1 .
/* материалистический смешанный тип
*/ if <vl08 = 1 and vl09 = 2)
ingl_ind = 3 . if (vl08 = 1
and vl11= 2) ingl_ind = 3 .
if {vl10 = 1 and vl09 = 2) ingl_ind = 3 .
if (vl10 = 1 and vl11 = 2)
ingl_ind = 3 .
/* постматериалистические
смешанные типы */
if (v!09 = 1 and v!08 = 2)
ingl_ind = 2 .
if (vl09 = 1 and vl10 = 2)
ingl_ind = 2 .
if (vl11 = 1 and vl08 = 2)
ingl_ind = 2 .
if (vl11 = 1 and vk10 = 2)
ingl_ind = 2 .
/* He знаю */
if (vl08 = 8 and vl09 = 8
and vl10 = 8 and vl11 = 8)
ingl_ind = 8 .
if (vl08 = 8 and vl09 = 8
and vl10 = 8) ingl_ind = 8 .
if (vl08 = 8 and vl09 = 8
and vl11 = 8) ingl_ind = 8 .
if (vl08 = 8 and vl10 = 8
and vl11 = 8) ingl_ind = 8 .
if (vl09 = 8 and vl10 = 8
and vl11 = 8) ingl_ind = 8 .
/* нет данных */
if (vl08 = 9 and vl09 = 9
and vl10 = 9 and vl11 = 9)
ingl_ind = 9 .
if (vl08 = 9 and vl09 = 9
and vl10 = 9) ingl~ind = 9 .
if (vl08 = 9 and vl09 = 9
and vl11 = 9) ingl_ind = 9 .
if (vl08 = 9 and vl10 = 9
and vl11 = 9) ingl_ind = 9 .
if (vl09 = 9 and vl10 = 9
and vl11 = 9) ingl~ind = 9 .
variable labels ingl_ind
'Индекс Инглхарта'
value labels ingl_ind 1
'Постматериалисты'
2 'ПМ, смешанный тип'
3 'M, смешанный тип'
4 ' Материалисты'
8 'Не знаю'
9 'нет данных' .
execute .
Программа начинается с двух строк комментариев, которые содержат информацию о том, что целью ее выполнения является построение индекса на примере теоремы Рональда Инглхарта об изменении ценностей. Комментарии обозначаются в SPSS символами /* в начале строки комментария и */ — в конце комментария. При выполнении программы процессор SPSS пропускает эти строки.
Далее вычисляется индекс для чистых материалистов. Если выполняется условие, что переменная v!08 имеет значение 1, а переменная v110 — значение 2, то переменная индекса ingMnd должна иметь значение 4 (Материалисты). После этого вычисляется индекс для чистых постматериалистов. Он равен 1. Для материалистических и постматериалистических смешанных типов имеется по четыре сочетания, которые обрабатываются в двух следующих блоках. Два последних блока программы обрабатывают ответы не знаю и нет данных. Индекс Инглхарта равен 8 (не знаю), если на три или четыре вопроса дан ответ не знаю, и 9 (нет данных), если на три или четыре вопроса дан ответ нет данных. Например, если респондент придал элементу v!08 первостепенную важность, а на три остальных вопроса ответил не знаю, он попадает в категорию не знаю.
Следует отметить, что находящиеся друг под другом в программе операторы AND (конъюнкции) можно преобразовать в дизъюнкцию, связав их операторами OR (см. главу 7). Следующая команда variable labels присваивает переменной ingl_ind метку «Индекс Инглхарта». Команда value labels устанавливает шесть меток значений для этой переменной. Команда execute в конце программы запускает выполнение всех необходимых преобразований.
Эта программа находится на компакт-диске примеров или в рабочем каталоге C:\SPSSBOOK. Она называется ingle.sps.
-
Загрузите программу в редактор синтаксиса ingle.sps, вызвав команды меню File (Файл) Open (Открыть).
-
Выделите текст программы следующими командами меню Edit (Правка) Select All (Выделить все)
-
Запустите программу, щелкнув на значке Run (Запуск).
-
Перейдите в редактор данных.
-
Выполните частотный анализ переменной ingljnd. Вы получите следующий результат:
Индекс Инглхарта
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | Постматериалисты | 673 | 22,0 | 22,0 | 22,0 |
ПМ, смешанный тип | 789 | 25,8 | 25,8 | 47,8 | |
М, смешанный тип | 956 | 31,3 | 31,3 | 79,1 | |
Материалисты | 598 | 19,6 | 19,6 | 98,6 | |
Не знаю | 19 | ,6 | ,6 | 99,2 | |
нет данных | 23 | ,8 | ,8 | 100,0 | |
Total | 3058 | 100,0 | 100,0 |
Из 3058 опрошенных 98,6% поддаются классификации; 41,6% относятся к чистым типам. В группу материалистического смешанного типа попадает почти треть всех наблюдений. Постматериалистическому смешанному типу соответствует чуть больше четверти. В чистых группах постматериалисты выражены несколько сильнее материалистов. Материалисты и материалистические смешанные типы составляют вместе 50,9%; постматериалисты и постматериалистические смешанные типы — 47,8%. Таким образом, наблюдается небольшой перевес в сторону материализма.
Данные четырех классических элементов Инглхарта содержит также файл beamte.sav. Он касается опроса ALLBLJS, проводившегося в 1988 г.. Для упражнения постройте индекс Инглхарта для этих данных. При сравнении с данными 1991 г. следует учитывать, что опрос ALLBUS 1991 впервые проводился во всех землях Германии, включая восточные.
8.5 Агрегирование данных
8.5 Агрегирование данных
На базе значений одной или нескольких группирующих переменных (переменных разбиения) можно объединить наблюдения в группы (агрегировать) и создать новый файл данных, содержащий по одному наблюдению для каждой группы разбиения. Для этого SPSS предоставляет большое количество функций агрегирования.
В сельскохозяйственном исследовании рассматривалось содержание свиней в двух различных типах свинарников. При этом в каждом из двух свинарников осуществлялся мониторинг поведения восьми свиней в течение двадцатидневного периода. На протяжении этого периода фиксировалась длительность определенных действий животных (то есть сколько времени свиньи рылись, ели, чесали голову и туловище). Данные хранятся в файле schwein.sav, содержащем следующие переменные:
Имя переменной | Пояснение |
stall | Тип свинарника (1 или 2) |
nr | Порядковый номер свиньи (от 1 до 8) |
zert | Номер дня (от 1 до 20) |
wuehlen | Длительность рытья (в секундах) |
fressen | Длительность кормежки (в секундах) |
massage | Длительность чесания (в секундах) |
Следует выяснить, значительно ли различается по длительности эти три действия в свинарниках обоих типов, для чего необходимо применить соответствующий статистический текст, например, тест Стьюдента (см. главу 13).
В каждой из двух выборок для каждого из трех действий имеется по 8 + 20=160 измерений. Однако выполнение статистического тест на основе этих данных будет не совсем корректно, так как они относятся к восьми особям, для каждой из которых было проведено по двадцать измерений.
Поэтому мы просуммируем длительности для каждой отдельной свиньи и для каждого отдельного действия. Затем полученные наборы сумм мы сравним при помощи теста Стьюдента. Это типичный пример агрегирования данных.
-
Загрузите файл schwein.sav.
-
Выберите в меню команды Data (Данные) Aggregate... (Агрегировать)
Откроется диалоговое окно Aggregate Data (Агрегировать данные).
-
В качестве переменных разбиения перенесите переменные stall и nr в поле Break Variable(s), а в качестве переменных агрегирования (Aggregate Variable(s)) выберите wuehlen, fressen и massage. Диалоговое окно приобретет вид, показанный на рис. 8.8.
Будут показаны три новые переменные wuehle_l, fresse_l и massag_l, имена которых состоят из первых шести букв имен соответствующих переменных агрегирования и комбинации символов _1. По умолчанию в качестве функции агрегирования принято среднее значение. Мы должны выбрать вместо него сумму.
-
Для этого щелкните на первой переменной, а затем на кнопке Funktion... (Функция). Откроется диалоговое окно Aggregate Data: Aggregate Function (Агрегировать данные: Функция агрегирования) (см. рис. 8.9).
Можно выбрать одну из шестнадцати функций агрегирования, имена которых не требуют особых пояснений.
-
Выберите пункт Sum of values (Сумма значений) и щелчком на кнопке Continue вернитесь в первое диалоговое окно.
-
Выполните те же действия для двух других переменных агрегирования. Агрегированные данные будут сохранены в новом файле.
-
Щелкните на кнопке File... и выберите для нового файла имя pigaggr.sav.
Рис. 8.8: Диалоговое окно Aggregate Data
Рис. 8.9: Диалоговое окно Aggregate Data: Aggregate Function
После щелчка на кнопке Отбудет создан новый файл, содержащий 2 х 8=16 наблюдений и переменные stall, nr, wuehle_l, fresse_l и massag_l.
-
Загрузите этот файл и просмотрите его содержимое в редакторе данных.
-
Как описано в разделе 13.1, проведите тест Стьюдента для независимых выборок с группирующей переменной stall и тестируемыми переменными fresse_l, massag_l и wuehle_l. Вы получите следующий результат:
Group Statistics (Статистика группы)
STALL | N | Mean (Среднее значение) | Std. Deviation (Стандартное отклонение) | Std. Error Mean (Стандартная ошибка среднего значения) |
FRESSE 1 1 2 | 8 8 | 339,0125 231,6750 | 98,2384 109,5381 | 34,7325 38,7276 |
MASSAG 1 1 2 | 8 8 | 2,2875 40,3625 | 3,3689 54,1795 | 1,1911 19,1553 |
WUEHLE 1 1 2 | 8 8 | 1996,587 1964.600 | 326,3919 642,5314 | 115,3970 227,1692 |
Independent Samples Test (Тест для независимых выборок)
Levne's Test forEquality of Variancies (Tecт Левена на равенство дисперсий) | Т-Test for Equality of Means (Тест Стьюдента на равенство средних) | |||||||||
F | Значи-мость | Т | df | (дву сторон-няя) | Разность средних | Стан-дартная ошибка разницы | 95% доверительный интервал разности Нижняя и Верхняя | |||
FRES-SE_.1 | Equal variances assumed (Дис-персии равны) Equal variances not assumed (Дис-персии не равны) | .128 | .726 | 2,063 2,063 | 14 13, 837 | ,058 ,058 | 107 ,3375 107 ,3375 | 52, 0209 52 ,0209 | -4,2362 -4,3594 | 218, 9112 219, 0344 |
MAS-SAG 1 | Equal variances assumed (Дис-персии равны) Equal variances not assumed (Дис-персии не равны) | 7.390 | ,017 | -1,984 -1,984 | 14 7,054 | ,067 ,087 | -38, 0750 -38,0750 | 19, 1923 19. 1923 | -79,2385 -83,3872 | 3,0885 7,2372 |
WU-EHLE_1 | variances assumed (Дис-персии равны) Equal variances not assumed (Дис-персии не равны) | 2,274 | ,154 | ,126 ,126 | 14 10 ,387 | ,902 ,902 | 31, 9875 31 ,9875 | 254 ,7985 254 ,7985 | -514 ,5010 -532, 8844 | 578. 4760 596 ,8594 |
В первом свинарнике свиньи ели в продолжение наблюдаемого периода в среднем 339,0 секунд в день, а в другом — только 231,7 секунд. Это различие является почти статистически значимым (р= 0,058).
8.gif

9.gif

8.6 Ранговые преобразования
8.6 Ранговые преобразования
В SPSS существует возможность задавать ранги для измеренных значений переменной, проводить оценки Сэвиджа, вычислять процентные ранги и формировать процентильные группы, добавляя в файл данных соответствующие переменные.
Так, например, в формулах для непараметрических тестов (см. главу 14) вместо исходных измеренных значений переменной используются присвоенные им ранги. Однако эти процедуры производят автоматическое присвоение рангов и в явном виде выполнять предварительные ранговые преобразования не требуется. Поэтому они играют второстепенную роль.
Мы продемонстрируем присвоение рангов на более наглядном примере, а затем проведем обзор различных типов рангов.
8.6.1 Пример рангового преобразования
8.6.1 Пример рангового преобразования
В главе 20 представлен файл europa.sav, содержащий отдельные статистические показатели по 28 европейским странам. В частности, он включает переменные land (краткое обозначение страны) и tjul (средняя дневная температура в июле). Требуется расположить страны в нисходящем порядке согласно значениям последней переменной и затем вывести их в отсортированном виде.
-
Загрузите файл europa.sav.
-
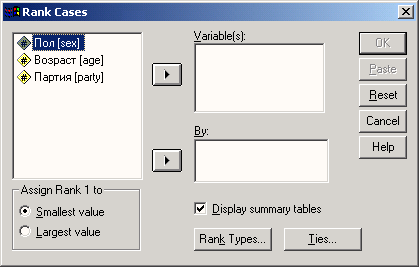
Выберите в меню команды Transform (Преобразовать) Rank Cases... (Присвоить ранги наблюдениям) Откроется диалоговое окно Rank Cases.
Рис. 8.10: Диалоговое окно Rank Cases
-
Щелкните в списке переменных на переменной tju1. В поле By: (По) можно задать группирующую переменную. В этом случае назначение рангов будет выполнено раздельно по группам, образуемым этой переменной.
-
Присвоим самой теплой стране (с максимальным значением переменной tju1) ранг 1; для этого щелкните в поле Assign Rank I to (Присвоить ранг 1) на опции Largest value (Максимальное значение).
Щелкнув на кнопке Rank types... (Типы рангов), можно увидеть стандартную настройку Rank. Пока оставим ее без изменений; остальные настройки мы рассмотрим в разделе 8.6.2.
-
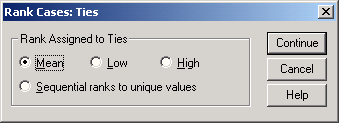
Кнопка Ties... (Связки) открывает диалоговое окно Rank Cases: Ties.
Его настройки указывают, как программа будет поступать при появлении одинаковых измеренных величин. По умолчанию принято (и, как правило, это наилучший вариант), что присваивается среднее (Mean) из значений рангов этих величин. При установке Low все значения получают наименьший, при установке High — наибольший из этих рангов. При выбранной опции Sequential ranks to unique values (Присваивать последовательные ранги) все связанные наблюдения получают одинаковый ранг; следующему наблдению присваивается следующее по порядку целое число. Поэтому максимальный присвоенный ранг равен не общему количеству значений, а количеству различных значений.
Перечисленные четыре способа присвоения рангов можно пояснить с помощью простого примера, в котором семь значений расположены по убыванию.
Рис. 8.11: Диалоговое окно Rank Cases: Ties
Значение | Mean | Low | High | Sequential ranks to unique values |
190 | 1 | 1 | 1 | 1 |
187 | 2,5 | 2 | 3 | 2 |
187 | 2,5 | 2 | 3 | 2 |
185 | 5 | 4 | 6 | 3 |
185 | 5 | 4 | 6 | 3 |
185 | 5 | 4 | 6 | 3 |
184 | 7 | 7 | 7 | 4 |
-
Оставьте стандартную настройку и закройте диалоговое окно кнопкой Continue.
-
Начните присвоение рангов, щелкнув на ОК.
В файл данных будет добавлена переменная rtju1, содержащая ранги, присвоенные значениям переменной tju1. Для обозначения ранговой переменной к имени исходной переменной спереди дописывается буква г.
Затем отсортируем файл данных по этой ранговой переменной.
-
Для этого, как описано в разделе 7.3, выберите в меню команды Data (Данные) Son Cases... (Сортировать наблюдения) и в появившемся диалоговом окне выберите в качестве переменной сортировки rtjul. Примите предлагаемый по умолчанию порядок сортировки по возрастанию.
-
Запустите сортировку кнопкой ОК. Теперь выведем значения переменных rtju1, land и tju1 в отсортированном виде.
-
Для этого выберите в меню команды (см. раздел 4.8) Analyze (Анализ) Reports (Отчеты) Case summaries... (Итоги по наблюдениям) и перенесите в поле Variables переменные rtjul, land и tjul в указанной последовательности.
-
Запустите создание отчета кнопкой ОК. В окне просмотра будет показана следующая таблица.
Отсюда можно заключить, что Греция является самой теплой страной (ранг 1), за ней следует Италия (ранг 2), следующий ранг имеют две страны — Албания и Румыния (средний ранг 3,5) и т.д.
Case Processing Summary a (Сводка случаев)
RANK TJU | LAN | Средняя дневная температура в июле | |
1 | 1,00 | GRI | 33 |
2 | 2,00 | ITA | 31 |
3 | 3,50 | ALB | 30 |
4 | 3,50 | RUM | 30 |
5 | 5,50 | JUG | 29 |
6 | 5,50 | TUE | 29 |
7 | 7,50 | BUL | 28 |
8 | 7,50 | UNG | 28 |
9 | 9,50 | FOR | 27 |
10 | 9,50 | SPA | 27 |
11 | 13,00 | DEU | 25 |
12 | 13,00 | FRA | 25 |
13 | 13,00 | OES | 25 |
14 | 13,00 | SCH | 25 |
15 | 13,00 | TSC | 25 |
16 | 17,00 | DD | 24 |
17 | 17,00 | POL | 24 |
18 | 17,00 | SOW | 24 |
19 | 19,50 | BEL | 23 |
20 | 19,50 | LUX | 23 |
21 | 23,50 | DAE | 22 |
22 | 23,50 | FIN | 22 |
23 | 23,50 | GRO | 22 |
24 | 23,50 | NIE | 22 |
25 | 23,50 | NOR | 22 |
26 | 23,50 | SCH | 22 |
27 | 27,00 | IRL | 20 |
28 | 28,00 | ISL | 15 |
| Total (Всего)N | 28 | 28 | 28 |
a. Limited to first 100 cases(Ограничено первыми 100 случаями) | |||
10.gif
11.gif
8.6.2 Типы рангов
8.6.2 Типы рангов
В диалоге Rank Cases можно, щелкнув на кнопке Rank Types... (Типы рангов), от-крыть диалоговое окно Rank Cases: Types (Ранги: Типы). В этом окне представлены шесть типов рангов; щелкнув на кнопке More » (Еще), можно увидеть еще два.
Ниже приведено объяснение различных типы рангов.
-
Rank (Ранг): Абсолютные значения рангов (см. раздел 8.6.1). Это установка по умолчанию.
-
Savage score (Оценка Сэвиджа): Это значения ранга, полученное на основе экспоненциального распределения. При общем количестве значений переменной т оценка Сэвиджа для i-го ранга определяется по формуле
Рис. 8.12: Диалоговое окно Rank Cases: Types
-
Fractional Rank (Относительный ранг): Это значение ранга деленное на количество наблюдений.
-
Fractional Rank as % (Относительный ранг в %): Это численные значения относительных рангов, умноженные на 100. Например, процентный ранг 33,93 означает, что 33,93% всех наблюдений имеют более низкий ранг.
-
Sum of case weights (Сумма весов наблюдений): Эта величина представляет интерес только при определении рангов для подгрупп и является постоянной в каждой подгруппе; она соответствует количеству случаев в подгруппе.
-
Ntiles (N-процентили): Пользователь может задать число групп процентилей, на которые должны быть разбиты наблюдения (по умолчанию 4). Тогда каждому случаю присваивается значение процентильной группы, к которой он принадлежит.
-
Proportion estimates (Долевые оценки): Вычисление накопленной доли при предположении нормальном распределении переменной. Для ранга г и количества наблюдений я соответствующие долевые оценки вычисляются по четырем нижеследующим формулам.
Blom: | (r-3/8)/(n+1/4) |
Tukey: | (r-1/3)/(n+1/3) |
Rankit: | (r-1/2)/n |
Van der Waerden: | r/(n+1) |
-
Normal scores (Нормальные ранги): Значения процентилей, относящиеся к долевым оценкам.
Для перечисленных рангов SPSS автоматически задает имена переменных, которые приведены в нижеследующей таблице. При этом имеет значение, был ли выбран единственный тип ранга или одновременно вычислялись ранги нескольких типов (что является исключением). В последнем случае, для обеспечения однозначности переменных имена должны различаться. В таблице приводятся также принятые в SPSS метки этих переменных. Для долевых оценок и нормальных рангов здесь приведен вариант, когда применяется формула Блома (Blom); при выборе других формул расчета этих рангов метки соответственно изменяются. Имя исходной переменной — lem (в нашем примере — это средняя ожидаемая продолжительность жизни мужчин).
Тип ранга | Единственный тип ранга | Несколько типов | Метка переменной |
Ранг | rlem | rlem | RANK of LEM |
Оценка Сэвиджа | slem | slem | SAVAGE of LEM |
Относительный ранг | rlem | rfrOO-1 | RFRACTION of LEM |
Относительный ранг в % | plem | perOO! | PERCENT of LEM |
Сумма весов наблюдений | nlem | nOOl | N of LEM |
N-процентили | nlem | ntiOOl | NTILES of LEM |
Долевые оценки (по Блому) | plern | plem | PROPORTION of LEM using BLOM |
Нормальные ранги (по Блому) | nlem | nlem | NORMAL of LEM using BLOM |
Если провести ранговые преобразования всех возможных типов и вывести получившиеся значения с помощью средства формирования сводки наблюдений, мы получим следующую таблицу.
Case Processinq Summary3 (Сводка наблюдений)
| LAN | RANK LE | SAVAG of | RFRACT Nof | PERCE of | Nof | NTILES LE | PROPOR Nof using | NORM of usin BLO |
1 | ALB | 3,00 |
| ,107 | 10,7 | 28 | 1 | ,092 |
|
2 | BEL | 11,50 |
| ,410 | 41,0 | 28 | 2 | ,393 |
|
3 | BUL | 15,50 |
| ,553 | 55,3 | 28 | 3 | ,535 | ,088 |
4 | DAE | 24,00 | ,843 | ,857 | 85,7 | 28 | 4 | ,836 | ,979 |
5 | DEU | 13,00 |
| ,464 | 46,4 | 28 | 2 | ,446 |
|
6 | DO | 17,00 |
| ,607 | 60,7 | 28 | 3 | ,588 | ,223 |
7 | FIN | 4,00 |
| ,142 | 14,2 | 28 | 1 | ,128 |
|
8 | FRA | 19.00 | ,098 | ,678 | 67,8 | 28 | 3 | ,659 | ,410 |
9 | GRI | 11,50 |
| ,410 | 41,0 | 28 | 2 | ,393 |
|
10 | GRO | 20,00 | ,209 | ,714 | 71,4 | 28 | 3 | ,694 | ,509 |
11 | IRL | 15,50 |
| ,553 | 55,3 | 28 | 3 | ,535 | ,088 |
12 | ISL | 27,00 | 1,927 | ,964 | 96,4 | 28 | 4 | ,942 | 1,575 |
13 | ITA | 18,00 |
| ,642 | 64,2 | 28 | 3 | ,623 | ,315 |
14 | JUG | 1,00 |
| ,035 | 3,5 | 28 | 1 | ,022 |
|
15 | LUX | 14,00 |
| ,500 | 50,0 | 28 | 2 | ,482 |
|
16 | NIE | 25,00 | 1,093 | ,892 | 89,2 | 28 | 4 | ,871 | 1,134 |
17 | NOR | 28,00 | 2,927 | 1,000 | 100,0 | 28 | 4 | ,977 | 2,011 |
18 | OES | 9,00 |
| ,321 | 32,1 | 28 | 2 | ,305 |
|
19 | POL | 7,00 |
| ,250 | 25,0 | 28 | 1 | ,234 |
|
20 | POR | 2,00 |
| ,071 | 7,1 | 28 | 1 | ,057 |
|
21 | RUM | 6,00 | - | ,214 | 21,4 | 28 | 1 | ,199 |
|
22 | SCH | 26,00 | 1,427 | ,928 | 92,8 | 28 | 4 | ,907 | 1,323 |
23 | SCH | 23,00 | ,643 | ,821 | 82,1 | 28 | 4 | ,800 | ,844 |
24 | sow | 22.00 | ,477 | ,785 | 78,5 | 28 | 4 | ,765 | ,724 |
25 | SPA | 21,00 | ,334 | ,750 | 75,0 | 28 | 3 | ,730 | ,613 |
26 | TSC | 5,00 | - | ,178 | 17,8 | 28 | 1 | ,163 |
|
27 | TUE | 10,00 | - | ,357 | 35,7 | 28 | 2 | ,340 | - |
28 | UNG | 8,00 |
| ,285 | 28,5 | 28 | 2 | ,269 |
|
Total (Всего) N | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 |
a. Limited to first 100 cases (Ограничено первыми 100 наблюдениями)
12.gif
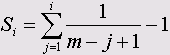
13.gif
8.7 Веса случаев
8.7 Веса случаев
SPSS предоставляет возможность определения веса данных. При этом данным, относящимся к разным наблюдениям, присваиваются различные весовые коэффициенты посредством так называемой переменной взвешивания. Эта процедура может быть полезной в следующих ситуациях:
-
Данная выборка не является репрезентативной, то есть частотные характеристики выборки, состоящей из переменных, достаточных для обеспечения репрезентативности, не соответствуют частотным характеристикам генеральной совокупности.
-
Анализ данных, которые уже представлены в виде частотных таблиц.
Эти ситуации рассматриваются в двух следующих разделах. Подробнее о таблицах сопряженности, которые используются при этом, см. в главе 11.
8.7.1 Коррекция при отсутствии репрезентативности
8.7.1 Коррекция при отсутствии репрезентативности
Перед служащими и представителями других социальных групп были поставлены четыре классических вопроса Инглхарта, уже известные нам из раздела 8.4.2, то есть, было предложено выбрать одну из четырех степеней важности для каждого из нижеследующих пунктов:
1. Поддержание спокойствия и порядка
2. Усиление влияния граждан на власть
3. Борьба с инфляцией
4. Обеспечение свободного выражения мнений
Данные, взятые из опроса ALLBUS 1988 г., хранятся в файле beamte.sav. При этом переменной beamier присваивается кодировка 1 или 2 в зависимости от того, является ли респондент служащим; переменные themal-Hhema4 содержат оценки четырех вышеприведенных пунктов.
-
Загрузите файл beamte.sav и командами меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты) создайте частотные таблицы переменных beamier и themaS:
Служащий?
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | Да | 137 | 10,5 | 10,5 | 10,5 |
Нет | 1162 | 89,5 | 89,5 | 100,0 | |
Total | 1299 | 100,0 | 100,0 |
Борьба с инфляцией
Valid | первостепенная важность | Frequency 109 | Percent 8,4 | Valid Percent 8,4 | Cumulative Percent 8,4 |
второстепенная важность | 237 | 18,2 | 18,2 | 26,6 | |
важность третьей степени | 374 | 28,8 | 28,8 | 55,4 | |
важность четвертой степени | 579 | 44,6 | 44,6 | 100,0 | |
Total | 1299 | 100,0 | 100,0 |
Из частотной таблицы переменной beamier можно заключить, что в данной выборке 10,5% респондентов являются служащими, хотя известно, что доля служащих в общем населении составляет только 8,4%.
Прежде чем мы скорректируем это небольшое искажение при помощи переменной взвешивания, составим таблицу сопряженности для переменных themaS (строки) и beamter (столбцы).
-
Командами меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности) создайте таблицу сопряженности из этих переменных.
-
Дополнительно кнопкой Cells... (Ячейки) задайте вывод процентов по строкам (Percentages — Row) и столбцам (Column), а кнопкой Statistics... (Статистика) — выполнение теста %2(Chi-square):
Таблица сопряженности Борьба с инфляцией* Служащий?
Служащий? | |||||
Да | нет | Total | |||
Борьба с инфля- цией | первостепен ная важность | Count (Коли- чество) | 6 | 103 | 109 |
% от Борьба с инфляцией | 5,5% | 94,5% | 100,0% | ||
%от Служащий? | 4,4% | 8,9% | 8,4% | ||
второстепенн ая важность | Count | 14 | 223 | 237 | |
% от Борьба с инфляцией | 5,9% | 94,1% | 100,0% | ||
%от Служащий? | 10,2% | 19,2% | 18,2% | ||
важность третьей степени | Count | 37 | 337 | 374 | |
% от Борьба с инфляцией | 9,9% | 90,1% | 100,0% | ||
%от Служащий? | 27,0% | 29,0% | 28,8% | ||
важность четвертой степени | Count | 80 | 499 | 579 | |
% от Борьба с инфляцией | 13,8% | 86,2% | 100,0% | ||
%от Служащий? | 58,4% | 42,9% | 44,6% | ||
Total | Count | 137 | 1162 | 1299 | |
% от Борьба с инфляцией | 10,5% | 89,5% | 100,0% | ||
%от Служащий? | 100,0% | 100,0% | 100,0% | ||
Chi-Square Tests (Тесты хи-квадрат)
Value (Значение) | df | Asymp. Sig. (2-sided) (Асимптотическая значимость (двусторонняя)) | |
Pearson Chi-Square хи-квадрат по Пирсону) | 15,077 (а) | 3 | ,002 |
Likelihood Ratio (Степень правдоподобия) | 16,032 | 3 | ,001 |
Linearly-Linear Association (Зависимость линейный-линейный) | 14,302 | 1 | ,000 |
N of Valid Cases (Кол-во допустимых случаев) | 1299 |
a. 0 cells (,0%) have expected count less than 5. The minimum expected count is 11,50. (Ячейки с нулями (,0%) имеют ожидаемую частоту менее 5. Минимальная ожидаемая частота 11,50.)
Результаты показывают, что для служащих борьба с инфляцией имеет меньшее значение, чем для остальных респондентов.
Теперь путем взвешивания мы попробуем скорректировать искажение доли служащих, имеющееся в выборке. Принцип заключается в том, что для каждого значения переменной (в данном случае переменной beamier) вычисляется весовой коэффициент как отношение необходимого значения к существующему.
Весовой коэффициент = (необходимое значение)/(существующее значение)
Для служащих весовой коэффициент равен
8,4/10,5=0,8
а для остальных —
91,5/89,5 = 1,023
-
Командами меню File (Файл) New (Создать) Syntax (Синтаксис) откройте редактор синтаксиса.
-
Чтобы создать переменную взвешивания, введите следующие команды:
IF beamter=1 gewicht=8.4/10.5 .
IF beamter=2 gewicht=91.6/89. 5 .
EXECUTE .
Исходя из соображений точности расчета рекомендуется вводить сами значения, а не их отношения, и предоставлять их вычисление компьютеру.
-
Выделите введенные команды, выбрав в меню Edit (Правка) Select All (Выделить все)
-
Щелкните на символе Run, и в файл данных будет добавлена новая переменная gewicht. Ее мы и будем использовать как переменную взвешивания.
Для создания переменных взвешивания можно и не использовать команды синтаксиса SPSS, а повторить подход, описанный в разделе 8.4.1.
-
Выберите в меню команды Data (Данные) ; Weight Cases... (Взвесить наблюдения)
Появится диалоговое окно Weight Cases.
Рис. 8.13: Диалоговое окно Weight Cases
-
Выберите в этом диалоговом окне опцию Weight cases by и перенесите переменную gewicht в поле под ней (в диалоге это поле называется Frequency Variable).
-
Описанным выше путем создайте частотные таблицы переменных beamier и thema3 и таблицу сопряженности из этих переменных. Вы получите следующий результат:
Служащий?
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | да | 110 | 8,4 | 8,4 | 8,4 |
нет | 1189 | 91,6 | 61,6 | 100,0 | |
Total | 1299 | 100,0 | 100,0 |
Борьба с инфляцией
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | первостепенная важность | 110 | 8,5 | 8,5 | 8,5 |
второстепенная важность | 239 | 18,4 | 18,4 | 26,9 | |
важность третьей степени | 375 | 28,8 | 28,8 | 55,8 | |
важность четвертой степени | 575 | 44,2 | 44,2 , | 100,0 | |
Total | 1299 | 100,0 | 100,0 |
Таблица сопряженности Борьба с инфляцией * Служащий?
Служащий? | |||||
да | Нет | Total | |||
Борьба с инфляцией | первосте- пенная важность | Count | 5 | 105 | 110 |
% от Борьба с инфляцией | 4,5% | 95,5% | 100,0% | ||
%от Служащий? | 4,5% | 8,8% | 8,5% | ||
второсте- пенная важность | Count | 11 | 228 | 239 | |
% от Борьба с инфляцией | 4,6% | 95,4% | 100,0% | ||
%от Служащий? | 10,0% | 19,2% | 18,4% | ||
важность третьей степени | Count | 30 | 345 | 375 | |
% от Борьба с инфляцией | ,U /0 | 92,0% | 100,0% | ||
%от Служащий? | 27,3% | 29,0% | 28,9% | ||
важность четвертой степени | Count | 64 | 511 | 575 | |
% от Борьба с инфляцией | 11,1% | 88,9% | 100,0% | ||
%от Служащий? | 58,2% | 43,0% | 44,3% | ||
Total | Count | 110 | 1189 | 1299 | |
% от Борьба с инфляцией | 8,5% | 91,5% | 100,0% | ||
%от Служащий? | 100,0% | 100,0% | 100,0% | ||
Chi-Square Tests
Value | Df | Asymp. Sig. (2-sided) | |
Pearson Chi-Square | 12,156 a | 3 | ,007 |
Likelihood Ratio | 12,972 | 3 | ,005 |
Linear-by-Linear Association | 11,410 | 1 | ,001 |
N of Valid Cases | 1299 |
а. 0 cells (,0%) have expected count less than 5. The minimum expected count is 9,31. (Ячейки с нулями (,0%) имеют ожидаемую частоту менее 5. Минимальная ожидаемая частота 9,31.)
Общая частота осталась неизменной — 1299, но взаимное отношение частот изменилось. В переменной beamter количество служащих снизилось с 137 до 110, что соответствует реальной доле служащих 8,4%. Также незначительно изменилась частотная таблица для переменной themaS; взвешивание повлияло и на нее.
То же можно сказать и о таблице сопряженности. Однако здесь процентные значения по столбцам не изменились; сохранились соотношения между отдельными значениями переменных в ячейках.
Установленное взвешивание будет действовать до тех пор, пока вы снова не выберете в диалоговом окне Weight Cases опцию Do not weight cases (He взвешивать наблюдения).
Описанный метод взвешивания при отсутствии репрезентативности может привести к возникновению некоторых проблем, которые, впрочем, не проявляются в изученном примере.
Если мы рассмотрим, например, взвешенную частотную таблицу переменной «Борьба с инфляцией», то обнаружим, что общее количество наблюдений (1299) не меняется при взвешивании. Это связано с тем, что сумма весовых коэффициентов по всем случаям равна числу случаев. Однако в варианте взвешивания, который будет изложен в разделе 8.7.2, это не так.
Если вы попробуете вручную просуммировать частоты упоминания всех четырех вариантов ответов, то в результате вы также получите число 1299. Однако это не закономерность, а скорее счастливое совпадение, о чем свидетельствует следующий пример.
-
Загрузите файл mai.sav, содержащий результаты опроса членов профсоюза на тему 1 мая (см. главу 24).
-
С помощью команд меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты) создайте частотные таблицы переменных v2 (Пол) и v20 (Занятие).
Пол
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | женский | 77 | 28,4 | 28,4 | 28,4 |
мужской | 184 | 71,6 | 71,6 | 100,0 | |
Total | 271 | 100,0 | 100,0 |
Занятие
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | Учащийся | 8 | 3,0 | 3,0 | 3,0 |
Рабочий | 47 | 17,3 | 17,3 | 20,3 | |
Квалифици- рованный рабочий | 47 | 17,3 | 17,3 | 37,6 | |
Специалист | 4 | 1,5 | 1,5 | 39,1 | |
Служащий | 66 | 24,4 | 24,4 | 63,5 | |
Менеджер | 8 | 3,0 | 3,0 | 66,4 | |
Государствен- ный служащий | 31 | 11,4 | 11,4 | 77,9 | |
Пенсионер | 42 | 15,5 | 15,5 | 93,4 | |
Домохозяйка | g | 3,3 | 3,3 | 96,7 | |
Нетрудоспо- собный | 1 | ,4 | ,4 | 97,0 | |
Безработный Total | 8 271 | 3,0 100,0 | 3,0 100,0 | 100,0 |
-
Взвесим наблюдения так, чтобы устранить неравномерность между количествами респондентов обоих полов. Учитывая частотное распределение полов, характерное для имеющейся выборки, это выполняется при помощи следующих команд:
IF v2=1 w=135.5/77.
IF v2=2 w=135.5/194.
EXECUTE
-
Теперь описанным выше способом проведем взвешивание, используя только что полученную переменную w, и построим обе частотные таблицы заново:
Пол
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | женский | 135 | 50,0 | 50,0 | 50,0 |
мужской | 135 | 50,0 | 50,0 | 100,0 | |
Total | 271 | 100,0 | 100,0 |
Занятие
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | Учащийся | 10 | 3,6 | 3,6 | 3,6 |
Рабочий | 46 | 16,8 | 16,8 | 20,4 | |
Квалифици- рованный рабочий | 35 | 12,9 | 12,9 | 33,3 | |
Специалист | 3 | 1,0 | 1,0 | 34,4 | |
Служащий | 83 | 30,7 | 30,7 | 65,1 | |
Менеджер | 7 | 2,5 | 2,5 | 67,5 | |
Государствен- ный служащий | 32 | 11,9 | 11,9 | 79,4 | |
Пенсионер | 36 | 13,2 | 13,2 | 92,6 | |
Домохозяйка | 9 | 3,5 | 3,5 | 96,1 | |
Нетрудоспо- собный | 2 | ,6 | ,6 | 96,8 | |
Безработный | 9 | 3,2 | 3,2 | 100,0 | |
Total | 271 | 100,0 | 100,0 |
Хотя общее число наблюдений, 271, опять не изменилось, но суммирование частот по категориям дает несколько другие результаты.
Это особенно заметно для переменной Пол. Так как после определения переменной взвешивания обе категории должны иметь одинаковые частоты, с самого начала ясно, что сумма не может быть нечетной. Для переменной занятие сложение частот по категориям также дает результат 272, что на единицу отличается от общего количества наблюдений — 271, выводимого в окне просмотра. SPSS всегда, в том числе при взвешивании, выдает целочисленные частоты. Поэтому негативное влияние округления будет неизбежным. Другие статистические программы, например, Stata, обходят эту ситуацию, вычисляя взвешенные частоты с дробной частью.
Если сделать выборку наблюдений, то отображаемые программой суммы до и после взвешивания, как правило, также будут различаться. Это связано с тем, что в частичной выборке количество наблюдений обычно не соответствует сумме весовых коэффициентов, попадающих в эту выборку. Это можно проверить, создав на основе открытого файла данных частотную таблицу переменной «Занятие» до взвешивания и после взвешивания, но только для приверженцев партии СДПГ (v22=2). Тогда мы получим соответственно суммы 91 и 83.
Взвешивание для выравнивания характеристик при нарушении репрезентативности применяется в первую очередь при эпидемиологических исследованиях. Так как при весовом коэффициенте, превосходящем единицу, количество наблюдений искусственно увеличивается по сравнению с фактически измеренным, к результатам теста на значимость следует подходить весьма критически.
14.gif
8.7.2 Анализ концентрированных данных
8.7.2 Анализ концентрированных данных
На предприятии с семнадцатью работниками девять из них удовлетворены условиями труда. Двое из этой последней группы в текущем году болели гриппом; из восьми работников, которые не удовлетворены условиями труда, гриппом болели пятеро. Это дает нам следующую таблицу:
удовлетворены | не уловлетворены | |
болели не болели | 1 7 | 5 3 |
Следует выяснить, является ли значимой большая доля болевших среди неудовлетворенных условиями труда. Подходящим статистическим тестом для этой задачи будет точный тест Фишера и Йейтса, который выполняется после создания таблицы сопряженности в дополнении к обычному тесту %2, если количество наблюдений очень мало.
Чтобы можно было решить эту задачу с применением SPSS, в первую очередь следует построить соответствующий файл данных, состоящий из наблюдений и переменных. Примером такого файла служит grippe.sav. Загрузите этот файл. В окне редактора данных вы получите структуру с четырьмя наблюдениями и тремя переменными.
Она содержит переменную grippe с категориями 1 и 2 (болели — не болели), переменную zuf с категориями 1 и 2 (удовлетворены — не удовлетворены) и переменную freq, которая указывает частоту каждого сочетания и будет использоваться в качестве переменной взвешивания.
-
Выберите в меню команды Data (Данные) Weight Cases... (Взвесить наблюдения)
-
В диалоговом окне Weight Cases выберите опцию Weight cases by и перенесите переменную freq в поле Frequency variable.
-
Закройте диалоговое окно и выберите команды меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
-
Перенесите переменную grippe в список переменных строк (Rows), переменную zuf— в список переменных столбцов (Columns), и в диалоге, открываемом кнопкой Statistics..., задайте проведение теста %2 (Chi-square).
В окне просмотра появится следующий результат:
Таблица сопряженности Болели? * Удовлетворены?
Count (Количество) | ||||
Удовлетворены? | Total | |||
| да нет | |||
Болели? | Да | 2 | 5 | 7 |
Нет | 7 | 3 | 10 | |
Total | 9 | 8 | 17 | |
Chi-Square Tests
Value | df | Asymp. Sig. (2-sided) | Exact Sig. (2-sided) (Точная значимость (двусторон-няя)) | Exact Sig. (1-sided) (Точная значимость (односторон-няя)) |
Pearson Chi-Square (?2 пo Пирсону) | 2,837 " | 1 | ,092 | |
Continuity Correction (b) (Коррекция непреры-вности) | 1,418 | 1 | ,234 | |
Likelihood Ratio (Отношение правдопо-добия) | 2,915 | 1 | ,088 | |
Fisher's Exact Test (Точный тест Фишера) | ,153 | ,117 | ||
Linear-by-Linear Association (Зависимость линейный-линейный) | 2,670 | 1 | ,102 | |
N of Valid Cases (Кол-во допустимых случаев) | 17 |
a. Computed only for a 2x2 table (Вычислено только для таблицы 2Х2)
b. 3 cells (75,0%) have expected count less than 5. The minimum expected count is 3,29 (3 ячейки (75%) имеют ожидаемую частоту менее 5. Минимальная ожидаемая частота 11,50.)
Односторонний тест Фишера-Йейтса даст в этом случае р =0,117, т.е. отсутствие значимой разницы.
Следующий пример взят из биологии. Исследовалось количество особей девяти различных видов кузнечиков на пяти разных лугах. Частоты сведены в следующую таблицу
Луг
Вид кузнечика 1 | 2 | 3 | 4 | 5 | |
1 | 0 | 0 | 1 | 1 | 1 |
2 | 1 | 1 | 1 | 1 | 0 |
3 | 61 | 51 | 17 | 122 | 54 |
4 | 36 | 32 | 23 | 38 | 11 |
5 | 2 | 0 | 2 | 6 | 0 |
6 | 3 | 1 | 2 | 2 | 1 |
7 | 0 | 0 | 0 | 2 | 0 |
8 | 26 | 50 | 25 | 54 | 22 |
9 | 35 | 33 | 36 | 25 | 12 |
Следует выяснить, являются ли повышенная концентрация или недостаток отдельных видов кузнечиков на определенных лугах статистически значимыми. Для этого следует применить тест по критерию хи-квадрат.
И в этом случае решение задачи SPSS должна начаться с составления файла данных, содержащего три переменные: переменную для вида кузнечиков (с категориями 1—9), переменную для луга (категории 1—5) и переменную, содержащую частоту данного вида на данном лугу.
-
Загрузите файл wiese.sav и исследуйте его структуру в редакторе данных.
-
Выберите в меню команды Data (Данные) Weight Cases... (Взвесить наблюдения) Откроется диалоговое окно Weight Cases.
-
Выберите опцию Weight cases by и перенесите переменную h в поле Frequency variable.
-
Закройте диалоговое окно кнопкой ОК и выберите команды меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
Появится диалоговое окно Crosstabs.
-
Перенесите переменную heuschr в список переменных строк, переменную wiese — в список переменных столбцов, и в диалоге, открываемом кнопкой Cells..., кроме вывода наблюдаемых частот (флажок Observed в группе Counts), задайте также вывод ожидаемых частот (флажок Expected) и нормированных остатков (флажок Standardized в группе Residuals). После закрытия диалогового окна будет выведена следующая таблица.
Таблица сопряженности HFUSflHR * WIFSF
WIESE | Total | ||||||
1 | 2 | 3 | 4 | 5 | |||
HEUSCHR | |||||||
1 | Count (Количество) | 0 | 0 | 1 | 1 | 1 | 3 |
Expected Count (Ожидаемое количество) | ,6 | ,6 | ,4 | 1,0 | ,4 | 3,0 | |
Std. Residual (Нормиро- ванный остаток) | -,8 | -,8 | ,9 | ,0 | 1,0 | ||
2 | Count | 1 | 1 | 1 | 1 | 0 | 4 |
Expected Count | ,8 | ,8 | ,5 | 1,3 | ,5 | 4,0 | |
Std. Residual | ,2 | ,2 | ,6 | -,2 | -,7 | ||
3 | Count | 61 | 51 | 17 | 122 | 54 | 305 |
Expected Count | 63,2 | 64,8 | 41,3 | 96,8 | 38,9 | 305,0 | |
Std. Residual | -,3 | -1,7 | -3,8 | 2,6 | 2,4 | ||
4 | Count | 36 | 32 | 23 | 38 | 11 | 140 |
Expected Count | 29,0 | 29,7 | 18,9 | 44,4 | 17,9 | 140,0 | |
Std. Residual | 1,3 | ,4 | ,9 | -1,0 | -1,6 | ||
5 | Count | 2 | 0 | 2 | 6 | 0 | 10 |
Expected Count | 2,1 | 2,1 | 1,4 | 3,2 | 1,3 | 10,0 | |
Std. Residual | -,1 | -1,5 | ,6 | 1,6 | -1,1 | ||
6 | Count | 3 | 1 | 2 | 2 | 1 | 9 |
Expected Count | 1,9 | 1,9 | 1,2 | 2,9 | 1,1 | 9,0 | |
Std. Residual | ,8 | -,7 | ,7 | -,5 | -,1 | ||
7 | Count | 0 | 0 | 0 | 2 | 0 | 2 |
Expected Count | ,4 | ,4 | ,3 | ,6 | ,3 | 2,0 | |
Std. Residual | -,6 | -,7 | -,5 | 1,7 | -,5 | ||
8 | Count | 26 | 50 | 25 | 54 | 22 | 177 |
Expected Count | 36,7 | 37,6 | 23,9 | 56,2 | 22,6 | 177,0 | |
Std. Residual | -1,8 | 2,0 | ,2 | -,3 | -,1 | ||
9 | Count | 35 | 33 | 36 | 25 | 12 | 141 |
Expected Count | 29,2 | 29,9 | 19,1 | 44,7 | 18,0 | 141,0 | |
Std. Residual | 1,1 | ,6 | 3,9 | -3,0 | -1,4 | ||
Total | |||||||
Count | 164 | 168 | 107 | 251 | 101 | 791 | |
Expected Count | 164,0 | 168,0 | 107.0 | 251,0 | 101,0 | 791,0 | |
В ячейках таблицы последовательно располагаются наблюдаемые частоты (fy), ожидаемые частоты (fg) и нормированные остатки, определяемые по формуле:
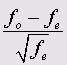
Считается, что существует значимое различие между наблюдаемой и ожидаемой частотой, если нормированный остаток больше или равен 2. Другие предельные значения принимаются в соответствии со следующей таблицей.
Нормированный остаток | Уровень значимости |
>=2,0 | р<0,05 (*) |
>=2,6 | р<0,01 (**) |
>=3,3 | P<0,001 (***) |
Однако эти правила применимы, только в том случае, если ожидаемая частота не меньше 5. Если, к примеру, взять вид кузнечиков № 3, то для него наблюдается значимый недостаток на лугу 3, очень значимая концентрация на лугу 4 и значимая концентрация на лугу 5.
15.gif
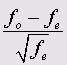
8.8 Примеры вычисления новых переменных
8.8 Примеры вычисления новых переменных
Два следующих примера демонстрируют возможности языка программирования SPSS.
8.8.1 Первый пример: вычисление расхода бензина
8.8.1 Первый пример: вычисление расхода бензина
Предположим, что мы ведем книгу учета расхода бензина. При каждой заправке в нее записывается дата, пробег в километрах и объем заправки в литрах:
Дата | Пробег | Литров |
16.12.1992 | 20580 | 60,3 |
23.12.1992 | 21250 | 57,4 |
04.01.1993 | 21874 | 56,6 |
17.01.1993 | 22476 | 56,3 |
28.01.1993 | 22954 | 45,4 |
12.02.1993 | 23450 | 48,6 |
27.02.1993 | 24020 | 57,0 |
14.03.1993 | 24611 | 56,7 |
Эти данные записаны соответственно в переменных tag, monat, jaehr, kmstand и liter файла tank.sav. Для каждой даты (кроме первой, где это невозможно) требуется вычислить пробег за день и средний расход бензина в расчете на сто километров, а также вывести их через новые переменные.
Это типичный случай, где рационально применить функций LAG и YRMODA. Используя пояснения к этим функциям, которые содержатся в разделе 8.1.2, попробуйте самостоятельно интерпретировать смысл следующих команд:
COMPUTE ntage=yrmoda(jahr,monat,tag) .
COMPUTE difftage=ntage-lag(ntage,1)
COMPUTE diffkm=kmstand-lag(kmstand/1).
COMPUTE verbr=liter*100/diffkm .
COMPUTE kmtag=diffkm/difftage .
EXECUTE .
-
Загрузите файл tank.sav.
-
Введите приведенные выше команды в редактор синтаксиса или примените для этого диалоговое окно Compute Variable.
-
В заключение командами меню Analyze (Анализ) Reports (Отчеты) Case summaries... (Сводка наблюдений) выведите значения переменных tag, monat, jahr, kmtag и verbr.
8.8.2 Второй пример: вычисление даты пасхи
8.8.2 Второй пример: вычисление даты пасхи
Никейский собор в 325 г. установил, что пасху следует праздновать в первое воскресенье после первого весеннего полнолуния. На этом основан метод Гаусса для определения даты пасхального воскресенья. Согласно нему, если задан год jahr (например, 1994), то дату пасхального воскресенья, можно вычислить с помощью следующих операций:
k = целый результат деления jahr/100
р = целый результат деления k/3
q = целый результат деления k/4
m = 15 + k — p — q
ml = остаток от деления т/30
n = 4 + k - q
nl = остаток от деления п/7
а = остаток от деления jahr/19
Ь = остаток от деления jahr/4
с = остаток от деления jahr/7
d = 19 * а + ml
dl = остаток от деления d/30
e = 2*b + 4*c + 6*dl + nl
el = остаток от деления е/7
х = 22 + dl + el
Для определения х существует два исключения
-
Если x=57, то х принимается равным 50
-
Если d1=28 и el=6, а остаток деления в выражении (11*m+11)/30 меньше 19, то х принимается равным 49
Пасхальное воскресенье выпадает на х-ое марта или, если х больше 31, — на х— 31-ое апреля. Этот алгоритм дает превосходный пример для знакомства с арифметическими функциями TRUNC и MOD (см. раздел 7.1.3). Кроме того, можно еще раз потренироваться в использовании оператора IF (раздел 8.4).
Сначала в редакторе данных следует создать файл данных, содержащий единственную переменную jahr. Затем в строках редактора необходимо ввести годы, для которых вы желаете вычислить дату пасхи. Можно также загрузить файл примеров ostern.sav, содержащий годы с 1995 по 2030.
Затем откройте редактор синтаксиса и введите следующую программу. Команды COMPUTE вплоть до вычисления х можно также ввести в соответствующем диалоговом окне (см. раздел 8.1). Команды, приведенные ниже, вводятся в редакторе синтаксиса. Для того, чтобы избежать ручного ввода этой программы, можно просто загрузить в редактор синтаксиса файл ostern.sps.
COMPUTE k=TRUNC(jahr/100) .
COMPUTE p=TRUNC(k/3) .
COMPUTE q=TRUNC(k/4) .
COMPUTE m=15+k-p-q .
COMPUTE ml=MOD(m,30) .
COMPUTE n=4+k-g .
COMPUTE nl=MOD(n,7) .
COMPUTE a=MOD(jahr,19) .
COMPUTE b=MOD(jahr,4) .
COMPUTE c=MOD(jahr,7)
COMPUTE d=19*a+ml .
COMPUTE dl=MOD(d,30) .
COMPUTE e=2*b+4*c+6*dl+nl .
COMPUTE el=MOD(e,7) .
COMPUTE x=22+dl+el .
IF x=57 x=50 .
IF dl=28 AND el=6
AND MOD (ll*m+ll,30)<19 x=49 .
COMPUTE tag=x .
COMPUTE monat=3 .
IF (x > 31) tag=x-31 .
IF (x > 31) monat=4 .
COMPUTE odatum=DATE.MDY(raonat,tag,jahr) .
FORMATS odatum(DATEll) .
LIST odatum .
Переменные tag и monat определяют дату пасхального воскресенья заданного года (переменной jahr). На их основе функция DATE.MDY вычисляет значение времени во внутреннем формате SPSS (число секунд после введения григорианского календаря). Затем это значение записывается в переменную odatum, которая преобразуется в формат даты DATE11.
После ввода программы или открытия файла в редакторе синтексиса с помощью меню Edit (Правка) выделите все строки и запустите программу. С помощью команды LIST в окне просмотра буде сформирована следующая таблица, фрагмент которой с 1995 до 2002 года, приводится ниже:
ODATUM
16-APR-1995
07-APR-1996
30-MAR-1997
12-APR-1998
04-APR-1999
23-APR-2000
15-APR-2001
31-MAR-2002
Обладая некоторой фантазией и знанием командного синтаксиса SPSS, можно решать задачи, не связанные непосредственно со статистическими вычислениями.