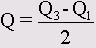6.2 Вывод статистических характеристик
6.2 Вывод статистических характеристик
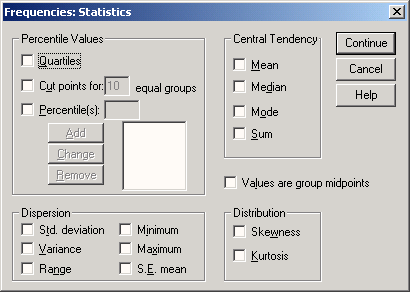
Чтобы получить описательную статистику числовых переменных, можно щелкнуть в диалоге Frequencies на кнопке Statistics... (Статистика). Откроется диалоговое окно Frequencies: Statistics (Частоты: Статистика).
В группе Percentile Values (Значения процентилей) можно выбрать следующие варианты:
-
Quartiks (Квартили): Будут показаны первый, второй и третий квартили. Первый квартиль (Q,) — это точка на шкале измеренных значений, ниже (левее) которой располагаются 25 % измеренных значений. Второй квартиль (Q2) — это точка, ниже которой располагаются 50 % измеренных значений. Второй квартиль также называется медианой. Третий квартиль (Q3) — это точка на шкале измеренных значений, ниже которой располагаются 75 % значений. Если данные имеются только в форме порядкового отношения, то качестве меры разброса используется межквартильная широта. Она определяется как
Рис. 6.2: Диалоговое окно frequencies: Statistics
-
Cut points (Точки раздела): Будут вычислены значения процентилей, разделяющие выборку на группы наблюдений, которые имеют одинаковую ширину, то есть включают одно и то же количество измеренных значений. По умолчанию предлагается количество групп 10. Если задать, к примеру, 4, то будут показаны квартили, то есть квартили соответствуют процентилям 25, 50 и 75. Видно, что число показываемых процентилей на единицу меньше заданного числа групп.
-
Percentile(s) (Процентили): Здесь имеются в виду значения процентилей, определяемые пользователем. Введите значение процентиля в пределах от 0 до 100 и щелкните на кнопке Add (Добавить). Повторите эти действия для всех желаемых значений процентилей. Значения в порядке возрастания будут показаны в списке. Например, если ввести значения 25, 50 и 75, то мы получим квартили. Можно задавать любые значения процентилей, например, 37 и 83. В первом случае (37) будет показано значение выбранной переменной, ниже которого лежат 37 % значений, а во втором случае (83) — значение, ниже которого располагаются 83 % значений.
В группе Dispersion (Разброс) можно выбрать следующие меры разброса:
-
Std. deviation (Стандартное отклонение): Стандартное отклонение — это мера разброса измеренных величин; оно равно квадратному корню из дисперсии. В интервале шириной, равной удвоенному стандартному отклонению, который отложен по обе стороны от среднего значения, располагается примерно 67% всех значений выборки, подчиняющейся нормальному распределению.
-
Variance (Дисперсия): Дисперсия — это квадрат стандартного отклонения и, следовательно, эта характеристика также является мерой разброса измеренных величин. Она определяется как сумма квадратов отклонений всех измеренных значений от их среднеарифметического значения, деленная на количество измерений минус 1.
-
Range (Размах): Размах — это разница между наибольшим значением (максимумом) и наименьшим значением (минимумом).
-
Minimum (Минимум): Наименьшее значение.
-
Maximum (Максимум): Наибольшее значение.
-
S.E. mean (Стандартная ошибка): Это стандартная ошибка среднего значения. В интервале шириной, равной удвоенной стандартной ошибке, отложенному вокруг среднего значения, располагается среднее значение генеральной совокупности с вероятностью примерно 67 %. Стандартная ошибка определяется как стандартное отклонение, деленное на квадратный корень из объема выборки.
Обычно мерами разброса переменных, относящихся к интервальной шкале и подчиняющихся нормальному распределению, служат стандартное отклонение и стандартная ошибка. Как было сказано выше, стандартное отклонение позволяет задать диапазон разброса отдельных значений. По так называемому правилу кулака, в одном диапазоне стандартного отклонения (охватывающем ширину стандартного отклонения в обе стороны от среднего значения) располагается примерно 67 % значений, в диапазоне удвоенного стандартного отклонения — примерно 95 %, а в диапазоне утроенного стандартного отклонения — примерно 99 % значений.
С другой стороны, стандартная ошибка позволяет задать доверительный интервал для среднего значения. В диапазоне удвоенной стандартной ошибки по обе стороны от среднего значения с вероятностью примерно 95 % находится среднее значение генеральной совокупности. С вероятностью примерно 99 % она лежит в диапазоне утроенной стандартной ошибки. Часто указывают только одну из этих двух мер разброса, обычно — стандартную ошибку, так как ее значение меньше. Во всех случаях следует точно выяснить, какая из мер разброса имеется в виду.
В группе Central Tendency (Средние) можно выбрать следующие характеристики:
-
Mean (Среднее значение): Среднее значение — это арифметическое среднее измеренных значений; оно определяется как сумма значений, деленная на их количество. Например, если имеется 12 измеренных значений и их сумма составляет 600, то среднее значение будет х = 600 : 12 = 50.
-
Median (Медиана): Медиана — это точка на шкале измеренных значений, выше и ниже которой лежит по половине всех измеренных значений. Например, если измеренные значения таковы:
37854639284,
то сначала они располагаются в порядке возрастания: 23344567889.
В данном случае медианой будет значение 5. Всего у нас 11 измеренных значений, следовательно, медианой является шестое значение. Выше него располагается 5 значений, и ниже — тоже 5. При нечетном количестве значений медиана всегда будет совпадать с одним из измеренных значений. При четном количестве медиана будет средним арифметическим двух соседних значений. Например, если имеются следующие измеренные значения:
3445678899
то медиана в этом случае будет равна: (6 + 7) : 2 = 6,5.
-
Mode (Мода): Мода — это значение, которое наиболее часто встречается в выборке. Если одна и та же наибольшая частота встречается у нескольких значений, то выбирается наименьшее из них.
-
Sum (Сумма): Сумма всех значений.
В группе Distribution (Распределение) можно выбрать следующие меры несимметричности распределения:
-
Skewness (Коэффициент асимметрии): Коэффициент асимметрии — это мера отклонения распределения частоты от симметричного распределения, то есть такого, у которого на одинаковом удалении от среднего значения по обе стороны выборки данных располагается одинаковое количество значений. Если наблюдения подчиняются нормальному распределению, то асимметрия равна нулю. Для проверки на нормальное распределение можно применять следующее правило: Если асимметрия значительно отличается от нуля, то гипотезу о том, что данные взяты из нормально распределенной генеральной совокупности, следует отвергнуть. Если вершина асимметричного распределения сдвинута к меньшим значениям, то говорят о положительной асимметрии, в противоположном случае — об отрицательной.
-
Kurtosis (Коэффициент вариации или эксцесс): Коэффициент вариации указывает, является ли распределение пологим (при большом значении коэффициента) или крутым. Коэффициент вариации равен нулю, если наблюдения подчиняются нормальному распределению. Поэтому для проверки на нормальное распределение можно применять еще одно правило: Если коэффициент вариации значительно отличается от нуля, то гипотезу о том, что данные взяты из нормально распределенной генеральной совокупности, следует отвергнуть.
Как правило, для переменных, относящихся к интервальной шкале и подчиняющихся нормальному распределению, в качестве основной характеристики используют среднее значение, а в качестве меры разброса — стандартное отклонение или стандартную ошибку. Для порядковых или интервальных переменных, не подчиняющихся нормальному распределению, — соответственно медиану или первый и третий квартили. Для переменных относящихся к номинальной шкале, нельзя дать других значимых характеристик кроме моды.
В диалоге есть еще один флажок:
-
Values are group midpoints (Значения являются средними точками групп): Если установить этот флажок, то при вычислении медианы и остальных значений процен-тилей оценки этих характеристик будут определяться для концентрированных данных. Этому вопросу посвящен отдельный раздел.
Для переменной alter (возраст) мы определим следующие характеристики: среднее значение, медиану, моду, квартили, стандартное отклонение, дисперсию, размах, минимум, максимум, стандартную ошибку, асимметрию и эксцесс. Поступите следующим образом:
-
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты)
-
В диалоге Frequencies щелкните на кнопке Reset (Сброс), чтобы отменить прежние настройки.
-
Перенесите переменную alter в список выходных переменных.
-
Щелкните на кнопке Statistics... (Статистика).
-
В диалоге Frequencies: Statistics установите флажки желаемых характеристик. Затем щелкните на кнопке Continue (Продолжить). Вы вернетесь в диалог Frequencies.
-
В диалоге Frequencies деактивируйте опцию Display frequency tables (Показывать частотные таблицы). Щелкните на кнопке ОК.
В окне просмотра появятся следующие результаты:
Статистика
Alter | ||
N | Допустимые | 106 |
Утерянные | 2 | |
Среднее значение | 22,24 | |
Стандартная ошибка среднего значения | 21 | |
Медиана | 22,00 | |
Мода | 21 | |
Стандартное отклонение | 2,19 | |
Дисперсия | 4,79 | |
Асимметрия | ,859 | |
Стандартная ошибка асимметрии | ,235 | |
Эксцесс | 1,042 | |
Стандартная ошибка эксцесса | ,465 | |
Размах | 11 | |
Минимум | 18 | |
Максимум | 29 | |
Процентили | 25 | 21,00 |
50 | 22,00 | |
75 | 23,00 | |
Респонденты опроса о психическом состоянии и социальном положении имеют средний возраст 22,24 года. Медиана составляет 22. Большинству респондентов 21 год (это мода). Самому молодому респонденту 18 лет (минимум), самому старшему — 29 лет (максимум). Самый старший респондент на 11 лет старше самого молодого (размах). Стандартное отклонение составляет 2,19. Следовательно, дисперсия — квадрат стандартного отклонения — равна (2,19)2 = 4,79. Асимметрия и коэффициент вариации даны с соот-ветсвующими стандартными ошибками.
3.gif