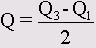Глава 6. Частотный анализ.
Глава 6. Частотный анализ
1. Частотный анализ
Частотный анализ
Первым этапом статистического анализа данных, как правило, является частотный анализ. В этой главе мы проведем частотный анализ на примере файла Studium.sav. Этот файл находится на компакт-диске примеров или в рабочем каталоге \SPSSBOOK. Он содержит результаты опроса студентов об их психическом состоянии и социальном положении. Опрос касался таких предметов, как социальное положение, психическая ситуация и успеваемость. Кроме того, затрагивались такие данные, как изучаемый предмет, пол, возраст и национальность.
6.1 Частотные таблицы
6.1 Частотные таблицы
-
Сначала загрузите файл Studium.sav, выбрав команды меню File (Файл) Open... (Открыть...) Появится диалог Open File (Открыть файл).
-
Выберите указанный выше файл Studium.sav и подтвердите выбор кнопкой Open (Открыть). Файл появится в Редакторе данных.
-
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies (Частоты) Появится диалоговое окно Frequencies (см. рис. 6.1).
-
Кнопкой с треугольником перенесите переменную psyche в список выходных переменных и подтвердите операцию кнопкой ОК.
Рис. 6.1: Диалоговое окно Frequencies (Частоты)
Результаты появятся в окне просмотра результатов. Перед самой частотной таблицей выводится небольшая таблица с обзором допустимых и отсутствующих значений. Здесь она не показана.
Психическое состояние
Частота | Проценты | Допус- тимые проценты | Нако- пленные проценты | ||
Крайне неустой- чивое | 20 | 18,5 | 18,7 | 18,7 | |
Неустой- чивое | 40 | 37,0 | 37,4 | 56,1 | |
Допус- тимые | Устойчивое | 41 | 38,0 | 38,3 | 94,4 |
Очень устойчивое | 6 | 5,6 | 5,6 | 100,0 | |
Всего | 107 | 99,1 | 100,0 | ||
Отсут-ствующие | нет данных | 1 | ,9 | ||
Всего | 108 | 100,0 |
Каждая строка частотной таблицы описывает одно возможное значение. Строка с пометкой нет данных представляет наблюдения, в которых не было дано никакого ответа. Всего имеется 107 допустимых ответов, а также одно наблюдение, в котором психическое состояние неизвестно (данные отсутствуют либо утеряны). Первый столбец содержит метки отдельных значений (крайне неустойчивое, неустойчивое, устойчивое, ...). Во втором столбце под заголовком «Частота» приведена частота каждого из вариантов ответа на вопрос из теста. Так, к примеру, 20 человек на вопрос о психическом состоянии дали ответ: «крайне неустойчивое», а 40 человек — «неустойчивое». В третьем столбце показана процентная частота каждого ответа. Процентная частота соответствует отношению каждого из вариантов ответа к общему количеству опрашиваемых, включая утерянные значения. В четвертом столбце дано допустимое процентное значение. При определении этого значения утерянные данные исключаются. Последний столбец содержит накопленные процентные значения. Накопленные проценты — это сумма процентных частот допустимых ответов. Так, например, процент респондентов, которые дали ответ крайне неустойчивое или неустойчивое, составляет 56,1%. Это число определяется выражением: 18,7% + 37,4% = 56,1%. В последней строке содержится сумма всех столбцов (Всего).
1.gif

6.2 Вывод статистических характеристик
6.2 Вывод статистических характеристик
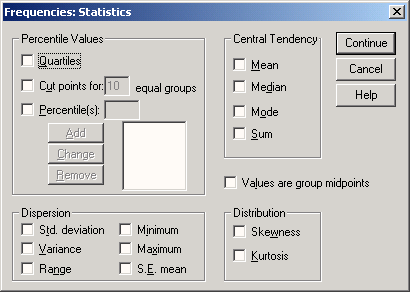
Чтобы получить описательную статистику числовых переменных, можно щелкнуть в диалоге Frequencies на кнопке Statistics... (Статистика). Откроется диалоговое окно Frequencies: Statistics (Частоты: Статистика).
В группе Percentile Values (Значения процентилей) можно выбрать следующие варианты:
-
Quartiks (Квартили): Будут показаны первый, второй и третий квартили. Первый квартиль (Q,) — это точка на шкале измеренных значений, ниже (левее) которой располагаются 25 % измеренных значений. Второй квартиль (Q2) — это точка, ниже которой располагаются 50 % измеренных значений. Второй квартиль также называется медианой. Третий квартиль (Q3) — это точка на шкале измеренных значений, ниже которой располагаются 75 % значений. Если данные имеются только в форме порядкового отношения, то качестве меры разброса используется межквартильная широта. Она определяется как
Рис. 6.2: Диалоговое окно frequencies: Statistics
-
Cut points (Точки раздела): Будут вычислены значения процентилей, разделяющие выборку на группы наблюдений, которые имеют одинаковую ширину, то есть включают одно и то же количество измеренных значений. По умолчанию предлагается количество групп 10. Если задать, к примеру, 4, то будут показаны квартили, то есть квартили соответствуют процентилям 25, 50 и 75. Видно, что число показываемых процентилей на единицу меньше заданного числа групп.
-
Percentile(s) (Процентили): Здесь имеются в виду значения процентилей, определяемые пользователем. Введите значение процентиля в пределах от 0 до 100 и щелкните на кнопке Add (Добавить). Повторите эти действия для всех желаемых значений процентилей. Значения в порядке возрастания будут показаны в списке. Например, если ввести значения 25, 50 и 75, то мы получим квартили. Можно задавать любые значения процентилей, например, 37 и 83. В первом случае (37) будет показано значение выбранной переменной, ниже которого лежат 37 % значений, а во втором случае (83) — значение, ниже которого располагаются 83 % значений.
В группе Dispersion (Разброс) можно выбрать следующие меры разброса:
-
Std. deviation (Стандартное отклонение): Стандартное отклонение — это мера разброса измеренных величин; оно равно квадратному корню из дисперсии. В интервале шириной, равной удвоенному стандартному отклонению, который отложен по обе стороны от среднего значения, располагается примерно 67% всех значений выборки, подчиняющейся нормальному распределению.
-
Variance (Дисперсия): Дисперсия — это квадрат стандартного отклонения и, следовательно, эта характеристика также является мерой разброса измеренных величин. Она определяется как сумма квадратов отклонений всех измеренных значений от их среднеарифметического значения, деленная на количество измерений минус 1.
-
Range (Размах): Размах — это разница между наибольшим значением (максимумом) и наименьшим значением (минимумом).
-
Minimum (Минимум): Наименьшее значение.
-
Maximum (Максимум): Наибольшее значение.
-
S.E. mean (Стандартная ошибка): Это стандартная ошибка среднего значения. В интервале шириной, равной удвоенной стандартной ошибке, отложенному вокруг среднего значения, располагается среднее значение генеральной совокупности с вероятностью примерно 67 %. Стандартная ошибка определяется как стандартное отклонение, деленное на квадратный корень из объема выборки.
Обычно мерами разброса переменных, относящихся к интервальной шкале и подчиняющихся нормальному распределению, служат стандартное отклонение и стандартная ошибка. Как было сказано выше, стандартное отклонение позволяет задать диапазон разброса отдельных значений. По так называемому правилу кулака, в одном диапазоне стандартного отклонения (охватывающем ширину стандартного отклонения в обе стороны от среднего значения) располагается примерно 67 % значений, в диапазоне удвоенного стандартного отклонения — примерно 95 %, а в диапазоне утроенного стандартного отклонения — примерно 99 % значений.
С другой стороны, стандартная ошибка позволяет задать доверительный интервал для среднего значения. В диапазоне удвоенной стандартной ошибки по обе стороны от среднего значения с вероятностью примерно 95 % находится среднее значение генеральной совокупности. С вероятностью примерно 99 % она лежит в диапазоне утроенной стандартной ошибки. Часто указывают только одну из этих двух мер разброса, обычно — стандартную ошибку, так как ее значение меньше. Во всех случаях следует точно выяснить, какая из мер разброса имеется в виду.
В группе Central Tendency (Средние) можно выбрать следующие характеристики:
-
Mean (Среднее значение): Среднее значение — это арифметическое среднее измеренных значений; оно определяется как сумма значений, деленная на их количество. Например, если имеется 12 измеренных значений и их сумма составляет 600, то среднее значение будет х = 600 : 12 = 50.
-
Median (Медиана): Медиана — это точка на шкале измеренных значений, выше и ниже которой лежит по половине всех измеренных значений. Например, если измеренные значения таковы:
37854639284,
то сначала они располагаются в порядке возрастания: 23344567889.
В данном случае медианой будет значение 5. Всего у нас 11 измеренных значений, следовательно, медианой является шестое значение. Выше него располагается 5 значений, и ниже — тоже 5. При нечетном количестве значений медиана всегда будет совпадать с одним из измеренных значений. При четном количестве медиана будет средним арифметическим двух соседних значений. Например, если имеются следующие измеренные значения:
3445678899
то медиана в этом случае будет равна: (6 + 7) : 2 = 6,5.
-
Mode (Мода): Мода — это значение, которое наиболее часто встречается в выборке. Если одна и та же наибольшая частота встречается у нескольких значений, то выбирается наименьшее из них.
-
Sum (Сумма): Сумма всех значений.
В группе Distribution (Распределение) можно выбрать следующие меры несимметричности распределения:
-
Skewness (Коэффициент асимметрии): Коэффициент асимметрии — это мера отклонения распределения частоты от симметричного распределения, то есть такого, у которого на одинаковом удалении от среднего значения по обе стороны выборки данных располагается одинаковое количество значений. Если наблюдения подчиняются нормальному распределению, то асимметрия равна нулю. Для проверки на нормальное распределение можно применять следующее правило: Если асимметрия значительно отличается от нуля, то гипотезу о том, что данные взяты из нормально распределенной генеральной совокупности, следует отвергнуть. Если вершина асимметричного распределения сдвинута к меньшим значениям, то говорят о положительной асимметрии, в противоположном случае — об отрицательной.
-
Kurtosis (Коэффициент вариации или эксцесс): Коэффициент вариации указывает, является ли распределение пологим (при большом значении коэффициента) или крутым. Коэффициент вариации равен нулю, если наблюдения подчиняются нормальному распределению. Поэтому для проверки на нормальное распределение можно применять еще одно правило: Если коэффициент вариации значительно отличается от нуля, то гипотезу о том, что данные взяты из нормально распределенной генеральной совокупности, следует отвергнуть.
Как правило, для переменных, относящихся к интервальной шкале и подчиняющихся нормальному распределению, в качестве основной характеристики используют среднее значение, а в качестве меры разброса — стандартное отклонение или стандартную ошибку. Для порядковых или интервальных переменных, не подчиняющихся нормальному распределению, — соответственно медиану или первый и третий квартили. Для переменных относящихся к номинальной шкале, нельзя дать других значимых характеристик кроме моды.
В диалоге есть еще один флажок:
-
Values are group midpoints (Значения являются средними точками групп): Если установить этот флажок, то при вычислении медианы и остальных значений процен-тилей оценки этих характеристик будут определяться для концентрированных данных. Этому вопросу посвящен отдельный раздел.
Для переменной alter (возраст) мы определим следующие характеристики: среднее значение, медиану, моду, квартили, стандартное отклонение, дисперсию, размах, минимум, максимум, стандартную ошибку, асимметрию и эксцесс. Поступите следующим образом:
-
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты)
-
В диалоге Frequencies щелкните на кнопке Reset (Сброс), чтобы отменить прежние настройки.
-
Перенесите переменную alter в список выходных переменных.
-
Щелкните на кнопке Statistics... (Статистика).
-
В диалоге Frequencies: Statistics установите флажки желаемых характеристик. Затем щелкните на кнопке Continue (Продолжить). Вы вернетесь в диалог Frequencies.
-
В диалоге Frequencies деактивируйте опцию Display frequency tables (Показывать частотные таблицы). Щелкните на кнопке ОК.
В окне просмотра появятся следующие результаты:
Статистика
Alter | ||
N | Допустимые | 106 |
Утерянные | 2 | |
Среднее значение | 22,24 | |
Стандартная ошибка среднего значения | 21 | |
Медиана | 22,00 | |
Мода | 21 | |
Стандартное отклонение | 2,19 | |
Дисперсия | 4,79 | |
Асимметрия | ,859 | |
Стандартная ошибка асимметрии | ,235 | |
Эксцесс | 1,042 | |
Стандартная ошибка эксцесса | ,465 | |
Размах | 11 | |
Минимум | 18 | |
Максимум | 29 | |
Процентили | 25 | 21,00 |
50 | 22,00 | |
75 | 23,00 | |
Респонденты опроса о психическом состоянии и социальном положении имеют средний возраст 22,24 года. Медиана составляет 22. Большинству респондентов 21 год (это мода). Самому молодому респонденту 18 лет (минимум), самому старшему — 29 лет (максимум). Самый старший респондент на 11 лет старше самого молодого (размах). Стандартное отклонение составляет 2,19. Следовательно, дисперсия — квадрат стандартного отклонения — равна (2,19)2 = 4,79. Асимметрия и коэффициент вариации даны с соот-ветсвующими стандартными ошибками.
3.gif
6.3 Медиана для концентрированных данных
6.3 Медиана для концентрированных данных
Для данных, имеющих форму частотной таблицы, определение медианы и остальных процентилей обычным методом будет слишком неточным. В таких случаях есть возможность вычислить медиану и любые другие процентили более точным методом. Мы поясним это на примере стоматологических данных.
-
Загрузите файл cpitn.sav, содержащий результаты стоматологического исследования.
Кроме переменных schule и mhfreq, которые определяют уровень образования и то, сколько раз в день обследуемый чистит зубы, этот файл содержит шесть переменных cpitnl—cpitn6, которые указывают степень пародонтального заболевания каждой из шести частей челюсти — так называемый параметр CPITN, задаваемый с помощью следующей кодировочной таблицы:
0 | Здоровый пародонт |
1 | Кровоточивость |
2 | Зубные отложения |
3 | Глубина десенных карманов 3,5-5,5 мм |
4 | Глубина десенных карманов 6 мм и более |
-
С помощью команд меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies (Частоты) создайте частотную таблицу, к примеру, для переменной cpitnl. Если задать вычисление среднего значения и медианы, мы получим следующий результат:
Статистика
CPITN1 | ||
N | Допустимые | 2548 |
Утерянные | 0 | |
Среднее значение | 2,24 | |
Медиана | 2,00 | |
CPITN1
Частота | Проценты | допустимые проценты | накопленные проценты | |
Допустимые здоровый | 109 | 4,3 | 4,3 | 4,3 |
кровоточивость | 389 | 15,3 | 15,3 | 19,5 |
отложения | 921 | 36,1 | 36,1 | 55,7 |
глубина карманов | 1042 | 40,9 | 40,9 | 96,6 |
3,5-5,5 глубина карманов >=6 | 87 | 3,4 | 3,4 | 100,0 |
Всего | 2548 | 100,0 | 100,0 |
При определении медианы обычным методом ее значение равно 2. Это значение, хотя формально и правильное, но дает совершенно неудовлетворительный, недостаточно значимый результат. В данном случае, когда данные являются концентрированным, для уточнения медианы применяется следующая расчетная формула:

Здесь:
n | Количество измеренных значений |
m | Класс, в котором находится медиана |
u | Нижняя граница класса m |
fm | Абсолютная частота в классе m |
Fm-1 | Накопленная частота вплоть до предыдущего класса m — 1 |
B | Ширина класса |
Следовательно, решающее значение имеет правильный выбор границ классов; их следует выбирать так, чтобы значения кодовых чисел соответствовали середине каждого класса. В данном примере для границ классов следует выбрать значения
-0,5 0,5 1,5 2,5 3,5 4,5
Ширина класса равна 1.
Следовательно,
n = 2548
m = 3 (так как медиана находится в третьем классе)
u = 1,5
fm = 921
Fm-1 = 109 + 389 = 498
b = 1
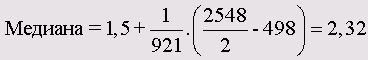
Если сравнить это значение со средним значением (2,24), то можно установить следующее правило — оказывается, что при распределении со сдвигом вправо (как в данном случае) медиана больше среднего значения.
Описанный точный метод вычисления медианы будет использован в SPSS, если в диалоге Frequencies: Statistics установить флажок Values are group midpoints.
В этом случае мы получим точное значение медианы (2,32).
По определению, медиана — это значение, выше и ниже (правее и левее) которого расположено по 50 % всех значений, если они упорядочены по величине. Обобщая эту характеристику, мы приходим к определению так называемых процентилей. Эти характеристики позволяют, например, указать значение, ниже которого лежит 10 % всех значений (а выше расположено 90 % значений). Чаше всего применяются процентили 25 % и 75 %, называемые также соответственно первым и третьим квартилями.
В диалоге Frequencies: Statistics можно последовательно задать любые значения процентилей. Если данные концентрированы, снова следует установить флажок Values are group midpoints.
Формула вычисления процентиля для любого значения:
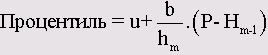
Здесь:
n | Класс, в котором находится процентиль |
m | Нижняя граница класса т |
P | Процентное значение процентиля |
Нm | Процентная частота в классе m-1 |
Hm-1 | Процентная накопленная частота в классе m-1 |
b | Ширина класса |
Для процентиля 50 % (Р = 50) после некоторых преобразований получается формула для медианы, приведенная выше.
В столбчатых, линейных, круговых диаграммах и диаграммах с областями, на которых предусмотрено отображение медианы и других процентилей, при наличии концентрированных данных используется модифицированный способ расчета (см. раздел 22.1.1).
4.gif

5.gif
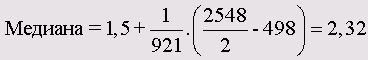
6.gif
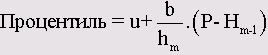
6.4 Форматы частотных таблиц
6.4 Форматы частотных таблиц
-
Загрузите файл studium.sav (см. раздел 6.1).
Сейчас мы попробуем вывести частотную таблицу переменной fach, отсортированную по убыванию частоты. Поступите следующим образом:
-
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты)
-
Перенесите переменную fach (специальность) в список выходных переменных.
-
Щелкните на кнопке Format.... Откроется диалоговое окно Frequencies: Format (Частоты: Формат).
Рис. 6.3: Диалоговое окно Frequencies: Format
В группе Order by (Сортировать по) можно выбрать порядок, в котором будут отображены значения в частотной таблице. Возможны следующие варианты:
-
Ascending values (По возрастанию значений): Данные сортируются по возрастанию значений. Это настройка по умолчанию.
-
Descending values (По убыванию значений): Данные сортируются по убыванию значений.
-
Ascending counts (По возрастанию частот): Данные сортируются по возрастанию частот.
-
Descending counts (По убыванию частот): Категории сортируются по убыванию частот.
Кроме того, флажок Suppress tables -with more than ... categories (He выводить таблицы с более чем... категориями) позволяет избежать вывода длинных частотных таблиц.
-
Выберите вариант Descending counts.
-
Подтвердите выбор кнопкой Continue (Продолжить).
-
Щелкните на кнопке ОК, чтобы начать вычисление. Мы получим следующие результаты:
Специальность
Частота | Проценты | Допустимые проценты | Накоплен- ные проценты | ||
Допус-тимые | Гуманитар- ные науки | 25 | 23,1 | 23,1 | 23,1 |
Юриспру- денция | 22 | 20,4 | 20,4 | 43,5 | |
Экономика | 19 | 17,6 | 17,6 | 61,1 | |
Психология | 11 | 10,2 | 10,2 | 71,3 | |
Медицина | 10 | 9,3 | 9,3 | 80,6 | |
Теология | 9 | 8,3 | 8,3 | 88,9 | |
Естествен- ные науки | 9 | 8,3 | 8,3 | 97,2 | |
Техника | 2 | 1,9 | 1,9 | 99,1 | |
Прочие | 1 | ,9 | ,9 | 100,0 | |
Всего | 108 | 100,0 | 100,0 |
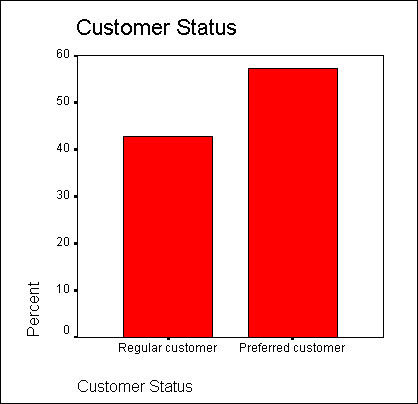
Основные специальности респондентов отображены в порядке убывания частоты.
7.gif
6.5 Графическое представление
6.5 Графическое представление
Результаты частотного распределения можно представить графически. Для примера мы создадим столбчатую диаграмму для частотного распределения основных специальностей. Поступите следующим образом:
-
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies (Частоты)
-
Перенесите переменную fach в список выходных переменных.
-
Щелкните на кнопке Charts... (Диаграммы). Откроется диалоговое окно Frequencies: Charts (Частоты: Диаграммы).
-
Выберите в группе Chart Type (Тип диаграммы) пункт Bar charts (Столбчатая диаграмма), а в группе Chart Values (Значения диаграммы) — пункт Percentages (Проценты). Подтвердите выбор кнопкой Continue (Продолжить). Вы вернетесь в диалог Frequencies.
-
В диалоговом окне Frequencies снимите флажок Display frequency tables (Показывать частотные таблицы). — Щелкните на кнопке ОК. Диаграмма будет показана в окне просмотра (см. рис. 6.5).
Рис. 6.4: Диалоговое окно Frequencies: Charts
Усовершенствуем вид этой диаграммы.
-
Чтобы начать редактирование, дважды щелкните в области столбчатой диаграммы. Диаграмма будет показана в редакторе диаграмм.
-
На панели инструментов редактора диаграмм щелкните на символе меток столбцов:

Рис. 6.5: Столбчатая диаграмма в средстве просмотра
Откроется диалоговое окно Bar Label Style (Стиль меток столбцов). Выберите пункт Framed (В рамке), щелкните на кнопке Apply all (Применить для всех) и затем на Close (Закрыть). На каждом столбце появится надпись с его процентным значением.
-
Щелкните мышью на любом из столбцов. На верхней стороне каждого столбца появится по два маленьких черных квадрата. Это означает, что области столбцов готовы для редактирования.
-
Щелкните мышью на символе образца заливки:

Откроется диалоговое окно Fill Patterns (Образцы заливки).
-
Выберите в нем подходящий образец заливки. Подтвердите выбор кнопкой Apply (Применить) и закройте диалоговое окно.
Рис. 6.6: Диалоговое окно Fill Patterns
Столбцы будут заполнены выбраннои заливкой.
-
Щелкните мышью на символе вида столбцов:

-
Выберите пункт Drop shadow (Тень), щелкните на кнопке Apply all (Применить для всех) и затем на Close (Закрыть).
-
Дважды щелкните на заголовке диаграммы Fachbereich. Откроется диалоговое окно Titles (Заголовки) (см. рис. 6.7).
-
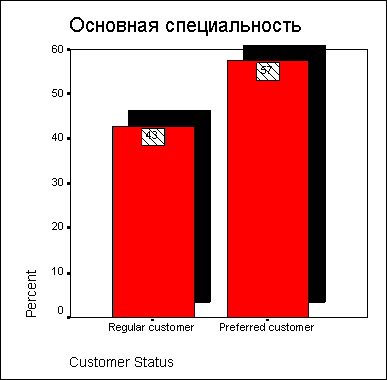
Измените заголовок на «Основная специальность» и закройте диалог кнопкой ОК.
-
В меню Chart (Диаграмма) установите флажок Outer Frame (Внешняя рамка). Закройте редактор диаграмм; получившийся график показан на рис. 6.8.
Рис. 6.7: Диалоговое окно Tirles
Рис. 6.8: Отредактированная диаграмма
Рассмотрим другой пример — визуальное представление частотного анализа.
-
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies (Частоты)
-
Щелкните на кнопке Reset (Сброс), чтобы установить стандартные настройки.
-
Перенесите переменную sozial (социальное положение) в список выходных переменных.
-
Щелкните на кнопке Charts... (Диаграммы). В диалоговом окне Frequencies: Charts выберите пункт Histograms (Гистограмма). Установите флажок With normal curve (С кривой нормального распределения). Щелкните на кнопке Continue.
-
В диалоговом окне Frequencies снимите флажок Display frequency tables (Показывать частотные таблицы). Щелкните на кнопке ОК. Гистограмма будет показана в окне просмотра (см. рис. 6.9).
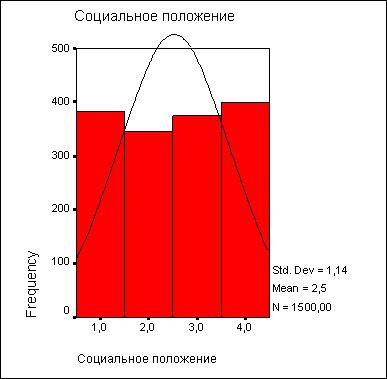
Рис. 6.9: Гистограмма
Частоты на гистограмме обозначены колонками, которые, но отличие от столбчатой диаграммы, не изолированы, а примыкают друг к другу. Отображаются также стандартное отклонение, среднее значение и общее количество наблюдений(М). Кроме того, показана кривая нормального распределения.
-
Дважды щелкните на области гистограммы — откроется редактор диаграмм, в котором можно придать гистограмме желаемый вид. График отобразится в редакторе диаграмм.
-
Выберите другой образец заливки и снабдите колонки надписями.
-
При желании проверьте другие функции редактора диаграмм.
На этом мы завершаем тему частотного анализа. Попробуйте самостоятельно выполнить частотный анализ переменной studium (время обучения) и представьте результаты распределения частот в графическом виде.
8.gif
10.gif
12.gif

14.gif

15.gif
16.gif