Самоучитель по SPSS
|
Глава 1. Программа SPSS
Глава 1. Программа SPSS
1. Программа SPSS
Программа SPSS
SPSS является самой распространённой программой для обработки статистической информации. В настоящем разделе описан путь этой программы к такому выдающемуся успеху. Затем приведен обзор отдельных модулей программы.
1.1 История SPSS
1.1 История SPSS
Два студента Норман Най (Norman Nie) и Дейл Вент (Dale Bent), специализировавшиеся в области политологии в 1965 году пытались отыскать в Стенфордском университете Сан-Франциско компьютерную программу, подходящую для анализа статистической информации. Вскоре они разочаровались в своих попытках, так как имеющиеся программы оказывались более или менее непригодными, неудачно построенными или не обеспечивали наглядность представления обработанной информации. К тому же принципы пользования менялись от программы к программе.
Так, не долго думая, они решили разработать собственную программу, со своей концепцией и единым синтаксисом. В их распоряжении тогда был язык программирования FORTRAN и вычислительная машина типа IBM 7090. Уже через год была разработана первая версия программы, которая, еще через год, в 1967, могла работать на IBM 360. К этому времени к группе разработчиков присоединился Хэдлай Халл (Hadlai Hull).
Как известно из истории развития информатики, программы тогда представляли собой пакеты перфокарт. Как раз на это указывает и исходное название программы, которое авторы дали своему продукту: SPSS — это аббревиатура от Statistical Package for the Social Science.
В 1970 году работа над программой была продолжена в Чикагском университете, а Норман Най основал соответствующую фирму — к тому моменту уже было произведено шестьдесят инсталляций. Первое руководство для пользователей описывало одиннадцать различных процедур.
Спустя пять лет SPSS была уже инсталлирована шестьсот раз, причём под разными операционными системами. С самого начала версиям программы присваивали соответствующие порядковые номера. В 1975 была разработана уже шестая версия (SPSS6). До 1981 последовали версии 7, 8 и 9.
Командный язык (синтаксис) SPSS в то время был ещё не так хорошо развит, как сейчас, и естественно ориентирован на перфокарты. Поэтому так называемые управляющие карты SPSS состояли из идентификационного поля (столбцы 1-15) и из поля параметров (столбцы 16-80).
В 1983 году командный язык SPSS был полностью переработан, синтаксис стал значительно удобней. Что бы отметить этот факт, программа была переименована в SPSSX, где буква X должна была служить как номером версии в римскими числами, так и сокращением для extended (расширенный).
Так как применение перфокарт к этому моменту уже стало историей, то программа SPSS и информация, подлежащая обработке, сохранялись в отдельных файлах на винчестерах больших ЭВМ, которые тогда использовались повсеместно. Год от года постоянно увеличивалось и количество процедур.
С появлением персональных компьютеров была разработана также и PC-версия SPSS, с 1983 года появилась PC-версия SPSS\PC+. рассчитанная на MS-DOS. Позже, с момента основания в 1984 году европейского торгового представительства в Горинхеме в Нидерландах, SPSS стал широко применяться и в Европе. В настоящее время это самое распространённое программное обеспечение для статистического анализа во всём мире.
Для того, чтобы отразить возможность использования программы во всех областях, имеющих отношение к статистическому анализу, буква X вновь была удалена из названия марки, а исходной аббревиатуре присвоено новое значение: Superior Performance Software System (система программного обеспечения высшей производительности).
Если PC версия SPSS/PC+ была чуть усовершенствованной версией для больших ЭВМ, то SPSS для операционной системой Windows (SPSS for Windows) стала большим шагом вперёд. Во первых эта версия SPSS обладает всеми возможностями версии для больших ЭВМ, во вторых, за некоторыми немногочисленными исключениями, программой можно пользоваться без особых знаний в области прикладного программирования. Вызов необходимых процедур статистического анализа происходит при помощи стандартной техники, применяемой в Windows, то есть с помощью мыши и соответствующих диалоговых окон.
Первая версия SPSS для Windows имела порядковый номер 5. Затем последовали версии 6.0 и 6.1 с некоторыми нововведениями в статистической и графической областях; версия 6.1 была первой статистической программой для Windows, которая использовала 32 битную архитектуру Windows 3.1. Это можно было заметить по более высокой скорости выполнения вычислений. Усовершенствования коснулись также и интерфейса пользователя. В конце концов, была выпущена версия 6.1.3, которая уже могла работать и под Windows 95 и под NT.
В начале 1996 года появилась 7-я версия SPSS, сначала как версия 7.0, а затем 7.5. Наряду с расширением возможностей в сфере статистики, разница между этими двумя версиями заключалась в том, что в версии 7.5 как меню, так и интерфейс программы были выполнены уже не только на английском, но и на других наиболее распространенных языках.
Самым весомым отличием версии 7 по отношению к предыдущим версиям, был абсолютно новый подход к выводу информации на экран. Так, во первых, получил новые очертания так называемый Viewer (Окно просмотра), и, во вторых, более приятный внешний вид приобрели таблицы результатов расчётов (мобильные таблицы). Появившаяся технология мобильных таблиц позволяет перестраивать полученные таблицы различным способами.
Если предшественница данной версии — версия 6.1.3 могла работать как под старой Windows 3.1 так и под новой Windows 95 (NT), то SPSS версии 7 могла работать только при наличии Windows 95 (NT).
За версией 7.5 последовала версия 8.0, прогресс которой заключался в усовершенствовании графической оболочки. Возможность составления интерактивных графиков предоставляет рад преимуществ по сравнению с традиционными графиками, которые являются стандартом для многих других пакетов.
Версия 9.0 включала в себя несколько новых статистических методов, в т.ч. многозначную логистическую регрессию, и несколько новых графических возможностей, расширяющих область интерактивных графиков.
Версия, описываемая в этой книге имеет порядковый номер 10.0. Ниже изложены важнейшие нововведения, относящиеся к этой версии.
1.2 Новое в версии 10.0
1.2 Новое в версии 10.0
Версия 10.0 SPSS имеет два самых существенных отличия по сравнению с предыдущей версией 9.0. Они будут рассмотрены в этой книге:
Было изменено строение Редактора данных. Благодаря закладкам Данные и Переменные облегчён переход между областями ввода данных и описания переменных. Таким образом, форма описания переменных была упрощена и соответствует теперь общепринятым стандартам, применяемым в сфере табличных расчётов.
В области статистики был добавлен регрессионный анализ с категориальной целевой переменной.
1.3 Модули SPSS
1.3 Модули SPSS
Основу программы SPSS составляет SPSS Base (базовый модуль), предоставляющий разнообразные возможности доступа к данным и управления данными. Он содержит методы анализа, которые применяются чаще всего.
Традиционно вместе с SPSS Base (базовым модулем) поставляются ещё два модуля: Advanced Models (продвинутые модели) и Regression Models (регрессионные модели). Эти три модуля охватывают тот спектр методов анализа, который входил в раннюю версию программы для больших ЭВМ.
В приложении А Вы сможете найти информацию о том, какие методы анализа относятся к тому или иному модулю. Пользователь, который приобрёл все эти три модуля, может не обращать внимания на данное приложение.
Наряду с тремя упомянутыми, существует еще ряд специальных дополнительных модулей и самостоятельных программ, число которых постоянно растёт, так что пользователям следует постоянно знакомиться с информацией о нововведениях в SPSS.
В этой книге описываются базисный модуль, а также модули Regression Models, Advanced Models и Tables. Назначением последнего модуля является составление презентационных таблиц. В книге не рассматриваются логлинейные модели, анализ выживания и многомерное шкалирование, а также процедура составления презентаций.
SPSS Base (Базовый модуль)
SPSS Base входит в базовую поставку. Он включает все процедуры ввода, отбора и корректировки данных, а также большинство предлагаемых в SPSS статистических методов. Наряду с простыми методиками статистического анализа, такими как частотный анализ, расчет статистических характеристик, таблиц сопряженности, корреляций, построения графиков, этот модуль включает t-тесты и большое количество других непараметрических тестов, а также усложненные методы, такие как многомерный линейный регрессионный анализ, дискриминантный анализ, факторный анализ, кластерный анализ, дисперсионный анализ, анализ пригодности (анализ надежности) и многомерное шкалирование.
Regression Models
Данный модуль включает в себя различные методы регрессионного анализа, такие как: бинарная и мультиномиальная логистическая регрессия, нелинейная регрессия и пробит-анализ.
Advanced Models
В этот модуль входят различные методы дисперсионного анализа (многомерный, с учетом повторных измерений), общая линейная модель, анализ выживания, включая метод Каплана-Майера и регрессию Кокса, логлинейные, а также логитлоглинсйные модели.
Tables
Модуль Tables служит для создания презентационных таблиц. Здесь предоставляются более широкие возможности по сравнению со упрощенными частотными таблицами и таблицами сопряженности, которые строятся в SPSS Base (базовом модуле).
Ниже в алфавитном порядке приведен список остальных модулей и программ предлагаемых для расширения SPSS.
Amos
Amos (Analysis of moment structures — анализ моментных структур) включает методы анализа с помощью линейных структурных уравнений. Целью программы является проверка сложных теоретических связей между различными признаками случайного процесса и их описание при помощи подходящих коэффициентов. Проверка проводится в форме причинного анализа и анализа траектории. При этом пользователь в графическом виде должен задать теоретическую модель, в которую вместе с данными непосредственных наблюдений могут быть включены и так называемые скрытые элементы. Программа Amos включена в состав модулей расширения SPSS, как преемник L1SREL (Linear Structural RELationships — линейные структурные взаимоотношения).
AnswerTree
AnswerTree (дерево решений) включает четыре различных метода автоматизированного деления данных на отдельные группы (сегменты). Деление проводится таким образом, что частотные распределения целевой (зависимой) переменной в различных сегментах значимо различаются. Типичным примером применения данною метода является создание характерных профилей покупателей при исследовании потребительского рынка. AnswerTree является преемницей программы СНАШ (Chi squared interaction Detector — детектор взаимодействий на основе хи-квадрата).
Categories
Модуль содержит различные методы для анализа категориальных данных, а именно: анализ соответствий и три различных метода оптимального шкалирования (анализ однородности, нелинейный анализ главных компонент, нелинейный канонический корреляционный анализ).
Clementine
Clementine — это программа для data mining (добычи знаний), в которой пользователю предлагаются многочисленные подходы к построению моделей, к примеру, нейронные сети, деревья решений, различные виды регрессионного анализа. Clementine представляет собой "верстак" аналитика, при помощи которого можно визуализировать процесс моделирования, перепроверять модели, сравнивать их между собой. Для удобства пользования программой имеется вспомогательная среда внедрения результатов.
Conjoint (совместный анализ)
Совместный анализ применяется при исследовании рынка для изучения потребительских свойств продуктов на предмет их привлекательности. При этом опрашиваемые респонденты по своему усмотрению должны расположить предлагаемые наборы потребительских свойств продуктов в порядке предпочтения, на основании которого можно затем вывести так называемые детализированные показатели полезности отдельных категорий каждого потребительских свойства.
Data Entry (ввод данных)
Программа Data Entry предназначена для быстрого составления вопросников, а также ввода и чистки данных. Заданные на этапе создания вопросника вопросы и категории ответов потом используются в качестве меток переменных и значений.
Exact Tests (Точные тесты)
Данный модуль служит для вычисления точного значения вероятности ошибки (величины р) в условиях ограниченности данных при проверке по критерию х2 (Chi-Quadrat-Test) и при непараметрических тестах. В случае необходимости для этого также может быть применён метод Монте-Карло (Monte-Carlo).
GOLDMineR
Программа содержит специальную регрессионную модель для регрессионного анализа упорядоченных зависимых и независимых переменных.
SamplePower
При помощи SamplePower может быть определён оптимальный размер выборки для большинства методов статистического анализа, реализованных в SPSS.
SPSS Missing Value Analysis
Данный модуль служит для анализа и восстановления закономерностей, которым подчиняются пропущенные значения. Он предоставляет различные варианты замены недостающих значений.
Trends
Модуль Trends содержит различные методы для анализа временных рядов, такие как: модели ARIMA, экспоненциальное сглаживание, сезонная декомпозиция и спектральный анализ.
Модули Amos, AnswerTree, Categories, Conjoint, LISREL и Trends описаны в книге этих же авторов: "SPSS. Методы исследования рынка и мнений".
Глава 2. Инсталляция
Глава 2. Инсталляция
1. Инсталляция
Инсталляция
В этой главе мы покажем, как установить SPSS с компакт-диска, создать ярлык на эту программу и задать рабочий каталог. Далее мы расскажем об установке прилагаемого к книге компакт-диска примеров.
2.1 Системные требования для инсталляции SPSS
2.1 Системные требования для инсталляции SPSS 10.0
Чтобы вы могли использовать SPSS 10.0 для Windows на своем компьютере, аппаратное и программное обеспечение должны удовлетворять следующим минимальным требованиям:
-
Windows 95, Windows 98, Windows NT 4.0 или Windows 2000,
-
процессор Pentium 90 МГц (или более),
-
не менее 16 Мбайт оперативной памяти (рекомендуется 64 Мбайт),
-
не менее 80 Мбайт свободного места на жестком диске (для базовой системы) и еше 80 Мбайт для работы SPSS,
-
привод CD-ROM,
-
видеокарта с минимальным разрешением 800*600 (SVGA).
Кроме того, для инсталляции необходимы:
-
серийный номер SPSS, который указан на коробке компакт-диска,
-
лицензионный код для SPSS, который прилагается на отдельном листке.
Лицензионный код дает возможность инсталлировать базовую систему и модули расширения SPSS, приобретаемые дополнительно.
2.2 Инсталляция SPSS
2.2 Инсталляция SPSS 11.5
В следующем описании мы исходим из того, что на вашем компьютере установлена операционная система Windows 98 или Windows 2000.
-
Вставьте инсталляционный компакт-диск SPSS 11.5 для Windows в привод CD-ROM.
-
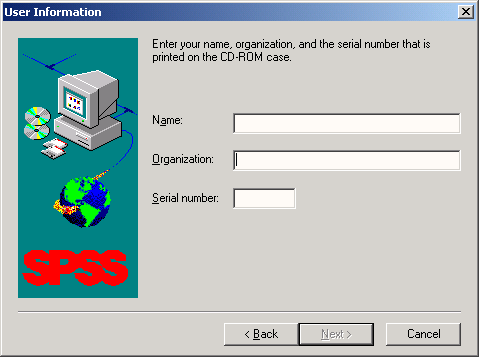
Немного подождите — должна автоматически запуститься программа инсталляции. На рабочем столе Windows вы увидите следующее окно.
-
Щелкните на пункте Install SPSS (Установить SPSS).
Программа инсталляции SPSS подготовит так называемый "мастер InstallShield", который будет сопровождать вас в процессе инсталляции.
-
Подождите, пока подготовка к инсталляции не завершится.
Рис. 2.1: Начальный экран программы инсталляции
Наконец, программа инсталляции SPSS 11.5 для Windows готова к работе. Прежде чем запускать ее, рекомендуется закрыть все программы Windows.
-
Если все остальные программы Windows закрыты, щелкните на кнопке Next (Далее). На экране появится Лицензионное соглашение SPSS.
-
Примите предлагаемые условия, щелкнув на кнопке "Yes" (Да). Теперь можно задать каталог, в который будет инсталлирована SPSS 10.0 для Windows.
-
Чтобы принять предлагаемый по умолчанию каталог (C:\Program Files\SPSS), щелкните на кнопке Далее.
Но если вы хотите установить SPSS в другой каталог, щелкните на кнопке Browse (Обзор). Откроется диалоговое окно Select Directory (Выбрать каталог). Здесь можно установить желаемый каталог.
На следующем этапе работы мастера требуется ввести данные пользователя. Здесь следует указать серийный номер SPSS.
-
Введите соответствующие данные и подтвердите их кнопкой Next.
Теперь вы должны выбрать один из трех типов инсталляции:
-
Standard (Стандартная): Программа будет установлена в наиболее употребительной конфигурации. Этот тип инсталляции рекомендуется для большинства пользователей.
-
Minimal (Минимальная): Будет инсталлирована лишь минимально необходимая конфигурация.
Рис. 2.2: Сведения о пользователе
-
Custom (Специальная): Здесь можно выбрать, какие функции программы будут инсталлированы. Этот тип инсталляции рекомендуется для опытных пользователей.
-
Подтвердите настройку по умолчанию Standard щелчком на кнопке Next. Затем мастер потребует от вас указать вид инсталляции.
-
Подтвердите установку для одной рабочей станции щелчком на кнопке Next.
-
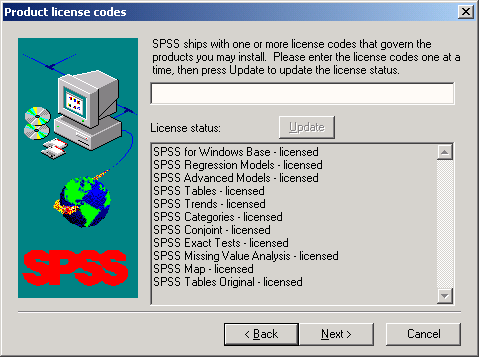
На следующем этапе мастер требует ввести код лицензии, который вы должны были получить для SPSS.
-
Введите код лицензии на программу. Обратите внимание, что группы цифр в коде обязательно должны быть разделены пробелом.
-
Подтвердите ввод, щелкнув на кнопке Next. Теперь можно выбрать, какие модули SPSS должны быть установлены. Свой выбор так же подтвердите кнопкой Next.
После этого SPSS будет искать файлы модулей, выбранных для инсталляции ("Files to install are determined..." — Определяются файлы для инсталляции).
-
Наконец, на заключительном этапе вы можете еще раз проверить сделанные ранее установки ("Ready to install files" — Готов к инсталляции файлов).
Рис. 2.3: Ввод кода лицензии
-
Подтвердите сделанные установки щелчком на кнопке Next. SPSS начнет инсталляцию файлов.
-
После инсталляции файлов программы мастер спросит в вас, когда вы желаете зарегистрировать SPSS — сейчас или позже. Выберите нужный вариант и щелкните на Next.
Теперь инсталляция SPSS для Windows 10.0 завершена; вы получаете соответствующее указание ("Setup was finished" — Инсталляция завершена). Вы можете запустить интерактивную обучающую программу или вернуться на рабочий стол Windows.
-
Чтобы выйти из процесса инсталляции, щелкните на кнопке Finish (Готово); в этом случае интерактивная обучающая программа не запустится.
-
В результате вы вернетесь на рабочий стол Windows и снова увидите начальный экран программы инсталляции (см. рис. 2.1). Щелкните здесь на кнопке Exit (Выход).
1.gif

2.gif
3.gif
2.3 Создание ярлыка
2.3 Создание ярлыка
Мы предполагаем, что в дальнейшем вы часто будете работать с SPSS и вам будет необходим быстрый доступ к этой программе. Поэтому мы предлагаем вам создать для нее ярлык.
-
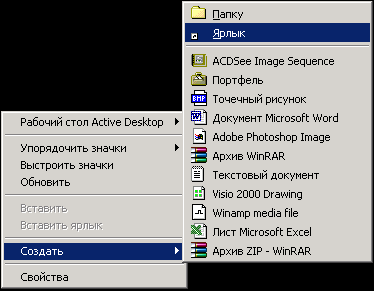
Щелкните правой кнопкой мыши на свободном месте рабочего стола Windows 98. Появится контекстное меню.
-
Выберите в контекстном меню команду Создать (New).
-
Щелкните на пункте Ярлык (Shortcut). Рабочий стол Windows 98 приобрет вид, показанный на рис. 2.4.
Откроется диалоговое окно Создать ярлык (Create Shortcut).
-
Введите в этом диалоговом окне путь и имя исполняемого файла — как правило, это будет "C:\Program Files\SPSS\spsswin.exe" — или выберите путь и файл с помощью кнопки Обзор (Browse), если вы не помните их в точности. Эта кнопка открывает структуру каталогов, в которой можно найти файл spsswin.exe.
-
Подтвердите ввод, щелкнув на кнопке Далее (Next).
Откроется диалоговое окно Выбор названия программы (Select a Title for the Program).
-
Введите в поле Укажите название ярлыка (Select a name for the shortcut) текст "SPSS 10".
-
Завершите создание ярлыка, подтвердив введенные данные кнопкой Готово (Finish).
Теперь ярлык создан.
Вы можете запускать SPSS прямо с рабочего стола. Для этого достаточно просто дважды щелкнуть на значке SPSS.
2.4 Установка рабочего каталога
2.4 Установка рабочего каталога
Теперь мы должны установить рабочий каталог. В этом каталоге будут храниться создаваемые вами файлы данных и выходные файлы. В дальнейшем в рабочий каталог надо будет скопировать файлы с компакт-диска примеров (см. главу 2.5). Мы рекомендуем дать этому каталогу имя SPSSBOOK.
Чтобы задать рабочий каталог, поступите следующим образом.
Рис. 2.4: Создание ярлыка
-
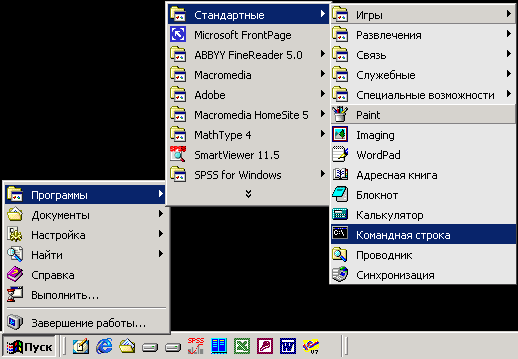
Через окно MS-DOS (Меню Пуск Программы | Сеанс MS-DOS) перейдите на уровень MS-DOS.
-
Командой CD (change directory) перейдите в корневой каталог С:\:Prompt:\> CD C:\
-
Командой MD (make directory) создайте подкаталог "SPSSBOOK": С : \> MD SPSSBOOK
-
Закройте сеанс DOS командой EXIT: С:\> EXIT
Вы снова окажетесь на рабочем столе Windows 98.
Теперь мы должны зарегистрировать вновь созданный каталог SPSSBOOK как рабочий каталог для SPSS 10.0.
-
Для этого поместите курсор на значок SPSS и щелкните правой кнопкой мыши. Откроется контекстное меню.
-
Выберите пункт Свойства (Properties).
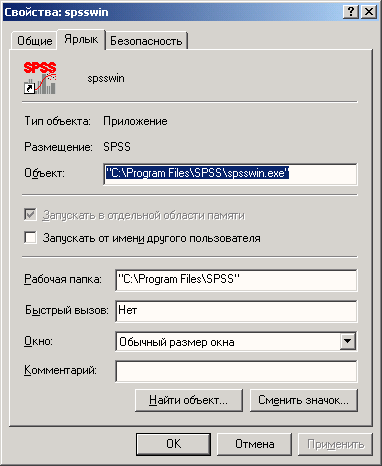
Откроется диалоговое окно SPSS 10: Свойства (SPSS 10 Properties).
-
Введите в поле Рабочий каталог (Working directory) текст "C:\SPSSBOOK".
-
Подтвердите ввод кнопкой ОК.
Рис. 2.5: Переход на уровень MS-DOS
Рис. 2.6: Диалоговое окно Свойства: SPSS 10
Теперь рабочий каталог задан. В дальнейшем SPSS будет использовать его как стандартный каталог (Default Directory).
4.gif
5.gif
6.gif
2.5 Инсталляция прилагаемого компакт-диска
2.5 Инсталляция прилагаемого компакт-диска
Сейчас мы скопируем содержимое компакт-диска примеров в только что установленный каталог SPSSBOOK. Поступите следующим образом:
-
Через окно сеанса MS-DOS перейдите на уровень MS-DOS.
-
Командой CD (change directory) перейдите в каталог SPSSBOOK: Prompt:\> CD C:\SPSSBOOK
После этого приглашение DOS приобретет следующий вид:
C:\SPSSBOOK\>
-
Командой DOS COPY скопируйте содержимое компакт-диска примеров в каталог C:\SPSSBOOK: C:\SPSSBOOK> COPY D:\*.* или вместо буквы D укажите обозначение привода CD-ROM на вашей машине.
-
Закройте сеанс DOS командой EXIT: C:\SPSSBOOK> EXIT
Вы вернетесь на рабочий стол Windows 98. Все этапы инсталляции успешно завершены.
2.6 Возобновление лицензии
2.6 Возобновление лицензии
Если срок действия вашей лицензии на SPSS истек и вы приобрели лицензию на новый период, можно возобновить лицензию, не повторяя весь процесс инсталляции заново. Для этого служит программа licrenew.exe.
-
Откройте окно сеанса MS-DOS.
-
Перейдите в каталог SPSS.
-
Введите licrenew.exe.
-
Введите код лицензии и подтвердите его.
2.7 Добавление компонентов
2.7 Добавление компонентов
Чтобы добавить компоненты, например, другие модули SPSS, следует запустить файл setup.exe с компакт-диска. После этого можно выбрать любые компоненты или функции. Убедитесь, что выбраны все функции — как вновь добавляемые, так и уже установленные. Если в SPSS добавляется новый модуль, следует также ввести новый код лицензии.
Глава 3. Подготовка данных
Глава 3. Подготовка данных
1. Подготовка данных
Подготовка данных
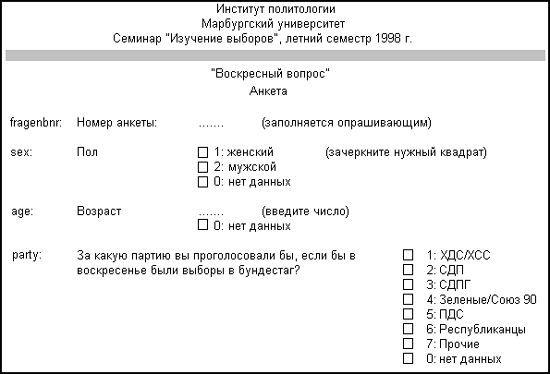
В этой главе мы на небольшом примере опишем процесс подготовки данных. За основу мы возьмем вымышленный опрос — так называемый "воскресный вопрос", который студенты, изучающие политологию в Марбургском университете, задавали избирателям:
"За кого бы вы голосовали, если бы в воскресенье были выборы в бундестаг?" С помощью следующей анкеты был проведен телефонный опрос 30 человек. Мы ограничили количество респондентов, чтобы избавить вас от ввода слишком большого количества данных.
После заполнения анкет, их следует подготовить для ввода данных в компьютер и обработки с помощью программы SPSS для Windows.
1.gif

3.1 Кодирование и кодировочная таблица
3.1 Кодирование и кодировочная таблица
Для того чтобы полученные данные можно было обработать, прежде всего следует создать кодировочную таблицу. Кодировочная таблица устанавливает соответствие между отдельными вопросам анкеты и переменными. используемыми при компьютерной обработке данных. Например, пункту анкеты "Пол" может быть поставлена в соответствие переменная sex.
Переменные — это ячейки памяти, в которые можно записывать значения, введенные с клавиатуры. Мы выбрали для переменной имя sex, так как имена переменных в SPSS для Windows могут содержать до восьми символов. Другое, более подробное имя было бы слишком длинным. Имена переменных могут состоять из букв латинского алфавита, цифр и специальных символов; причем первым символом имени должна быть буква.
Переменные могут принимать различные значения. Переменная sex может иметь два возможных значения: "женский" и "мужской". Кодировочная таблица определяет кодовые числа, соответствующие отдельным значениям переменных; например, значению "женский" может соответствовать цифра "1", а значению "мужской" — "2".
Подитожим задачи, которые решаются при составлении кодировочной таблицы:
-
Кодировочная таблица устанавливает соответствие между отдельным вопросам анкеты и переменными.
-
" Кодировочная таблица устанавливает соответствие между возможным значениями переменных и кодовыми числами.
Для нашей анкеты мы можем составить следующую кодировочную таблицу. Она приводится в самой анкете.
2.gif
3.2 Матрица данных
3.2 Матрица данных
Предположим, что 30 анкет были заполнены следующим образом:
fragebnr | Sex | age | party | |
1 | W-001 | женский | 45 | ХДС/ХСС |
2 | W-002 | мужской | 22 | СДПГ |
3 | W-003 | мужской | 19 | сдпг |
4 | W-004 | женский | 42 | ХДС/ХСС |
5 | W-005 | мужской | 34 | Зеленые/Союз 90 |
6 | W-006 | женский | 72 | сдп |
7 | W-007 | мужской | 38 | СДПГ |
8 | W-008 | женский | 56 | СДПГ |
9 | W-009 | мужской | 61 | ХДС/ХСС |
10 | W-010 | женский | 77 | ХДС/ХСС |
11 | W-01 1 | женский | 23 | Зеленые/Союз 90 |
12 | W-012 | мужской | 67 | Республиканцы |
13 | W-013 | мужской | 79 | Прочие |
14 | W-01 4 | женский | 26 | СДПГ |
15 | W-01 5 | мужской | 59 | ХДС/ХСС |
16 | O-001 | женский | 34 | Зеленые/Союз 90 |
17 | O-002 | мужской | 18 | Республиканцы |
18 | O-003 | женский | 44 | ХДС/ХСС |
19 | O-004 | мужской | 68 | ХДС/ХСС |
20 | O-005 | женский | 33 | пдс |
21 | O-006 | мужской | 66 | ХДС/ХСС |
22 | O-007 | женский | 22 | нет данных |
23 | O-008 | мужской | нет данных | СДПГ |
24 | O-009 | женский | 67 | СДПГ |
25 | O-010 | мужской | 33 | сдп |
26 | O-011 | мужской | 44 | ХДС/ХСС |
27 | O-012 | женский | 22 | СДПГ |
28 | O-013 | женский | 19 | Прочие |
29 | O-014 | женский | 55 | ХДС/ХСС |
30 | O-015 | мужской | 39 | СДПГ |
Приведенная выше таблица называется матрицей данных. Данные, предназначенные для обработки в SPSS для Windows, должны быть представлены в виде такой матрицы. Матрица данных состоит из определенного числа строк и столбцов. Строки и столбцы образуют прямоугольную таблицу. При этом каждая строка соответствует одной анкете, а каждый столбец — одной переменной. Так как в нашем небольшом опросе участвовало 30 респондентов, матрица содержит 30 строк. Каждая строка включает четыре столбца для переменных fragebnr, sex, age и party.
Мы предполагаем, что опрос проводился как в старых, так и в новых федеральных землях. Опрашивающие должны были отмечать это с помощью буквы перед номером анкеты. Буква "W" с дефисом должна была обозначать старые федеральные земли (West), а буква "О" — новые (Ost). Например, W-001 означает первую анкету, которая была заполнена в старых федеральных землях, а О-005 — пятую анкету, которая была заполнена в новых федеральных землях.
3.3 Запуск SPSS
3.3 Запуск SPSS
Начнем с ввода данных для небольшого примера анализа.
-
Запустите SPSS для Windows, дважды щелкнув левой кнопкой мыши на значке SPSS.
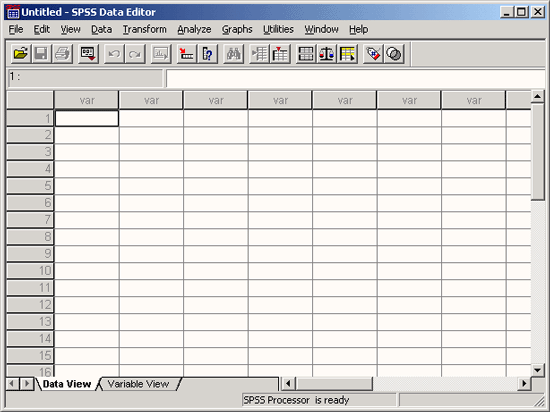
Откроется редактор данных SPSS (см. рис. 3.1).
Редактор данных — это одно из многих окон SPSS. Здесь можно вводить новые данные или загружать существующие из файлов данных с помощью команд меню File (Файл) Open... (Открыть...)
Так как при запуске SPSS ни один файл данных еще не загружен, в заголовке редак тора данных стоит "Untitled" (Без имени). Над изображением таблицы в редакторе данных имеются строка меню и панель символов.
3.4 Редактор данных
3.4 Редактор данных
Сейчас с помощью редактора данных мы создадим файл данных. Редактор данных это приложение, напоминающее электронную таблицу. Под электронной таблицей подразумевается рабочий лист, разделенный на строки и столбцы, который позволяет про сто и эффективно вводить данные. Отдельные строки таблицы соответствуют отдельным наблюдениям. Например, при обработке данных опроса одна строка содержит данные одного респондента. Отдельные столбцы соответствуют отдельным переменным. При обработке данных наблюдений анкеты в одной переменной хранятся ответы на отдельный вопрос. Отдельные ячейки таблицы содержат значения переменных для каждого отдельного наблюдения; в каждой ячейке хранится одно значение переменной.
Рис. 3.1: Редактор данных: просмотр данных
3.gif
3.4.1 Определение переменных
3.4.1 Определение переменных
Начнем с определения переменных. Переменную можно определить следующим образом:
-
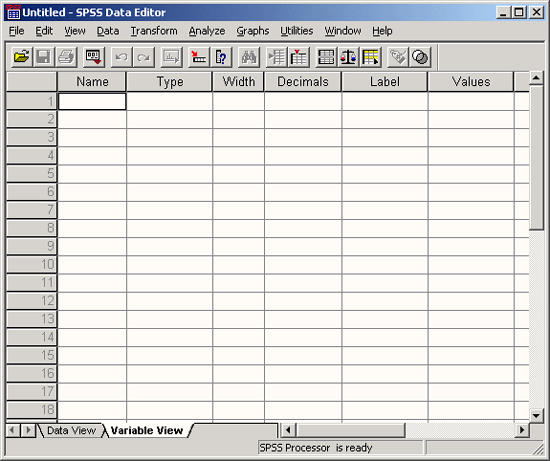
В редакторе данных дважды щелкните на ячейке с надписью var или щелкните на ярлычке Variable view (Просмотр переменных) на нижнем краю таблицы.
В обоих случаях вы перейдете в режим просмотра переменных, который обеспечивает редактор данных (см. рис. 3.2). Здесь мы можем последовательно, строка за строкой определить необходимые переменные.
Имя переменной
Чтобы задать имя переменной, поступите следующим образом:
-
Введите в текстовом поле Name (Имя) выбранное имя переменной. В нашем примере мы сначала определим переменную fragebnr. Для этого введите в поле Name текст "fragebnr".
При выборе имени переменной следует соблюдать определенные правила:
-
Имена переменных могут содержать буквы латинского алфавита и цифры. Кроме того, допускаются специальные символы _ (подчеркивание), . (точка), а также символы @ и #. Не разрешаются, например, пробелы, знаки других алфавитов и специальные символы, такие как !, ?," и *.
-
Имя переменной должно начинаться с буквы.
-
Последний символ имени не может быть точкой или знаком подчеркивания (_).
-
Длина имени переменной не должна превышать восьми символов.
Рис. 3.2: Редактор данных: просмотр переменных
-
Имена переменных нечувствительны к регистру, то есть прописные и строчные буквы не различаются.
Примеры допустимых имен переменных:
budget99
gender
zarplata
quest_13
var3_1_2
Примеры недопустимых имен переменных:
1nа1 | Имя начинается не с буквы |
Assignment | Имя длиннее 8 символов |
Прибыль | Имя содержит символы другого алфавита |
State 94 | Имя содержит пробел |
None! | Символ "!" не разрешается |
-
Нажмите на клавишу <Таb>, чтобы подтвердить ввод и перейти к установке типа переменной.
Тип переменной
Как видно из электронной таблицы, вновь созданные в SPSS переменные по умолчанию являются численными с максимальной длиной восемь знаков, причем дробная часть состоит из двух знаков (формат F8.2).
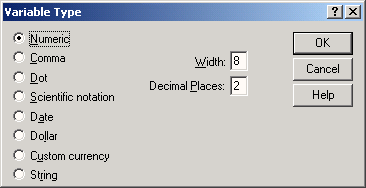
• Если требуется изменить тип переменной, щелкните в ячейке на кнопке с тремя точками:

Откроется диалоговое окно Define Variable Type (Определение типа переменной).
Рис. 3.3: Диалоговое окно Define Variable Type (для численной переменной)
В SPSS существуют следующие типы переменных:
Numeric (Численный) | К допустимым значениям относятся цифры, перед которыми стоит знак плюс или минус и десятичный разделитель. Знак плюс перед числом, в отличие от минуса, не отображается. В текстовом поле Length (Длина) задается максимальное количество знаков, включая позицию для десятичного разделителя. В текстовом поле Decimals (Десятичные разряды) вводится количество отображаемых знаков дробной части. |
Comma (Запятая) | К допустимым значениям относятся цифры, перед которыми стоит знак плюс или минус, точка, как десятичный разделитель и одна или несколько запятых в качестве разделителей групп разрядов. Если запятые опускаются при вводе, они вставляются автоматически. Длина такой переменной равна максимальному количеству знаков, включая десятичный разделитель и запятые между группами разрядов. |
Dot (Точка) | К допустимым значениям относятся цифры, перед которыми стоит знак плюс или минус, запятая, как десятичный разделитель и одна или несколько точек в качестве разделителей групп разрядов. Если точки опускаются при вводе, они вставляются автоматически. |
Scientific notation (Экспоненциальное представление) | При вводе данных разрешаются все допустимые численные значения, включая экспоненциальное представление, о котором свидетельствует содержащаяся в числе буква Е или D, а также знак плюс или минус. |
Date (Дата) | Допустимые значения — дата и/или время. |
Dollar (Доллар) | К допустимым значениям относятся: знак доллара, точка, как десятичный разделитель и запятые, как разделители групп разрядов. Если знак доллара или запятые опускаются при вводе, они вставляются автоматически. |
Special currency (Специальная валюта) | Пользователь может задавать собственные форматы валюты. В поле Length в этом случае задается максимальное количество знаков, включая все знаки, заданные пользователем. Обозначение валюты при вводе не указывается; оно вставляется автоматически. |
String (Строка) | Строка символов. К допустимым значениям относятся: буквы, цифры и специальные символы. Различаются короткие и длинные строковые переменные. Короткие строковые переменные могут содержать не более восьми знаков. В большинстве процедур SPSS применение длинных строковых переменных ограничивается или вообще не допускается. |
При вводе и выводе данных надо учитывать следующие особенности:
-
Численные форматы: В численных форматах десятичным разделителем может быть либо точка, либо запятая. Тип десятичного разделителя зависит от настроек диалогового окна Язык и стандарты (Regional Settings) на панели управления Windows. Точное значение переменной хранится внутри программы, а Редактор данных отображает на экране лишь заданное число десятичных разрядов. Значения, которые имеют больше десятичных разрядов, округляются. Для вычислений применяется точное значение.
-
Строковые форматы: В длинных строковых переменных значения дополняются пробелами до максимальной длины. Например, в строковой переменной длины 10 значение "SPSS" хранится внутри программы как "SPSS
-
Форматы даты и времени: В форматах даты в качестве разделителей между значениями дня, месяца и числа могут применяться косая черта, дефис, пробел, запятая или точка. Можно выбрать один из нескольких форматов даты (dd-mm-yyyy, dd-mmm-yy, mm/dd/yyyy и т.д.). Дата в формате dd-mmm-yy отображается с разделителем-дефисом и сокращением названия месяца из трех букв. Дата в форматах dd/mm/yy и mm/dd/yy отображается с разделителем-косой чертой и номером месяца вместо названия.
-
Всего доступно 27 различных форматов даты и времени, которые отображаются в разворачивающемся списке. В форматах времени в качестве разделителей между значениями часов, минут и секунд могут использоваться двоеточие, точка или пробел.
-
Специальная валюта: Форматы отображения валюты ССА, ССВ, ССС, CCD и ССЕ задаются с помощью вкладки Currency (Валюта), которая открывается командой меню Edit (Правка) Options... (Параметры...)
-
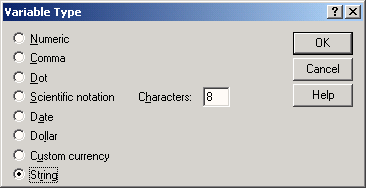
Установите для переменной fragebnr тип String и длину пять символов и щелкните на кнопке ОК.
Рис. 3.4: Диалоговое окно Define Variable Type (для строковой переменной).
Переменная fragebnr получила строковый тип. С такими переменными нельзя выполнять никаких вычислительных операций, но можно проводить, например, подсчеты повторяемости. Кроме того, становится возможным ввод букв, например, "W" для старых федеральных земель и "О" — для новых. Мы выбрали длину пять символов, чтобы можно было кодировать до 999 анкет для обеих групп земель. В этом случае для анкет в старых федеральных землях можно будет задавать номера анкет от "W-001" до "W-999", а для новых федеральных земель — от "О-001" до "О-999".
-
Нажмите клавишу <ТаЬ>, чтобы перейти к установке формата столбца.
Формат столбца (Width)
-
Для переменной fragebnr задано число позиций в столбце, равное "5". Это значение следует из длины переменной, указанной в диалоге Define Variable Type.
-
Чтобы изменить этот формат представления переменной, перенесенный из диалога Define Variable Type, щелкните на кнопке лифта:

-
В этом случае выбранное значение ширины подтверждается клавишей <Таb>.
Десятичные разряды (Decimals)
-
Так как переменная fragebnr является строковой, для нее задано количество десятичных разрядов "0". Увеличение или уменьшение этого значения, определенного настройкой в диалоге Define Variable Type, также производится при помощи кнопки лифта:
 Подтвердите значение "0", нажав клавишу <Таb>.
Подтвердите значение "0", нажав клавишу <Таb>.
Метка переменной (Label)
Метка переменной — это название, позволяющая описать переменную более подробно. Метка переменной может содержать до 256 символов. В метках переменных различаются прописные и строчные буквы. Они отображаются в том виде, в каком были введены. Для переменной fragebnr введите в качестве метки в поле Variable label текст "Номер анкеты".
Метки значений (Values)
Метки значений — это название, позволяющее более подробно описать возможные значения переменной. Так, например, в случае переменной sex можно задать метку "женский" для значения "1" и метку "мужской" для значения "2". Подтвердите настройку по умолчанию None (Нет) клавишей <Таb>. Впрочем, ввод данных также можно подтвердить клавишей <Enter>.
Пропущенные значения (Missing values)
В SPSS допускаются два вида пропущенных значений:
-
Пропущенные значения, определяемые системой (System-defined missing values): Если в матрице данных есть незаполненные численные ячейки, система SPSS самостоятельно идентифицирует их как пропущенные значения. Этот факт отображается в матрице данных с помощью запятой (,).
-
Пропущенные значения, задаваемые пользователем ( User-defined missing values): Если в определенных случаях у переменных отсутствуют значения, например, если на вопрос не был дан ответ, ответ неизвестен, или существуют другие причины, пользователь может с помощью кнопки Missing объявить эти значения как пропущенные. Пропущенные значения можно исключить из последующих вычислений. В нашем примере пропущенным значением, определяемым пользователем мы объявим вариант ответа "0" (нет данных) для переменной sex.
-
Подтвердите настройку по умолчанию None (Нет) клавишей <Enter>.
Столбцы (Columns)
Поле Columns определяет ширину, которую будет иметь в таблице данный столбец при отображении значений. Ширину столбца также можно изменить непосредственно в окне редактора данных. Для этого поместите указатель мыши на разделитель между двумя заголовками столбцов с именами переменных. Вид указателя изменится. Появившаяся двойная стрелка указывает, что соответствующий столбец можно расширить или сузить путем перетаскивания.
-
Подтвердите настройку по умолчанию "8" клавишей <Enter>.
Выравнивание (Alignment)
Здесь можно задать вид выравнивания значений, т.е. определить, как они будут отображаться в таблице. Возможные виды выравнивания — "Right" (по правому краю), "Left" (no левому краю) и "Center" (по центру). Чтобы задать вид выравнивания, щелкните на кнопке 
-
Подтвердите настройку по умолчанию Right клавишей <Enter>.
Шкала измерения (Measure)
Здесь можно задать шкалу переменной, которая может быть номинальной (шкала наименований), порядковой или метрической (см. главу 5.1.1). По умолчанию принимается метрическая шкала измерения. Правда, это различие имеет значение только при создании интерактивных графиков, где номинальная и порядковая шкала измерений объединяются в "категориальный" тип.
Если вы загружаете файлы, созданные в предыдущих версиях SPSS, или шкала измерений не определяется явно, SPSS вначале автоматически предполагает метрическую шкалу. Однако если соответствующая переменная имеет метки значений или принимает менее 24 различных значений, то задается порядковая шкала.
-
Подтвердите настройку по умолчанию Nominal (шкала наименований) клавишей <Таb>. Затем снова поместите курсор в поле Name, чтобы начать объявление следующей переменной.
Теперь мы займемся определением переменной sex.
-
Введите в поле Name текст "sex" и подтвердите ввод нажатием на клавишу <Enter> или <Таb>.
-
Чтобы задать тип переменной, щелкните в поле Туре на кнопке с тремя точками. Откроется диалоговое окно Define Variable Type (Определение типа переменной). Примите предлагаемую настройку Numeric (Численный) и установите длину "1" и количество десятичных разрядов "0", так как в этой переменной будут храниться только значения 1, 2 или 0. Подтвердите настройку кнопкой ОК и перейдите к следующему полю клавишей <Таb>.
-
Для формата столбца примите без изменений предлагаемые значения формата "1" и количества десятичных разрядов "0". На этом этапе можно было бы изменить сделанные ранее настройки.
-
Для метки переменной задайте текст "Пол".
-
Щелкните в поле Value Labels на кнопке
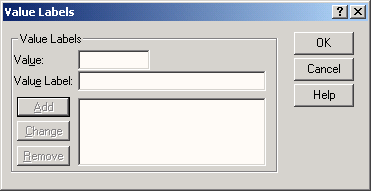
 . Откроется диалоговое окно Define Value Labels (Определение меток значений).
. Откроется диалоговое окно Define Value Labels (Определение меток значений).
Рис. 3.5: Диалоговое окно Define Value Labels
Метки значений определяются следующим образом:
-
Вначале введите в поле Value (Значение) число "1". Нажмите клавишу <Таb>.
-
Введите в поле Value label (Метка значения) текст "женский".
-
Щелкните на кнопке Add (Добавить). Метка значения будет добавлена в список. Для этой цели можно также нажать комбинацию клавиш <Alt>+<h>.
-
Повторите эти действия для значений "2" — "мужской" и "0" — "нет данных". Максимально допустимая длина метки значения составляет 60 знаков.
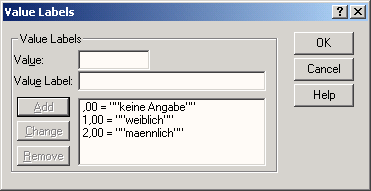
Результат ввода всех значений в диалоговом окне показан на рис. 3.6.
Рис. 3.6: Заполненное диалоговое окно Define Value Labels (Определение меток значений)
-
Подтвердите введенные данные кнопкой ОК, а затем — клавишей <ТаЬ>.
-
Чтобы задать пропущенные значения, щелкните в поле Missing на кнопке с тремя точками
 . Откроется диалоговое окно Define Missing Values (Определение пропущенных значений).
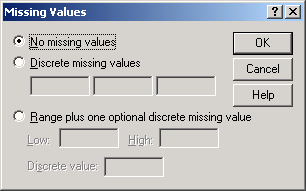
. Откроется диалоговое окно Define Missing Values (Определение пропущенных значений).
Рис. 3.7: Диалоговое окно Define Missing Values
По умолчанию предлагается вариант No missing values (Нет пропущенных значений), то есть все значения в настоящее время рассматриваются как допустимые.
-
Щелкните на пункте Discrete missing values (Отдельные пропущенные значения). Для одной переменной нужно задать до трех пользовательских пропущенных значений. Введите значение "О".
Существует еще один вариант:
-
Range and one optional Discrete missing value (Диапазон и единичное отсутствующее значение): при выборе этого варианта все значения в диапазоне от Minimum (Наименьшее значение) до Maximum (Наибольшее значение) включительно объявляются как пропущенные. Кроме того, можно объявить как отсутствующее еще одно значение вне этого диапазона.
К сожалению, при сборе данных, как правило, не удается избежать пропущенных значений. Во многих статистических методах, прежде всего одномерных, учет пропущенных значений не составляет проблемы, так как кроме соответствующего уменьшения количества наблюдений не нужно вносить никаких дополнительных изменений в расчетный метод. Однако при двумерном, а тем более при многомерном анализе пропущенные значения в списках переменных создают более значительные проблемы, так как одного-единственного отсутствующего значения достаточно, чтобы сделать всю выборку непригодной для анализа. Впрочем, для многих методов анализа SPSS предлагает выход из такой ситуации.
-
Подтвердите выбор пропущенных значений для переменной sex кнопкой ОК.
-
В полях Columns и Alignment примите настройки, предлагаемые по умолчанию.
-
В поле Measure щелкните на кнопке
 — откроется список с тремя возможными шкалами измерения:
— откроется список с тремя возможными шкалами измерения:
-
Измените первоначальную настройку Scale (Метрическая) на Nominal (Номинальная) и нажмите клавишу <Таb>.
Теперь мы займемся определением переменной age.
-
Введите в поле Name текст "age" и подтвердите ввод.
-
Чтобы задать тип переменной, щелкните в поле Туре на кнопке с тремя точками
 .Откроется диалоговое окно Define Variable Type. Примите предлагаемую настройку Numeric и установите длину "2" (мы предполагаем, что все респонденты не старше 99 лет) и количество десятичных разрядов "0". Подтвердите настройку кнопкой ОК и перейдите к следующему полю клавишей <Таb>.
.Откроется диалоговое окно Define Variable Type. Примите предлагаемую настройку Numeric и установите длину "2" (мы предполагаем, что все респонденты не старше 99 лет) и количество десятичных разрядов "0". Подтвердите настройку кнопкой ОК и перейдите к следующему полю клавишей <Таb>. -
В полях Column format и Decimals примите настройки, предлагаемые по умолчанию.
-
Для метки переменной введите текст "Возраст", а для меток значений примите предлагаемую настройку None, нажав <Enter>.
-
Чтобы задать пропущенные значения, щелкните в поле Missing values на кнопке с тремя точками
 . Откроется диалоговое окно Define Missing Values. По умолчанию предлагается вариант No missing values (Нет пропущенных значений), то есть все значения рассматриваются как допустимые. Введите единичное отсутствующее значение "0" и закройте диалоговое окно кнопкой ОК.
. Откроется диалоговое окно Define Missing Values. По умолчанию предлагается вариант No missing values (Нет пропущенных значений), то есть все значения рассматриваются как допустимые. Введите единичное отсутствующее значение "0" и закройте диалоговое окно кнопкой ОК. -
Примите предлагаемые настройки "8" в поле Columns, "Right" в поле Alignment и "Scale" в поле Measure.
Создание маски данных мы завершаем объявлением переменной party.
-
Введите в поле Name текст "party" и подтвердите ввод нажатием клавиши <Таb>.
-
Чтобы задать тип переменной, щелкните в поле Туре на кнопке с тремя точками. Откроется диалоговое окно Define Variable Type. Примите предлагаемую настройку Numeric и установите длину "1" и количество десятичных разрядов "0", так как в этой переменной будут храниться только значения от 1 до 7 и 0 как отсутствующее значение. Подтвердите настройку кнопкой ОК и перейдите к следующему полю клавишей <Таb>.
-
Для формата столбца примите значение "1" и количество десятичных разрядов "0".
-
Для метки переменной задайте текст "Партия".
-
Щелкните в поле Value labeb на кнопке
 .Откроется диалоговое окно Define Value Labels (см. рис. 3.5).
.Откроется диалоговое окно Define Value Labels (см. рис. 3.5). -
Вначале введите в поле Value (Значение) число "1". Нажмите клавишу <Таb>.
-
Введите в поле Value label (Метка значения) текст "ХДС/ХСС".
-
Щелкните на кнопке Add (Добавить). Метка значения будет добавлена в список.
-
Повторите эти действия для значений "2" — "СДП", "3" — "СЕПГ", 4 — "Зеленые/ Союз90", 5 — "ПДС", 6 — "Республиканцы", "7" — "Прочие" и "0" — "Нет данных".
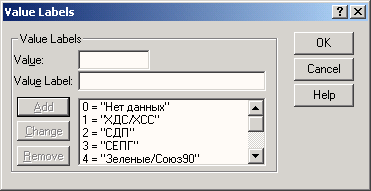
Результат ввода всех значений в диалоговом окне показан на рис. 3.8.
Рис. 3.8: Заполненное диалоговое окно Define Value Labels для переменной party
-
Подтвердите введенные данные кнопкой О К, а затем — клавишей <Таb>.
-
Чтобы задать пропущенные значения, щелкните в поле Missing на кнопке с тремя точками
 . Откроется диалоговое окно Define Missing Values. Щелкните на пункте Discrete missing values и задайте значение "0".
. Откроется диалоговое окно Define Missing Values. Щелкните на пункте Discrete missing values и задайте значение "0". -
Подтвердите выбор пропущенных значений для переменной party кнопкой ОК и нажмите клавишу <Таb>.
-
В полях Columns и Alignment примите настройки, предлагаемые по умолчанию.
-
В поле Measure щелкните на кнопке с тремя точками
 и выберите вариант Nominal.
и выберите вариант Nominal.
4.gif
6.gif
7.gif
11.gif
12.gif
13.gif
15.gif
19.gif
3.4.2 Ввод данных
3.4.2 Ввод данных
Приступим ко вводу данных:
fragebnr | sex | age | party | |
1 | W-001 | 1 | 45 | 1 |
2 | W-002 | 2 | 22 | 3 |
3 | W-003 | 2 | 19 | 3 |
4 | W-004 | 1 | 42 | 1 |
5 | W-005 | 2 | . 34 | 4 |
6 | W-006 | 1 | 72 | 2 |
7 | W-007 | 2 | 38 | 3 |
8 | W-008 | 1 | 56 | 3 |
9 | W-009 | 2 | 61 | 1 |
10 | W-010 | 1 | 77 | 1 |
11 | W-011 | 1 | 23 | 4 |
12 | W-012 | 2 | 67 | 6 |
13 | W-013 | 2 | 79 | 7 |
14 | W-014 | 1 | 26 | 3 |
15 | W-015 | 2 | 59 | 1 |
16 | О-001 | 1 | 34 | 4 |
17 | О-002 | 2 | 18 | 6 |
18 | О-00З | 1 | 44 | 1 |
19 | О-004 | 2 | 68 | 1 |
20 | О-005 | 1 | 33 | 5 |
21 | О-006 | 2 | 66 | 1 |
22 | О-007 | 1 | 22 | 0 |
23 | О-008 | 2 | 0 | 3 |
24 | О-009 | 1 | 67 | 3 |
25 | О-010 | 2 | 33 | 2 |
26 | 0-011 | 2 | 44 | 1 |
27 | О-012 | 1 | 22 | 3 |
28 | О-013 | 1 | 19 | 7 |
29 | О-014 | 1 | 55 | 1 |
30 | 0-01 5 | 2 | 39 | 3 |
Данные можно вводить по отдельным наблюдениям (строкам) или по отдельным переменным (столбцам). Действуйте следующим образом:
-
Щелкните на ячейке в левом верхнем углу. Вокруг ячейки появится рамка. Таким образом эта ячейка обозначается как активная.
-
Введите значение, в нашем примере это "W-001". Это значение отобразится в редакторе ячеек в верхней части окна редактора данных.
-
Нажмите клавишу <Таb>. Значение из редактора ячеек отобразится в ячейке.
В следующих таблицах показано, каким клавишам в редакторе данных соответствует какая функция. Здесь, как и далее, мы предполагаем, что активизирована таблица просмотра данных.
Позиционирование
Клавиша | Функция |
<Таb> или <стрелка вправо> | Перемещает курсор на ячейку вправо. |
<Enter> или <стрелка вниз> | Перемещает курсор на ячейку вниз. |
<стрелка вверх> | Перемещает курсор на ячейку вверх. |
<Shift> <Tab> или <стрелка влево> | Перемещает курсор на ячейку влево, т.е. в предыдущее поле. |
<Ноте> | Перемещает курсор в первую ячейку строки или случая. |
<End> | Перемещает курсор в последнюю ячейку случая. |
<Ctrl> <стрелка вверх> | Перемещает курсор в первый случай столбца. |
<Ctrl> <стрелка вниз> | Перемещает курсор в последний случай столбца. |
<Ctrl> <Home> | Перемещает курсор в первую ячейку первого случая. |
<Ctrl> <End> | Перемещает курсор в последнюю ячейку последнего случая. |
<Page Up> | Прокручивает таблицу на одну страницу вверх. |
<Page Down> | Прокручивает таблицу на одну страницу вниз. |
Выделение
<Shift> <пробел> | Выделяет всю строку. |
<Ctri> <пробел> | Выделяет весь столбец. |
<Shift> <клавиши со стрелками> | Выделение области случаев и переменных. Также можно щелкнуть мышью и перетянуть ее из верхнего левого угла области в нижний правый угол. |
Редактирование
F2 | Переключает в режим редактирования. Следующее нажатие <F2> отключает режим редактирования. |
<стрелка вправо> | Переместить позицию редактирования в ячейке вправо на один знак. |
<стрелка влево> | Переместить позицию редактирования в ячейке влево на один знак. |
<Ноте> | Перейти в начало значения ячейки. |
<End> | Перейти в конец значения ячейки. |
3.5 Сохранение файла данных
3.5 Сохранение файла данных
Сейчас мы сохраним созданный файл данных. Поступите следующим образом:
-
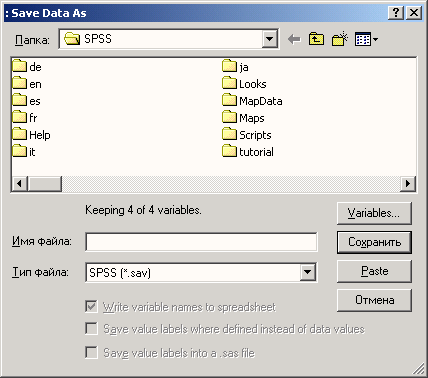
Выберите в меню команды File (Файл) Save as... (Сохранить как...) Откроется диалоговое окно Save Data as (Сохранить данные как).
По умолчанию SPSS сохраняет файл данных в текущем каталоге с расширением .sav.
Если вы следовали указаниям по инсталляции и задали рабочий каталог \SPSSBOOK, он будет предлагаться по умолчанию.
-
Задайте имя файла, соответствующее соглашению об именах в DOS. Для рассматриваемого примера мы предлагаем имя файла "btwahl.sav". Расширение .sav SPSS присваивает файлам данных по умолчанию. Поэтому расширение .sav вводить необязательно.
Рис. 3.9: Диалоговое окно Save Data as
22.gif
3.6 Копирование описаний переменных
3.6 Копирование описаний переменных
В исследовании на тему "Здоровье и питание", в частности, проводится опрос о предпочитаемых диетах. Респонденты должны ответить, насколько к ним относится одно из следующих высказываний.
Я предпочитаю следующую диету | Да, конечно | Да | Частично | В малой степени | Нет |
вегетарианскую | X | X | X | X | X |
биодинамическую | X | X | X | X | X |
с низким содержанием животных белков | X | X | X | X | X |
фаст-фуд | X | X | X | X | X |
с учетом калорийности | X | X | X | X | X |
сытную | X | X | X | X | X |
дешевую | X | X | X | X | X |
Так как в этом случае описания семи переменных в матрице данных почти одинаковы, можно сэкономить время, просто перенеся параметры описания первой переменной на остальные шесть. Для этого поступите следующим образом.
-
Активизируйте вид данных редактора данных, введите в поле Name текст "vegetar" и подтвердите ввод нажатием клавиши <Таb>.
-
Чтобы задать тип переменной, щелкните в поле Туре на кнопке с тремя точками
 Откроется диалоговое окно Define Variable Type. Примите предлагаемую настройку Numeric и установите длину 1 и количество десятичных разрядов I) , так как в этой переменной будут храниться только значения от 1 до 5 и 0 как отсутствующее значение. Подтвердите настройку кнопкой ОК и перейдите к следующему полю клавишей <Таb>.
Откроется диалоговое окно Define Variable Type. Примите предлагаемую настройку Numeric и установите длину 1 и количество десятичных разрядов I) , так как в этой переменной будут храниться только значения от 1 до 5 и 0 как отсутствующее значение. Подтвердите настройку кнопкой ОК и перейдите к следующему полю клавишей <Таb>. -
Для формата столбца примите значение "1" и количество десятичных разрядов "0".
-
Для метки переменной задайте текст "вегетарианская".
-
Щелкните в поле Values на кнопке
 Откроется диалоговое окно Define Value Labels.
Откроется диалоговое окно Define Value Labels. -
Вначале введите в поле Value число "1". Нажмите клавишу <Таb>.
-
Введите в поле Label текст "да, конечно".
-
Щелкните на кнопке Add. Метка значения будет добавлена в список.
-
Повторите эти действия для значений "2" — "да", "3" — "частично", "4" — "в малой степени", "5" — "нет" и "0" — "нет данных".
-
Подтвердите введенные данные кнопкой ОК, а затем — клавишей <Таb>.
-
Чтобы задать пропущенные значения, щелкните в поле Missing на кнопке с тремя точками
 . Откроется диалоговое окно Define Missing Values. Щелкните на пункте Discrete missing values и задайте значение 0 .
. Откроется диалоговое окно Define Missing Values. Щелкните на пункте Discrete missing values и задайте значение 0 . -
Подтвердите выбор пропущенных значений для переменной vegetar кнопкой ОК и нажмите клавишу <Таb>.
-
В полях Columns, Alignment и Measure примите настройки, предлагаемые по умолчанию.
-
Поместите курсор в ячейку с номером 1, т.е. в начало первой строки, и нажмите левую кнопку мыши. Параметры описания первой переменной будут выделены (см. рис. 3.10).
Рис. 3.10: Выделенное описание переменной
-
Выберите в меню команды Edit (Правка) Сору (Копировать)
-
Поместите курсор в ячейку с номером 2, т.е. в начало второй строки, и нажмите левую кнопку мыши — будет выделена вторая строка.
-
Выберите в меню команды Edit (Правка) Paste (Вставить)
Параметры объявления первой переменной будут скопированы во вторую строку.
Рис. 3.11: Скопированные параметры описания .переменной
-
Далее измените предлагаемое имя переменной var0000l на biolog и повторите эти действия для всех остальных переменных.
-
После пометки и копирования описания переменной, когда выделена вторая строка для вставки описания, вместо команд Edit Paste можно также использовать команду меню Edit Paste variables... (Вставить переменные) Откроется диалоговое окно Paste Variables.
Рис. 3.12: Диалоговое окно Paste Variables
-
Замените предлагаемое имя vege на новое имя biolog и щелкните на кнопке ОК.
Диалоговое окно Paste Variables (см. рис. 3.12) дает возможность указать количество новых переменных. Если задать здесь число 6, параметры объявления переменной vegetar можно будет перенести на все остальные переменные за одну операцию. В этом случает таблица будет выглядеть так:
Рис. 3.13: Таблица после вставки нескольких переменных
Нам остается только заменить имена переменных vege I — vege6 на желаемые, например, biolog, lowprot, fastfood, calbal, rich и cheap, и все переменные шкалы "Предпочтения в питании" будут объявлены.
26.gif

27.gif

28.gif

29.gif

3.7 Завершение сеанса работы
3.7 Завершение сеанса работы
Сейчас мы завершим наш сеанс работы с SPSS.
-
Выберите в меню команды File (Файл) Exit (Выход)
Для каждого из открытых окон SPSS спрашивает, надо ли сохранить его содержимое. Если щелкнуть на кнопке "Yes" (Да) или нажать <Enter>, SPSS открывает специальное диалоговое окно, в котором надо указать тип сохраняемого файла (файл данных, вывода или синтаксиса).
Так как у нас было открыто только окно редактора данных и мы уже сохранили его содержимое в разделе 3.5, программа ничего не запрашивает и просто закрывается.
Глава 4. SPSS для Windows — обзор
Глава 4. SPSS для Windows — обзор
1. PSS для Windows — обзор
SPSS для Windows — обзор
В этой главе мы хотим дать обзор использования SPSS для Windows на примере файлов данных wahl.sav и zahri.sav. Наш обзор в первую очередь будет касаться технических приемов работы с программой.
-
Запустите SPSS, дважды щелкнув мышью на значке SPSS.
-
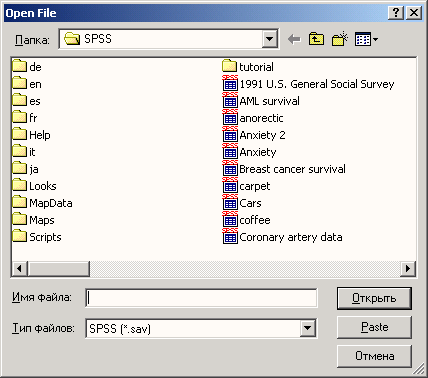
Загрузите файл wahl.sav из каталога \SPSSBUCH. Этот файл соответствует файлу btwahl.sav, который мы сохранили ранее (см. главу 3). Для этого выберите в меню команды File (Файл) Open... (Открыть)... Появится диалоговое окно Open file (Открыть файл) (см. рис. 4.1).
Если вы следовали нашим инструкциям по установке примеров с компакт диска (см. главу 2) и создали рабочий каталог под названием SPSSBOOK, вы увидите список файлов в каталоге \SPSSBOOK.
-
Щелкните на кнопке со стрелкой вправо на линейке прокрутки этого списка. Удерживайте кнопку мыши нажатой, пока не появится файл wahl.sav. Выделите этот файл. Его имя должно появиться в текстовом поле File name (Имя файла). Имя нужного файла можно ввести в этом поле и непосредственно.
Рис. 4.1. Диалоговое окно Open file
-
Подтвердите выбор, щелкнув на кнопке Open (Открыть). Подтвердить выбор файла также можно, дважды щелкнув мышью на имени wahl.sav. После этого содержимое файла wahl.sav отобразится в окне редактора данных, как показано на рис. 4.2. Если был активизирован просмотр переменных, потребуется еще перейти на вкладку Data View (просмотр данных).
1.gif

2.gif
4.1 Выбор статистической процедуры
4.1 Выбор статистической процедуры
Меню статистики, которое открывается по команде меню Analyze (Анализ), содержит список статистических методов. После каждого пункта этого меню стоит стрелка. Она указывает на существование следующего уровня меню.
Доступный набор статистических методов зависит, в частности, от того, какие модули были установлены. В варианте установки SPSS, показанного на рис. 4.3, кроме модулей, описанных в этой книге, установлены дополнительные модули Amos, AnswerTree и Trends. Эти модули рассматриваются в нашей книге "SPSS. Методы изучения рынка и общественного мнения" (SPSS. Methoden fur die Markt- und Meinungs-forschung").
В качестве примера попробуем построить частотное распределение. Выполните следующие действия.
Выберите в меню команды Analyze (Анализ) Descriptive statistics (Описательная статистика) Frequency... (Частоты...)
Рис. 4.2: Фрагмент файла данных wahl.sav
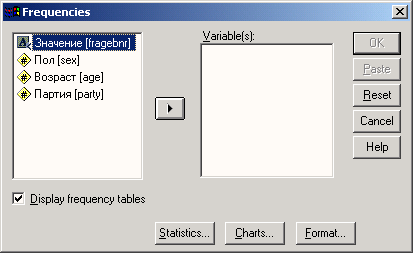
Рис. 4.3: Меню статистики Появится диалоговое окно Frequency (см. рис. 4.4).
Рис. 4.4: Диалоговое окно Frequency
Диалоговые окна статистических процедур содержат следующие компоненты:
-
Список исходных переменных — список всех переменных в файле данных. В данный момент в списке исходных переменных присутствуют следующие переменные: age, fragebnr, partei, sex. Перед именем каждой переменной стоит значок; по которому можно определить, является ли эта переменная численной или строковой.
-
Список выбранных переменных — список, содержащий переменные файла данных, которые были выбраны для анализа. Список выбранных переменных также называют целевым списком или списком тестируемых переменных. Этот список имеет заголовок Variable(s) (Переменная(ые)). Так как мы еще не выбрали ни одной переменной, этот список пуст.
-
Командные кнопки — кнопки, при щелчке на которые выполняются определенные действия. В этом диалоговом окне расположены кнопки OK, Paste (Вставить), Reset (Сброс или Отклонить), Cancel (Отмена) и Help (Справка), а также кнопки, открывающие вспомогательные диалоговые окна: Statistics... (Статистика), Charts... (Диаграммы или Графики) и Format... (Формат). Кнопки вспомогательных диалоговых окон отличаются троеточием (...) после названия.
Пять стандартных командных кнопок в главном диалоговом окне имеют следующее назначение:
-
ОК — кнопка ОК запускает соответствующую процедуру. Одновременно она закрывает диалоговое окно.
-
Paste — эта кнопка переносит выбранный в диалоговом окне синтаксис команды в редактор синтаксиса. Здесь можно отредактировать синтаксис команды и дополнить его другими опциями, недоступными в данном диалоговом окне.
-
Reset — эта кнопка отменяет перенос выделенной переменной в целевой список переменных.
-
Cancel — эта кнопка отменяет все изменения, сделанные с момента последнего открытия диалогового окна, и закрывает его.
-
Help — эта кнопка выводит контекстно-чувствительную справку. При щелчке на ней открывается окно справки, содержащее сведения о текущем диалоговом окне.
Выбор переменных
Сначала мы построим частотное распределение для переменной partei. Выполните следующие действия:
-
Выделите переменную party в списке исходных переменных.
-
Щелкните на кнопке, которая находится рядом со списком выбранных переменных. Переменная party будет перенесена из списка исходных переменных в список выбранных переменных. Можно также дважды щелкнуть на нужной переменной, и она будет перенесена в список выбранных переменных.
-
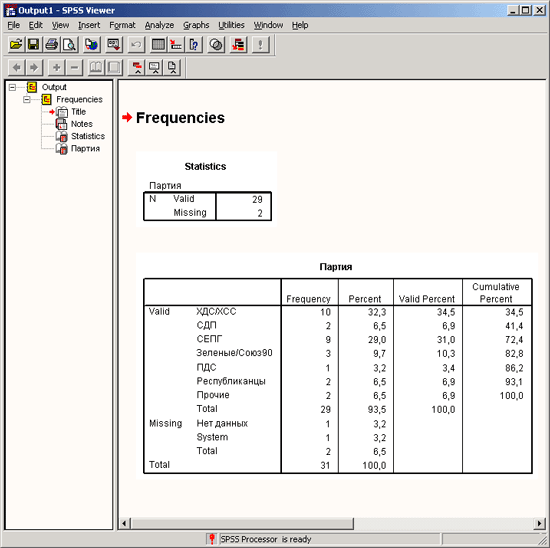
Подтвердите операцию, щелкнув на кнопке ОК. Результаты будут отображены в окне просмотра (Viewer).
Окно просмотра разделено на две части. В левой отображается структура вывода, а в правой — собственно выводимые данные. В разделе вывода отображаются как таблицы, так и графики. Подробное описание окна просмотра и возможностей, которое оно предоставляет, приводится в разделе 4.5.
Вернемся в редактор данных. Это можно сделать двумя различными способами:
-
Выберите в меню команды Window (Окно) 1 Wahl.sav — SPSS Data Editor или щелкните на панели инструментов на символе редактора данных

Рис. 4.5: Окно просмотра
Чтобы для построения частотного распределения выбрать все переменные, содержащиеся в файле данных, выполните следующие действия:
-
Щелкните на имени первой переменной и задержите нажатой левую кнопку мыши. Перетащите мышь, пока не будут выделены все переменные.
-
Затем, щелкнув на кнопке с треугольником, перенесите переменные в список выбранных переменных.
Для выполнения этой же задачи можно также щелкнуть на первой переменной, а затем, нажав клавишу <Shift> — на последней переменной (метод "Shift-клик"). Чтобы выделить несколько переменных, которые находятся в разных местах списка, следует поступить следующим образом:
-
Щелкните на первой переменной, а затем, при нажатой клавише <Ctrl>, — на следующей и т.д. (метод "Ctrl-клик").
Вспомогательные диалоговые окна
Сейчас мы попробуем определить наименьшее, наибольшее и среднее значения переменной age.
-
Выберите в меню команды Analyze (Анализ) Descriptive statistics (Дескриптивные статистики) Frequency... (частота распределения)
-
В диалоговом окне Frequency щелкните сначала на кнопке Reset(C6poc). Затем перенесите переменную age в конечный список переменных.
-
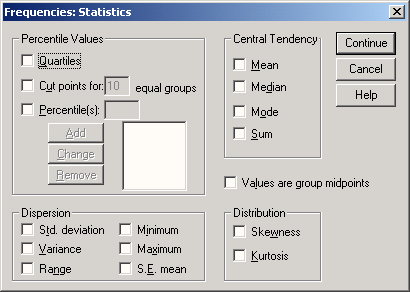
Щелкните на кнопке Statistics... Откроется диалоговое окно Frequency: Statistics (Частотное распределение: Статистика) (см. рис. 4.6).
Рис. 4.6: Диалоговое окно Frequency: Statistics
-
Установите флажки Minimum (Наименьшее значение), Maximum (Наибольшее значение) и Average (Среднее значение).
-
Щелкните на кнопке Next (Далее). Настройки будут сохранены и мы вернемся в главное диалоговое окно.
-
Снимите флажок Display frequency tables (Показывать частотные таблицы).
-
Запустите вычисление, щелкнув на кнопке ОК. Результаты будут показаны в окне просмотра:
Статистика
Возраст | ||
N | Имеется | 29 |
Отсутствует | 1 | |
Среднее | 44,28 | |
Наименьшее | 18 | |
Наибольшее | 79 | |
3.gif
4.gif
5.gif
7.gif
8.gif
4.10 Настройки
4.10 Настройки
-
Для того, чтобы изменить системные настройки SPSS, выберите в меню Edit (Правка) Options... (Параметры)
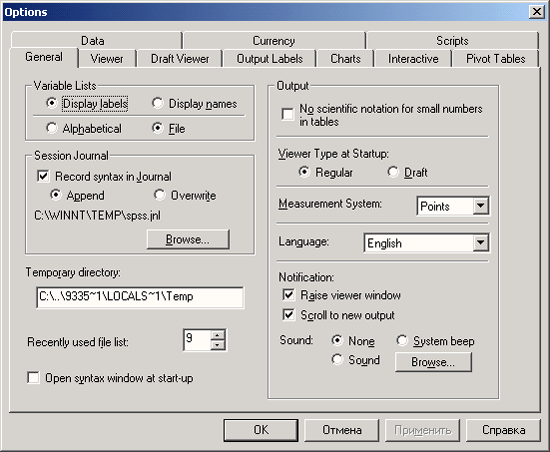
Откроется диалоговое окно Options (Параметры).
В этом диалоговом окне находятся десять регистрационных карт. Названия отдельных параметров говорят сами за себя, поэтому мы остановимся только на описании самих регистрационных карт.
-
General (Общие): здесь вы можете задать тип сортировки списков переменных. Сортировка в алфавитном порядке, установленная по умолчанию, может быть изменена на порядок, в котором переменные были расположены в рабочем файле. Вы можете также задать, что указывать во всех диалоговых окнах — метки значений или имена переменных.
-
Viewer (Окно просмотра): здесь можно установить тип и размер шрифта заголовков и текста, отображаемых в окне просмотра, а также задать размеры страницы.
-
DraftViewer (Окно текстового режима): на этой карте присутствуют различные установки внешнего вида таблиц и текста.
-
Output Labels (Обозначение выводимых значений): Вы можете выбрать, будут ли для обозначения переменных указываться их имена или соответствующие метки (установка по умолчанию) или и то и другое одновременно. Для обозначения категорий переменной вы можете выбрать значение переменной или метку значения (установка по умолчанию) или оба варианта одновременно.
Рис. 4.35: Диалоговое окно Параметры SPSS
-
Charts (Диаграммы): наряду с установками шрифта вы можете также задать, будут ли различные столбцы, линии, области и т.д. отображаться разными цветами (установка по умолчанию) или же при помощи разных штриховок и соответственно типов линий. Вы также можете управлять компоновкой рамки (рамка снаружи или внутри) и организовывать отображение координатной сетки.
-
Interactive (Интерактивный режим): Вы можете выбрать параметры интерактивных графиков задав, к примеру, некоторый образец. Если из соображений последующей обработки и вывода на печать вы хотите, чтобы диаграмма была построена в чёрно-белом виде, активируйте для этого образец Grayscale.do (Оттенки серого).
-
Pivot Tables (Мобильные таблицы): здесь Вы можете выбрать внешний вид (компоновку) мобильных таблиц.
-
Data (Данные): в этой карте может быть изменён формат представления рассчитанных переменных (установка по умолчанию: восемь позиций, причём две из них приходятся десятичные знаки). Для отображения года двумя последними цифрами Вы можете дополнительно указать столетие. Если вы активируете автоматическую опцию, столетие будет отсчитываться будет в пределах от 1931 до 2030.
-
Currency (Денежная единица): здесь можно указать денежный формат (см. гл. 3.4.1).
-
Scripts (Сценарии): Вы можете активировать автоматические сценарии.
Теперь Вы разбираетесь в технических тонкостях управления программой.
55.gif
4.2. Настройки редактора данных
4.2. Настройки редактора данных
Меню View (Вид) редактора данных содержит множество опций, с помощью которых можно произвести индивидуальную настройку редактора данных. В частности, можно:
-
Показать или скрыть строку состояния. Команда: Status bar (Строка состояния)
-
Увеличить значки на панели символов и включить или отключить отображение кратких сведений. Команда: Toolbars... (Панели символов)
-
Выбрать другой тип, начертание и размер шрифта. Команда: Fonts... (Шрифты)
-
Включить или отключить отображение линий сетки. Команда: Grid lines (Линии сетки)
-
Отображать метки значений вместо фактических значений переменных. Команда: Value labels (Метки значений)
Рассмотрим следующий пример:
Мы хотим, чтобы вместо значений переменных файла wahl.sav отображались метки значений.
-
В первую очередь командами меню Window 1 Wahl.sav — SPSS Data Editor перейдите в редактор данных, если окно вывода еще активно.
-
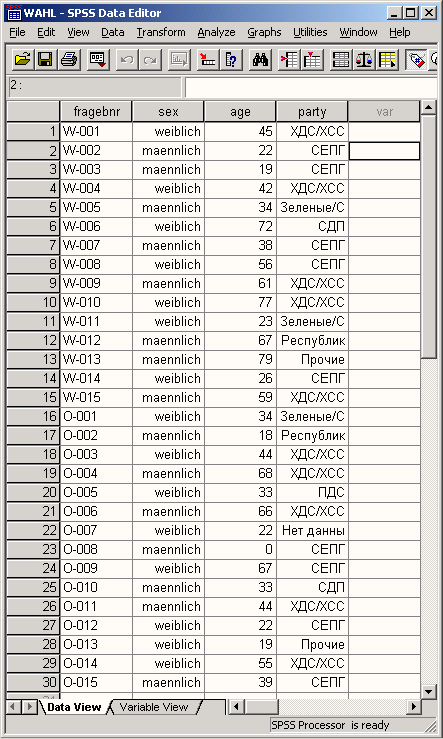
Выберите в меню команды: View Value labels
Теперь в редакторе данных файл wahl.sav будет отображен с метками значений вместо значений переменных.
Метки значений также позволяют как вводить данные, так и изменять их. Выполните следующие действия:
-
Щелчком мыши выделите, например, ячейку переменной partei. Появится кнопка

-
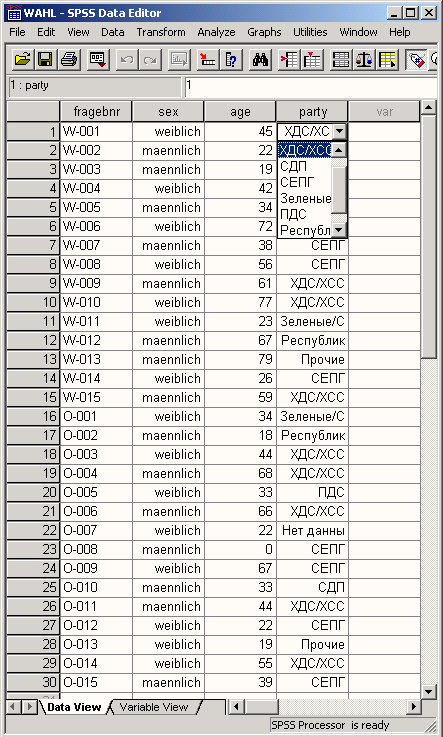
Щелкните на этой кнопке. Отобразится список меток значений переменной party (см. рис. 4.8).
Рис. 4.7: Редактор данных с метками значений
Рис. 4.8: Список меток значений в редакторе данных
-
Выберите из списка метку, которую хотите ввести. После щелчка выделенная метка значения будет перенесена в ячейку. Это позволяет относительно быстро исправлять ошибки в содержимом ячеек данных.
10.gif
11.gif
4.3 Панели символов
4.3 Панели символов
SPSS имеет следующие окна:
-
Редактор данных (Data Editor)
-
Окно просмотра (Viewer)
-
Окно просмотра текста (Text Viewer)
-
Редактор мобильных таблиц (Pivot Table Editor)
-
Редактор диаграмм (Diagram Editor)
-
Редактор текстового вывода (Text Output Editor)
-
Редактор синтаксиса (Syntax Editor)
-
Редактор скриптов (Script Editor)
Редактор данных был подробно описан в разделе 3.4, другие окна мы рассмотрим позже. Каждое окно, кроме редактора мобильных таблиц, имеет одну или две панели символов для вызова часто используемых команд. Краткие сведения о каждом символе можно получить, если поместить на него указатель мыши.
Ниже представлены прежде всего те символы, которые встречаются в большинстве или во всех окнах.
 Открыть файл: Этот символ активизирует диалоговое окно открытия файла, причем по умолчанию предлагается открыть документ того же типа, который находится в активном окне. Следовательно, при помощи этого символа можно открыть файл данных, файл вывода или файл синтаксиса.
Открыть файл: Этот символ активизирует диалоговое окно открытия файла, причем по умолчанию предлагается открыть документ того же типа, который находится в активном окне. Следовательно, при помощи этого символа можно открыть файл данных, файл вывода или файл синтаксиса.
 Сохранить файл: Этот символ предназначен для сохранения рабочего файла. Если рабочему файлу еще не присвоено имя, этот символ активизирует диалоговое Save as (Сохранить как). Если вы находитесь не в окне редактора данных, активизируется диалоговое окно сохранения файла соответствующего типа — файла вывода или синтаксиса.
Сохранить файл: Этот символ предназначен для сохранения рабочего файла. Если рабочему файлу еще не присвоено имя, этот символ активизирует диалоговое Save as (Сохранить как). Если вы находитесь не в окне редактора данных, активизируется диалоговое окно сохранения файла соответствующего типа — файла вывода или синтаксиса.
 Печать: Этот символ вызывает диалоговое окно вывода на печать в соответствии с типом активного окна. Он позволяет напечатать весь документ или только выделенную область.
Печать: Этот символ вызывает диалоговое окно вывода на печать в соответствии с типом активного окна. Он позволяет напечатать весь документ или только выделенную область.
 История вызова диалоговых окон: Этот символ выводит список 12 последних вызванных диалоговых окон. Это дает возможность быстро перейти к одному из недавно вызванных диалоговых окон. Окно, вызванное в последнюю очередь, всегда находится в начале списка.
История вызова диалоговых окон: Этот символ выводит список 12 последних вызванных диалоговых окон. Это дает возможность быстро перейти к одному из недавно вызванных диалоговых окон. Окно, вызванное в последнюю очередь, всегда находится в начале списка.
Чтобы заново вызвать диалоговое окно, просто щелкните на соответствующем пункте списка.
 Перейти в редактор данных: Этот символ обеспечивает переход в редактор данных из любого окна.
Перейти в редактор данных: Этот символ обеспечивает переход в редактор данных из любого окна.
 Перейти к наблюдению: Этот символ открывает диалоговое окно Go to case (Перейти к наблюдению). Его можно использовать для перехода к определенному наблюдению, так в SPSS называется набор значений переменных, набранных в строке редактора данных.
Перейти к наблюдению: Этот символ открывает диалоговое окно Go to case (Перейти к наблюдению). Его можно использовать для перехода к определенному наблюдению, так в SPSS называется набор значений переменных, набранных в строке редактора данных.
 Выбрать наблюдения: -этот символ открывает диалоговое окно select cases (Выбрать наблюдения). Его можно использовать для отбора наблюдений, для которых выполняется определенное условие.
Выбрать наблюдения: -этот символ открывает диалоговое окно select cases (Выбрать наблюдения). Его можно использовать для отбора наблюдений, для которых выполняется определенное условие.
 Информация о переменных: Этот символ открывает диалоговое окно Variables, в котором отображаются описания выделенных переменных. Из множества символов, которые возникают только в одном определенном окне, мы покажем лишь несколько. О назначении остальных легко можно узнать из кратких сведений (Quick Info) по данному символу.
Информация о переменных: Этот символ открывает диалоговое окно Variables, в котором отображаются описания выделенных переменных. Из множества символов, которые возникают только в одном определенном окне, мы покажем лишь несколько. О назначении остальных легко можно узнать из кратких сведений (Quick Info) по данному символу.
В редакторе синтаксиса большое значение имеет символ Syntax-Start (Синтаксис-Начать), в случае если для вызова статистических процедур Вы пользуетесь командным синтаксисом SPSS (см. главу 26):
 Синтаксис-Начать: В окне редакторе синтаксиса этот символ запускает на выполнение выделенные команды SPSS. Если не выделено ни одной команды, запускается команда, на которой находится курсор.
Синтаксис-Начать: В окне редакторе синтаксиса этот символ запускает на выполнение выделенные команды SPSS. Если не выделено ни одной команды, запускается команда, на которой находится курсор.Три следующих символа могут быть задействованы в редакторе данных.
 Вставить наблюдение: В редакторе данных щелчок на этом символе вызывает вставку наблюдения над активной ячейкой.
Вставить наблюдение: В редакторе данных щелчок на этом символе вызывает вставку наблюдения над активной ячейкой.
 Вставить переменную: В редакторе данных щелчок на этом символе вызывает вставку новой переменной слева от активной переменной.
Вставить переменную: В редакторе данных щелчок на этом символе вызывает вставку новой переменной слева от активной переменной.
 Метки значений: Этот символ позволяет переключаться между отображением значений и меток значений.
Метки значений: Этот символ позволяет переключаться между отображением значений и меток значений.
Символы, доступные в редакторе диаграмм, подробно описаны в разделе 22.16.
16.gif
4.4 Построение и редактирование графиков
4.4 Построение и редактирование графиков
Представим в графическом виде значения переменной partei (партия).
-
Выберите в меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты)
-
При помощи кнопки Reset (Сброс) удалите все предыдущие установки.
-
Щёлкните дважды на переменной partei (партия), чтобы поместить её в список отобранных переменных.
-
Щёлкните на выключателе Charts... (Диаграммы). Откроется диалоговое окно Frequencies: Charts (Частоты: Диаграммы) (см. рис. 4.9).
-
Щёлкните на опции Bar Charts (Столбчатые диаграммы), в области Chart Values (Значения диаграммы) щёлкните на опции Percentages (Проценты) и затем на Continue (Далее).
-
В главном диалоговом окне деактивируйте опцию Display frequency tables (Показать частотные таблицы).
-
Щёлкните на ОК. В окне просмотра появится столбчатая диаграмма (см. рис. 4.10).
Рис. 4.9: Диалоговое окно Frequencies: Charts (Частоты: Диаграммы)
Предположим, у Вас появилось желание отредактировать построенный график в соответствии со своими требованиями.
-
Щёлкните дважды на какой-либо точке в пределах графика. После этого он будет помещён в редактор диаграмм (см. рис. 4.11).
Панель меню изменилась. Теперь в меню присутствуют только опции, предназначенные для обработки графиков (см. гл. 22.16). Также претерпели изменения и панели инструментов. Изменим сначала метод представления столбцов. Столбцы, в соответствии с нашим желанием, должны быть представлены в трёхмерном виде.
Рис. 4.10: Столбчатая диаграмма в окне просмотра
Рис. 4.11: Столбчатая диаграмма в окне редактора диаграмм
-
В меню редактора диаграмм выберите Format (Формат) Bar Style... (Вид столбца)
Откроется диалоговое окно Bar Styles (Виды столбцов) (см. рис. 4.12).
Рис. 4.12: Диалоговое окно Ва Styles (Виды столбцов)
-
Щёлкните на области 3-D effect (3-D эффект).
-
В поле Depth (Глубина) введите число "40".
-
Щёлкните Apply All (Применить для всех) и затем на выключателе Close (Закрыть). Теперь столбчатая диаграмма выглядит так, как изображено на рисунке 4.13.
Рис. 4.13: Столбиковая диаграмма с 3D эффектом
Теперь дадим графику название.
-
Выберите в меню Chart (Диаграмма) Title... (Заголовок)
-
Откроется диалоговое окно Titles (Заголовки).
-
В поле Title 1 (Заголовок 1) введите текст "Парламентские выборы", а в поле ТШе2 (Заголовок 2) "Воскресный опрос". Выберите для заголовка и подзаголовка центральное выравнивание — Center (Центр). Подтвердите нажатием ОК.
Теперь выделим график при помощи рамки.
-
Выберите в меню Chart (Диаграмма) Outer Frame (Рамка снаружи) Пометим столбцы точными процентными показателями.
Рис. 4.14: Диалоговое окно Titles (Заголовки)
-
Выберите в меню Format (Формат) Bar Label Style... (Метки столбцов)
Откроется диалоговое окно Bar Label Styles (Метки столбцов).
-
Щёлкните на области Framed (В рамке), затем на Apply All (Применить для всех) и в заключение на Close (Закрыть). Отредактированная нами диаграмма отображена на рисунке 4.16.
Рис. 4.15: Диалоговое окно Bar Label Styles (Метки столбцов)
Рас. 4.16: Столбиковая диаграмма с метками столбцов
Если Вы желаете сохранить построенный график, то поступите следующим образом:
-
При помощи щелчка на значке
 закройте редактор диаграмм.
закройте редактор диаграмм.
Отредактированный график останется в окне просмотра. Этот график (а в общем случае и любые другие результаты, выведенные в окно просмотра) мы хотим сохранить в файле, который имеет формат Viewer (средства просмотра SPSS).
-
Выберите в меню File (Файл) Save As... (Сохранить как)
Откроется диалоговое окно Save As (Сохранить как) (см. рис. 4.17).
Согласно предварительным установкам, SPSS обозначает файлы, которые имеют формат средства просмотра, присваивая им расширение .spo.
-
Задайте подходящее имя файла и щёлкните на ОК.
Рис. 4.17: Диалоговое окно Save As (Сохранить как)
Теперь распечатаем график на принтере.
-
Выберите в меню File (Файл) Print... (Печать)
-
Подтвердите установки диалогового окна Print (Печать) при помощи кнопки ОК.
25.gif
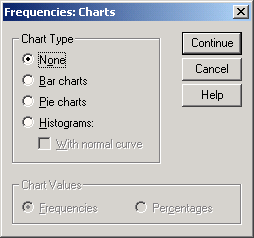
26.gif
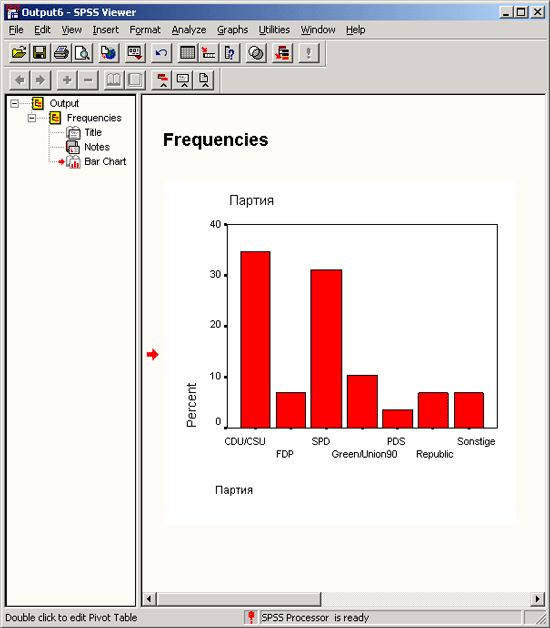
27.gif
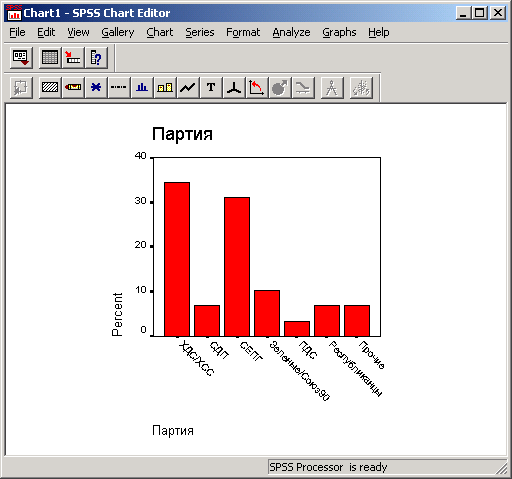
28.gif
29.gif
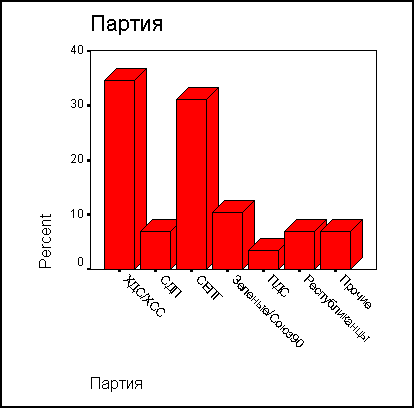
30.gif
31.gif
32.gif
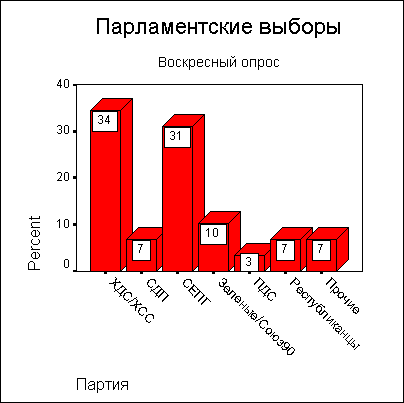
34.gif
4.5 Окно просмотра
4.5 Окно просмотра
Рассмотрим на конкретном примере возможности, предоставляемые пользователю окном средства просмотра результатов. Для того, чтобы иметь рабочий материал в окне просмотра, произведём некоторые операции с файлом wahl.sav и построим несколько таблиц и график.
На первом шаге подсчитаем частоты переменной partei (партия).
-
Выберите в меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты)
-
Перенесите переменную partei (партия) в поле тестируемых переменных и подтвердите действие при помощи ОК.
Теперь создадим таблицу сопряженности для переменных partei (партия) и sex (пол).
-
Выберите в меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
-
Поместите переменную partei (партия) в поле строчных переменных (Row), а переменную sex (пол) в поле столбцовых (Column).
-
При помощи выключателя Cells... (Ячейки) организуйте вывод процентных показателей по столбцам (опция Column (Столбец)).
-
Щёлкните на выключателе Statistics (Статистики) и активируйте тест Chi-square (Тест Хи-квадрат).
Представим распределение частотных показателей переменной partei (партия) в виде круговой диаграммы.
-
Выберите в меню Graphs (Графики) Pie... (Круговые)
-
Оставьте, установленную по умолчанию, опцию Summaries for groups of cases (Обработка категорий одной переменной), щелкните на кнопке Define (Определить), поместите переменную partei (партия) в поле для сегментов, озаглавленное Define slices by (Создать сектора на основе).
В заключение подсчитаем для переменной alter (возраст) статистические показатели.
-
Выберите в меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Descriptives... (Дескриптивные)
-
Перенесите переменную alter (возраст) в поле тестируемых переменных.
Результаты производимых нами расчётов будут по очереди появляться в окне просмотра, согласно установкам, каждый последующий результат расчёта будет помещаться в конец окна. Если Вас вся эта процедура сильно утомляет, Вы можете просто в окне просмотра открыть файл beispiel.spo, в котором сохранены все рассчитанные нами данные. Окно просмотра Viewer будет выглядеть так, как изображено на рисунке 4.18.
Окно просмотра состоит из двух частей. В левой части находится иерархия (обзор содержания) результатов; в правую часть помещаются таблицы с результатами расчётов и построенные графики. Ширину этих частей окна можно изменять перетаскиванием разделительной границы при помощи мыши.
Рассмотрите полученные результаты, помещенные в правую часть окна и ознакомьтесь с формой таблиц. В качестве примера рассмотрим поподробнее таблицу сопряженности между полом (sex) и переменной partei (партия), характеризующей партийные предпочтения респондентов.
Рис. 4.18: Окно просмотра
Partei * Geschlecht Crosstabulation (Таблица сопряженности Партия * Пол)
Geschiecnt (Пол) | lTotal | ||||
weiblich (женский) | mannlich (мужской) | (Сумма) | |||
Partei (Партия) | CDU/CSU | Count (Количество) | 5 | 5 | 10 |
% within Geschiecht (% для пола) | 35,7% | 33,3% | 34,5% | ||
FDP | Count (Количество) | 1 | 1 | 2 | |
% within Geschlecht (% для пола) | 7,1% | 6,7% | 6,9% | ||
SPD | Count (Количество) | 4 | 5 | 9 | |
% within Geschlecht (% для пола) | 28,6% | 33,3% | 31,0% | ||
Grbne/ Bundnis (Зелёные / Союз 90) | Count (Количество) | 2 | 1 | 3 | |
% within Geschlecht (% для пола) | 14,3% | 6,7% | 10,3% | ||
PDS | Count (Количество) | 1 | 1 | ||
% within Geschlecht (% для пола) | 7,1% | 3,4% | |||
Republikaner (Респуб- ликанцы) | Count (Количество) | 2 | 2 | ||
% within Geschlecht (% для пола) | 13,3% | 6,9% | |||
Sonstige (прочие) | Count (Количество) | 1 | 1 | 2 | |
% within Geschlecht (% для пола) | 7,1% | 6,7% | 6,9 | ||
Total (Сумма) | Count (Количество) | 14 | 15 | 29 | |
% within Geschlecht (% для пола) | 100,0% | 100,0% | 100,0% | ||
Иерархию окна просмотра можно увидеть в левой части рисунка 4.18.
Результаты каждой выполненной статистической процедуры, а также графический вывод, отображаются в окне просмотра в виде блока, причём каждый блок является отдельным объектом. В иерархии каждый блок озаглавливается соответствующим именем процедуры, перед которым устанавливается значок блока. Этому значку предшествует небольшой четырёхугольник, в котором сначала указывается знак минус. Внутри каждого блока сначала Вы видите заголовок и примечания. Далее идёт перечисление элементов блока, которым тоже предшествуют соответствующие символы. Благодаря такой конструкции иерархии объектов, вы можете производить поиск необходимых элементов, переставлять их местами, копировать, удалять и т.д.
Поиск в окне просмотра
-
Чтобы увидеть в области вывода необходимый объект или элемент, Вам не нужно прокручивать всё окно просмотра. Чтобы попасть в нужное место, щёлкните на соответствующем символе в иерархии.
Удаление в окне просмотра
-
Чтобы удалить некоторые элементы результатов расчётов, щёлкните на соответствующем символе и выберите в меню Edit (Правка) Delete (Удалить)
Вы можете также просто нажать на клавиатуре клавишу <Delete>.
Скрытый режим
Вместо того, чтобы удалять части блоков, Вы можете на некоторое время их "скрыть". Они становятся невидимыми на экране и при печати.
-
Чтобы скрыть части результатов, щёлкните дважды на соответствующем символе в иерархии или выделите нужный элемент одним щелчком с последующим выбором меню View (Вид) Hide (Скрыть)
-
Если Вы вновь хотите сделать элемент видимым, повторно щёлкните дважды на значке или выделите его одним щелчком с последующим выбором меню View (Вид) Show (Показать)
-
Если же Вы хотите скрыть целый блок, содержащий весь вывод отдельной процедуры, щёлкните на маленьком квадратике слева от значка блока. При этом знак минус в квадратике превратится в знак плюс и данная процедура вместе со всем её содержимым исчезнет.
-
Вы можете также выделить значок блока и произвести следующий выбор меню View (Вид) Collapse (Свернуть)
-
Блок можно вновь сделать видимым при помощи повторного щелчка на квадратике; при этом знак плюс опять будет заменён знаком минус. Можно также щелчком выделить значок блока и выбрать в меню View (Вид) Expand (Развернуть)
Перестановка в окне просмотра
-
Если Вы хотите переместить некоторую часть результатов на другое место, выделите соответствующий значок (если необходимо, то значок блока) и удерживая нажатой левую кнопку мыши, переместите его к тому элементу, после которого Вы бы хотели расположить данные результаты или блок.
-
Альтернативная возможность перемещения элементов заключается в выделении значка, соответствующего необходимой части информации с последующим выбором меню Edit (Правка) Cut (Вырезать)
-
Затем выделите значок, позади которого вы бы хотели вставить вырезанный элемент и выберите в меню Edit (Правка) Paste After (Вставить после)
Копирование в окне просмотра
-
Если вы хотите скопировать какую-либо часть информации в другое место (при этом сохранив её на прежнем месте), щёлкните на значке, соответствующем нужному элементу или блоку, не отпуская кнопку мыши, нажмите на клавиатуре клавишу <Ctrl> и перетащите значок к тому элементу, после которого должен быть вставлен копируемый элемент.
-
Вы можете также щёлкнуть на значке копируемого элемента и выбрать в меню следующие опции: Edit (Правка) Сору (Копировать)
-
Затем щёлкните на значке элемента, после которого должен быть вставлен копируемый элемент и выберите в меню Edit (Правка) Paste After (Вставить после)
Вывод примечаний
При чтении результатов расчётов очень помогают примечания. В них содержится информация о соответствующем файле и общих установках программы. По умолча--ию эти примечания сначала являются скрытыми, но их можно сделать видимыми, если, к примеру, дважды щёлкнуть на значке примечания (Notes). В качестве приме-га отобразим примечание для процедуры подсчёта частоты.
Notes (Примечания)
Output Created (Расчёт произведен) | 18-ОСТ-2001 16:26:51 | |
Comments (Комментарии) | ||
input (Ввод) | Data (Данные) | E:\WAHL.SAV |
Filter (Фильтр) | <nоnе> (отсутствует) | |
Weight (Вес) | <nоnе> (отсутствует) | |
Split File (Разделение файла) | <nоnе> (отсутствует) | |
N of Rows in Working Data File (Количество строк в рабочем файле) | 30 | |
Missing Value Handling (Обработка отсутствующих значений) | Definition of Missing (Определение отсутствующих значений) | User-defined missing values are treated as missing. (Отсутствующие значения указанные пользователем, обрабатываются как отсутствующие) |
Cases Used (Использованные случаи) | Statistics are based on all cases with valid data. (Статистики базируются на всех случаях с допустимыми переменными) | |
Syntax (Синтаксис) | FREQUENCIES VARIABLES=partei /ORDER= ANALYSIS . (Частотная переменная=раг1е1/Команда = анализ) | |
Resources (Ресурсы) | Total Values Allowed (Данные, пригодные для расчёта) | 18724 |
Elapsed Time (Продолжительность расчёта) | 0:00:00,22 | |
Изменение размера и типа шрифта иерархического списка
-
Чтобы изменить размер знаков и тип шрифта в иерархическом списке, выберите в меню View (Вид) Outline Size (Размер знаков) и соответственно View (Вид) Outline Font (Шрифт знаков)
У Вас появится возможность выбора среди трёх размеров (Small (Мелкий), Medium (Средний), Large (Крупный)) и большого количества шрифтов.
35.gif
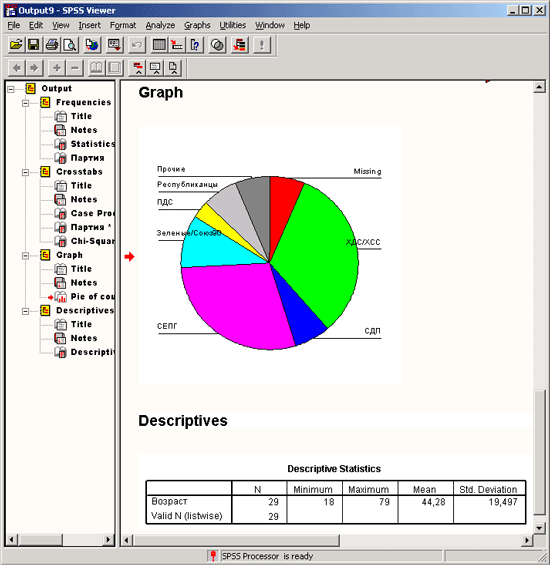
4.6 Редактирование таблиц
4.6 Редактирование таблиц
В главе 4.5 мы уже рассматривали, как при помощи иерархического списка в окне просмотра можно управлять выводом элементов результатов расчётов. Теперь мы расскажем о возможностях, которые существуют для редактирования элементов результатов. Так как приёмы редактирования графиков уже рассматривались в разделе 4.4, здесь мы остановимся только на редактировании таблиц.
Многие элементы результатов расчетов представлены в виде так называемых мобильных таблиц. Это новая форма таблиц, которая позволяет менять местами строки, столбцы и слои таким образом, чтобы результаты можно было бы оценить с разных точек зрения. Хорошим примером их применения могут послужить, прежде всего, таблицы сопряженности.
-
Откройте файл zahn.sav и выберите в меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
Переменной рu (периодичность чистки) присвойте статус строчной переменной, а переменной g (пол) статус столбцовой переменной. Через выключатель Cells... (Ячейки) наряду с установленным по умолчанию выводом наблюдаемых частот, организуйте вывод процентных показателей по столбцам (опция Column (Столбец)). Эти действия приведут к отображению следующей перекрёстной таблицы (предшествующая таблица "Case Processing Summary" (Итоги для обработанных наблюдений) была пропущена).
Putzhaeufigkeit * Geschlecht Crosstabulation (Перекрёстная таблица Периодичность чистки * Пол)
Geschlecht (Пол) | Total (Сумма) | ||||
weiblich (женский) | mannlich (мужской) | ||||
Putzha-eufigkeit (Перио-дичность чистки) | < 1-mal taeglich (< 1 раза в день) | Count (Количество) | 14 | 4 | 18 |
% within Geschlecht (% для пола) | 2,0% | ,9% | 1,6% | ||
1-mal taeglich (1 раз в день) | Count (Количество) | 177 | 56 | 233 | |
% within Geschlecht (% для пола) | 25,1% | 13,2% | 20,6% | ||
2-mal taeglich (2 раза в день) | Count (Количество) | 490 | 342 | 832 | |
% within Geschlecht (% для пола) | 69,4% | 80,7% | 73,6% | ||
> 2-mal taeglich (> 2 раз в день) | Count (Количество) | 25 | 22 | 47 | |
% within Geschlecht (% для пола) | 3,5% | 5,2% | 4,2% | ||
Total (Сумма) | Count (Количество) | 706 | 424 | 1130 | |
% within Geschlecht (% для пола) | 100,0% | 100,0% | 100,0% | ||
-
Если Вы хотите узнать о возможностях редактирования, которые предоставляет техника мобильных таблиц, щёлкните дважды на этой таблице. В результате будет активирован редактор мобильных таблиц.
4.6.1 Редактор мобильных таблиц
4.6.1 Редактор мобильных таблиц
Об активировании редактора мобильных таблиц Вы узнаете по изменившейся панели меню.
-
Выберите в меню Pivot (Мобильная таблица) Pivoting Trays (Поля вращения)
Откроется окно Pivoting Trays (Поля вращения) (см. рис. 4.20), содержащее три панели, обозначенные как Layer (Слой), Row (Строка) и Column (Столбец). На панели строк расположены два значка, а на панели столбцов один значок. Для того, чтобы получить информацию о назначении этих значков, пройдитесь по ним указателем, ненадолго задерживая его над значками — будут выведены метки соответствующих переменных.
Два значка на панели строк соответствуют переменной ри (периодичности чистки) и "статистике" соответственно, причём под статистикой в данном случае понимаются процентные показатели по столбцам, затребованные нами при построении таблицы сопряженности. Значок на панели столбцов соответствует переменной g (полу). На панели слоев значки отсутствуют; они бы там были, если бы Вы в диалоговом окне Crosstabs... (Таблицы сопряженности) ввели одну или несколько переменных слоя.
Рис. 4.19: Редактор мобильных таблиц
Рис. 4.20: Окно Pivoting Trays
-
При помощи этих значков Вы можете изменить структуру таблицы. Щёлкните, например, на значке Statistics панели строк и перетащите его мышью за значок, находящийся на панели столбцов. После этого процентные показатели будут отображаться в колонках таблицы.
Putzhaeufigkeit * Geschlecht Crosstabulation (Таблица сопряженности Периодичность чистки * Пол)
Geschlecht (Пол)
| Total(Сумма) | ||||||
rnannlicn (мужской) | weiblicn (женский) | ||||||
Count (Количе ство) | % within Geschle cht (% для пола) | Count (Количе ство) | % within Geschle cht (% для пола) | Count (Количе ство) | % within Geschle cht (% для пола) | ||
Putzhaeufigkeit (Перио дичность чистки) | < 1-mal taeglich (< 1 раза в день) | 14 | 2,0% | 4 | ,9% | 18 | 1,6% |
1-mal taeglich (1 раз в день) | 177 | 25,1% | 56 | 13,2% | 233 | 20,6% | |
2-mal taeglich (2 раза в день) | 490 | 69,4% | 342 | 80,7% | 832 | 73,6% | |
> 2-mal taeglich | 25 | 3,5% | 22 | 5,2% | 47 | 4,2% | |
Total (Сумма) | 706 | 100,0% | 424 | 100,0% | 1130 | 100,0% | |
-
Теперь щёлкните на значке Geschlecht (пол), находящемся на панели столбцов, и разместите его позади значка, оставшегося на панели строк. Теперь обе переменные расположены по строкам. Испытайте самостоятельно и другие возможности изменения структуры таблицы.
-
Если у Вас появилось желание выйти из редактора мобильных таблиц, щёлкните в какой-либо точке за пределами выделенной таблицы.
-
Чтобы увидеть пример таблицы сопряженности с использованием переменных слоя, в диалоговом окне Crosstabs (Таблицы сопряженности) дополнительно к произведенным установкам поместите переменную s (образование) в поле переменных слоя. После этого построенная ранее таблица сопряженности будет разбита ещё и по категориям этой переменной. Это разбиение можно наблюдать в нижеследующей таблице.
Putzhaeufigkeit * Geschlecht * Schulbildung Crosstabulation (Таблица сопряженности Периодичность чистки * Пол * Образование)
Schulbildung (Обрэзование) | Geschleсht(Пол) | Total (Сумма) | ||||
mannlich (мужской) | weiblich (женский) | |||||
Sonderschule Специальное) | Putzha- euflgkeit (Перио- дичность чистки) | < 1-mal taeglich (< 1 раза в цень) | Count (Количество | 1 |
| 1 |
% within Geschlecht (% для пола) | 100,0% |
| 100,0% | |||
Total (Сумма) | Count (Количество | 1 |
| 1 | ||
% within Geschlecht (% для пола) | 100,0% |
| 100,0% | |||
Hauptschule Начальная школа)
| Putzha- euflgkeit (Перио- дичность чистки) | < 1-mal taeglich (< 1 раза в цень) | Count (Количество | 8 | 2 | 10 |
% within Geschlecht (% для пола) | 5,6% | 3,0% | 4,7% | |||
1-mal taeglich | Count (Количество | 71 | 2С | 91 | ||
(1 раз в день) | % within Geschlecht (% для пола) | 49,3% | 29,9% | 43,1% | ||
2-mal taeglich (2 раза в день) | Count (Количество | 65 | 42 | 107 | ||
% within Geschlecht (% для попа) | 45,1% | 62,7% | 50,7% | |||
> 2-mal taeglich > 2 раз в день) | Count (Количество |
| 2 | т | ||
% within Geschlecht (% для пола) |
| 4,5% | 1,4% | |||
Total (Сумма) | Count (Количество | 144 | 67 | 211 | ||
% within Geschlecht (% для попа)_ | 100,0% | 100,0% | 100,0% | |||
mittlere Reife Незаконченное среднее)
| Putzha- eufigkeit Перио- дичность | < 1-mal taeglich | Count (Количество | 6 | 2 | 8 |
(< 1 раза в день | % within Geschlecht (% для пола) | 1,6% | ,8% | 1,2% | ||
1-mal taeglich 1 раза в день | Count (Количество | 89 | 31 | 120 | ||
% within Geschlecht (% для пола) | 23.1% | 11,9% | 18,6% | |||
2-mal taeglich | Count (Количество | 284 | 216 | 500 | ||
(2 раза в день) | % within Geschlecht (% для пола) | 73,6% | 83,1% | 77,4% | ||
> 2-mal taeglich | Count (Количество | 7 | 11 | 18 | ||
'> 2 раз в день) | % within Geschlecht (% для пола) | 1,8% | 4,2% | 2,8% | ||
Total (Сумма) | Count (Количество | 386 | 260 | 646 | ||
% within Geschlecht (% для пола) | 100,0% | 100,0% | 100,0% | |||
Abitur Аттестат зрелости) | Putzha- eufigkeit (Перио- дичность чистки) | 1-mal taeglich 1 раз в день) | Count (Количество | 9 | 1 | 10 |
% within Geschlecht (% для пола) | 12,7% | 10,0% | 12,3% | |||
2-mal taeglich (2 раза в день) | Count (Количество | 56 | 8 | 64 | ||
% within Geschlecht (% для пола) | 78,9% | 80,0% | 79,0% | |||
> 2-mal taeglich > 2 раз в день) | Count (Количество | 6 | 1 | 7 | ||
% within Geschlecht (% для пола) | 8,5% | 10,0% | 8,6% | |||
Total (Сумма) | Count (Количество | 71 | 10 | 81 | ||
% within Geschlecht (% для пола) | 100,0% | 100,0% | 100,0% | |||
Hochschule Высшее) | Putzha- eufigkeit (Перио- дичность чистки)
| 1-mal taeglich '1 раз в день) | Count (Количество | 7 | 4 | 11 |
% within Geschlecht (% для пола) | 6,7% | 4,6% | 5,8% | |||
2-mal taeglich '2 раза в день) | Count (Количество | 85 | 76 | 161 | ||
% within Geschlecht (% для пола) | 81,7% | 87,4% | 84,3% | |||
> 2-mal taeglich > 2 раз в день) | Count (Количество | 12 | 7 | 19 | ||
% within Geschlecht (% для пола) | 11,5% | 8,0% | 9,9% | |||
Total (Сумма) | Count (Количество | 104 | 87 | 191 | ||
% within Geschlecht (% для пола) | 100,0% | 100,0% | 100,0% | |||
-
Дважды щёлкните на таблице и выберите в меню Pivot (Мобильная таблица) Pivoting Trays (Поля вращения) На панели строк появился ещё один значок.
-
Если Вы пройдётесь указателем мыши по этим значкам, то заметите, что первый из трёх значков соответствует переменной Schulbildung (образование). Щёлкните на этом значке и, не отпуская кнопку мыши, перетащите его на панель переменных слоя.
Теперь в редакторе мобильных таблиц будет представлена таблица сопряженности между периодичностью чистки зубов и полом для первой категории образования Sonderschule (специальное).
-
Закройте окно Pivoting Trays (Поля вращения)
-
Выберите в меню Pivot (Мобильная таблица) Go to Layer... (Перейти к слою)
Откроется диалоговое окно Go to Layer Category (Переход к категории слоя) (см. рис. 4.21).
Рис. 4.21: Диалоговое окно Go to Layer Category (Переход к категории слоя)
-
Выделите категорию "Hauptschule" (Начальная школа), теперь в окне просмотра будет отображена таблица только для этой категории.
Putzhaeufigkeit * Geschlecht * Schulbildung Crosstabulation (Таблица сопряженности Периодичность чистки * Пол * Образование)
Schulbildung: He suptschule (Образ ование: Начальная школа) | |||||
Geschle:ht (Пол) | Total (Сумма) | ||||
nannlich (мужской) | weiblich (женский) | ||||
Putzhaeufigkeit (Периодичность чистки) | < 1-mal taeglich (< 1 раза в день) | Count (Количество) | 8 | 2 | 10 |
% within Geschlecht (% для пола) | 5,6% | 3,0% | 4,7% | ||
1-mal taeglich (1 раз в день) | Count (Количество) | 71 | 2С | 91 | |
% within Geschlecht (% для пола) | 49,3% | 29,9% | 43,1% | ||
2-mal taeglich (2 раза в день) | Count (Количество) | 65 | 42 | 107 | |
% within Geschlecht (% для пола) | 45,1% | 62,7% | 50,7% | ||
>2-mal taeglich (> 2 раз в день) | Count (Количество) |
| f. | Т | |
% within Geschlecht (% для пола) |
| 4,5% | 1,4% | ||
Total (Сумма) | Count (Количество) | 144 | 67 | 211 | |
% within Geschlecht (% для пола) | 100,0% | 100,0% | 100,0% | ||
Остальные возможности изменения положения строк, столбцов и слоев испытайте, пожалуйста, самостоятельно.
36.gif
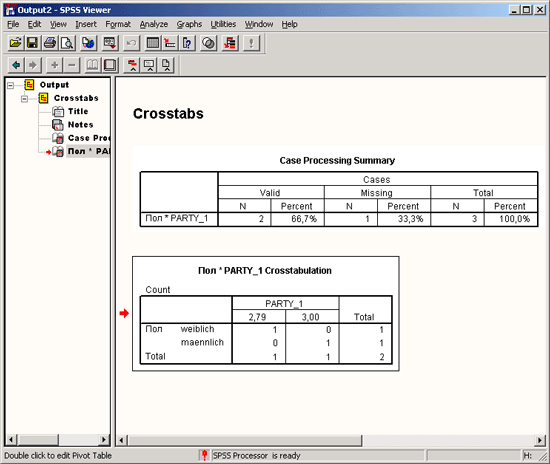
37.gif
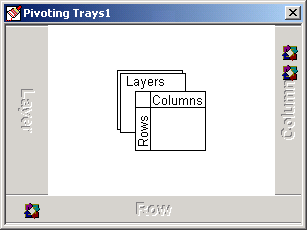
38.gif
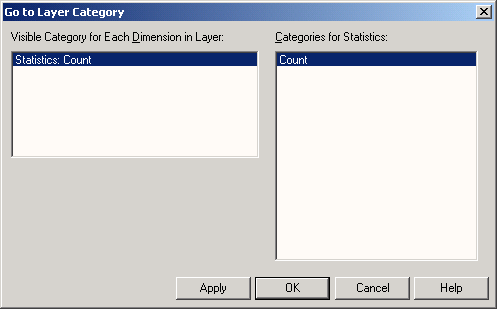
4.6.2 Дополнительные возможности редактирования таблиц
4.6.2 Дополнительные возможности редактирования таблиц
Применение техники мобильных таблиц для изменения структуры таблиц результатов статистических расчетов была представлена в разделе 4.6.1. Однако для изменения внешнего вида таблиц и их содержания, помимо описанной техники, существуют также и следующие возможности:
-
выбор внешнего вида таблицы из библиотеки таблиц
-
изменение свойств таблицы
-
изменение свойств ячеек
-
изменение текста в таблице
-
добавление пояснений
-
добавление сносок
-
ввод названия объекта и дополнительного текста
Рассмотрим самые важные аспекты перечисленных возможностей редактирования таблиц.
Выбор внешнего вида таблицы
В качестве примера таблицы, для которой нужно будет применить редактирование, рассмотрим повторно перекрёстную таблицу между периодичностью чистки и полом.
-
Дважды щёлкните на таблице; это приведёт к активированию редактора мобильных таблиц.
-
Чтобы выбрать другой внешний вид таблицы, выберите в меню Format (Формат) TabelLooks... (Дизайн таблиц) Откроется диалоговое окно TabelLooks (Дизайн таблиц) (см. рис. 4.22).
-
В этом диалоговом окне Вы можете выбрать среди более чем пятидесяти различных заготовок внешнего вида (дизайна) таблиц. Выберите, к примеру, заготовку Avant-gard и покиньте диалоговое окно нажатием ОК.
Рис. 4.22: Диалоговое окно Tabe/Looks (Дизайн таблиц)
Наша таблица теперь будет выглядеть следующим образом.
Putzhaeufigkeit * Geschlecht * Schulbildung Crosstabulation (Таблица сопряженности Периодичность чистки * Пол)
Geschlecht(Пол) | Total (Сумма) | |||||
mannlich (мужской) | weiblich (женский) | |||||
Putzhaeufigkeit (Периодичность чистки) | < 1-mal taeglich < 1 раза в день) | Count (Количество) |
| 14 | 4 | 18 |
% within Geschlecht | (% для пола) | 2,0% | ,9% | 1 ,6% | ||
1-mal taeglich (1 раз в день) | Count (Количество |
| 177 | 56 | 233 | |
% within Geschlecht | (% для пола) | 25,1% | 13,2% | 20,6% | ||
2-mal taeglich (2 раза в день) | Count (Количество) |
| 490 | 342 | 832 | |
% within Geschlecht | (% для пола) | 69,4% | 80,7% | 73,6% | ||
> 2-mal taeglich (> 2 раз в день) | Count (Количество |
| 25 | 22 | 47 | |
% within Geschlech | (% для пола) | 3,5% | 5,2% | 4,2% | ||
Total (Сумма) | Count (Количество) |
| 706 | 424 | 1130 | |
% within Geschlechl | (% для пола) | 100,0% | 100,0% | 100,0% | ||
-
При помощи выключателя Edit Look (Редактировать дизайн) диалогового окна TabelLooks (Дизайн таблиц) Вы можете открыть вспомогательное диалоговое окно Table Properties (Свойства таблицы), в котором можно дополнительно изменить отдельные элементы компоновки таблицы. Отредактированный дизайн Вы можете сохранить при помощи команд Save Look (Сохранить дизайн) и Save as... (Сохранить как).
Изменение свойств таблицы
-
Чтобы изменить свойства таблицы, выберите в меню Format (Формат) Table Properties... (Свойства таблицы) Откроется диалоговое окно Table Properties (Свойства таблицы).
Рис. 4.23: Диалоговое окно Table Properties (Свойства таблицы)
Вы можете по своему вкусу изменить представление некоторых данных, ссылки, форматы ячеек и виды рамок. Для отдельных областей таблицы, таких как индивидуальные ячейки, вы можете также изменить и шрифт.
-
Выделите щелчком одну из таких областей активированной мобильной таблицы и выберите в меню Format (Формат) Font... (Шрифт)
-
Если вы хотите установить одинаковую ширину для всех ячеек таблицы, то это можно сделать посредством выбора меню Format (Формат) Set Data Cell Widths... (Ширина ячеек данных)
Изменение свойств ячеек
Наряду со свойствами всей таблицы можно также изменять и свойства отдельных ячеек.
-
Выделите щелчком в активированной мобильной таблице необходимую ячейку и выберите в меню Format (Формат) Cell Properties... (Свойства ячейки) Откроется диалоговое окно Cell Properties (Свойства ячейки).
Рис. 4.24: Диалоговое окно Cell Properties (Свойства ячейки)
При помощи регистрационных карт, имеющихся в этом диалоговом окне, Вы можете выбрать необходимый формат чисел, выравнивание в ячейке, поля и оттенок. В поле образца (Sample) всегда будет приводиться образец надписи с учетом соответствующих установок.
Изменение текста в таблице
-
Создадим сначала частотную таблицу. Если файл zahn.sav уже открыт, выберите в меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты)
-
В диалоговом окне Frequencies (Частоты) поместите переменную s (образование) в поле тестируемых переменных. Вы получите соответствующую частотную таблицу.
-
Двойным щелчком на таблице активируйте редактор мобильных таблиц и затем тоже дважды щёлкните на ячейке с текстом "Frequency" (Частота). В таком режиме можно вместо имеющегося текста указать в данной ячейке другой текст, к примеру, "Count" (Количество); после ввода текста нажмите клавишу Enter. Таким же образом можно поступить и с другими текстами, имеющимися в таблице.
-
Если Вы произвели все необходимые замены, покиньте редактор мобильных таблиц щелчком на области за пределами выделенной таблицы. Теперь таблица будет выглядеть следующим образом.
Schulbildung (Образование)
Count (Количество) | Percent (Процент) | Valid Percent (Действи- тельный процент) | Cumulative Percent (Совокупный процент) | ||
Valid (Действи- тельные значения) | Sonderschule (Специальное) | 1 | ,1 | ,1 | ,1 |
Hauptschule (Начальная школа) | 211 | 18,7 | 18,7 | 18,8 | |
mittlere Reife (Незаконченное среднее) | 646 | 57,2 | 57,2 | 75,9 | |
Abitur (Аттестат зрелости) | 81 | 7,2 | 7,2 | 83,1 | |
Hochschule (Высшее) | 191 | 16,9 | 16,9 | 100 | |
Total (Сумма) | 1130 | 100,0 | 100,0 |
| |
Добавление пояснений
-
Чтобы под таблицей разместить пояснение, активируйте двойным щелчком режим редактирования таблиц и выберите в меню Insert (Вставка) Caption (Подпись)
-
Под таблицей появится рамка с текстом Table Caption (Подпись таблицы) внутри. Щёлкните дважды на этом тексте и наберите, к примеру, "Данные 1994 года".
Добавление сносок
-
Везде в таблице можно добавлять сноски. Нужную таблицу двойным щелчком перенесите в редактор мобильных таблиц и выделите щелчком любой текст в таблице. Рассмотрим, например, созданную нами частотную таблицу и текст "Hochschule" (Высшее).
-
После выделения текста выберите в меню Insert (Вставка) Footnote (Сноска)
-
В появившейся рамке дважды щёлкните на тексте "Footnote" (Сноска) и наберите вместо него необходимый текст, для данного случая, к примеру, "Включая специальные высшие учебные заведения".
-
Если Вы посмотрите на сноску, то заметите, что перед ней в соответствии с установками появился маркер в виде буквы уменьшенного размера (для первой сноски это буква а). Если вы хотите изменить маркер, выделите щелчком сноску и выберите в меню Format (Формат) Footnote Marker... (Маркер сноски)
-
Активируйте опцию Special marker (Специальный маркер) и введите цифру 1. Изменённая частотная таблица теперь выглядит следующим образом.
Schulbildung (Образование)
|
| Count (Количество) | Percent (Процент) | Valid Percent (Действи- тельный процент) | Cumulative Percent (Совокупный процент) |
Valid (Действи- | Sonderschule (Специальное) | 1 | ,1 | ,1 | ,1 |
тельные значения) | Hauptschule (Начальная школа) | 211 | 18,7 | 18,7 | 18,8 |
| mittlere Reife (Незаконченное среднее) | 646 | 57,2 | 57,2 | 75,9 |
| Abitur (Аттестат зрелости) | 81 | 7,2 | 7,2 | 83,1 |
| Hochschule1 (Высшее) | 191 | 16,9 | 16,9 | 100,0 |
| Total (Сумма) | 1130 | 100,0 | 100,0 |
|
Данные 1994 года
1. Включая специальные высшие учебные заведения
Ввод названия объекта и дополнительного текста
-
Чтобы добавить название или какой-либо текст, выделите щелчком соответствующий объект (заголовок, таблицу, график и т.д.), после которого вы хотите добавить подзаголовок или текст. Затем выберите в меню Insert (Вставка) New Title (Новое название) и соответственно Insert (Вставка) New Text (Новый текст)
-
После двойного щелчка на новом объекте Вы можете ввести необходимое название или текст.
-
Если необходимый текст находится в текстовом файле, то выберите в меню Insert (Вставка) Text File... (Текстовый файл) И в появившемся диалоговом окне укажите имя файла.
39.gif
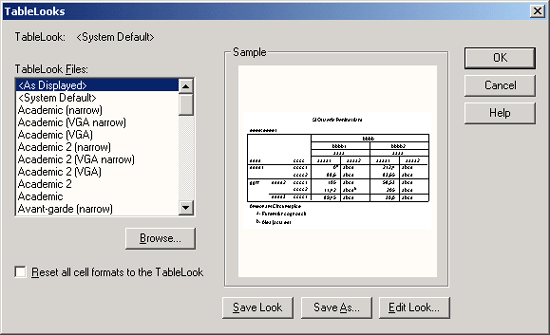
40.gif
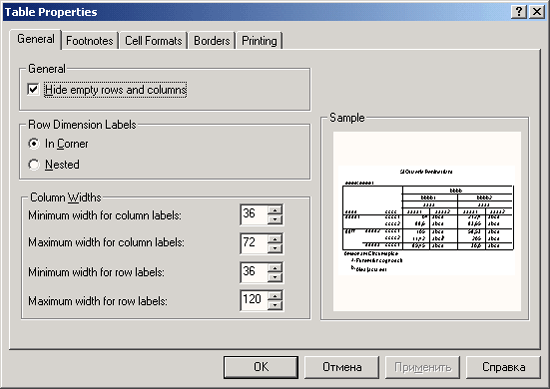
41.gif
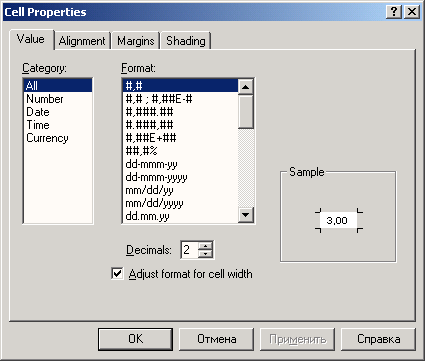
4.6.3 Операции с таблицами большого размера
4.6.3 Операции с таблицами большого размера
Очень длинные таблицы полностью не помещаются в окне просмотра. Визуально это отмечается при помощи маркировки красного цвета в месте разрыва. В этом случае щёлкните дважды на таблице и при нажатой левой кнопке мыши Вы сможете переместить этот маркер вниз.
4.6.4 Окно просмотра текста
4.6.4 Окно просмотра текста
Если Вы хотите работать не с интерактивными мобильными таблицами, а с простой текстовой выдачей пропорциональным (системным) шрифтом, то используйте для этого окно просмотра текста.
-
Режим просмотра текста можно установить при помощи выбора меню Edit (Правка) Options... (Параметры) с последующим активированном на регистрационной карте General (Общие) опции вывода информации в виде окна просмотра текста (DraftViewer). Чтобы установки вступили в силу необходимо перезапустить программу.
-
Различные возможности редактирования элементов при данном режиме работы окна просмотра находятся на регистрационной карте DraftViewer (Окно текстового режима) диалогового окна Options (Параметры). Данные, находящиеся в окне текстового режима, будут сохранены в формате RTF (Rich Text).
-
Дополнительную информацию о текстовом режиме просмотра результатов Вы можете получить после выбора меню Help (Помощь) Topics (Темы)
-
В окне Help: SPSS for Windows (Справочная система: SPSS для Windows) выберите закладку Index (Указатель), в поисковом поле наберите "Draft Viewer" и дважды щёлкните на нужной позиции.
4.7 Редактор синтаксиса
4.7 Редактор синтаксиса
Редактор синтаксиса представляет собой текстовое окно, применяемое для набора и запуска на исполнение команд SPSS. Вы можете вводить команды непосредственно в окне набора или просто переносить установки диалоговых окон при помощи выключателя Paste (Вставить), находящегося в самих диалоговых окнах. Этот перенос возможен благодаря тому, что все диалоговые окна написаны на командном языке SPSS. С целью реализации дополнительных возможностей или каких-либо индивидуальных подходов к обработке данных, команды, помещённые в редактор синтаксиса, можно изменять.
-
Откройте сначала файл wahl.sav.
-
Чтобы открыть редактор синтаксиса, выберите в меню File (Файл) New (Новый) Syntax (Синтаксис)
-
Наберите следующую команду
FREQUENCIES VARIABLES = sex alter partei.
Редактор синтаксиса будет выглядеть так, как на рисунке 4.25.
Рис. 4.25: Редактор синтаксиса
-
Запустите команду SPSS на исполнение путём нажатия кнопки со значком Run . Current (Выполнить текущую команду).

SPSS перейдёт в окно просмотра результатов. В окне просмотра будет отображены распределения частот переменных sex, alter и partei.
Для выполнения команд SPSS при помощи редактора синтаксиса, поступайте следующим образом:
-
Выделите щелчком и перетаскиванием курсора команды, которые Вы хотели бы выполнить.
-
Если вы хотите выполнить одну команду, расположите курсор в любом месте этой команды.
-
Если Вы желаете выполнить все команды, находящиеся в редакторе, выберите в меню Edit (Правка) Select All (Выделить всё) В редакторе будут выделены все команды.
-
Затем для выполнения команд щёлкните на кнопке Run Current (Выполнить текущую команду) редактора синтаксиса или нажмите одновременно клавиши <Ctrl> <R>.
Перенос синтаксиса команд из диалоговых окон
Установки диалоговых окон можно переносить в редактор синтаксиса при помощи переключателя Paste (Вставить). Рассмотрим пример:
-
Выберите в меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты)
-
При необходимости для устранения всех предыдущих установок щёлкните на выключателе Reset (Сброс).
-
Перенесите переменную alter (возраст) в список целевых переменных.
-
Щёлкните на переключателе Statistics (Статистики) и проставьте флажки активации опций Mean (Среднее значение), Minimum (Минимум) и Maximum (Максимум). Подтвердите нажатием Continue (Далее).
-
В главном диалоговом окне деактивируйте опцию Display frequency tables (Показать частотные таблицы).
-
Теперь щёлкните на Paste (Вставить).
Установки диалогового окна будут размещены в редакторе синтаксиса.
Рис. 4.26: Командный язык SPSS
Сохранение файла синтаксиса
Для сохранения файла синтаксиса необходимо выполнить следующие шаги:
-
Активируйте редактор синтаксиса, в котором содержатся команды, предназначенные для сохранения.
-
Выберите в меню File (Файл) Save (Сохранить)
Откроется диалоговое окно Save as... (Сохранить как). В соответствии с установками программа SPSS прибавляет к своим синтаксическим файлам расширение .sps.
-
Введите название сохраняемого файла и подтвердите нажатием кнопки Save (Сохранить).
Можно также щёлкнуть на значке сохранения Save File (Сохранить файл). 
Больше подробностей о работе с синтаксисом программы вы узнаете в главе 26.
42.gif
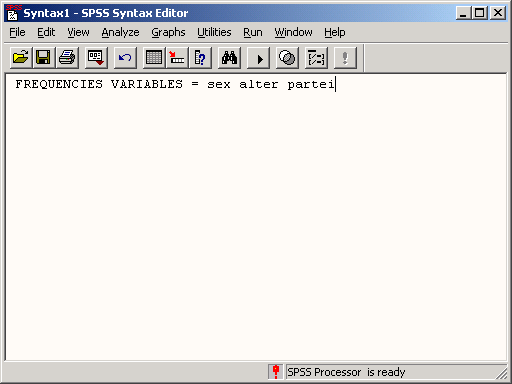
44.gif
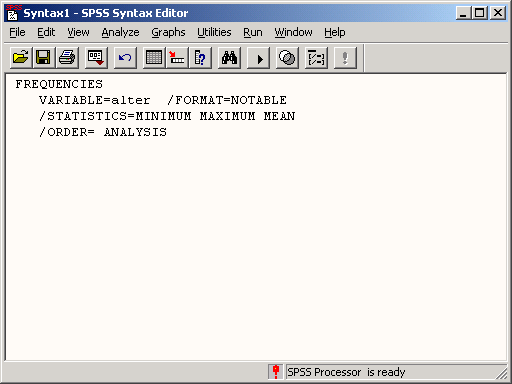
4.8 Информация о файле
4.8 Информация о файле
Для любого файла SPSS Вы можете получить следующую информацию:
-
список переменных с их описанием,
-
полную информацию обо всех переменных и
-
перечень наблюдений.
-
Откройте файл wahl.sav.
-
Если вы хотите просмотреть информацию о значениях переменных, их формате и метках, выберите в меню Utilities (Дополнительные возможности) Variables... (Переменные)
-
Если в появившемся диалоговом окне Вы щёлкните, к примеру, на переменной sex (пол), то увидите информацию, отображаемую на рисунке 4.27.
-
Рис. 4.27: Диалоговое окно Variables (Переменные)
В информационном окне выводится имя переменной, значения и метки переменной, тип переменной, а также указывается количество пропущенных значений. Из диалогового окна Variables (Переменные) можно сразу перейти к рассматриваемой переменной в окно данных.
-
Щёлкните для этого на выключателе Go to (Перейти к).
Окно данных прокручивается горизонтально таким образом, что переменная, отмеченная нами в диалоговом окне Variables (Переменные), оказывается в окне данных на первой позиции. Выключатель Paste (Вставить) копирует имена всех выделенных переменных в редактор синтаксиса.
Некоторую информацию о переменной можно также получить и в любой момент, находясь в диалоговом окне какой-либо статистической процедуры. Для изучения этой операции рассмотрим следующий пример. Допустим, Вы исследуете частотное распределение переменной partei (партия).
-
В диалоговом окне Frequencies (Частоты) перенесите переменную partei (партия) в поле целевых переменных.
Теперь Вам захотелось, не покидая диалогового окна, вскользь взглянуть на значения этой переменной.
-
Выделите её так же, как Вы выделяете и другие переменные в диалоговых окнах и нажмите правую кнопку мыши.
-
В появившемся меню выберите опцию Variable Information (Информация о переменной).
Откроется информационное окно переменной изображённое на рисунке 4.28. В этом окне также приводится имя переменной, тип статистической шкалы, к которой она относится и метки значений.
-
Если Вы щёлкните на стрелке, указывающей вниз, то увидите список всех значений и их меток.
Рис. 4.28: Информационное окно переменной
Чтобы закрыть информационное окно, просто щёлкните на любой точке за его пределами.
-
Если же Вы хотите получить полную информацию обо всех переменных текущего (рабочего) файла, выберите в меню Utilities (Дополнительные возможности) File Info (Информация о файле)
В окне просмотра появится следующая информация по файлу wahl.sav:
List of variables on the working file (Список переменных рабочего файла)
Name (Имя) Position (Позиция)
FRAGEBNR Fragebogen-Nr. (Номер анкеты) 1
Measurement Level: Nominal (Шкала: номинальная)
Column Width: Unknown (Ширина столбцов: неизвестна)
Alignment: Left (Выравнивание: влево)
Print Format: AS (Формат печати: А5)
Write Format: AS (Формат записи: AS)
SEX Geschlecht (Пол) 2
Measurement Level: Nominal (Шкала: номинальная)
Column Width: Unknown (Ширина столбцов: неизвестна)
Alignment: Right (Выравнивание: вправо)
Print Format: Fl (Формат печати: Fl)
Write Format: Fl (Формат записи: Fl)
Missing Values: 0 (Отсутствующие значения: 0)
Value (Значение) Label (Метка)
0 М keine Angabe (Данные отсутствуют)
1 weiblich (Женский)
2 maennlich (Мужской)
ALTER Lebensalter (Возраст) 3
Measurement Level: Scale (Шкала: метрическая)
Column Width: Unknown (Ширина столбцов: неизвестна)
Alignment: Right (Выравнивание: вправо)
Print Format: F2 (Формат печати: F2)
Write Format: F8.2 (Формат записи: F8.2)
Missing Values: 0 (Отсутствующие значения: 0)
Value (Значение) Label (Метка)
0 М keine Angabe (Данные отсутствуют)
PARTEI Partei (Партия) 4
Measurement Level: Nominal (Шкала: номинальная)
Column Width: Unknown (Ширина столбцов: неизвестна)
* Alignment: Right (Выравнивание: вправо)
Print Format: Fl (Формат печати: Fl)
Write Format: F8.2 (Формат записи: F8.2)
Missing Values: 0 (Отсутствующие значения: 0)
Value (Значение) Label (Метка)
0 М keine Angabe (Данные отсутствуют)
1 CDU/CSU
2 FDP
3 SPD
4 Gruene/Buendnis 90 (Зелёные/Союз 90)
5 PDS
6 Republikaner (Республиканцы)
7 Sonstige (Прочие)
-
Если вы хотите получить такую информацию о файле, который не является в данный момент рабочим, то выберите в меню File (Файл) Display Data Info... (Показать информацию о файле) Откроется соответствующее диалоговое окно (см. рис. 4.29).
Рис. 4.29: Диалоговое окно Display Data Info (Показат< информацию о файле)
-
Выделите необходимый файл, к примеру, wahl.sav и подтвердите выбор нажатием кнопки Open (Открыть).
Информация о выбранном файле появится в окне просмотра.
-
Если же у Вас появится желание проверить фактическое содержание некоторого файла, к примеру, список наблюдений, то выберите в меню Analyze (Анализ) Reports (Отчёты) Case Summaries... (Сводка по наблюдениям)
Вы увидите диалоговое окно Summarize Cases (Формирование итогов по наблюдениям) (см. рис. 4.30).
Рис. 4.30: Диалоговое окно Summarize Cases (Формирование сводки по наблюдениям)
Переменные файла будут показаны в списке исходных переменных. Здесь Вы можете выделить одну или несколько переменных, наблюдения для которой должны быть помещены в сводку. Опции диалогового окна говорят сами за себя.
-
В качестве упражнения перенесите в список выбираемых переменных переменную partei (партия) и активируйте опцию Show case numbers (Отобразить номера наблюдений).
-
Подтвердите установки нажатием ОК. В окне просмотра будут отображены значения переменной partei (партия) для всех наблюдений.
46.gif
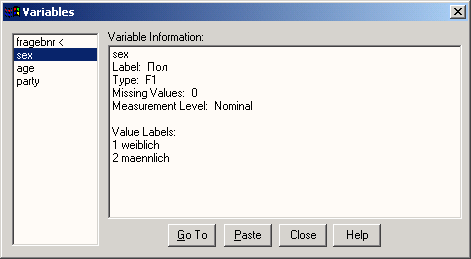
47.gif
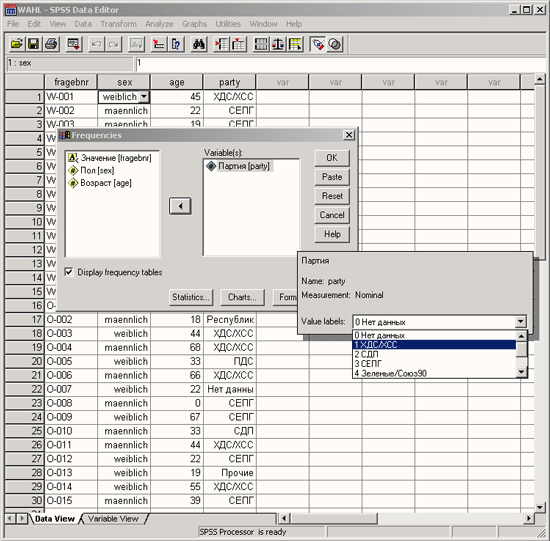
48.gif
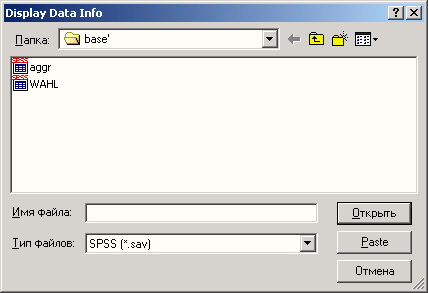
49.gif
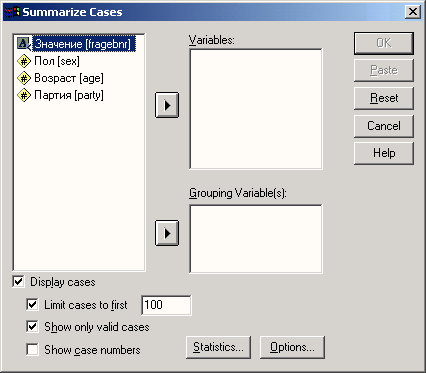
4.9 Справочная система
4.9 Справочная система
Справку в SPSS можно вызвать несколькими способами:
-
Нажать в любой момент работы функциональную клавишу <F1>. Откроется диалоговое окно Help: SPSS for Windows (Справочная система: SPSS для Windows).
-
Выбрать в главном меню опцию Help (Справка).
-
Находясь в любом диалоговом окне, нажать переключатель с названием Help (Справка) и Вы получите справку по текущей теме.
Изучим вызов справки при помощи нескольких примеров:
-
Выберите в меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты)
-
Щёлкните на переключателе Help (Справка). Откроется диалоговое окно справки SPSS (см. рис. 4.31).
Рис. 4.31: Справка SPSS
Рассмотрим следующий пример:
-
Выберите в меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты)
-
Перенесите переменную partei (партия) в поле целевых переменных. Щёлкните на переключателе Paste (Вставить). Установки диалогового окна будут перенесены в редактор синтаксиса.
-
В редакторе синтаксиса щёлкните в панели инструментов на кнопке со значком Syntax-Help (Справка по теме синтаксиса)

В окне справки появится синтаксис соответств. команды SPSS (см. рис. 4.32).
Если Вы щёлкните на переключателе Index (Указатель), то в окне справки будет отображён список тем SPSS (см. рис. 4.33).
Чтобы, находясь в справочной системе, параллельно иметь возможность работать в редакторе синтаксиса Вы можете уменьшить окно справки до любого необходимого Вам, размера и расположить его в удобном для Вас месте. Рассмотрим ещё один пример:
-
В редакторе данных в списке меню шёлкните на опции Help (Справка). Откроется вспомогательное меню.
-
Щёлкните на позиции Topics (Темы). Появится перечень тем SPSS. В списке тем SPSS присутствуют и определения статистических терминов.
-
В списке тем выделите строку 25th percentile (25-й процентиль) и щёлкните на кнопке Display (Показать). Вы увидите информацию, отображаемую на рисунке 4.34.
-
Любую информацию, находящуюся в диалоговом окне справки, можно напечатать с помощью принтера. Для этого выберите команду Print (Печать).
Рис. 4.32: Окно справки синтаксиса SPSS
Рис. 4.33: Список тем SPSS
Рис. 4.34: Информация о значениях процентиля
50.gif
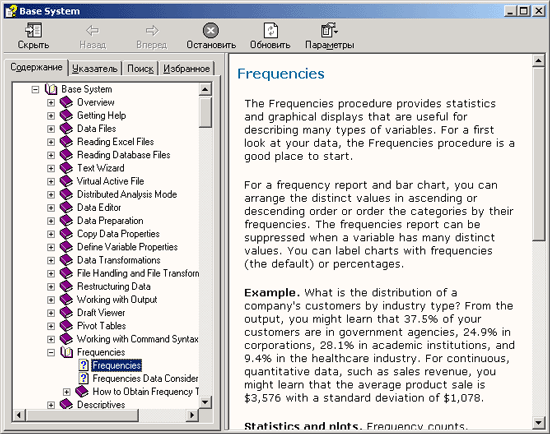
52.gif
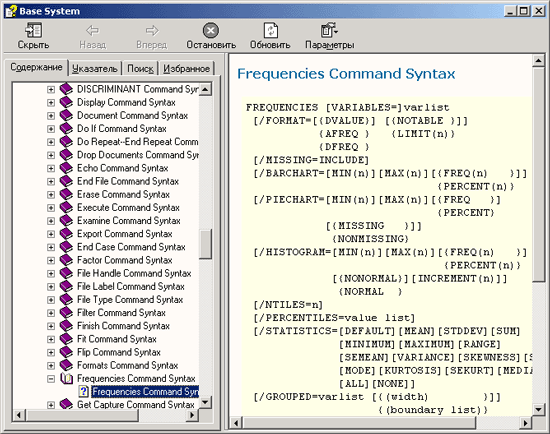
53.gif
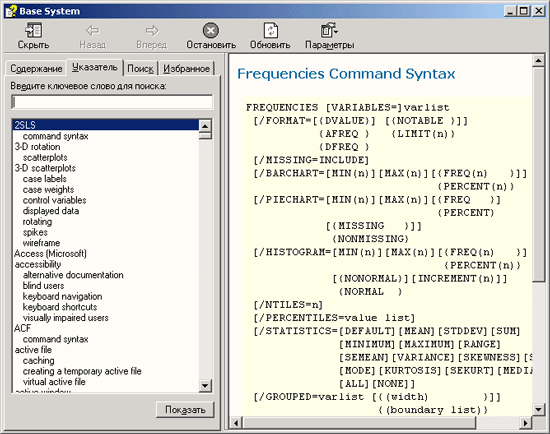
54.gif
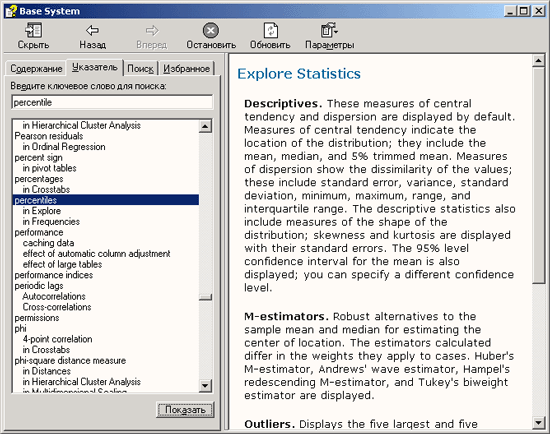
Глава 5. Основы статистики
Глава 5. Основы статистики
1. Основы статистики
Основы статистики
Овладение приемами работы с такой программой, как SPSS требует предварительных познаний в области статистики. Здесь мы коротко остановимся на некоторых основных понятиях, с которыми непременно должен быть знаком пользователь, если он хочет использовать SPSS. В первую очередь сюда относятся предварительные оценки, которые выполняются перед проведением любого статистического теста: классификация переменных по статистическим шкалам, проверка наличия нормального распределения и выделение независимых и зависимых выборок. В следующих разделах представлено описание наиболее часто проводимой процедуры проверки гипотезы о среднем значении и рассматривается значение вероятности ошибки р. Завершает главу обзор методов статистической обработки с указанием глав, в которых они будут рассматриваться в этой книге.
5.1 Предварительные условия для проведения статистического теста
5.1 Предварительные условия для проведения статистического теста
В большинстве случаев перед применением статистического теста ставится вопрос: каков характер заданных условий? В частности, необходимо выяснить следующие моменты:
-
К какой статистической шкале относится данная переменная?
-
Если речь идёт о переменных с интервальной шкалой, то подчиняются ли они закону нормального распределения?
-
Являются ли сравниваемые выборки зависимыми или независимыми?
5.1.1 Типы статистических шкал
5.1.1 Типы статистических шкал
В эмпирическом исследовании могут встречаться, к примеру, следующие переменные (указано их наиболее вероятное кодирование):
Пол | 1 = мужской |
2 = женский | |
Семейное положение | 1 = холост/не замужем |
2 = женат/замужем | |
3 = вдовец/вдова | |
4 = разведен(а) | |
Курение | 1 = некурящий |
2 = изредка курящий | |
3 = интенсивно курящий | |
4 = очень интенсивно курящий | |
Месячный доход | 1 = до 3000 DM |
2 = 3001 - 5000 DM | |
Коэффициент интеллекта (I.Q.) | 3 = более 5000 DM |
Возраст, лет |
Рассмотрим сначала графу Пол. Мы видим, что назначение соответствия цифр 1 и 2 обоим полам абсолютно произвольно, их можно было поменять местами или обозначить другими цифрами
Мы, конечно, не имеем в виду, что женщины стоят на ступеньку ниже мужчин, или :о мужчины значат меньше, чем женщины. Следовательно, отдельным числам не соответствует никакою эмпирического значения. В этом случае говорят о переменных, относящихся к номинальной шкале. В нашем примере рассматривается переменная с номинальной шкалой, имеющая две категории. Такая переменная имеет еще одно название- дихотомическая.
Такая же ситуация и с переменной Семейное положение. Здесь также соответствие -:жду числами и категориями семейного положения не имеет никакого эмпирического значения. Но в отличии от Пола, эта переменная не является дихотомической — у нее четыре категории вместо двух. Возможности обработки переменных, относящихся к номинальной шкале очень ограничены. Собственно говоря, можно провести только частотный анализ таких переменных. К примеру, расчет среднего значения для переменной Семейное положение, совершенно бессмысленен. Переменные, относящиеся к номинальной шкале часто используются для группировки, с помощью которых совокупная выборка разбивается по категориям этих переменных. В частичных выборках проводятся одинаковые статистические тесты, результаты которых затем сравниваются друг с другом.
В качестве следующего примера рассмотрим переменную Курение. Здесь кодовым цифрам присваивается эмпирическое значение в том порядке, в котором они расположены в списке. Переменная Курение, в итоге, сортирована в порядке значимости снизу вверх: умеренный курильщик курит больше, нежели некурящий, а сильно курящий — больше, чем умеренный курильщик и т.д. Такие переменные, для которых используются численные значения, соответствующие постепенному изменению эмпирической значимости, относятся к порядковой шкале.
Однако эмпирическая значимость этих переменных не зависит от разницы между соседними численными значениями. Так, несмотря на то, что разница между значениями кодовых чисел для некурящего и изредка курящего и изредка курящего и интенсивно курящего в обоих случаях равна единице, нельзя утверждать, что фактическое различие между некурящим и изредка курящим и между изредка курящим и интенсивно курящим одинаково. Для этого данные понятия слишком расплывчаты.
К классическими примерами переменных с порядковой шкалой относятся также переменные, полученные в результате объединения величин в классы, как Месячный доход в нашем примере.
Кроме частотного анализа, переменные с порядковой шкалой допускают также вычисление определенных статистических характеристик, таких как медианы. В некоторых случаях возможно вычисление среднего значения. Если должна быть установлена связь (корреляция) с другими переменными такого рода, для этой цели можно использовать коэффициент ранговой корреляции.
Для сравнения различных выборок переменных, относящихся к порядковой шкале, могут применяться непараметрические тесты, формулы которых оперируют рангами.
Рассмотрим теперь коэффициент интеллекта (IQ). Не только его абсолютные значения отображают порядковое отношение между респондентами, но и разница между двумя значениями также имеет эмпирическую значимость. Например, если у Ганса IQ равен 80, у Фрица — 120 и у Отто — 160, можно сказать, что Фриц в сравнении с Гансом настолько же интеллектуальнее насколько Отто в сравнении с Фрицем (а именно — на 40 единиц IQ). Однако, основываясь только на том, что значение IQ у Ганса в два раза меньше, чем у Отто, исходя из определения IQ нельзя сделать вывод, что Отто вдвое умнее Ганса.
Такие переменные, у которых разность (интервал) между двумя значениями имеет эмпирическую значимость, относятся к интервальной шкале. Они могут обрабатываться любыми статистическим методами без ограничений. Так, к примеру, среднее значение является полноценным статистическим показателем для характеристики таких переменных.
Наконец, мы достигли наивысшей статистической шкалы, на которой эмпирическую значимость приобретает и отношение двух значений. Примером переменной, относящейся к такой шкале является возраст: если Максу 30 лет, а Морицу 60, можно сказать, что Мориц вдвое старше Макса. Шкала, к которой относятся данные называется шкалой отношений. К этой шкале относятся все интервальные переменные, которые имеют абсолютную нулевую точку. Поэтому переменные относящиеся к интервальной шкале, как правило, имеют и шкалу отношений.
Подводя итоги, можно сказать, что существует четыре вида статистических шкал, на которых могут сравниваться численные значения:
Статистическая шкала | Эмпирическая значимость |
Номинальная | Нет |
Порядковая | Порядок чисел |
Интервальная | Разность чисел |
Шкала отношений | Отношение чисел |
На практике, в том числе в SPSS, различие между переменными, относящимися к интервальной шкале и шкале отношений обычно несущественно. То есть в дальнейшем практически всегда речь будет идти о переменных, относящихся к интервальной шкале.
Пользователь SPSS должен четко разбираться в видах статистических шкал и при выборе метода обращать внимание на то, чтобы были определены надлежащие виды шкал.
Мы уже указывали, что переменные, относящиеся к номинальной шкале допускают весьма ограниченные возможности для проведения анализа. Исключение в некоторых ситуациях составляют дихотомические переменные. Для них можно, по крайней мере, определять ранговую корреляцию. Если, например, обнаруживается корреляция коэффициента интеллекта с полом, то положительный коэффициент корреляции означает, что женщины интеллектуальнее, чем мужчины. Однако если переменные, относящиеся к номинальной шкале не являются дихотомическими, вычисление коэффициентов ранговой корреляции не имеет смысла.
5.1.2 Нормальное распределение
5.1.2 Нормальное распределение
Многочисленные методы, с помощью которых обрабатываются переменные, относящиеся к интервальной шкале, исходят из гипотезы, что их значения подчиняются нормальному распределению. При таком распределении большая часть значений группируется около некоторого среднего значения, по обе стороны от которого частота наблюдений равномерно снижается.
В качестве примера рассмотрим нормальное распределение возраста, которое строится по данным исследований гипертонии (файл hyper.sav) с помощью команд меню Graphs (Графы) Histogramm... (Гистограмма) (см. рис. 5.1).
На диаграмме нанесена кривая нормального распределения (Колокол Гаусса). Реальное распределение в большей или меньшей степени отклоняется от этой идеальной кривой. Выборки, строго подчиняющиеся нормальному распределению, на практике, как правило, не встречаются. Поэтому почти всегда необходимо выяснить, можно ли реальное распределение считать нормальным и насколько значительно заданное распределение отличается от нормального.
Перед применением любого метода, который предполагает существование нормального распределения, наличие последнего нужно проверять в первую очередь. Классическим примером статистического теста, который исходит из гипотезы о нормальном распределении, можно назвать t-тест Стьюдента, с помощью которого сравнивают две независимые выборки. Если же данные не подчиняются нормальному распределению, следует использовать соответствующий непараметрический тест, в случае двух независимых выборок — U-тест Манна и Уитни.
Если визуальное сравнение реальной гистограммы с кривой нормального распределения кажется недостаточным, можно применить тест Колмогорова-Смирнова, который находится в меню Analyze (анализ данных) в наборе непараметрических тестов (см. раздел 14.5).
Рис. 5.1: Распределение возраста
В нашем примере с распределением возрастов тест Колмогорова-Смирнова не показывает значительного отклонения от нормального распределения.
Еще одну возможность проверки наличия нормального распределения дает построение графика нормального распределения (см. разделы 10.4.1, 22.12), в котором наблюдаемые значения сопоставляются с ожидаемыми при нормальном распределении.
1.gif

5.1.3 Зависимость и независимость выборок
5.1.3 Зависимость и независимость выборок
Две выборки зависят друг от друга, если каждому значению одной выборки можно закономерным и однозначным способом поставить в соответствие ровно одно значение другой выборки. Аналогично определяется зависимость нескольких выборок.
Чаще всего зависимые выборки возникают, когда измерение проводится для нескольких моментов времени. Зависимые выборки образуют значения параметров изучаемого процесса, соответствующие различным моментам времени.
В SPSS зависимые (также связанные, спаренные) выборки будут представляться разными переменными, которые сопоставляются друг с другом в соответствующем тесте на одной и той же совокупности наблюдений.
Если закономерное и однозначное соответствие между выборками невозможно, эти выборки являются независимыми. В SPSS независимые выборки содержат разные наблюдения (например, относящиеся к различным респондентам), которые обычно различаются с помощью групповой переменной, относящейся к номинальной шкале.
5.2 Обзор распространенных тестов для проверки гипотез о среднем
5.2 Обзор распространенных тестов для проверки гипотез о среднем
В наиболее распространенной ситуации, когда требуется сравнить друг с другом разные выборки по их средних значениям или медианам, с учетом условий, описанных в разделе 5.1, обычно применяется один из восьми следующих тестов.
Переменные, относящиеся к интервальной шкале и подчиняющиеся нормальному распределению
Количество сравниваемых выборок | Зависимость | Тест |
1 | Независимые | t-тест Стьюдента |
1 | Зависимые | t-тест для зависимых выборок |
>2 | Независимые | Простой дисперсионный анализ |
>2 | Зависимые | Простой дисперсионный анализ с повторными измерениями |
Переменные, относящиеся к порядковой шкале или переменные, относящиеся к интервальной шкале, но не подчиняющиеся нормальному распределению
Количество сравниваемых выборок | Зависимость | Гест |
1 | Независимые | U-тест Манна и Уитни |
2 | Зависимые | тест Уилкоксона |
>2 | Независимые | Н-тест Крускала и Уоллиса |
>2 | Зависимые | тест Фридмана |
Для каждой из этих двух групп тестов в SPSS имеются отдельные пункты меню, а именно Analyze (Анализ) Compare Means (Сравнение средних) или Analyze (Анализ) Nonparametric Tests (Непараметрические тесты)
Исключение составляет простой дисперсионный анализ с повторными измерениями. Этот метод нельзя найти в разделе Compare Means. Он вызывается командой меню General Linear Model (Общая линейная модель).
5.3 Вероятность ошибки р
5.3 Вероятность ошибки р
Если следовать подразделению статистики на описательную и аналитическую, то задача аналитической статистики - предоставить методы, с помощью которых можно было бы объективно выяснить, например, является ли наблюдаемая разница в средних значениях или взаимосвязь (корреляция) выборок случайной или нет.
Например, если сравниваются два средних значения выборок, то можно сформулировать две предварительных гипотезы:
-
Гипотеза 0 (нулевая): Наблюдаемые различия между средними значениями выборок находятся в пределах случайных отклонений.
-
Гипотеза 1 (альтернативная): Наблюдаемые различия между средними значениями нельзя объяснить случайными отклонениями.
В аналитической статистике разработаны методы вычисления так называемых тестовых (контрольных) величин, которые рассчитываются по определенным формулам на основе данных, содержащихся в выборках или полученных из них характеристик. Эти тестовые величины соответствуют определенным теоретическим распределениям (t-pacnpe-лелению, F-распределению, распределению X2 и т.д.), которые позволяют вычислить так называемую вероятность ошибки. Это вероятность равна проценту ошибки, которую можно допустить отвергнув нулевую гипотезу и приняв альтернативную.
Вероятность определяется в математике, как величина, находящаяся в диапазоне от 0 до 1. В практической статистике она также часто выражаются в процентах. Обычно вероятность обозначаются буквой р:
0<р< 1
Вероятности ошибки, при которой допустимо отвергнуть нулевую гипотезу и принять альтернативную гипотезу, зависит от каждого конкретного случая. В значительной степени эта вероятность определяется характером исследуемой ситуации. Чем больше требуемая вероятность, с которой надо избежать ошибочного решения, тем более узкими выбираются границы вероятности ошибки, при которой отвергается нулевая гипотеза, так называемый доверительный интервал вероятности.
Существует общепринятая терминология, которая относится к доверительным интервалам вероятности. Высказывания, имеющие вероятность ошибки р <= 0,05. называются значимыми; высказывания с вероятностью ошибки р <= 0,01 - очень значимыми, а высказывания с вероятностью ошибки р <= 0,001 - максимально значимыми. В литературе такие ситуации обозначают одной, двумя или тремя звездочками.
Вероятность ошибки | Значимость | Обозначение |
р > 0.05 | Не значимая | ns |
р <= 0.05 | Значимая | * |
р <= 0.01 | Очень значимая | ** |
р <= 0.001 | Максимально значимая | *** |
В SPSS вероятность ошибки р имеет различные обозначения; звездочки для указания степени значимости применяются лишь в немногих случаях.
Времена, когда не было компьютеров, пригодных для статистического анализа, давали практикам по крайней мере одно преимущество.: Так как все вычисления надо было выполнять вручную, статистик должен был сначала тщательно обдумать, какие вопросы можно решить с помощью того или иного теста. Кроме того, особое значение придавалось точной формулировке нулевой гипотезы.
Нос помощью компьютера и такой мощной программы, как SPSS, очень легко можно провести множество тестов за очень короткое время. К примеру, если в таблицу сопряженности свести 50 переменных с другими 20 переменными и выполнить тест %2, то получится 1000 результатов проверки значимости или 1000 значений р. Некритический подбор значимых величин может дать бессмысленный результат, так как уже при граничном уровне значимости р = 0,05 в пяти процентах наблюдений, то есть в 50 возможных наблюдениях, можно ожидать значимые результаты.
Этим ошибкам первого рода (когда нулевая гипотеза отвергается, хотя она верна) следует уделять достаточно внимания. Ошибкой второго рода называется ситуация, когда нулевая гипотеза принимается, хотя она ложна. Вероятность допустить ошибку первого рода равна вероятности ошибки р. Вероятность ошибки второго рода тем меньше, чем больше вероятность ошибки р.
5.4 Обзор статистических методов
5.4 Обзор статистических методов
В этом разделе мы попытаемся составить небольшой путеводитель по данной книге, дав обзор последовательности действий, которые выполняются при статистическом анализе.
5.4.1 Структурирование, вводи проверка данных
5.4.1 Структурирование, ввод и проверка данных
Прежде чем мы сможем применить статистические методы или строить графики, естественно, следует представить собранные данные в форме, пригодной для обработки. При этом рекомендуется придерживаться следующего плана действий:
-
Проведите структурирование набора данных; прежде всего выясните, к какими категориям относятся Ваши наблюдения и к каким — переменные. В большинстве случаев это ясно сразу. Если структурирование провести не удается, SPSS применять нельзя, да и все остальные статистические программы также требуют, чтобы данные были структурированы. Подробнее об этом см. раздел 3.2.
-
Определите шкалу, к которой относятся переменные (см. раздел 5.1.1).
-
Составьте кодировочную таблицу (см. раздел 3.1).
-
Введите данные в Редакторе данных (см. раздел 3.4), учитывая кодировочную таблицу. Если для ввода данных вы хотите использовать другие программы (например, Excel, dBase), это вполне допустимо; SPSS может работать с файлами данных этих программ. Не вводите данные, которые можно вычислить на основе других данных. Эти вычисления следует предоставить компьютеру (см. главу 8). Если данные уже были введены в других программах статистики (например, SAS, Stata. Statistica), их можно преобразовать в файлы SPSS с помощью таких утилит, как, к примеру, DBMS/COPY.
-
Проверьте введенные данные на отсутствие ошибок и осмысленность. Подробнее об этом см. раздел 10.1.
-
Установите, подчиняются ли нормальному распределению переменные, относящиеся к интервальной шкале (см. раздел 5.1.2).
Теперь можно начинать статистическую обработку введенных данных. Учтите, что анализ может быть выполнен только для наблюдений, сгруппированных определенным образом см. главу 7). Об основных принципах работы с версией 9 можно прочесть в главе 4.
5.4.2 Описательный (дескриптивный) анализ
5.4.2 Описательный (дескриптивный) анализ
Этот вид анализа включает описательное представление отдельных переменных. К нему относятся создание частотной таблицы, вычисление статистических характеристик или графическое представление. Частотные таблицы строятся для переменных, относящихся к номинальной шкале и для порядковых переменных, имеющих не слишком много категорий; об этом см. главы 6, 12 и 24.
Для переменных относящихся к номинальной шкале нельзя вычислить никаких значимых статистических характеристик. Наиболее часто для порядковых переменных и переменных, относящихся к интервальной шкале, но не подчиняющихся нормальному распределению, вычисляются медианы и оба квартиля (см. раздел 6.2); при небольшом числе категорий можно использовать вариант для концентрированных данных см. раздел 6.3).
Для переменных, относящихся к интервальной шкале и подчиняющихся нормальному распределению, чаще всего вычисляется среднее значение и стандартное отклонение пли стандартная ошибка (см. раздел 6.2). Однако следует выбрать только одну из этих двух характеристик разброса. Для переменных, относящихся ко всем статистическим шкалам, можно построить большое разнообразных графиков, на которых представлены частоты, средние значения или другие характеристики. Подробнее об этом в главах 22 и 23.
5.4.3 Аналитическая статистика
5.4.3 Аналитическая статистика
Практически любой статистический анализ наряду с чисто описательными операциями включает те или иные аналитические методы (тесты значимости), при применении которых в конечном счете определяется вероятности ошибки р (см. раздел 5.3).
Большая группа тестов служит для выяснения того, различаются ли две или более различных выборки по своим средним значениям или медианам. При этом учитывается разница между независимыми выборками (разные наблюдения) и зависимыми выборками (разные переменные; см. раздел 5.1.3). В зависимости количества выборок (две или более), от того, зависимы ли выборки или нет, относятся ли переменные к интервальной или порядковой шкале, подчиняются ли нормальному распределению — применяются специализированные тесты (см. раздел 5.2).
Очень часто встречается ситуация, когда сравниваются различные группы наблюдений или значений переменных, относящихся к номинальной шкале. В этом случае строятся таблицы сопряженности (см. главу 11). Другая группа тестов касается исследования связей между двумя переменными, то есть выявления корреляций и восстановления регрессий (см. главу 15, раздел 16.1).
Кроме этих довольно простых статистических методов существуют также более сложные методы многомерного анализа, в которых обычно одновременно используется очень много переменных. К примеру, если требуется свести большое количество переменных к меньшему количеству "пучков переменных", называемых факторами, то проводится факторный анализ (глава 19). Если же наша цель, противоположна — объединить заданные наблюдения, образовав из них кластеры, то применяется кластерный анализ (глава 20).
В определенной группе многомерных тестов вводится различие между зависимой переменной, называемой также целевой и несколькими независимыми переменными (переменными влияния или прогнозирования).
Зависимая переменная | Независимые переменные | Многомерный метол |
Дихотомическая | Любые | Двоичная логистическая регрессия (раздел 16.4); дискриминантный анализ (глава 18) |
Дихотомическая | С номинальной или порядковой шкалой | Логит-логарифмические линейные модели |
С номинальной шкалой | С номинальной или порядковой шкалой | Мультиномиальная логистическая регрессия (раздел 16.5) |
С порядковой шкалой | С номинальной или порядковой шкалой | Порядковая регрессия (раздел 16.6) |
С интервальной шкалой | С номинальной или порядковой шкалой | Дисперсионный анализ (раздел 17.1) |
С интервальной шкалой | Любые | Ковариационный анализ (раздел 17.2); множественный регрессионный анализ (раздел 16.2) |
При мультиномиальной логистической регрессии и порядковой регрессии могут также использоваться ковариации, относящиеся к интервальной шкале.
Независимые переменные, относящиеся к номинальной шкале, при двоичной логистической регрессии, дискриминантном анализе и многозначном регрессионном анализе должны быть дихотомическими либо раскладываться на набор дихотомических переменных (см. раздел 16.2). Логит-логарифмические линейные модели рассматриваются не в этой книге, а во втором томе, посвященном методам исследования рынка и общественного мнения.
Кроме упомянутых здесь, существует еще несколько методов анализа, например, пробит-анализ или анализ надежности; об их назначении можно узнать из соответствующих глав.
Глава 6. Частотный анализ.
Глава 6. Частотный анализ
1. Частотный анализ
Частотный анализ
Первым этапом статистического анализа данных, как правило, является частотный анализ. В этой главе мы проведем частотный анализ на примере файла Studium.sav. Этот файл находится на компакт-диске примеров или в рабочем каталоге \SPSSBOOK. Он содержит результаты опроса студентов об их психическом состоянии и социальном положении. Опрос касался таких предметов, как социальное положение, психическая ситуация и успеваемость. Кроме того, затрагивались такие данные, как изучаемый предмет, пол, возраст и национальность.
6.1 Частотные таблицы
6.1 Частотные таблицы
-
Сначала загрузите файл Studium.sav, выбрав команды меню File (Файл) Open... (Открыть...) Появится диалог Open File (Открыть файл).
-
Выберите указанный выше файл Studium.sav и подтвердите выбор кнопкой Open (Открыть). Файл появится в Редакторе данных.
-
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies (Частоты) Появится диалоговое окно Frequencies (см. рис. 6.1).
-
Кнопкой с треугольником перенесите переменную psyche в список выходных переменных и подтвердите операцию кнопкой ОК.
Рис. 6.1: Диалоговое окно Frequencies (Частоты)
Результаты появятся в окне просмотра результатов. Перед самой частотной таблицей выводится небольшая таблица с обзором допустимых и отсутствующих значений. Здесь она не показана.
Психическое состояние
Частота | Проценты | Допус- тимые проценты | Нако- пленные проценты | ||
Крайне неустой- чивое | 20 | 18,5 | 18,7 | 18,7 | |
Неустой- чивое | 40 | 37,0 | 37,4 | 56,1 | |
Допус- тимые | Устойчивое | 41 | 38,0 | 38,3 | 94,4 |
Очень устойчивое | 6 | 5,6 | 5,6 | 100,0 | |
Всего | 107 | 99,1 | 100,0 | ||
Отсут-ствующие | нет данных | 1 | ,9 | ||
Всего | 108 | 100,0 |
Каждая строка частотной таблицы описывает одно возможное значение. Строка с пометкой нет данных представляет наблюдения, в которых не было дано никакого ответа. Всего имеется 107 допустимых ответов, а также одно наблюдение, в котором психическое состояние неизвестно (данные отсутствуют либо утеряны). Первый столбец содержит метки отдельных значений (крайне неустойчивое, неустойчивое, устойчивое, ...). Во втором столбце под заголовком «Частота» приведена частота каждого из вариантов ответа на вопрос из теста. Так, к примеру, 20 человек на вопрос о психическом состоянии дали ответ: «крайне неустойчивое», а 40 человек — «неустойчивое». В третьем столбце показана процентная частота каждого ответа. Процентная частота соответствует отношению каждого из вариантов ответа к общему количеству опрашиваемых, включая утерянные значения. В четвертом столбце дано допустимое процентное значение. При определении этого значения утерянные данные исключаются. Последний столбец содержит накопленные процентные значения. Накопленные проценты — это сумма процентных частот допустимых ответов. Так, например, процент респондентов, которые дали ответ крайне неустойчивое или неустойчивое, составляет 56,1%. Это число определяется выражением: 18,7% + 37,4% = 56,1%. В последней строке содержится сумма всех столбцов (Всего).
1.gif

6.2 Вывод статистических характеристик
6.2 Вывод статистических характеристик
Чтобы получить описательную статистику числовых переменных, можно щелкнуть в диалоге Frequencies на кнопке Statistics... (Статистика). Откроется диалоговое окно Frequencies: Statistics (Частоты: Статистика).
В группе Percentile Values (Значения процентилей) можно выбрать следующие варианты:
-
Quartiks (Квартили): Будут показаны первый, второй и третий квартили. Первый квартиль (Q,) — это точка на шкале измеренных значений, ниже (левее) которой располагаются 25 % измеренных значений. Второй квартиль (Q2) — это точка, ниже которой располагаются 50 % измеренных значений. Второй квартиль также называется медианой. Третий квартиль (Q3) — это точка на шкале измеренных значений, ниже которой располагаются 75 % значений. Если данные имеются только в форме порядкового отношения, то качестве меры разброса используется межквартильная широта. Она определяется как
Рис. 6.2: Диалоговое окно frequencies: Statistics
-
Cut points (Точки раздела): Будут вычислены значения процентилей, разделяющие выборку на группы наблюдений, которые имеют одинаковую ширину, то есть включают одно и то же количество измеренных значений. По умолчанию предлагается количество групп 10. Если задать, к примеру, 4, то будут показаны квартили, то есть квартили соответствуют процентилям 25, 50 и 75. Видно, что число показываемых процентилей на единицу меньше заданного числа групп.
-
Percentile(s) (Процентили): Здесь имеются в виду значения процентилей, определяемые пользователем. Введите значение процентиля в пределах от 0 до 100 и щелкните на кнопке Add (Добавить). Повторите эти действия для всех желаемых значений процентилей. Значения в порядке возрастания будут показаны в списке. Например, если ввести значения 25, 50 и 75, то мы получим квартили. Можно задавать любые значения процентилей, например, 37 и 83. В первом случае (37) будет показано значение выбранной переменной, ниже которого лежат 37 % значений, а во втором случае (83) — значение, ниже которого располагаются 83 % значений.
В группе Dispersion (Разброс) можно выбрать следующие меры разброса:
-
Std. deviation (Стандартное отклонение): Стандартное отклонение — это мера разброса измеренных величин; оно равно квадратному корню из дисперсии. В интервале шириной, равной удвоенному стандартному отклонению, который отложен по обе стороны от среднего значения, располагается примерно 67% всех значений выборки, подчиняющейся нормальному распределению.
-
Variance (Дисперсия): Дисперсия — это квадрат стандартного отклонения и, следовательно, эта характеристика также является мерой разброса измеренных величин. Она определяется как сумма квадратов отклонений всех измеренных значений от их среднеарифметического значения, деленная на количество измерений минус 1.
-
Range (Размах): Размах — это разница между наибольшим значением (максимумом) и наименьшим значением (минимумом).
-
Minimum (Минимум): Наименьшее значение.
-
Maximum (Максимум): Наибольшее значение.
-
S.E. mean (Стандартная ошибка): Это стандартная ошибка среднего значения. В интервале шириной, равной удвоенной стандартной ошибке, отложенному вокруг среднего значения, располагается среднее значение генеральной совокупности с вероятностью примерно 67 %. Стандартная ошибка определяется как стандартное отклонение, деленное на квадратный корень из объема выборки.
Обычно мерами разброса переменных, относящихся к интервальной шкале и подчиняющихся нормальному распределению, служат стандартное отклонение и стандартная ошибка. Как было сказано выше, стандартное отклонение позволяет задать диапазон разброса отдельных значений. По так называемому правилу кулака, в одном диапазоне стандартного отклонения (охватывающем ширину стандартного отклонения в обе стороны от среднего значения) располагается примерно 67 % значений, в диапазоне удвоенного стандартного отклонения — примерно 95 %, а в диапазоне утроенного стандартного отклонения — примерно 99 % значений.
С другой стороны, стандартная ошибка позволяет задать доверительный интервал для среднего значения. В диапазоне удвоенной стандартной ошибки по обе стороны от среднего значения с вероятностью примерно 95 % находится среднее значение генеральной совокупности. С вероятностью примерно 99 % она лежит в диапазоне утроенной стандартной ошибки. Часто указывают только одну из этих двух мер разброса, обычно — стандартную ошибку, так как ее значение меньше. Во всех случаях следует точно выяснить, какая из мер разброса имеется в виду.
В группе Central Tendency (Средние) можно выбрать следующие характеристики:
-
Mean (Среднее значение): Среднее значение — это арифметическое среднее измеренных значений; оно определяется как сумма значений, деленная на их количество. Например, если имеется 12 измеренных значений и их сумма составляет 600, то среднее значение будет х = 600 : 12 = 50.
-
Median (Медиана): Медиана — это точка на шкале измеренных значений, выше и ниже которой лежит по половине всех измеренных значений. Например, если измеренные значения таковы:
37854639284,
то сначала они располагаются в порядке возрастания: 23344567889.
В данном случае медианой будет значение 5. Всего у нас 11 измеренных значений, следовательно, медианой является шестое значение. Выше него располагается 5 значений, и ниже — тоже 5. При нечетном количестве значений медиана всегда будет совпадать с одним из измеренных значений. При четном количестве медиана будет средним арифметическим двух соседних значений. Например, если имеются следующие измеренные значения:
3445678899
то медиана в этом случае будет равна: (6 + 7) : 2 = 6,5.
-
Mode (Мода): Мода — это значение, которое наиболее часто встречается в выборке. Если одна и та же наибольшая частота встречается у нескольких значений, то выбирается наименьшее из них.
-
Sum (Сумма): Сумма всех значений.
В группе Distribution (Распределение) можно выбрать следующие меры несимметричности распределения:
-
Skewness (Коэффициент асимметрии): Коэффициент асимметрии — это мера отклонения распределения частоты от симметричного распределения, то есть такого, у которого на одинаковом удалении от среднего значения по обе стороны выборки данных располагается одинаковое количество значений. Если наблюдения подчиняются нормальному распределению, то асимметрия равна нулю. Для проверки на нормальное распределение можно применять следующее правило: Если асимметрия значительно отличается от нуля, то гипотезу о том, что данные взяты из нормально распределенной генеральной совокупности, следует отвергнуть. Если вершина асимметричного распределения сдвинута к меньшим значениям, то говорят о положительной асимметрии, в противоположном случае — об отрицательной.
-
Kurtosis (Коэффициент вариации или эксцесс): Коэффициент вариации указывает, является ли распределение пологим (при большом значении коэффициента) или крутым. Коэффициент вариации равен нулю, если наблюдения подчиняются нормальному распределению. Поэтому для проверки на нормальное распределение можно применять еще одно правило: Если коэффициент вариации значительно отличается от нуля, то гипотезу о том, что данные взяты из нормально распределенной генеральной совокупности, следует отвергнуть.
Как правило, для переменных, относящихся к интервальной шкале и подчиняющихся нормальному распределению, в качестве основной характеристики используют среднее значение, а в качестве меры разброса — стандартное отклонение или стандартную ошибку. Для порядковых или интервальных переменных, не подчиняющихся нормальному распределению, — соответственно медиану или первый и третий квартили. Для переменных относящихся к номинальной шкале, нельзя дать других значимых характеристик кроме моды.
В диалоге есть еще один флажок:
-
Values are group midpoints (Значения являются средними точками групп): Если установить этот флажок, то при вычислении медианы и остальных значений процен-тилей оценки этих характеристик будут определяться для концентрированных данных. Этому вопросу посвящен отдельный раздел.
Для переменной alter (возраст) мы определим следующие характеристики: среднее значение, медиану, моду, квартили, стандартное отклонение, дисперсию, размах, минимум, максимум, стандартную ошибку, асимметрию и эксцесс. Поступите следующим образом:
-
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты)
-
В диалоге Frequencies щелкните на кнопке Reset (Сброс), чтобы отменить прежние настройки.
-
Перенесите переменную alter в список выходных переменных.
-
Щелкните на кнопке Statistics... (Статистика).
-
В диалоге Frequencies: Statistics установите флажки желаемых характеристик. Затем щелкните на кнопке Continue (Продолжить). Вы вернетесь в диалог Frequencies.
-
В диалоге Frequencies деактивируйте опцию Display frequency tables (Показывать частотные таблицы). Щелкните на кнопке ОК.
В окне просмотра появятся следующие результаты:
Статистика
Alter | ||
N | Допустимые | 106 |
Утерянные | 2 | |
Среднее значение | 22,24 | |
Стандартная ошибка среднего значения | 21 | |
Медиана | 22,00 | |
Мода | 21 | |
Стандартное отклонение | 2,19 | |
Дисперсия | 4,79 | |
Асимметрия | ,859 | |
Стандартная ошибка асимметрии | ,235 | |
Эксцесс | 1,042 | |
Стандартная ошибка эксцесса | ,465 | |
Размах | 11 | |
Минимум | 18 | |
Максимум | 29 | |
Процентили | 25 | 21,00 |
50 | 22,00 | |
75 | 23,00 | |
Респонденты опроса о психическом состоянии и социальном положении имеют средний возраст 22,24 года. Медиана составляет 22. Большинству респондентов 21 год (это мода). Самому молодому респонденту 18 лет (минимум), самому старшему — 29 лет (максимум). Самый старший респондент на 11 лет старше самого молодого (размах). Стандартное отклонение составляет 2,19. Следовательно, дисперсия — квадрат стандартного отклонения — равна (2,19)2 = 4,79. Асимметрия и коэффициент вариации даны с соот-ветсвующими стандартными ошибками.
3.gif
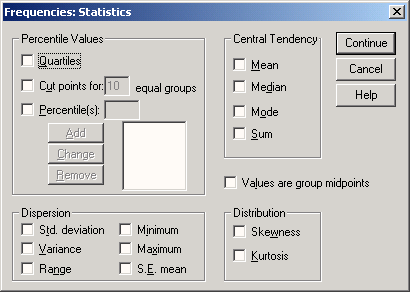
6.3 Медиана для концентрированных данных
6.3 Медиана для концентрированных данных
Для данных, имеющих форму частотной таблицы, определение медианы и остальных процентилей обычным методом будет слишком неточным. В таких случаях есть возможность вычислить медиану и любые другие процентили более точным методом. Мы поясним это на примере стоматологических данных.
-
Загрузите файл cpitn.sav, содержащий результаты стоматологического исследования.
Кроме переменных schule и mhfreq, которые определяют уровень образования и то, сколько раз в день обследуемый чистит зубы, этот файл содержит шесть переменных cpitnl—cpitn6, которые указывают степень пародонтального заболевания каждой из шести частей челюсти — так называемый параметр CPITN, задаваемый с помощью следующей кодировочной таблицы:
0 | Здоровый пародонт |
1 | Кровоточивость |
2 | Зубные отложения |
3 | Глубина десенных карманов 3,5-5,5 мм |
4 | Глубина десенных карманов 6 мм и более |
-
С помощью команд меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies (Частоты) создайте частотную таблицу, к примеру, для переменной cpitnl. Если задать вычисление среднего значения и медианы, мы получим следующий результат:
Статистика
CPITN1 | ||
N | Допустимые | 2548 |
Утерянные | 0 | |
Среднее значение | 2,24 | |
Медиана | 2,00 | |
CPITN1
Частота | Проценты | допустимые проценты | накопленные проценты | |
Допустимые здоровый | 109 | 4,3 | 4,3 | 4,3 |
кровоточивость | 389 | 15,3 | 15,3 | 19,5 |
отложения | 921 | 36,1 | 36,1 | 55,7 |
глубина карманов | 1042 | 40,9 | 40,9 | 96,6 |
3,5-5,5 глубина карманов >=6 | 87 | 3,4 | 3,4 | 100,0 |
Всего | 2548 | 100,0 | 100,0 |
При определении медианы обычным методом ее значение равно 2. Это значение, хотя формально и правильное, но дает совершенно неудовлетворительный, недостаточно значимый результат. В данном случае, когда данные являются концентрированным, для уточнения медианы применяется следующая расчетная формула:

Здесь:
n | Количество измеренных значений |
m | Класс, в котором находится медиана |
u | Нижняя граница класса m |
fm | Абсолютная частота в классе m |
Fm-1 | Накопленная частота вплоть до предыдущего класса m — 1 |
B | Ширина класса |
Следовательно, решающее значение имеет правильный выбор границ классов; их следует выбирать так, чтобы значения кодовых чисел соответствовали середине каждого класса. В данном примере для границ классов следует выбрать значения
-0,5 0,5 1,5 2,5 3,5 4,5
Ширина класса равна 1.
Следовательно,
n = 2548
m = 3 (так как медиана находится в третьем классе)
u = 1,5
fm = 921
Fm-1 = 109 + 389 = 498
b = 1
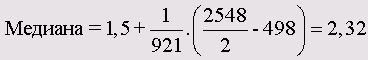
Если сравнить это значение со средним значением (2,24), то можно установить следующее правило — оказывается, что при распределении со сдвигом вправо (как в данном случае) медиана больше среднего значения.
Описанный точный метод вычисления медианы будет использован в SPSS, если в диалоге Frequencies: Statistics установить флажок Values are group midpoints.
В этом случае мы получим точное значение медианы (2,32).
По определению, медиана — это значение, выше и ниже (правее и левее) которого расположено по 50 % всех значений, если они упорядочены по величине. Обобщая эту характеристику, мы приходим к определению так называемых процентилей. Эти характеристики позволяют, например, указать значение, ниже которого лежит 10 % всех значений (а выше расположено 90 % значений). Чаше всего применяются процентили 25 % и 75 %, называемые также соответственно первым и третьим квартилями.
В диалоге Frequencies: Statistics можно последовательно задать любые значения процентилей. Если данные концентрированы, снова следует установить флажок Values are group midpoints.
Формула вычисления процентиля для любого значения:
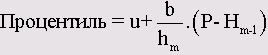
Здесь:
n | Класс, в котором находится процентиль |
m | Нижняя граница класса т |
P | Процентное значение процентиля |
Нm | Процентная частота в классе m-1 |
Hm-1 | Процентная накопленная частота в классе m-1 |
b | Ширина класса |
Для процентиля 50 % (Р = 50) после некоторых преобразований получается формула для медианы, приведенная выше.
В столбчатых, линейных, круговых диаграммах и диаграммах с областями, на которых предусмотрено отображение медианы и других процентилей, при наличии концентрированных данных используется модифицированный способ расчета (см. раздел 22.1.1).
4.gif

5.gif
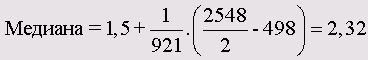
6.gif
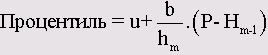
6.4 Форматы частотных таблиц
6.4 Форматы частотных таблиц
-
Загрузите файл studium.sav (см. раздел 6.1).
Сейчас мы попробуем вывести частотную таблицу переменной fach, отсортированную по убыванию частоты. Поступите следующим образом:
-
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты)
-
Перенесите переменную fach (специальность) в список выходных переменных.
-
Щелкните на кнопке Format.... Откроется диалоговое окно Frequencies: Format (Частоты: Формат).
Рис. 6.3: Диалоговое окно Frequencies: Format
В группе Order by (Сортировать по) можно выбрать порядок, в котором будут отображены значения в частотной таблице. Возможны следующие варианты:
-
Ascending values (По возрастанию значений): Данные сортируются по возрастанию значений. Это настройка по умолчанию.
-
Descending values (По убыванию значений): Данные сортируются по убыванию значений.
-
Ascending counts (По возрастанию частот): Данные сортируются по возрастанию частот.
-
Descending counts (По убыванию частот): Категории сортируются по убыванию частот.
Кроме того, флажок Suppress tables -with more than ... categories (He выводить таблицы с более чем... категориями) позволяет избежать вывода длинных частотных таблиц.
-
Выберите вариант Descending counts.
-
Подтвердите выбор кнопкой Continue (Продолжить).
-
Щелкните на кнопке ОК, чтобы начать вычисление. Мы получим следующие результаты:
Специальность
Частота | Проценты | Допустимые проценты | Накоплен- ные проценты | ||
Допус-тимые | Гуманитар- ные науки | 25 | 23,1 | 23,1 | 23,1 |
Юриспру- денция | 22 | 20,4 | 20,4 | 43,5 | |
Экономика | 19 | 17,6 | 17,6 | 61,1 | |
Психология | 11 | 10,2 | 10,2 | 71,3 | |
Медицина | 10 | 9,3 | 9,3 | 80,6 | |
Теология | 9 | 8,3 | 8,3 | 88,9 | |
Естествен- ные науки | 9 | 8,3 | 8,3 | 97,2 | |
Техника | 2 | 1,9 | 1,9 | 99,1 | |
Прочие | 1 | ,9 | ,9 | 100,0 | |
Всего | 108 | 100,0 | 100,0 |
Основные специальности респондентов отображены в порядке убывания частоты.
7.gif
6.5 Графическое представление
6.5 Графическое представление
Результаты частотного распределения можно представить графически. Для примера мы создадим столбчатую диаграмму для частотного распределения основных специальностей. Поступите следующим образом:
-
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies (Частоты)
-
Перенесите переменную fach в список выходных переменных.
-
Щелкните на кнопке Charts... (Диаграммы). Откроется диалоговое окно Frequencies: Charts (Частоты: Диаграммы).
-
Выберите в группе Chart Type (Тип диаграммы) пункт Bar charts (Столбчатая диаграмма), а в группе Chart Values (Значения диаграммы) — пункт Percentages (Проценты). Подтвердите выбор кнопкой Continue (Продолжить). Вы вернетесь в диалог Frequencies.
-
В диалоговом окне Frequencies снимите флажок Display frequency tables (Показывать частотные таблицы). — Щелкните на кнопке ОК. Диаграмма будет показана в окне просмотра (см. рис. 6.5).
Рис. 6.4: Диалоговое окно Frequencies: Charts
Усовершенствуем вид этой диаграммы.
-
Чтобы начать редактирование, дважды щелкните в области столбчатой диаграммы. Диаграмма будет показана в редакторе диаграмм.
-
На панели инструментов редактора диаграмм щелкните на символе меток столбцов:

Рис. 6.5: Столбчатая диаграмма в средстве просмотра
Откроется диалоговое окно Bar Label Style (Стиль меток столбцов). Выберите пункт Framed (В рамке), щелкните на кнопке Apply all (Применить для всех) и затем на Close (Закрыть). На каждом столбце появится надпись с его процентным значением.
-
Щелкните мышью на любом из столбцов. На верхней стороне каждого столбца появится по два маленьких черных квадрата. Это означает, что области столбцов готовы для редактирования.
-
Щелкните мышью на символе образца заливки:

Откроется диалоговое окно Fill Patterns (Образцы заливки).
-
Выберите в нем подходящий образец заливки. Подтвердите выбор кнопкой Apply (Применить) и закройте диалоговое окно.
Рис. 6.6: Диалоговое окно Fill Patterns
Столбцы будут заполнены выбраннои заливкой.
-
Щелкните мышью на символе вида столбцов:

-
Выберите пункт Drop shadow (Тень), щелкните на кнопке Apply all (Применить для всех) и затем на Close (Закрыть).
-
Дважды щелкните на заголовке диаграммы Fachbereich. Откроется диалоговое окно Titles (Заголовки) (см. рис. 6.7).
-
Измените заголовок на «Основная специальность» и закройте диалог кнопкой ОК.
-
В меню Chart (Диаграмма) установите флажок Outer Frame (Внешняя рамка). Закройте редактор диаграмм; получившийся график показан на рис. 6.8.
Рис. 6.7: Диалоговое окно Tirles
Рис. 6.8: Отредактированная диаграмма
Рассмотрим другой пример — визуальное представление частотного анализа.
-
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies (Частоты)
-
Щелкните на кнопке Reset (Сброс), чтобы установить стандартные настройки.
-
Перенесите переменную sozial (социальное положение) в список выходных переменных.
-
Щелкните на кнопке Charts... (Диаграммы). В диалоговом окне Frequencies: Charts выберите пункт Histograms (Гистограмма). Установите флажок With normal curve (С кривой нормального распределения). Щелкните на кнопке Continue.
-
В диалоговом окне Frequencies снимите флажок Display frequency tables (Показывать частотные таблицы). Щелкните на кнопке ОК. Гистограмма будет показана в окне просмотра (см. рис. 6.9).
Рис. 6.9: Гистограмма
Частоты на гистограмме обозначены колонками, которые, но отличие от столбчатой диаграммы, не изолированы, а примыкают друг к другу. Отображаются также стандартное отклонение, среднее значение и общее количество наблюдений(М). Кроме того, показана кривая нормального распределения.
-
Дважды щелкните на области гистограммы — откроется редактор диаграмм, в котором можно придать гистограмме желаемый вид. График отобразится в редакторе диаграмм.
-
Выберите другой образец заливки и снабдите колонки надписями.
-
При желании проверьте другие функции редактора диаграмм.
На этом мы завершаем тему частотного анализа. Попробуйте самостоятельно выполнить частотный анализ переменной studium (время обучения) и представьте результаты распределения частот в графическом виде.
8.gif
10.gif
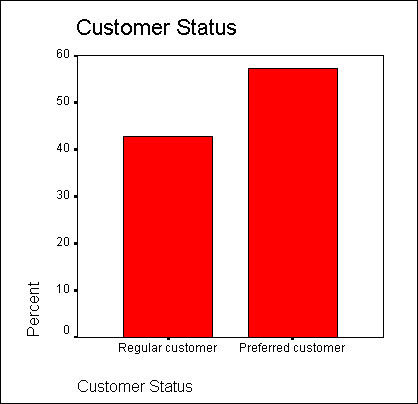
12.gif

14.gif

15.gif
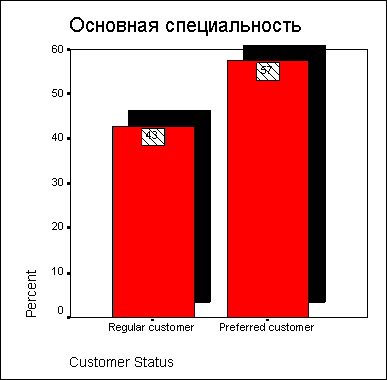
16.gif
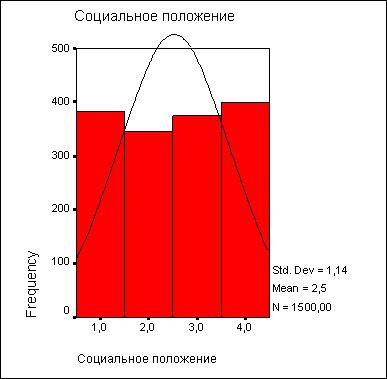
Глава 7. Отбор данных
Глава 7. Отбор данных
1. Отбор данных
Отбор данных
В этой главе мы на примере файлов wahl.sav и studium.sav покажем разнообразные возможности, предоставляемые в SPSS для отбора данных. Отбор данных — это выбор наблюдений по определенным критериям; так, например, при опросе избирателей (файл wahl.sav) можно отобрать только мужчин, голосующих за ХДС/ХСС, а при опросе студентов (файл studium.sav) — только студенток, изучающих психологию и медицину. После этого все вычисления будут проводиться только с этими отобранными наблюдениям.
Для этого в SPSS существует три принципиальные возможности:
-
Выбор наблюдений по определенному условию (логическому выражению),
-
Извлечение случайной выборки наблюдений из файла данных,
-
Разделение наблюдений на группы в соответствии со значениями одной или нескольких переменных.
Данная глава разбита на три раздела, посвященные каждой из этих возможностей. Еще в одном разделе рассматривается вопрос сортировки наблюдений, содержащихся в файле данных, по значениям выбранных переменных.
7.1 Выбор наблюдений
7.1 Выбор наблюдений
Проведем частотный анализ переменной partei (партия). При этом мы будем учитывать только респондентов-женщин. Поступите следующим образом:
-
Загрузите файл wahl.sav в редактор данных.
-
Выберите в меню команды Data (Данные) Select Cases... (Выбрать наблюдения)
Откроется диалоговое окно Select Cases (см. рис. 7.1). По умолчанию в этом диалоге выбран пункт All cases (Все наблюдения).
-
Выберите пункт If condition is satisfied (Если выполняется условие) и щелкните на кнопке If... (Если). Откроется диалоговое окно Select Cases: If (см. рис. 7.2).
Это диалоговое окно разделено на следующие части:
-
Список исходных переменных: Содержит переменные, содержащиеся в открытом файле данных. В нашем случае это переменные fragebnr, sex, alter и partei.
-
Редактор условий: Здесь записывается логическое выражение, по которому должны быть отобраны наблюдений. В данный момент редактор условий пока пуст.
Рис. 7.1: Диалоговое окно Select Cases
Рис. 7.2: Диалоговое окно Select Cases: If
-
Кнопка с треугольником: Эта кнопка позволяет перенести переменную из списка исходных переменных в редактор условий.
-
Клавиатура: Содержит цифры, а также арифметические, логические операторы и операторы отношения; с ней можно работать как с обыкновенным калькулятором. Если щелкнуть на какой-нибудь кнопке мышью, соответствующий знак, например, +, *, 7, будет скопирован в редактор условий.
-
Список функций: Содержит около 140 функций. Каждую из функции можно скопировать в редактор условий двойным щелчком.
1.gif
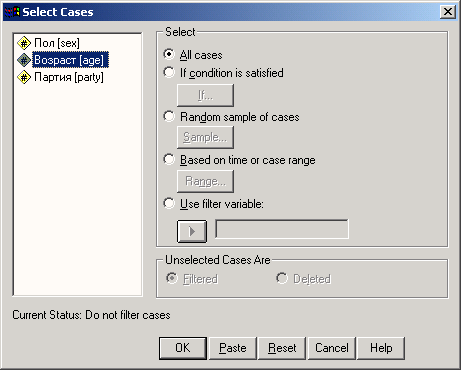
2.gif
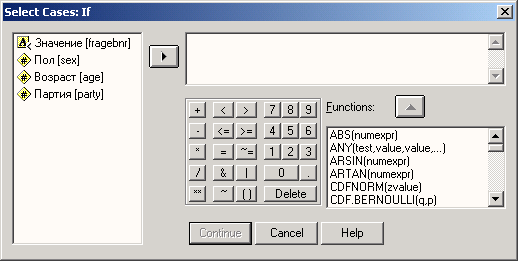
7.1.1 Классификация операторов
7.1.1 Классификация операторов
Операторы делятся на арифметические, логические и операторы отношения. Арифметические операторы применяются в так называемых арифметических выражениях (математических формулах), которые при отборе данных имеют лишь второстепенное значение. Арифметические операторы всегда можно использовать в логических выражениях, однако это встречается нечасто. Решающую роль эти операторы играют при модификации данных; поэтому они и описаны в разделе 8.1, посвященном модификации данных.
Логические операторы и операторы отношения применяются исключительно в логических выражениях, которые рассматриваются в настоящей главе.
7.1.2 Операторы отношения
7.1.2 Операторы отношения
Отношение — это логическое выражение, в котором два значения сравниваются друг с другом посредством оператора отношения. В областях, где применяется SPSS в операторах отношения значения переменной сравниваются с каким-либо численным значением (константой), например
sex = 2 partei ~= 3 alter > 30
Для построения логических выражений могут применяться следующие операторы отношения:
Знак на кнопке | Альтернативный текст | Значение (рус./англ.) |
< | LT | меньше (less than) |
> | GT | больше (greater than) |
<= | LE | меньше или равно (less than or equal to) |
>— | GE | больше или равно (greater than or equal to) |
= | EQ | равно (equal to) |
~= | NE или <> | не равно (not equal to) |
Операторы можно ввести в редактор условий либо щелкнув в диалоговом окне на кнопке с соответствующим знаком, либо введя с клавиатуры альтернативный текст. Например, вместо ~= можно ввести NE или <>.
7.1.3 Логические операторы
7.1.3 Логические операторы
Для построения условных выражений могут применяться следующие логические операторы:
Знак на кнопке | Альтернативный текст | Значение |
& | AND | Логическое И |
| | OR | Логическое ИЛИ |
~ | NOT | Логическое НЕ |
Логические операторы AND и OR связывают два отношения, а логический оператор МОТ меняет значение истинности условного выражения на противоположное. Между логическими операторами устанавливаются следующие приоритеты:
Приоритет | Оператор |
1 | NOT |
2 | AND |
3 | OR |
7.1.4 Булева алгебра
7.1.4 Булева алгебра
Логические операторы основаны на принципах булевой алгебры (логики высказываний), краткий обзор которых приводится в данном разделе.
Оператор И (конъюнкция)
Выражение 1 | Выражение 2 | Результат |
и | и | и |
и | л | л |
л | и | л |
л | л | л |
Легенда: и = истина (true); л = ложь (false)
При конъюнкции все участвующие выражения (отношения) должны быть истинными, чтобы общий результат также являлся истинным. Примеры:
Выражение | Истинность |
(3<7) AND (8>5) | и |
(12=8) AND (4=4) | л |
(3<=5) AND (4>=1) | и |
(8=4) AND (7=3) | л |
Оператор ИЛИ (дизъюнкция)
Выражение 1 | Выражение 2 | Результат |
и | и | и |
и | л | и |
л | и | и |
л | л | л |
При дизъюнкции хотя бы одно из участвующих отношений должно быть истинным, чтобы общий результат также был истинным. Примеры:
Выражение | Истинность |
(3<5) OR (47+1 0<10) | и |
(3=8) OR (7>5) | и |
(4:7=2) OR (8*4=21) | л |
(42=16) OR (23=3) | и |
Логическое НЕ (отрицание)
Выражение | Результат |
и | л |
л | и |
Отрицание меняет истинность выражения на противоположную. Примеры:
Выражение | Истинность |
NOT [(3<5) AND (4>5)] | и |
NOT [(4<5) AND (8<12)] | л |
При отрицании следует учитывать эквивалентность операторов:
отрицаемый оператор | эквивалентный оператор |
< | >- |
> | < = |
<= | > |
> = | < |
В заключение приведем пример более сложного логического выражения: [(NOT A) AND (NOT В)] OR С
Согласно правилам приоритета скобки здесь не нужны. Мы поместили их только для повышения наглядности. Истинность выражения можно определить при помощи следующей таблицы:
А | И | С | NOT A | NОТ В | (NОT A) AND (NОT В) | OR С |
и | и | и | л | л | л | и |
и | и | л | л | л | л | л |
и | л | и | л | и | л | и |
и | л | л | л | л | л | л |
л | и | и | и | л | л | и |
л | и | л | и | л | л | л |
л | л | и | и | и | и | и |
л | л | л | и | и | и | и |
Для более сложных выражений также следует составлять подобные таблицы.
Если все эти элементы логики высказываний кажутся вам слишком математизированными или абстрактными, вполне можно ориентироваться по разговорному употреблению союза "и". Высказывание: "Я был в кино и видел интересный фильм", истинно тогда и только тогда, когда истинны обе его части. Если, несмотря на то, что вы ходили в кино, но на сеансе заснули от скуки, это выражение не будет истинным. Также оно не будет истинным, если вы смотрели интересный фильм по телевизору. И, конечно же, оно будет совершенно ложным (хотя здесь нас не интересует степень ложности), если вы и не были в кино, и не смотрели там интересный фильм.
Иначе обстоит дело при разговорном применении союза "или", которое в основном означает исключающее "или", когда, например, дети хотят получить на Рождество или компьютер, или велосипед.
7.1.5 Функции
7.1.5 Функции
Список функций, который мы сейчас рассмотрим, — следующая важная часть диалогового окна Select Cases: If.
Этот список содержит множество математических функций, большая часть из которых, однако, имеет отношение только к модификации данных (расчету новых переменных). Поэтому обзор этих функций представлен в соответствующем разделе (см. раздел 8.1.2). Здесь мы рассмотрим только логические и строковые функции.
Логические функции
В SPSS реализованы две логические функции:
-
RANGE (variable, begin, end): Функция RANGE возвращает значение 1, или true, если значение переменной лежит в диапазоне между заданными начальным и конечным значениями. Переменная может иметь как численный, так и строковый тип. RANGE (alter, 18, 22) возвращает значение 1, то есть true, если значение переменной alter лежит между 18 и 22 включительно. Можно задавать несколько диапазонов, например, RANGE (alter, 1,17, 63, 99). В этом случае функция возвращает true, если значение переменной alter лежит между 1 или 17 или между 63 и 99 включительно. В функции RANGE можно также использовать переменные строкового типа, например, RANGE (name, A, Mzzzzzz). Тогда функция будет возвращать 1 для имен, начинающихся с букв от А до М включительно. Если имя начинается с другой буквы, функция возвратит 0.
-
ANY (variable, vail, va!2, val3,...): Функция ANY возвращает значение 1, или true, если значение переменной (значение первого аргумента) совпадает по крайней мере с одним из значений, указанных в последующем списке параметров (vail, va!2, va!3, ...). В противном случае возвращается значение 0 или false. Первый элемент, как правило, — переменная численного или символьного типа. Примеры: ANY (jahr, 1991, 1992, 1993, 1994) возвращает true, если значение переменной jahr равно 1991, 1992, 1993 или 1994. ANY (name, Schmidt, Meier, Raabe) возвращает значение true или 1 в тех случаях, когда переменная name содержит значения Schmidt, Meier или Raabe. Во всех остальных случаях возвращается значение 0. Не забывайте заключать строковые значения в двойные кавычки.
Строковые функции
Из общего количества 18 строковых функций мы рассмотрим три самых важных, на наш взгляд.
-
SUBSTR (variable, begin, length): Эта функция извлекает определенную часть из строки. Она возвращает подстроку или отдельный символ. Например, если строковая переменная name содержит значение Mannheim, то следующий вызов функции
SUBSTR (name, 1, 2)
возвратит значение Ма. Здесь из переменной name извлекаются два знака (третий аргумент) начиная с первой позиции (второй аргумент). Выражение
SUBSTR (name, I, 2) = Ma
будет истинным для значений переменной Maus, Mannesmann или Mahlmann. При сравнении со строками вместо двойных кавычек (= "Ма") можно также применять простые (= 'Ма'). Однако смешение простых и двойных кавычек (= 'Ма") не допускается.
-
UPCASE (argument): Функция UPCASE преобразует строчные буквы в прописные. В качестве аргумента можно задавать строку или переменную символьного типа. UPCASE (vorname) возвращает значение ANNA, если переменная vorname имеет значение Anna.
-
LOWER (argument): Функция LOWER преобразует прописные буквы в строчные.
В качестве параметра можно задавать строку или переменную символьного типа.
-
LOWER (vorname) возвращает значение anna, если переменная vorname имеет значение ANNA или Anna.
Функции переносятся в редактор условий следующим образом:
-
Поместите курсор на место в условном выражении, на котором должна быть вставлена функция.
-
Дважды щелкните на функции в списке функций или выделите функцию и щелкните на кнопке с треугольником около списка функций.
Функция будет вставлена в выражение. Вместо аргументов в этой функции будут стоять вопросительные знаки. Количество вопросительных знаков указывает минимальное количество аргументов, которое следует вставить. Отредактировать функцию можно следующим образом:
-
Выделите вопросительные знаки во вставленной функции.
-
Замените их соответствующими аргументами. Имена переменных для аргументов можно перенести из списка исходных переменных.
В заключение мы составим список приоритетов при построении логических выражений:
Приоритет | Оператор/функция | Значение |
1 | 0 | Оператор скобок |
2 | Функции | Различные значения |
3 | < | Меньше |
<= | Меньше или равно | |
> | Больше | |
>= | Больше или равно | |
= | Равно | |
"= | Не равно | |
4 | — | Логическое НЕ |
5 | 6, | Логическое И |
6 | I | Логическое ИЛИ |
7.1.6 Ввод условного выражения
7.1.6 Ввод условного выражения
Теперь попробуем снова выполнить отбор, но в этот раз будем выбирать только респондентов-женщин. Выполните следующие действия:
-
Перенесите переменную sex в редактор условий, дважды щелкнув на ней или выделив ее и щелкнув на кнопке с треугольником.
-
Щелкните на кнопке со знаком равенства на клавиатуре. Этот знак будет скопирован в редактор условий.
-
Щелкните на кнопке 1 на клавиатуре. Знак будет скопирован в редактор условий. Вид диалогового окна показан на рис. 7.3.
Условие имеет вид sex = 1, то есть будут выбраны все наблюдения, для которых переменная sex имеет значение 1 (женский).
Рис. 7.3: Условие в редакторе условий
-
Подтвердите выбор кнопкой Continue (Продолжить). Вы вернетесь в диалог Select Cases. Однако теперь в диалоговом окне появилось условие sex = 1.
-
Щелкните на кнопке ОК. Вы снова окажетесь в редакторе данных.
Примечание: Выбранные опции соответствуют следующему командному синтаксису:
SELECT IF sex = 1.
EXECUTE .
Теперь фильтрация наблюдений включена. О том, что отбор, заданный с помощью диалоговых окон осуществлен свидетельствует сообщение Filter on (Фильтр включен), которое появляется в строке состояния в нижней части окна SPSS. Система создает переменную filter_S. Это численная переменная с длиной один байт. Она имеет следующие метки значений: 0 = Not Selected (Не выбрано), 1 = Selected (Выбрано), так как нуль обозначает ложь (false), а единица — истину (true). При всех последующих операциях будут учитываться только наблюдения, для которых значение этой переменной равно 1, то есть те, для которых выполняется условие sex = 1. Номера неотобранных наблюдений отображаются зачеркиванием в левом крае редактора данных. Теперь проведем частотный анализ переменной partei. Мы получим следующий результат:
Партия
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | ХДС/ХСС | 5 | 33,3 | 35,7 | 35,7 |
СДП | 1 | 6,7 | 7,1 | 42,9 | |
сдпг | 4 | 26,7 | 28,6 | 71,4 | |
Зеленые/Союз 90 | 2 | 13,3 | 14,3 | 85,7 | |
пдс | 1 | 6,7 | 7,1 | 92,9 | |
Прочие | 1 | 6,7 | 7,1 | 100,0 | |
Всего | 14 | 93,3 | 100,0 | ||
Missing Total | нет данных | 1 15 | 6,7 100,0 |
Из 30 наблюдений файла wahl.sav условие отбора выполняется в 15 наблюдениях; для них sex = 1. Эти 15 наблюдений и учитываются при частотном анализе переменной partei. Для одного из отобранных наблюдений данных о партии нет.
Обратите внимание, что фильтр действует и при остальных статистических процедурах. Команда SPSS SELECT IF или соответствующие настройки в диалоговых окнах фильтруют наблюдения постоянно, то есть до тех пор, пока фильтр не будет удален или деактивирован. Чтобы удалить фильтр, поступите следующим образом:
-
Щелкните на имени переменной filter_$. Весь столбец будет выделен.
-
Нажмите клавишу <Backspace>. Переменная фильтра будет удалена.
Если требуется не удалять фильтр, а лишь временно деактивизировать его, выполните следующие действия:
-
Выберите в меню команды Data (Данные) elect Cases... (Выбрать наблюдения)
-
В диалоговом окне Select Cases щелкните на кнопке All cases (Все наблюдения). Условие фильтра будет деактивировано, однако переменная filter_S сохранится. В любой момент ее можно будет активизировать снова.
На уровне синтаксических команд отбор можно выполнить при помощи единственной процедуры, которая показана ниже. Для этого применяется команда TEMPORARY:
TEMPORARY.
SELECT IF sex = 1. FREQUENCIES VARIABLES = partei.
Временный фильтр можно ввести только вручную в редакторе синтаксиса SPSS; через диалоговые окна этого сделать невозможно. Этот пример показывает, что непосредственный ввод команд в редакторе синтаксиса имеет некоторые преимущества. Об этом мы еще расскажем в главе 26 (Программирование).
При вводе команд в редакторе синтаксиса следует обращать внимание на различие между численными и строковыми переменными.
Численная переменная:
SELECT IF sex = 1.
Строковая переменная:
SELECT IF fragebnr = "W-001".
Для строковых переменных (как fragebnr (код анкеты) в этом примере) следует применять простые или двойные кавычки. Слова SELECT IF необходимы только при непосредственном вводе команды в редакторе синтаксиса; та же самая строка в редакторе условий диалога Select Cases: If будет более компактной:
sex = 1 ИЛИ
fragebnr = "W-001"
Здесь также следует учитывать различие между численными и строковыми переменными.
3.gif

7.1.7 Примеры отбора данных
7.1.7 Примеры отбора данных
Здесь мы представим некоторые примеры отбора данных. Рассмотрим следующие условия:
1. Требуется отобрать только респондентов-мужчин. В редакторе условий вводится следующая строка:
sex = 2
Эту строку можно набрать непосредственно или перенести с помощью кнопки с треугольником и кнопок клавиатуры.
2. Требуется отобрать только респондентов-женщин, которые голосовали за ХДС/ХСС. В редакторе условий вводится следующая строка:
sex = 1 & partei = 1
ИЛИ
sex = 1 AND partei = 1
Обратите внимание на значение переменной фильтра в наблюдении 22 (fragebnr = 0-007). Здесь это системное пропущенное значение. В этом случае SPSS не может сделать никакого вывода об истинности, так как переменная partei имеет значение О = нет данных или данные не введены. Поэтому условие sex =1 & partei = 1 в наблюдении 22 нельзя проверить на истинность. Оно может быть как истинным, так и ложным. Для такого неопределенного случая SPSS присваивает переменной filter_$ системное пропущенное значение.
Следовательно, таблицу истинности можно дополнить случаем отсутствующих значений:
Конъюнкция
Логическое выражение | Результат |
true AND true | true |
true AND false | false |
false AND true | false |
false AND false | false |
true AND missing | missing |
false AND missing | false |
missing AND missing | missing |
Дизъюнкция
Логическое выражение | Результат |
true OR true | true |
true OR false | true |
false OR true | true |
false OR false | false |
true OR missing | true |
false OR missing | missing |
missing OR missing | missing |
Отрицание:
Логическое выражение | Результат |
true | false |
false | true |
missing | missing |
Если результат логического выражения равен missing (отсутствует), то данный случай, как и при результате false, не учитывается при дальнейшей обработке.
3. Требуется отобрать только респондентов, имеющих возраст от 40 до 60 лет включительно.
alter >= 40 & alter <= 60
ИЛИ
alter >= 40 AND alter <= 60
Более изящным будет применение здесь функции
RANGE: RANGE (alter, 40, 60).
4. Требуется отобрать только респондентов-женщин, которые старше 60 лет. sex =1 & alter > 60 ИЛИ sex =1 AND alter > 60.
5. Требуется отобрать только респондентов-мужчин, возраст которых не превышает 25 лет и которые голосовали за СДПГ. При формулировке условия не старше 25 лет применяется оператор NOT:
sex = 2 S partei = 3 & ~ alter > 25
ИЛИ
sex = 2 S partei = 3 S NOT alter > 25.
Оператор NOT обязательно должен стоять в начале логического выражения. Выражение & alter ~> 25 не допускается в SPSS. В этом случае вы получите сообщение об ошибке с подсказкой, где должен находиться оператор NOT.
6. Требуется отобрать респондентов, которые голосовали за ХДС, СДП или республиканцев.
partei = 1 | partei = 2 | partei = 6
ИЛИ
partei = 1 OR partei = 2 OR partei = 6.
Здесь более изящным будет применение функции ANY:
ANY (partei, 1, 2, 6).
7. Отберем респондентов, которые опрашивались в Западной Германии:
fragebnr >= "W-"
Здесь более изящным будет применение функции SUBSTR:
SUBSTR (fragebnr,1,1) = "W"
ИЛИ
SUBSTR (fragebnr,1,2) = "W-"
Можно также применить функцию RANGE:
RANGE (fragebnr, W-001, W-999)
ИЛИ
RANGE (fragebnr, "W-001", "W-999").
8. Отберем респондентов, которые опрашивались в Восточной Германии: fragebnr >= "0-" & fragebnr < "W-"
Достаточно также просто ввести
fragebnr < "W-"
И в этом случае изящнее будет вариант с SUBSTRING:
SUBSTR(fragebnr,1,1) = "О"
или
SUBSTR(fragebnr,1,2) = "0-"
Можно также применить функцию RANGE:
RANGE (fragebnr, "O-001", "0-999")
Удобно использовать оператор NOT:
~ fragebnr >= "W"
Далее мы рассмотрим применение функций UPCASE и LOWER. При этом будем исходить из следующей ситуации.: При вводе номеров анкет иногда по ошибке вме-^то прописного "W" для Западной Германии было закодировано строчное "w". Эти наблюдения не будут отобраны по условию SUBSTR(fragebnr, 1,1) = "W". В таком ^лучае может помочь функция UPCASE или LOWER:
SUBSTR (UPCASE (fragebnr,1,1) = "W".
Рассмотренная конструкция называется вложенной функцией. Вложенные функции вычисляются в направлении изнутри наружу. Функция UPCASE преобразует содержимое переменной fragebnr в прописные буквы. Преобразованное содержимое затем передается в функцию SUBSTR. Эта функция выделяет из строки первую букву. Полученная буква сравнивается с буквой W. Если они совпадают, данное наблюдение выбирается, то есть переменная фильтра filter_S приобретает значение 1. Если применяется функция LOWER, строка в редакторе условий будет выглядеть так:
SUBSTR (LOWER (fragebnr, 1,1) = "w".
Функция LOWER преобразует содержимое переменной fragebnr в строчные буквы. Преобразованное содержимое передается в функцию SUBSTR. Эта функция выделяет из строки первую букву. Полученная буква сравнивается с буквой w. Если они совпадают, данное наблюдение отбирается.
7.2 Извлечение случайной выборки
7.2 Извлечение случайной выборки
При большом количестве наблюдений для экономии времени может быть полезно использовать небольшую случайную выборку при первой предварительной проверке гипотезы. Чтобы извлечь случайную выборку из совокупности всех наблюдений, выполните следующие действия:
-
Выберите в меню команды Data (Данные) Select Cases... (Выбрать наблюдения)
-
Выберите пункт Random sample of cases (Случайная выборка), а затем щелкните на кнопке Sample... (Выборка). Откроется диалоговое окно Select Cases: Random Sample (Выбрать наблюдения: Случайная выборка).
Рис. 7.4: Диалоговое окно Select Cases: Random Sample
В группе Sample Size (Размер выборки) можно выбрать один из следующих способов определения объема выборки:
-
Approximately (Приблизительно): Пользователь может указать здесь процентного значение. SPSS создаст случайную выборку с объемом, приблизительно соответствующим указанному проценту наблюдений.
-
Exactly (Точно): Пользователь должен указать здесь точное количество наблюдений в случайной выборке. Кроме того, здесь надо задать количество наблюдений, из которых будет извлечена выборка. Второе число не должно превышать общего количества наблюдений в файле данных. Для каждой случайной выборки генератор случайных чисел SPSS использует новое начальное значение. Таким образом, каждый раз при обращении к данному диалогу создается новая выборка наблюдений, отличная от прежних. Если требуется, чтобы случайная выборка повторялась, надо задать начальное значение самостоятельно.
-
Для этого выберите в меню команды Transform (Преобразовать) Random Number Seed... (Установить начальное положение генератора случайных чисел)
Откроется диалоговое окно Random Number Seed.
Начальное значение может быть любым положительным целым числом. Это значение можно задать самостоятельно или предоставить сделать это SPSS (вариант Random Seed, принятый по умолчанию).
Рис. 7.5: Диалоговое окно Random Number Seed.
4.gif
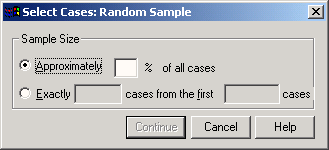
5.gif
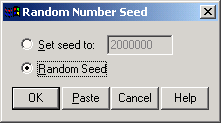
7.3 Сортировка наблюдений
7.3 Сортировка наблюдений
Данные в SPSS можно сортировать в соответствии со значениями одной или нескольких переменных. Рассмотрим следующий пример: Требуется упорядочить данные файла wahl.sav по возрасту. Для этого поступите следующим образом:
-
Выберите в меню команды Data (Данные) Sort Cases... (Сортировать наблюдения)
Откроется диалоговое окно Sort Cases. Переменные файла данных будут отображены в списке исходных переменных.
Рис. 7.6: Диалоговое окно Sort Cases
-
Перенесите переменную alter в список Sort by (Сортировать по). В группе Sort order (Порядок сортировки) по умолчанию выбран вариант Ascending (По возрастанию). Эта опция сортирует наблюдения в порядке возрастания значения переменной сортировки, а следующая опция, Descending — в порядке убывания.
-
Подтвердите настройки кнопкой ОК. В редакторе данных файл wahl.sav будет отсортирован по возрастанию значений переменной alter.
Примечание: Выбранные опции соответствуют следующему командному синтаксису:
SORT CASES BY alter (A) .
или, если надо сортировать по убыванию:
SORT CASES BY alter (D) .
Здесь А обозначает ascending (возрастание), a D — descending (убывание). Если выбрать несколько переменных сортировки, их последовательность в списке Sort by будет определять порядок, в котором будут отсортированы наблюдения. Рассмотрим следующий пример: Необходимо отсортировать файл wahl.sav по значениям переменных nartei и alter. Переменная partei должна быть первым критерием сортировки, а переменная alter — вторым. Сортировка по переменной partei должна быть в порядке возрастания, а по переменной alter — в порядке убывания. Для этого перенесите в список переменных сортировки вначале переменную partei, а затем переменную alter. Выделите переменную alter и щелкните на опции Ascending.
Примечание: Выбранные опции соответствуют следующему командному синтаксису:
SORT CASES BY partei (A) alter (D) .
В редакторе данных файл wahl.sav будет отсортирован по возрастанию значений переменной partei. Наблюдения, относящиеся к одной и той же партии будут отсортированы по убыванию возраста.
6.gif

7.4 Разделение наблюдений на группы
7.4 Разделение наблюдений на группы
В SPSS можно выполнять анализ данных раздельно по группам. Группой в этом контексте называется определенное количество наблюдений с одинаковыми значениями признаков. Чтобы можно было производить обработку по группам, файл должен быть отсортирован по группирующим переменным. Такой переменной может быть, например, переменная sex. В этом случае все переменные со значением признака 1 (женский) образуют одну группу, а все переменные со значением признака 2 (мужской) — другую группу. С каждой группой можно проводить определенные операции, например, выполнять частотный анализ. При этом частотный анализ проводится раздельно для признаков мужской и женский. В SPSS такое разделение на группы можно выполнять автоматически. Рассмотрим следующий пример, основанный на опросе студентов об их психическом состоянии и социальном положении:
Проведем частотный анализ переменной psyche (психическое состояние) раздельно для всех изучаемых специальностей. В соответствии со значениями переменной fach (специальность) у нас образуются 9 групп (1 = Юриспруденция, 2 = Экономика, 3 = Гуманитарные науки, 4 = Психология и т.д.). В этом случае файл данных studium.sav должен быть сначала отсортирован по переменной fach. Поступите следующим образом:
-
Загрузите файл studium.sav в редактор данных.
-
Выберите в меню команды Data (Данные) Split File... (Разделить файл) Откроется диалоговое окно Split File.
Рис. 7.7: Диалоговое окно Split File
По умолчанию разделение на группы не предполагается. Если выбрать пункт Organize output by groups (Разделить вывод на группы), мы получим вывод результатов по каждой группе отдельно. Эти группы должны быть определены в поле Groups based on (Группы, созданные на основе) на базе соответствующих переменных.
Еще одну возможность предоставляет опция Compare Groups (Сравнить группы). Она организует вывод таким образом, что можно визуально сравнить разные группы друг с другом. Но сначала мы рассмотрим раздельный вывод.
-
Выберите опцию Organize output by groups. Для раздельного выполнения операций по группам необходимо, чтобы файл данных был предварительно отсортирован по этим группирующим переменным. По этой причине опция Sort the file by grouping variables (Сортировать файл по группирующим переменным) выбрана по умолчанию.
-
Перенесите переменную fach в поле Groups based on. Если выбирается несколько группирующих переменных, то последовательность, в которой они стоят в списке, определяет порядок или приоритет сортировки.
-
Щелкните на кнопке ОК. Файл studium.sav будет отсортирован по переменной fach, то есть разбит на группы в соответствии с ее значениями. Сообщение File split on (Разделение файла включено) в строке состояния внизу окна SPSS информирует об активации режиме разделения.
-
Выполните частотный анализ переменной psyche.
Вы получите следующий результат (ниже для экономии места показаны частотные таблицы только для специальностей Юриспруденция и Естественные науки).
Специальность = Юриспруденция
Статистика(а)
Психическое состояние | |
N Valid Missing | 22 0 |
а. Специальность = Юриспруденция | |
Психическое состояние(а)
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | Крайне неустойчивое | 2 | 9,1 | 9,1 | 9,1 |
Неустойчивое | 5 | 22,7 | 22,7 | 31,8 | |
Устойчивое | 12 | 54,5 | 54,5 | 86,4 | |
Очень устойчивое | 3 | 13,6 | 13,6 | 100,0 | |
| Total | 22 | 100,0 | 100,0 | ||
Спциальность = юриспруденция | |||||
Специальность = Естественные науки
Статистика(а)
N Valid Missing | 18 1 | |
а. Специальность = Естественные науки | ||
Психическое состояние(а)
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | Крайне неустойчивое | 1 | 5,3 | 5,6 | 5,6 |
Неустойчивое | 4 | 21,1 | 22,2 | 27,8 | |
Устойчивое | 11 | 57,9 | 61,1 | 88.9 | |
Очень устойчивое | 2 | 10,5 | 11,1 | 100,0 | |
Всего | 18 | 94,7 | 100,0 | ||
Missing | нет данных | 1 | 5,3 | ||
Всего | 19 | 100,0 |
а. Специальность = Естественные науки
Как видно, результаты частотного анализа переменной psyche выводятся раздельно по специальностям студентов.
-
Теперь выберите другой пункт — Compare groups (Сравнить группы).
-
Снова выполните частотный анализ переменной psyche. Вы получите следующую результирующую таблицу:
Психическое состояние
Специальность |
|
| Frequency | Percent | Valid Percent | Cumulative Percent |
Юриспру- денция | Valid | Крайне неустойчивое | 2 | 9,1 | 9,1 | 9,1 |
| Неустойчивое | 5 | 22,7 | 22,7 | 31,8 | |
| Устойчивое | 12 | 54,5 | 54,5 | 86,4 | |
| Очень устойчивое | 3 | 13,6 | 13,6 | 100,0 | |
| Всего | 22 | 100,0 | 100,0 |
| |
Экономика | Valid | Крайне неустойчивое | 1 | 5,3 | 5,6 | 5,6 |
| Неустойчивое | 4 | 21,1 | 22,2 | 27,8 | |
| Устойчивое | 11 | 57,9 | 61,1 | 88,9 | |
| Очень устойчивое | 2 | 10,5 | 11,1 | 100,0 | |
| Всего | 18 | 94,7 | 100,0 |
| |
Missing | нет данных | 1 | 5,3 |
|
| |
Total | 19 | 100,0 |
|
|
| |
Гуманитар- ные науки | Valid | Крайне неустойчивое | 10 | 40,0 | 40,0 | 40,0 |
| Неустойчивое | 14 | 56,0 | 56,0 | 96,0 | |
| Устойчивое | 1 | 4,0 | 4,0 | 100,0 | |
| Всего | 25 | 100,0 | 100,0 |
| |
Психология | Valid | Крайне неустойчивое | 3 | 27,3 | 27,3 | 27,3 |
| Неустойчивое | 6 | 54,5 | 54,5 | 81,8 | |
| Устойчивое | 2 | 18,2 | 18,2 | 100,0 | |
| Всего | 11 | 100,0 | 100,0 |
| |
Теология | Valid | Крайне неустойчивое | 2 | 22,2 | 22,2 | 22,2 |
| Неустойчивое | 5 | 55,6 | 55,6 | 77,8 | |
| Устойчивое | 2 | 22,2 | 22,2 | 100,0 | |
| Всего | 9 | 100,0 | 100,0 |
| |
Медицина | Valid | Крайне неустойчивое | 1 | 10,0 | 10,0 | 10,0 |
| Неустойчивое | 3 | 30,0 | 30,0 | 40,0 | |
| Устойчивое | 5 | 50,0 | 50,0 | 90,0 | |
| Очень устойчивое | 1 | 10,0 | 10,0 | 100,0 | |
| Всего | 10 | 100,0 | 100,0 |
| |
Естествен- ные науки | Valid | Неустойчивое | 3 | 33,3 | 33,3 | 33,3 |
| Устойчивое | 6 | 66,7 | 66,7 | 100,0 | |
| Всего | 9 | 100,0 | 100,0 |
| |
Техника | Valid | Крайне неустойчивое | 1 | 50,0 | 50,0 | 50,0 |
| Устойчивое | 1 | 50,0 | 50,0 | 100,0 | |
| Всего | 2 | 100,0 | 100,0 |
| |
Прочие | Valid | Устойчивое | 1 | 100,0 | 100,0 | 100,0 |
Учтите, что файл данных останется разделенным на подгруппы, пока вы не деактивируете соответствующие опции. Для этого поступите следующим образом:
-
Выберите в меню команды Data (Данные) Split File... (Разделить файл)
-
В диалоговом окне Split File выберите опцию Analyze all cases, do not create groups (Анализировать все наблюдения, не создавать группы). Теперь разделение файла убрано.
-
Если требуется дополнительно убрать сортировку по специальностям, выберите в меню следующие команды Data (Данные) Sort Cases... (Сортировать наблюдения)
-
Перенесите переменную fragebnr (код анкеты) в список переменных сортировки и подтвердите операцию кнопкой ОК. Данные будут отсортированы в исходном порядке — по номерам анкет.
На этом мы заканчиваем обзор возможностей отбора данных в SPSS и переходим к изучению средств модификации данных.
7.gif
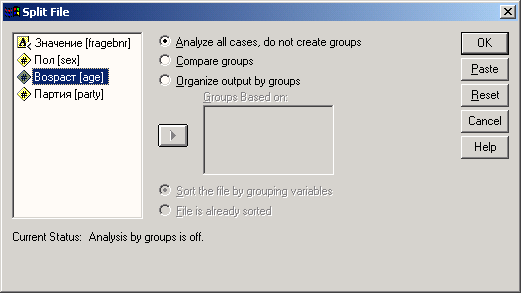
Глава 8. Модификация данных
Глава 8. Модификация данных
1. Модификация данных
Модификация данных
Для проведения анализа часто бывает необходимо выполнить преобразование данных. На основе первоначально собранных данных можно создать новые переменные и изменить кодирование. Подобные преобразования называются модификацией данных.
В SPSS существует много возможностей для модификации данных. К важнейшим из них относятся:
-
Вычисление новых переменных путем использования различных арифметических выражений (математических формул)
-
Подсчет частоты появлений определенных значений
-
Перекодирование значений
-
Вычисление новых переменных при выполнении определенного условия
-
Агрегирование данных
-
Ранговые преобразования
-
Вычисление весов наблюдений
Разделы этой главы посвящены всем перечисленным возможностям модификации данных.
8.1 Вычисление новых переменных
8.1 Вычисление новых переменных
Путем вычислений в SPSS можно образовать новые переменные и добавить их в файл данных. Так, например, в медицинском исследовании (см. главу 9, файл hyper.sav) в два момента времени (до и после приема лекарства) проводились измерения систолического кровяного давления, которые фиксировались в переменных rrs0 и rrsl.
Если нас интересует изменение давления между двумя этими моментами, было бы глупо каждый раз вычислять разницу двух значений и вручную вводить ее в новую переменную. Эту работу можно переложить на компьютер, который сделает ее быстро и, главное, без ошибок. Для этого поступите следующим образом:
-
Загрузите файл hyper.sav в редактор данных.
-
Выберите в меню команды Transform (Преобразовать) Compute... (Вычислить) Откроется диалоговое окно Compute Variable (Вычислить переменную).
Рис. 8.1: Диалоговое окно Compute Variable
В поле Target Variable (Выходная переменная) указывается имя переменной, которой присваивается вычисленное значение. В качестве выходной переменной может служить уже существующая или новая переменная. В поле Numeric Expression (Численное выражение) вводится выражение, применяемое для определения значения выходной переменной. 3 этом выражении могут использоваться имена существующих переменных, константы, арифметические операторы и функции.
-
Введите в поле Target Variable имя rrsdiff, а в поле Numeric Expression формулу rrs0— rrsl. Зту формулу можно ввести либо вручную, либо используя список переменных и клавиатуру диалогового окна. Кнопка с треугольником позволяет копировать в поле формулы имена переменных, а кнопки клавиатуры — вставлять цифры и знаки.
-
Щелкните на кнопке Type&Label... (Тип и метка).
Откроется диалоговое окно Compute Variable: Type and Label (Вычислить переменную: Тип и метка).
Здесь можно задать метку для новой переменной rrsdiff. В поле Label введите текст Изменение сист. кровяного давления и щелкните на кнопке Continue.
-
В диалоговом окне Compute Variable щелкните на кнопке ОК.
Рис. 8.2: Диалоговое окно Compute Variable: Type and Label
Примечание: Выбранные опции соответствуют следующему командному синтаксису:
COMPOTE rrsdiff = rrs0 - rrsl.
VARIABLE LABELS rrsdiff = "Изменение сист. кровяного давления".
EXECUTE.
Общий формат команды COMPUTE имеет следующий вид:
COMPUTE целевая_переменная = арифметическое_выражение.
Команда EXECUTE считывает данные и выполняет предшествующие команды преобразования. В файл данных добавляется новая переменная rrsdiff. Теперь ее, как и прочие переменные, можно применять для вычислений. Для SPSS нет разницы, введены ли значения переменных через редактор данных или вычислены по формуле.
Вместо слова формула мы будем использовать в дальнейшем понятие численное выражение. При формулировке таких численных выражений нужно соблюдать определенные правила, которые представлены в следующем разделе.
1.gif

2.gif

8.1.1 Формулировка численных выражений
8.1.1 Формулировка численных выражений
Для построения численных выражений можно применять следующие арифметические операторы:
Арифметические операторы
+ | Сложение |
- | Вычитание |
* | Умножение |
/ | Деление |
** | Возведение в степень |
С помощью арифметических операторов в численных (арифметических) выражениях можно задавать такие основные действия, как сложение и вычитание.
Так как структура выражений может быть сложной, следует учитывать следующие приоритеты арифметических операторов:
Приоритет | Оператор | Значение |
1 | () | Оператор скобок |
2 | ** | Возведение в степень |
3 | * | Умножение |
/ | Деление | |
4 | + | Сложение |
— | Вычитание |
Операции более высокого приоритета выполняются раньше операций с более низким приоритетом; приоритет 1 наивысший, а 4 — самый низкий. Далее на нескольких типичных примерах показано, на что следует обращать внимание при записи численных выражений. Если вы хотите выразить только что вычисленное изменение кровяного давления в процентах от исходного значения, надо составить следующую команду:
COMPUTE rrsdiff = (rrsl - rrsO) / rrs0 * 100 .
В этой формуле выполняются операции трех разных видов, имеющие разные приоритеты. Так, умножение и деление выполняются всегда перед сложением и вычитанием, если только, как в данном примере, скобки не определяют другую последовательность выполнения.
Если рост (в см) записан в переменной gr, и вы хотите определить на его основе нормальный вес, который обычно равен росту в см минус 100, команда, которая создает для этой величины новую переменную, будет следующей:
COMPUTE ng = gг - 100 .
Если же требуется вычислить избыточный вес как разницу фактического веса, который хранится в переменной gew, и этой новой величины, для этого служит команда
COMPUTE uegew = gew — ng .
Отрицательное значение uegew указывает на недостаточный вес. Оба выражения можно объединить:
COMPUTE uegew = gew — (gr — 100) .
Это можно также записать в виде
COMPUTE uegew = gew — gr + 100 .
Формула для определения избыточного веса в процентах к нормальному:
COMPUTE puegew = (gew — ng) / ng * 100 .
Без использования вспомогательной переменной ng эта формула имеет вид
COMPUTE puegew = (gew - (gr - 100)) / (gr - 100) * 100 .
Эта запись выглядит уже довольно сложной и имеет тот недостаток, что выражение gr — 100 должно быть вычислено дважды. Разумеется, при высокой производительности компьютера это не так важно.
Мы уже видели, что в арифметических выражениях могут участвовать переменные и константы. Сейчас мы рассмотрим применение и них функций, которые встроены в SPSS. Если нас интересует не само изменение кровяного давления, а только его абсолютная ветчина, в этом случае можно применить функцию ABS:
COMPUTE rrsd = ABS(rrsl - rrs0)
Чтобы вычислить десятичный логарифм переменной х, применяется функция LG10:
COMPUTE у = LG10(x)
Мы также можем вычислить гипотенузу по теореме Пифагора, использовав функцию SQRT для извлечения квадратного корня и оператор возведения в степень:
COMPUTE с = SQRTfa ** 2 + b ** 2) .
Аргументы функций сами могут быть арифметическими выражениями: Если вы не хо-:ите работать с командами синтаксиса SPSS, можно, как показано в начале главы, применить диалоговое окно Compute Variable. В этом случае в редакторе условий достаточно вместо
COMPUTE rrsd = rrs1 - rrs0 .
ввести просто
rrsd = rrsl - rrs0 для достижения той же цели — вычисления изменения кровяного давления rrsd.
8.1.2 Функции
8.1.2 Функции
Из числа функций, которые отображаются в диалоговом окне Select Cases: If, мы рассмотрели только логические и строковые функции. Остальные функции можно разделить на следующие классы:
-
арифметические функции
-
статистические функции
-
функции даты и времени
-
функции обработки отсутствующих значений
-
функции извлечения значений наблюдений
-
статистические функции распределения
-
функции генерации случайных чисел.
Параметрами функций могут быть переменные, константы или выражения. Параметры заключаются в круглые скобки; несколько параметров отделяются друг от друга запятыми, например, SUM (5, 8, 10). Функция SUM вычисляет сумму трех параметров. SUM (5, 8, 10) возвращает значение 23.
Арифметические функции
-
ABS (numexpr): Функция ABS возвращает абсолютное значение. Если переменная celsius имеет значение -6,5, ABS (celsius) возвращает 6,5, a ABS (celsius + 3) — значение 3,5.
-
RND (numexpr): Функция RND округляет до ближайшего целого числа. Если переменная celsius имеет значение 3,6, RND (celsius) возвращает 4, a RND (celsius + 6) — значение 10.
-
TRUNC (numexpr): Функция отбрасывает дробную часть значения; округления не происходит. Если переменная celsius имеет значение 3,9, TRUNC (celsius) возвращает 3, a TRUNC (celsius + 4) — значение 7.
-
MOD (numexpr, modulus): Функция MOD возвращает остаток от деления первого аргумента (numexpr) на второй (modulus). Если переменная jaehr имеет значение 1994, MOD (jaehr, 100) возвращает 94.
-
SQRT (numexpr): Функция SQRT возвращает квадратный корень. Если переменная zahll имеет значение 9, SQRT (zahll) возвращает значение 3.
-
ЕХР (numexpr): Показательная функция.
-
LG10 (numexpr): Десятичный логарифм.
-
LN (numexpr): Натуральный логарифм.
-
ARSIN (numexpr): Арксинус.
-
ARTAN (numexpr): Арктангенс.
-
SIN (numexpr): Синус.
-
COS (numexpr): Косинус.
В тригонометрических функциях аргументы задаются в радианах.
Статистические функции
Статистические функции могут иметь любое количество параметров.
-
SUM (numexpr, numexpr,...): Функция SUM возвращает сумму значений допустимых аргументов. SUM (zahll, zahll, zah!3) возвращает сумму значений трех переменных.
-
MEAN (numexpr, numexpr,...): Функция MEAN возвращает среднее арифметическое допустимых аргументов. MEAN (42, 19, 29) возвращает значение 30.
-
SD (numexpr, numexpr,...): Функция SD возвращает стандартное отклонение значений допустимых аргументов.
-
VARIANCE (numexpr, numexpr,...): Функция VARIANCE возвращает дисперсию значений допустимых аргументов.
-
CFVAR (numexpr, numexpr,...): Функция CFVAR возвращает коэффициент вариации значений допустимых аргументов.
-
MIN (numexpr, numexpr,...): Функция MIN возвращает наименьшее из значений допустимых аргументов.
-
MAX (numexpr, numexpr,...): Функция МАХ возвращает набольшее из значений допустимых аргументов.
Функциям SUM, MEAN, MIN и МАХ требуется хотя бы один допустимый аргумент, функциям SD, VARIANCE и CFVAR — два. Остальные аргументы могут содержать отсуттвуюшие значения. Если это свойство, принятое по умолчанию, требуется деактивировать, то к имени функции через точку прибавляют количество необходимых аргументов, например, MEAN. 10. В этом случае значение функции вычисляется только тогда, когда существует хотя бы указанное количество аргументов (в данном примере 10).
Функции даты и времени
В SPSS очень часто в различных целях используются дата и время. Для ввода данных гтого типа в редакторе данных SPSS предоставляет ряд различных форматов, описанных в разделе 3.4.1. Существующие форматы можно просмотреть в диалоговом окне Variable Tуре (Тип переменной).
Мы рекомендует использовать общепринятый формат даты: указание числа месяца двумя цифрами, месяца — также двумя цифрами и года — четырьмя цифрами через течку: dd.mm.yyyy.
Экономии места за счет отбрасывания двух первых цифр года в последнее время, как известно, уделяется много внимания. При указании года двумя цифрами в качестве столетнего диапазона в SPSS принят срок с 1931 по 2030 г., следовательно, год 28 интерпретируется как 2028, а 32 — как 1932. В меню Edit (Правка) Options... (Параметры...) на вкладке Data (Данные) пользователь может самостоятельно задать столетний диапазон..
Если число или месяц можно записать одной цифрой, их не нужно дополнять спереди нулями. Таким образом, указание даты в следующих форматах будет допустимым:
20.6.1998
13.12.1887
1.10.2003
5.2.1997
Компьютер замечает противоречивое указание даты при вводе. Например, если попытаться ввести дату 29.2.1997, это значение не записано принято в ячейку.
Для времени мы рекомендуем формат hh:mm:ss, т.е. одна или две цифры для часов, минут и секунд через двоеточие. При отсутствии секунд можно также применять формат hh:mm. Примеры:
23:34:55
8:5:12
12:17:5
12:47 8:12
Дату и время, введенные в любом виде, SPSS преобразует во внутренний формат. Для даты это количество секунд, прошедших с 0 часов 15.10.1582 г. (момента введения григорианского календаря) до 0 часов заданного дня; для времени — количество секунд с 0 часов до заданного момента времени.
В принципе можно также хранить число, месяц, год, часы, минуты и секунды в отдельных переменных и определять дату или время во внутреннем формате при помощи соответствующих функций.
Всего в SPSS имеется 25 различных функций для работы с датой и временем. Важнейшие из них представлены ниже.
XDATE.MDAY(arg) | Выделяет из даты число |
XDATE.MONTH(arg) | Выделяет из даты месяц |
XDATE.YEAR(arg) | Выделяет из даты год |
XDATE.WKDAY(arg) | Номер дня недели (1 =' воскресенье, ,..., 7 = суббота) |
XDATE.JDAY(arg) | Номер дня в году |
XDATE.QUARTER(arg) | Номер квартала в году |
XDATE.WEEK(arg) | Номер недели в году |
XDATE.TDAY(arg) | Количество дней начиная с 15.10.1582 |
XDATE.DATE(arg) | Количество секунд начиная с 15.10.1582 |
DATE.DMY(d,m,y) | Преобразует данные числа месяца, месяца и года во внутреннюю дату |
DATE.MOYR(m.y) | Преобразует данные месяца и года во внутреннюю дату |
YRMODA(y,m,d) | Преобразует данные года, месяца и числа месяца (строго в приведенной последовательности) в количество дней начиная с 15.10.1582 |
XDATE.TIME(arg) | Количество секунд начиная с 0 часов |
TIME.HMS(h,m,s) | Преобразует данные часов, минут и секунд в секунды |
Функции даты и времени применяются чаще всего в ситуациях, когда требуется вычислить промежуток между двумя датами или моментами времени. Например, если имеется две даты, записанные в переменных datum 1 и datum2, длительность промежутка между ними в днях можно рассчитать по следующей формуле:
COMPUTE tage=XDATE.TDAY(datum2) - XDATE.TDAY(datural). EXECUTE.
Пример использования функции YRMODA приводится в разделе 8.8. Функции обработки пропущенных значений
-
VALUE (variable): Функция VALUE объявляет недействительным пользовательское пропущенное значение.
-
MISSING (variable): Функция MISSING возвращает значение 1 (или true), если переменная содержит пользовательское или системное пропущенное значение.
-
SYSMIS (variable): Функция SYSMIS возвращает значение 1 (или true), если переменная содержит системное пропущенное значение.
-
NMISS (variable,variable,...): Функция NMISS возвращает количество пропушен-нных значений в списке переменных.
-
NVALID (variable,variable,...): Функция NMISS возвращает количество допустимых значений в списке переменных.
Функции извлечения значений наблюдений
-
LAG (variable,n): Функция LAG возвращает значение соответствующей переменной за я наблюдений до текущего. Так, например, LAG( variable, I) позволяет получить значение переменной в предыдущем случае (см. первый пример в разделе 8.8).
Статистические функции распределения
В SPSS реализовано в совокупности 20 статистических функций распределения. Эти функций вычисляют значение вероятности для следующих распределений: ß-распределения, распределения Коши, хи-квадрат, экспоненциального распределения, Г-распределения, F-распределения, распределения Лапласа, логистического, логарифмически нормального. нормального распределений, распределения Парето, распределения Стьюдента, равномерного распределения, распределения Вейбулла (непрерывные функции), а также распределения Бернулли, биномиального, геометрического, гипергеометрического, негативно-биномиального распределений и распределения Пуассона (дискретные функции). Для 14 непрерывных функций распределения существуют соответствующие обратные функции.
Так, например, функция CDF.T(t,df) возвращает вероятность ошибки р для заданного значения функции распределения Стьюдента, t и числа степеней свободы df, функция IDF. T(p,df) возвращает значение t для заданных вероятности ошибки р и числа степеней свободы df.
Функции генерации случайных чисел
В SPSS реализовано в совокупности 24 функции генерации случайных чисел, в том теле для 20 встроенных статистических функций распределения; например функция RV.T(df) возвращает случайные числа, подчиняющиеся распределению Стьюдента при df степенях свободы. Функция UNIFORM (numexpr) генерирует равномерно распределенные случайные величины, находящиеся в интервале от 0 до 1, а ее аргумент задает начальное значение для генератора случайных чисел.
8.2 Подсчет частоты появлений определенных значений
8.2 Подсчет частоты появлений определенных значений
В SPSS есть возможность подсчитать количество появления одного и того же значения или значений для определенной переменной. Например, членам Дортмундского спортивного клуба задавались следующие вопросы:
Вопрос1: Вопрос 2: Вопрос3: | Укажите Ваш пол ... |
Укажите Ваш возраст ... | |
Какими из следующих видов спорта Вы активно занимаетесь: 3_1 : Плаванием: да/нет? 3_2: Гимнастикой: да/нет? 3_3: Легкой атлетикой: да/нет? 3_4: Волейболом: да/нет? 3_5: Теннисом: да/нет? 3 6: Велосипедным спортом: да/нет? 3_7: Футболом: да/нет? 3_8: Гандболом: да/нет? 3_9: Баскетболом: да/нет? |
Если во всех наблюдениях этого примера подсчитать число появлений значения 1 (= да) для переменных 3_1—3_9, то для каждого респондента мы получим количество видов спорта, которыми он активно занимается.
Для этого поступите следующим образом:
-
Загрузите файл sport.sav в редактор данных.
-
Выберите в меню команды Transform (Преобразовать) Count... (Подсчитать)
Откроется диалоговое окно Count Occurences of Values within Cases (Подсчитать количество значений в наблюдениях).
Рис. 8.3: Диалоговое окно Count Occurences of Values wirhin Cases
Это диалоговое окно разделено на следующие части:
-
Target variable (Выходная переменная): В поле Target variable указывается имя переменной, в которой будут содержаться подсчитанные значения.
-
Target Label (Метка): В поле Target Label указывается метка для выходной переменной.
-
Variables (Переменные): Этот список содержит переменные, выбранные из списка исходных переменных, хранящихся в файле данных, для которых нужно подсчитать определенные значения. Список не может одновременно содержать численные и строковые переменные.
-
Выделите в списке исходных переменных переменные v3_l—v3_9. Перенесите их в список переменных.
-
Присвойте выходной переменной имя sports и метку: «Количество разных видов спорта».
-
Щелкните на кнопке Define values... (Определить значения). Откроется диалоговое окно Count Values within Cases: Values to Count (Подсчитать значения в наблюдениях: какие значения?). (См. рис. 8.4.)
Рис. 8.4: Диалоговое окно Count Values within Cases:values to Count
Это диалоговое окно служит для определения подсчитываемых значений. Можно задать отдельное значение, диапазон или сочетание того и другого. В группе Value (Значение) можно выбрать один из следующих вариантов:
-
Value: Вводится отдельное значение, частоту которого необходимо подсчитать.
-
System missing (Системное пропущенное): Подсчитывается количество появлений системного пропущенного значения. В списке Values to count (Подсчитываемые значения) оно отображается как SYSMIS. Для строковых переменных этот вариант неприменим.
-
System- or user-missing (Пользовательские или системные пропущенные): Если выбрать этот вариант, будет подсчитано количество появлений всех пропущенных значений, как системных, так и пользовательских. В списке Values to count эти значения отображаются как MISSING.
-
Range through (Дипазон): Подсчитывается количество значений, находящихся в определенном диапазоне. Этот вариант также неприменим для строковых переменных.
-
Range: Lowest through (Диапазон: от наименьшего до): Подсчитывается количество значений, находящихся в диапазоне от наименьшего наблюдаемого до указанного. Этот вариант неприменим для строковых переменных.
-
Range: through highest (Диапазон: до наибольшего): Подсчитывается количество значений, находящихся в диапазоне от указанного до наибольшего наблюдаемого. Этот вариант неприменим для строковых переменных.
Если требуется подсчитать повторяемость нескольких значений, щелкните после выбора опции на кнопке Add (Добавить). В этом случае будет подсчитана частота повторений каждого значения, присутствующего в списке Values to count.
-
Задайте отдельное значение 1 и щелкните на кнопке Add.
-
Подтвердите ввод кнопкой Continue, а затем — ОК. В файл данных будет добавлена переменная sports, содержащая количество видов спорта, которыми занимается респондент.
3.gif
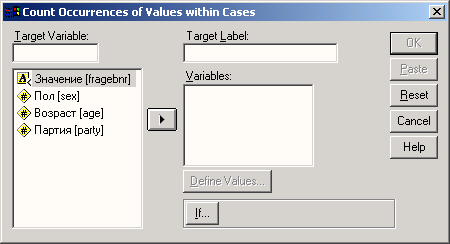
4.gif
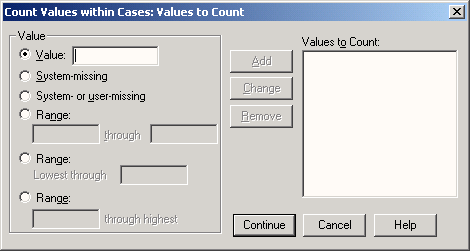
8.3 Перекодирование значений
8.3 Перекодирование значений
Первоначально собранные данные можно перекодировать с помощью средств SPSS. Перекодирование численных данных необходимо, например, тогда, когда первоначальное разнообразие исходных данных не нужно для последующего анализа. В этом случае перекодирование означает уменьшение объема обрабатываемой информации. Перекодирование данных можно выполнить вручную или автоматически. Мы рассмотрим оба этих метода.
8.3.1 Ручное перекодирование
8.3.1 Ручное перекодирование
Для примера мы проанализируем результаты воскресного опроса (файл wahl.sav). Нас интересует процентное распределение опрашиваемых в классическом политическом спектре правые-левые. В этом случае переменную partei следует перекодировать и создать новую переменную lire (левые-правые). Новые значения будут определены следующим образом:
Левые:
СПДГ
Зеленые/Союз 90
ПДС
Правые:
ХДС/ХСС
СДП
Республиканцы
не определено:
нет данных
Прочие
Сравним значения переменной partei со значениями переменной lire:
Переменная partei Значения | Метки значений | Переменная lire Значения | Метки значений |
0 | нет данных | 0 | не определено |
1 | ХДС/ХСС | 2 | правые |
2 | СДП | 2 | правые |
3 | СДПГ | 1 | левые |
4 | Зеленые/Союз 90 | 1 | левые |
5 | ПДС | 1 | левые |
6 | Республиканцы | 2 | правые |
7 | Прочие | 0 | не определено |
Значение 1 (ХДС/ХСС) переменной partei соответствует значению 2 (правые) переменной lire, значение 2 (СДП) — значению 2 (правые), значение 3 (СДПГ) — значению 1 (левые) и т.д. Значение 0 переменной lire объявляется как отсутствующее.
Перекодирование производится следующим образом:
-
Загрузите файл wahl.sav в редактор данных.
-
Выберите в меню команды Transform (Преобразовать) Recede (Перекодировать)
Можно хранить перекодированные значения в той же переменной или перенести их в другую переменную. Если мы проведем перекодировку в прежней переменной, все ее старые значения будут стерты.
-
Выберите в подменю пункт Into Different Variables... (В другие переменные). Откроется диалоговое окно Recede into Different Variables (Перекодировать в другие переменные).
Рис. 8.5: Диалоговое окно Recede into Different Variables
Список исходных переменных содержит переменные файла данных. Здесь можно выбрать одну или несколько переменных для перекодирования. Если выбираются несколько переменных, все они должны быть одного типа.
-
Перенесите переменную partei (партия) в поле Input Variable -> Output Variable (Входная переменная > Выходная переменная). Вопросительный знак, добавленный в поле, говорит о том, что надо задать имя выходной переменной.
-
Введите в поле Name (Имя) текст lire. Щелкните на кнопке Change (Изменить). Вопросительный знак в поле Input Variable -> Output Variable будет заменен на lire.
-
Введите в поле Label обозначение: «Политический спектр». Подтвердите ввод, щелкнув на Change.
-
Чтобы установить значения, которые следует перекодировать, щелкните на кнопке Old and New Values... (Старые и новые значения). Откроется диалоговое окно Recede into Different Variables: Old and New Values.
Для осуществления каждого перекодирования надо указать значение или диапазон входной переменной и соответствующее значение выходной переменной. Перекодирование завершается щелчком на кнопке Add.
Это диалоговое окно разделено на следующие части. В группе Old Value (Старое значение) можно выбрать один из следующих вариантов:
Рис. 8.6: Диалоговое окно Recede into Different Variables: Old and New Values
-
Value: Вводится отдельное значение.
-
System missing (Системное пропущенное): С помощью этой опции значение входной переменной обозначается, как системное пропущенное. Это значение обозначается в списке значений переменных как SYSMIS. Такой вариант неприменим для строковых переменных.
-
System- or user-missing (Пользовательские или системные пропущенные): Эта опция служит для обозначения всех пользовательских или системных пропущенных значений. В списке значений переменных пользовательские пропущенные значения отображаются как MISSING.
-
Range through (Дипазон): Здесь можно задать замкнутый интервал значений. Этот вариант неприменим для строковых переменных.
-
Range: Lowest through (Диапазон: от наименьшего до): В этом случае будут перекодированы все значения от наименьшего наблюдаемого до указанного. Этот вариант неприменим для строковых переменных.
-
Range: through highest (Диапазон: до наибольшего): В этом случае будут перекодированы все значения от указанного до наибольшего наблюдаемого. Этот вариант неприменим для строковых переменных.
-
All other values (Все остальные значения): Эта опция касается всех еще не указанных значений. В списке значений переменных они отображаются как ELSE.
В группе New Value (Новое значение) можно выбрать один из следующих вариантов:
-
Value: Здесь вводится новое значение.
-
System missing (Системное отсутствующее): Эта опция служит для обозначения значения выходной переменной как системного отсутствующего значения. Значение появляется в списке значений переменных в виде SYSM1S. Этот вариант неприменим для строковых переменных.
-
Copy old value(s) (Копировать старые значения): Значения входной переменной сохранятся без изменений.
Если новые выходные переменные являются строковыми, следует установить флажок Output variables are strings (Выходные переменные являются строками). Теперь выполните следующие действия:
-
Введите старые и новые значения согласно следующей таблице:
1->22->23->14->15->16->2ELSE -> 0.
-
При этом старое значение вводите в поле Value в группе Old Value, новое значение — в поле Value в группе New Value и щелкайте на кнопке Add.
-
Чтобы перекодировать старые значения 0 и 7, выберите опцию All other values. Введите 0 в поле Value в группе New Value и щелкните на кнопке Add.
-
Щелкните на кнопке Continue, а затем на ОК. Новая переменная lire будет добавлена в файл wahl.sav.
Примечание: Выбранные опции соответствуют следующему командному синтаксису:
RECODE partei
(1=2) (2=2) (3=1) (4=1) (5=1) (6=2) (ELSE=0)
INTO lire . VARIABLE LABELS
lire "Политический спектр" EXECUTE .
-
В редакторе данных дважды щелкните на lire, чтобы перейти в редактор вида переменных.
-
Установите следующие параметры: тип переменной — численный, ширина — 1, десятичные разряды — 0. Укажите следующие метки значений:
0 = не определено
1 = левые
2 = правые.
-
Объявите нуль как пропущенное значение.
-
В заключение выполните частотный анализ переменной lire. Вы получите следующий результат:
Политический спектр
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | левые | 13 | 43,3 | 48,1 | 48,1 |
правые | 14 | 46,7 | 51,9 | 100,0 | |
Total | 27 | 90,0 | 100,0 | ||
Missing | не определено | 3 | 10,0 | ||
Total | 30 | 100,0 |
Из 30 респондентов 46,7% выбрали партии правого направления, а 43,3% — партии левого направления. Трое опрашиваемых (10%) не дали никакого ответа на вопрос: «За кого бы вы голосовали, если бы в воскресенье были выборы в бундестаг?».
5.gif
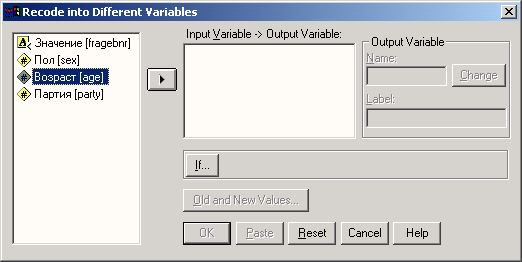
6.gif

8.3.2 Автоматическое перекодирование
8.3.2 Автоматическое перекодирование
Если категории не были закодированы непрерывно начиная с 1, то это может приводить к негативным последствиям при решении многих задач в SPSS. Поэтому для преобразования значений численных или строковых переменных в непрерывную последовательность целых чисел в SPSS реализована возможность автоматического перекодирования. В качестве примера рассмотрим автоматическое перекодирование строковой переменной в численную.
-
Загрузите файл string.sav.
В редакторе данных отобразятся значения строковой переменной beschw (недуги), соответствующие характеру жалоб пациентов. Они состоят не более чем из двадцати символов.
-
Выберите в меню команды Transform (Преобразовать) Automatic Recode... (Автоматическое перекодирование)
Откроется диалоговое окно Automatic Recede (см. рис. 8.7).
Рис. 8.7: Диалоговое окно Automatic Recede
-
Перенесите строковую переменную в поле Variable -> New Name (Переменная > Новое имя). В текстовое поле под ним введите новое имя, например, beschwn, и щелкните на кнопке New Name (Новое имя).
-
Щелкните на кнопке ОК.
В окне просмотра будет отображена таблица соответствия, отрывок из которой приводится ниже:
BESCHW Old Value | BESCHWN New Value | Жалобы Value Label |
Абсцесс | 1 | Абсцесс |
Аллергия | 2 | Аллергия |
Стенокардия | 3 | Стенокардия |
Одышка | 4 | Одышка |
Бактерии в моче | 5 | Бактерии в моче |
Боли в позвоночнике | 6 | Боли в позвоночнике |
Боли в животе | 7 | Боли в животе |
Затруднения | 8 | Затруднения |
Метеоризм | 9 | Метеоризм |
Гипертония | 10 | Гипертония |
Жжение | 11 | Жжение |
Бронхит | 12 | Бронхит |
Воспаление кишечника | 13 | Bocпаление кишечника |
Диабет | 14 | Диабет |
Диализ | 15 | Диализ |
Нарушения кровообр . | 1б | Нарушения кровообращения |
Понос | 17 | Понос |
Воспаления | 18 | Воспаления |
Лихорадка | 19 | Лихорадка |
Различным значениям строковой переменной beschw, выстроенным в алфавитном порядке, поставлена в соответствие непрерывная последовательность натуральных чисел от 1 до 58; эти численные значения сохраняются в переменной beschwn. Прежние строковые значения стали метками значений этой переменной.
7.gif
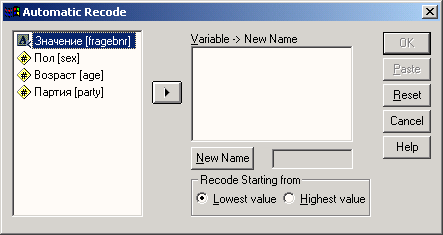
8.4 Вычисление новых переменных в соответствии с определенными условиями
8.4 Вычисление новых переменных в соответствии с определенными условиями
Вычисление новых переменных может быть поставлено в зависимость от определенных условий, как показано в разделе 8.4.1. Во втором разделе этого параграфа приводится практический пример использования условного вычисления — создание индекса.
8.4.1 Формулировка условий
8.4.1 Формулировка условий
В файле studium.sav (психологическое состояние и социальное положение студентов), в частности, содержатся переменные alter (возраст), fach (специальность), semester (количество семестров) и sex (пол).
Допустим, нам требуется образовать из переменных alter и semester новую переменную, которая будет показывать возраст студента в начале обучения. Кроме того, это значение следует вычислять только для старших курсов (semester>6).
-
Загрузите файл Studium.sav и выберите команды меню Transform (Преобразовать) Compute... (Вычислить)
-
В открывшемся диалоговом окне в поле выходной переменной (см. раздел 8.1) задайте, например, studbeg, а для численного выражения — alter — semester /2.
-
Щелкните на кнопке If... (Если). Откроется диалоговое окно Compute Variable: If Cases (Вычислить переменную: Если выполняется условие). Измените начальную настройку Include all cases (Включить все наблюдения) на Include if case satisfies condition (Включить, если для наблюдения выполняется условие). В поле под этой опцией введите условие: semester>6.
-
Закройте это диалоговое окно, щелкнув на кнопке Continue, и диалог Compute Variable кнопкой ОК.
Теперь в файле данных появилась переменная studbeg, которая в случаях, когда заданное условие не выполняется, содержит системное отсутствующее значение.
Примечание: Выбранные опции соответствуют следующему командному синтаксису:
IF (semester > 6) studbeg = alter - semester /2 .
EXECUTE .
Ниже приведен другой типичный пример условного вычисления новых переменных.
Если, к примеру, требуется определить, значительно ли отличаются юристы (fach = 1) от гуманитариев (fach = 3) по количеству семестров, которые прозанимались эти студенты, можно использовать переменную fach как группирующую и сравнить результаты U-теста по Манну и Уитни для переменной semester при значениях fach=l и fach=3 (см. раздел 14.1). Если же требуется сравнить юристов-мужчин с гуманитариями-мужчинами, то оба набора значений надо дополнительно ограничить условием sex = 2 (см. раздел 7. 1).
Однако, когда надо сравнить, например, юристов-мужчин со студентками-гуманитариями, возникает проблема — в этом случае появляются две группирующих переменных. В подобных ситуациях помогает создание вспомогательной переменной. Этой переменной присваивается значение 1, когда наблюдение соответствует студенту-юристу, и 2 — когда студентке гуманитарной специальности. Затем вспомогательная переменная используется как группирующая при проведении теста по Манну и Уитни.
-
Чтобы построить такую переменную, выберите в меню команды Transform (Преобразовать) Compute... (Вычислить)
-
Задайте выходную переменную, например, gruppe, а в поле численного выражения введите значение 1. В диалоговом окне If... укажите условие fach=l and sex=2.
-
Закройте диалоги кнопками Continue и ОК.
-
Повторите процесс; снова задайте выходную переменную gruppe, но численное выражение 2. В диалоге If... сформулируйте условие fach=3 and sex=l. На вопрос Change existing variables?, который появляется после закрытия диалогов, ответьте утвердительно (ОК).
В редакторе данных появится новая переменная gruppe, которая в наблюдениях, соответствующих сформулированным условиям, имеет значения ] или 2, Эту операцию можно выполнить быстрее при помощи командного синтаксиса SPSS.
-
Для этого командами меню File (Файл) New (Создать) Syntax (Синтаксис) откройте редактор синтаксиса и введите следующие команды:
IF (fach = 1 and sex = 2) gruppe = 1.
IF (fach = 3 and sex = 1) gruppe = 2. EXECUTE.
-
После выделения всех строк командами меню Edit (Правка) Select All (Выделить все) и щелчка на значке запуска (Run) в открытый файл данных будет добавлена новая переменная со значениями 1 (мужчины-юристы) и 2 (женщины-гуманитарии), которая может служить группирующей переменной, например, при U-тесте Манна и Уитни.
8.4.2 Создание индекса
8.4.2 Создание индекса
Индексом называют объединение нескольких отдельных вопросов (элементов) в едином показателе, который характеризует сложные, многоплановые состояния — например, показатель уровня жизни или уровня интеллекта. Создание такого индекса мы рассмотрим на примере теоремы об изменении ценностей американского политолога Рональда Инглхарта (Inglehart).
В своей работе «Культурный сдвиг. Смена ценностей в западном мире» (см. список литературы) Инглхарт выдвинул положение о том, что представления о ценностях в западном обществе претерпели значительное изменение. Ранее на первом месте стояли материальное благополучие и физическая безопасность, тогда как сегодня больше значения придается качеству жизни. Таким образом, ценностные приоритеты сместились от материализма к постматериализму. Это смещение Инглхарт объясняет, в частности, тем, что после второй мировой войны, прежде всего в западноевропейских странах и США, люди ощутили большую экономическую и физическую безопасность чем когда-либо до сих пор. Более молодые поколения, годы формирования которых пришлись на период безопасности и стабильности, будут постепенно отдаляться от традиционных норм и представлений о ценностях, свойственных старшим поколениям. Основываясь на факте достижения высокой экономической безопасности и стабильности, Инглхарт делает вывод о смене ценностей между поколениями, которая влечет за собой значительные социальные последствия.
Далее мы построим индекс, который будет указывать, придерживается ли респондент материалистических или же постматериалистических ценностей, согласно Рональду Ингчарту. Этот индекс будет построен на основе опроса ALLBUS, проведенного в 1991 г. В опpoce ALLBUS фигурировало четыре вопроса, касающиеся теоремы Инглхарта об изменении ценностей. В частности, респондента спрашивали, какое значение он придает ценностям «Спокойствие и порядок в стране» (переменная v108), «Увеличение степени частая народа в решениях власти» (переменная v109), «Борьба с ростом цен» (переменная v110) и «Право на свободное выражение мнения» (переменная v111). Респондент, :гавнивая эти четыре ценности между собой, мог указать для каждой из них один из четырех приоритетов: первостепенное значение, второстепенное значение, значение третье степени и значение четвертой степени. Данные находятся в файле ingle.sav.
-
Загрузите файл ingle.sav.
-
Чтобы получить первоначальное представление, проведите частотный анализ переменных v108, v109, v110 и v111. В окне просмотра вы увидите следующие результаты:
ВАЖНОСТЬ СПОКОЙСТВИЯ И ПОРЯДКА
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | первостепенная важность | 1313 | 42,9 | 42,9 | 42,9 |
второстепенная | 691 | 22,6 | 22,6 | 65,5 | |
важность третьей степени | 597 | 19,5 | 19,5 | 85,1 | |
важность четвертой степени | 395 | 12,9 | 12,9 | 98,0 | |
не знаю | 30 | 1,0 | 1,0 | 99,0 | |
нет данных | 32 | 1,0 | 1,0 | 100,0 | |
total | 3058 | 100,0 | 100,0 |
ВАЖНОСТЬ ВЛИЯНИЯ ГРАЖДАН НА ВЛАСТЬ
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | первостепенная важность | 976 | 31,9 | 31,9 | 31,9 |
второстепенная важность | 790 | 25,8 | 25,8 | 57,8 | |
важность третьей степени | 736 | 24,1 | 24,1 | 81,8 | |
важность четвертой степени | 477 | 15,6 | 15,6 | 97,4 | |
не знаю | 44 | 1,4 | 1.4 | 98,9 | |
нет данных | 35 | 1,1 | 1,1 | 100,0 | |
total | 3058 | 100,0 | 100,0 |
ВАЖНОСТЬ БОРЬБЫ С ИНФЛЯЦИЕЙ
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | первостепенная важность | 248 | 8,1 | 8,1 | 8,1 |
второстепенная важность | 696 | 22.8 | 22,8 | 30,9 | |
важность третьей степени | 879 | 28,7 | 28.7 | 59,6 | |
важность четвертой степени | 1142 | 37,3 | 37,3 | 97,0 | |
не знаю | 48 | 1.6 | 1.6 | 98,5 | |
нет данных | 45 | 1,5 | 1,5 | 100,0 | |
total | 3058 | 100,0 | 100,0 |
ВАЖНОСТЬ СВОБОДНОГО ВЫРАЖЕНИЯ МНЕНИЙ
Частота | Проценты | Допустимые | Накопленные проценты | ||
Valid | первосте- пенная важность | 488 | 16,0 | 16,0 | 16,0 |
второсте- пенная важность | 839 | 27,4 | 27,4 | 43,4 | |
важность третьей степени | 762 | 24,9 | 24,9 | 68,3 | |
важность четвертой степени | 880 | 28,8 | 28,8 | 97,1 | |
не знаю | 49 | 1,6 | 1,6 | 98,7 | |
нет данных | 40 | 1,3 | 1,3 | 100,0 | |
total | 3058 | 100,0 | 100,0 |
Элементы vl08 (Спокойствие и порядок) и v110 (Борьба с ростом цен/инфляцией) соответствуют материалистическим ценностям, а элементы v!09 (Влияние граждан на власть) и vl11 (Свободное выражение мнений) — постматериалистическим. Таким образом, за каждым материалистическим элементом следует постматериалистический элемент. Именно так эти четыре классических элемента были расположены в исследовании Инглхарта Это. В своих многочисленных работах, которые выходили с начала 70-х гг., Рональд Инглхарт объединял эти четыре элемента в шкалу из четырех степеней, или индекс. При этом элементы v!08 (Спокойствие и порядок) и v110 (Борьба с ростом цен/ инфляцией) служили для выделения материалистов, а элементы v!09 (Влияние граждан на власть) и v111 (Свободное выражение мнений) — для выделения постматериалистов. В зависимости от сочетания ответов Инглхарт классифицировал опрашиваемого как
-
чистого материалиста
-
чистого постматериалиста
-
материалистический смешанный тип
-
постматериалистический смешанный тип.
Сочетание ответов v108/v110 соответствует чистому материалисту, а сочетание v109/ v111 — чистому постматериалисту. При оставшихся сочетаниях ответов, в зависимости от того, был ли главной целью респондента материалистический или постматериалистический элемент, опрашиваемый классифицируется как материалистический или постматериалистический смешанный тип. Таким образом, мы получаем следующие варианты сочетаний для создаваемого индекса:
Индекс Инглхарта
Цель первостепенной важности | Цель второстепенной важности | Инлекс Инглхарта |
v108 | v110 | чистый материалист |
v110 | v108 | чистый материалист |
v109 | v111 | чистый постматериалист |
v111 | v109 | чистый постматериалист |
v108 | v109 | материалистический смешанный тип |
v108 | v111 | материалистический смешанный тип |
v110 | v109 | материалистический смешанный тип |
v110 | v111 | материалистический смешанный тип |
v109 | v108 | постматериалистический смешанный тип |
v109 | v110 | постматериалистический смешанный тип |
v111 | v108 | постматериалистический смешанный тип |
V111 | v110 | постматериалистический смешанный тип |
Рассмотрим теперь нижеследующую программу SPSS, которая строит индекс в соответствии с вышеприведенной таблицей.
/* Создание индекса */
.'* на примере теоремы Рональда
Инглхарта об изменении ценностей */
/* чистые материалисты */
if (v!08 = 1 and vl10 = 2)
ingl_ind = 4 . if (vl10 = 1
and vl08 = 2) ingl_ind = 4 .
/* чистые постматериалисты */
if (v!09 = 1 and vlll = 2)
ingl_ind = 1 .
if (vl11 = 1 and vl09 = 2)
ingl_ind = 1 .
/* материалистический смешанный тип
*/ if <vl08 = 1 and vl09 = 2)
ingl_ind = 3 . if (vl08 = 1
and vl11= 2) ingl_ind = 3 .
if {vl10 = 1 and vl09 = 2) ingl_ind = 3 .
if (vl10 = 1 and vl11 = 2)
ingl_ind = 3 .
/* постматериалистические
смешанные типы */
if (v!09 = 1 and v!08 = 2)
ingl_ind = 2 .
if (vl09 = 1 and vl10 = 2)
ingl_ind = 2 .
if (vl11 = 1 and vl08 = 2)
ingl_ind = 2 .
if (vl11 = 1 and vk10 = 2)
ingl_ind = 2 .
/* He знаю */
if (vl08 = 8 and vl09 = 8
and vl10 = 8 and vl11 = 8)
ingl_ind = 8 .
if (vl08 = 8 and vl09 = 8
and vl10 = 8) ingl_ind = 8 .
if (vl08 = 8 and vl09 = 8
and vl11 = 8) ingl_ind = 8 .
if (vl08 = 8 and vl10 = 8
and vl11 = 8) ingl_ind = 8 .
if (vl09 = 8 and vl10 = 8
and vl11 = 8) ingl_ind = 8 .
/* нет данных */
if (vl08 = 9 and vl09 = 9
and vl10 = 9 and vl11 = 9)
ingl_ind = 9 .
if (vl08 = 9 and vl09 = 9
and vl10 = 9) ingl~ind = 9 .
if (vl08 = 9 and vl09 = 9
and vl11 = 9) ingl_ind = 9 .
if (vl08 = 9 and vl10 = 9
and vl11 = 9) ingl_ind = 9 .
if (vl09 = 9 and vl10 = 9
and vl11 = 9) ingl~ind = 9 .
variable labels ingl_ind
'Индекс Инглхарта'
value labels ingl_ind 1
'Постматериалисты'
2 'ПМ, смешанный тип'
3 'M, смешанный тип'
4 ' Материалисты'
8 'Не знаю'
9 'нет данных' .
execute .
Программа начинается с двух строк комментариев, которые содержат информацию о том, что целью ее выполнения является построение индекса на примере теоремы Рональда Инглхарта об изменении ценностей. Комментарии обозначаются в SPSS символами /* в начале строки комментария и */ — в конце комментария. При выполнении программы процессор SPSS пропускает эти строки.
Далее вычисляется индекс для чистых материалистов. Если выполняется условие, что переменная v!08 имеет значение 1, а переменная v110 — значение 2, то переменная индекса ingMnd должна иметь значение 4 (Материалисты). После этого вычисляется индекс для чистых постматериалистов. Он равен 1. Для материалистических и постматериалистических смешанных типов имеется по четыре сочетания, которые обрабатываются в двух следующих блоках. Два последних блока программы обрабатывают ответы не знаю и нет данных. Индекс Инглхарта равен 8 (не знаю), если на три или четыре вопроса дан ответ не знаю, и 9 (нет данных), если на три или четыре вопроса дан ответ нет данных. Например, если респондент придал элементу v!08 первостепенную важность, а на три остальных вопроса ответил не знаю, он попадает в категорию не знаю.
Следует отметить, что находящиеся друг под другом в программе операторы AND (конъюнкции) можно преобразовать в дизъюнкцию, связав их операторами OR (см. главу 7). Следующая команда variable labels присваивает переменной ingl_ind метку «Индекс Инглхарта». Команда value labels устанавливает шесть меток значений для этой переменной. Команда execute в конце программы запускает выполнение всех необходимых преобразований.
Эта программа находится на компакт-диске примеров или в рабочем каталоге C:\SPSSBOOK. Она называется ingle.sps.
-
Загрузите программу в редактор синтаксиса ingle.sps, вызвав команды меню File (Файл) Open (Открыть).
-
Выделите текст программы следующими командами меню Edit (Правка) Select All (Выделить все)
-
Запустите программу, щелкнув на значке Run (Запуск).
-
Перейдите в редактор данных.
-
Выполните частотный анализ переменной ingljnd. Вы получите следующий результат:
Индекс Инглхарта
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | Постматериалисты | 673 | 22,0 | 22,0 | 22,0 |
ПМ, смешанный тип | 789 | 25,8 | 25,8 | 47,8 | |
М, смешанный тип | 956 | 31,3 | 31,3 | 79,1 | |
Материалисты | 598 | 19,6 | 19,6 | 98,6 | |
Не знаю | 19 | ,6 | ,6 | 99,2 | |
нет данных | 23 | ,8 | ,8 | 100,0 | |
Total | 3058 | 100,0 | 100,0 |
Из 3058 опрошенных 98,6% поддаются классификации; 41,6% относятся к чистым типам. В группу материалистического смешанного типа попадает почти треть всех наблюдений. Постматериалистическому смешанному типу соответствует чуть больше четверти. В чистых группах постматериалисты выражены несколько сильнее материалистов. Материалисты и материалистические смешанные типы составляют вместе 50,9%; постматериалисты и постматериалистические смешанные типы — 47,8%. Таким образом, наблюдается небольшой перевес в сторону материализма.
Данные четырех классических элементов Инглхарта содержит также файл beamte.sav. Он касается опроса ALLBLJS, проводившегося в 1988 г.. Для упражнения постройте индекс Инглхарта для этих данных. При сравнении с данными 1991 г. следует учитывать, что опрос ALLBUS 1991 впервые проводился во всех землях Германии, включая восточные.
8.5 Агрегирование данных
8.5 Агрегирование данных
На базе значений одной или нескольких группирующих переменных (переменных разбиения) можно объединить наблюдения в группы (агрегировать) и создать новый файл данных, содержащий по одному наблюдению для каждой группы разбиения. Для этого SPSS предоставляет большое количество функций агрегирования.
В сельскохозяйственном исследовании рассматривалось содержание свиней в двух различных типах свинарников. При этом в каждом из двух свинарников осуществлялся мониторинг поведения восьми свиней в течение двадцатидневного периода. На протяжении этого периода фиксировалась длительность определенных действий животных (то есть сколько времени свиньи рылись, ели, чесали голову и туловище). Данные хранятся в файле schwein.sav, содержащем следующие переменные:
Имя переменной | Пояснение |
stall | Тип свинарника (1 или 2) |
nr | Порядковый номер свиньи (от 1 до 8) |
zert | Номер дня (от 1 до 20) |
wuehlen | Длительность рытья (в секундах) |
fressen | Длительность кормежки (в секундах) |
massage | Длительность чесания (в секундах) |
Следует выяснить, значительно ли различается по длительности эти три действия в свинарниках обоих типов, для чего необходимо применить соответствующий статистический текст, например, тест Стьюдента (см. главу 13).
В каждой из двух выборок для каждого из трех действий имеется по 8 + 20=160 измерений. Однако выполнение статистического тест на основе этих данных будет не совсем корректно, так как они относятся к восьми особям, для каждой из которых было проведено по двадцать измерений.
Поэтому мы просуммируем длительности для каждой отдельной свиньи и для каждого отдельного действия. Затем полученные наборы сумм мы сравним при помощи теста Стьюдента. Это типичный пример агрегирования данных.
-
Загрузите файл schwein.sav.
-
Выберите в меню команды Data (Данные) Aggregate... (Агрегировать)
Откроется диалоговое окно Aggregate Data (Агрегировать данные).
-
В качестве переменных разбиения перенесите переменные stall и nr в поле Break Variable(s), а в качестве переменных агрегирования (Aggregate Variable(s)) выберите wuehlen, fressen и massage. Диалоговое окно приобретет вид, показанный на рис. 8.8.
Будут показаны три новые переменные wuehle_l, fresse_l и massag_l, имена которых состоят из первых шести букв имен соответствующих переменных агрегирования и комбинации символов _1. По умолчанию в качестве функции агрегирования принято среднее значение. Мы должны выбрать вместо него сумму.
-
Для этого щелкните на первой переменной, а затем на кнопке Funktion... (Функция). Откроется диалоговое окно Aggregate Data: Aggregate Function (Агрегировать данные: Функция агрегирования) (см. рис. 8.9).
Можно выбрать одну из шестнадцати функций агрегирования, имена которых не требуют особых пояснений.
-
Выберите пункт Sum of values (Сумма значений) и щелчком на кнопке Continue вернитесь в первое диалоговое окно.
-
Выполните те же действия для двух других переменных агрегирования. Агрегированные данные будут сохранены в новом файле.
-
Щелкните на кнопке File... и выберите для нового файла имя pigaggr.sav.
Рис. 8.8: Диалоговое окно Aggregate Data
Рис. 8.9: Диалоговое окно Aggregate Data: Aggregate Function
После щелчка на кнопке Отбудет создан новый файл, содержащий 2 х 8=16 наблюдений и переменные stall, nr, wuehle_l, fresse_l и massag_l.
-
Загрузите этот файл и просмотрите его содержимое в редакторе данных.
-
Как описано в разделе 13.1, проведите тест Стьюдента для независимых выборок с группирующей переменной stall и тестируемыми переменными fresse_l, massag_l и wuehle_l. Вы получите следующий результат:
Group Statistics (Статистика группы)
STALL | N | Mean (Среднее значение) | Std. Deviation (Стандартное отклонение) | Std. Error Mean (Стандартная ошибка среднего значения) |
FRESSE 1 1 2 | 8 8 | 339,0125 231,6750 | 98,2384 109,5381 | 34,7325 38,7276 |
MASSAG 1 1 2 | 8 8 | 2,2875 40,3625 | 3,3689 54,1795 | 1,1911 19,1553 |
WUEHLE 1 1 2 | 8 8 | 1996,587 1964.600 | 326,3919 642,5314 | 115,3970 227,1692 |
Independent Samples Test (Тест для независимых выборок)
Levne's Test forEquality of Variancies (Tecт Левена на равенство дисперсий) | Т-Test for Equality of Means (Тест Стьюдента на равенство средних) | |||||||||
F | Значи-мость | Т | df | (дву сторон-няя) | Разность средних | Стан-дартная ошибка разницы | 95% доверительный интервал разности Нижняя и Верхняя | |||
FRES-SE_.1 | Equal variances assumed (Дис-персии равны) Equal variances not assumed (Дис-персии не равны) | .128 | .726 | 2,063 2,063 | 14 13, 837 | ,058 ,058 | 107 ,3375 107 ,3375 | 52, 0209 52 ,0209 | -4,2362 -4,3594 | 218, 9112 219, 0344 |
MAS-SAG 1 | Equal variances assumed (Дис-персии равны) Equal variances not assumed (Дис-персии не равны) | 7.390 | ,017 | -1,984 -1,984 | 14 7,054 | ,067 ,087 | -38, 0750 -38,0750 | 19, 1923 19. 1923 | -79,2385 -83,3872 | 3,0885 7,2372 |
WU-EHLE_1 | variances assumed (Дис-персии равны) Equal variances not assumed (Дис-персии не равны) | 2,274 | ,154 | ,126 ,126 | 14 10 ,387 | ,902 ,902 | 31, 9875 31 ,9875 | 254 ,7985 254 ,7985 | -514 ,5010 -532, 8844 | 578. 4760 596 ,8594 |
В первом свинарнике свиньи ели в продолжение наблюдаемого периода в среднем 339,0 секунд в день, а в другом — только 231,7 секунд. Это различие является почти статистически значимым (р= 0,058).
8.gif

9.gif

8.6 Ранговые преобразования
8.6 Ранговые преобразования
В SPSS существует возможность задавать ранги для измеренных значений переменной, проводить оценки Сэвиджа, вычислять процентные ранги и формировать процентильные группы, добавляя в файл данных соответствующие переменные.
Так, например, в формулах для непараметрических тестов (см. главу 14) вместо исходных измеренных значений переменной используются присвоенные им ранги. Однако эти процедуры производят автоматическое присвоение рангов и в явном виде выполнять предварительные ранговые преобразования не требуется. Поэтому они играют второстепенную роль.
Мы продемонстрируем присвоение рангов на более наглядном примере, а затем проведем обзор различных типов рангов.
8.6.1 Пример рангового преобразования
8.6.1 Пример рангового преобразования
В главе 20 представлен файл europa.sav, содержащий отдельные статистические показатели по 28 европейским странам. В частности, он включает переменные land (краткое обозначение страны) и tjul (средняя дневная температура в июле). Требуется расположить страны в нисходящем порядке согласно значениям последней переменной и затем вывести их в отсортированном виде.
-
Загрузите файл europa.sav.
-
Выберите в меню команды Transform (Преобразовать) Rank Cases... (Присвоить ранги наблюдениям) Откроется диалоговое окно Rank Cases.
Рис. 8.10: Диалоговое окно Rank Cases
-
Щелкните в списке переменных на переменной tju1. В поле By: (По) можно задать группирующую переменную. В этом случае назначение рангов будет выполнено раздельно по группам, образуемым этой переменной.
-
Присвоим самой теплой стране (с максимальным значением переменной tju1) ранг 1; для этого щелкните в поле Assign Rank I to (Присвоить ранг 1) на опции Largest value (Максимальное значение).
Щелкнув на кнопке Rank types... (Типы рангов), можно увидеть стандартную настройку Rank. Пока оставим ее без изменений; остальные настройки мы рассмотрим в разделе 8.6.2.
-
Кнопка Ties... (Связки) открывает диалоговое окно Rank Cases: Ties.
Его настройки указывают, как программа будет поступать при появлении одинаковых измеренных величин. По умолчанию принято (и, как правило, это наилучший вариант), что присваивается среднее (Mean) из значений рангов этих величин. При установке Low все значения получают наименьший, при установке High — наибольший из этих рангов. При выбранной опции Sequential ranks to unique values (Присваивать последовательные ранги) все связанные наблюдения получают одинаковый ранг; следующему наблдению присваивается следующее по порядку целое число. Поэтому максимальный присвоенный ранг равен не общему количеству значений, а количеству различных значений.
Перечисленные четыре способа присвоения рангов можно пояснить с помощью простого примера, в котором семь значений расположены по убыванию.
Рис. 8.11: Диалоговое окно Rank Cases: Ties
Значение | Mean | Low | High | Sequential ranks to unique values |
190 | 1 | 1 | 1 | 1 |
187 | 2,5 | 2 | 3 | 2 |
187 | 2,5 | 2 | 3 | 2 |
185 | 5 | 4 | 6 | 3 |
185 | 5 | 4 | 6 | 3 |
185 | 5 | 4 | 6 | 3 |
184 | 7 | 7 | 7 | 4 |
-
Оставьте стандартную настройку и закройте диалоговое окно кнопкой Continue.
-
Начните присвоение рангов, щелкнув на ОК.
В файл данных будет добавлена переменная rtju1, содержащая ранги, присвоенные значениям переменной tju1. Для обозначения ранговой переменной к имени исходной переменной спереди дописывается буква г.
Затем отсортируем файл данных по этой ранговой переменной.
-
Для этого, как описано в разделе 7.3, выберите в меню команды Data (Данные) Son Cases... (Сортировать наблюдения) и в появившемся диалоговом окне выберите в качестве переменной сортировки rtjul. Примите предлагаемый по умолчанию порядок сортировки по возрастанию.
-
Запустите сортировку кнопкой ОК. Теперь выведем значения переменных rtju1, land и tju1 в отсортированном виде.
-
Для этого выберите в меню команды (см. раздел 4.8) Analyze (Анализ) Reports (Отчеты) Case summaries... (Итоги по наблюдениям) и перенесите в поле Variables переменные rtjul, land и tjul в указанной последовательности.
-
Запустите создание отчета кнопкой ОК. В окне просмотра будет показана следующая таблица.
Отсюда можно заключить, что Греция является самой теплой страной (ранг 1), за ней следует Италия (ранг 2), следующий ранг имеют две страны — Албания и Румыния (средний ранг 3,5) и т.д.
Case Processing Summary a (Сводка случаев)
RANK TJU | LAN | Средняя дневная температура в июле | |
1 | 1,00 | GRI | 33 |
2 | 2,00 | ITA | 31 |
3 | 3,50 | ALB | 30 |
4 | 3,50 | RUM | 30 |
5 | 5,50 | JUG | 29 |
6 | 5,50 | TUE | 29 |
7 | 7,50 | BUL | 28 |
8 | 7,50 | UNG | 28 |
9 | 9,50 | FOR | 27 |
10 | 9,50 | SPA | 27 |
11 | 13,00 | DEU | 25 |
12 | 13,00 | FRA | 25 |
13 | 13,00 | OES | 25 |
14 | 13,00 | SCH | 25 |
15 | 13,00 | TSC | 25 |
16 | 17,00 | DD | 24 |
17 | 17,00 | POL | 24 |
18 | 17,00 | SOW | 24 |
19 | 19,50 | BEL | 23 |
20 | 19,50 | LUX | 23 |
21 | 23,50 | DAE | 22 |
22 | 23,50 | FIN | 22 |
23 | 23,50 | GRO | 22 |
24 | 23,50 | NIE | 22 |
25 | 23,50 | NOR | 22 |
26 | 23,50 | SCH | 22 |
27 | 27,00 | IRL | 20 |
28 | 28,00 | ISL | 15 |
| Total (Всего)N | 28 | 28 | 28 |
a. Limited to first 100 cases(Ограничено первыми 100 случаями) | |||
10.gif
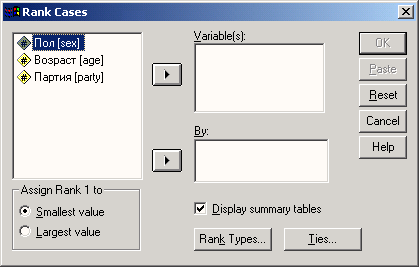
11.gif
8.6.2 Типы рангов
8.6.2 Типы рангов
В диалоге Rank Cases можно, щелкнув на кнопке Rank Types... (Типы рангов), от-крыть диалоговое окно Rank Cases: Types (Ранги: Типы). В этом окне представлены шесть типов рангов; щелкнув на кнопке More » (Еще), можно увидеть еще два.
Ниже приведено объяснение различных типы рангов.
-
Rank (Ранг): Абсолютные значения рангов (см. раздел 8.6.1). Это установка по умолчанию.
-
Savage score (Оценка Сэвиджа): Это значения ранга, полученное на основе экспоненциального распределения. При общем количестве значений переменной т оценка Сэвиджа для i-го ранга определяется по формуле
Рис. 8.12: Диалоговое окно Rank Cases: Types
-
Fractional Rank (Относительный ранг): Это значение ранга деленное на количество наблюдений.
-
Fractional Rank as % (Относительный ранг в %): Это численные значения относительных рангов, умноженные на 100. Например, процентный ранг 33,93 означает, что 33,93% всех наблюдений имеют более низкий ранг.
-
Sum of case weights (Сумма весов наблюдений): Эта величина представляет интерес только при определении рангов для подгрупп и является постоянной в каждой подгруппе; она соответствует количеству случаев в подгруппе.
-
Ntiles (N-процентили): Пользователь может задать число групп процентилей, на которые должны быть разбиты наблюдения (по умолчанию 4). Тогда каждому случаю присваивается значение процентильной группы, к которой он принадлежит.
-
Proportion estimates (Долевые оценки): Вычисление накопленной доли при предположении нормальном распределении переменной. Для ранга г и количества наблюдений я соответствующие долевые оценки вычисляются по четырем нижеследующим формулам.
Blom: | (r-3/8)/(n+1/4) |
Tukey: | (r-1/3)/(n+1/3) |
Rankit: | (r-1/2)/n |
Van der Waerden: | r/(n+1) |
-
Normal scores (Нормальные ранги): Значения процентилей, относящиеся к долевым оценкам.
Для перечисленных рангов SPSS автоматически задает имена переменных, которые приведены в нижеследующей таблице. При этом имеет значение, был ли выбран единственный тип ранга или одновременно вычислялись ранги нескольких типов (что является исключением). В последнем случае, для обеспечения однозначности переменных имена должны различаться. В таблице приводятся также принятые в SPSS метки этих переменных. Для долевых оценок и нормальных рангов здесь приведен вариант, когда применяется формула Блома (Blom); при выборе других формул расчета этих рангов метки соответственно изменяются. Имя исходной переменной — lem (в нашем примере — это средняя ожидаемая продолжительность жизни мужчин).
Тип ранга | Единственный тип ранга | Несколько типов | Метка переменной |
Ранг | rlem | rlem | RANK of LEM |
Оценка Сэвиджа | slem | slem | SAVAGE of LEM |
Относительный ранг | rlem | rfrOO-1 | RFRACTION of LEM |
Относительный ранг в % | plem | perOO! | PERCENT of LEM |
Сумма весов наблюдений | nlem | nOOl | N of LEM |
N-процентили | nlem | ntiOOl | NTILES of LEM |
Долевые оценки (по Блому) | plern | plem | PROPORTION of LEM using BLOM |
Нормальные ранги (по Блому) | nlem | nlem | NORMAL of LEM using BLOM |
Если провести ранговые преобразования всех возможных типов и вывести получившиеся значения с помощью средства формирования сводки наблюдений, мы получим следующую таблицу.
Case Processinq Summary3 (Сводка наблюдений)
| LAN | RANK LE | SAVAG of | RFRACT Nof | PERCE of | Nof | NTILES LE | PROPOR Nof using | NORM of usin BLO |
1 | ALB | 3,00 |
| ,107 | 10,7 | 28 | 1 | ,092 |
|
2 | BEL | 11,50 |
| ,410 | 41,0 | 28 | 2 | ,393 |
|
3 | BUL | 15,50 |
| ,553 | 55,3 | 28 | 3 | ,535 | ,088 |
4 | DAE | 24,00 | ,843 | ,857 | 85,7 | 28 | 4 | ,836 | ,979 |
5 | DEU | 13,00 |
| ,464 | 46,4 | 28 | 2 | ,446 |
|
6 | DO | 17,00 |
| ,607 | 60,7 | 28 | 3 | ,588 | ,223 |
7 | FIN | 4,00 |
| ,142 | 14,2 | 28 | 1 | ,128 |
|
8 | FRA | 19.00 | ,098 | ,678 | 67,8 | 28 | 3 | ,659 | ,410 |
9 | GRI | 11,50 |
| ,410 | 41,0 | 28 | 2 | ,393 |
|
10 | GRO | 20,00 | ,209 | ,714 | 71,4 | 28 | 3 | ,694 | ,509 |
11 | IRL | 15,50 |
| ,553 | 55,3 | 28 | 3 | ,535 | ,088 |
12 | ISL | 27,00 | 1,927 | ,964 | 96,4 | 28 | 4 | ,942 | 1,575 |
13 | ITA | 18,00 |
| ,642 | 64,2 | 28 | 3 | ,623 | ,315 |
14 | JUG | 1,00 |
| ,035 | 3,5 | 28 | 1 | ,022 |
|
15 | LUX | 14,00 |
| ,500 | 50,0 | 28 | 2 | ,482 |
|
16 | NIE | 25,00 | 1,093 | ,892 | 89,2 | 28 | 4 | ,871 | 1,134 |
17 | NOR | 28,00 | 2,927 | 1,000 | 100,0 | 28 | 4 | ,977 | 2,011 |
18 | OES | 9,00 |
| ,321 | 32,1 | 28 | 2 | ,305 |
|
19 | POL | 7,00 |
| ,250 | 25,0 | 28 | 1 | ,234 |
|
20 | POR | 2,00 |
| ,071 | 7,1 | 28 | 1 | ,057 |
|
21 | RUM | 6,00 | - | ,214 | 21,4 | 28 | 1 | ,199 |
|
22 | SCH | 26,00 | 1,427 | ,928 | 92,8 | 28 | 4 | ,907 | 1,323 |
23 | SCH | 23,00 | ,643 | ,821 | 82,1 | 28 | 4 | ,800 | ,844 |
24 | sow | 22.00 | ,477 | ,785 | 78,5 | 28 | 4 | ,765 | ,724 |
25 | SPA | 21,00 | ,334 | ,750 | 75,0 | 28 | 3 | ,730 | ,613 |
26 | TSC | 5,00 | - | ,178 | 17,8 | 28 | 1 | ,163 |
|
27 | TUE | 10,00 | - | ,357 | 35,7 | 28 | 2 | ,340 | - |
28 | UNG | 8,00 |
| ,285 | 28,5 | 28 | 2 | ,269 |
|
Total (Всего) N | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 |
a. Limited to first 100 cases (Ограничено первыми 100 наблюдениями)
12.gif
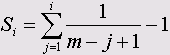
13.gif
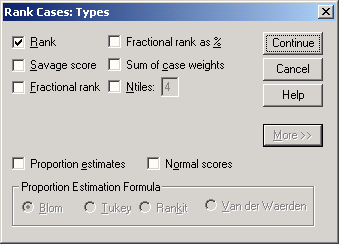
8.7 Веса случаев
8.7 Веса случаев
SPSS предоставляет возможность определения веса данных. При этом данным, относящимся к разным наблюдениям, присваиваются различные весовые коэффициенты посредством так называемой переменной взвешивания. Эта процедура может быть полезной в следующих ситуациях:
-
Данная выборка не является репрезентативной, то есть частотные характеристики выборки, состоящей из переменных, достаточных для обеспечения репрезентативности, не соответствуют частотным характеристикам генеральной совокупности.
-
Анализ данных, которые уже представлены в виде частотных таблиц.
Эти ситуации рассматриваются в двух следующих разделах. Подробнее о таблицах сопряженности, которые используются при этом, см. в главе 11.
8.7.1 Коррекция при отсутствии репрезентативности
8.7.1 Коррекция при отсутствии репрезентативности
Перед служащими и представителями других социальных групп были поставлены четыре классических вопроса Инглхарта, уже известные нам из раздела 8.4.2, то есть, было предложено выбрать одну из четырех степеней важности для каждого из нижеследующих пунктов:
1. Поддержание спокойствия и порядка
2. Усиление влияния граждан на власть
3. Борьба с инфляцией
4. Обеспечение свободного выражения мнений
Данные, взятые из опроса ALLBUS 1988 г., хранятся в файле beamte.sav. При этом переменной beamier присваивается кодировка 1 или 2 в зависимости от того, является ли респондент служащим; переменные themal-Hhema4 содержат оценки четырех вышеприведенных пунктов.
-
Загрузите файл beamte.sav и командами меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты) создайте частотные таблицы переменных beamier и themaS:
Служащий?
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | Да | 137 | 10,5 | 10,5 | 10,5 |
Нет | 1162 | 89,5 | 89,5 | 100,0 | |
Total | 1299 | 100,0 | 100,0 |
Борьба с инфляцией
Valid | первостепенная важность | Frequency 109 | Percent 8,4 | Valid Percent 8,4 | Cumulative Percent 8,4 |
второстепенная важность | 237 | 18,2 | 18,2 | 26,6 | |
важность третьей степени | 374 | 28,8 | 28,8 | 55,4 | |
важность четвертой степени | 579 | 44,6 | 44,6 | 100,0 | |
Total | 1299 | 100,0 | 100,0 |
Из частотной таблицы переменной beamier можно заключить, что в данной выборке 10,5% респондентов являются служащими, хотя известно, что доля служащих в общем населении составляет только 8,4%.
Прежде чем мы скорректируем это небольшое искажение при помощи переменной взвешивания, составим таблицу сопряженности для переменных themaS (строки) и beamter (столбцы).
-
Командами меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности) создайте таблицу сопряженности из этих переменных.
-
Дополнительно кнопкой Cells... (Ячейки) задайте вывод процентов по строкам (Percentages — Row) и столбцам (Column), а кнопкой Statistics... (Статистика) — выполнение теста %2(Chi-square):
Таблица сопряженности Борьба с инфляцией* Служащий?
Служащий? | |||||
Да | нет | Total | |||
Борьба с инфля- цией | первостепен ная важность | Count (Коли- чество) | 6 | 103 | 109 |
% от Борьба с инфляцией | 5,5% | 94,5% | 100,0% | ||
%от Служащий? | 4,4% | 8,9% | 8,4% | ||
второстепенн ая важность | Count | 14 | 223 | 237 | |
% от Борьба с инфляцией | 5,9% | 94,1% | 100,0% | ||
%от Служащий? | 10,2% | 19,2% | 18,2% | ||
важность третьей степени | Count | 37 | 337 | 374 | |
% от Борьба с инфляцией | 9,9% | 90,1% | 100,0% | ||
%от Служащий? | 27,0% | 29,0% | 28,8% | ||
важность четвертой степени | Count | 80 | 499 | 579 | |
% от Борьба с инфляцией | 13,8% | 86,2% | 100,0% | ||
%от Служащий? | 58,4% | 42,9% | 44,6% | ||
Total | Count | 137 | 1162 | 1299 | |
% от Борьба с инфляцией | 10,5% | 89,5% | 100,0% | ||
%от Служащий? | 100,0% | 100,0% | 100,0% | ||
Chi-Square Tests (Тесты хи-квадрат)
Value (Значение) | df | Asymp. Sig. (2-sided) (Асимптотическая значимость (двусторонняя)) | |
Pearson Chi-Square хи-квадрат по Пирсону) | 15,077 (а) | 3 | ,002 |
Likelihood Ratio (Степень правдоподобия) | 16,032 | 3 | ,001 |
Linearly-Linear Association (Зависимость линейный-линейный) | 14,302 | 1 | ,000 |
N of Valid Cases (Кол-во допустимых случаев) | 1299 |
a. 0 cells (,0%) have expected count less than 5. The minimum expected count is 11,50. (Ячейки с нулями (,0%) имеют ожидаемую частоту менее 5. Минимальная ожидаемая частота 11,50.)
Результаты показывают, что для служащих борьба с инфляцией имеет меньшее значение, чем для остальных респондентов.
Теперь путем взвешивания мы попробуем скорректировать искажение доли служащих, имеющееся в выборке. Принцип заключается в том, что для каждого значения переменной (в данном случае переменной beamier) вычисляется весовой коэффициент как отношение необходимого значения к существующему.
Весовой коэффициент = (необходимое значение)/(существующее значение)
Для служащих весовой коэффициент равен
8,4/10,5=0,8
а для остальных —
91,5/89,5 = 1,023
-
Командами меню File (Файл) New (Создать) Syntax (Синтаксис) откройте редактор синтаксиса.
-
Чтобы создать переменную взвешивания, введите следующие команды:
IF beamter=1 gewicht=8.4/10.5 .
IF beamter=2 gewicht=91.6/89. 5 .
EXECUTE .
Исходя из соображений точности расчета рекомендуется вводить сами значения, а не их отношения, и предоставлять их вычисление компьютеру.
-
Выделите введенные команды, выбрав в меню Edit (Правка) Select All (Выделить все)
-
Щелкните на символе Run, и в файл данных будет добавлена новая переменная gewicht. Ее мы и будем использовать как переменную взвешивания.
Для создания переменных взвешивания можно и не использовать команды синтаксиса SPSS, а повторить подход, описанный в разделе 8.4.1.
-
Выберите в меню команды Data (Данные) ; Weight Cases... (Взвесить наблюдения)
Появится диалоговое окно Weight Cases.
Рис. 8.13: Диалоговое окно Weight Cases
-
Выберите в этом диалоговом окне опцию Weight cases by и перенесите переменную gewicht в поле под ней (в диалоге это поле называется Frequency Variable).
-
Описанным выше путем создайте частотные таблицы переменных beamier и thema3 и таблицу сопряженности из этих переменных. Вы получите следующий результат:
Служащий?
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | да | 110 | 8,4 | 8,4 | 8,4 |
нет | 1189 | 91,6 | 61,6 | 100,0 | |
Total | 1299 | 100,0 | 100,0 |
Борьба с инфляцией
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | первостепенная важность | 110 | 8,5 | 8,5 | 8,5 |
второстепенная важность | 239 | 18,4 | 18,4 | 26,9 | |
важность третьей степени | 375 | 28,8 | 28,8 | 55,8 | |
важность четвертой степени | 575 | 44,2 | 44,2 , | 100,0 | |
Total | 1299 | 100,0 | 100,0 |
Таблица сопряженности Борьба с инфляцией * Служащий?
Служащий? | |||||
да | Нет | Total | |||
Борьба с инфляцией | первосте- пенная важность | Count | 5 | 105 | 110 |
% от Борьба с инфляцией | 4,5% | 95,5% | 100,0% | ||
%от Служащий? | 4,5% | 8,8% | 8,5% | ||
второсте- пенная важность | Count | 11 | 228 | 239 | |
% от Борьба с инфляцией | 4,6% | 95,4% | 100,0% | ||
%от Служащий? | 10,0% | 19,2% | 18,4% | ||
важность третьей степени | Count | 30 | 345 | 375 | |
% от Борьба с инфляцией | ,U /0 | 92,0% | 100,0% | ||
%от Служащий? | 27,3% | 29,0% | 28,9% | ||
важность четвертой степени | Count | 64 | 511 | 575 | |
% от Борьба с инфляцией | 11,1% | 88,9% | 100,0% | ||
%от Служащий? | 58,2% | 43,0% | 44,3% | ||
Total | Count | 110 | 1189 | 1299 | |
% от Борьба с инфляцией | 8,5% | 91,5% | 100,0% | ||
%от Служащий? | 100,0% | 100,0% | 100,0% | ||
Chi-Square Tests
Value | Df | Asymp. Sig. (2-sided) | |
Pearson Chi-Square | 12,156 a | 3 | ,007 |
Likelihood Ratio | 12,972 | 3 | ,005 |
Linear-by-Linear Association | 11,410 | 1 | ,001 |
N of Valid Cases | 1299 |
а. 0 cells (,0%) have expected count less than 5. The minimum expected count is 9,31. (Ячейки с нулями (,0%) имеют ожидаемую частоту менее 5. Минимальная ожидаемая частота 9,31.)
Общая частота осталась неизменной — 1299, но взаимное отношение частот изменилось. В переменной beamter количество служащих снизилось с 137 до 110, что соответствует реальной доле служащих 8,4%. Также незначительно изменилась частотная таблица для переменной themaS; взвешивание повлияло и на нее.
То же можно сказать и о таблице сопряженности. Однако здесь процентные значения по столбцам не изменились; сохранились соотношения между отдельными значениями переменных в ячейках.
Установленное взвешивание будет действовать до тех пор, пока вы снова не выберете в диалоговом окне Weight Cases опцию Do not weight cases (He взвешивать наблюдения).
Описанный метод взвешивания при отсутствии репрезентативности может привести к возникновению некоторых проблем, которые, впрочем, не проявляются в изученном примере.
Если мы рассмотрим, например, взвешенную частотную таблицу переменной «Борьба с инфляцией», то обнаружим, что общее количество наблюдений (1299) не меняется при взвешивании. Это связано с тем, что сумма весовых коэффициентов по всем случаям равна числу случаев. Однако в варианте взвешивания, который будет изложен в разделе 8.7.2, это не так.
Если вы попробуете вручную просуммировать частоты упоминания всех четырех вариантов ответов, то в результате вы также получите число 1299. Однако это не закономерность, а скорее счастливое совпадение, о чем свидетельствует следующий пример.
-
Загрузите файл mai.sav, содержащий результаты опроса членов профсоюза на тему 1 мая (см. главу 24).
-
С помощью команд меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты) создайте частотные таблицы переменных v2 (Пол) и v20 (Занятие).
Пол
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | женский | 77 | 28,4 | 28,4 | 28,4 |
мужской | 184 | 71,6 | 71,6 | 100,0 | |
Total | 271 | 100,0 | 100,0 |
Занятие
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | Учащийся | 8 | 3,0 | 3,0 | 3,0 |
Рабочий | 47 | 17,3 | 17,3 | 20,3 | |
Квалифици- рованный рабочий | 47 | 17,3 | 17,3 | 37,6 | |
Специалист | 4 | 1,5 | 1,5 | 39,1 | |
Служащий | 66 | 24,4 | 24,4 | 63,5 | |
Менеджер | 8 | 3,0 | 3,0 | 66,4 | |
Государствен- ный служащий | 31 | 11,4 | 11,4 | 77,9 | |
Пенсионер | 42 | 15,5 | 15,5 | 93,4 | |
Домохозяйка | g | 3,3 | 3,3 | 96,7 | |
Нетрудоспо- собный | 1 | ,4 | ,4 | 97,0 | |
Безработный Total | 8 271 | 3,0 100,0 | 3,0 100,0 | 100,0 |
-
Взвесим наблюдения так, чтобы устранить неравномерность между количествами респондентов обоих полов. Учитывая частотное распределение полов, характерное для имеющейся выборки, это выполняется при помощи следующих команд:
IF v2=1 w=135.5/77.
IF v2=2 w=135.5/194.
EXECUTE
-
Теперь описанным выше способом проведем взвешивание, используя только что полученную переменную w, и построим обе частотные таблицы заново:
Пол
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | женский | 135 | 50,0 | 50,0 | 50,0 |
мужской | 135 | 50,0 | 50,0 | 100,0 | |
Total | 271 | 100,0 | 100,0 |
Занятие
Frequency | Percent | Valid Percent | Cumulative Percent | ||
Valid | Учащийся | 10 | 3,6 | 3,6 | 3,6 |
Рабочий | 46 | 16,8 | 16,8 | 20,4 | |
Квалифици- рованный рабочий | 35 | 12,9 | 12,9 | 33,3 | |
Специалист | 3 | 1,0 | 1,0 | 34,4 | |
Служащий | 83 | 30,7 | 30,7 | 65,1 | |
Менеджер | 7 | 2,5 | 2,5 | 67,5 | |
Государствен- ный служащий | 32 | 11,9 | 11,9 | 79,4 | |
Пенсионер | 36 | 13,2 | 13,2 | 92,6 | |
Домохозяйка | 9 | 3,5 | 3,5 | 96,1 | |
Нетрудоспо- собный | 2 | ,6 | ,6 | 96,8 | |
Безработный | 9 | 3,2 | 3,2 | 100,0 | |
Total | 271 | 100,0 | 100,0 |
Хотя общее число наблюдений, 271, опять не изменилось, но суммирование частот по категориям дает несколько другие результаты.
Это особенно заметно для переменной Пол. Так как после определения переменной взвешивания обе категории должны иметь одинаковые частоты, с самого начала ясно, что сумма не может быть нечетной. Для переменной занятие сложение частот по категориям также дает результат 272, что на единицу отличается от общего количества наблюдений — 271, выводимого в окне просмотра. SPSS всегда, в том числе при взвешивании, выдает целочисленные частоты. Поэтому негативное влияние округления будет неизбежным. Другие статистические программы, например, Stata, обходят эту ситуацию, вычисляя взвешенные частоты с дробной частью.
Если сделать выборку наблюдений, то отображаемые программой суммы до и после взвешивания, как правило, также будут различаться. Это связано с тем, что в частичной выборке количество наблюдений обычно не соответствует сумме весовых коэффициентов, попадающих в эту выборку. Это можно проверить, создав на основе открытого файла данных частотную таблицу переменной «Занятие» до взвешивания и после взвешивания, но только для приверженцев партии СДПГ (v22=2). Тогда мы получим соответственно суммы 91 и 83.
Взвешивание для выравнивания характеристик при нарушении репрезентативности применяется в первую очередь при эпидемиологических исследованиях. Так как при весовом коэффициенте, превосходящем единицу, количество наблюдений искусственно увеличивается по сравнению с фактически измеренным, к результатам теста на значимость следует подходить весьма критически.
14.gif
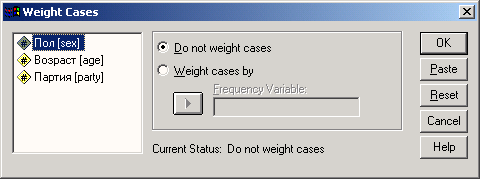
8.7.2 Анализ концентрированных данных
8.7.2 Анализ концентрированных данных
На предприятии с семнадцатью работниками девять из них удовлетворены условиями труда. Двое из этой последней группы в текущем году болели гриппом; из восьми работников, которые не удовлетворены условиями труда, гриппом болели пятеро. Это дает нам следующую таблицу:
удовлетворены | не уловлетворены | |
болели не болели | 1 7 | 5 3 |
Следует выяснить, является ли значимой большая доля болевших среди неудовлетворенных условиями труда. Подходящим статистическим тестом для этой задачи будет точный тест Фишера и Йейтса, который выполняется после создания таблицы сопряженности в дополнении к обычному тесту %2, если количество наблюдений очень мало.
Чтобы можно было решить эту задачу с применением SPSS, в первую очередь следует построить соответствующий файл данных, состоящий из наблюдений и переменных. Примером такого файла служит grippe.sav. Загрузите этот файл. В окне редактора данных вы получите структуру с четырьмя наблюдениями и тремя переменными.
Она содержит переменную grippe с категориями 1 и 2 (болели — не болели), переменную zuf с категориями 1 и 2 (удовлетворены — не удовлетворены) и переменную freq, которая указывает частоту каждого сочетания и будет использоваться в качестве переменной взвешивания.
-
Выберите в меню команды Data (Данные) Weight Cases... (Взвесить наблюдения)
-
В диалоговом окне Weight Cases выберите опцию Weight cases by и перенесите переменную freq в поле Frequency variable.
-
Закройте диалоговое окно и выберите команды меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
-
Перенесите переменную grippe в список переменных строк (Rows), переменную zuf— в список переменных столбцов (Columns), и в диалоге, открываемом кнопкой Statistics..., задайте проведение теста %2 (Chi-square).
В окне просмотра появится следующий результат:
Таблица сопряженности Болели? * Удовлетворены?
Count (Количество) | ||||
Удовлетворены? | Total | |||
| да нет | |||
Болели? | Да | 2 | 5 | 7 |
Нет | 7 | 3 | 10 | |
Total | 9 | 8 | 17 | |
Chi-Square Tests
Value | df | Asymp. Sig. (2-sided) | Exact Sig. (2-sided) (Точная значимость (двусторон-няя)) | Exact Sig. (1-sided) (Точная значимость (односторон-няя)) |
Pearson Chi-Square (?2 пo Пирсону) | 2,837 " | 1 | ,092 | |
Continuity Correction (b) (Коррекция непреры-вности) | 1,418 | 1 | ,234 | |
Likelihood Ratio (Отношение правдопо-добия) | 2,915 | 1 | ,088 | |
Fisher's Exact Test (Точный тест Фишера) | ,153 | ,117 | ||
Linear-by-Linear Association (Зависимость линейный-линейный) | 2,670 | 1 | ,102 | |
N of Valid Cases (Кол-во допустимых случаев) | 17 |
a. Computed only for a 2x2 table (Вычислено только для таблицы 2Х2)
b. 3 cells (75,0%) have expected count less than 5. The minimum expected count is 3,29 (3 ячейки (75%) имеют ожидаемую частоту менее 5. Минимальная ожидаемая частота 11,50.)
Односторонний тест Фишера-Йейтса даст в этом случае р =0,117, т.е. отсутствие значимой разницы.
Следующий пример взят из биологии. Исследовалось количество особей девяти различных видов кузнечиков на пяти разных лугах. Частоты сведены в следующую таблицу
Луг
Вид кузнечика 1 | 2 | 3 | 4 | 5 | |
1 | 0 | 0 | 1 | 1 | 1 |
2 | 1 | 1 | 1 | 1 | 0 |
3 | 61 | 51 | 17 | 122 | 54 |
4 | 36 | 32 | 23 | 38 | 11 |
5 | 2 | 0 | 2 | 6 | 0 |
6 | 3 | 1 | 2 | 2 | 1 |
7 | 0 | 0 | 0 | 2 | 0 |
8 | 26 | 50 | 25 | 54 | 22 |
9 | 35 | 33 | 36 | 25 | 12 |
Следует выяснить, являются ли повышенная концентрация или недостаток отдельных видов кузнечиков на определенных лугах статистически значимыми. Для этого следует применить тест по критерию хи-квадрат.
И в этом случае решение задачи SPSS должна начаться с составления файла данных, содержащего три переменные: переменную для вида кузнечиков (с категориями 1—9), переменную для луга (категории 1—5) и переменную, содержащую частоту данного вида на данном лугу.
-
Загрузите файл wiese.sav и исследуйте его структуру в редакторе данных.
-
Выберите в меню команды Data (Данные) Weight Cases... (Взвесить наблюдения) Откроется диалоговое окно Weight Cases.
-
Выберите опцию Weight cases by и перенесите переменную h в поле Frequency variable.
-
Закройте диалоговое окно кнопкой ОК и выберите команды меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
Появится диалоговое окно Crosstabs.
-
Перенесите переменную heuschr в список переменных строк, переменную wiese — в список переменных столбцов, и в диалоге, открываемом кнопкой Cells..., кроме вывода наблюдаемых частот (флажок Observed в группе Counts), задайте также вывод ожидаемых частот (флажок Expected) и нормированных остатков (флажок Standardized в группе Residuals). После закрытия диалогового окна будет выведена следующая таблица.
Таблица сопряженности HFUSflHR * WIFSF
WIESE | Total | ||||||
1 | 2 | 3 | 4 | 5 | |||
HEUSCHR | |||||||
1 | Count (Количество) | 0 | 0 | 1 | 1 | 1 | 3 |
Expected Count (Ожидаемое количество) | ,6 | ,6 | ,4 | 1,0 | ,4 | 3,0 | |
Std. Residual (Нормиро- ванный остаток) | -,8 | -,8 | ,9 | ,0 | 1,0 | ||
2 | Count | 1 | 1 | 1 | 1 | 0 | 4 |
Expected Count | ,8 | ,8 | ,5 | 1,3 | ,5 | 4,0 | |
Std. Residual | ,2 | ,2 | ,6 | -,2 | -,7 | ||
3 | Count | 61 | 51 | 17 | 122 | 54 | 305 |
Expected Count | 63,2 | 64,8 | 41,3 | 96,8 | 38,9 | 305,0 | |
Std. Residual | -,3 | -1,7 | -3,8 | 2,6 | 2,4 | ||
4 | Count | 36 | 32 | 23 | 38 | 11 | 140 |
Expected Count | 29,0 | 29,7 | 18,9 | 44,4 | 17,9 | 140,0 | |
Std. Residual | 1,3 | ,4 | ,9 | -1,0 | -1,6 | ||
5 | Count | 2 | 0 | 2 | 6 | 0 | 10 |
Expected Count | 2,1 | 2,1 | 1,4 | 3,2 | 1,3 | 10,0 | |
Std. Residual | -,1 | -1,5 | ,6 | 1,6 | -1,1 | ||
6 | Count | 3 | 1 | 2 | 2 | 1 | 9 |
Expected Count | 1,9 | 1,9 | 1,2 | 2,9 | 1,1 | 9,0 | |
Std. Residual | ,8 | -,7 | ,7 | -,5 | -,1 | ||
7 | Count | 0 | 0 | 0 | 2 | 0 | 2 |
Expected Count | ,4 | ,4 | ,3 | ,6 | ,3 | 2,0 | |
Std. Residual | -,6 | -,7 | -,5 | 1,7 | -,5 | ||
8 | Count | 26 | 50 | 25 | 54 | 22 | 177 |
Expected Count | 36,7 | 37,6 | 23,9 | 56,2 | 22,6 | 177,0 | |
Std. Residual | -1,8 | 2,0 | ,2 | -,3 | -,1 | ||
9 | Count | 35 | 33 | 36 | 25 | 12 | 141 |
Expected Count | 29,2 | 29,9 | 19,1 | 44,7 | 18,0 | 141,0 | |
Std. Residual | 1,1 | ,6 | 3,9 | -3,0 | -1,4 | ||
Total | |||||||
Count | 164 | 168 | 107 | 251 | 101 | 791 | |
Expected Count | 164,0 | 168,0 | 107.0 | 251,0 | 101,0 | 791,0 | |
В ячейках таблицы последовательно располагаются наблюдаемые частоты (fy), ожидаемые частоты (fg) и нормированные остатки, определяемые по формуле:
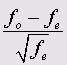
Считается, что существует значимое различие между наблюдаемой и ожидаемой частотой, если нормированный остаток больше или равен 2. Другие предельные значения принимаются в соответствии со следующей таблицей.
Нормированный остаток | Уровень значимости |
>=2,0 | р<0,05 (*) |
>=2,6 | р<0,01 (**) |
>=3,3 | P<0,001 (***) |
Однако эти правила применимы, только в том случае, если ожидаемая частота не меньше 5. Если, к примеру, взять вид кузнечиков № 3, то для него наблюдается значимый недостаток на лугу 3, очень значимая концентрация на лугу 4 и значимая концентрация на лугу 5.
15.gif
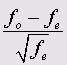
8.8 Примеры вычисления новых переменных
8.8 Примеры вычисления новых переменных
Два следующих примера демонстрируют возможности языка программирования SPSS.
8.8.1 Первый пример: вычисление расхода бензина
8.8.1 Первый пример: вычисление расхода бензина
Предположим, что мы ведем книгу учета расхода бензина. При каждой заправке в нее записывается дата, пробег в километрах и объем заправки в литрах:
Дата | Пробег | Литров |
16.12.1992 | 20580 | 60,3 |
23.12.1992 | 21250 | 57,4 |
04.01.1993 | 21874 | 56,6 |
17.01.1993 | 22476 | 56,3 |
28.01.1993 | 22954 | 45,4 |
12.02.1993 | 23450 | 48,6 |
27.02.1993 | 24020 | 57,0 |
14.03.1993 | 24611 | 56,7 |
Эти данные записаны соответственно в переменных tag, monat, jaehr, kmstand и liter файла tank.sav. Для каждой даты (кроме первой, где это невозможно) требуется вычислить пробег за день и средний расход бензина в расчете на сто километров, а также вывести их через новые переменные.
Это типичный случай, где рационально применить функций LAG и YRMODA. Используя пояснения к этим функциям, которые содержатся в разделе 8.1.2, попробуйте самостоятельно интерпретировать смысл следующих команд:
COMPUTE ntage=yrmoda(jahr,monat,tag) .
COMPUTE difftage=ntage-lag(ntage,1)
COMPUTE diffkm=kmstand-lag(kmstand/1).
COMPUTE verbr=liter*100/diffkm .
COMPUTE kmtag=diffkm/difftage .
EXECUTE .
-
Загрузите файл tank.sav.
-
Введите приведенные выше команды в редактор синтаксиса или примените для этого диалоговое окно Compute Variable.
-
В заключение командами меню Analyze (Анализ) Reports (Отчеты) Case summaries... (Сводка наблюдений) выведите значения переменных tag, monat, jahr, kmtag и verbr.
8.8.2 Второй пример: вычисление даты пасхи
8.8.2 Второй пример: вычисление даты пасхи
Никейский собор в 325 г. установил, что пасху следует праздновать в первое воскресенье после первого весеннего полнолуния. На этом основан метод Гаусса для определения даты пасхального воскресенья. Согласно нему, если задан год jahr (например, 1994), то дату пасхального воскресенья, можно вычислить с помощью следующих операций:
k = целый результат деления jahr/100
р = целый результат деления k/3
q = целый результат деления k/4
m = 15 + k — p — q
ml = остаток от деления т/30
n = 4 + k - q
nl = остаток от деления п/7
а = остаток от деления jahr/19
Ь = остаток от деления jahr/4
с = остаток от деления jahr/7
d = 19 * а + ml
dl = остаток от деления d/30
e = 2*b + 4*c + 6*dl + nl
el = остаток от деления е/7
х = 22 + dl + el
Для определения х существует два исключения
-
Если x=57, то х принимается равным 50
-
Если d1=28 и el=6, а остаток деления в выражении (11*m+11)/30 меньше 19, то х принимается равным 49
Пасхальное воскресенье выпадает на х-ое марта или, если х больше 31, — на х— 31-ое апреля. Этот алгоритм дает превосходный пример для знакомства с арифметическими функциями TRUNC и MOD (см. раздел 7.1.3). Кроме того, можно еще раз потренироваться в использовании оператора IF (раздел 8.4).
Сначала в редакторе данных следует создать файл данных, содержащий единственную переменную jahr. Затем в строках редактора необходимо ввести годы, для которых вы желаете вычислить дату пасхи. Можно также загрузить файл примеров ostern.sav, содержащий годы с 1995 по 2030.
Затем откройте редактор синтаксиса и введите следующую программу. Команды COMPUTE вплоть до вычисления х можно также ввести в соответствующем диалоговом окне (см. раздел 8.1). Команды, приведенные ниже, вводятся в редакторе синтаксиса. Для того, чтобы избежать ручного ввода этой программы, можно просто загрузить в редактор синтаксиса файл ostern.sps.
COMPUTE k=TRUNC(jahr/100) .
COMPUTE p=TRUNC(k/3) .
COMPUTE q=TRUNC(k/4) .
COMPUTE m=15+k-p-q .
COMPUTE ml=MOD(m,30) .
COMPUTE n=4+k-g .
COMPUTE nl=MOD(n,7) .
COMPUTE a=MOD(jahr,19) .
COMPUTE b=MOD(jahr,4) .
COMPUTE c=MOD(jahr,7)
COMPUTE d=19*a+ml .
COMPUTE dl=MOD(d,30) .
COMPUTE e=2*b+4*c+6*dl+nl .
COMPUTE el=MOD(e,7) .
COMPUTE x=22+dl+el .
IF x=57 x=50 .
IF dl=28 AND el=6
AND MOD (ll*m+ll,30)<19 x=49 .
COMPUTE tag=x .
COMPUTE monat=3 .
IF (x > 31) tag=x-31 .
IF (x > 31) monat=4 .
COMPUTE odatum=DATE.MDY(raonat,tag,jahr) .
FORMATS odatum(DATEll) .
LIST odatum .
Переменные tag и monat определяют дату пасхального воскресенья заданного года (переменной jahr). На их основе функция DATE.MDY вычисляет значение времени во внутреннем формате SPSS (число секунд после введения григорианского календаря). Затем это значение записывается в переменную odatum, которая преобразуется в формат даты DATE11.
После ввода программы или открытия файла в редакторе синтексиса с помощью меню Edit (Правка) выделите все строки и запустите программу. С помощью команды LIST в окне просмотра буде сформирована следующая таблица, фрагмент которой с 1995 до 2002 года, приводится ниже:
ODATUM
16-APR-1995
07-APR-1996
30-MAR-1997
12-APR-1998
04-APR-1999
23-APR-2000
15-APR-2001
31-MAR-2002
Обладая некоторой фантазией и знанием командного синтаксиса SPSS, можно решать задачи, не связанные непосредственно со статистическими вычислениями.
Глава 9. Статистические характеристики
Глава 9. Статистические характеристики
1. Статистические характеристики
Статистические характеристики
Статистические характеристики вычисляются в основном для переменных, относящихся к интервальной шкале. Для этого используются следующие четыре команды меню.
Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Descriptives.., (Описательная статистика). Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты). Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Explore... (Исследовать)Analyze (Анализ) Reports (Отчеты)Case summaries... (Итоги по наблюдениям)
Создание частотных таблиц рассматривается в главе 6, а исследование данных — в главе 10.
В нижеследующей таблице приведен обзор характеристик, рассчитываемых в SPSS. В меню Descriptives... можно также провести стандартизацию переменных (z-преобразование).
Характе- ристика | Descrip-tives | Frequen- cies | Explore | Case summaries |
Среднее значение | X | X | X | X |
Сумма | X | X | X | |
Медиана | X | X | X | |
Групповая медиана | X | X | ||
Квартиль | X | |||
Процеитиль | X | X | ||
Мода | X | |||
Стандартное отклонение | X | X | X | X |
Стандартная ошибка | X | X | X | X |
Дисперсия | X | X | X | X |
Минимум | X | X | X | X |
Максимум | X | X | X | X |
Размах | X | X | X | X |
Межквартильная широта | X | |||
Эксцесс (вариация) | X | X | X | X |
Асимметрия | X | X | X | X |
Стандартная ошибка эксцесса | X | X | X | X |
Стандартная ошибка асимметрии | X | X | X | X |
Доверительный интервал | X | |||
Гармоническое среднее | X | |||
Геометрическое среднее | X | |||
М-оценка (Хампеля) | X | |||
Выброс | X | |||
Усеченное среднее | X |
Статистические характеристики, которые задаются в меню Case summaries, можно также вычислить раздельно по категориям группирующих переменных, относящихся к номинальной или порядковой шкале.
В качестве примера для этой и следующей главы мы рассмотрим исследование, относящееся к области медицины — анализ действия двух различных лекарств (с вымышленными названиями альфасан и бетасан) на снижение кровяного давления у гипертоников. Эти данные хранятся в файле hyper.sav, содержащем 174 наблюдения и значения следующих переменных:
nr | Номер пациента |
med | Лекарство (1 = альфасан, 2 = бетасан) |
g | Пол (1 = мужской, 2 = женский) |
а | Возраст, лет |
gr | Рост, см |
gew | Вес, кг |
rrs0 | Систолическое кровяное давление, исходное значение |
rrs1 | то же, через 1 месяц |
rrs6 | то же, через 6 месяцев |
rrs12 | то же, через 12 месяцев |
rrd0 | Диастолическое кровяное давление, исходное значение |
rrd1 | то же, через 1 месяц |
rrd6 | то же, через 6 месяцев |
rrd12 | то же, через 12 месяцев |
chol0 | Холестерин, исходное значение |
chol1 | то же, через 1 месяц |
chol6 | то же, через 6 месяцев |
chol12 | то же, через 12 месяцев |
bz0 | Сахар в крови, исходное значение |
bz1 | то же, через 1 месяц |
bz6 | то же, через 6 месяцев |
bz12 | то же, через 12 месяцев |
ak | Возрастной класс (1 = до 55 лет, 2 = 56-65 лет, 3 = 66-75 лет, 4 = более 75) |
9.1 Описательная статистика
9.1 Описательная статистика
Для ознакомления с характеристиками описательной статистики рассмотрим переменную а, отражающую возраст.
-
Загрузите файл hyper, sav и выберите команды меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Descriptives... (Описательная статистика) Откроется диалоговое окно Descriptives.
Рис. 9.1: Диалоговое окно Descriptives
-
Перенесите переменную а в список тестируемых переменных, и щелкните на кнопке Options... (Параметры).
Здесь можно задать вычисление следующих статистических характеристик:
-
Среднего значения,
-
Суммы,
-
Стандартного отклонения,
-
Стандартной ошибки,
-
Дисперсии,
-
Минимума,
-
Максимума,
-
Размаха,
-
Эксцесса (вариации),
-
Асимметрии.
-
Установите флажки для вывода следующих характеристик: Mean (Среднее значение), Minimum (Минимум), Maximum (Максимум) и S.E. mean (Стандартная ошибка).
Если анализируется несколько переменных, можно также задать последовательность вывода:
-
в порядке возрастания средних значений,
-
в порядке убывания средних значений,
-
по алфавиту (по именам переменных),
-
согласно списку выбранных целевых переменных.
По умолчанию выбран последний вариант. Если имеется только одна переменная, как в данном примере, порядок не имеет значения.
-
Пометив желаемые характеристики, щелкните на кнопке Continue... (Далее). В главном диалоговом окне укажите, чтобы стандартизованные значения были сохранены в новой переменной открытого файла данных, для чего установите флажок Save standardized values as variables.
-
Запустите вычисление, щелкнув на кнопке ОК. Результат будет показан в окне просмотра:
Descriptive Statistics (Описательная статистика)
N | Minimum | Maximum | Mean | ||
Statistic | Statistic | Statistic | Statistic | Std. Error | Statistic |
Возраст | 174 | 36 | 87 | 62,11 | ,88 |
Valid N (listvise) (Допустимых значений (по списку)) | 174 | ||||
О значении отдельных характеристик описательной статистики можно прочесть в главе 6.
Видно, что в файле данных появилась новая переменная za. Она содержит нормированные значения переменной а (Возраст). По умолчанию к имени исходной переменной спереди дописывается буква z. При этом стандартизация (z-преобразование) значения х выполняется по формуле
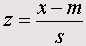
Здесь m — среднее значение переменной, a s — стандартное отклонение.
Проведение стандартизации переменных может быть целесообразным при использовании некоторых статистических методов. Его также можно выполнять в тех случаях, когда несколько переменных, которые имеют различный размах или отличаются на порядки по значению, должны быть приведены к общему показателю. В подобной ситуации сначала необходимо провести стандартизацию этих переменных, а затем, путем усреднения, вывести общее значение из полученных стандартизованых значений (z-зна-чений).
1.gif
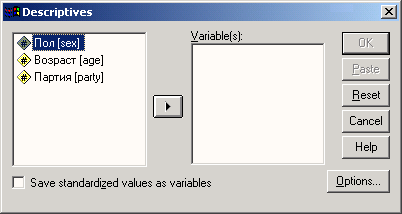
9.2 Сводка наблюдений
9.2 Сводка наблюдений
Этот пункт меню позволяет как выводить значения переменных по наблюдениям, так и вычислять статистические характеристики.
Первую из этих возможностей мы рассмотрели в разделе 4.7; сейчас мы опишем вычисление статистических характеристик. В качестве примера снова выберем файл hyper.sav.
-
Загрузите файл hyper.sav и выберите команды меню Analyze (Анализ) Reports (Отчеты) Case summaries... (Сводка наблюдений)
Откроется диалоговое окно Summarize Cases (Вывести сводку наблюдений) (см. рис. 9.2).
-
Перенесите переменную а в правый список и снимите флажок Display Cases (Показывать наблюдения).
-
Щелкните на кнопке Statistics... (Статистика). Откроется диалоговое окно Summary Report: Statistics (Сводка: Статистика) (см. рис. 9.3).
-
Выберите в списке вычисление среднего значения (Mean), медианы (Median), гармонического среднего (Harmonic Mean) и геометрического среднего (Geometric Mean).
-
Кнопка Options... позволяет задать заголовок для сводной таблицы и способ обработки пропущенных значений.
Рис. 9.2: Диалоговое окно Summarize Cases
Рис. 9.3: Диалоговое окно Summary Report: Statistics
В окне просмотра будут показаны следующие результаты:
Case Processing Summary (Обработанные наблюдения)
Cases (Случаи) | ||||||
Included (Включенные) | Excluded (Исключенные) | Total (Всего) | ||||
N | Percent | N | Percent | N | Percent | |
Возраст | 174 | 100,0% | 0 | ,0% | 174 | 100,0% |
Case Summaries (Сводка наблюдений)
Возраст | ||||||
Mean | Median | Harmonic Mean | Geometric | Mean | ||
62,11 | 63,00 | 59,80 | 60,98 | |||
Описательные характеристики можно также вычислить раздельно по категориям группирующей переменной.
-
Выберите в качестве тестируемой переменной chol0, а в качестве группирующей переменной — g.
-
Задайте вычисление среднего значения, стандартного отклонения, стандартной ошибки среднего (Std. Error of Mean) и медианы.
В окне просмотра будут показаны следующие результаты:
Case Processing Summary
Cases | ||||||
Included | Excluded | Total | ||||
N | Percent | N | Percent | N | Percent | |
Холестерин, исходный * Пол | 174 | 100,0% | 0 | ,0% | 174 | 100,0% |
Case Summaries
Холестерин, исходный | ||||
Пол | Mean | Std. Deviation | Std. Error Mean | Median |
мужской | 228,95 | 54,63 | 7,11 | 216,00 |
женский | 241,54 | 46,19 | 4,31 | 241,00 |
Total | 237,27 | 49,42 | 3,75 | 234,50 |
О настройках, предназначенных для вывода значений по наблюдениям см. раздел 4.8. Раздельное вычисление по категориям группирующей переменной можно также выполнить при помощи команд меню Analyze (Анализ) Compare Means (Сравнение средних) Means... (Средние). Analyze (Анализ) Reports (Отчеты) OLAP Cubes... (OLAP-кубы)
Здесь доступны те же характеристики, что и в меню Case summaries...
Метод вычисления в форме OLAP-кубов (Online Analytical Processing) впервые появился в версии 9 SPSS. Он отличается тем, что таблицы, получающиеся при разбиении по группирующим переменным, можно активировать, пользуясь мобильными таблицами.
3.gif
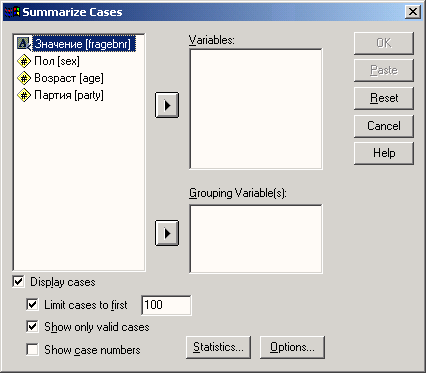
4.gif
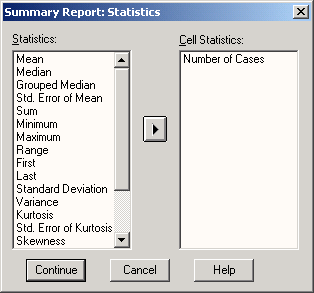
Глава 10. Исследование данных
Глава 10. Исследование данных
1. Исследование данных
Исследование данных
Когда данные введены в компьютер, не следует сразу же приступать к анализу. На первом этапе сами данные следует подвергнуть подробному и всестороннему исследованию. Подобное исследование преследует три основных цели:
-
Обнаружение ошибок ввода,
-
Проверка закона распределения,
-
Описание данных подходящими статистическими характеристиками.
10.1 Обнаружение ошибок ввода
10.1 Обнаружение ошибок ввода
Самый точный метод проверки данных (то есть значений всех переменных) на ошибки при вводе состоит в том, чтобы командами меню Analyze (Анализ) Reports (Отчеты) Case summaries... (Сводка наблюдений) вывести их список (см. раздел 4.6) и сравнить каждое значение с оригиналом (например, анкетой). Однако этот способ требует очень много времени, особенно при большом объеме данных. Поэтому решиться на проведение такой скучной и утомительной работы можно только в редких случаях — как правило, когда объем данных ограничен. В общем случае рекомендуется проводить частотный анализ значений переменных; для этого служат команды меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты) (см. главу 6). Результаты этого анализа при внимательном рассмотрении позволяют выявить недопустимые значения. Например, если переменная содержит данные роста в сантиметрах, то значение 384, обнаруживаемое при частотном анализе, явно свидетельствует о том, что в данных имеется ошибка. После проведения частотного анализа это значение можно отыскать в файле данных и исправить. Следовательно, при изучении частотных таблиц особое внимание надо обращать на максимальное и минимальное значения. Однако если вместо возраста 65 лет было введено, например, значение 56, то при помощи частотной таблицы эту ошибку обнаружить невозможно. Часто имеется также возможность провести смысловой анализ данных путем создания таблиц сопряженности (см. главу 11). Например, если данные взяты из анкеты, в которой имелся вопрос о семейном положении (холост/не замужем, женат/замужем, вдовец/вдова, разведен(а)), то, построив таблицу сопряженности для этого вопроса и вопроса типа: «Если у вас есть семья, то приемлемо ли для вас проводить отпуск раздельно?», легко можно обнаружить, ответили ли на него только женатые/замужние опрашиваемые.
Обладая некоторыми практическими навыками и фантазией, с помощью описанных и им подобных способов можно выявить большое количество ошибок ввода. Все такие ошибки обязательно должны быть исправлены. Даже если наблюдений несколько тысяч, то даже одно-единственное противоречивое значение наносит вред вашему исследованию: создается впечатление, что работа по сбору о подготовке информации выполнена поверхностно.
10.2 Проверка закона распределения
10.2 Проверка закона распределения
В первую очередь представляет интерес закон распределения, особенно для переменных, относящихся к интервальной шкале и шкале отношений. Чаще всего при этом ставится вопрос, подчиняются ли значения переменных нормальному распределению. Именно от этого практически всегда зависит выбор соответствующих аналитических тестов.
В этом отношении самым распространенным и рекомендуемым является графическое изображение распределения данных в форме гистограммы (см. главы 6 и 22). Объективная проверка на нормальное распределение проводится с помощью подходящего статистического критерия (теста Колмогорова-Смирнова). Эта операция представлена в разделе 14.5.
10.3 Вычисление характеристик
10.3 Вычисление характеристик
SPSS предоставляет различные возможности для вычисления статистических характеристик, помогающих оценить положение вершины и разброс распределения. К таким характерам относятся, например, среднее значение, медиана, стандартное отклонение и т.д. Эти возможности перечислены в обзоре в начале главы 9.
В рамках исследования данных можно определить другие характеристики, называемые робастными оценками. Этот метод исследования данных также предоставляет возможности для обнаружения ошибок ввода (например, путем выявления выбросов) и проверки формы распределения.
10.4 Исследование данных
10.4 Исследование данных
Чтобы понять, что может предложить нам SPSS для решения этой задачи, возьмем для примера переменную а (Возраст) из исследования эффективности лекарств (см. главу 9).
-
Загрузите файл hyper.sav.
-
Перейдите к исследованию данных, выбрав команды меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Explore... (Исследовать) Откроется диалоговое окно Explore.
Рис. 10.1: Диалоговое окно Explore
Поначалу вас может смутить то, что в этом диалоговом окне проводится различие между зависимыми переменными и факторами. Это означает, что можно выполнять анализ раздельно по группам наблюдений. В этом случае анализируемой переменной будет зависимая переменная, а группирующей переменной — фактор. Если же такой раздельный анализ проводить не требуется, список факторов не используется.
В следующем разделе мы рассмотрим для начала такой анализ данных, который не должен производиться по группам раздельно.
1.gif
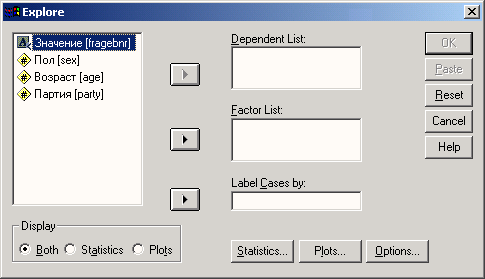
10.4.1 Анализ без группирующей переменной
10.4.1 Анализ без группирующей переменной
Проведем анализ возраста пациентов.
-
Перенесите переменную а в список зависимых переменных (Dependent List). Так как сначала мы хотим выяснить, какие методы анализа выполняются по умолчанию, то не будем пока вносить никаких изменений в настройки.
-
Запустите вычисление, щелкнув на кнопке ОК. Будут созданы следующие таблицы:
Case Processing Summary (Обработанные наблюдения)
Cases (Случаи) | |||||
Valid (Допустимые) | Missing (Отсутствующие) | Total (Всего) | |||
N | Percent | N Percent | N | Percent | |
Возраст | 174 | 100,0% | 0 ,0% | 174 | 100,0% |
Descriptives (Описательная статистика)
Statistic | Std. Error | ||
Возраст | Mean (Среднее) | 62,11 | ,88 |
95% Confidence Interval for Mean (95% доверительный интервал среднего) | Lower Bound (Нижняя граница) Upper Bound (Верхняя граница) | 60,38 63,84 | |
5% Trimmed Mean (5% усеченное среднее) | 62,25 | ||
Median (Медиана) | 63,00 | ||
Variance (Дисперсия) | 133,358 | ||
Std. Deviation (Стандартное отклонение) | 11,55 | ||
Minimum (Минимум) | 36 | ||
Maximum (Максимум) | 87 | ||
Range (Размах) | 51 | ||
Interquartile Range (Межквартильная широта) | 17,25 | ||
Skewness (Асимметрия) | -,143 | ,184 | |
Kurtosis (Коэффициент вариации) | -,635 | ,366 |
Возраст Stem-and-Leaf Plot (диаграмма ветвей и листьев)
Frequency | Stem & | Leaf |
6,00 | 3 . | 677999 |
7,00 | 4 . | 0223333 |
14,00 | 4 . | 66677788888999 |
23,00 | 5 . | 01111111122223333333444 |
20,00 | 5 . | 55667777778888888899 |
27,00 | 6 . | 000011111222333333333444444 |
27,00 | 6 . | 555555666666677888888999999 |
24,00 | 7 . | 000000011111122233333444 |
13,00 | 7 . | 5566666788899 |
11,00 | 8 . | 00001111224 |
2,00 | 8 . | 67 |
Stem width : | 10 | |
Each leaf: | 1 case(s) |
В этом случае окно вывода результатов содержит:
-
статистические характеристики,
-
диаграмму stem-and-leaf (ветвей и листьев)
-
коробчатую диаграмму (box plot).
Большую часть статистических характеристик мы уже рассмотрели в главах 6 и 9. Появились новые характеристики:
-
5% усеченное среднее: среднее значение, вычисленное без учета 5% наименьших и 5% наибольших значений.
-
95% доверительный интервал: доверительный интервал, в котором находится среднее значение с вероятностью 95%.
-
Межквартилъная широта: расстояние между первым и третьим квартилями.
Диаграмма ветвей и листьев представляет собой комбинацию гистограммы и табличного списка. Как на гистограмме, длина каждой строки соответствует количеству наблюдений, попадающих в определенный интервал. Но, сверх этого, на данной диаграмме выводится также наблюдаемое численное значение для каждого наблюдения. Для этой цели численное значения разбиваются на два компонента: ветвь, представляющую собой первую цифру или группу цифр и лист — последующие цифры. Ветвь соответствует тем разрядам численного значения наблюдаемой переменной, которые не изменяются, а листья — разрядам, которые изменяются в пределах избранного интервала. В рассматриваемом примере ветви разбиты на две части — одну для листьев с 0 по 4 и другую — для листьев с 5 по 9.
Коробчатая диаграмма состоит из прямоугольника, занимающего пространство от первого до третьего квартиля (то есть, от 25 до 75 процентиля). Линия внутри этого прямоугольника соответствует медиане. Кроме того, на коробчатой диаграмме отмечаются максимальное и минимальное значения, если только они не являются выбросами (см. ниже).
Значения, удаленные от границ более чем на три длины построенного прямоугольника (экстремальные значения), помечаются на диаграмме звездочками. Значения, удаленные более чем на полторы длины прямоугольника, помечаются кружками.
Теперь посмотрим, какие еще статистические характеристики можно вычислить в дополнение к стандартным.
Рис. 10.2: Коробчатая диаграмма
-
В диалоговом окне Explore щелкните на кнопке Statistics... (Статистика).
Откроется диалоговое окно Explore: Statistics (см. рис. 10.3).
-
Статистические характеристики, установленные по умолчанию уже вычислены, поэтому флажок для них (Descriptives) можно снять.
-
Установите флажки для вычисления М-оценок Губера, Тьюки, Эндрюса и Хампеля (М-estimators), выбросов (Outliers) и процентилей (Percentiles).
-
Закройте диалог, щелкнув на Continue, и запустите вычисления кнопкой ОК. Результат этих вычислений приводится ниже.
Рис. 10.3: Диалоговое окно Explore: Statistics
M-Estimators
Huber's M-Estimator ia) (М-оценка Губера) | Tukey's Biweight (b) (Оценка Тьюки) | Hampel M-Estimator (с) (М-оценка Хампеля) | Andrews' Wave (d) (Волна Эндрюса) | |
Возраст | 62,38 | 62,51 | 62,31 | 62,51 |
a. The weighting constant is 1,339 (Весовая константа равна 1,339).
b. The weighting constant is 4,685 (Весовая константа равна 4,685).
с. The weighting constants are 1,700, 3,400 and 8,500 (Весовые константы равны 1,700, 3,400 и 8,500).
d. The weighting constant is 1,340*pi (Весовая константа равна 1,340*pi).
Percentiles
Percentiles | |||||||
| 5 | 10 | 25 | 50 | 75 | 90 | 95 |
Weighted Возраст Average(Definition 1 ) (Взвешенное среднее, определение 1 ) | 42,00 | 47,00 | 53,00 | 63,00 | 70,25 | 78,00 | 81,00 |
Tukey's Hinges Возраст (угловые точки Тьюки) | 53,00 | 63,00 | 70,00 | ||||
Extreme Values (Экстремальные значения)
Case Number (Номер случая) | Value (Значение) | |||
Возраст | Highest (Наибольшие значения) | 1 | 96 | 87 |
2 | 53 | 86 | ||
3 | 99 | 84 | ||
4 | 86 | 82 | ||
5 | 62 | 82 | ||
Lowest (Наименьшие значения) | 1 | 68 | 36 | |
2 | 23 | 37 | ||
3 | 64 | 37 | ||
4 | 122 | 39 | ||
5 | 45 | .а |
a. Only a partial list of cases with the value 39 are shown in the table of lower extremes (В таблице наименьших экстремальных значений показан только частичный список наблюдений со значением 39).
В этих таблицах выводятся М-оценки Губера, Тьюки, Хампеля и волна Эндрюса. Основная идея М-оценок состоит в том, чтобы перед вычислением среднего значения присвоить отдельным наблюдениям разные веса. В распространенных М-оценках применяются веса, уменьшающиеся с удалением от центра распределения. Следовательно, обычное среднее значение можно рассматривать как М-оценку с единичными весами для всех наблюдений.
Из возможных процентилей выводятся семь значений: для 5, 10, 25, 50, 75, 90 и 95 процентов. Дополнительно вычисляются угловые точки Тьюки: 25%, 50% и 75%-про-центили.
В таблице «Экстремальные значения» выводятся пять наибольших и пять наименьших значений (выбросы).
Теперь обратимся к диаграммам, которые можно построить при исследовании данных в SPSS.
-
В диалоговом окне Explore щелкните на кнопке Plots... (Диаграммы). Откроется диалоговое окно Explore: Plots (см. рис. 10.4).
С коробчатой диаграммой и диаграммой ветвей и листьев мы уже ознакомились.
-
Поэтому в поле Boxplots (Коробчатые диаграммы) выберите опцию None (Нет) и снимите флажок Stem-and-leaf; вместо него установите флажок Histogram (Гистограмма).
-
Щелкните на кнопке Continue, а затем на ОК. В окне просмотра появится гистограмма.
Рис. 10.4: Диалоговое окно Explore: Plots
Рис. 10.5: Гистограмма возрастной структуры
Далее мы посмотрим, какие результаты можно получить, если установить в диалоговом окне Explore: Plots флажок Normality plots with tests (Диаграмма нормального распределения с тестами).
-
Установите этот флажок и подтвердите настройку кнопкой ОК.
В окне просмотра будет показан результат теста Лиллифора (модификации теста Колмогорова-Смирнова) на нормальное распределение.
Если в результате получена вероятность ошибки р менее 0,05, то данное распределение значимо отличается от нормального. В данном примере при р = 0,200 распределение можно считать нормальным. При объеме выборки менее 50 наблюдений проводится также тест Шапиро-Уилкса.
Tests of Normality (Тесты на нормальное распределение)
Kolmoqorov-Smirnov (а) (Колмогоров-Смирнов) | |||
Statistic | df | Sig. | |
Возраст | ,059 | 174 | ,200* |
*. This is a lower bound of the true significance (Это нижняя граница истинной значимости), a. Lilliefors Significance Correction (Коррекция значимости по Лиллифору).
В окне просмотра будут показаны две диаграммы:
-
диаграмма нормального распределения
-
диаграмма с исключенным трендом
По диаграмме нормального распределения (также называемой диаграммой Q-Q) можно визуально определить, достаточно ли близко заданное распределение приближается к нормальному. Здесь каждое наблюдаемое значение сравнивается со значением, ожидаемым при нормальном распределении. При условии точного выполнения нормального распределения все точки лежат на прямой. Наблюдаемые значения откладываются по оси X, а ожидаемые — по оси Y, при этом все значения подвергаются стандартизации (z-преобразованию). В данном примере (см. рис. 10.6) наблюдаемые значения достаточно близки к прямой.
Рис. 10.6: Диаграмма нормального распределения
На диаграмме с исключенным трендом отклонения наблюдаемых значений от ожидаемых при нормальном распределении представлены в зависимости от наблюдаемых значений. В случае нормального распределения все точки лежат на горизонтальной прямой, проходящей через нуль. Явное отклонение от прямой указывает на отличие распределения от нормального. На этой диаграмме все значения, также подвергаются стандартизации (z-преобразованию) (см. рис. 10.7).
Рис. 10.7: Диаграмма с исключенным трендом
Заканчивая рассмотрение диалога Explore... (Исследовать), следует упомянуть еще кнопку Options... (Параметры), которая позволяет задать способ обработки пропущенных значений, и содержит группу опций Display (Показывать). Последняя позволяет запретить вывод диаграмм или статистических таблиц.
2.gif
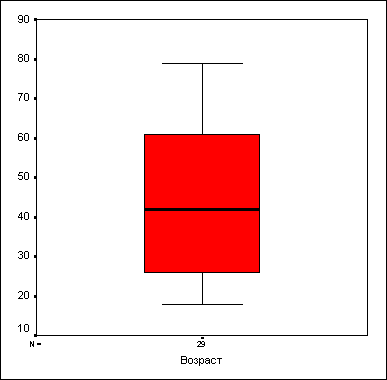
3.gif

4.gif
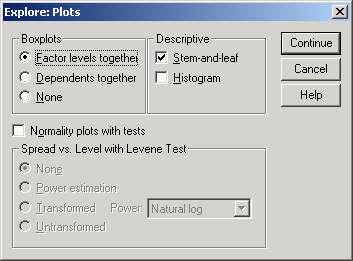
5.gif
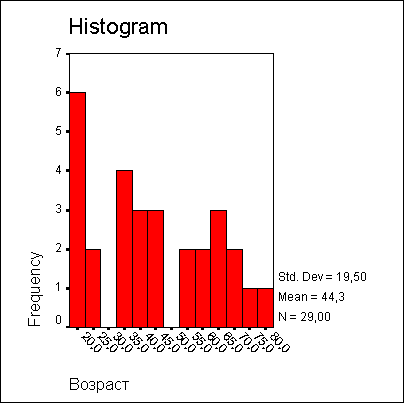
6.gif
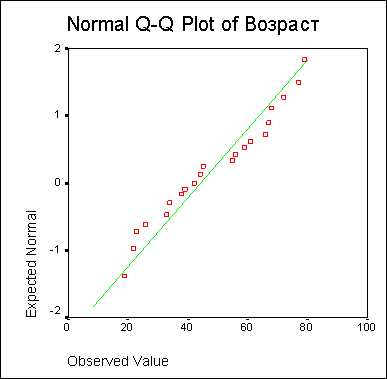
7.gif
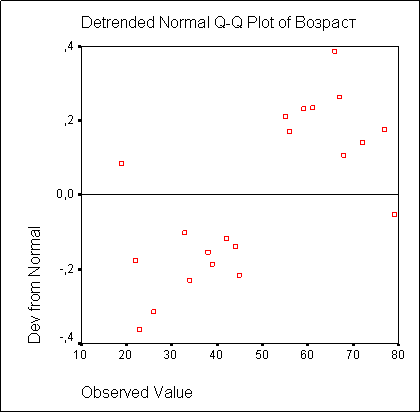
10.4.2 Анализ для групп наблюдений
10.4.2 Анализ для групп наблюдений
Проанализируем исходное содержание холестерина (переменная cho10), которое содержится в файле hyper.sav, для четырех возрастных классов (переменная ak).
-
В диалоговом окне Explore кнопкой Reset (Сброс) восстановите настройки по умолчанию и перенесите переменную cholO в список зависимых переменных (Dependent List), а переменную ak — в список факторов (Factor List).
-
Щелкните на кнопке ОК.
В результате будут вычислены характеристики описательной статистики и построена диаграмма ветвей и листьев раздельно по четырем возрастным классам. На коробчатой диаграмме соответственно появятся четыре прямоугольника (см. рис. 10.8).
Остальные статистические параметры также можно вычислить раздельно по разным значениям группирующей переменной (в данном случае по возрастным классам). Это относится и к выводу гистограмм и диаграмм нормального распределения в окне просмотра.
Далее можно проверить, значимо ли различаются группы наблюдений, образованные в соответствии со списком факторов, по дисперсиям зависимых переменных. В нашем примере можно выяснить, существуют ли значимые различия между пациентами четырех возрастных классов по разбросу содержания холестерина. Такая проверка гомогенности дисперсий необходима, например, если требуется провести для четырех возрастных группах простой дисперсионный анализ на сравнение средних (см. главу 13). Дисперсионный анализ как раз предусматривает гомогенность распределения дисперсий по отдельным ячейкам.
-
В диалоговом окне Explore: Plots в группе Spread vs. Level with Levene Test (Зависимость «Разброс — средний уровень по тесту Левена») выберите опцию Power estimation (Экспоненциальная оценка).
-
Запустите вычисления, щелкнув на Continue и ОК.
Рис. 10.8: Коробчатая диаграмма по группам
В результате во всех четырех вариантах будет проведен тест Левена на гомогенность дисперсий. Этот тест определяет уровень значимости (допустимую вероятность ошибки р. При р > 0,05 различие дисперсии между данными группами не значимо. Следовательно, их можно рассматривать как гомогенные. В данном примере тест Левена не дает значимого результата.
Test of Homogenity of Variances (Тест на гомогенность дисперсий)
Levene Statistic (Статистика Левена) | df1 | df2 | Sig. (Значи-мость) | ||
холестерин, исходный | Based on Mean (На основе среднего) | ,190 | 3 | 170 | ,903 |
Based on Median (На основе медианы) | ,157 | 3 | 170 | ,925 | |
Based on Median and with adjusted df (Ha основе медианы и с уточненным df) | ,157 | 3 | 169,024 | ,925 | |
Based on trimmed mean (На основе усеченного среднего) | ,178 | 3 | 170 | ,912 |
Далее выводится диаграмма, на которой для каждой группы изображена зависимость разброса значений от центрального значения. Точнее говоря, на оси X откладывается логарифм медианы, а на оси Y — логарифм межквартильной широты. Если дисперсии не гомогенны, а гетерогенны (тест Левена дает значимый результат, SPSS дает возможность провести так называемое степенное преобразование данных. Для этого выберите в диалоговом окне Explore: Plots опцию Transformed (С пре-5разованием) и в списке Power (Степень) выберите подходящую степень. Возможные степеные преобразования показаны в нижеследующей таблице.
Степень | Преобразование |
3 | кубическое |
2 | квадратное |
| | квадратный корень |
В | натуральный логарифм. |
-1/2 | величина, обратная квадратному корню |
-1 | обратная величина |
Успешность преобразования можно оценить, вновь построив зависимость разброса от среднего уровня (Spread vs. Level with Levene Test). Однако с такими преобразованиями следует обходиться очень осторожно. Нелинейные преобразования изменяют отношения между группами, и, кроме того, статистические суждения в таком случае основываются уже не на исходных, а на преобразованных значениях.
8.gif
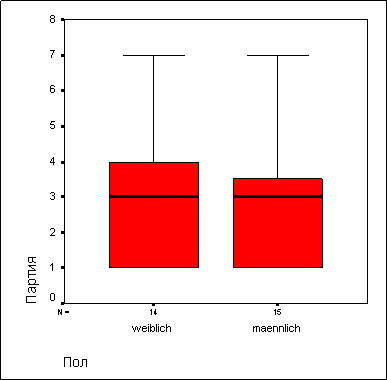
Глава 11. Таблицы сопряженности
Глава 11. Таблицы сопряженности
1. Таблицы сопряженности
Таблицы сопряженности
До сих пор мы рассматривали только отдельные переменные. Мы проводили частотный анализ, а также описывали отдельные переменные статистическими характеристиками, такими как минимум, максимум и среднее значение. Методы анализа такого рода называются одномерными. В текущей главе мы перейдем к двумерному анализу и займемся выяснением вопроса, существует ли взаимосвязь между двумя или более переменными.
В SPSS имеется большое количество разнообразных процедур, при помощи которых можно произвести анализ связи между двумя переменными. Связь между неметрическими переменными, то есть переменными, относящимися к номинальной шкалу или к порядковой шкале с не очень большим количеством категорий, лучше всего представить в форме таблиц сопряженности. Для этой цели в SPSS реализован тест %2, при котором проверяется, есть ли значимое различие между наблюдаемыми и ожидаемыми частотами. Кроме того, существует возможность расчета различных мер связанности. Восстановление зависимостей между метрическими переменными, то есть имеющими интервальную шкалу или шкалу отношений, рассматривается в главе 15.
11.1 Создание таблиц сопряженности
11.1 Создание таблиц сопряженности
-
Загрузите файл studium.sav.
-
Для создания таблиц сопряженности и вычисления меры связанности на их основе, выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности) Откроется диалоговое окно Crosstabs (см. рис. 11.1).
Список исходных переменных содержит переменные открытого файла данных. Здесь можно выбрать переменные для строк и столбцов таблицы сопряженности. Для каждого сочетания двух переменных будет создана таблица сопряженности. Например, если в списке строк (Rows) находится три переменных, а в списке столбцов (Columns) — две, то мы получим 3*2 = 6 таблиц сопряженности. Сначала мы построим таблицу сопряженности из переменных sex (пол) и psyche (психическое состояние). Поступите следующим образом:
-
Перенесите переменную sex в список строк, а переменную psyche — в список столбцов.
Рис. 11.1: Диалоговое окно Crosstabs (Таблицы cопряженности)
-
Щелкните на ОК, и будет создана таблица сопряженности в стандартном формате. В окне просмотра будут показаны следующие таблицы:
Case Processing Summary (Обработанные наблюдения)
Cases (Случаи) | ||||||
Valid (Допусти-мые) | Missing (Отсутству-ющие) | Total (Всего) | ||||
N | Percent | N | Percent | N | Percent | |
Пол* Психическое состояние | 106 | 98,1% | 2 | 1,9% | 108 | 100,0% |
Пол * Психическое состояние Crosstabulation (Таблица сопряженности)
Count (Число)
Психическое состояние | Total | |||||
| Крайне неустой- чивое | Неустой-чивое | Устой-чивое | Очень устойчивое | ||
Пол | Женский | 16 | 18 | 9 | 1 | 44 |
Мужской | 3 | 22 | 32 | 5 | 62 | |
Total | 19 | 40 | 41 | 6 | 106 | |
Первая таблица содержит информацию о числе самих наблюдений; два наблюдения содержат пропущенные значения по крайней мере в одной из двух участвующих переменных. Вторая таблица — это собственно таблица сопряженности. Переменная 'Психическое состояние" (psyche) является столбцовой переменной, так как каждое ее значение (крайне неустойчивое, устойчивое, ...) отображается в отдельном столбце. Переменная "Пол" (sex) — это переменная строк, так как каждое ее значение (женский, мужской) отображается в отдельной строке таблицы. Значение в каждой ячейке таблицы — количество наблюдений (частота). Так, например, здесь видно, что 16 респонденток оценивают свое психическое состояние как "крайне неустойчивое", а 5 респондентов-мужчин — как "очень устойчивое". Если для таблицы сопряженности приняты параметры по умолчанию, в каждой ячейке отображается только абсолютная частота. Метки переменных и значений в таблице соответствуют определениям переменных в файле данных SPSS. Числа в последней строке и в последнем столбце (Всего) показывают суммы значений соответственно по строкам и столбцам. В данном примере суммы по строкам указывают, что 44 (16+18+9+1) опрошенных — лица женского пола, а 62 — мужского. Суммы по столбцам показывают, что
19 опрошенных (16 + 3) оценивают свое психическое состояние как "крайне неустойчивое", 40 как неустойчивое, 41 как устойчивое и 6 как очень устойчивое. При анализе принимались в расчет 106 допустимых наблюдений. Полученные результаты мы можем интерпретировать следующим образом:
-
Из 106 опрошенных, которые учитывались при анализе, — 44 женщины и 62 мужчины.
-
16 женщин оценивают свою психику как "крайне неустойчивую", тогда как для мужчин это количество составляет только 3.
-
Лишь одна женщина считает свое психическое состояние "очень устойчивым", а мужчин с таким состоянием пятеро.
Даже первое впечатление, которое возникает при анализе таблицы сопряженности, свидетельствует о том, что зависимость между переменными Пол и Психическое состояние существует. Женщины считают свое психическое состояние более неустойчивым, чем мужчины. Исследуем эту зависимость чуть более детально; для этого нам понадобится точно ответить на следующие вопросы:
-
Существует ли зависимость вообще?
-
Что можно сказать об интенсивности этой зависимости?
-
Что можно сказать о направлении и характере этой зависимости?
Более тщательно исследовать существование зависимости позволяет вычисление значений ожидаемых частот. Чтобы определить эти значения, выполните следующие действия:
-
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
В списке строк у нас должна стоять переменная sex, а в списке столбцов — переменная psyche.
-
Щелкните на кнопке Cells... (Ячейки). Откроется диалоговое окно Crosstabs: Cell Display (Таблицы сопряженности: Отображение ячеек).
По умолчанию в ячейках таблицы сопряженности отображаются только наблюдаемые значения частот. В группе Counts (Частоты) можно выбрать один или более следующих вариантов отображения:
-
Observed (наблюдаемые): Будут отображаться наблюдаемые частоты. Это настройка по умолчанию.
-
Expected (Ожидаемые): Если установить этот флажок, будут отображаться ожидаемые частоты. Они вычисляются как произведение сумм соответствующей строки и столбца, деленное на общую сумму частот.
Рис. 11.2: Диалоговое окно Crosstabs: Cell Display
-
Установите флажок Expected.
-
Щелкните на кнопке Continue, а затем на ОК. Вы получите следующую таблицу сопряженности.
Пол * Психическое состояние Crosstabulation (Таблица сопряженности)
Психическое состояние | |||||||
Крайне неустой-чивое | Неусто- йчивое | Устой-чивое | Очень устой-чивое | Total | |||
Пол | женский | Count | 16 | 18 | 9 | 1 | 44 |
Expected Count (Ожида- емое число) | |||||||
7,9 | 16,6 | 17,0 | 2,5 | 44,0 | |||
мужской | Count | 3 | 22 | 32 | 5 | 62 | |
Expected Count | 11,1 | 23,4 | 24,0 | 3,5 | 62,0 | ||
"Total | Count | 19 | 40 | 41 | 6 | 106 | |
Expected Count | 19,0 | 40,0 | 41,0 | 6,0 | 106,0 | ||
Теперь под наблюдаемыми частотами (Count) появились ожидаемые значения Expected Count). Эти данные мы можем интерпретировать так:
Для значений переменной "психическое состояние" "крайне неустойчивое" и "неустойчивое" абсолютная частота у опрашиваемых женщин выше, чем ожидаемая (16 и 7,9; j и 16,6), тогда как при значениях "устойчивое" и "очень устойчивое" она ниже (9 и ".0; 1 и 2,5).
У опрашиваемых мужчин мы находим противоположную тенденцию. Для значений ' крайне неустойчивое" и "неустойчивое" абсолютная частота ниже, чем ожидаемая (3 и ' 1.1; 22 и 23,4), тогда как для значений "устойчивое" и "очень устойчивое" она выше :2 и 24,0; 5и 3,5). Эти результаты мы можем объединить в следующую таблицу:
крайне неустойчивое; неустойчивое | очень устойчивое; устойчивое | |
| Женщины | абс. частота > ожидаемой частоты | абс. частота < ожидаемой частоты |
Мужщины | абс. частота < ожидаемой частоты | абс. частота > ожидаемой частоты |
Таким образом, наше первоначальное впечатление, что женщины считают свое психическое состояние менее устойчивым, чем мужчины, подтверждается. Еще одну возможность выявления существования зависимости между переменными дает вычисление остатков. Эти остатки являются показателем того, насколько сильно наблюдаемые и ожидаемые частоты отклоняются друг от друга. Чтобы получить остатки частот, выполните следующие действия:
-
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
В списке переменных строк у нас должна стоять переменная sex, а в списке переменных столбцов — переменная psyche.
-
Щелкните на кнопке Cells... Флажки Observed и Expected следует оставить помеченными.
В группе Residuals (Остатки) можно выбрать один или более следующих вариантов отображения:
-
Unstandardized (Ненормированные): Отображаются ненормированные остатки, то есть разность наблюдаемых (f) и ожидаемых (f) частот.
-
Standardized (Нормированные): Отображаются нормированные остатки. Для этого ненормированные остатки делятся на квадратный корень из ожидаемой частоты:
Нормированные остатки полезны при последующем проведении анализа тестов по критерию х2 (см. раздел 11.3.1).
-
Adj. standardized (Уточненные нормированные): Нормированные остатки вычисляются с учетом сумм по строкам и столбцам:
Здесь z — сумма по текущей строке, a s — сумма по текущему столбцу; N — общая сумма частот.
-
Установите флажок Unstandardized.
-
Щелкните на кнопке Continue, а в главном диалоговом окне — на ОК. Вы получите следующую таблицу сопряженности.
Пол * Психическое состояние Таблица сопряженности
| Психическое состояние | Total | |||||
|
|
| Крайне неустой-чивое | Неустой-чивое | Устой-чивое | Очень устой-чивое | |
Пол | жен-ский | Count | 16 | 18 | 1 | 44 | |
Expected Count | 7,9 | 16,6 | 17,0 | 2,5 | 44,0 | ||
Residual (Остаток) | 8,1 | 1,4 | -8,0 | -1,5 |
| ||
муж-ской | Count | 3 | 22 | 32 | 5 | 62 | |
Expected Count | 11,1 | 23,4 | 24,0 | 3,5 | 62,0 | ||
Residual | -8,1 | -1,4 | 8,0 | 1,5 |
| ||
Total |
| Count | 19 | 40 | 41 | 6 | 106 |
Expected Count | 19,0 | 40,0 | 41,0 | 6,0 | 106,0 | ||
Можно заметить, что каждый остаток равен разности наблюдаемой и теоретически ожидаемой частот в данной ячейке (например, в первой ячейке 16 - 7,9 = 8,1). Остатки делают еще более заметной противоположную тенденцию самооценки у мужчин и женщин.
Таблицы сопряженности, которые мы рассмотрели выше, имеют тот недостаток, что в них приводятся только абсолютные значения. Чтобы узнать, насколько эти значения важны по отношению к общему количеству, надо определить их процентную долю для вычисления процентных значений выполните следующие действия:
-
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Cmsstabs... (Таблицы сопряженности)
-
Не изменяя прежних настроек, щелкните на кнопке Cells... Откроется диалоговое окно Crosstabs: Cell Display (Таблицы сопряженности: Отображение ячеек). В группе Percentages (Проценты) можно выбрать один или более из нижеследующих вариантов отображения:
-
Row (По строкам): Вычисляются процентные значения по строкам: количество наблюдений в каждой ячейке, отнесенное к сумме по строке.
-
Column (По столбцам): Вычисляются процентные значения по столбцам: количество наблюдений в каждой ячейке в отношении к сумме столбца.
-
Total (Полные): Вычисляются полные процентные значения: количество наблюдений в каждой ячейке, отнесенное к общей сумме наблюдений.
Пол * Психическое состояние Таблица сопряженности
Психическое состояние | Total | ||||||
|
|
| Крайне неустой-чивое | Неустой-чивое | Устой-чивое | Очень устой-чивое | |
Пол | жен-ский | Count | 16 | 18 | 9 | 1 | 44 |
Expected Count | 7,9 | 16,6 | 17,0 | 2,5 | 44,0 | ||
% от Пол | 36,4% | 40,9% | 20,5% | 2,3% | 100,0 % | ||
% от Психическое состояние | 84,2% | 45,0% | 22,0% | 16,7% | 41,5% | ||
% of Total | 15,1% | 17,0% | 8,5% | ,9% | 41.5% | ||
Residual | 8,1 | 1,4 | -8,0 | -1.5 |
| ||
муж-ской | Count | 3 | 22 | 32 | 5 | 62 | |
Expected Count | 11,1 | 23,4 | 24,0 | 3,5 | 62,0 | ||
% от Пол | 4,8% | 35,5% | 51,6% | 8.1% | 100,0 % | ||
% от Психическое состояние | 15,8% | 55,0% | 78,0% | 83,3% | 56,5% | ||
% of Total | 2,8% | 20,8% | 30,2% | 4,7% | 58,5% | ||
Residual | -8,1 | -1,4 | 8,0 | 1,5 |
| ||
Тotal | Count | 19 | 40 | 41 | 6 | 106 | |
Expected Count | 19,0 | 40,0 | 41,0 | 6,0 | 106,0 | ||
% от Пол | 17,9% | 37,7% | 38,7% | 5,7% | 100.0 % | ||
% от Психическое состояние | 100,0% | 100,0% | 100,0 % | 100.0% | 100,0 % | ||
% of Total | 17,9% | 37,7% | 38,7% | 5,7% | 100,0 % | ||
-
Установите флажки Row, Column и Total.
-
Щелкните на кнопке Continue, а в главном диалоговом окне — на ОК. В окне просмотра результатов будет получена таблица сопряженности, приведенная выше.
В ней дополнительно отображаются процентные значения частот по отношению к суммам строк, столбцов и общей сумме.
Возьмем для примера первую ячейку. Значения, содержащиеся в ней можно интерпретировать следующим образом:
-
16 из 44 женщин-респонденток или 36,4% от общего числа опрашиваемых охарактеризовали свое психическое состояние как "крайне неустойчивое".
-
Из 19 респондентов с "крайне неустойчивым" состоянием 16 — женщины, что составляет 84,2%.
-
16 женщин-респонденток дали ответ "крайне неустойчивое", что по отношению ко всей таблице (общему количеству респондентов) составляет 15,1%.
Можно также сделать следующие общие выводы:
-
36,4% женщин оценивают свою психику как "крайне неустойчивую", тогда как среди мужчин эта доля составляет только 4,8%.
-
Среди опрашиваемых, оценивающих свою психику как "крайне неустойчивую", женщины составляют 84,2%, а мужчины — лишь 15,8%.
-
77,3% (36,4% + 40,9%) женщин считают свое психическое состояние "крайне неустойчивым" или "неустойчивым", в то время, как только 40,3 % (4,8 % + 35,5 %) мужчин дают такую же оценку своего психического состояния.
-
22,8% (20,5 %+ 2,3%) женщин и 59,7% (51,6% + 8,1%) мужчин оценивают свою психику как "устойчивую" или "очень устойчивую".
-
2,3% женщин оценивают свое психическое состояние как "очень устойчивое", а среди мужчин эта доля составляет 8,1%.
-
Среди опрашиваемых, оценивающих свою психику как "очень устойчивую", женщины составляют 16,7%, а мужчины — 83,3%.
На вопрос, существует ли зависимость между переменными sex и psyche, наиболее ясный ответ в данном примере дают процентные частоты по столбцам. Эти частоты сведены в следующую таблицу:
Крайне неустойчивое | Неустой-чивое | Устой-чивое | Очень устойчивое | |
| Женский | 84,2 | 45,0 | 22,0 | 16,7 |
| Мужской | 1 5,8 | 55,0 | 78,0 | 83,3 |
Так как в нашем случае процентные распределения значительно различаются, мы можем сделать вывод о существовании статистической зависимости между признаками sex и psyche. Значительно больше женщин, чем мужчин, оценивают свое психическое состояние как "крайне неустойчивое", и значительно больше мужчин, чем женщин, оценивают свое психическое состояние как "очень устойчивое". Таким образом, наблюдается различие в оценках психического состояния, связанное с полом. Является ли это различие значимым, можно выяснить при помощи хи-квадрат-теста (см. раздел 11.3.1).
Форматы таблиц сопряженности
Можно изменить порядок сортировки переменных строк в таблице сопряженности, щелкнув в диалоговом окне Crosstabs на кнопке Formal... (Формат). Откроется диалоговое окно Crosstabs: Table Format (Таблицы сопряженности: Формат таблицы).
В группе Row Order (Порядок строк) можно выбрать один из следующих вариантов сортировки значений:
-
Ascending (По возрастанию): Значения переменных строк отображаются в порядке возрастания от наименьшего к наибольшему. Это настройка по умолчанию.
-
Descending (По убыванию): Значения переменных строк отображаются в порядке убывания от наибольшего к наименьшему.
Рис. 11.3: Диалоговое окно Crosstabs: Table Format
Применение переменных групп и слоев
Созданные выше таблицы сопряженности можно разделить по специальностям. Вполне может быть, что переменная fach (Специальность) оказывает влияние на зависимость между sex и psyche. Чтобы выявить возможные различия, следует создать отдельные таблицы, в нашем случае — по одной таблице для каждой специальности. Такие таблицы могут выявить интересные различия между отдельными специальностями. В рассматриваемом примере переменная fach играет роль переменной слоев. Анализ производится по группам, то есть для каждой группы — в нашем случае для каждой специальности — составляется отдельная таблица сопряженности.
Чтобы задать переменную слоев, поступите так:
-
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблица сопряженности)
В списке строк у нас должна стоять переменная sex, а в списке столбцов — переменная psyche.
-
Перенесите переменную fach в список переменных слоев. В диалоговом окне это третий сверху список; он еще пуст. Диалоговое окно Crosstabs приобретет вид, показанный на рис. 11.4.
Рис. 11.4: Заполненное диалоговое окно Crosstabs
Можно выбрать другие уровни переменных слоев. Для каждой категории каждой из переменной слоев будет создана отдельная таблица сопряженности. Чтобы добавить новый слой, щелкните на кнопке Next (Следующий). Каждый последующий уровень делит таблицу сопряженности на меньшие подгруппы. Переходить от одного слоя к другому можно при помощи кнопок Next и Previous (Предыдущий).
-
Щелкните на ОК. Вы получите таблицы сопряженности переменных sex и psyche отдельно для каждой специальности. Предоставляем вам самостоятельно интерпретировать их содержание.
1.gif
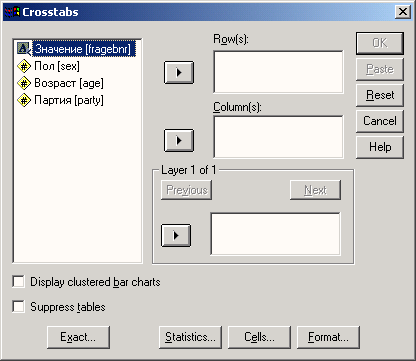
2.gif
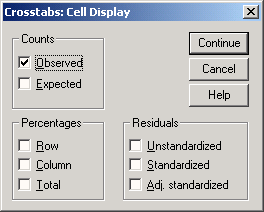
3.gif
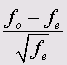
4.gif
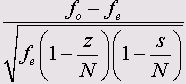
5.gif
6.gif
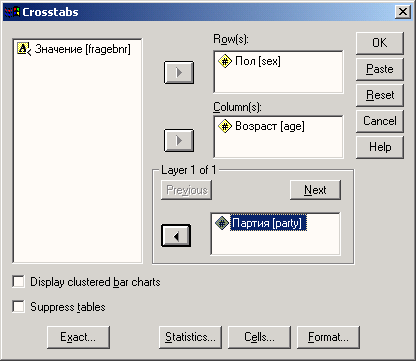
11.2 Графическое представление таблиц сопряженности
11.2 Графическое представление таблиц сопряженности
Чтобы сделать более наглядными данные, содержащиеся в таблицах сопряженности, их можно представить визуально. Для этого поступите следующим образом:
-
Выберите в меню команды Graphs (Графики) Ваr... (Столбчатые) Откроется диалоговое окно Bar Charts (Столбчатые диаграммы).
-
Выберите пункт Clustered (Группированные), оставьте предлагаемую по умолчанию опцию Summaries for groups of cases (Сводка категорий переменной) и щелкните на кнопке Define (Определить). Откроется диалоговое окно Define Clustered Bar: Summaries for groups of cases (Определить столбчатую диаграмму: Сводка категорий переменной).
-
Выберите пункт % of cases (% наблюдений).
-
Перенесите переменную psyche в поле Category Axis (Ось категорий), а переменную sex — в поле Define Clusters by (Определить группы по).
-
Щелкните на кнопке Titles... (Заголовки). Откроется диалоговое окно Titles (см. рис. 11.6).
-
В поле Line 1 (Строка 1) введите заголовок "Психическое состояние в зависимости от пола", в поле Subtitle — подзаголовок "Изучение психического состояния и социального положения студентов", а в поле Footnote, Line 1 (Нижний колонтитул, строка 1) — текст "Опрос студентов WS 93/94". Подтвердите ввод кнопкой Continue.
-
Щелкните на кнопке Options... (Параметры). Откроется диалоговое окно Options.
Рис. 11.5: Диалоговое окно Define Clustered Bar: Summaries for groups of cases
Рис. 11.6: Диалоговое окно Titles
Рис. 11.7: Диалоговое окно Options
-
Снимите в нем флажок Display groups defined by missing values (Отображать группы, образование пропущенными значениями).
-
Щелкните на кнопке Continue, а затем на ОК. В окне просмотра появится график.
-
Дважды щелкните на этом графике — откроется редактор диаграмм, в котором его можно править.
-
Выберите в меню команды Format (Формат) Bar Label Style... (Стиль меток столбцов) Откроется диалоговое окно Bar Label Style.
-
Выберите пункт Framed (В рамках), щелкните на кнопке Apply all (Применить для всех) и затем на Close (Закрыть).
-
Щелкните на одном из столбцов, отображающем психическое состояние женщин, или в легенде на поле "женский". Столбцы, отображающие психическое состояние женщин, будут выделены. Это можно определить по маленьким черным квадратикам на углах столбцов.
-
Выберите в меню команды Format (Формат) Color... (Цвет)
Откроется диалоговое окно Colors (Цвета). Здесь можно изменить стандартный цвет столбцов, а также цвет их контура.
-
Щелкните на сером поле, а затем на кнопках Apply (Применить) и Close (Закрыть).
-
Таким же способом измените цвет столбцов для мужчин на черный.
-
В заключение вызовите команды меню Chart (Диаграмма) Outer Frame (Внешняя рамка)
Получится графическое представление таблицы сопряженности, показанное на рис. 11.8.
Можно не вызывать меню Graph, а просто установить в диалоге Crosstabs флажок Display clustered bar charts (Показывать столбчатые кластеризованные диаграммы). Тогда на диаграмме будут показаны две группы столбцов для двух переменных строк. Чтобы придать диаграмме такой вид, как на рис. 11.8, надо поменять переменные строк и столбцов местами.
7.gif
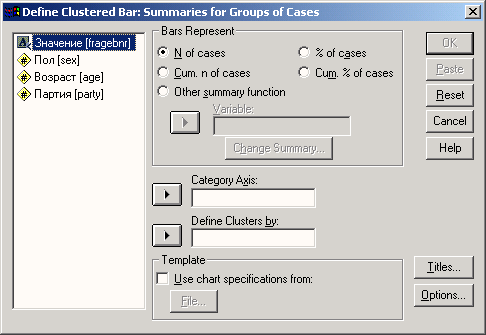
8.gif
9.gif
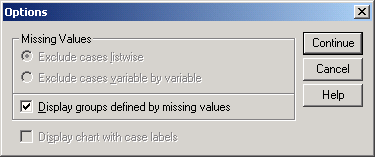
11.3 Статистические критерии для таблиц сопряженности
11.3 Статистические критерии для таблиц сопряженности
Чтобы получить статистические критерии для таблиц сопряженности, щелкните на кнопке Statistics... (Статистика) в диалоговом окне Crosstabs. Откроется диалоговое окно Crosstabs: Statistics (Таблицы сопряженности: Статистика) (см. рис. 11.9).
Флажки в этом диалоговом окне позволяют выбрать один или несколько критериев.
-
Тест хи-квадрат (X2)
-
Корреляции
-
Меры связанности для переменных, относящихся к номинальной шкале
-
Меры связанности для переменных, относящихся к порядковой шкале
-
Меры связанности для переменных, относящихся к интервальной шкале
-
Коэффициент каппа (к)
Рис. 11.8: Графическое представление: столбчатая диаграмма
Рис. 11.9: Диалоговое окно Crosstabs: Statistics
-
Мера риска
-
Тест Мак-Немара
-
Статистики Кохрана и Мантеля-Хэнзеля
Эти критерии рассматриваются в двух последующих разделах, причем из-за того, что критерий хи-квадрат имеет большое значение в статистических вычислениях, ему посвящен отдельный раздел.
10.gif
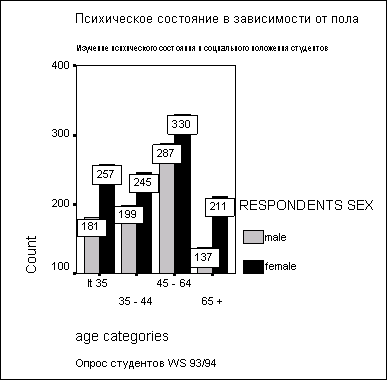
11.gif
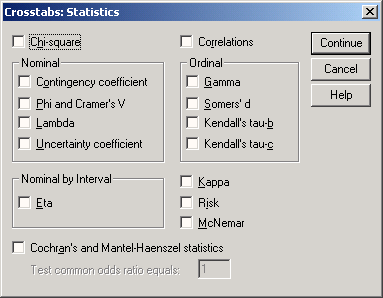
11.3.1 Тест хи-квадрат
11.3.1 Тест хи-квадрат (X2)
При проведении теста хи-квадрат проверяется взаимная независимость двух переменных таблицы сопряженности и благодаря этому косвенно выясняется зависимость обоих переменных. Две переменные считаются взаимно независимыми, если наблюдаемые частоты (f0) в ячейках совпадают с ожидаемыми частотами (fe).
Для того, чтобы провести тест хи-квадрат с помощью SPSS, выполните следующие действия:
-
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
-
Кнопкой Reset (Сброс) удалите возможные настройки.
-
Перенесите переменную sex в список строк, а переменную psyche — в список столбцов.
-
Щелкните на кнопке Cells... (Ячейки). В диалоговом окне установите, кроме предлагаемого по умолчанию флажка Observed, еще флажки Expected и Standardized. Подтвердите выбор кнопкой Continue.
-
Щелкните на кнопке Statistics... (Статистика).
Откроется описанное выше диалоговое окно Crosstabs: Statistics.
-
Установите флажок Chi-square (Хи-квадрат). Щелкните на кнопке Continue, а в главном диалоговом окне — на ОК.
Вы получите следующую таблицу сопряженности.
Пол * Психическое состояние Таблица сопряженности
Психическое состояние | Total | ||||||
|
|
| Крайне неустой-чивое | Неустой-чивое | Устой-чивое | Очень устойчивое | |
Пол | женский | Count | 16 | 18 | 9 | 1 | 44 |
Expected Count | 7,9 | 16,6 | 17,0 | 2,5 | 44,0 | ||
Std. Residual | 2,9 | ,3 | -1,9 | -.9 |
| ||
Мужской | Count | 3 | 22 | 32 | 5 | 62 | |
Expected Count | 11,1 | 23,4 | 24,0 | 3,5 | 62,0 | ||
Std. Residual | -2,4 | -,3 | 1,6 | ,8 |
| ||
Total |
| Count | 19 | 40 | 41 | 6 | 106 |
Expected Count | 19,0 | 40,0 | 41,0 | 6,0 | 106,0 | ||
Кроме того, в окне просмотра будут показаны результаты теста хи-квадрат:
Chi-Square Tests (Тесты хи-квадрат)
Value (Значение) | df | Asymp. Sig. (2-sided) (Асимптотическая значимость (двусторонняя)) | |
Pearson Chi-Square (Хи-квадрат по Пирсону) | 22,455 (а) | 3 | ,000 |
Likelihood Ratio (Отношение правдоподобия) | 23,688 | 3 | ,000 |
Linear-by-Linear Association (Зависимость линейный-линейный) | 20,391 | 1 | ,000 |
N of Valid Cases (Кол-во допустимых случаев) | 106 |
а. 2 cells (25,0%) have expected count less than 5. The minimum expected count is 2,49 (2 ячейки (25%) имеют ожидаемую частоту менее 5. Минимальная ожидаемая частота 2,49.)
Для вычисления критерия хи-квадрат применяются три различных подхода: формула Пирсона, поправка на правдоподобие и тест Мантеля-Хэнзеля. Если таблица сопряженности имеет четыре поля и ожидаемая вероятность менее 5, дополнительно выполняется точный тест Фишера.
Критерий хи-квадрат по Пирсону
Обычно для вычисления критерия хи-квадрат используется формула Пирсона:
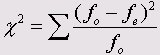
Здесь вычисляется сумма квадратов стандартизованных остатков по всем полям таблицы сопряженности. Поэтому поля с более высоким стандартизованным остатком вносят более весомый вклад в численное значение критерия хи-квадрат и, следовательно, — в значимый результат. Согласно правилу, приведенному в разделе 8.7.2, стандартизованный остаток 2 или более указывает на значимое расхождение между наблюдаемой и ожидаемой частотами.
В рассматриваемом нами примере формула Пирсона дает максимально значимую величину критерия хи-квадрат (р<0,001). Если рассмотреть стандартизованные остатки в отдельных полях таблицы сопряженности, то на основе вышеприведенного правила можно сделать вывод, что эта значимость в основном определяется полями, в которых переменная psyche имеет значение "крайне неустойчивое". У женщин это значение сильно повышено, а у мужчин — понижено.
Корректность проведения теста хи-квадрат определяется двумя условиями: во-первых, ожидаемые частоты < 5 должны встречаться не более чем в 20 % полей таблицы; во-вторых, суммы по строкам и столбцам всегда должны быть больше нуля.
Однако в рассматриваемом примере это условие выполняется не полностью. Как указывает примечание после таблицы теста хи-квадрат, 25 % полей имеют ожидаемую частоту менее 5. Однако, так как допустимый предел4в 20 % превышен лишь ненамного и эти поля, вследствие своего очень малого стандартизованного остатка, вносят весьма незначительную долю в величину критерия хи-квадрат, это нарушение можно считать несущественным.
Критерий хи-квадрат с поправкой на правдоподобие
Альтернативой формуле Пирсона для вычисления критерия хи-квадрат является поправка на правдоподобие:

При большом объеме выборки формула Пирсона и подправленная формула дают очень близкие результаты. В нашем примере критерий хи-квадрат с поправкой на правдоподобие составляет 23,688.
Тест Мантеля-Хэнзеля
Дополнительно в таблице сопряженности под обозначением linear-by-linear ("линейный-по-линейному") выводится значение теста Мантеля-Хэнзеля (20,391). Эта форма критерия хи-квадрат с поправкой Мантеля-Хэнзеля — еще одна мера линейной зависимости между строками и столбцами таблицы сопряженности. Она определяется как произведение коэффициента корреляции Пирсона на количество наблюдений, уменьшенное на единицу:
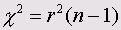
Полученный таким образом критерий имеет одну степень свободы. Метод Мантеля-Хэнзеля используется всегда, когда в диалоговом окне Crosstabs: Statistics установлен флажок Chi-square. Однако для данных, относящихся к с номинальной шкале, этот критерий неприменим.
12.gif
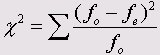
13.gif

11.3.2 Коэффициенты корреляции
11.3.2 Коэффициенты корреляции
До сих пор мы выясняли лишь сам факт существования статистической зависимости между двумя признаками. Далее мы попробуем выяснить, какие заключения можно сделать о силе или слабости этой зависимости, а также о ее виде и направленности. Критерии количественной оценки зависимости между переменными называются коэффициентами корреляции или мерами связанности. Две переменные коррелируют между собой положительно, если между ними существует прямое, однонаправленное соотношение. При однонаправленном соотношении малые значения одной переменной соответствуют малым значениям другой переменной, большие значения — большим. Две переменные коррелируют между собой отрицательно, если между ними существует обратное, разнонаправленное соотношение. При разнонаправленном соотношении малые значения одной переменной соответствуют большим значениям другой переменной и наоборот. Значения коэффициентов корреляции всегда лежат в диапазоне от -1 до +1.
В качестве коэффициента корреляции между переменными, принадлежащими порядковой шкале применяется коэффициент Спирмена, а для переменных, принадлежащих к интервальной шкале — коэффициент корреляции Пирсона (момент произведений). При этом следует учесть, что каждую дихотомическую переменную, то есть переменную, принадлежащую к номинальной шкале и имеющую две категории, можно рассматривать как порядковую.
Для начала мы проверим существует ли корреляция между переменными sex и psyche из файла studium.sav. При этом мы учтем, что дихотомическую переменную sex можно считать порядковой. Выполните следующие действия:
-
Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
-
Перенесите переменную sex в список строк, а переменную psyche — в список столбцов.
-
Щелкните на кнопке Statistics... (Статистика). В диалоге Crosstabs: Statistics установите флажок Correlations (Корреляции). Подтвердите выбор кнопкой Continue.
-
В диалоге Crosstabs откажитесь от вывода таблиц, установив флажок Supress tables (Подавлять таблицы). Щелкните на кнопке ОК.
Будут вычислены коэффициенты корреляции Спирмена и Пирсона, а также проведена проверка их значимости:
Symmetric Measures (Симметричные меры)
Value (Значение) | Asympt. Std. Error (а) Асимпто-тическая стандарт-ная ошибка) | Approx. Т (b) (Приблиз. Т) | Approx. Sig. (Приблизи- тельная значи-мость) | ||
Interval by Interval (Интерваль- ный-интерваль- ныи) | Pearson's R (R Пирсона) | ,441 | ,081 | 5,006 | ,000 (с) |
Ordinal by Ordinal (Порядковый-порядковый) | Spearman Correlation (Корреляци я по Спирмену) | .439 | ,083 | 4,987 | ,000 (с) |
N of Valid Cases (Кол-во допустимых случаев) |
| 106 |
|
|
|
a. Not assuming the null hypothesis (Нулевая гипотеза не принимается).
b. Using the asymptotic standard error assuming the null hypothesis (Используется асимптотическая стандартная ошибка с принятием нулевой гипотезы).
с. Based on normal approximation (На основе нормальной аппроксимации).
Так как здесь нет переменных с интервальной шкалой, мы рассмотрим коэффициент корреляции Спирмена. Он составляет 0,439 и является максимально значимым (р<0,001).
Для словесного описания величин коэффициента корреляции применяется следующая таблица:
Значение коэффициента корреляции r | Интерпретация |
0 < г <= 0,2 0,2 < г <= 0,5 0,5 < г <= 0,7 0,7 < г <= 0,9 0,9 < г <= 1 | Очень слабая корреляция Слабая корреляция Средняя корреляция Сильная корреляция Очень сильная корреляция |
Исходя из вышеприведенной таблицы, можно сделать следующие заключения: Между переменными sex и psyche существует слабая корреляция (заключение о силе зависимости), переменные коррелируют положительно (заключение о направлении зависимости).
В переменной psyche меньшие значения соответствуют отрицательному психическому состоянию, а большие — положительному. В переменной sex, в свою очередь, значение "1" соответствует женскому полу, а "2" — мужскому.
Следовательно, однонаправленность соотношения можно интерпретировать следующим образом: студентки оценивают свое психическое состояние более негативно, чем '.х коллеги-мужчины или, что вероятнее всего, в большей степени склонны согласиться на такую оценку при проведении анкетирования. Строя подобные интерпретации, нужно учитывать, что корреляция между двумя признаками не обязательно равнозначна их Функциональной или причинной зависимости. Подробнее об этом см. в разделе 15.3.
Теперь проверим корреляцию между переменными alter и semester. Применим методику, описанную выше. Мы получим следующие коэффициенты:
Symmetric Measures
Value | Asympt. Std. Error (a) | Approx. Т (b) | Approx. Sig. | ||
Interval by Interval | Pearson's R | ,807 | ,041 | 13,930 | ,000 (c) |
Ordinal by Ordinal | Spearman Correlation | ,743 | ,060 | 11,310 | ,000 (c) |
N of Valid Cases | 106 | ||||
a. Not assuming the null hypothesis (Нулевая гипотеза не принимается).
э. Using the asymptotic standard error assuming the null hypothesis (Используется асимптотическая стандартная ошибка с принятием нулевой гипотезы).
с. Based on normal approximation (На основе нормальной аппроксимации).
Так как переменные alter и semester являются метрическими, мы рассмотрим коэффициент Пирсона (момент произведений). Он составляет 0,807. Между переменными alter и semester существует сильная корреляция. Переменные коррелируют положительно. Следовательно, старшие по возрасту студенты учатся на старших курсах, что, собственно, не является неожиданным выводом.
Проверим на корреляцию переменные sozial (оценку социального положения) и psyche. Мы получим следующие коэффициенты:
Symmetric Measures
Value | Asympt. Std. Error (a) | Approx. Т (b) | Approx. Sig. | ||
Interval by Interval | Pearson's R | -,688 | ,057 | -9,703 | ,000 (c) |
Ordinal by Ordinal | Spearman Correlation | -,703 | ,059 | -10,123 | ,000 (c) |
N of Valid Cases | 107 | ||||
a. Not assuming the null hypothesis (Нулевая гипотеза не принимается).
b. Using the asymptotic standard error assuming the null hypothesis (Используется асимптотическая стандартная ошибка с принятием нулевой гипотезы).
с. Based on normal approximation (На основе нормальной аппроксимации).
В этом случае мы рассмотрим коэффициент корреляции Спирмена; он составляет -0,703. Между переменными sozial и psyche существует средняя или сильная корреляция (граничное значение 0,7). Переменные коррелируют отрицательно, то есть чем больше значения первой переменной, тем меньше значения второй и наоборот. Так как малые значения переменной sozial характеризуют позитивное состояние (1 = очень хорошее, 2 = хорошее), а большие значения psyche — отрицательное состояние (1 = крайне неустойчивое, 2 = неустойчивое), следовательно, психологические затруднения во многом обусловлены социальными проблемами.
11.3.3 Меры связанности для переменных с номинальной шкалой
11.3.3 Меры связанности для переменных с номинальной шкалой
Коэффициент корреляции нельзя применять в качестве характеристики зависимости между переменными, если эти переменные принадлежат к номинальной шкале и имеют более двух категорий, потому что между их кодировками невозможно установить порядкового отношения и, следовательно, они не могут быть расположены в определенном, рационально объяснимом порядке.
Наилучшим средством для анализа таких зависимостей считается представленный в разделе 11.3.1 тест хи-квадрат, после которого при необходимости можно провести анализ наблюдаемых и ожидаемых частот, а также нормированных остатков. Этот анализ был описан в разделе 8.7.2.
Тем не менее и в этом случае также производились попытки разработать критерии количественной оценки степени связанности двух переменных, поставленных во взаимное соответствие. Эти критерии показывают степень взаимной зависимости или независимости двух переменных, принадлежащих к с номинальной шкале, причем значение 0 соответствует полной независимости переменных, а 1 — их максимальной зависимости. Меры связанности не могут иметь отрицательных значений, так как при отсутствии порядкового отношения нельзя дать ответа на вопрос о направлении зависимости.
В опросе членов городской организации одной из политических партий среди прочего выяснялось их занятие и определялось, выполняет ли респондент какую-либо партийную функцию. Выдержка из ответов респондентов-мужчин содержится в файле partei.sav.
-
Загрузите файл partei.sav и создайте таблицу сопряженности с переменной funk в строках и переменной beruf в столбцах.
-
Задайте вывод ожидаемых частот, стандартизованных остатков, процентов по столбцам и критерия хи-квадрат.
Занятие * Партийная работа Crosstabulation (Таблица сопряженности)
Занятие | Total | ||||||
|
|
| Наемный работник | Государст- венный служащий | Предпри-ниматель | ||
Партийная работа | да | Count | 13 | 16 | 7 | 36 | |
Expected Count | 12,4 | 10,1 | 13,5 | 36,0 | |||
% от Занятие | 59,1% | 88,9% | 29,2% | 56,3% | |||
Std. Residual | ,2 | 1,8 | -1,8 |
| |||
нет | Count | 9 | 2 | 17 | 28 | ||
Expected Count | 9,6 | 7,9 | 10,5 | 28,0 | |||
% от Занятие | 40,9% | 11,1% | 70.8% | 43,8% | |||
Std. Residual | -,2 | -2,1 | 2,0 |
| |||
Total | Count | 22 | 18 | 24 | 64 | ||
Expected Count | 22,0 | 18,0 | 24,0 | 64,0 | |||
% от Занятие | 100,0% | 100,0% | 100,0% | 100,0% | |||
Chi-Square Tests
Value | df | Asymp. Sig. (2-sided) | |
Pearson Chi-Square (Критерий хи-квадрат по Пирсону) | 15,01 7 (a) | 2 | ,001 |
Likelihood Ratio (Отношение правдоподобия) | 16,421 | 2 | ,000 |
Li near-by-Li near Association (Зависимость линейный-линейный) | 4,420 | 1 | ,036 |
N of Valid Cases | 64 |
а. и cells (,0%) have expected count less than 5. The minimum expected count is 11,50. (0 ячеек (,0%) имеют ожидаемую частоту менее 5. Минимальная ожидаемая частота 7,88.)
Результат получился максимально значимым: участие в партийной работе весьма характерно для государственных служащих, а для предпринимателей — совсем не характерно, тогда как наемные работники находятся посредине. Теперь зададим (кнопкой Statistics...) вывод всех мер связанности для переменных, принадлежащих к номинальной шкале (флажки в группе Nominal).
Directional Measures (Направленные меры)
| Value | Asympt. Std. Error (a) | Approx. Т (b) | Approx. sig. | ||
Nominal by Nominal (Номиналь- ный-номина- льный) | Lambda (Лямбда) | Symmetric (Симметри- ческая) | ,279 | ,104 | 2,554 | ,011 |
Партийная работа Dependent (B зависимости от Партийная работа) | ,357 | ,140 | ,211 | ,035 | ||
Занятие Dependent (В зависимости от Занятие) | ,225 | ,106 | 1,930 | ,054 | ||
Goodman and Kruskal tau (Tay Гудмена-Крускала) | Партийная работа Dependent | ,235 | ,093 |
| ,001 (c) | |
Занятие Dependent | ,116 | ,051 |
| ,001 (c) | ||
Uncertainty Coefficient (Коэффициент неопреде- ленности) | Симметричный | ,144 | ,063 | 2,269 | ,000 (d) | |
Партийная работа Dependent | ,187 | ,082 | 2,269 | ,000 (d) | ||
Занятие Dependent | ,118 | ,052 | 2,269 | ,000 (d) | ||
a. Not assuming the null hypothesis (Нулевая гипотеза не принимается).
b. Using the asymptotic standard error assuming the null hypothesis (Используется асимптотическая стандартная ошибка с принятием нулевой гипотезы).
с. Based on chi-square approximation (На основе аппроксимации по распределению хи-квадрат).
d. Likelihood ratio chi-square probability (Степень правдоподобия при распределении вероятности по закону хи-квадрат).
Symmetric Measures (Симметричные меры)
Value | Approx. Sig. | ||
Nominal by Nominal (Номинальный-номинальный) | Phi (Фи) | ,484 | ,001 |
Cramer's V (V Крамера) | ,484 | ,001 | |
Contingency Coefficient (Коэффициент сопряженности признаков) | ,436 | ,001 | |
N of Valid Cases | 64 | ||
a. Not assuming the null hypothesis (Нулевая гипотеза не принимается).
b. Using the asymptotic standard error assuming the null hypothesis (Используется асимптотическая стандартная ошибка с принятием нулевой гипотезы).
Коэффициент сопряженности признаков (Пирсона)
Его величина всегда находится в пределах от 0 до 1 и вычисляется (как и значения критериев Фишера (<р) и Крамера (V)) с использованием значения критерия хи-квадрат:

Здесь N — общая сумма частот в таблице сопряженности. Так как N всегда больше нуля, коэффициент сопряженности признаков никогда не достигает единицы. Максимальное значение зависит от количества строк и столбцов таблицы сопряженности и в таблице размером 3*2 составляет (как в данном примере) 0,762. По этой причине коэффициенты сопряженности признаков для двух таблиц с разным количеством полей несопоставимы.
Критерий Фишера (<р)
Этот коэффициент можно использовать только для таблиц 2*2, так как в других случаях он может превысить значение 1:

Критерий Крамера (V)
Этот критерий представляет собой модификацию критерия Фишера и для любых таблиц сопряженности он дает значение в пределах от 0 до 1, включая 1:

Здесь k — наименьшее из количеств строк и столбцов.
Три названных критерия основаны на использовании критерия хи-квадрат. Они различными способами нормируют его значение по отношению к размеру выборки. Так, если формуле для V Крамера положить k = 2, то значения (р и V Крамера совпадут. Определение значимости основано на значении критерия хи-квадрат.
При оценке полученных значений мер связанности, находящихся в нашем примере в промежутке между 0,4 и 0,5, следует учесть, что значение 1 достигается очень редко или вообще никогда. Другие меры связанности (Я, т Гудмена-Крускала и коэффициент неопределенности) определяются на основе так называемой концепции пропорционального сокращения ошибки. При определении этих критериев одна переменная рассматривается как зависимая; по этой причине данные критерии называются "направленными мерами".
Лямбда
В данном примере вопрос о партийной работе можно рассматривать как зависимую переменную, определяемую родом занятий. Если для какого-то отдельно взятого человека надо сделать предположение о том, выполняет ли он партийную работу или нет, то, естественно, делается наиболее вероятное предположение, соответствующее наиболее часто даваемому ответу — в данном случае, предположение о том, что опрашиваемый занимается партийной работой. Такой ответ дают 56,3% респондентов; однако в 43,7% наблюдений наше предположение будет неверным.
Вероятность предположения можно повысить, если учитывать другую переменную — род занятий. Для наемных работников, как и для государственных служащих, можно достаточно уверенно прогнозировать участие в партийной работе, причем этот прогноз окажется неверным для 9 наемных работников и для 2 государственных служащих. В то же время для предпринимателей можно с большими основаниями предположить, что они не занимаются партийной работой, и ошибиться в 7 наблюдениях. Таким образом, для общего числа 64 опрашиваемых мы получаем 9 + 2 + 7=18 наблюдений, или 28,1 %, в которых прогноз будет неверен. Легко видеть, что первоначальная вероятность ошибки 43,7% значительно сократилась.
На основе этих двух вероятностей можно вычислить относительное сокращение ошибки, которое и называется лямбда:
Лямбда=(Ошибка при первом прогнозе — Ошибка при втором прогнозе)/Ошибка при первом
В нашем примере:
Лямбда =( 43,7% - 28.1%)/43,7% = ,357
Если ошибка при втором прогнозе сокращается до 0, лямбда будет равна 1. Если ошибки при первом и при втором прогнозе одинаковы, лямбда = 0. В этом случае вторая переменная никак не помогает в уточнении предсказания значения первой (зависимой переменной); то есть выбранные две переменные совершенно не зависят друг от друга.
Так как ваш быстрый, но совершенно не умеющий соображать компьютер не знает, какую переменную следует считать зависимой, SPSS вычисляет оба значения Я, поочередно рассматривая каждую из переменных как зависимую. В случае, если выясняется, что ни одну из выбранных переменных нельзя объявить зависимой, выводится среднее двух этих значений с обозначением "лямбда -симметричная".
Тау (т) Гудмена-Крускала
Это вариант меры связанности , который SPSS всегда вычисляет совместно с ней. При определении этой меры количество правильных предсказаний определяется по-иному: наблюдаемые частоты взвешиваются с учетом своих процентов и складываются. Для первого прогноза это дает:
36 * 56,3% + 28 * 43,8% =32,53
Согласно этому выражению, из 64 респондентов неверное предположение сделано для 31,47, что составляет 49,17%.
С учетом второй переменной количество верных предположений (второй прогноз) составляет:
13 * 59,1 % + 16 * 88,9 % + 7 * 29,2 % + 9 * 40,9 % + 2 * 11,1 % + 17 * 70,8 % = 39,89
Итак, при втором прогнозе сделано 24,11 неверных прогнозов из 64, что составляет 37,67%. Тогда сокращение ошибки равно
(49.17 %-37.67%)/49,17 %=0,235
Это значение выводится под названием "тау Гудмена-Крускала". И в этом случае SPSS выдает второе значение т, рассматривая вторую переменную, как зависимую.
Коэффициент неопределенности
Это еще один вариант критерия лямбда, при определении которого имеется в виду не ошибочное предсказание, а "неопределенность", то есть степень неточности предсказаний. Эта неопределенность вычисляется по достаточно сложным формулам, которые мы опускаем. Коэффициент неопределенности также принимает значения в диапазоне от 0 до 1. Значение 1 говорит о том, что одну переменную можно точно предсказать по значениям другой.
15.gif

16.gif

17.gif

11.3.4 Меры связанности для переменных с порядковой шкалой
11.3.4 Меры связанности для переменных с порядковой шкалой
Все эти критерии основаны на количестве нарушений порядка (так называемых инверсий, обозначаемых через 1). Количество инверсий можно определить, если расположить в порядке возрастания значения одной из двух переменной между которыми необходимо установить степень взаимосвязи, а рядом с ними записать соответствующие значения другой переменной. Число нарушений порядка расположения второй переменной и есть количество инверсий. Это количество вместе с количеством соблюдений порядка (проверсий, обозначаемых через Р) используется в различных формулах для определения меры связанности, которые дают значения этого параметра в диапазоне от -1 до +1.
Гамма (ÿ)
Гамма вычисляется по простой формуле:

Если инверсий не наблюдается (I = 0), то мы имеем у =1 (полную зависимость). Если же не встречается проверсий, а только инверсии (Р = 0), то говорят о максимально разнонаправленной зависимости (у = -1). Если Р= I, зависимости вообще не существует (y=0).
d Сомера
Существуют две асимметричных и симметричная меры связанности d Сомера. Для их вычисления используется формула для ус корректирующим членом Т, который учитывает количество связей зависимых переменных (одинаковых значений, встречающихся в измерениях):
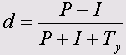
Для сопряженной асимметричной меры связанности d Сомера используется корректирующий член Г, соответствующий количеству связей независимой переменной. В знаменателе симметричной rf-статистики Сомера стоит среднее значение двух асимметричных коэффициентов.
Тау-б (Tb Кендалла)
Этот коэффициент одновременно учитывает связи как зависимых, так и независимых переменных:
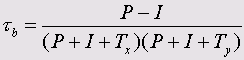
tb может приобретать значения -1 и +1 только для квадратных таблиц сопряженности.
Тау-ц (tc) Кендалла
Этот критерий может достигать значений -1 и +1 в любых таблицах:
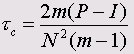
Здесь N — общая сумма частот; m — наименьшее из количеств строк и столбцов.
19.gif
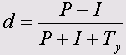
20.gif
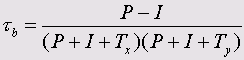
21.gif
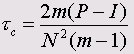
11.3.5 Другие меры связанности
11.3.5 Другие меры связанности
SPSS позволяет вычислить другие специальные меры связанности, обзор которых приводится ниже.
Эта
Этот коэффициент применяется, если зависимая переменная принадлежит к интервальной шкале, а независимая — к порядковой или шкале наименований, эта2 представляет собой долю общей дисперсии, которую можно объяснить влиянием независимой переменной.
Коэффициент каппа (к)
Коэффициент каппа Козна (к) можно вычислить только для квадратных таблиц сопряженности, в которых применяются одинаковые числовые кодировки для переменных строк и столбцов. Типичный случай применения этого критерия — оценка людей или объектов двумя экспертами. В таком случае к указывает на степень согласия между экспертами.
Мера риска
С помощью этой опции в SPSS реализован расчет трех различных коэффициентов, которые могут быть определены для таблицы сопряженности, состоящей из 2 строк и 2 столбцов, созданной на основании строго определенных правил, которые будут сформулированы в конце данного параграфа. При расчете меры риска анализируется так называемая переменная риска, которая имеет две категории и указывает, произошло ли определенное событие или нет. Анализ переменной риска проводится в зависимости от причинной (независимой) переменной, которая должна также быть дихотомической.
Это положение можно пояснить на типичном примере. Исследование депрессии на базе 294 респондентов дало следующую частотную таблицу:
Депрессия | Да | Нет |
Женщины | а = 40 | Ь = 143 |
| Мужчины | с = 10 | d = 101 |
Обе переменные, входящие в таблицу, — являются дихотомическими. Депрессия, имеющая две категории (да-нет), является переменной риска, а пол с двумя категориями (женщины-мужчины) — независимой (причинной) переменной.
Исследование, проводимое в такой форме, называется групповым или когортным. При когортном исследовании определенная группа наблюдений, в которых анализируемое событие еще не произошло, изучается на протяжении известного промежутка времени. Определяется, в каких наблюдениях данное событие произошло, а в каких — нет, и различается ли риск наступления события между разными категориями независимой переменной. При групповых исследованиях группа наблюдений, в которых событие уже произошло, сравнивается с контрольной группой.
Два из трех коэффициентов риска, определяемых в SPSS, обычно относятся к когортным исследованиям, а третий — к групповым. При когортном исследовании для обеих категорий независимой переменной (в данном случае пола) определяется инцидентность. У респондентов-женщин инцидентность наступления депрессии равна:
40/(40 + 143)=0,219
У респондентов-мужчин инцидентность равна
10/(10 + 101)=0,09
Отношение инцидентностей составляет
0,219/0,090 = 2,426
и называется относительным риском или мерой относительного риска. Риск попасть в депрессию у женщин в 2,426 раза выше, чем у мужчин. Так как компьютер не знает, какое из двух кодовых значений переменной риска соответствует наличию депрессии, относительный риск вычисляется для обоих значений.
При групповом исследовании применяется несколько отличный вариант коэффициента, называемый также "отношением шансов" (отношением перекрестных произведений). "Шансы" попасть в депрессию у женщин составляют 40/143, а у мужчин — 10/101. Следовательно, отношение шансов равно
(40 * 101)/(143 * 10)= 2,825
Если обозначить четыре частоты в таблице буквами а, Ь, с и d (см. выше), то формулы, которые SPSS использует для вычисления мер риска, можно записать так:
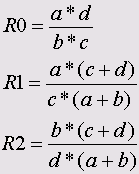
Проведем анализ приведенного примера в SPSS.
-
Загрузите файл depr.sav.
Этот файл содержит переменную риска depr с кодовыми значениями 1 = да и 2 = нет и независимую (причинную) переменную sex с кодовыми значениями 1 = женщины и 2 = мужчины. Еще одна переменная, n, содержит частоты наблюдений.
-
Выберите в меню команды Data (Данные) Weight Cases... (Взвесить наблюдения) и задайте n как переменную взвешивания.
-
В диалоговом окне Crosstabs определите переменную sex как переменную строк и depr — как переменную столбцов, а во вспомогательном диалоге Statistics установите флажок Risk (Риск).
В окне просмотра будут показаны следующие результаты.
Пол * Депрессия Таблица сопряженности
Депрессия | Total | |||
да | нет | |||
Пол | Женщины | 40 | 143 | 183 |
| Мужчины | 10 50 | 101 | 111 | |
Total | 244 | 294 | ||
Risk Estimate (Оценка риска)
| Value |
| 95% Confidence Interval (95% доверительный интервал) | |
| Lower (Нижняя граница) | Upper (Верхняя граница) | |
Odds Ratio for (Отношение шансов для) Пол (Женщины / Мужчины) | 2,825 | 1,350 | 5,911 |
For cohort (Для когорты) Депрессия = да | 2,426 | 1,265 | 4,655 |
For cohort (Для когорты) Депрессия = нет | ,859 | ,780 | ,946 |
N of Valid Cases | 294 |
|
Здесь последовательно показаны отношение шансов (RO) и оба коэффициента относительного риска (R1 и R2). Кроме того, для каждой величины определен 95 % доверительный интервал.
Чтобы правильно вычислить отношение шансов и относительный риск, надо учитывать следующие правила построения таблиц сопряженности:
-
Определяйте причинную (независимую) переменную как переменную строк, а переменную риска — как переменную столбцов.
-
В первой ячейке каждой строки таблицы должна находиться группа с наибольшим риском.
-
В первой ячейке каждого столбца таблицы должно стоять кодовое значение совершения события.
Тест хи-квадрат по Мак-Немару
Тест хи-квадрат по Мак-Немару применяется при наличии двух независимых дихотомических переменных; он рассматривается в разделе 14.2.
Статистика Кохрана и Мантеля-Хзнзеля
Эта статистика включает метод вычисления отношения шансов в таблицах сопряженности 2x2. Расчет этой статистики задается флажком Risk. При вычислениях используется переменная слоев (ковариация) и определяется, значительно ли отличаются категории этой переменной по своему отношению шансов от 1 (или другой величины). Это можно пояснить на примере.
-
Загрузите файл angst.sav.
В этом файле в трех переменных хранятся сведения о 1737 людях: их пол (1 = женский, 2 = мужской), наличие тревожной депрессии (1 = да, 2 = нет) и избыточного веса (1 = нет, 2 = да). Для людей с избыточным весом и с недостатком веса составим раздельные таблицы сопряженности пола и наличия тревожной депрессии, а затем вычислим отношение шансов.
-
Выберите в меню команды Data (Данные) Split File... (Разделить файл)
Выберите опцию Organize output by groups (Разделить вывод на группы) и задайте gewicht как группирующую переменную.
-
Выберите команды меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
-
Перенесите переменную sex в список переменных строк, а переменную angst — в список переменных столбцов.
-
Кнопкой Cells... (Ячейки) задайте вывод процентов по строкам (Percentages — Row), а кнопкой Statistics... (Статистика) — вывод риска (Risk):
Основная часть результатов приводится ниже.
Пол * Тревожная депрессия Crosstabulation (a)
Тревожная депрессия | Total | ||||
|
| Да | нет | ||
Пол | женский | Count | 154 | 592 | 746 |
% от Пол | 20,6% | 79,4% | 100,0% | ||
мужской | Count | 79 | 715 | 794 | |
% от Пол | 9,9% | 90,1% | 100,0% | ||
Total | Count | 233 | 1307 | 1540 | |
% от Пол | 15,1% | 84,9% | 100,0% | ||
Избыточный вес = нет | |||||
Risk Estimate (a)
| 95% Confidence Interval
| ||||
| Value | Lower | Upper | |
Odds Ratio for Пол (женский / мужской) | 2,354 | 1,758 | 3,154 | |
For cohort Тревожная депрессия = да | 2,075 | 1,612 | 2,670 | |
For cohort Тревожная депрессия = нет | ,881 | ,844 | ,920 | |
N of Valid Cases | 1540 | |||
а. Избыточный вес = нет | ||||
Пол * Тревожная депрессия Crosstabulation (a)
Тревожная депрессия | Total | ||||
| Да | нет | ||||
Пол | женский | Count | 22 | 62 | 84 |
% от Пол | 26,2% | 73,8% | 100,0% | ||
мужской | Count | 9 | 104 | 113 | |
% от Пол | 8,0% | 92,0% | 100,0% | ||
Total | Count | 31 | 166 | 197 | |
% от Пол | 15,7% | 84,3% | 100,0% | ||
Избыточный вес; = да | |||||
Risk Estimate (a)
| Value | 95% Confidence Interval | ||
| Lower | Upper | |
Odds Ratio for Пол (женский / мужской) | 4,100 | 1,776 | 9,468 |
For cohort Тревожная депрессия = да | 3,288 | 1,597 | 6,771 |
For cohort Тревожная депрессия = нет | ,802 | ,698 | ,921 |
N of Valid Cases | 197 |
| |
а. Избыточный вес = да
В обоих случаях тревожная депрессия у женщин наступает значительно чаще. Отношение шансов для людей с недостатком веса составляет 2,354, а для людей с избыточным весом — 4,100.
Теперь вычислим статистику Кохрана и Мантеля-Хэнзеля.
-
Чтобы отменить разделение на группы, после вызова команд меню Data (Данные) Split File... (Разделить файл) выберите опцию Analyze all cases, do not create groups (Анализировать все наблюдения, не создавать группы).
-
В диалоговом окне Crosstabs задайте gewicht как переменную слоев, во вспомогательном диалоге Statistics снимите флажок Risk и установите флажок Cochran and Mantel-Haenszel statistics (Статистика Кохрана и Мантеля-Гензеля).
-
В поле Test common odds ratio equals (Общее отношение шансов) оставьте значение 1, установленное по умолчанию.
Из полученных результатов ниже приводится только статистика Кохрана и Мантеля-Гензеля.
Test of Homogenity of the Odds Ratio (Тест на гомогенность отношения шансов) Statistics
Statistics | Chi-Squared (Хи-квадрат) | df | Asymp. Sig. (2-sided) | |
Conditional (Условная независимость) | Cochran (Кохран) | 44,665 | 1 | ,000 |
Mantel-Haenszel (Мантель-Гензель) | 43,724 | 1 | ,000 | |
Homogeneity (Гомогенность) | Breslow-Day (Бреслоу-Дэй) | 1,522 | 1 | ,217 |
Tarone (Тарой) | 1,522 | 1 | ,217 | |
Under the conditional independence assumption, Cochran's statistic is asymptotically distributed as a 1 df chi-squared distribution, only if the number of strata is fixed, while the Mantel-Haenszel statistic is always asymptotically distributed as a 1 df chi-squared distribution. Note that the continuity correction is removed from the Mantel-Haenszel statistic when the sum of the differences between the observed and the expected is 0. (При гипотезе условной независимости статистика Кохрана дает распределение, асимптотически приближающееся к распределению хи-квадрат с 1-ой степенью свободы, только при фиксированном количестве слоев, в то время как статистика Мантеля-Хэнзеля при той же гипотезе всегда дает такое распределение. Обратите внимание, что в статистике Мантеля-Хэнзеля опускается коррекция на непрерывность, если сумма разностей наблюдаемых и ожидаемых величин равна 0.)
Mantel-Haenszel Common Odds Ratio Estimate (Оценка общего отношения шансов Мантеля-Гензеля)
Estimate (Оценка) | 2,503 | ||
ln(Estimate) | ,918 | ||
Std. Error of (Стандартная ошибка) In(Estimate) | ,141 | ||
Asymp. Sig. (2-sided) (Асимптотическая значимость (двусторонняя) | ,000 | ||
Asymp. 95% Confidence Interval (Асимптотический 95 % доверительный интервал) | Common Odds Ratio (Общее отношение шансов) | Lower Bound (Нижняя граница) | 1,901 |
Upper Bound (Верхняя граница) | 3,297 | ||
ln(Common Odds Ratio) | Lower Bound (Нижняя граница) | ,642 | |
Upper Bound (Верхняя граница) | 1,193 | ||
The Mantel-Haenszel common odds ratio estimate is asymptotically normally distributed under the common odds ratio of 1,000 assumption. So is the natural log of the estimate. (Оценка общего отношения шансов Мантеля-Хэнзеля при условии, что общее отношение шансов равно 1,000, имеет асимптотически нормальное распределение. То же распределение сохраняется и для натурального логарифма оценки.)
Результаты тестов Кохрана и Мантеля-Хэнзеля очень близки; в обоих случаях для весовых групп наблюдается максимально значимое отличие отношения шансов от 1 (р<0,001). Тесты как Бреслоу-Дэя, так и Тарона позволяют сохранить допущение о гомогенности отношения шансов для весовых групп (р = 0,217).
Оценка объединенного отношения шансов дает те значения, которые будут получены при вычислении риска, если не разделять данные по переменной слоев.
22.gif
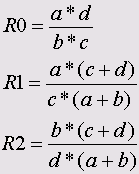
Глава 12. Анализ множественных ответов
Глава 12. Анализ множественных ответов
1. Анализ множественных ответов
Анализ множественных ответов
В этой главе мы рассмотрим особенности кодирования и анализа множественных ответов. Вопросы, на которые можно дать несколько ответов одновременно ( это и есть множественные ответы), имеются во многих анкетных исследованиях. Для кодировкии анализа таких множественных ответов SPSS представляет два различных метода: метод множественной дихотомии и категориальный метод. Оба этих метода рассматриваются в последующих разделах на одном и том же примере. Пример взят из анкетирования членов городской организации политической партии, в котором исследовались их мнения и пожелания.
12.1 Дихотомный метод
12.1 Дихотомный метод
В упомянутой анкете был задан вопрос: "Как можно сделать партию более привлекательной?" Предлагались следующие варианты ответов:
-
больше активности в период между выборами
-
повышение эффективности общих собраний
-
больше неформальных встреч
-
открытые общие собрания
-
большая близость к населению на местах
-
лучше информировать членов партии об актуальных событиях
-
привлечение не членов партии к различным партийным проектам
-
больше мероприятий по актуальным политическим темам на местах
В методе множественной дихотомии для каждой из возможностей ответа определяется отдельная переменная. В рассматриваемом примере для этого понадобится восемь переменных. Если член партии отметит ответ "больше активности в период между выборами ",соответствующая переменная получит значение "1", если нет-"0", если член партии отметит ответ "повышение эффективности общих собраний", соответствующая переменная получит значение "1", если нет-"0",и т.д. для остальных переменных. Таким образом мы получили восемь переменных с кодовыми значениями 0 и 1. Кодовые значения при этом выбираются произвольно, однако для всех ответов они должны быть одинаковы и введены в компьютер на правильном месте.
Ответы на этот и другие вопросы анкетирования членов партии содержаться в файле meinug.sav. Сначала мы посмотрим частотную таблицу ответов на вопрос "Как можно сделать партию более привлекательной?", а затем перекрестную таблицу этого вопроса и пола.
12.1.1 Определение наборов
12.1.1 Определение наборов
Ответы на наш вопрос закодированы вышеописанным способом в переменных att1+attS. В первую очередь мы должны сообщить компьютеру, что эти восемь переменных принадлежат к одному "набору переменных".
-
Загрузите файл meinung.sav.
-
Выберите в меню команды Analyze (Анализ) Multiple Response (Множественные ответы) Define Sets... (Определить наборы)
Откроется диалоговое окно Define Multiple Response Sets (Определение наборов ответов).
-
Выделите в списке исходных переменных переменные att1+att8 и перенесите их в список Variables in Set (Переменные в наборе).
-
Задайте дихотомическую кодировку переменных (опция Dichotomies в группе Variables Are Coded As). Эта настройка выбирается по умолчанию. В поле Counted Value (Учитываемое значение) введите "1".
-
Присвойте набору имя "attrak" и метку "Повышение привлекательности".
-
Щелкните на кнопке Add (Добавить), и созданный набор будет внесен в список наборов множественных ответов (Mult Response Sets).
SPSS начинает имена наборов переменных со знака доллара; следовательно, вновь созданный набор получит имя Sattrak.
-
Щелкните на кнопке Close (Закрыть), чтобы закончить процесс определения набора.
12.1.2 Частотные таблицы для дихотомических наборов
12.1.2 Частотные таблицы для дихотомических наборов
-
Чтобы создать частотную таблицу для дихотомического набора, выберите команды меню Analyze (Анализ) Multiple Response (Множественные ответы) Frequencies... (Частоты)
Рис. 12.1: Диалоговое окно Define Multiple Response Sets
Рис. 12.2: Диалоговое окно Multiple Response Frequencies
Откроется диалоговое окно Multiple Response Frequencies (Частоты множественных ответов).
В списке Mult Response Sets этого диалога отображаются уже определенные наборы переменных; в нашем примере это набор Sattrak.
-
Перенесите набор Sattrak в список Table(s) for (Таблицы для).
-
Щелкните на кнопке ОК.
В окне просмотра появятся следующие результаты:
Group $ATTRAK Повышение привлекательности (Value tabulated = 1) | Pet of Pet of | |||||
dichotomy label | Name Count Responses | Cases | ||||
больше активности в период между выборами | ATT1 | 81 | 20 | ,4 | 77 | ,1 |
повышение эффективности общих собраний | ATT2 | 24 | 6 | ,0 | 22 | ,9 |
больше неформальных встреч | ATT3 | 24 | 6 | ,0 | 22 | ,9 |
открытые общие собрания | ATT4 | 25 | 6 | ,3 | 23 | ,8 |
большая близость к населению на местах | ATT5 | 80 | 20 | ,1 | 76 | ,2 |
лучше информировать членов партии | ATT6 | 51 | 12 | ,8 | 48 | , 6 |
привлечение не членов партии | ATT7 | 46 | 11 | ,6 | 43 | ,8 |
больше мероприятий по актуальным темам | ATT8 | 67 | 16 | ,8 | 63 | ,8 |
Total responses | 398 | 100 | ,0 | 379 | ,0 | |
5 missing cases; 105 valid cases | ||||||
В столбце "Dichotomy label" (Метка дихотомии) приводятся метки переменных, принадлежащих к набору. Показано, что имеется 5 пропущенных и 105 допустимых наблюдений. Отсутствующим наблюдением считается, если ни одна из переменных набора не имеет учитываемого значения (в данном примере значения "1").
Можно получить еще один вариант таблицы, если в диалоговом окне Multiple Response Frequencies установить флажок Exclude cases listwise with dichotomies (Для дихотомических переменных исключать наблюдения по списку). Тогда к пропущенным будут причисляться и те наблюдения, в которых хотя бы одна переменная набора имеет отсутствующее значение — в данном примере не закодирована ни единицей, ни нулем. Это вариант представления может быть полезен, если данный ответ в анкете не определен однозначно.
Для наблюдаемых частот выводятся два разных процентных значения. При определении первого из них наблюдаемая частота отнесена к общему числу ответов "да" (398), а при определении второго — к общему числу допустимых наблюдений (105). Однако самая удобная процентная характеристика, а именно процент от количества всех наблюдений (110), отсутствует. Первую строку частотной таблицы можно интерпретировать, например, так: 81 член партии считает, что большая активность в период между выборами может повысить привлекательность партии. Это 20,4 % от общего количества положительных ответов или 77,1 % членов партии, которые дали хотя бы один вариант ответа.
Как мы уже говорили, в этой таблице, к сожалению, отсутствует процент от общего количества опрошенных членов партии (НО наблюдений). Если вам нужна эта наиболее информативная характеристика, ее можно вычислить вручную или применить следующий прием.
-
С помощью команд синтаксиса
COMPUTE att9 = 1.
EXECUTE.
создайте новую переменную и поместите ее в набор. Вы получите следующую частотную таблицу:
Group $ATTRAK Повышение привлекательности (Value tabulated = 1) | Pct of | Pct of | ||||
Dichotomy label | Name | Count Responses | Cases | |||
больше активности в период между выборам | ATT1 | 81 | 15 | , 9 | 73 | ,6 |
повышение эффективности общих собраний | ATT2 | 24 | 4 | ,7 | 21 | / & |
больше неформальных встреч | ATT3 | 24 | 4 | , 7 | 21 | ,8 |
открытые общие собрания | ATT4 | 25 | 4 | , 9 | 22 | , 7 |
большая близость к населению на местах | ATT5 | 80 | 15 | ,7 | 72 | , 7 |
лучше информировать членов партии | ATT6 | 51 | 10 | ,0 | 46 | ,4 |
привлечение не членов партии | ATT7 | 46 | 9 | ,1 | 41 | ,8 |
больше мероприятий по актуальным темам | ATT8 | 67 | 13 | ,2 | 60 | ,9 |
ATT9 | 110 | 21 | ,7 | 100 | ,0 | |
Total responses | 508 | 100 | ,0 | 461 | ,8 | |
0 missing cases; 110 valid cases | ||||||
Теперь расчет процентов от общего количества ответов потерял смысл, а второй столбец процентов относится к фактическому числу всех наблюдений. То есть 73,6 % всех опрошенных членов партии считают, что большая активность в период между выборами может повысить привлекательность партии.
1.gif

2.gif

12.1.3 Таблицы сопряженности с дихотомическими наборами
12.1.3 Таблицы сопряженности с дихотомическими наборами
Таблицы сопряженности можно создавать между двумя наборами переменных, а также между набором и "обычной" переменной. Так, к примеру, нам необходимо в одной таблице сопряженности отобразить соотношение между набором Sattrak и переменной geschl, которая с помощью кодировок 1 = женский и 2 = мужской характеризует пол респондентов.
-
Выберите в меню команды Analyze (Анализ) Multiple Response (Множественные ответы) Crosstabs... (Таблицы сопряженности) Появится диалоговое окно Multiple Response Crosstabs.
Рис. 12.3: Диалоговое окно Multiple Response Crosstabs
В списке исходных переменных показаны переменные файла meinung.sav. В списке наборов множественных ответов показан ранее определенный набор.
-
Перенесите в список переменных строк набор Sattrak, а в список переменных столбцов — переменную geschl. Эта переменная появится в списке столбцов с двумя вопросительными знаками, заключенными в скобки. Если таблица сопряженности строится между элементарными переменными (не являющимися наборами) и наборами, то для первых следует задать диапазон значений.
-
Щелкните на кнопке Define Ranges... (Определить диапазоны).
Откроется диалоговое окно Multiple Response Crosstabs: Define Variable Range (Таблицы сопряженности для множественных ответов: Определить диапазон переменной).
-
Задайте минимальное значение (Minimum) "1", а максимальное (Maximum) — "2".
-
Подтвердите выбор кнопкой Continue. Теперь вопросительные знаки заменены значениями "1" и "2".
-
Щелкните на кнопке Options... (Параметры).
Откроется диалоговое окно Multiple Response Crosstabs: Options.
Рис. 12.4: Диалоговое окно Multiple Response Crosstabs: Define Variable Range
Абсолютные частоты в ячейках выводятся всегда. Дополнительно в группе Cell Percentages (Проценты в ячейках) можно выбрать одну или несколько характеристик:
-
Row (По строкам): Отображаются проценты для строки.
-
Column (По столбцам). Отображаются проценты для столбца.
-
Total (Полные): Отображаются общие проценты для таблицы.
В группе Percentages based on (Проценты вычисляются на основе) можно выбрать одну из следующих опций:
Рис. 12.5: Диалоговое окно Multiple Response Crosstabs: Options
-
Cases (Наблюдения): Это настройка по умолчанию. Основанием для расчёта процентных показателей в ячейках является число наблюдений, соответствующие количеству опрошенных респондентов.
-
Responses (ответы): Основой расчета процентного отношения в ячейке является количество ответов. Для наборов множественных дихотомий количество ответов равно частоте учитываемого значения во всех наблюдениях.
Обработка пропущенных значений уже рассматривалась в разделе 12.1.2.
Флажок Match variables across response sets (Учитывать переменные из наборов попарно) имеет смысл, только если таблица сопряженности строится на основе двух наборов переменных. В этом случае первая переменная из первого набора сочетается с первой переменной из второго набора, и т.д.
-
В группе Percentages based on сохраните настройку по умолчанию Cases.
-
В группе Cell Percentages установите флажок Column.
-
Подтвердите ввод кнопкой Continue, а затем — ОК. В окне просмотра будет показана следующая таблица.
* * * СR0SSТABULATION * * * | |||||
$ATTRAK (tabulating 1) | Erhohung | der Attraktivitat | |||
by GESCHL Geschlecht | |||||
GESCHL | |||||
Count Iweiblich | maennlic | ||||
Col pet Ih | Row | Total | |||
I |
| ||||
I | 1 | I | 2 | I | |
$ATTRAK X | |||||
ATT1 I | 21 | + -I | 60 | + I | 81 |
mehr Prasenz zwische I | 72,4 | I | 78,9 | I | 77,1 |
+ — | _ _ _ | + — | _ _ _ | + | |
ATT2 I | 6 | I | 18 | I | 24 |
Verbesserung der Hit I | 20,7 | I | 23,7 | I | 22,9 |
+ — | _ _ _ | + — | _ _ _ | + | |
ATT3 I | 5 | I | 19 | I | 24 |
mehr gesellige Zusam I + - | 17 ,2 | I | 25, 0 | I | 22, 9 |
ATT4 I | 2 | + - I | 23 | + I | 25 |
offentlich zuganglic I | 6,9 | I | 30,3 | I | 23,8 |
+ - | _ _ _ | + - | _ _ _ | + | |
ATT5 I | 23 | I | 57 | I | 80 |
mehr Burgernahe mit I | 79,3 | I | 75,0 | I | 76,2 |
+ - | _ _ _ | + — | _ _ _ | + | |
ATT6 I | 14 | I | 37 | I | 51 |
bessere Information I | 48,3 | I | 48,7 | I | 48,6 |
+ - | _ _ _ | + - | _ _ _ | + | |
ATT7 I | 12 | I | 34 | I | 46 |
Beteiligung von Nich I | 41,4 | I | 44,7 | I | 43,8 |
+ - | _ _ _ | + — | _ _ _ | + | |
ATT 8 I | 18 | I | 49 | I | 67 |
mehr Veranstaltungen I | 62,1 | I | 64,5 | I | 63,8 |
| _ _ _ | + — | _ _ _ | + | |
Column | 29 | 76 | 105 | ||
Total | 27, 6 | 72,4 | 100,0 | ||
Percents and totals based on respondents 105 valid cases; 5 missing cases
Полученные проценты соответствуют отношению частот к числу допустимых наблюдений; ср. заключения сделанные в разделе 12.1.2. К сожалению, длина меток переменных ограничивается лишь двадцатью символами.
Если сравнить оба пола, то значительное различие заметно только при анализе переменной att4: 30,3 % мужчин считают, что открытые собрания повышают привлекательность партии, но лишь 6,9 % женщин придерживаются этого мнения.
К сожалению, для множественных ответов SPSS не проводит проверку значимости с помощью критерия хи-квадрат. Если выполнение такой проверки необходимо, то следует поступить, как указано в разделе 8.7.2.
3.gif
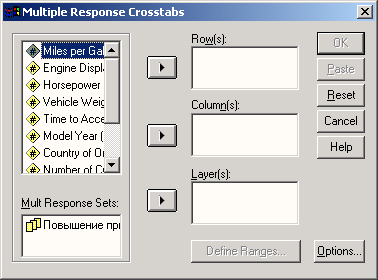
4.gif

5.gif
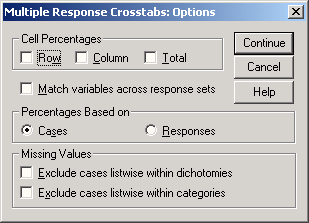
12.2 Категориальный метод
12.2 Категориальный метод
Альтернативный способ кодирования множественных ответов предоставляет метод множественных категорий, или категориальный. Для применения этого метода должно быть известно максимальное количество возможных ответов. Это количество можно, например, задать в анкете (указанием типа "Отмечайте не более пяти вариантов") или установить после проверки анкет.
Чтобы узнать, почему члены партии, не имеющие партийного поручения, не хотят его получить или не участвуют в партийной работе иным образом, в анкете задавался вопрос "Что мешает Вашему участию в партийной работе?". После вопроса было помещено указание, что можно отметить не более пяти из приводимых вариантов ответа:
Мне неизвестны возможности для участия в работе | 1 |
Функции уже распределены | 2 |
Поведение функционеров | 3 |
Групповщина не дает стимула для участия | 4 |
У меня слишком мало политического опыта | 5 |
Я опасаюсь негативного влияния на свою работу/карьеру | 6 |
Я опасаюсь негативного влияния на свою личную жизнь | 7 |
Не желаю | 8 |
Здоровье не позволяет | 9 |
Так как количество ответов составляет не более пяти, для того, чтобы закодировать все варианты ответов будет достаточно пяти переменных. В файле meinung.sav это переменные mit1+mitS, которые после загрузки файла отображаются в редакторе данных.
Каждая из пяти переменных кодируется одинаковыми категориями, причем вне зависимости от количества данных ответов область этих пяти переменных заполняется слева направо.
Так, в первом наблюдении при ответе на вопрос отмечены категории 3, 4 и 6 (Поведение функционеров, Групповщина, Негативное влияние в работе). Следующие три респондента не отметили ни одного ответа, в наблюдении 8 дан только один ответ (Категория 1, "Неизвестны возможности участия") и т.д. Для этого вопроса мы также построим частотную таблицу и таблицу сопряженности с полом. Но сначала определим набор переменных.
Рис. 12.6: Множественные отпеты при категориальном методе
6.gif
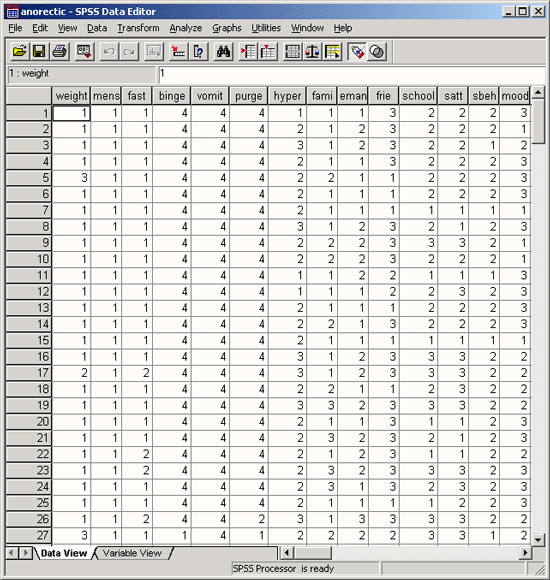
12.2.1 Определение наборов
12.2.1 Определение наборов
Сначала следует определить набор. Выполите следующие действия:
-
Выберите в меню команды Analyze (Анализ) Multiple Response (Множественные ответы) Define Sets... (Определить наборы)
Появится уже известное вам диалоговое окно Define Multiple Response Sets. В списке исходных переменных Set Definition (Определение набора) показаны переменные файла meimmg.sav.
-
Выделите переменные mit1+mitS и перенесите их в список Variables in Set (Переменные в наборе).
-
Задайте категориальную кодировку переменных (опция Categories). В полях Range — through укажите диапазон "1" + "9".
-
Присвойте набору имя "mitwirk" и метку "Препятствия в сотрудничестве".
-
Щелкните на кнопке Add (Добавить), и созванный набор будет внесен в список наборов множественных ответов (Mult Response Sets).
-
Щелкните на кнопке Close, чтобы завершить определение набора.
12.2.2 Частотные таблицы для категориальных наборов
12.2.2 Частотные таблицы для категориальных наборов
-
Для того, чтобы создать частотную таблицу, выберите в меню команды Analyze (Анализ) Multiple Response (Множественные ответы) Frequencies... (Частоты) Откроется диалоговое окно Multiple Response Frequencies.
-
Перенесите набор Smitwirk в список Table(s) for.
-
Щелкните на кнопке ОК.
В окне просмотра будет показана следующая частотная таблица.
Group $MITWIRK Препятствия в сотрудничестве Pet of Pet of | ||||||
Category label Code | CountResponses | Cases | ||||
Неизвестны возможности участия | 1 | 24 | 12 | ,8 | 27 | ,6 |
Функции уже распределены | 2 | 26 | 13 | ,9 | 29 | , 9 |
Поведение функционеров | 3 | 36 | 19 | ,3 | 41 | ,4 |
Групповщина | 4 | 20 | 10 | ,7 | 23 | ,0 |
Недостаток политического опыта | 5 | 29 | 15 | ,5 | 33 | , 3 |
Негативное влияние, в работе | 6 | 8 | 4 | ,3 | 9 | ,2 |
Негативное влияние в личной жизни | 7 | 6 | 3 | ,2 | 6 | , 9 |
Нежелание | 8 | 14 | 7 | ,5 | 16 | , 1 |
Здоровье | 9 | 24 | 12 | ,8 | 27 | , 6 |
Total responses | 187 | 100 | ,0 | 214 | ,9 | |
23 missing cases; 87 valid cases | ||||||
В столбце "Category label" (Метки категорий) показаны (единообразные) метки значений переменных, объединенных в набор. Показано, что имеется 23 пропущенных и 87 допустимых наблюдений. Наблюдение считается пропущенным, если ни одна из переменных, принадлежащих к набору не имеет кодового значения
Можно получить еще один вариант таблицы, если в диалоговом окне Multiple Response Frequencies установить флажок Exclude cases listwise with categories (Для категориальных переменных исключать наблюдения по списку). Тогда допустимыми будут считаться только наблюдения, в которых все переменные набора имеют кодовые значения.
Обе процентные характеристики уже рассматривались в разделе 12.1.2. Первую строку частотной таблицы можно интерпретировать следующим образом: 24 члена партии считают, что их участию в партийной работе мешает то, что им неизвестны возможности такого участия. Это 12,8 % данных ответов и 27,6 % респондентов, которые дали хотя бы один вариант ответа.
12.2.3 Таблицы сопряженности с категориальными наборами
12.2.3 Таблицы сопряженности с категориальными наборами
На основе наборов со множественными категориями также можно строить таблицы сопряженности с другими переменными. Для примера рассмотрим таблицу сопряженности между набором Smitwirk и переменной geschl. Выполните следующие действия:
-
Выберите в меню команды Analyze (Анализ) Multiple Response (Множественные ответы) Crosstabs... (Таблицы сопряженности)
Появится диалоговое окно Multiple Response Crosstabs.
-
Перенесите в список переменных строк набор Smitwirk, а в список переменных столбцов — переменную geschl. Эта переменная появится в списке столбцов с двумя вопросительными знаками, заключенными в скобки.
-
Щелкните на кнопке Define Ranges... (Определить диапазоны).
Откроется диалоговое окно Multiple Response Crosstabs: Define Variable Range.
-
Введите минимальное значение 1 и максимальное "2".
-
Подтвердите выбор кнопкой Continue.
-
Щелкните на кнопке Options... (Параметры).
Откроется диалоговое окно Multiple Response Crosstabs: Options.
-
В группе Percentages based on сохраните настройку по умолчанию Cases.
-
В группе Cell Percentages установите флажок Column.
-
Подтвердите ввод кнопкой Continue, а затем — ОК.
В окне просмотра будет показана следующая таблица сопряженности.
*** CROSSTABULATION * ** | |||||||||
$MITWIRK (group) Scheiterungby GESCHL Geschlecht der Mitwirkung | |||||||||
GESCHL | |||||||||
Count Iweiblich maennlic | |||||||||
Col pet | I | h | ROW | ||||||
I | Total | ||||||||
I | 1 | I | 2 | I + I | 24 | ||||
1 | + - I | 7 | + - - I | 17 | |||||
Moglichkeiten nicht | I | 30,4 | I 26 | ,6 | I | 27,6 | |||
+ - | _ _ _ | + — — | — — | + | |||||
2 | I | 3 | I | 23 | I | 26 | |||
Mandate bereits bese | I | 13,0 | I 35 | ,9 | I | 29,9 | |||
+ - | + — — | + | |||||||
3 | I | 10 | I | 26 | I | 36 | |||
Fuhrungs verbal ten de | I | 43,5 | I 40 | ,6 | I | 41,4 | |||
+ - | _ _ _ | •f - — | — — | + | |||||
4 | I | 4 | I | 16 | I | 20 | |||
keine Forderung wage | I | 17 ,4 | I 25 | ,0 | I | 23,0 | |||
+ - | — — — | + — — | — — | + | |||||
5 | I | 11 | I | 18 | I | 29 | |||
zu wenig politische 6 | I + — I | 47 ,8 | I 28 | ,1 | I + I | 33,3 8 | |||
0 | + - - I | 8 | |||||||
Befurchtung beruflic 7 | I + -I | , 0 | I 12 | ,5 | I + I | 9,2 6 | |||
0 | + - — I | 6 | |||||||
Befurchtung persqnli | I | , 0 | I 9 | ,4 | I | 6,9 | |||
+ — | _ _ _ | + - - | — — | + | |||||
8 | I | 4 | I | 10 | I | 14 | |||
nichts bewegen konne | I | 17,4 | I 15 | ,6 | I | 16,1 | |||
+ - | _ _ _ | + - - - | - - + | ||||||
9 | I | 7 | I | 17 I | 24 | ||||
gesundheitliche | Grun | I | 30,4 | I | 26,6 I | 27,6 | |||
+ — | _ _ _ | + - - | - — - + | ||||||
Column | 23 | 64 | 87 | ||||||
Total | 26,4 | 73,6 | 100,0 | ||||||
Percents | and | totals based | on | respondents | |||||
S7 | valid | cases ; | 23 | missing cases | |||||
Процентные значения рассчитываются на основе количества допустимых наблюдений. Если сравнить оба пола, то значительное различие заметно только в частоте упоминания мнения, что функции уже распределены и в боязни негативного влияния на работу и личную жизнь; такие ответы мужчины дают чаще. Женщины, напротив, чаще ссылаются на недостаток политического опыта.
12.3 Упражнение
12.3 Упражнение
В заключение проведем анализ множественных ответов на следующем примере. При анкетировании 530 туристов в Кении задавался вопрос о влиянии туризма. Рассмотрим интересующий нас отрывок из этой анкеты:
Варианты ответов на вопрос "Какое влияние, по Вашему мнению, оказывает туризм в Кении?" закодированы по методу множественных категорий. При этом установлено, что было зачеркнуто не более шести возможных ответов. Для шести вариантов определены переменные vnl+vn6. Эти переменные могут иметь следующие значения:
1 = "Приток валюты"
2 = "Подорожание"
3 = "Нагрузка на окр. среду"
4 = "Рабочие места"
5 = "Развитие инфраструктуры"
6 = "Переселение в города"
7 = "Взаимопонимание"
8 = "Разрушение культуры"
9 = "Сохранение культуры"
Загрузите файл kenia.sav.
-
Определите набор переменных. Перенесите в набор переменные vnKvn6. Задайте категориальную кодировку (активируйте опцию Categories в группе Variables Coded by...). Установите диапазон от 1 до 9.
-
Присвойте набору имя "tour" и метку "Влияние туризма".
-
Щелкните на кнопке Add, чтобы добавить сформированный набор в список наборов.
-
Проведите частотный анализ набора Stour как было описано выше. Вы получите следующий результат:
Group $TOUR Влияние туризма | ||||
Pet of | Pet of | |||
Category label Code | Count | Responses | Cases | |
Приток валюты | 1 | 457 | 22,7 | 88,2 |
Подорожание | 2 | 105 | 5,2 | 20,3 |
Нагрузка на окр. среду | 3 | 209 | 10,4 | 40,3 |
Рабочие места | 4 | 441 | 21,9 | 85,1 |
Развитие инфраструктуры | 5 | 170 | 8,4 | 32,8 |
Переселение в города | 6 | 125 | 6,2 | 24,1 |
Взаимопонимание | 7 | 206 | 10,2 | 39,8 |
Разрушение культуры | 8 | 262 | 13,0 | 50,6 |
Сохранение культуры | 9 | 41 | 2,0 | 7,9 |
Total responses | 2016 | 100,0 | 389 ,2 | |
12 missing cases; 518 valic | i cases | |||
Постройте перекрестные таблицы набора Stour последовательно с переменными g (пол), s (образование) и alter (возраст). Проинтерпретируйте результаты самостоятельно.
7.gif

12.4 Сравнение дихотомного и категориального методов
12.4 Сравнение дихотомного и категориального методов
Дихотомный метод | Категориальный метод |
Особенности: | Особенности: |
• Определяется по одной переменной для каждого варианта ответа. | • Оценка максимального количества возможных ответов. |
• Отображение множественных ответов с помощью нескольких дихотомических переменных. | в Определение такого же числа переменных, соответствующего максимальному количеству возможных ответов. |
• Переменные объединяются в наборы из нескольких дихотомий. | • В наборы, соответствующие множественным ответам, объединяются переменные из нескольких категорий. |
Преимущества: | Преимущества: |
• Предварительная оценка максимального количества выбранных вариантов ответов не требуется. | • Меньшее число переменных, если количество вариантов ответов, выбранных в каждом отдельном случае, меньше совокупного количества возможных вариантов ответов. |
Недостатки: | Недостатки: |
• Если количество всех возможных ответов велико, а максимальное количество ответов, выбранных в каждом отдельном случае мало, то затрачивается слишком много переменных по сравнению с категориальным методом. | • Вследствие распределения по разным переменным при проведении последующего анализа затруднено получение совокупного результата. |
О недостатке категориального метода, отмеченном в таблице, следует рассказать подробнее. Например, если потребуется подвергнуть переменную с дихотомическим кодированием att3 из файла mcinung.sav ("неформальные встречи повышают привлекательность партии") какому-либо последующему анализу, то это можно будет сделать без особого труда. Это такая же переменная, как и все остальные.
Но если мы рассмотрим ответ "У меня слишком мало политического опыта" на вопрос "Что мешает Вашему участию в партийной работе", то этот вариант ответа нельзя идентифицировать с помощью однозначно определенной переменной. Этому варианту ответа будет соответствовать одна из переменных mitl-mit5, причем привязка к одной их этих переменных будет меняется от наблюдения к наблюдению.
Чтобы решить эту проблему, следует с помощью команды DO REPEAT (см. раздел 26.3) создать новую переменную:
COMPUTE wenigerf=0.
DO REPEAT mit=mitl to mit5.
IF mit=5 wenigerf=1
END REPEAT.
EXECUTE.
Переменная wenigerf своими кодовыми значениями 1 = да и 0 = нет будет указывать, ответил ли член партии, что у него мало политического опыта, или нет. Эту переменную можно использовать при последующем анализе.
Данный недостаток категориального метода мы считаем настолько значительным, что рекомендуем применять дихотомный метод.
Глава 13. Сравнение средних
Глава 13. Сравнение средних
1. Сравнение средних
Сравнение средних
Сравнение средних значений различных выборок относится к наиболее часто применяемым методам статистического анализа. При этом всегда должен быть выяснен вопрос, можно ли объяснить имеющееся различие средних значений статистическими колебаниями или нет. В последнем случае говорят о значимом различии.
При сравнении средних значений выборок предполагается, что обе выборки подчиняются нормальному распределению. Если это не так, то вычисляются медианы и для сравнения выборок используется непараметрический тест.
При сравнении средних значений выборок выделяют четыре различные тестовые ситуации:
-
сравнение двух независимых выборок
-
сравнение двух зависимых (спаренных) выборок
-
сравнение более двух независимых выборок
-
сравнение более двух зависимых выборок
В этих ситуациях соответственно применяются следующие статистические тесты:
-
t-тест для независимых выборок (тест Стьюдента)
-
t-тест для зависимых выборок
-
однофакторный дисперсионный анализ
-
однофакторный дисперсионный анализ с повторными измерениями
Первые три из этих тестов вызываются с помощью меню Analyze (Анализ) Compare Means (Сравнение средних)
Чтобы провести однофакторный дисперсионный анализ с повторными измерениями (очень часто встречающаяся тестовая ситуация) надо вызвать команду меню Analyze (Анализ) General Linear Model (Общая линейная модель) Repeated Measures... (Повторные измерения)
Сначала мы рассмотрим тесты, вызов которых происходит посредством пункта меню Compare Means. Для примера мы возьмем данные исследования гипертонии в файле hyper.sav (см. главу 9).
-
Загрузите файл hyper.sav.
-
Выберите в меню команды Analyze (Анализ) Compare Means (Сравнение средних)
В подменю содержатся, в частности, t-тест для независимых выборок (Independent-Samples Т Test), t-тест для парных выборок (Paired-Samples Т Test) и однофакторный дисперсионный анализ (ANOVA) для сравнения нескольких независимых выборок ( One-Way ANOVA).
Еще один тест, включенный в данное подменю, это t-тест случайной выборки, используемый для сравнения с заданным значением (One-Sample T Test), рассматривается в разделе 13.5. В подпункте меню Means... (Средние) вычисляются средние значения раздельно по категориям группирующей переменной; здесь также можно проверить существование значимого различия при помощи однофакторного дисперсионного анализа. В этом отношении данный подпункт предоставляет меньше возможностей, чем подпункт One-Way ANOVA..., и поэтому здесь не рассматривается.
13.1 Сравнение двух независимых выборок
13.1 Сравнение двух независимых выборок
Мы хотим проверить, значительно ли различается действие двух групп медикаментов на людей в зависимости от их возраста. Такое различие было бы, конечно, нежелательным, так как в этом случае разницу в действии лекарств можно было бы объяснить разным возрастным составом пациентов.
-
Выберите в подменю команду Independent-Samples T Test... (t-тест для независимых выборок)
Откроется диалоговое окно Independent-Samples T Test (см. рис. 13.1).
-
В списке исходных переменных щелкните на переменной а и щелчком на кнопке с треугольником перенесите ее в список тестируемых переменных (Test Variable(s)).
-
Таким же способом перенесите переменную med в поле Grouping Variable (Группирующая переменная).
-
Щелчком на кнопке Define Groups... (Определить группы) открывается окно, в котором можно ввести значения двух категорий для группирующей переменной. Мы будем сравнивать две группы, удовлетворяющие условиям соответственно med = 1 и med = 2. Поэтому внесите в поле Group 1 (Группа 1) значение 1, а в поле Group2 — значение 2.
-
Щелчком на кнопке Continue вернитесь в основное диалоговое окно.
-
Теперь следует выяснить, какие параметры установлены по умолчанию. Щелкните для этого на кнопке Options... (Параметры). Не изменяя настроек, щелкните на кнопке Continue и вернитесь в основное диалоговое окно.
Рис. 13.1: Диалоговое окно Independent-Samples T Test
-
Запустите t-тест, щелкнув на ОК. В окне просмотра появятся следующие результаты:
Group Statistics (Статистика групп)
Лекарство | N | Mean (Среднее) | Std. Deviation (Стандартное отклонение) | Std. Error Mean (Стандартная ошибка среднего) | |
Возраст | Альфасан | 87 | 62,24 | 11,19 | 1,20 |
Бетасан | 87 | 61,98 | 11,96 | 1,28 |
Independent Samples Test (Тест для независимых выборок)
Levene's Test for Equality of Variancies (Тест Левена на равенство дисперсий) | t-test for Equality of Means (Тест Стьюдента на равенство средних) | |||||||||
F | Sig. (Значи-мость) | Т | df | Sig. (2-tailed) (Значимость (двусто- ронняя)) | Mean Diffe-rence (Разность средних) | Std. Error Differe-псе (Станда- ртная ошибка разницы) | 95 % Confidence Interval of the Difference (Довери-тельный интервал разницы) | |||
Lower (Нижняя граница) | Upper (Верхняя граница) | |||||||||
Возраст | Equal variances assumed (Дис-персии равны) | ,54 | ,462 | ,151 | 172 | ,880 | ,26 | 1,76 | -3,20 | 3,73 |
Equal variances not assumed (Ди- сперсии не равны) |
|
| ,15' | 171,249 | ,880 | ,26 | 1,76 | -3,20 | 3,73 | |
Выведенные результаты содержат:
-
количество наблюдений, средние значения, стандартные отклонения и стандартные ошибки средних в обеих группах,
-
результаты теста Левена на равенство дисперсий.
Как правило, гипотеза о равенстве (гомогенности) дисперсий не принимается, если тест Левена дает значение р < 0,05 (гетерогенность дисперсий). Для случаев как гомогенности (равенства), так и гетерогенности (неравенства) выводятся следующие характеристики:
-
результаты t-теста: значение распределения t, количество степеней свободы df, вероятность ошибки р (под обозначением "Значимость (2-сторонняя)"), а также
-
разница средних значений, ее стандартная ошибка и доверительный интервал.
В данном примере мы не получаем значимого различия воздействия двух группами лекарств по возрасту (р = 0,880).
В следующем t-тесте мы проверим, различается ли действие двух групп лекарств по так называемому индексу Брока. Этот индекс, разработанный одним парижским хирургом, предусматривает, что нормальный вес человека можно определить из следующего уравнения:
Нормальный вес (кг) = Рост (см) — 100
Если взять отношение фактического веса человека к нормальному весу по этой рормуле, то мы получим процентный показатель, который у людей с нормальным весом равен 100, у людей с избытком веса > 100 и т.д.
Индекс Брака =((Вес в кг)/(Рост в см - 100)) • 100
-
Определим на основе существующих переменных новую переменную, для чего выберем команды меню Transform (Преобразовать) Compute... (Вычислить)
-
В поле выходной переменной (Target Variable) задайте новое имя "broca", а в поле численного выражения (Numeric Expression) введите выражение gew I (gr- 100) * 100
-
Щелкните на кнопке ОК. Теперь можно командами меню Analyze (Анализ) Compare Means (Сравнение средних) Independent Samples T Test... (t-тест для независимых выборок) описанным выше способом провести t-тест для новой переменной broca.
И этот тест показывает, что между двумя труппами лекарств не наблюдается значимого различия по индексу Брока (р = 0,233).
1.gif
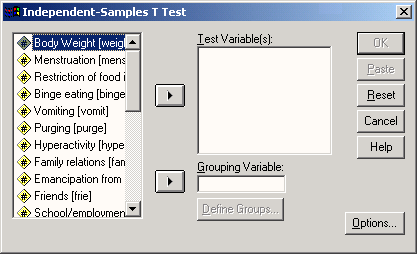
13.2. Сравнение двух зависимых выборок
13.2. Сравнение двух зависимых выборок
Сейчас мы выясним, значимо ли изменяется содержание холестерина через месяц : осле начала приема лекарств. Для этого мы сравним переменные cho10 и cho11 при помощи t-теста для зависимых выборок. В этом тесте будут участвовать данные всех пациентов, независимо от группы принимаемых лекарств.
-
Выберите в соответствующем подменю команду Paired-Samples Т Test... (t-тсст для парных выборок)
Откроется диалоговое окно Paired-Samples T Test.
Рис. 13.2: Диалоговое окно Paired-Samples T Test
-
Перенесите переменные cholO и choll из списка исходных переменных в поле парных переменных (Paired Variables).
-
Щелкните на ОК, чтобы начать вычисления. В окне просмотра появятся следующие результаты:
Paired Samples Statistics (Статистика для парных выборок)
Mean | N | Std. Deviation | Std. Error Mean | ||
Pair (Пары) | Холестерин, исходный | 237,27 | 174 | 49,42 | 3,75 |
Холестерин, через 1 мес. | 239,20 | 174 | 49,51 | 3,75 |
Paired Samples Correlations (Корреляции для парных выборок)
N | Correlation (Корреляция) | Sig. (Значимость) | ||
Pair (Пары) | Холестерин, исходный & Холестерин, через 1 мес. | 174 | ,861 | ,000 |
Paired Samples Test (Тест для парных выборок)
|
Paired Differences (Парные разницы) |
Т |
df |
Sig. (2-tailed) |
||||||
|
Mean |
Std. Devi-ation |
Std. Error Mean |
95% Confi-dence Interval of the Diffe-rence |
||||||
|
Lower |
Upper |
||||||||
|
Pair (Пары) |
Холе- стерин, исходный -Холе- стерин, через 1 мес. |
-1,93 |
26,09 |
1,98 |
-5,83 |
1,98 |
-,974 |
173 |
,332 |
Результаты, выведенные в окне просмотра, содержат:
-
средние значения, количество наблюдений, стандартные отклонения и стандартные ошибки средних для обеих переменных,
-
коэффициент корреляции (момент произведений Пирсона) между переменными и значимость его отклонения от нуля,
-
среднее значение, количество наблюдений, стандартное отклонение и стандартная ошибка разницы,
-
результаты t-теста: тестовая величина, полученная из распределения Стьюден-та, количество степеней свободы df, вероятность ошибки р, обозначенная "Sig. (2-tailed)").
Значимого изменения содержания холестерина за один месяц после начала приема лекарств не наблюдается (р = 0,332).
Повторим вычисления, но теперь только для пациентов, принимавших альфасан (переменная med имеет значение 1; условие med = 1).
-
Выберите в меню команды Data (Данные) Select Cases... (Выбрать наблюдения)
-
Выберите опцию If condition is satisfied... (Если выполняется условие). Щелчком на кнопке If... (Если) откройте диалоговое окно, в котором можно сформулировать условие. Введите в соответствующем поле условие "med = 1".
-
Щелкните на кнопке Continue, а в основном диалоге — на кнопке ОК.
-
Снова запустите t-тест. Теперь он будет выполнен только для наблюдений (N = 87), относящихся к первой группе лекарств. Мы снова получим незначимый результат (р = 0,666).
-
Чтобы последующий анализ снова можно было проводить с использованием всех наблюдений, откройте диалоговое окно Select Cases и выберите в нем опцию All cases (Все наблюдения).
2.gif
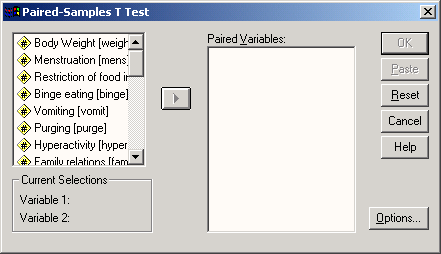
13.3 Сравнение более двух независимых выборок
13.3 Сравнение более двух независимых выборок
Далее мы исследуем, существует ли значимое различие веса (переменная gr) между четырьмя разными возрастными группами (переменная ak).
-
Выберите в подменю команду One-Way ANOVA... (Однофакторный дисперсионный анализ)
Подобная возможность есть и в первом пункте подменю (Means...), но она дает значительно более ограниченные возможности для анализа, и поэтому мы ее не рассматриваем. Появится диалоговое окно One-Way AN OVA.
-
Перенесите переменную gr в список зависимых переменных (Dependent List), a переменную ak — в поле Factor (Фактор).
-
Посмотрите, какие параметры можно задать для этого теста (кнопка Options...). Задайте вывод описательной статистики (флажок Descriptive) и проверку на гомогенность дисперсий (флажок Homogeneity-of-variance).
-
Чтобы выполнить апостериорный тест, вернувшись в основное диалоговое окно, щелкните на кнопке Post Нос... Откроется диалоговое окно One-Way ANOVA: Post Hoc Multiple Comparisons (Однофакторный дисперсионный анализ: апостериорные множественные сравнения) рис. 13.4.
-
Выберите тест Дункана (флажок Duncan). При значимом результате дисперсионного анализа этот тест показывает, какие именно возрастные группы значимо отличаются друг от друга. По умолчанию установлен уровень значимости 0,05; можно выбрать и другое значение.
-
Запустите тест, щелкнув на ОК.
Рис. 13.3: Диалоговое окно One-Way ANOVA
Рис. 13.4: Диалоговое окно One-Way AN OVA: Post Hoc Multiple Comparisons
В окне просмотра появятся следующие результаты:
Descriptives (Описательная статистика)
Рост | ||||||||
N | Mean | Std. Devi-ation | Std. Error | 95 % Confidence Interval for Mean (95 % доверительный интервал среднего). | Mini-mum | Maxi-mum | ||
Lower Bound | Upper Bound | |||||||
до 55 лет | 52 | 169,10 | 8,21 | 1,14 | 166,81 | 171,38 | 150 | 185 |
56ч 65 лет | 51 | 164,82 | 7,62 | 1,07 | 162,68 | 166,97 | 146 | 185 |
66ч75 лет | 47 | 162,47 | 7,22 | 1,05 | 160,35 | 164,59 | 145 | 175 |
>75 лет | 24 | 162,67 | 7,38 | 1,51 | 159,55 | 165,78 | 150 | 178 |
Total | 174 | 165,17 | 8,08 | 61 | 16396 | 166,38 | 145 | 185 |
Test of Homogeneity of Variances (Тест гомогенности дисперсий)
Рост | |||
Levene Statistic (Статистика Левена) | dfl | df2 | Sig. |
,639 | 3 | 170 | 591 |
ANOVA (Дисперсионный анализ)
Рост | |||||
Sum of Squares (Сумма квадратов) | Df | Mean Square (Средний квадрат) | F | Sig. (Значимость) | |
Between Groups (Между группами) | 1301,200 | 3 | 433,733 | 7,380 | ,000 |
Within Groups (В группах) | 9990,966 | 170 | 58,770 | ||
Total | 111292,167 | 173 | |||
Апостериорные тесты Гомогенные подгруппы
Рост
Dunean" | |||
Возрастной класс | N | Subset for alpha = ,05 (Подгруппа для альфа = ,05). | |
1 | 2 | ||
66-75 лет | 47 | 162.47 | |
>75 лет | 24 | 162,67 | |
56-65 лет | 51 | 164,82 | |
до 55 лет | 52 | 169,10 | |
Sig. (Значимость) | ,201 | 1,000 | |
Means for groups in homogeneous subsets are displayed (Показаны средние значения для групп внутри гомогенных подгрупп).
a. Uses Harmonic Mean Sample Size = 39,300 (Используется гармоническое среднее для размера выборки = 39,300).
b. The group sizes are unequal. The harmonic mean of the group sizes is used. Type I error levels are not guaranteed. (Размеры групп неодинаковы. Используется гармоническое среднее размеров групп. Уровни ошибок типа I не гарантируются).
Выведенные результаты содержат:
-
количество наблюдений, средние значения, стандартные отклонения и стандартные ошибки средних, 95 % доверительные интервалы, минимумы и максимумы для всех слоев фактора,
-
результаты теста Левена на гомогенность дисперсий,
-
типовую схему дисперсионного анализа, включая вероятность ошибки р (значимость) для оценки общей значимости,
-
результаты многорангового теста Дункана.
В этом примере дисперсионный анализ дает максимально значимый результат (р < 0,001). Тест Дункана выделяет две гомогенные подгруппы (со стандартным значением р = 0,05), одна из которых включает возрастной класс до 55 лет, а другая — три остальных класса. Это означает, что возрастной класс до 55 лет значимо отличается от трех других возрастных классов, которые, в свою очередь, не обнаруживают значимого различия между собой.
Уменьшение роста с увеличением возраста может быть связано с тем, что в старших возрастных классах преобладают женщины, рост которых мал по сравнению с мужчинами, что и вызывает данный эффект. Повторим этот анализ для категорий пола. Окажется, что у мужчин факт уменьшения роста с увеличением возраста подтверждается, а для женщин — нет.
Далее мы подробно рассмотрим имеющиеся в диалоговом окне AN OVA кнопки Contrasts (Контрасты), Post Hoc... и Options..., а также возможности, которые они предоставляют.
3.gif
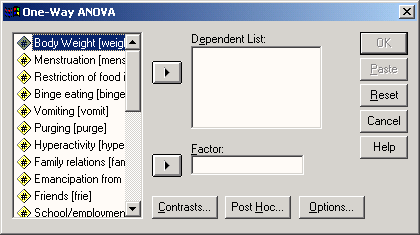
4.gif

13.3.1 Разложение на составляющие тренда
13.3.1 Разложение на составляющие тренда
Сумму квадратов между группами можно разложить на линейные или полиномиальные (до 5 степени включительно) составляющие тренда.
-
В диалоговом окне ANOVA щелкните на кнопке Contrasts... Появится диалоговое окно One-Way ANOVA: Contrasts (Однофакторный дисперсионный анализ: Контрасты).
Рис. 13.5: Диалоговое окно One-Way AN OVA: Contrasts
-
Установите флажок Polynomial (Многочлен); после этого в списке Degree (Степень) можно будет выбрать порядок многочлена (линейный, квадратный, кубический, биквадратный или 5-й степени).
5.gif
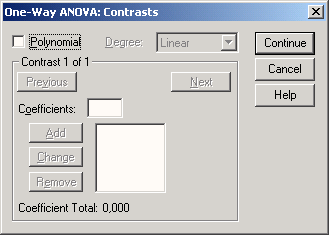
13.3.2 Априорные контрасты
13.3.2 Априорные контрасты
Различия средних значений зависимых переменных, получаемые на базе априорных контрастов, можно подвергнуть t-тесту. Эта процедура называется априорным множественным сравнением. Контрасты определяются как последовательность (линейная комбинация) коэффициентов, каждый из которых соответствует отдельной категории независимой переменной.
Для коэффициентов, используемых при определении контрастов, можно задавать положительные, отрицательные, целые и дробные значения. Категории независимой переменной, соответствующие отрицательным коэффициентам, комбинируются, эти комбинации сопоставляются с комбинациями категорий, которые соответствуют положительным коэффициентам. Категории, которым соответствуют нулевые коэффициенты, не учитываются. Сумма всех коэффициентов должна равняться нулю.
В нашем примере сравнивались четыре возрастных класса (категории 1 -4) по переменной роста. Допустим, нам требуется сопоставить первую возрастную группу и комбинацию из трех остальных групп; для этого мы выберем нижеследующие априорные коэффициенты:
-3 1 1 1
Если же требуется сравнить комбинацию первых двух групп с последней группой, следует выбрать такие коэффициенты:
-1-1 0 2
Для определения описанных контрастов по вышеописанной процедуре множественного сравнения откроем в диалоге AN OVA вспомогательное диалоговое окно Contrasts. В поле Coefficients этого диалогового окна введем первый коэффициент и щелкнем на кнопке Add. Таким же образом вводятся остальные коэффициенты.
Когда все коэффициенты задачи введены, можно кнопкой Next (Следующий) перейти ко вводу следующей комбинации коэффициентов. После задания коэффициентов для всех требуемых контрастов кнопкой Continue закройте это диалоговое окно. Можно задать до десяти контрастов, каждый из которых содержит до пятидесяти коэффициентов.
13.3.3 Апостериорные тесты
13.3.3 Апостериорные тесты
Чтобы провести апостериорные тесты множественного сравнения средних, щелкните в диалоговом окне ANOVA на кнопке Post Hoc... В появившемся окне можно выбрать 'Мин или несколько из восемнадцати тестов, которые производят такие сравнения для всех групп:
-
Наименьшая значимая разность (многократный t-тест без альфа-коррекции) —LSD
-
Тест Бонферрони (многократный t-тест с альфа-коррекцией) — Bonferroni
-
t-тест Сидака (Sidak)
-
Тест Шеффе (Scheffe)
-
Процедура Райана-Эйно-Габриеля-Уэлша, или F-тест (R-E-G-W-F)
-
Процедура Райана-Эйно-Габриеля-Уэлша, или определение стьюдентизированного критерия размаха выборки (R-E-G-W-Q)
-
Тест Стьюдента-Иьюмена-Кейлса (S-N-K)
-
Тест Тьюки (Tukey)
-
b Тьюки (Tukey's b)
-
Тест Дункана (Duncari)
-
GT2 Хохберга (Hochberg's GT2)
-
Тест Габриеля (Gabriel)
-
Тест Уоллера-Дункана (Waller-Duncan)
-
t-тест Даннета, одно- и двусторонний (Dunnetf)
-
Т2 Тэмхена (Tamehane 's T2)
-
ТЗ Даннета (Dunnett's ТЗ)
-
Тест Геймса-Ховелла (Games-Howell)
-
С Даннета (Dunnett's С).
Средние значения групп выводятся в порядке возрастания.
13.3.4 Другие параметры
13.3.4 Другие параметры
В диалоговом окне ANOVA: Options, кроме способа обработки пропущенных значений, можно дополнительно задать вывод описательной статистики по группам (средних значений, стандартных отклонений, стандартных ошибок, минимумов, максимумов, 95 % доверительных интервалов и количеств наблюдений), а также проверку на гомогенность дисперсий посредством теста Левена. Можно также задать вывод линейчатых графиков средних значений.
13.4. Сравнение более чем двух зависимых выборок
13.4. Сравнение более чем двух зависимых выборок
На основе данных по гипертонии исследуем, значимо ли изменяется содержание холестерина в течение четырёх промежутков времени (такое сравнение для первых двух промежутков времени мы уже провели в параграфе 13.2).
Для достижения этой цели подходит однофакторный дисперсионный анализ с повторными измерениями. Пользователи SPSS, работавшие с этим пакетом на больших компьютерах, знают, что выполнить эту весьма распространенную операцию можно было только с помощью процедуры MANOVA (многомерный дисперсионный анализ). Ясно, что эта процедура предназначена для разнообразных методов многомерного анализа, но может быть использована при одномерном дисперсионном анализе с повторными измерениями.
Начиная с версии 7 SPSS процедура MANOVA была заменена процедурой GLM (General Linear Model). Однако и в текущей версии процедура MANOVA по прежнему остается доступной при использовании программного синтаксиса.
Разнообразные возможности анализа, предоставляемые этими процедурами (GLM и MANOVA), обеспечиваются ценой уже практически необозримого количества команд, спецификаций, параметров и ключевых слов. Даже при решении такой простой задачи, как рассматриваемая, надо уметь ориентироваться в этом многообразии. Несколько подробнее процедура GLM рассматривается в главе 17; однако в рамках этой книги невозможно охватить всю широту диапазона возможностей, предоставляемых этой процедурой. Теперь перейдем к решению нашей задачи при помощи однофакторного дисперсионного анализа с повторными измерениями.
-
Загрузите файл hyper, sav.
-
Выберите в меню команды Analyze (Анализ) General Linear Model (Общая линейная модель) Repeated Measures... (Повторные измерения)
Откроется диалоговое окно Repeated Measures Define Factors) (Определить фактор(ы) для повторных измерений).
В данном примере мы подвергнем анализу четыре переменных: cho10, cho11, cho16 и chol12; следовательно, фактор повторных измерений будет задаваться четырьмя уровнями (слоями).
-
Введите число 4 в поле Number of Levels (Количество уровней). По умолчанию принимается имя фактора faktorl; при желании можно задать для него любое другое i имя (например, "время").
-
Щелкните на кнопке Add. Других факторов повторных измерений у нас нет, поэтому можно сразу закрыть этот диалог кнопкой Define (Определить). Появится диалоговое окно Repeated Measures (Повторные измерения) (см. рис. 13.7).
-
Перенесите переменные cho10, choll, cho16 и chol12 в список Within-Subject Variables (Переменные внутри субъекта); далее кнопками, которые находятся внизу диалогового окна, можно установить дополнительные параметры но мы не будем их рассматривать.
-
Запустите вычисления, щелкнув на ОК.
Рис. 13.6: Диалоговое окно Repeated Measures Define Factor(s)
Рис. 13.7: Диалоговое окно Repeated Measures
-
Проанализируйте результаты, появившиеся в окне просмотра.
Вы убедитесь, что для неподготовленного пользователя толкование полученных результатов расчёта может составить большие трудности. Подробнее о них мы поговорим в главе 17. Теперь же мы ограничимся указанием, что результаты обычного дисперсионного анализа содержатся в строке "Sphericity assumed" (Предположение о сферичности) таблицы вывода, приведенной ниже:
Tests of Within-Subjects Effects (Тест эффектов внутри субъекта)
Measure: MEASURE_1 | ||||||
Source (Источник) | Type III Sum of Squares (Сумма квадратов типа III) | df | Mean Square (Среднее квадратов) | F | Sig. (Значи-мость) | |
FACTOR1 | Sphericity Assumed (Прини- мается гипотеза о сферич- ности) | 3381,822 | 3 | 1127,274 | 2,653 | ,048 |
Greenhouse- Geisser | 3381,822 | 2,509 | 1347,779 | 2,653 | ,058 | |
Huynh-Feldt | 3381 ,822 | 2,549 | 1326,675 | 2,653 | ,058 | |
Lower Bound | 3381,822 | 1,000 | 3381,822 | 2,653 | ,105 | |
Error (FACTOR1) | Sphericity Assumed (Прини- мается гипотеза о сферич- ности) | 220504,678 | 519 | 424,865 |
|
|
Greenhouse- Geisser | 220504,678 | 434,088 | 507,972 |
|
| |
Huynh-Feldt | 220504,678 | 440,994 | 500,018 |
|
| |
Lower Bound | 220504,678 | 173,000 | 1274,594 |
|
| |
Вероятность ошибки р составляет 0,048, что указывает на значимое различие между отдельными моментами времени. К сожалению, даже в 10-й версии SPSS отсутствует возможность провести апостериорный тест для повторных измерений, чтобы выяснить, какие именно промежутки времени значимо отличаются друг от друга. В случае, если выявлены значимые отличия, как в рассмотренном примере, пользователю не остается ничего другого, кроме выполнения парного t-теста.
6.gif

7.gif
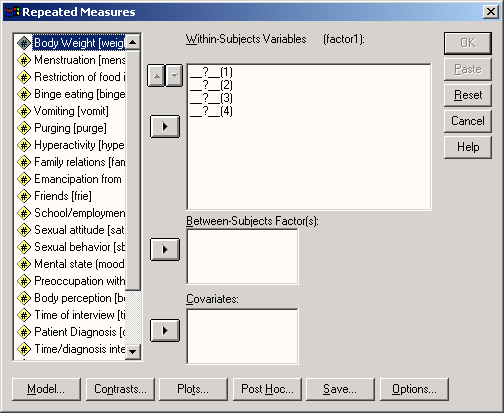
13.5 t-тест одной выборки
13.5 Мест одной выборки
Этот тест позволяет выяснить, отличается ли среднее значение, полученное на основе данной выборки, от предварительно заданного контрольного значения.
Мы проверим, отличается ли средний показатель холестерина, полученный при исследовании гипертонии, от значения 229, которое могло быть определено в каком-либо другом исследовании.
-
Загрузите файл hyper.sav.
-
Выберите в меню команды Analyze (Анализ) Compare Means (Сравнение средних) One-Sample T Test... (t-тест для одной выборки) Откроется диалоговое окно One-Sample T Test (см. рис. 13.8).
-
Перенесите переменную cho10 в поле Test Variable(s) и введите в поле Test Value (Контрольное значение) значение 229.
-
Запустите вычисления, щелкнув на ОК.
Результаты, показанные в окне просмотра, свидетельствуют о том, что в данном исследовании средний исходный уровень холестерина составляет 237,27, что значимо (р = 0,029) отличается от контрольного значения 229.
Рис. 13.8: Диалоговое окно One-Sample T Test
One-Sample Statistics (Статистика одной выборки)
N | Mean | Std. Deviation | Std. Error Mean | |
Холестерин, исходный | 174 | 237,27 | 49,42 | 3,75 |
One-Sample Test (Тест пои одной выборке)
Test Value = 229 | ||||||
T | df | Sig. (2-tailed) | Mean Difference | 95 % Confidence Interval of the Difference | ||
Upper | Lower | |||||
Холестерин, исходный | 2,207 | 173 | ,029 | 8,27 | ,88 | 15,66 |
Кнопкой Options... (Параметры) можно задать вместо 95 % любой другой доверительный интервал. Значение доверительного интервала может принимать значения в промежутке от 1 до 99%.
8.gif
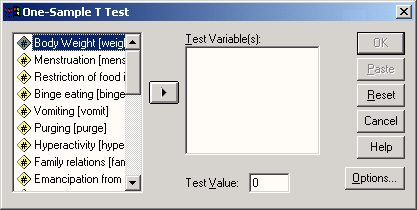
Глава 14. Непараметрические тесты
Глава 14. Непараметрические тесты
1. Непараметрические тесты
Непараметрические тесты
Непараметрические (не основанные на каком-либо распределении вероятности) тесты применяются там, где выборки из переменных, принадлежащих к интервальной шкале, не подчиняются нормальному распределению. Так как в этих тестах обрабатывается не само измеренное значение, а его ранг (положение внутри выборки), то эти тесты нечувствительны к выбросам. Непараметрические тесты применяются также в тех случаях, когда переменные относятся к порядковой, а не к интервальной шкале. В меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты)
SPSS предоставляет в распоряжение пользователей немалое количество непараметрических тестов. Все эти тесты приведены в нижеследующей таблице. В левой колонке находятся описания вспомогательных меню, а правая содержит описания тестов, вызываемых через соответствующие диалоговые окна.
Вспомогательные меню | Аналоговое окно |
Chi-Square (Хи-квадрат) | |
Binomial (Биномиальный) | |
Runs (Последовательности) | |
1 -Sample K-S... (Колмогоров-Смирнов для одной выборки) | |
2 Independent Samples (Две независимые выборки) | Mann-Withney-U-Test (U-тест Манна-Уитни) Moses extreme reactions (Экстремальные реакции по Мозесу) |
Z Kolomgorov-Smirnov (Z-тест Колмогорова-Смирнова | |
Wald-Wolfowitz runs (Последовательности Уалда-Вольфовица) | |
К Independent Samples (К независимых выборок) | Н Kruskal-Wallis (Н-тест Крускала-Уоллиса) Median (Медианный тест) |
2 Related Samples (Две связанные выборки) | Wilcoxon (Тест Уилкоксона) Sign (Знак) |
McNemar (Тест МакНемара) | |
К Related Samples (К связанных выборок) | Friedman (Тест Фридмана) |
W Kendall (W-тест Кендала) | |
Q Cochran (Q-тест Кохрана) |
Наиболее часто применяемыми тестами являются тесты для сравнения двух и более независимых или зависимых выборок. Наиболее известными тестами, служащими для этих целей являются U-тест Манна-Уитни, Н-тест Крускала-Уоллиса, тест Уилкоксона и тест Фридмана. Важную роль также играет тест Колмогорова-Смирнова для одной выборки, который может применяться для проверки наличия нормального распределения.
Непараметрические тесты могут, конечно, применяться и в случае нормального распределения значений. Но в этом случае они будут иметь лишь 95 %-ую эффективность по сравнению с параметрическими тестами. Если Вы хотите, к примеру, произвести множественное сравнение средних значений двух независимых выборок, причем выборки являются частично подчиняются нормальному распределению, а частично — нет, то рекомендуется всегда применять U-тест Манна и Уитни.
14.1 Сравнение двух независимых выборок
14.1.1 U-тест по методу Манна и Уитни
14.1.1 U-тест по методу Манна и Уитни
Это самый известный и самый распространенный тест непараметрического сравнения двух независимых выборок. Он основан на использовании одной общей последовательности значений обоих выборок.
Мы хотим проверить, отличаются ли показатели сахара в крови для мужчин и женщин в примере об исследовании гипертонии (файл hyper.sav).
Если Вы построите гистограмму показателя сахара в крови (переменная bz0), то заметите явную деформацию распределения в левую сторону. Тест Колмогорова-Смирнова (см. гл. 14.5) также показывает очень значительное отклонение от нормального распределения. Стало быть, для сравнения обоих выборок следует вместо t-теста Стьюдента применить U-тест по методу Манна и Уитни.
-
Откройте файл hyper.sav.
-
Выберите в меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) 2 Independent Samples... (Две независимые выборки)
Появится диалоговое окно Two Independent Samples Tests (Тесты для двух независимых выборок) (см. рис. 14.1).
U-тест по методу Манна и Уитни является предварительной установкой.
-
Перенесите переменную bz0 из поля исходных переменных в поле тестируемых переменных, а переменную g в поле групповых переменных.
-
После щелчка на кнопке Define Groups (Определить группы). Вы получите возможность внести коды (1 — мужской и 2 — женский), необходимые для идентификации групп.
-
После щелчка на Continue Вы опять попадаете в исходное диалоговое окно.
-
Запустите программу вычисления путём нажатия на ОК.
В окне просмотра появятся следующие результаты:
Рис. 14.1: Диалоговое окно Two Independent Samples Tests (Тесты для двух независимых выборок)
Ранги
Пол | N | Mean Rank (Усреднённый ранг) | Sum of Ranks (Ранговая сумма) | |
Blutzucker, Ausgangswert (Сахар, исходное значение) | maennlich (Мужской) | 59 | 81,66 | 4818,00 |
weiblich Женский | 115 | 90,50 | 10407,00 | |
Total (Сумма) | 174 |
Статистика теста а
Blutzucker, Ausgangswert (Сахар, исходное значение) | |
Mann-Whitney U jU-тест по Манну и Уитни) | 3048,000 |
W Уилкоксона | 4818,000 |
Z | -1,096 |
Asymp. Sig. (2-tailed) Асимптотическая значимость (2-сторонняя) | ,273 |
a Grouping Variable: Geschlecht (Групповая переменная: пол).
Выведенные результаты включают следующие показатели:
-
количество наблюдений, усреднённые ранги и ранговая сумма для двух выборок (причём большим значениям присваиваются низшие ранговые места),
-
тестовую величину U, определенную с помощью теста Манна и Уитни,
-
наименьшее значение из обоих ранговых сумм (W-тест Уилкоксона),
-
точное значение вероятности ошибки р при количестве наблюдений менее 30 и
-
тестовую величину z, определенную по тесту Колмогорова-Смирнова, а также относящуюся к ней вероятность ошибки р, которую следует использовать при количестве наблюдений более 30.
Выясняется, что в рассматриваемом примере разница показателей сахара в крови между полами не является статистически значимой (р = 0,273).
Нажав кнопку Options, Вы можете выбрать дополнительные возможности вывода данных, относящихся к рассмотренному и к другим непараметрическим тестам. Наряду с обычной обработкой пропущенных значений, можно организовать расчет дескриптивных статистик (среднее значение, минимум, максимум, стандартное отклонение, количество наблюдений) и квартилей (25, 50 и 75 процентили). Однако в этом случае характеристики дескриптивной статистики будут определяться одновременно для тестируемых и группирующих переменных. Это абсолютно бесполезно, так как в данном случае дескриптивная статистика имеет смысл только для тестируемых переменных, разбитых на группы по группирующим переменным. К сожалению, данная ошибка не была исправлена и в 10 версии SPSS.
В рассмотренном примере проведения U-теста был бы также очень полезен расчет медиан обеих групп. Медианы определяются с помощью других средств SPSS. В нашем примере медиана показателя сахара для мужчин равна 93, а для женщин 97.
1.gif
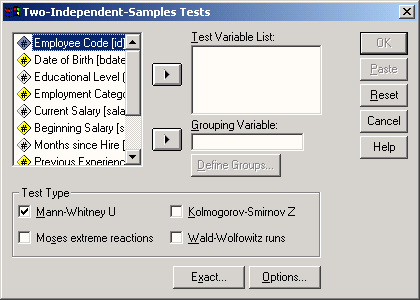
14.1.2 Тест Мозеса (Moses)
14.1.2 Тест Мозеса (Moses)
Данный тест проверяет различие размаха двух независимых выборок, которые состоят из переменных, относящихся к порядковой шкале, причем одна выборка рассматривается как контрольная группа, а другая как экспериментальная. Так как размах экстремальных значений может давать искаженные представления, то при помощи установки по умолчанию по обеим сторонам распределения контрольной группы отсекаются в обшей сложности 5 процентов значений.
Однако, это может привести к тому, что реальные различия в наблюдаемых значениях переменных, будут искусственно стёрты. Это можно увидеть на следующем примере, который уже рассматривался при изучении U-теста по Манну и Уитни.
-
Откройте файл hyper.sav.
-
В диалоговом окне Two Independent Samples Tests (Тесты для двух независимых выборок) удалите флажок для U-теста по методу Манна и Уитни и отметьте вместо этого тест Мозеса (Moses extreme reactions).
-
В качестве тестовой переменной выберите переменную rrsl, а в качестве групповой переменной переменную med с кодировками 1 и 2.
-
Запустите программу вычисления путём нажатия на ОК. В окне просмотра появятся следующие результаты:
Частоты
Медикамент | N | |
syst. Blutdruck, Ausgangswert (Систолическое давление, через 1 месяц) | Alphasan (контрольный) | 87 |
Betasan (экспериментальный) | 87 | |
Total (Сумма) | 174 |
Статистика теста a,b
Систолическое давление, через 1 месяц | ||
Observed Control Group Span (Наблюдаемый размах контрольной группы) | NSig. (1 -tailed) N Значимость (1 -сторонняя) | 167 ,032 |
Trimmed Control Group Span (Размах усеченной контрольной группы) | N Sig. (1-tailed) N Значимость (1-сторонняя) | 156 ,500 |
Outliers Trimmed from each End (Выбросы удалены с обеих сторон) | 4 |
а. Тест Мозеса
b. Групповая переменная: медикамент
При проведении теста Мозеса первая из двух групп рассматривается как контрольная. Значения обеих групп располагаются на порядковой шкале и им присваиваются соответствующие ранговые места. В контрольной группе подсчитывается размах между этими ранговыми местами, то есть разность между большим и меньшим рангом. Этот размах равен 167 с соответствующим значением вероятности ошибки р = 0,032. Полученное значение вероятности ошибки указывает на значимое отклонение от размаха, ожидаемого при равномерном распределении. Эта значимость полностью исчезает (р = 0,500), если при подсчёте размаха контрольной группы удалить по четыре самых больших и самых малых ранга.
14.1.3 Тест Колмогорова-Смирнова
14.1.3 Тест Колмогорова-Смирнова
Условия применения данного теста такие же, как и при использовании U-теста по методу Манна и Уитни. Тест Колмогорова-Смирнова является предпочтительным тогда, когда количество категорий для тестируемых переменных ограничено. Если для такого j случая применять U-тест Манна и Уитни, то появляется большое количество ранговых мест, к которым относится сразу несколько переменных, то есть возникают неоднозначные ранговые последовательности. Основой теста является расчет максимальной разности между кумулятивными частотами обеих выборок. Эта разность обозначается величиной z, на основании которой, выводится вероятность ошибки р. В главе 11 рассматривался файл studium.sav, в котором при помощи переменной psyche отражалось психологическое состояние студентов (закодированное цифрами от 1 до 4 для значений: очень неустойчивое до очень устойчивое), а при помощи переменной sex — пол (1 = женский, 2 = мужской). Раньше различия между полами проверялись при помощи теста хи-квадрат. В данном случае для определения различия I можно также применить тест Колмогорова-Смирнова.
-
Откройте файл studium.sav.
-
Активируйте в диалоговом окне Two Independent Samples (Тесты для двух независимых выборок) тест Колмогорова-Смирнова.
-
Перенесите переменную psyche в поле тестируемых переменных, а переменной sex присвойте статус групповой переменной с категориями 1 и 2.
-
Запустите вычисления путём нажатия на ОК.
В окне просмотра появятся следующие результаты расчёта:
Статистика теста а
Psychische Lage | ||
,370 ,000 -,370 | ||
Most Extreme Differences (Самые экстремальные разности) | Абсолютно Положительно Отрицательно | |
Z-Колмогорова-Смирнова |
| 1,875 |
| Asymp.Sig.(2-tailed) (Статистическая значимость (2-сторонняя) | ,002 |
a. Grouping Variable: Geschlecht (Групповая переменная: пол)
Получается очень значимая разница между полами в отношении психологического состояния (р = 0,002).
14.1.4 Тест Уалда-Вольфовица (Wald-Wolfowitz)
14.1.4 Тест Уалда-Вольфовица (Wald-Wolfowitz)
Условия применения данного теста те же, что и при U-тесте по методу Манна и Уитни или при тесте Колмогорова-Смирнова. Значения обоих групп выстраиваются в единую последовательность по рангу. Затем производится подсчёт количества смен группового признака, с помощью которого можно найти количество непрерывных
последовательностей (количество смен плюс 1). Если появляются одинаковые значения (ранговые связки), то выводятся значения минимального и максимального числа возможных непрерывных последовательностей. Исходя из количества непрерывных последовательностей, можно найти вероятность ошибки р. Данный тест не пригоден для переменных с малым числом категорий, так как в этом случае очень сильно возрастает количество ранговых связок.
В качестве примера рассмотрим уже многократно использовавшийся пример со сравнением показателя кровяного давления.
-
Откройте файл hyper.sav.
-
В диалоговом окне Two Independent Samples (Тесты для двух независимых выборок) активируйте тест Уалда-Вольфовица.
-
Перенесите переменную rrsl в поле для тестируемых переменных, переменной med присвойте статус групповой переменной с категориями 1 и 2.
-
Запустите вычисления путём нажатия ОК. В окне просмотра появятся следующие результаты:
Статистика теста b,c
Number of Runs (Число непрерывных последователь- ностей) | Z | Asymp. Sig. (1-tailed) (Статисти- ческая значимость , (1 -сторонняя)) | ||
Syst. Blutdruck, nach 1 Monat (Систолическое давление, через 1 месяц) | Minimum Possible (Минимально возможное) | 13" | -11,404 | ,000 |
Maximum Possible (Максимально возможное) | 146 а | 8,819 | 1,000 | |
a. There are 10 inter-group ties involving 165 cases. (Между группами насчитывается 10 связок, которые охватывают 165 наблюдений.)
b. Wald-Wolfowitz Test (Тест по методу Уалда-Вольфовица)
с. Grouping Variable: Medikament (Групповая переменная: медикамент)
В результате мы получаем различие между минимальной и максимальной возможной непрерывной последовательностью (значение Z) и связанную с ним вероятность ошибки. Так как рассчитываемые значения Z располагаются по обоим краям стандартного нормального распределения, то выборка может содержать исходные данные, не пригодные для проведения этого теста. Поэтому тест Уальда-Вольфовица является не очень убедительным, в особенности при наличии ранговых связок.
14.2 Сравнение двух зависимых выборок
14.2 Сравнение двух зависимых выборок
Понятие о зависимости выборок было рассмотрено в главе 5.1.3. Для проведения сравнения для таких выборок SPSS предлагает три различных теста, среди которых установленным по умолчанию является тест Уилкоксона. Заслуживает внимания так же и знаковый тест. При наличии дихотомических переменных применяется тест хи-квадрат по методу МакНемара.
14.2.1 Тест Уилкоксона (Wilcoxon)
14.2.1 Тест Уилкоксона (Wilcoxon)
Этот тест является традиционным непараметрическим тестом для сравнения двух зависимых выборок. Он основан на построении ранговой последовательности абсолютных разностей пар значений.
Мы уже установили (см. раздел 14.1), что для обоих медикаментов после 1 месяца приема наблюдается значительное понижение систолического кровяного давления. Теперь мы хотим проверить, является ли это изменение закономерным. Для простоты мы сначала должны быть рассмотрены все наблюдения подряд, то есть без разделения на группы по принимаемым медикаментам.
Переменные rrs0 и rrs1 (начальный уровень систолического давления и уровень через месяц после начала приема медикамента) представляют собой типичный пример связанных (зависимых) выборок.
-
Откройте файл hyper.sav.
-
Выберите в меню Analyze (Анализ) Nonparametric Tests... (Непараметрические тесты) 2 Related Samples... (Две связанные выборки)
Вы сможете убедиться в том, что предварительно по умолчанию установлен тест Уил-коксона (см. рис. 14.2)
-
Теперь в поле тестируемых переменных нужно выделить две необходимые переменные и эту пару перенести в поле для спаренных переменных. В нашем примере такими переменными являются rrsO и rrsl.
-
Запустите тест Уилкоксона на исполнение нажатием клавиши ОК. В окне просмотра появятся результаты расчёта:
Ranks (Ранги)
N | Mean Rank (Средний ранг) | Sum of Ranks (Ранговая сумма) | ||
syst. Blutdruck, nach 1 Monat - syst. Blutdruck, Ausgangswert (Систолическое кровяное давление, через 1 месяц -систолическое кровяное давление, исходная величина) | Negative Ranks (Отрицательные ранги) | 144а | 77,81 | 11204,00 |
Positive Ranks (Положительные ранги) | 8Ь | 53,00 | 424,00 | |
Ties (Связи) | 22е | |||
Total (Сумма) | 174 |
a. syst Blutdruck, nach 1 Monat < syst. Blutdruck, Ausgangswert (Систолическое кровяное давление, через 1 месяц < систолическое кровяное давление, исходная величина)
b. syst. Blutdruck, nach 1 Monat > syst. Blutdruck, Ausgangswert (Систолическое кровяное давление, через 1 месяц > систолическое кровяное давление, исходная величина)
с. syst. Blutdruck, nach 1 Monat = syst. Blutdruck, Ausgangswert (Систолическое кровяное давление, через 1 месяц = систолическое кровяное давление, исходная величина)
Статистика теста b
syst. Blutdruck, nach 1 Monat - syst. Blutdruck, Ausgangswert (Систолическое кровяное давление, через 1 месяц -систолическое кровяное давление, исходная величина) | |
Z | -9,970а |
Asymp. Sig. (2-tailed) (Статистическая значимость (2-сторонняя)) | ,000 |
a. Based on positive ranks (Основано на положительных рангах)
b. Wilcoxon test (Тест Вилоксона)
Результаты расчёта включают следующие данные:
Рис. 14.2: Диалоговое окно Two-Related-Samples Tests (Тесты для двух связанных выборок)
-
количества, средние ранги и ранговые суммы для отрицательных и положительных разностей (причём большим абсолютным разностям присваивается более высокое ранговое место)
-
количество нулевых разностей и
-
контрольную величину z с соответствующей вероятностью ошибки р.
Полученная в приведенном примере величина р = 0,000 свидетельствует об очень значимой разнице.
Теперь повторим тест, но отдельно для каждого медикамента. Это значит, что один раз расчёт нужно произвести с условием med = 1, а второй с условием med = 2.
Для расчёта можно применить метод "Выбрать наблюдения", однако метод "Разделить файл" является более быстрым (см. гл. 7.4).
-
Выберите в меню Data (Данные) Split file... (Разделить файл)
-
Активируйте опцию Organize output by groups (Выводить результаты по группам), и перенесите переменную med в поле Groups based on (Группы основываются на).
-
Т.к. данные не сортированы по групповым признакам, оставьте опцию Sort the File by grouping variables... (Файл сортировать по групповым признакам) включённой и щёлкните на ОК.
-
Проведите ещё раз тест Уилкоксона, как было описано в начале раздела. Теперь он производится отдельно для каждого медикамента.
2.gif
14.2.2 Знаковый тест
14.2.2 Знаковый тест
Условия применения данного теста те же, что и для теста Уилкоксона, но в отличие от него здесь ведётся подсчёт только положительных и отрицательных разностей, что может оказаться полезным тогда, когда различия между выборками будут не слишком заметны.
До и после проведения курса лечения 67 пациентов были опрошены на предмет их самочувствия со следующими вариантами ответов: "хорошее", "относительно нормальное" или "плохое". Из 5 пациентов, самочувствие которых до прохождения курса лечения было хорошим, 3 после лечения отметили ответ "хорошее", а 2 "относительно нормальное". 18 пациентов до курса лечения оценили своё самочувствие как "относительно нормальное". 9 из них после лечения дали ответ "хорошее", 7 — "относительно нормальное" и 2 — "плохое". 44 пациента до лечения отозвались о своём самочувствии как о плохом. Из них 8 после лечения дали ответ "хорошее", 22 — "относительно нормальное", а 14 как и прежде — "плохое". Требуется проверить, является ли значимым успех лечения.
Данные находятся в файле kur.sav, который содержит переменные befl и bef2 (самочувствие до и после лечения с кодировками 1 = хорошо, 2 = относительно нормально, 3 = плохо) и n (частоты соответствующих комбинаций состояния пациентов).
-
Откройте файл kur.sav.
-
Используя меню Data (Данные) Weight cases... (Взвесить наблюдения) присвойте переменной п статус частотной переменной (см. гл. 8.7.2).
-
После вызова меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) 2 Related Samples... (Две связанные выборки) откроется диалоговое окно Two-Related-Samples Tests (Тесты для двух связанных выборок).
-
Укажите переменные befl и bef2 в качестве тестируемой пары.
-
Из-за принятой кодировки переменных, вместо предварительно установленного теста Уилкоксона необходимо выбрать знаковый тест.
-
Запустите расчёт на исполнение при помощи нажатия ОК. В окне просмотра появятся следующие результаты расчёта:
Frequencies (Частоты)
N | ||
Befinden nach der Kur - Befinden vor der Kur (Самочувствие после лечения - самочувствие до лечения) | Negative Differences (Отрицательные разности) г | 39 |
Positive Differences (Положительные разности) " | 4 | |
Ties (Связки) с | 27 | |
Total (Сумма) | 67 |
a. Befinden nach der Kur < Befinden vor der Kur (Самочувствие после лечения < самочувствие до лечения)
b. Befinden nach der Kur > Befinden vor der Kur (Самочувствие после лечения > самочувствие до лечения)
с. Befinden nach der Kur = Befinden vor der Kur (Самочувствие после лечения = самочувствие до лечения)
Test Statistics3 (Статистика теста)
Befinden nach der Kur - Befinden vor der Kur (Самочувствие после лечения - самочувствие до лечения) | |
Z | -5,185 |
Asymp. Sig. (2-tailed) (Статистическая значимость (2-сторонняя)) | ,000 |
a. Sign test (Знаковый тест)
Результаты расчёта дают 39 отрицательных разностей (bef2 < befl), которые свидетельствуют о наступлении улучшений и 4 положительных разности, а в 24 наблюдениях изменений самочувствия не наблюдается. Вследствие того, что количества положительных и отрицательных разностей отличаются, значение z получается равным -5,185; этому показателю соответствует вероятность ошибки р < 0,001. Стало быть, наблюдается очень значимый успех лечения.
14.2.3 Тест хи-квадрат по методу МакНемара (McNemar)
14.2.3 Тест хи-квадрат по методу МакНемара (McNemar)
Данный тест применяется исключительно при наличии дихотомических переменных. При этом для двух зависимых переменных выясняется, происходят ли какие-либо изменения в структуре распределения их значений. В большинстве наблюдений сравнение проводится с учётом временного фактора по схеме "до — после".
В качестве примера рассмотрим исследование, проведенное в области стоматологии, где изучается факт кровоточивости дёсен до и после лечения.
-
Откройте файл zahnblut.sav.
Он содержит две переменные b1 и b2, которые своими кодировками (1 = да, 2 = нет) указывают на наличие кровоточивости дёсен соответственно до и после лечения.
-
В диалоговом окне Two-Related-Samples Tests (Тесты для двух связанных выборок) выберите тест МакНемара и перенесите обе переменные Ы и Ь2 в поле тестируемых пар.
-
Запустите расчёт на исполнение нажатием кнопки ОК. В окне просмотра появятся следующие результаты:
Zahnfleischbluten vor Behandlung & Zahnfleischbluten nach Behandlung (Кровоточивость дёсен до лечения & Кровоточивость дёсен после лечения)
Zahnfleischbluten vor Behandlung (Кровоточивость дёсен до лечения) | Zahnfleischbluten nach Behandlung (Кровоточивость дёсен после лечения) | |
2 | 1 | |
1 | 362 | 808 |
2 | 240 | 1565 |
Test Statistics (Статистика теста) b
Zahnfleischbluten vor Behandlung & Zahnfleischbluten nach Behandlung (Кровоточивость дёсен до лечения & Кровоточивость дёсен после лечения) | |
N | 2975 |
Chi-Square (Хи-квадрат) а | 306,764 |
Asymp. Sig. (Статистическая значимость) | ,000 |
a. Continuity Corrected (Непрерывность откорректирована) b. McNemar Test (Tea МакНемара)
Принимая во внимание кодировки выясняется, что в 808 наблюдениях после лечения кровоточивость дёсен исчезла, однако, с другой стороны, в 240 наблюдениях после прохождения курса лечения вновь появилась. В 362 наблюдениях кровоточивость оставалась постоянной. В 1565 наблюдениях кровоточивости не наблюдалось ни перед, ни после лечения. В соответствии с вероятностью ошибки, соответствующей величине критерия хи-квадрат (р < 0,001), можно констатировать, что разница между количеством улучшений (808) и количеством ухудшений (240) является очень значимой.
14.3 Сравнение более чем двух независимых выборок
14.3.1 Н-тест по методу Крускала и Уоллиса
14.3.1 Н-тест по методу Крускала и Уоллиса
Этот тест является модификацией U-теста Манна и Уитни на случай для более двух 1езависимых выборок. Он также базируется на общей ранговой последовательности значений всех выборок.
В данном случае нам необходимо протестировать четыре возрастные категории из рассмотренного выше исследования гипертонии на предмет значимости различия исходного показателя систолического кровяного давления.
-
Откройте файл hyper.sav Если бы Вы через меню Analyze (Анализ) Compare Means (Сравнить средние значения) Means... (Средние значения) вычислили средние значения исходного показателя давления (переменная rrs0) для четырёх возрастных категорий, то получили бы следующие результаты:
Report (Сводка)
jyst. Blutdruck, Ausgangswert (Систолическое кровяное давление, исходное значение)
Altersklassen (Возрастные категории) | Mean (Среднее значение) | N | Std. Deviation (Стандартное отклонение) |
до 55 лет | 170,38 | 52 | 15,37 |
56-65 лет | 172,16 | 51 | 13,12 |
66-75 лет | 175,64 | 47 | 13,62 |
> 75 лет | 168,75 | 24 | 11,44 |
Сумма | 172,10 | 174 | 13,86 |
-
Для проверки значимости выберите в меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) К Independent Samples... (Несколько независимых выборок)
Появится диалоговое окно Tests for Several Independent Samples (Тесты для нескольких независимых выборок) (см. рис. 14.3).
Н-тест по методу Крускала и Уоллиса является установкой по умолчанию.
-
Перенесите переменную rrs0 в поле тестируемых переменных, а переменную ak, которая описывает четыре возрастные категории, в список групповых переменных.
Рис. 14.3: Диалоговое окно Tests for Several Independent Samples (Тесты для нескольких независимых выборок)
-
Щёлкните на Define Range... (Определить диапазон) и введите значения 1 и 4 для минимального и максимального значения переменной соответственно.
-
Вернувшись снова в исходное диалоговое окно (щелчок на Далее), начните вычисления путём щелчка на ОК.
В окне просмотра появятся следующие результаты:
Ranks (Ранги)
Altersklassen (Возрастные категории) | N | Mean Rank (Средний ранг) | |
syst. Blutdruck, Ausgangswert (Систолическое давление, исходная величина) | до 55 лет | 52 | 79,76 |
56-65 лет | 51 | 87,51 | |
66-75 лет | 47 | 102,17 | |
> 75 лет | 24 | 75,52 | |
Total (Сумма) | 174 |
Test Statistics (Статистика теста) а, b
syst. Blutdruck, Ausgangswert (Систолическое кровяное давление, исходная величина) | |
Chi-Square (Хи-квадрат) | 6,801 |
Df | 3 |
Asymp. Sig. (Статистическая значимость) | ,079 |
a. Kruskal Wallis Test (Тест Крускала-Уолхлиса)
b. Grouping Variable: Altersklassen (Групповая переменная: Возрастные категории)
В результаты расчёта входят:
-
усреднённые ранги в отдельных группах (где большим значениям отдаются более высокие места) и
-
величина критерия хи-квадрат, соответствующее число степеней свободы (df) и вероятность ошибки р.
В данном примере для которого р = 0,079 граница значимости преодолена незначительно, это означает, что всё же наблюдается тенденция к проявлению закономерности. В случае выявления существенной закономерности, для определения групп, которые значимо отличаются друг от друга, необходимо протестировать все группы попарно (как в тесте по методу Манна и Уитни).
3.gif

14.3.2 Медианный тест
14.3.2 Медианный тест
Для всех независимых выборок вычисляется общая медиана; затем подсчитывается, какое количество измеряемых величин находится ниже и выше медианы. Это приводит к построению полевой таблицы, содержащей 2*k полей, которая затем подвергается тесту хи-квадрат. Как уже указывалось, эффективность данного теста не очень высока.
Используем пример, использованный для изучения Н-теста по Крускалу и Уоллису.
-
В этот раз вместо указанного теста активируйте медианный тест.
-
Запустите расчёт путём нажатия ОК.
В окне просмотра появятся следующие результаты:
Frequencies (Частоты)
Altersklassen (Возрастные категории) | |||||
| до 55 лет | 56-65 лет | 66-75лет | >75лет | |
syst. Blutdruck, Ausgangswert (Систолическое кровяное давление, исходная величина) | > медианы <= медианы | 18 | 19 | 24 | 7 |
34 | 32 | 23 | 17 | ||
Test Statistics (Статистика для теста) b
syst. Blutdruck, Ausgangswert (Систолическое кровяное давление, исходная величина) | |
N | 174 |
Медиана | 170,00 |
Хи-квадрат | 4,333а |
Df | 3 |
Asymp. Sig. (Статистическая значимость) | ,228 |
a. 0 cells (,0%) have expected frequencies less than 5. The minimum expected cell frequency is 9,4. (В 0 ячеек (,0%) ожидается значение частоты менее 5. Минимальная ожидаемая частота в ячейке равна 9,4.)
b Grouping Variable: Altersklassen (Групповая переменная: возрастные категории)
Так как в Н-тесте получилась р = 0,079, то он оказывается более подходящим для выявления закономерностей.
14.4 Сравнение более чем двух зависимых выборок
14.4.1 Тест Фридмана
14.4.1 Тест Фридмана
Этот тест представляет собой расширение теста Уилкоксона для случая наличия более чем двух зависимых выборок. Он основывается на ранговых последовательностях, которые строятся для значений всех переменных участвующих в тесте.
-
Если Вы с помощью меню Analyze (Анализ) Reports (Сводка) Case Summaries... (Итоги по наблюдениям)
произведёте расчёт медиан для диастолического кровяного давления из исследования гипертонии (файл hyper.sav) для четырёх последовательных моментов времени (переменные rrdO, rrdl, rrd6, rrd!2), то получите следующие значения:
Case Processing Summary (Сводная таблица наблюдений)
Median (Медианы) | |||
diast. Blutdruck, Ausgangswert (Диастоли- ческое кровяное давление, исходная величина) | diast. Blutdruck, nach 1 Monat (Диастолическое кровяное давление, через 1 месяц ) | diast. Blutdruck, nach 6 Monaten (Диастоли- ческое кровяное давление, через 6 месяцев) | diast. Blutdruck, nach 12 Monaten (Диастоли- ческое кровяное давление, через 12 месяцев) |
100,00 | 95,00 | 90,00 | 85,00 |
Видно, что Диастолическое кровяное давление непрерывно снижается. Этот факт следует проверить при помощи теста на значимость. В приведенном примере речь идёт о нескольких (а именно, — о четырёх) связанных выборках. Подходящим непараметрическим тестом для сравнения этих выборок является тест Фридмана.
-
Откройте файл hyper.sav.
-
Выберите в меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) К Related Samples... (Две связанные выборки)
В диалоговом окне Вы увидите, что предварительно установлен тест Фридмана (см. рис. 14.4).
-
Перенесите по очереди переменные rrd0, rrdl, rrd6 и rrd12 в поле тестируемых переменных. После щелчка на кнопке Statistics... (Статистики) у Вас появилась бы возможность организовать вывод дескриптивных статистик и квантилей, но в данном случае мы от этого воздержимся.
-
Запустите расчёт путём нажатия ОК.
Рис. 14.4: Диалоговое окно Tests for Several Related Samples (Тесты для нескольких связанных выборок)
В окне просмотра появятся следующие результаты:
Ranks (Ранговые ряды)
Mean Rank (Средний ранг) | |
diast. Blutdruck, Ausgangswert (Диастолическое кровяное давление, исходная величина ) | 3,81 |
diast. Blutdruck, nach 1 Monat Диастолическое кровяное давление, через 1 месяц ) | 2,57 |
diast. Blutdruck, nach 6 Monaten (Диастолическое кровяное давление, через 6 месяцев) | 2,02 |
diast. Blutdruck, nach 12 Monaten (Диастолическое кровяное давление, ЧЙПРЗ 1 9 Миля! ien^ | 1,60 |
Test Statistics (Статистика теста)a
N | 174 |
Chi-Square (Хи-квадрат) | 317,754 |
Df | 3 |
Asymp. Sig. (Статистическая значимость) | ,000 |
а. Тест Фридмана
Полученные результаты содержат:
-
усреднённые ранги участвующих переменных (где большим значениям присваиваются более высокие места) и
-
количество наблюдений, величина критерия хи-квадрат, полученная в результате теста, соответствующее число степеней свободы (df) и вероятность ошибки р.
В приведенном примере получился очень значимый показатель р < 0,001. Теперь, применяя попарное тестирование, при помощи теста Уилкоксона Вы самостоятельно можете выяснить, какие временные моменты по отдельности отличаются друг от друга.
4.gif
14.4.2 W Кендала
14.4.2 W Кендала
Коэффициент согласованности Кендала (W) измеряет степень согласованности между несколькими связанными выборками. Он был специально разработан для проведения тестов в ситуации, когда большое количество рецензентов высказывают своё мнение о большом количестве рецензируемых персон (объектов).
При этом рецензируемые образуют отдельные переменные, а рецензенты — отдельные наблюдения. На этом несколько неожиданном разделении следует остановиться подробнее. Каждый рецензент при помощи заданных наперед оценок выстраивает рецензируемых по рангу. Затем для каждого рецензируемого определяется сумма ранговых номеров. Исходя из этих сумм, определяется масштаб различных отзывов. Коэффициент согласованности W, вычисленный на основании этого масштаба, указывает на меру согласия между рецензентами. Коэффициент согласованности может принимать значения между 0 и 1. Значение 1 соответствует наличию полного согласия.
Три крупные спортивные газеты оценивали футболистов высшей лиги, игравших в прошлом туре чемпионата, при помощи оценок от 1 до 6 (к примеру 1 за "мировой уровень" и 6 за "не отработал свои деньги"). Оценки для 22 футболистов, участвовавших в одной игре, находятся в файле fussball.sav, который содержит три наблюдения, соответствующие трем рецензентам и 22 переменные (sl-s22), соответствующие 12 рецензируемым игрокам.
-
Откройте файл fussball.sav.
-
Переместите в диалоговом окне Tests for Several Related Samples (Тесты для нескольких связанных выборок) переменные sl-s22 в поле тестируемых переменных.
-
Вместо предварительно установленного теста Фридмана активируйте РК-тест Кендала.
-
Запустите расчёт путём нажатия ОК. В окне просмотра появятся следующие результаты:
Ranks (Ранги)
Mean Rank (Усреднённый ранг) | |
S1 | 12,33 |
S2 | 6,17 |
S3 | 10,33 |
S4 | 3,50 |
S5 | 8,50 |
S6 | 19,33 |
S7 | 18,50 |
S8 | 10,50 |
S9 | 6,17 |
S10 | 14,67 |
S11 | 16,67 |
S12 | 12,67 |
S13 | 6,67 |
S14 | 15,33 |
S15 | 19,67 |
S16 | 3,33 |
S17 | 12,33 |
S18 | 17,00 |
S19 | 2,17 |
S20 | 12,33 |
S21 | 16,33 |
S22 | 8,50 |
Test Statistics (Статистика теста)
N | 3 |
W Кендала а | ,741 |
Хи-квадрат | 46,695 |
Df | 21 |
Asymp. Sig. (Статистическая значимость) | ,001 |
a. Kendall's Coefficient of Concordance (Коэффициент согласованности Кендала)
Очень значимый (р = 0,001) коэффициент согласованности W (0,741) указывает на высокую согласованность всех трёх спортивных газет при оценке 22 игроков.
14.4.3 ОКохрана
14.4.3 Q Кохрана
Этот тест представляет собой расширенный хи-квадрат-тест по МакНемару для случая с несколькими зависимыми выборками; стало быть, он может применяться при наличии более чем двух дихотомических переменных.
В главе 21 будет описан файл neugier.sav, который содержит 18 вопросов, с помощью которых исследовалась степень любопытства респондентов. Следующие три вопроса взяты из этого файла:
Вопрос 10: | Хотели бы Вы полететь на Луну? |
Вопрос 12: | Спрашивали ли Вы себя когда-нибудь, как будет выглядеть мир через сто лет? |
Вопрос 14: | Предоставили бы Вы себя в руки учёных для проведения научных экспериментов? |
Переменные, соответствующие ответам на эти вопросы, имеют кодировки 1 (да) и 2 (нет). Мы должны найти ответ на вопрос, существуют ли значимые отличия в ответах на эти три вопроса.
-
Откройте файл neugier.sav.
-
В диалоговом окне Tests for Several Related Samples (Тесты для нескольких связанных выборок) переместите переменные item10, item12 и item14 в поле тестируемых переменных.
-
Вместо установленного теста Фридмана активируйте Q-тест Кохрана.
-
Запустите расчёт путём нажатия ОК. В окне просмотра появятся следующие результаты:
Frequencies (Частоты)
Value (Значение) | ||
2 | ||
item 10 | 9 | 21 |
item 12 | 15 | 15 |
item14 | 12 | 18 |
Test Statistics (Статистика теста)
N | 30 |
Q тест Кохрана | 3,375" |
df | 2 |
Asymp. Sig. (Статистическая значимость) | ,185 |
a. 2 is treated as a success. (2 рассматривается, как успешный результат).
К результатам данного теста относятся частоты для обеих категорий переменных и тестовое значение Q, полученное на основании распределения хи-квадрат. Между частотными распределениями ответов на эти вопросы не существует значимого различия (р = 0,185).
14.5 Тест Колмогорова-Смирнова для проверки формы распределения
14.5 Тест Колмогорова-Смирнова для проверки формы распределения
При помощи этого теста по выбору можно проверить, соответствует ли реальное распределение переменной нормальному, равномерному, экспоненциальному распределению или распределению Пуассона. Разумеется, самым распространённым видом проверки является проверка наличия нормального распределения.
Чтобы продемонстрировать работу данного теста, проверим на предмет наличия нормального распределения исходные значения холестерина, то есть переменную cho10 из файла hyper.sav.
-
Откройте файл hyper.sav.
-
Выберите в меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) 1-Sample KS (К-С одной выборки)
Появится диалоговое окно One Sample .\olomgorov-Smirnov Test (Тест Колмогорова-Гмирнова для одной выборки) (см. рис. 4.5).
-
Перенесите переменную cho10 в поле тестируемых переменных.
-
Если Вы щёлкните на кнопке Options... (Опции), то сможете дополнительно организовать вывод характеристик дескриптивной статистики и квартилей.
-
Щёлкните на ОК.
Рис. 14.5: Диалоговое окно One Sample Kolomgorov-Smirnov Test (Тест Колмогорова-Смирнова для одной выборки)
Предварительно установленной является проверка на нормальное распределение. В окне просмотра появятся следующие результаты:
One-Sample Kolmogorov-Smirnov Test (Тест Колмогорова-Смирнова для одной выборки)
Cholesterin, Ausgangswert (Холестерин, исходная величина) | ||
N | 174 | |
Normal Parameters (Параметр нормального распределения) а' ь | Mean (Среднее значение) Std. Deviation (Стандартное отклонение) | 237,27 49,42 |
Most Extreme Differences (Экстремальные разности) | Absolute (Абсолютные) Positive (Положительные) Negative (Отрицательные) | ,057 ,057 -,046 |
Z Колмогорова-Смирнова | ,756 | |
Asymp. Sig. (2-tailed) (Статистическая значимость (2-сторонняя)) | ,616 |
a. Test distribution is Normal. (Тестируемое распределение является нормальным распределением.)
b. Calculated from data. (Рассчитано исходя из исходных данных.)
Полученные результаты включают:
-
среднее значение и стандартное отклонение
-
промежуточные результаты, полученные в результате теста Колмогорова-Смирнова
-
вероятность ошибки р.
Отклонение от нормального распределения считается существенным при значении р < 0,05; в этом случае для соответствующих переменных следует применять непараметрические тесты. В рассматриваемом примере ( значение р = 0,616), то есть вероятность ошибки является не значимой; поэтому значения переменной достаточно хорошо подчиняются нормальному распределению.
5.gif
14.6 Отдельный тест по критерию хи-квадрат
14.6 Отдельный тест по критерию хи-квадрат
С помощью этого теста проверяют, насколько значительно отличаются друг от друга наблюдаемые и ожидаемые частоты переменных, относящихся к номинальной шкале. Как правило, при этом ожидаемая частота подчиняется равномерному распределения; однако в SPSS существует возможность задать соответствующие пропорции.
Одним из примеров ожидаемого равномерного распределения частот являются кости. Предположим, Вы бросили один игральную кость 3000 раз и получили следующее частоты для выпавших очков.
Число очков | Частота | Число очков | Частота |
1 | 511 | 4 | 498 |
2 | 472 | 5 | 513 |
3 | 572 | 6 | 434 |
Исходя из предположения об идеальности игральную кость (равной вероятности выпадения любого числа очков), ожидаемая частота для каждого из выпавших чисел составит 3000 / 6 = 500. Необходимо проверить, значимо ли отличаются наблюдаемые частоты от ожидаемых. Данные, а именно переменные augen (число очков) и n (частота), находятся в файле wuerfel.sav. Последнюю переменную следует применить в качестве весовой переменной.
-
Откройте файл wuerfel.sav.
-
Сначала выберите в меню Data (Данные) Weight Case (Взвесить наблюдения)
-
Переменную n объявите частотной (см. гл. 8.7), выберите в меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) Chi-Square (Хи-квадрат) Откроется диалоговое окно Chi-Square Test (Тест хи-квадрат) (см. рис. 14.6).
-
Перенесите переменную augen в поле тестируемых переменных.
Если Вы, как в рассматриваемом примере, хотите подвергнуть анализу все категории тестируемых переменных, то оставьте в разделе Expected range (Ожидаемый диапазон) включённой опцию Get from Data (Из исходных данных); в противном случае у Вас есть возможность ограничить вовлекаемые категории посредством ввода нижней и верхней границ. Так как ожидаемые частоты одинаковы для всех категорий (была принята гипотеза о равномерном распределении), то эта предварительная установка остаётся в силе.
После нажатия кнопки Опции... у Вас появится возможность организовать вывод характеристик дескриптивной статистики и квартилей (что в данном случае является абсолютно бессмысленным).
-
Запустите расчёт путём нажатия ОК.
В окне просмотра появятся следующие результаты:
Augenzahl (Число очков)
Observed N (Наблюдаемое N) | Expected N (Ожидаемое N) | Residuals (остатки) | |
1 | 511 | 500,0 | 11,0 |
2 | 472 | 500,0 | -28,0 |
3 | 572 | 500,0 | 72,0 |
4 | 498 | 500,0 | -2,0 |
5 | 513 | 500,0 | 13,0 |
6 | 434 | 500,0 | -66,0 |
Total (Сумма) | 3000 |
Test Statistics (Статистика теста)
Augenzahl (Число) | |
Chi-Square (Хи-квадрат) а | 21,236 |
Df | 5 |
Asymp. Sig. (Статистическая значимость) | ,001 |
a. 0 cells (,0%) have expected frequencies less than 5. The minimum expected cell frequency is 500,0. (В 0 ячеек (,0%) ожидаемая частота имеет значение менее 5. Минимальная ожидаемая частота в одной ячейке равна 500,0.)
Получилось очень значимое значение критерия хи-квадрат (р = 0,001). В рассматриваемом случае желателен вывод не абсолютных, а стандартизированных остатков, определяемых по формуле:
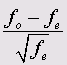
Рис. 14.6: Диалоговое окно СЫ-Square Test (Хи-квадрат-тест)
(см. гл. 11.1). При помощи основополагающего правила, приведенного в главе 8.7.2, можно точно определить те категории, для которых наблюдается значительное отклонение наблюдаемых частот от ожидаемых:
Стандартизированные остатки >= 2,0 указывают на значительное, >= 2,6 на очень значительное и >= 3,3 на сверх значительное отклонение. Если следовать этому правилу, то в экспериментах с игральной костью наблюдается очень значимое превышение количества выпадений 3 очков и очень, очень значимое занижение количества выпадений 6 очков.
Во втором примере, который принадлежит к области ботаники, нужно проверить не равномерное распределение, а наличие распределения подчиняющегося заданному соотношению.
Потомки трёх сортов бобовой культуры были разделены на три типа, которые находятся в соотношении между собой как 1:2:1. Во время некоторого эксперимента, проведенного с сотней таких потомков тип 1 появился 29 раз, тип 2 — 44 раза и тип 3 — 27 раз. Необходимо исследовать значительно ли отклоняется полученное распределение от теоретического распределения 1:2:1.
Данные находятся в файле bohnen.sav, причём переменная typ соответствует типу, а переменная n частоте.
-
Откройте файл bohnen.sav.
-
Сначала действуйте так же, как в первом примере, и взвесьте наблюдения с частотной переменной n.
-
В диалоговом окне Chi-Square Test (тест Хи-квадрат) присвойте переменной typ статус тестируемой переменной.
-
В поле Expected values (Ожидаемые значения) активируйте в этот раз опцию Values (Значения). Введите числа 1, 2 и 1 в предусмотренное для этого поле, и щёлкните дополнительно на кнопке Add (Добавить).
-
Запустите расчёт путём нажатия ОК. В окне просмотра появятся следующие результаты:
Тур (Тип)
Observed N (Наблюдаемое N) | Expected N (Ожидаемое N ) | Residual (Остаток) | |
1 | 29 | 25,0 | 4,0 |
2 | 44 | 50,0 | -6,0 |
3 | 27 | 25,0 | 2,0 |
Total (Сумма) | 100 |
Test Statistics (Статистика теста)
Тур (Тип) | |
Chi-Square (Хи-квадрат) а | 1,520 |
Of | 2 |
Asymp. Sig. (Статистическая значимость) | ,468 |
а. 0 cells (,0%) have expected frequencies less than 5. The minimum expected cell frequency is 25,0. (В 0 ячеек (,0%) ожидаемая частота имеет значение менее 5. Минимальная ожидаемая частота в одной ячейке равна 25,0.)
Ожидаемые частоты выстроены в соответствии с заданным соотношением. На сей раз значимого отклонения наблюдаемых частот от ожидаемых не наблюдается (р = 0,468).
6.gif
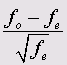
7.gif
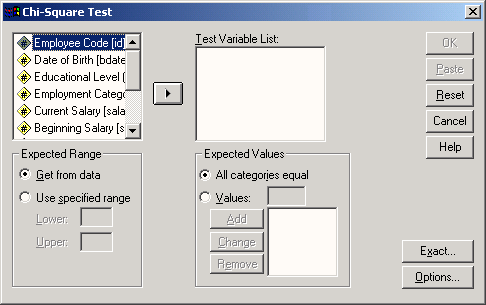
14.7 Биномиальный тест
14.7 Биномиальный тест
Этот тест проверяет дихотомические переменные на наличие различия между частотами обоих проявлений признака. Недихотомические переменные могут быть диэтомизированы (разделены на две категории) при помощи задания некоторой разделительной величины.
Представьте себе, что Вы играете со своим партнёром по теннису 50 матчей и выигрываете 29. Ваш партнёр, выигравший 21 раз, думает, что Вы ничем не лучше, а эта разница является случайной.
Чтобы это проверить можно выполнить биномиальный тест.
-
Откройте файл match.sav, содержащий две переменные: spieler и n.
Первая переменная имеет кодировки 1 и 2, которые соответствуют двум игрокам. Переменная n указывает на частоту выигрыша; ей присваивается статус весовой переменной.
-
Сначала выберите в меню Data (Данные) Weight Cases (Взвесить наблюдения)
-
Укажите переменную п как частотную переменную (см. гл. 8.7).
-
Затем выберите в меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) Binomial (Биномиальное распределение)
Откроется диалоговое окно Binomial Test (Тест на биномиальное распределение) см. рис. 14. 7.
-
Перенесите щелчком переменную spieler в поле тестируемых переменных.
Если бы эта переменная не была дихотомической, Вы бы могли в поле Определить дихотомию (Define Dichotomy) ввести разделительную величину для проведения раздвоения (дихотомизации). Предварительно установленная тестовая пропорция (0,50) показывает на ожидаемую относительную частоту появления первой из двух дихотомических категорий. Здесь Вы можете задать и другое значение. После нажатия кнопки Options... (Опции) Вы можете организовать вывод (абсолютно бессмысленных) характеристик дескриптивной статистики.
-
Запустите расчёт путём нажатия ОК.
В окне просмотра появятся следующие результаты:
Binomial Test (Тест на биномиальное распределение)
Category (Категория) | N | Observed Prop. (Наблюда- емая пропорция) | Test Prop. (Тестовая пропорция) | Asymp. Sig. (2-tailed) (Статисти- ческая значимость (2-сторонняя)) | ||
SPIELER (Игрок) | Группа 1 | 1 | 29 | ,58 | ,50 | ,322а |
Группа 2 | 2 | 21 | ,42 |
|
| |
Total (Сумма) |
| 50 | 1,00 |
|
| |
a. Based on Z Approximation. (Основываясь на Z-аппроксимации.)
Рис. 14.7: Диалоговое окно Тест на биномиальное распределение
В выводимые результаты включают наблюдаемые абсолютные и относительные частоты обеих категорий, а так же ожидаемую относительную частоту первой категории Полученная вероятность ошибки (р = 0,322) говорит о том, что между наблюдаемой и ожидаемой относительными частотами не существует значимого различия. Стало быть и разница между обеими частотами выигрыша не является значимой.
8.gif
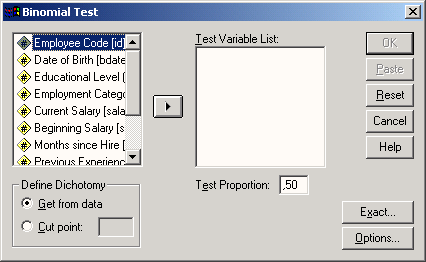
14.8 Анализ последовательностей
14.8 Анализ последовательностей
При проверке последовательности дихотомических значений переменной выясняется следующий вопрос: идёт ли речь о случайном ряде или ряд построен в соответствии с определённой закономерностью.
В качестве примера рассмотрим три различные очереди людей, стоящих у кассы кинотеатра, учитывая пол.
1. Очередь: мжмжмжмжмжмжмжмжмжмж
2. Очередь: жмжммжжммжмжмжжмжммж
3. Очередь: мжжжжммммжжжжмжжмжмж
В первой очереди можно заметить явную закономерность, т.к. посетители стоят всегда по парам, при чём мужчина всегда стоит впереди. Во второй очереди, также просматривается попарный рисунок, хотя очерёдность мужчин и женщин меняется Третья очередь была выстроена генератором случайных чисел. Для первой очереди следует ожидать значительное отклонение от случайной последовательности, для второй очереди скорее всего так же, а для третьей нет.
Данные рассматриваемого примера соответствуют трем переменными rl, r2 и r3 в файле kino.sav. Мужчинам присвоен код 0, а женщинам 1.
-
Откройте файл kino.sav.
-
Выберите в меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) Runs (Последовательности) Появится диалоговое окно Runs Test (Критерий серий) см. рис. 14.8.
-
Перенесите переменные rl, г2 и гЗ в поле тестируемых переменных.
Рис. 14.8: Диалоговое окно Runs Test (Тест для последовательностей)
-
Для дихотомических переменных, закодированных при помощи 0 и 1, как в рассматриваемом примере, активируйте в поле Cut Point (Разделительная величина) опцию Custom (Пользовательская) и введите значение 1.
-
Запустите расчёт путём нажатия ОК.
В окне просмотра появятся следующие результаты.
Runs Test (Критерий серий)
Test Value (Проверяемое значение) " | R1 1 | R2 1 | R3 1 |
Total Cases (Общее количество случаев) | 20 | 20 | 20 |
Number of Runs (Количество последовательностей) | 20 | 15 | 10 |
Z | 3,905 | 1,608 | -,048 |
Asymp. Sig. (2-tailed) (Статистическая значимость (2-сторонняя)) | ,000 | ,108 | ,962 |
а. User-specified. (Определяется пользователем) | |||
Вычисленные программой значения р соответствуют ожиданиям.
9.gif
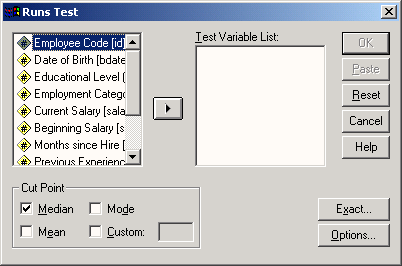
Глава 15. Корреляции
Глава 15. Корреляции
1. Корреляции
Корреляции
В этой главе речь пойдёт о связи (корреляции) между двумя переменными. Расчёты подобных двумерных критериев взаимосвязи основываются на формировании парных значений, которые образовываются из рассматриваемых зависимых выборок.
Если в качестве примера мы возьмём данные об уровне холестерина для первых двух моментов времени из исследования гипертонии (файл hyper.sav), то в данном случае следует ожидать довольно сильную связь: большие значения в исходный момент времени являются веским поводом для ожидания больших значений и через 1 месяц.
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая; пара значений маркируется при помощи определенного символа. Такой график, называемый «диаграммой рассеяния» для двух зависимых переменных можно построить путём вызова меню Graphs... (Графики) Scatter plots... (Диаграммы рассеяния) (см. гл. 22.8).
Образовавшееся скопление точек показывает, что обследованные пациенты с высокими исходными показателями, как правило, имеют высокие значения холестерина и при повторном опросе через месяц. Это, конечно же, не является неожиданностью; данный пример был выбран, чтобы продемонстрировать наличие явной связи.
Статистик говорит о корреляции между двумя переменными и указывает силу связи при помощи некоторого критерия взаимосвязи, который получил название коэффициента корреляции. Этот коэффициент, всегда обозначаемый латинской буквой г, может принимать значения между -1 и +1, причём если значение находится ближе к 1, то это означает наличие сильной связи, а если ближе к 0, то слабой.
Рис. 15.1.Диаграммы рассеяния
Если коэффициент корреляции отрицательный, это означает наличие противоположной связи: чем выше значение одной переменной, тем ниже значение другой. Сила связи характеризуется также и абсолютной величиной коэффициента корреляции. Для словесного описания величины коэффициента корреляции используются следуюшие градации:
Значение | Интерпретация |
до 0,2 | Очень слабая корреляция |
до 0,5 | Слабая корреляция |
до 0,7 | Средняя корреляция |
до 0,9 | Высокая корреляция |
свыше 0,9 | Очень высокая корреляция |
Метод вычисления коэффициента корреляции зависит от вида шкалы, которой относятся переменные.
-
Переменные с интервальной и с номинальной шкалой: коэффициент корреляции Пирсона (корреляция моментов произведений).
-
По меньшей мере, одна из двух переменных имеет порядковую шкалу либо не является нормально распределённой: ранговая корреляция по Спирману или т (тау-грого-соая) Кендала.
-
Одна из двух переменных является дихотомической: точечная двухрядная корреляция. Эта возможность в SPSS отсутствует. Вместо этого может быть применён расчёт ранговой корреляции.
-
Обе переменные являются дихотомическими: четырёхполевая корреляция. Данный вид корреляции рассчитываются в SPSS на основании определения мер расстояния и мер сходства (см. гл 15.4).
Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена). Если связь, к примеру, U-образная (неоднозначная), то коэффициент корреляции непригоден для использования в качестве меры силы связи: его значение стремится к нулю. В следующих разделах будут рассмотрены корреляции по Пирсону, Спирману и Кендалу. Ешё один раздел специально посвящён частной корреляции.
1.gif
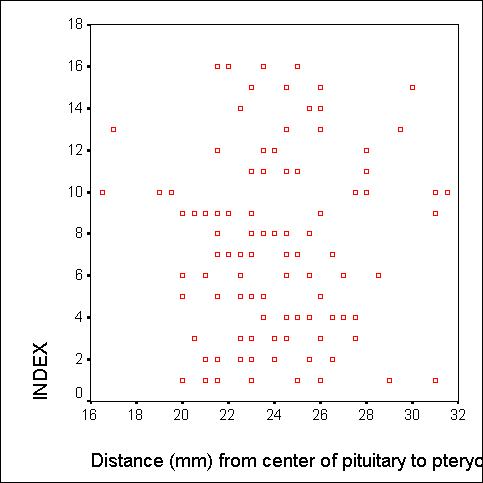
15.1 Коэффициент корреляции Пирсона
15.1 Коэффициент корреляции Пирсона
Данный коэффициент вычисляется по следующей формуле:
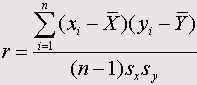
где xi и уi значения двух переменных, х- и у- их средние значения, a sx и sy их стандартные отклонения; n количество пар значений.
На основании данных исследования гипертонии нам нужно рассчитать коэффициент корреляции по Пирсону попарно для переменных cho10, cho11, cho!6 и chol12 (то есть сформировать для этих переменных корреляционную матрицу).
-
Откройте файл hyper.sav.
-
Выберите в меню Analyze... (Анализ) Correlate... (Корреляция) Bivariate... (Парные) Появится диалоговое окно Bivariate Correlations (Парные корреляции) (см. рис. 15.21.)
-
Переменные cho10, cho11, cho16 и chol12 перенесите по очереди в поле тести-! руемых переменных. Расчёт коэффициента корреляции по Пирсону является' предварительной установкой, также как двусторонняя проверка значимости и маркировка значимых корреляций.
-
Начните расчёт путём нажатия кнопки ОК.
В окне просмотра появятся следующие результаты:
Correlations (Корреляции)
Cholesterin, Ausga- ngswert (Холесте- рин, исходная величина) | Cholesterin, nach 1 Monat (Холесте- рин, через 1 месяц) | Cholesterin, nach 6 Monaten (Холесте- рин, через 6 месяцев) | Cholesterin, nach 12 Monaten (Холесте- рин, через 12 месяцев) | ||
Cholesterin, Ausga- ngswert (Холестерин, исходная величина) | Pearson Correlation (Корреляция по Пирсону) Sig. (2-tailed) (Значимость (2-сторонняя)) N | 1,000 174 | ,861" ,000 174 | ,775" ,000 174 | ,802" ,000 174 |
Cholesterin, nach 1 Monat (Холесте- рин, через 1 месяц) | Pearson Correlation (Корреляция по Пирсону) Sig. (2-tailed) (Значимость (2-сторонняя)) N | ,861" ,000 174 | 1,000 174 | ,852" ,000 174 | ,813" ,000 174 |
Cholesterin, nach 6 Monaten (Холесте-рин, через 6 месяцев) | Pearson Correlation (Корреляция по Пирсону) Sig. (2-tailed) (Значимость (2-сторонняя)) N | ,775" ,000 174 | ,852" ,000 174 | 1,000 174 | ,892" ,000 174 |
Cholesterin, nach 12 Monaten (Холесте- рин, через 12 месяцев) | Pearson Correlation (Корреляция по Пирсону) Sig. (2-tailed) (Значимость (2-сторонняя)) N | ,802" ,000 174 | ,813" ,000 174 | ,892" ,000 174 | 1,000 174 |
** Correlation is significant at the 0.01 level (2-tailed). (Корреляция является значимой на уровне 0,01 (2-стороння)).
Рис. 15.2: Диалоговое окно Bivariate Correlations (Двумерные корреляции)
Полученные результаты содержат: корреляционный коэффициент Пирсона r, количество использованных пар значений переменных и вероятность ошибки р, соответствующая предположению о ненулевой корреляции. В приведенном примере присутствует сильная корреляция, поэтому все коэффициенты конечно же являются сверхзначимыми (р < 0,001). Следовательно, маркировка корреляции, приведенная :-низу таблицы, должна была бы состоять из трёх звёздочек, которыми обозначается уровень р=0,001.
При помощи щелчка на кнопке Options... (Опции) можно организовать расчёт среднего значения и стандартного отклонения для двух переменных. Дополнительно могут выводиться отклонения произведений моментов (значений числителя формулы для коэффициента корреляции) и элементы ковариационной матрицы (числитель, делённый на n - 1).
2.gif
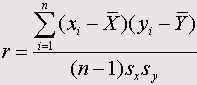
3.gif

15.2 Ранговые коэффициенты корреляции по Спирману и Кендалу
15.2 Ранговые коэффициенты корреляции по Спирману и Кендалу
Для переменных, принадлежащих к порядковой шкале или для переменных, не подчиняющихся нормальному распределению, а также для переменных принадлежащих к интервальной шкале, вместо коэффициента Пирсона рассчитывается ранговая корреляция по Спирману. Для этого отдельным значениям переменных присваиваются ранговые места, которые впоследствии обрабатываются с помощью соответствующих формул. Чтобы выявить ранговую корреляцию, уберите в диалоговом окне Bivariate Correlations... (Парные корреляции) метку для расчета корреляции по Пирсону, установленную по умолчанию. Вместо этого активируйте расчет корреляции Спирмана. Это расчет даст следующие результаты (см. стр. 260).
Коэффициенты ранговой корреляции весьма близки к соответствующим значениям коэффициентов Пирсона (исходные переменные имеют нормальное распределение). Ещё одним вариантом ранговых коэффициентов корреляции являются коэффициенты Кендала (tb Кендала), расчет которых можно вызвать в диалоговом окне Bivariate Correlations... (Парные корреляции). В этом методе одна переменная представляется в виде монотонной последовательности в порядке возрастания величин; другой переменной присваиваются соответствующие ранговые места. Количество инверсий (нарушений монотонности по сравнению с первым рядом) используется в формуле для корреляционных коэффициентов. Применение коэффициента Кендала является предпочтительным, если в исходных данных встречаются выбросы.
Correlations (Корреляции)
Chole- sterin, Ausgan-gswert (Холе-стерин, исходная величина) | Chole-sterin, nach 1 Monat (Холе-стерин, через 1 месяц) | Chole-sterin, nach 6 Monaten (Холе-стерин, через 6 месяцев) | Chole- sterin, nach 12 Monaten (Холе-стерин, через 12 месяцев) | |||
Spearman's rho (рСпир-мана) | Chole-sterin, Ausgang-swert (Холес-терин, исходная величина) | Correlation Coefficient (Коэф- фициент корре- ляции) Sig. (2-tailed) (Значимость (2-сторонняя)) N | 1,000 174 | ,877" ,000 174 | ,791" ,000 174 | ,792"! ,000 174 |
Chole-sterin, nach 1 Monat (Холес-терин, через 1 месяц) | Correlation Coefficient (Коэф- фициент корре- ляции) Sig. (2-tailed) (Значимость (2-сторонняя)) N | ,877" ,000 174 | 1,000 174 | ,874** ,000 174 | ,834" ,000 174 | |
Chole-sterin, nach 6 Monaten (Холес-терин, через 6 месяцев) | Correlation Coefficient (Коэф- фициент корр-еляции) Sig. (2-tailed) (Значимость (2-сторонняя)) N | ,791** ,000 174 | ,874** ,000 174 | 1,000 174 | ,879" ,000 174 | |
Choles-terin, nach 12 Monaten (Холес-терин, через 12 месяцев) | Correlation Coefficient (Коэф- фициент корре- ляции) Sig. (2-tailed) (Значимость (2-сторонняя)) N | ,792** ,000 174 | .834" ,000 174 | ,879" ,000 174 | 1,000 174 | |
** Correlation is significant at the .01 level (2-tailed). (Корреляция является значимой на уровне 0,01 (2-сгороння)).
Если рассчитать корреляционную матрицу Кендала, то станет заметно, что в данном случае коэффициенты значительно ниже корреляционных коэффициентов Спирмана.
15.3 Частная корреляция
15.3 Частная корреляция
Если исследовать достаточно большую совокупность мужчин и сопоставить размер их обуви с уровнем образованности, то между этими двумя переменными можно заметить хоть и небольшую, но в то же время значимую корреляцию. Это корреляция может послужить примером так называемой ложной корреляции. Здесь статистически значимый коэффициент корреляции является не проявлением некоторой причинной связи между двумя рассматриваемыми переменными, а в большей степени обусловлен некоторой третьей переменной.
В рассматриваемом примере такой переменной является рост. С одной стороны существует некоторая незначительная корреляция между ростом и уровнем образованности, а с другой — вполне объяснимая и логичная связь между ростом и размером обуви. Вместе эти две корреляции приводят к упоминавшейся ложной корреляции. Для исключения одной такой искажающей переменной необходим расчёт так называемой частной корреляции.
Если присвоить коррелирующим переменным индексы 1 и 2, а искажающей переменной — индекс 3, и попарно рассчитать корреляционный коэффициент (Пирсона) r12,r13, и r23 , то для частных корреляционных коэффициентов получим:
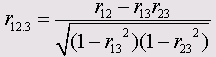
Достаточно давно в социологических исследованиях, проводимых в Германии, выяснялось отношение населения к приезжим рабочим-иностранцам. Для этого было сформулировано несколько отдельных вопросов. Ответы на вопросы суммировались. Сумма могла принимать значения от 0 до 30, причём большее значение соответствует более негативному отношению к приезжим рабочим.
Среди многочисленных дополнительных переменных учитывались: возраст опрашиваемых и частота посещения церкви. Последней характеристике были присвоены значения от 1 (никогда) до 6 (по меньшей мере, 2 раза в неделю). Небольшая выборка из оригинальных данных опроса (35 респондентов с этими тремя переменными) наводится в файле kirche.sav. Откройте этот файл, если Вы хотите самостоятельно провести следующие расчёты.
Если подсчитать корреляции между этими тремя переменными, то при выборе коэффициентов Пирсона для анализа взаимосвязи, получатся следующие результаты закроем глаза на то, что одна из переменных, а именно частота посещения церкви, имеет порядковую шкалу):
Correlations (Корреляции)
ALTER (Возраст) | GAST (Приезжий) | KIRCHE (Церковь) | ||
ALTER (Возраст) | Pearson Correlation (Корреляция по Пирсону) Sig. (2-tailed) (Значимость (2-сторонняя)) N | 1,000 35 | ,468" ,005 35 | ,779" ,000 35 |
GAST (Приезжий) | Pearson Correlation (Корреляция по Пирсону) Sig. (2-tailed) (Значимость (2-сторонняя)) N | ,468" ,005 35 | 1,000 35 | ,432** ,010 35 |
KIRCHE (Церковь) | Pearson Correlation (Корреляция по Пирсону) Sig. (2-tailed) (Значимость (2-сторонняя)) N | ,779" ,000 35 | ,432" ,010 35 | 1,000 35 |
"* Correlation is significant at the .01 level (2-tailed). Корреляция является закономерной на уровне 0,01 (2-стороння).
Принимая во внимание полярность, полученные результаты можно трактовать, к примеру, таким образом, что частые посещения церкви коррелируют с отрицательным отношением к приезжим рабочим (r = 0,432). Прежде, чем поставить в упрёк церкви враждебность по отношению к иностранцам, нужно учесть влияние возраста. Он также коррелирует с враждебным отношением к иностранным рабочим (r = 0,468) и сильно коррелирует с частотой посещения церкви (r = 0.779). Таким образом, возникает подозрение, что возраст является искажающим признаком, виновным в ложной корреляции между частотой посещения церкви и отрицательным отношением к иностранным рабочим. Докажем это путём расчёта частных корреляционных коэффициентов.
-
Откройте файл kirche.sav.
-
Выберите в меню Analyse... (Анализ) Correlate... (Корреляция) Partial... (Частная)
Откроется диалоговое окно Partial Correlations (Частные корреляции).
-
Перенесите переменные gast и kirche в поле признаков, а переменную alter в поле контрольных переменных и оставьте предварительную установку для двухстороннего теста значимости.
При помощи щелчка на кнопке Options... (Опции) наряду с традиционной обработкой пропущенных значений, Вы можете организовать расчёт среднего значения, стандартного отклонения и вывод «корреляций нулевого порядка» (то есть простых корреляционных коэффициентов).
В случае одной искажающей переменной, как в приведенном примере, возможен расчёт частной корреляции первого порядка, при наличии нескольких искажающих переменных, SPSS выдаёт корреляции высших порядков.
-
Начните расчёт щелчком на кнопке ОК. Вязкие просмотра появится следующий результат:
Partial correlation coefficients (Частичные корреляционные коэффициенты) | ||
Controlling for... A (Контрольная переменная) ( | LTER Возраст) | |
GAST (Приезжий) | GAST ( Приезжий)
1,0000 ( 0) P= , | KIRCHE (Церковь) ,1215 ( 32) P= ,494 |
KIRCHE (Церковь) | ,1215 ( 32) P= ,494 | 1,0000 ( 0) P= , |
Вас, возможно, удивит, что в данном случае всё ещё выводится старый вариант таблицы результатов, соответствующий прежним версиям SPSS. Результаты включают: частный корреляционный коэффициент, число степеней свободы (число наблюдений минус 3) и уровень значимости. Исходя из полученных результатов, можно сделать вывод, что при исключении искажающей переменной alter больше не наблюдается существенной корреляции между частотой посещения церкви и отрицательным отношением к иностранным рабочим.
Рис. 15.3: Диалоговое окно Partial Correlations (Частичные корреляции)
4.gif
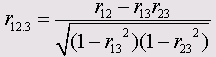
5.gif
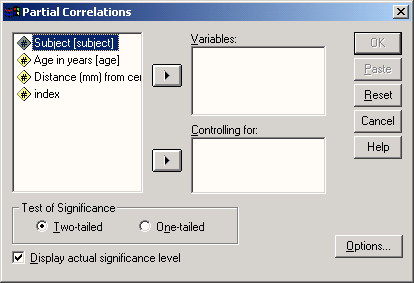
15.4 Мера расстояния и мера сходства
15.4 Мера расстояния и мера сходства
Наряду с приведенными корреляционными коэффициентами, SPSS дополнительно предлагает расчет ряда мер расстояния и мер сходства. Так, к примеру, реализован расчет многочисленных мер сходства при анализе взаимосвязи между дихотомическими переменными. Некоторые статистические процедуры, такие как факторный анализ, кластерный анализ, многомерное масштабирование, построены на применении этих мер, а иногда сами представляют добавочные возможности для вычисления 1 ер подобия. Если Вы во время выполнения этих процедур захотите использовать какую-либо меру, не предусмотренную в выбранной процедуре, то Вам следует воспользоваться дополнительными возможностями, предоставляемыми SPSS.
В качестве примера возьмем анкету, которая будет рассматриваться в главе 21. Она посвящена исследованию степени любознательности опрашиваемых.
-
Откройте файл neugier.sav.
-
Выберите в меню Analyze... (Анализ) Correlate... (Корреляция) Distances... (Расстояния)
Появится диалоговое окно Distances... (Расстояния).
В этом диалоговом окне Вы можете организовать расчет расстояния между наблюдениями или между переменными, а также выбрать тип рассчитываемой меры мера отличия или мера подобия). Щелчком на кнопке Measures... (Меры) можно выбрать формулу вычисления меры расстояния для интервальных или дихотомических (бинарных) переменных. В основу расчета мер отличия могут быть также положены и частоты.
Все меры отличия и сходства для переменных, принадлежащих к интервальной шкале, будут рассмотрены в главе 20.3. Эти меры являются важным элементом кластерного анализа. Ниже приведены формулы для мер сходства между бинарными (дихотомическими) переменными, принадлежащими к интервальной шкале. Символами а, b, с и d обозначены частоты, находящиеся в ячейках таблицы 2x2 (четырёхполевой таблицы). В случае необходимости, более подробное объяснение этих формул Вы найдёте в главе 20.3.3.
Рис. 15.4: Диалоговое окно Distances... (Расстояния).
Рассел и Рао (Russel and Rao)
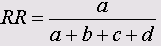
Простое согласование
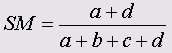
Джаккард (Jaccard)
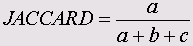
Игральная кость
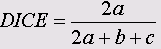
Роджерс и Танимото (Rogers and Tanimoto)
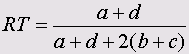
Соукал и Снис 1 (Sokal and Sneath)
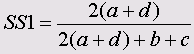
Соукал и Снис 2
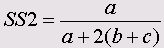
Соукал и Снис 3

Кульчинский 1 (Kulczynski)
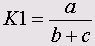
Кульчинский 2
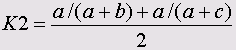
Соукал и Снис 4
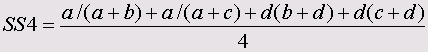
Хаманн (Hamann)
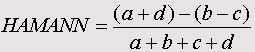
Лямбда
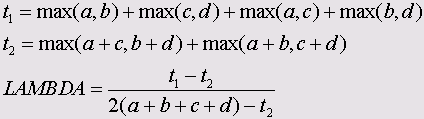
D Андерберга (Anderberg)
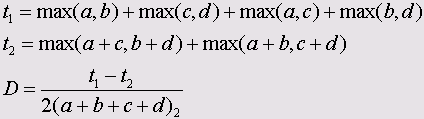
YtOiBi
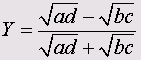
О Юля
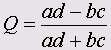
Очиаи lOchiai)
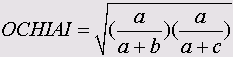
Соукал и Скис 5
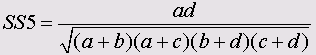
4 точечная ц-корреляция
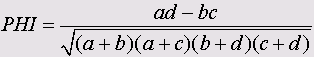
Дисперсия

Два следующих примера помогут нам разобраться в особенностях работы с мерами расстояния.
Пример первый: сходства между дихотомическими переменными.
-
Создайте сначала таблицу сопряженности для переменных item3 и item 14. Эти переменные соответствуют ответам на вопросы «Считаете ли Вы, что развитие космонавтики необходимо?» и соответственно «Согласились бы Вы предоставить себя в распоряжение учёным для научных экспериментов?» (с кодировками 1 = да и 2 = нет).
Частоты в таблице 2x2 распределились следующим образом:
Рис. 15.5: Частоты в таблице 2x2
-
Выберите в меню Analyze... (Анализ) Correlate... (Корреляция) Distances... (Расстояния)
-
Перенесите переменные item3 и item 14 в поле тестируемых переменных.
-
Активируйте расчёт расстояний Between Variables (Между переменными) и в качестве типа меры выберите Similarities... (Подобия).
-
Щёлкните на кнопке Measures... (Меры) и, в открывшемся диалоговом окне, активируйте Binary (Бинарные). Оставьте предварительную установку мер вычисления по методу Рассела и Рао.
-
Так как в приведенном примере отрицательному ответу присвоен код 2, а в предварительных установках предусмотрен 0, то Вам необходимо откорректировать это значение в поле Absent (Отсутствует).
-
Покиньте диалоговое окно мер нажатием Continue (Далее) и в главном диалоговом окне начните расчёт щелчком на ОК.
В результате Вы получите значение меры подобия равное 0,3. Оно определяется как частное от деления частоты а на сумму всех четырёх частот:
Proximity Matrix (Матрица близости)
Russell and Rao Measure (Мера подобия Рассела и Рао) | ||
ITEM3 | ITEM14 | |
ITEM3 ITEM 14 | ,300 | ,300 |
This is a similarity matrix (Это матрица подобия) ;
Пример второй: расчёт корреляционной матрицы 2x2 в качестве базиса для факторного анализа
Мы хотим рассчитать корреляционную матрицу для восемнадцати переменных item1-item18 с применением четырёхточечная корреляция фи. В этом случае корреляционную матрицу можно использовать в качестве базиса для факторного анализа. Для решения этой задачи нам предстоит поработать с программным синтаксисом SPSS.
-
Перенесите переменные item1-item18 в поле тестируемых переменных.
-
Активируйте расчёт расстояний Between Variables (Между переменными) и в качестве типа меры выберите Similarities... (Подобия).
-
Откройте щелчком на кнопке Measures... (Меры) соответствующее диалоговое окно, активируйте в нём Binary (Бинарные) и присвойте параметру Absent (Отсутствует) код 2. В заключении вместо меры по Расселу и Рао выберите 4 точечную µ-корреляцию.
-
При помощи щелчка на Continue (Далее) вернитесь в основное диалоговое окно, после прохождения кнопки Paste... (Вставить) просмотрите синтаксис команд.
-
Внесите в синтаксис следующие корректировки:
PROXIMITIES
item1 item2 item3 item4
item5 item6 item7 item8
item9 item10 item11 item12
Lzem13 item14 item15 item16
item17 item18
VIEW=VARIABLE
MEASURE= PHI (1,2)
MATRIX=OUT(*) .
SSCODE rowtype_ ( "PROX"='CORR') .
FACTOR /MATRIX=IN(COR=*).
-
Начните расчёт при помощи символа Syntax-Start (Синтаксис-Начать).
В окне просмотра появятся результаты факторного анализа, а в окне редактора данных будет показана корреляционная матрица.
6.gif
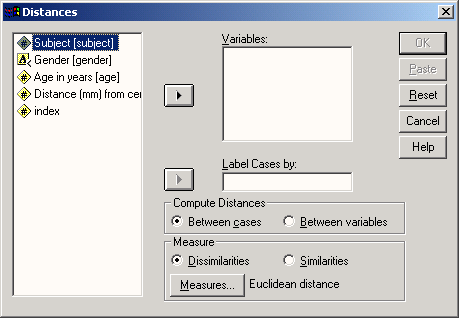
8.gif
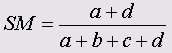
11.gif
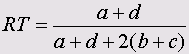
12.gif
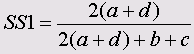
17.gif
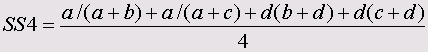
18.gif
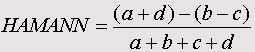
19.gif
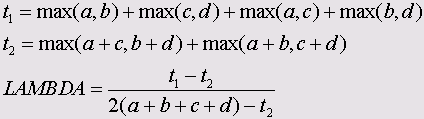
20.gif
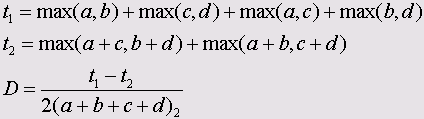
21.gif
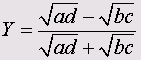
23.gif
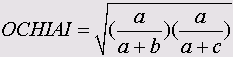
24.gif
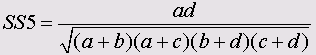
25.gif
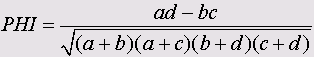
26.gif

27.gif

15.5 Внутриклассовый коэффициент корреляции (Intraclass Correlation Coefficient (ICC))
15.5 Внутриклассовый коэффициент корреляции (Intraclass Correlation Coefficient (ICC))
Внутриклассовый коэффициент корреляции (ICC) со значениями, находящимися в диапазоне между -1 и +1, применяется в качестве меры связанности в том случае, когда согласованность двух признаков должна быть проверена не так, как при расчете рассмотренных выше корреляционных коэффициентов, относительно её общей направленности ("чем больше одна переменная, тем больше вторая"), а также и относительно средних уровней обеих переменных. Таким образом, расчёт ICC считается уместным только тогда, когда обе переменные имеют приблизительно одинаковый уровень значений. Подобная ситуация вероятнее всего возникнет в случае, когда одной и той же величине дается двоякая оценка.
ICC играет также важную роль при анализе достоверности (гл. 21), где он применяется в качестве меры достоверности. При его расчёте используется более двух переменных, называемых в данном случае объектами. В связи с этим расчёт ICC в SPSS производится в рамках анализа достоверности.
Рассмотрим расчёт ICC на данных одного типичного примера.
-
Откройте файл alter.sav.
В файле находятся три переменные: a, agesch и agesch10. Переменной а обозначен фактический возраст респондентов, agesch — возраст по оценке со стороны. Переменная agesch10 соответствует возрасту по оценке со стороны минус 10 лет.
Если Вы произведёте расчёт корреляционных коэффициентов Пирсона (см. гл. 15.1) для переменных а и agesch, то получите значение г = 0,944. Такое же значение Вы получите при расчёте корреляции между переменными а и agesch2, так как соотношение между обоими переменными не изменилось.
Определим теперь ICC.
-
Выберите в меню Analyze... (Анализ) Scale... (Масштабировать) Reliability Analysis... (Анализ пригодности)
-
Перенесите обе переменные а и agesch в список объектов.
-
Через кнопку Statistics... (Статистика), активируйте опцию Intraclass Correlation Coefficient (Корреляционный коэффициент внутри классов).
-
В качестве модели выберите One-Way Random (Однократно, случайно), которая соответствует традиционному расчёту ICC.
-
Оставьте предварительно установленный 95 % доверительный интервал и подтвердите нажатием Continue (Далее) и ОК.
В окне просмотра появятся следующие результаты:
RELIABILITY ANALYSIS - SCALE (ALPHA)
Intraclass Correlation Coefficient
One-way random effect model: People Effect Random
Single Measure Intraclass Correlation = ,9367
95,00% C.I.: Lower = Л9156 Upper = ,9526
F = 30,5740 DF = ( 173, 174,0)
Sig. = ,0000 (Test Value = ,0000 )
Average Measure Intraclass Correlation = , 9673
95,00% C.I.: Lower = ,9559 Upper = ,9757
F = 30,5740 DF = ( 173, 174,0)
Sig. = ,0000 (Test Value = ,0000 )
Reliability Coefficients
N of Cases = 174,0 N of Items = 2
Alpha = ,9680
Результаты обычного расчёта ICC Вы найдёте под заголовком «Single Measure Intraclass Correlation». Вы получите значение ICC = 0,9367, которое с 95 %-м доверительным интервалом принадлежит к диапазону от 0,9156 до 0,9526. Это значение весьма близко к корреляционным коэффициентам Пирсона.
-
Повторите теперь расчёт для переменных а и agesch10.
В последней переменной из сторонней оценки возраста вычитается постоянная величина. Так как обе переменные теперь имеют различные уровни, то ICC теперь показывает заметно более низкое значение: ICC = 0,6957.
Ещё одним типичным случаем для применения расчёта ICC является определение связей между фактическим весом и весом по оценке со стороны или фактическим и оценочным ростом.
Глава 16. Регрессионный анализ
Глава 16. Регрессионный анализ
1. Регрессионный анализ
Регрессионный анализ
Если расчёт корреляции характеризует силу связи между двумя переменными, то регрессионный анализ служит для определения вида этой связи и дает возможность для прогнозирования значения одной (зависимой) переменной отталкиваясь от значения другой (независимой) переменной.
-
Чтобы вызвать регрессионный анализ в SPSS, выберите в меню Analyze... (Анализ) Regression... (Регрессия)
Откроется соответствующее подменю.
Разделы этой главы соответствуют опциям вспомогательного меню. Причём при изучении линейного регрессионного анализа снова будут проведено различие между простым анализом (одна независимая переменная) и множественным анализом (несколько независимых переменных). Собственно говоря, никаких принципиальных отличий между этими видами регрессии нет, однако простая линейная регрессия является простейшей и применяется чаще всех остальных видов.
Рис. 16.1: Вспомогательное меню Regression (Регрессия)
Для проведения линейного регрессионного анализа зависимая переменная должна иметь интервальную (или порядковую) шкалу. В то же время, бинарная логистическая регрессия выявляет зависимость дихотомической переменной от некой другой переменной, относящейся к любой шкале. Те же условия применения справедливы и для пробит-анализа. Если зависимая переменная является категориальной, но имеет более двух категорий, то здесь подходящим методом будет мультиномиальная логистическая регрессия. Новшеством в 10 версии SPSS является порядковая регрессия, которую можно использовать, когда зависимые переменные относятся к порядковой шкале. И, наконец, можно анализировать и нелинейные связи между переменными, которые относятся к интервальной шкале. Для этого предназначен метод нелинейной регрессии.
Методы криволинейного приближения, весовые оценки и 2-ступенчатые наименьшие квадраты исследуют соответственно приближённость пути прохождения кривых при помощи компенсационных кривых, регрессионный анализ для изменяющейся дисперсии и проблемы из области эконометрии.
1.gif

16.1 Простая линейная регрессия
16.1 Простая линейная регрессия
Этот вид регрессии лучше всего подходит для того, чтобы продемонстрировать основополагающие принципы регрессионного анализа. Рассмотрим для этого диаграмму рассеяния из главы 15.1, которая иллюстрирует зависимость показателя холестерина спустя один месяц после начала лечения от исходного показателя, полученную при исследовании гипертонии. Можно легко заметить очевидную связь: обе переменные развиваются в одном направлении и множество точек, соответствующих наблюдаемым значениям показателей, явно концентрируется (за некоторыми исключениями) вблизи прямой (прямой регрессии). В таком случае говорят о линейной связи.
у=b*х + а
где b — регрессионные коэффициенты, a — смещение по оси ординат.
Смещение по оси ординат соответствует точке на оси у (вертикальной оси), где прямая регрессии пересекает эту ось. Коэффициент регрессии b через соотношение
b = tg(a) указывает на угол наклона прямой.
При проведении простой линейной регрессии основной задачей является определение параметров b и а. Оптимальным решением этой задачи является такая прямая, для которой сумма квадратов вертикальных расстояний до отдельных точек данных является минимальной.
Если мы рассмотрим показатель холестерина через один месяц (переменная chol1) как зависимую переменную (у), а исходную величину как независимую переменную (х), то тогда для проведения регрессионного анализа нужно будет определить параметры соотношения
chol1 = b-chol0 + a
После определения этих параметров, зная исходный показатель холестерина, можно спрогнозировать показатель, который будет через один месяц.
16.1.1 Расчёт уравнения регрессии
16.1.1 Расчёт уравнения регрессии
Откройте файл hyper.sav.
-
Выберите в меню Analyze... (Анализ) Regression...(Регрессия) Linear... (Линейная) Появится диалоговое окно Linear Regression (Линейная регрессия).
-
Перенесите переменную chol1 в поле для зависимых переменных и присвойте переменной chol0 статус независимой переменной.
-
Ничего больше не меняя, начните расчёт нажатием ОК.
Вывод основных результатов выглядит следующим образом:
Model Summary (Сводная таблица по модели)
Model (Модель) | R | R Square (R-квадрат) | Adjusted R Square (Смещенный R-квадрат) | Std. Error of the Estimate (Стандартная ошибка оценки) |
1 | ,861а | ,741 | ,740 | 25,26 |
а. Predictors: (Constant), Cholesterin, Ausgangswert (Влияющие переменные: (константы), холестерин, исходная величина)
ANOVA b
Model (Модель) | Sum of Squares (Сумма Квадратов) | df | Mean Square (Сред-нее значе- ние квадра- та) | F | Sig. (Значи-мость) | |
1 | Regre- ssion (Регре- ссия) | 314337,948 | 1 | 314337,9 | 492,722 | ,000a |
Residual (Остатки) | 109729,408 | 172 | 637,962 | |||
Total (Сумма) | 424067,356 | 173 |
a. Predictors: (Constant), Cholesterin, Ausgangswert (Влияющие переменные: (константа), холестерин, исходная величина)
b. Dependent Variable: Cholesterin, nach 1 Monat (Зависимая переменная холестерин через 1 месяц)
Рис.16.2: Диалоговое окно Линейная регрессия
Coefficients (Коэффициенты) а
Model (Модель) | Unstan- dardized Coefficients (Не стандарти-зированные коэф-фициенты) | Standa-rdized Coef- ficients (Стандарти-зированные коэф- фициенты) | Т | Sig. (Значи-мость) | |||
|
| В | Std: Error (Стандар-тная ошибка) | ß (Beta) | |||
1 | (Constant) (Конста- нта) | 34,546 | 9,416 | 3,669 | ,000 | ||
Choles- terin, Ausga- ngswert (холес- терин, исходная величина) | ,863 | ,039 | ,861 | 22,197 | ,000 | ||
a. Dependent Variable (Зависимая переменная)
Рассмотрим сначала нижнюю часть результатов расчётов. Здесь выводятся коэффициент регрессии b и смещение по оси ординат а под именем "константа". То есть, уравнение регрессии выглядит следующим образом:
chol1 = 0,863-chol0 + 34,546
Если значение исходного показателя холестерина составляет, к примеру, 280, то через один месяц можно ожидать показатель равный 276.
Частные рассчитанных коэффициентов и их стандартная ошибка дают контрольную величину Т; соответственный уровень значимости относится к существованию ненулевых коэффициентов регрессии. Значение коэффициента (3 будет рассмотрено при изучении многомерного анализа.
Средняя часть расчётов отражает два источника дисперсии: дисперсию, которая описывается уравнением регрессии (сумма квадратов, обусловленная регрессией) и дисперсию, которая не учитывается при записи уравнения (остаточная сумма квадратов). Частное от суммы квадратов, обусловленных регрессией и остаточной суммы квадратов называется "коэфициентом детерминации". В таблице результатов это частное выводится под именем "R-квадрат". В нашем примере мера определённости равна
314337,948/ 424067,356 =0,741
Эта величина характеризует качество регрессионной прямой, то есть степень соответствия между регрессионной моделью и исходными данными. Мера определённости всегда лежит в диапазоне от 0 до 1. Существование ненулевых коэффициентов регрессии проверяется посредством вычисления контрольной величины F, к которой относится соответствующий уровень значимости.
В простом линейном регрессионном анализе квадратный корень из коэфициента детерминации, обозначаемый "R", равен корреляционному коэффициенту Пирсона. При множественном анализе эта величина менее наглядна, нежели сам коэфициент детерминации. Величина "смещенный R-квадрат" всегда меньше, чем несмещенный. При наличии большого количества независимых переменных, мера определённости корректируется в сторону уменьшения. Принципиальный вопрос о том, может ли вообще имеющаяся связь между переменными рассматриваться как линейная, проще и нагляднее всего решать, глядя на соответствующую диаграмму рассеяния. Кроме того, в пользу гипотезы о линейной связи говорит также высокий уровень дисперсии, описываемой уравнением регрессии. О том, как регрессионную прямую можно встроить в диаграмму рассеяния, будет рассказано в разделе 16.1.3.
И, наконец, стандартизированные прогнозируемые значения и стандартизированные остатки можно предоставить в виде графика. Вы получите этот график, если через кнопку Plots...(Графики) зайдёте в соответствующее диалоговое окно и зададите в нём параметры *ZRESID и *ZPRED в качестве переменных, отображаемых по осям у и х соответственно. В случае линейной регрессии остатки распределяются случайно по обе стороны от горизонтальной нулевой линии.
2.gif

16.1.2 Сохранение новых переменных
16.1.2 Сохранение новых переменных
Многочисленные вспомогательные значения, рассчитываемые в ходе построения уравнения регрессии, можно сохранить как переменные и использовать в дальнейших расчётах.
-
Для этого в диалоговом окне Linear Regression (Линейная регрессия) щёлкните на кнопке Save (Сохранить).
Откроется диалоговое окно Linear Regression: Save (Линейная регрессия: Сохранение) как изображено на рисунке 16.3.
В 10 версии SPSS появилась новая возможность сохранять информацию о модели в так называемом XML-файле. В дальнейшем он может использоваться некоторыми дополнительными SPSS-продуктами (к примеру, Whatlf?).
Интересными здесь представляются опции Standardized (Стандартизированные значения) и Unstandardized (Нестандартизированные значения), которые находятся под рубрикой Predicted values (Прогнозируемые величины опции). При выборе опции Не стандартизированные значения будут рассчитывается значения у, которое соответствуют уравнению регрессии. При выборе опции Стандартизированные значения прогнозируемая величина нормализуется. SPSS автоматически присваивает новое имя каждой новообразованной переменной, независимо от того, рассчитываете ли Вы прогнозируемые значения, расстояния, прогнозируемые интервалы, остатки или какие-либо другие важные статистические характеристики. Нестандартизированным значениям SPSS присваивает имена pre_1 (predicted value), pre_2 и т.д., а стандартизированным zpr_l.
Рис. 16.3: Диалоговое окно Линейная регрессия: Сохранение
-
Щёлкните в диалоговом окне Linear Regression: Save (Линейная регрессия: Сохранение) в поле Predicted values (Прогнозируемые значения) на опции Unstandardized (Нестандартизированные значения).
-
Подтвердите нажатием Continue (Далее) и в заключение ОК.
Вы увидите, что в редакторе данных была образована новая переменная под именем рrе_1 и добавлена в конец списка переменных в файле. Для объяснения значений, находящихся в переменной рrе_1, возьмём случай 5. Для случая 5 переменная рrе_1 содержит нестандартизированное прогнозируемое значение 263,11289. Это прогнозируемое значение слегка отличается в сторону увеличения от реального показателя содержания холестерина, взятого через один месяц (chol1) и равного 260. Нестандартизированное прогнозируемое значение для переменной chol1, так же как и другие значения переменной рге_1, было вычислено исходя из соответствующего уравнения регрессии.
Если мы в уравнение регрессии
chol1 = 0,863 • chol0 + 34,546
подставим исходное значение для chol0 (265), то получим chol1 = 0,863 -265 + 34,546 =263,241
Небольшое отклонение от значения, хранящегося в переменной рге_1 объясняется тем, что SPSS использует в расчётах более точные значения, чем те, которые выводятся в окне просмотра результатов. На этом этапе мы ещё раз проиллюстрируем возможность использования регрессии в качестве прогноза.
-
Добавьте для этого в конец файла hyper.sav, ещё два случая, используя фиктивные значения для переменной chol0. Пусть к примеру, это будут значения 282 и 314.
Мы исходим из того, что нам не известны значения показателя холестерина через месяц после начала лечения, и мы хотим спрогнозировать значение переменной chol1.
-
Оставьте предыдущие установки без изменений и проведите новый расчёт уравнения регрессии.
В конце списка переменных добавится переменная рге_2. Для нового добавленного случая (№175) для переменной chol1 будет предсказано значение 277,77567, а для случая №176 — значение 305,37620.
3.gif

16.1.3 Построение регрессионной прямой
16.1.3 Построение регрессионной прямой
Чтобы на диаграмме рассеяния изобразить регрессионную прямую, поступите следующим образом:
-
Выберите в меню следующие опции Graphs ... (Графики) Scatter plots... Диаграммы рассеяния
Откроется диалоговое окно Scatter plots... (Диаграмма рассеяния) как изображено на рисунке 16.4.
-
В диалоговом окне Scatter plots...(Диаграмма рассеяния) оставьте предварительную установку Simple (Простая) и щёлкните на кнопке Define (Определить).
Откроется диалоговое окно Simple Scatter plot (Простая диаграмма рассеяния) (см. рис. 16.5).
Рис. 16.4: Диалоговое окно Scatter plots... (Диаграмма рассеяния)
Рис. 16.5: Диалоговое окно Simple Scatterplot (Простая диаграмма рассеяния).
-
Перенесите переменную chol1 в поле оси Y, а переменную chol0 в поле оси X.
-
Подтвердите щелчком на ОК.
В окне просмотра результатов появится диаграмма рассеяния (см. рис. 16.6).
-
Щёлкните дважды на этом графике, чтобы перенести его в редактор диаграмм.
-
Выберите в редакторе диаграмм меню Chart... (Диаграмма) Options... (Опции)
Откроется диалоговое окно Scatterplot Options (Опции для диаграммы рассеяния) (см. рис. 16.7).
-
В рубрике Fit Line (Приближенная кривая) поставьте флажок напротив опции Total (Целиком для всего файла данных) и щёлкните на кнопке Fit Options (Опции для приближения). Откроется диалоговое окно Scatterplot Options: Fit Line (Опции для диаграммы рассеяния: приближенная кривая) (см. рис. 16.8).
-
Подтвердите предварительную установку Linear Regression (Линейная регрессия) щелчком Continue (Далее) и затем на ОК.
-
Закройте редактор диаграмм и щёлкните один раз где-нибудь вне графика.
Рис. 16.6: Диаграмма рассеяния в окне просмотра
Рис. 16.7: Диалоговое окно Scatterplot Options (Опции для диаграммы рассеяния)
Рис. 16.8: Диалоговое окно Scatterplot Options: Fit Line (Опции для диаграммы рассеяния:
Теперь в диаграмме рассеяния отображается регрессионная прямая (см. рис. 16.9).
4.gif

5.gif
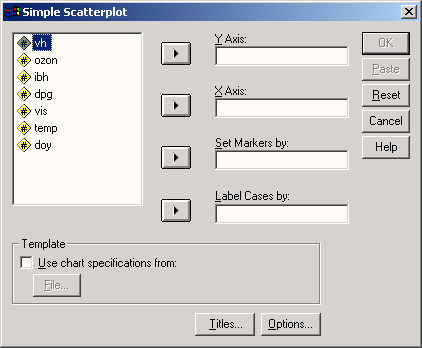
6.gif
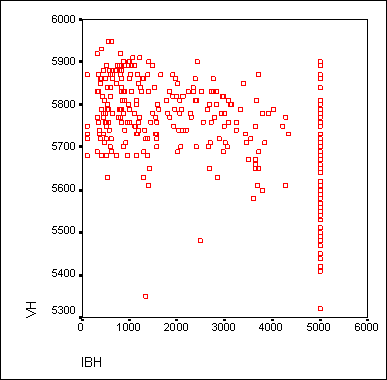
7.gif
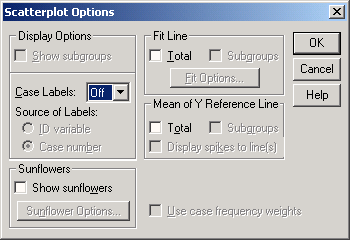
8.gif
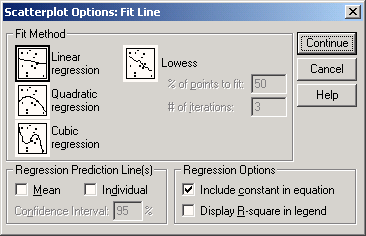
16.1.4 Выбор осей
16.1.4 Выбор осей
Для диаграмм рассеяния часто оказывается необходимой дополнительная корректировка осей. Продемонстрируем такую коррекцию при помощи одного примера. В файле raucher.sav находятся десять фиктивных наборов данных. Переменная konsum указывает на количество сигарет, которые выкуривает один человек в день, а переменная puls на количество времени, необходимое каждому испытуемому для восстановления пульса до нормальной частоты после двадцати приседаний. Как было показано ранее, постройте диаграмму рассеяния с внедрённой регрессионной прямой.
-
В диалоговом окне Simple Scatterplot (Простая диаграмма рассеяния) перенесите переменную puls в поле оси Y, а переменную konsum — в поле оси X.
Рис. 16.9: Диаграмма рассеяния с регрессионной прямой
После соответствующей обработки данных в окне просмотра появится диаграмма рассеяния, изображённая на рисунке 16.10.
Рис. 16.10: Диаграмма рассеяния с регрессионной прямой до коррекции осей
Так как никто не выкуривает минус 10 сигарет в день, точка начала отсчёта оси X является не совсем корректной. Поэтому попробуем эту ось откорректировать.
-
Дважды щёлкните на графике и в меню редактора диаграмм вберите опции Chart... (Диаграмма) Axis... (Оси) Откроется диалоговое окно Axis Selection (Выбор оси) (см. рис. 16.11).
-
Подтвердите предварительный выбор оси X нажатием кнопки ОК.
Откроется диалоговое окно X-Scale Axis (Ось X) (см. рис. 16.12).
-
В редактируемом поле Displayed (Отображаемый) в рубрике Range (Диапазон) измените минимальное значение на 0.
-
Подтвердите нажатием на ОК.
Рис. 16.11: Диалоговое окно Axis Selection (Выбор оси)
Рис. 16.12: Диалоговое окно X-Scale Axis (Ось X)
-
Выберите вновь в меню редактора диаграмм опции Chart... (Диаграмма* Axis... (Оси)
-
Активируйте в диалоговом окне Axis Selection (Выбор оси) опцию Y Scale (Ось Y). Откроется диалоговое окно Y-Scale Axis (Ось Y).
-
И здесь в рубрике Range (Диапазон) в редактируемом поле Displayed (Отображаемый) измените минимальное значение на "0".
-
Подтвердите нажатием на ОК.
В окне просмотра Вы увидите откорректированную диаграмму рассеяния (см. рис. 16.13).
На откорректированной диаграмме рассеяния теперь стало проще распознать начальную точку на оси Y, которая образуется при пересечении с регрессионной прямой. Значение этой точки примерно равно 2,9. Сравним это значение с уравнением регрессии для переменных puls (зависимая переменная) и konsum (независимая переменная). В результате расчёта уравнения регрессии в окне отображения результатов появятся следующие значения:
Coefficients (Коэффициенты)а
Model (Модель) | Unstandardized Coefficients (He стандартизированные коэф- фициенты) | Standar- dized Coefficients (Стандарти- зированные коэф- фициенты) | Т | Sig. (Значи- мость) | |||
| В | Std. Error (Стандар- тная ошибка) | ß (Beta) | ||||
1 | (Constant) (Константа) | 2,871 | ,639 | 4,492 | ,002 | ||
tgl. Zigaretten-konsum (Коли- чество сигарет в день) | ,145 | ,038 | ,804 | 3,829 | ,005 | ||
a. Dependent Variable: Pulsfrequenz unter 80 (Зависимая переменная: частота пульса ниже 80)
Рис. 16.13: Диаграмма рассеяния с регрессионной прямой после корректировки осей
Что дает следующее уравнение регрессии:
pids = 0,145-konsum + 2,871
Мы видим, что константа в вышеприведенном уравнении регрессии (2,871) соответствует точке на оси Y, которая образуется в точке пересечения с регрессионной прямой.
9.gif
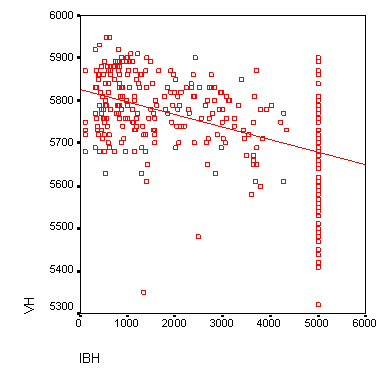
10.gif

11.gif
12.gif

13.gif
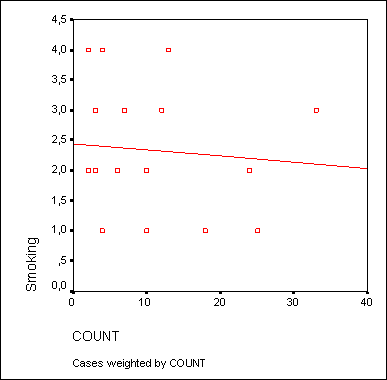
16.10 Двухступенчатый метод наименьших квадратов
16.10 Двухступенчатый метод наименьших квадратов
При помощи этого метода, используемого в эконометрии, производится анализ переменных, представленных в виде временных рядов. Примером может здесь послужить классическая эконометрическая модель, в которой спрос на некоторый продукт зависит от его цены, уровня обеспеченности (достатка) потенциальных покупателей и других неизвестных факторов:
Спрос = ß0 + ß1 • Цена + ß2 • Достаток + Ошибка
Наряду с независимыми переменными (называемыми также объявленными переменными) в этом уравнении должно быть указано, по меньшей мере, такое же количество так называемых инструментальных переменных. Они могут оказывать влияние на независимые переменные, при этом сами независимые переменные оказывать влияния на них не могут. Если речь идёт о сельскохозяйственном продукте, то такими переменными могут быть климатические переменные. Инструментальные переменные должны иметь сильную корреляцию с независимыми переменными, но совсем не иметь корреляции со слагаемыми ошибки.
В диалоговом окне для этого метода выводится запрос по поводу зависимых, объявленных и инструментальных переменных. На данном этапе рассмотрение конкретного примера мы опустим.
16.2 Множественная линейная регрессия
16.2 Множественная линейная регрессия
В общем случае в регрессионный анализ вовлекаются несколько независимых переменных. Это, конечно же, наносит ущерб наглядности получаемых результатов, так как подобные множественные связи в конце концов становится невозможно представить графически.
В случае множественного регрессионного анализа речь идёт необходимо оценить коэффициенты уравнения
у = b1-х1+b2-х2+... + bn-хn+а,
где n — количество независимых переменных, обозначенных как х1 и хn, а — некоторая константа.
Переменные, объявленные независимыми, могут сами коррелировать между собой; этот факт необходимо обязательно учитывать при определении коэффициентов уравнения регрессии для того, чтобы избежать ложных корреляций.
В качестве примера рассмотрим стоматологическое обследование 1130 человек, в котором исследуется вопрос необходимости лечения зубного ряда, измеряемой при помощи так называемого показателя CPITN, в зависимости от набора различных переменных.
При этом зубной ряд был разделён на секстанты, для которых и происходило определение показателя CPITN. Этот показатель может принимать значения от 0 до 4, где 0 соответствует здоровому состоянию, а 4 наибольшей степени развития заболевания. Затем значения показателя CPITN для всех секстант были усреднены.
Файл zahn.sav содержит следующие переменные:
Имя переменной | Расшифровка |
cpitn | Усредненное значение CPITN |
alter | Возраст |
g | Пол (1 = мужской, 2 = женский) |
s | Образование (1 = специальное школьное, 2 = неполное школьное, 3 = среднее, 4 = аттестат зрелости, 5 = высшее образование) |
pu | Периодичность чистки зубов (1 = меньше одного раза в день, 2 = один раз в день, 3 = два раза в день, 4 = долее двух раз в день) |
zb | Смена зубной щётки (1 = каждый месяц, 2 = каждые три месяца, 3 = раз в полгода, 4 = ещё реже) |
beruf (профессия) | Профессия (1 = государственный служащий/служащий, 2 = рабочий/профессиональный рабочий, 3 = занятость в области медицины, 4 = военный) |
Переменные cpitn и alter принадлежат к интервальной шкале, а переменные s, pu и zb при более подробном рассмотрении можно отнести к порядковой шкале, так что они могут быть подвергнуты регрессионному анализу. Переменная g относится к номинальной шкале, но в то же время является дихотомической. Поэтому если при оценке результатов обратить внимание на полярность, то и эта переменная так же может быть вовлечена в регрессионный анализ. Однако, переменная beruf относится к номинальной шкале и имеет более двух (а именно четыре) категории. Поэтому, без дополнительной обработки ее нельзя применять в дальнейших расчётах.
В данном случае можно прибегнуть к специальному трюку: разложить переменную beruf на четыре, так называемых, фиктивных переменных, с кодировками отвечающими О (действительно) и 1 (ложно). В файл добавляются четыре новые переменные: berufl-beruf4, которые поочередно соответствуют четырём различным кодировкам переменной beruf. Так, к примеру, переменная berafl указывает на то, является ли данный респондент государственным служащим/работником (кодировка 1) или нет (кодировка 0).
-
Откройте файл zahn.sav.
-
Выберите в меню Analyze... (Анализ) Regression...(Регрессия) Linear... (Линейная)
-
Поместите переменную cpitn в поле для зависимых переменных, объявите переменные: alter, berafl, bеrа0, beru0, beruf4, g, pu, S.H zb независимыми.
Для множественного анализа с несколькими независимыми переменными не рекомендуется оставлять метод включения всех переменных, установленный по умолчанию. Этот метод соответствует одновременной обработке всех независимых переменных, выбранных для анализа, и поэтому он может рекомендоваться для использования только в случае простого анализа с одной независимой переменной. Для множественного анализа следует выбрать один из пошаговых методов. При прямом методе независимые переменные, которые имеют наибольшие коэффициенты частичной корреляции с зависимой переменной пошагово увязываются в регрессионное уравнение. При обратном методе начинают с результата, содержащего все независимые переменные и затем исключают независимые переменные с наименьшими частичными корреляционными коэффициентами, пока соответствующий регрессионный коэффициент не оказывается незначимым (в данном случае уровень значимости равен 0,1).
Наиболее распространенным является пошаговый метод, который устроен так же, как и прямой метод, однако после каждого шага переменные, используемые в данный момент, исследуются по обратному методу. При пошаговом методе могут задаваться блоки независимых переменных; в этом случае заданные блоки на одном шаге обрабатываются совместно.
-
Выберите пошаговый метод, но воздержитесь от блочной формы ввода данных, не задавайте больше ни каких дополнительных расчётов и начните вычисление нажатием ОК.
Model Summary (Сводная таблица модели)
Model (Модель) | R | R Square (Коэф- фициент детерми- нации) | Adjusted R Square (Скорректи- рованный R-квадрат) | Std. Error of the Estimate (Станда- ртная ошибка оценки) |
1 2 3 4 5 | ,452а ,564b ,599с ,609d ,613е | ,204 ,318 ,359 ,371 ,375 | ,203 ,317 ,358 ,369 ,373 | ,8316 ,7698 ,7467 ,7402 ,7380 |
a. Predictors: (Constant), Alter (Влияющие переменные: (константа), возраст)
b. Predictors: (Constant), Alter, Putzhaeufigkeit (Влияющие переменные: (константа), возраст, периодичность чистки)
c Predictors: (Constant), Alter, Putzhaeufigkeit, Zahnbuerstenwechsel (Влияющие переменные: (константа), возраст, периодичность чистки, смена зубной щётки)
d Predictors: (Constant), Alter, Putzhaeufigkeit, Zahnbuerstenwechsel, Schulbildung (Влияющие переменные: (константа), возраст, периодичность чистки, смена зубной щётки, образование)
е. Predictors: (Constant), Alter, Putzhaeufigkeit, Zahnbuerstenwechsel, Schulbildung, Arbeiter/Facharbeiter (Влияющие переменные: (константа), возраст, периодичность чистки, смена зубной щётки, образование, рабочий/профессиональный работник) .
Из первой таблице следует, что вовлечение переменных в расчет производилось за пять шагов, то есть переменные возраст, периодичность чистки, смена зубной щётки, образование, рабочий/профессиональный работник поочерёдно внедрялись в уравнение регрессии. Для каждого шага происходит вывод коэффициентов множественной регрессии, меры определённости, смещенной меры определённости и стандартной ошибки.
К указанным результатам пошагово присоединяются результаты расчёта дисперсии (см. гл. 16.1.1), которые здесь не приводятся. Также, пошаговым образом, производится вывод соответствующих коэффициентов регрессии и значимость их отличия от нуля.
Coefficients (Коэффициенты) a
| Model (Модель) | UnStan- dardized Coefficients (He стандарти-зированные коэф- фициенты) | Standa- rdized Coefficients (Стандарти-зированные коэф-фициенты) | Т | Sig. (Значи мость) | ||
| В | Std. Error (Станда- ртная ошибка) | ß (Beta) | ||||
| (Constant) (Константа) Alter (Возраст) | 1,295 3,31 Е-02 | ,071
,002 |
,452 | 18,220 17,006 | ,000 ,000 | |
| 2 | (Константа) Возраст Перио- дичность чистки | 3,024 3.20Е-02 -,604 | ,142
,002 ,044 |
,437
-,339 |
21,317 17,765 -13,756 | ,000 ,000 ,000 |
| 3 | (Константа) Возраст Перио- дичность чистки Смена зубной щётки | 1,903 3.25Е-02 -,439 ,253 | ,191
,002 ,047 ,030 |
,443
-,246 ,222 |
9,976 18,555 -9,376 8,473 | ,000 ,000,
,000 ,000 |
| 4 | (Константа) Возраст Перио- дичность чистки Смена зубной щётки Образование | 2,188 3,31 Е-02 -,391 ,226 -,115 | ,199
,002 ,048 ,030 ,025 |
,451
-,220 ,199 -,116 |
10,992 19,011 -8,235 7,498 -4,580 | ,000 ,000
,000 ,000 ,000 |
| 5 | (Константа) Возраст Перио- дичность чистки Смена зубной щётки Образование Рабочий/ Профес- сиональный работник |
2,022 3.20Е-02 -,379 ,229 -8.3Е-02 ,143
|
,208 ,002 ,048 ,030 ,028 ,052
|
,437 -,213 ,201 -,084 ,075
|
9,743 18,041 -7,964 7,613 -2,983
2,757 |
,000 ,000 ,000 ,000 ,003
,006 |
а. Dереnаdеnt variable: Mittlerer CPITN-Wert (Зависимая переменная: усреднённое значение CPITN)
Вдобавок ко всему для каждого шага анализируются исключённые переменные. В вышеприведенной таблице в объяснениях нуждаются лишь коэффициенты ß. Это — регрессионные коэффициенты, стандартизованные соответствующей области значений, они указывают на важность независимых переменных, вовлечённых в регрессионное уравнение.
Уравнение регрессии для прогнозирования значения CPITN выглядит следующим образом:
cpitn = 0,032•alter - 0.379•рu + 0,229•zb - 0,083•s + 0,143- benif 2 + 2,022
Для 40-летнего рабочего с неполным школьным образованием, который ежедневно чистит зубы один раз в день и меняет щётку раз в полгода, с учётом соответствующих кодировок, получается следующее уравнение:
cpitn = 0,032•40-0,379•2 + 0,229•3- 0,083•2 + 0,143•1 + 2,022 = 3,208
При помощи соответствующих опций можно организовать вывод большого числа дополнительных статистических характеристик и графиков, на которых мы здесь останавливаться не будем. Можно также создать много дополнительных переменных и добавить их в исходный файл данных.
Важным моментом является анализ остатков, то есть отклонений наблюдаемых значений от теоретически ожидаемых. Остатки должны появляться случайно (то есть не систематически) и подчиняться нормальному распределению. Это можно проверить, если с помощью кнопки Charts... (Диаграммы) построить гистограмму остатков. В приведенном примере наблюдается довольно хорошее согласование гистограммы остатков с нормальным распределением.
Проверка на наличие систематических связей между остатками соседних случаев (что, однако, является уместным только при наличии так называемых данных с продольным сечением), может быть произведена при помощи теста Дарбина-Ватсона (Durbin-Watson) на автокорреляцию. Этот тест вычисляет коэффициент, лежащий в диапазоне от 0 до 4. Если значение этого коэффициента находится вблизи 2, то это означает, что автокорреляция отсутствует. Тест Дарбина-Ватсона можно активировать через кнопку Statistics (Статистические характеристики). В данном примере тест дает удовлетворительное значение коэффициента, равное 1,776.
Ещё одной дополнительной возможностью является задание переменной отбора в диалоговом окне Linear Regression (Линейная регрессия). Здесь, с помощью кнопки Rule... (Правило) в диалоговом окне Linear Regression: Define Selection Rule (Линейная регрессия: ввод условия отбора), Вы получаете возможность при помощи избирательного признака сформулировать условие, которое будет ограничивать количество случаев, вовлеченных в анализ.
Рис. 16.14: Гистограмма остатков
14.gif
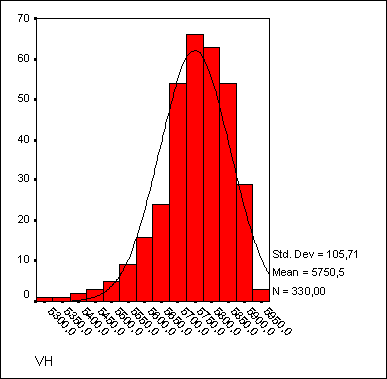
16.3 Нелинейная регрессия
16.3 Нелинейная регрессия
Многие связи по своей природе, то есть в реальной жизни, либо являются строго линейными, либо их можно привести к линейному виду. Один пример линейной связи из области медицины был приведен в главе 16.1; ещё одним, уже знакомым нам примером является линейная связь между весом и ростом. При условии наличия лопаточного количества респондентов, на основании измеренных пар значений можно вывести уравнение регрессионной прямой, к которой более или менее приближается '.тожество точек, соответствующие парам значений.
Существуют также линейные связи, следующие непосредственно из физических закономерностей. Так путь s, пройденный, при постоянной скорости с за промежуток времени : рассчитывается по формуле:
s=c•t
Стало быть, путь является линейной функцией времени. А если мы рассмотрим закон свободного падения, то в этом случае расстояние s. которое проходили падающее тело увеличивается пропорционально квадрату времени:

где g — ускорение свободного падения.
Если Вы захотите проверить это экспериментально, то Вам надлежит сделать серию опытов, в которых будет необходимо бросать некоторый предмет, например, камень, с различной высоты (лучше всего, конечно же, в разряжённом, безвоздушном пространстве) и засекать время падения. Предположим, у Вас получились следующие результаты:
s (см) | t (сек) |
5 | 1,0 |
9 | 1,4 |
16 | 1,8 |
26 | 2,3 |
40 | 2,8 |
65 | 3,6 |
98 | 4,5 |
Хотя связь между 5 и с и не является линейной, её можно перевести в линейную модель, если взять квадратный корень из обоих сторон закона свободного падения:

С помощью преобразования данных, мы разрешаем компьютеру создать новую переменную, содержащую значения квадратного корня из величины s и рассматривать её как зависимую переменную, а время / как независимую переменную. Рассчитаем коэффициент регрессии b так, как это было изложено в разделе 16.1.
Используя этот коэффициент, можно теперь рассчитать искомое ускорение свободного падения:
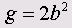
Если Вы выполните эти вычисления, то получите b = 0,2224 и g = 9,88.
При помощи соответствующих трансформаций в линейную модель можно перевести и другие исходно нелинейные связи. К примеру, очень часто встречающуюся экспоненциальную связь
у = а•еbx
можно преобразовать в линейную при помощи вычисления логарифма от обеих сторон уравнения
ln (у) = ln(a) + b•x
То есть в данном случае до проведения линейного регрессионного анализа необходимо прологарифмировать независимые переменные.
Связи, которые при помощи соответствующих трансформаций могут быть переведены в линейную связь, называются линейными по существу (Intrinsically Linear Model). Возможность перевода в линейную модель нужно использовать всегда, так как в этом случае параметры регресии вычисляются непосредственно, а не определяются с помощью итераций.
В качестве примера нелинейной по существу связи (Intrinsically Nonlinear Model) можно привести динамику роста населения США (этот пример взят из Справочника по SPSS):
Год | Лекала | Население |
1790 | 0 | 3,895 |
1800 | 1 | 5,267 |
1810 | 2 | 7,182 |
1820 | 3 | 9,566 |
1830 | 4 | 12,834 |
1840 | 5 | 1 6,985 |
1850 | 6 | 23,069 |
1860 | 7 | 31,278 |
1870 | 8 | 38,416 |
1880 | 9 | 49,924 |
1890 | 10 | 62,692 |
1900 | 11 | 75,734 |
1910 | 12 | 91,812 |
1920 | 13 | 109,806 |
1930 | 14 | 122,775 |
1940 | 15 | 131,669 |
1950 | 16 | 150,697 |
1960 | 17 | 178,464 |
В таблице приведена численность населения в миллионах и дополнительно количество декад (десятилетий), прошедших с 1790 года.
Зависимость численности населения (переменная pop) от времени t (выраженного здесь в декадах) часто описывается при помощи следующей формулы:
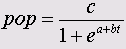
Эту связь нельзя перевести в линейную форму. Она включает три параметра: а, b и с, которые должны быть определены при помощи подходящего метода. Для этого необходимо задать начальные значения этих параметров.
Общего универсального метода определения параметров подобной нелинейной связи, к сожалению, не существует, поэтому описанная ниже последовательность действий может служить только примером.
В рассматриваемом примере параметр с является амплитудой, так что начальное значение может быть задано немного большим, чем максимум значения pop, то есть приблизительно с = 200.
При помощи значения параметра pop при t = 0 и начального значения параметра с можно получить начальную оценку параметра а:
3,895 = 200/(1+e2)
и следовательно
а = ln((200/3,895-1)) = 3,9
Исходя из значения параметра pop для первой декады, можно вычислить начальное значение параметра b:
5,267=200/(1+e3,9+b)
и следовательно
b=ln(5,267-1)-3,9 = -0,3
Определим теперь более точные значения параметров а, b и с с помощью итераций.
-
Откройте файл usa.sav.
-
Выберите в меню Analyze... (Анализ) Regression... (Регрессия) Nonlinear... (Нелинейная)
-
В диалоговом окне Nonlinear Regression (Нелинейная регрессия) перенесите переменную pop в поле для зависимых переменных.
-
Щёлкните на поле Model Expression (Модельное выражение) и внесите в него следующую формулу:
c/(l+exp(a+b*dekade))
При вводе формулы можно использовать клавиатуру, находящуюся в диалоговом окне. Диалоговое окно будет выглядеть так, как изображено на рисунке 16.15. Нам осталось только задать начальные значения параметров.
-
Щёлкните на кнопке Parameter... (Параметр)
Вы получите диалоговое окно, в котором сможете задавать начальные значения.
-
Укажите в поле имён имя первого параметра, то есть, к примеру, а, затем щёлкните в поле Starting value (Начальное значение), введите значение 3,9 и щёлкните на Add (Добавить).
Рис. 16.15: Диалоговое окно Nonlinear Regression (Нелинейная регрессия).
-
Поступите таким же образом с двумя другими параметрами бис (начальные значения —0,3 и 200 соответственно).
-
Покиньте диалоговое окно нажатием Далее.
-
Щёлкните на кнопке Save (Сохранить). Отметьте в диалоговом окне Nonlinear Regression: Save New Variables (Нелинейная регрессия: Сохранить новые переменные) параметры: Predicted Values (Прогнозируемые значения) и Residuals (Остатки). Таким образом, Вы создадите две новые переменные (с именами: pred_ и resid), которые содержат вычисленные значения и остатки для каждого года.
-
Начните расчёт нажатием ОК.
На экране появятся результаты, причём Вы можете заметить, что вывод происходит не в виде привычных современных таблиц. Сначала протоколируется процесс итерации; в рассматриваемом примере для достижения заданного уровня точности понадобилось 10 итерационных шагов. Дополнительно выводятся следующие статистические характеристики:
Nonlinear Regression | Summary Statistics Dependent Variable POP | ||
Source | DF | Sum of Squares | Mean Square |
Regression | 3 | 123048 ,61437 | 41016,20479 |
Residual | 15 | 186,50337 | 12,43356 |
Uncorrected Total | 18 | 123235,11774 |
|
(Corrected Total) | 17 | 53291,50763 |
|
R squared = 1Residual SS / CorrectedSS = ,99650 | |||
Здесь интерес может представлять только член, обозначенный R squared; его следует понимать как часть суммарной дисперсии, которая обусловлена построенной моделью. Вычисленное значение этого параметра, 0.9965, указывает на очень хорошую степень приближения. После этого вывода следует распечатка конечных значений всех трех параметров вместе с соответствующей стандартной ошибкой и доверительным интервалом:
Asymptotic 95 % Asymptotic Confidence Interval | ||||
Parameter Estimate | Std. Error | Lower Upper | ||
A | 3,888771432 , | 093688592 | 3,6890789254 ,088463938 | |
В | -,278834486, | 015593535 | -,312071318 - ,245597654 | |
С | 244,01372955 | 17,974966354 | 205, 70099568 282 | ,32646341 |
Завершает список выводимых результатов корреляционная матрица оценок параметров:
Asymptotic | Correlation А | Matrix of В | the | Parameter Estimates С |
А В С | 1,0000 -,7243 -,3759 | -,724: 1,000 ,904 | 3 '0 3 | -,3759 ,9043 1,0000 |
Очень высокие абсолютные значения корреляций указывают на то, что модель содержит неоправданно большое количество параметров. В рассматриваемом примере и модель с меньшим количеством параметров даст столь же хорошее приближение.
-
Если Вы хотите визуально сравнить рассчитанные значения с наблюдаемыми, то можете посредством меню Graph... (Графики) Scatter plots... (Диаграммы рассеяния)
построить многослойную диаграмму рассеяния (Staggered), на которой Вы можете представить переменные pop и pred_ в зависимости от переменной jahr. Также можно поступить и с остатками (переменная rcsid).
Согласно предварительным установкам при расчете нелинейной регрессии происходит минимизация суммы квадратов остатков. При помощи кнопки Loss...(Остаток) можно задать какую-либо другую минимизирующую функцию. Далее при помощи кнопки Constraints...(ограничения) может быть открыто окно, в котором можно задать ограничения для определяемых параметров нелинейной регрессии.
16.gif

19.gif

16.4 Бинарная логистическая регрессия
16.4 Бинарная логистическая регрессия
С помощью метода бинарной логистической регрессии можно исследовать зависимость дихотомических переменных от независимых переменных, имеющих любой вид шкалы.
Как правило, в случае с дихотомическими переменными речь идёт о некотором событии, которое может произойти или не произойти; бинарная логистическая регрессия в таком случае рассчитывает вероятность наступления события в зависимости от значений независимых переменных.
Вероятность наступления события для некоторого случая рассчитывается по формуле
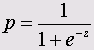
где z= b1*X1 + b2хХ2+ ...+ bnxXn+ a ,
X1 — значения независимых переменных, b1 — коэффициенты, расчёт которых является задачей бинарной логистической регрессии, а — некоторая константа.
Если для р получится значение меньшее 0,5, то можно предположить, что событие не наступит; в противном случае предполагается наступление события.
В качестве примера рассмотрим два диагностических теста из области медицины на предмет обнаружения карциномы (злокачественной опухоли) мочевого пузыря: подсчет количества (типизация) Т-клеток и тест LAI. Результатами первого теста являются значения, принадлежащие к интервальной шкале, а тест LAI дает дихотомический результат: "положительно" или "отрицательно".
Оба теста были проведены со здоровыми людьми и заведомо больными пациентами. Результаты представлены в следующей таблице:
Коллектив | Типизация t-клеток | LAI | Коллектив | Типизация t-клеток | LAI |
болен | 48.5 | положи-тельно | болен | 73.5 | положи-тельно |
болен | 55.5 | положи-тельно | здоров | 61.1 | положи-тельно |
болен | 57.5 | положи-тельно | здоров | 62.5 | отрица-тельно |
болен | 58.5 | положи-тельно | здоров | 63.5 | отрица-тельно |
болен | 61.0 | положи-тельно | здоров | 64.5 | положи-тельно |
болен | 61.5 | положи-тельно | здоров | 69.5 | положи-тельно |
болен | 61.5 | положи-тельно | здоров | 70.0 | отрица-тельно |
болен | 6,2.0 | положи-тельно | здоров | 70.0 | отрица-тельно |
болен | 62.0 | положи-тельно | здоров | 71.0 | положи-тельно |
болен | 62,0 | положи-тельно | здоров | 71,5 | положи-тельно |
болен | 62.5 | положи-тельно | здоров | 71.5 | отрица-тельно |
болен | 63.0 | положи-тельно | здоров | 72.0 | отрица-тельно |
болен | 63.5 | положи-тельно | здоров | 73.0 | отрица-тельно |
болен | 65.0 | положи-тельно | здоров | 76.0 | отрица-тельно |
болен | 65.0 | отрица-тельно | здоров | 72.5 | отрица-тельно |
болен | 66.5 | отрица-тельно | здоров | 73.0 | отрица-тельно |
болен | 66.5 | отрица-тельно | здоров | 73.5 | отрица-тельно |
болен | 66.5 | положи-тельно | здоров | 74.0 | отрица-тельно |
болен | 68.5 | положи-тельно | здоров | 75.0 | отрица-тельно |
болен | 69.0 | отрица-тельно | здоров | 77.0 | отрица-тельно |
болен | 71.0 | положи-тельно | здоров | 77.0 | отрица-тельно |
болен | 71.0 | положи-тельно | здоров | 78.5 | отрица-тельно |
болен | 71.0 | положи-тельно |
|
|
|
Если сначала посмотреть на результаты типизации Т-клеток, то можно заметить, что здесь для здоровых людей значения в среднем выше, чем для больных. Следовательно, исходя из значений, получившихся при типизации Т-клеток, можно попытаться, вывести вероятность наличия карциномы мочевого пузыря.
Приведенные в таблице данные находятся в файле hkarz.sav. Больным присвоена кодировка 1, а здоровым 2; для теста LA1 кодировка 0 соответствует положительному результату, а 1 отрицательному.
-
Откройте файл hkarz.sav.
-
Выберите в меню Analyze... (Анализ) Regression... (Регрессия) Binary logistic... (Бинарная логистическая)
Открывается диалоговое окно Logistic Regression (Логистическая регрессия).
-
Поместите переменную gruppe (группа), содержащую информацию о принадлежности к одному или второму коллективу (больным или здоровым), в поле для зависимых переменных, а переменную tzell — в поле ковариат. Результаты теста LAI сначала мы не будем использовать в расчёте.
Рис. 16.16: Диалоговое окно -Ogistic Regression (Логистическая регрессия).
В качестве метода использования переменных в вычислениях предварительно установлен метод Enter (Вложение), при котором в расчёт одновременно вовлекаются :-:е переменные объявленные ковариатами. Альтернативой здесь являются прогрессивная и обратная селекции. В случае наличия лишь одной ковариаты, как в указаном примере, для расчёта подходит только предварительно установленный метод.
Кнопка Select» (Выбрать) предоставляет возможность отбора определённых случаев для дальнейшего анализа.
Используя кнопку Categorical... (Категориальные) Вы можете подготовить для расчета категориальные переменные (то есть переменные, принадлежащие к номинальной шкале). На этом мы остановимся более подробно, рассматривая второй пример.
При помощи кнопки Save... (Сохранить) Вы можете добавить в файл дополнительные переменные; активируйте к примеру в разделе Predicted Values (Спрогнозированные значения) предварительные установки Probabilities (Вероятности) и Принадлежность к группе.
Нажав на кнопку Options... (Опции), Вы сможете организовать вывод дополнительных статистических характеристик, различных диаграмм и произвести некоторые дополнительные установки. В данном расчёте мы этого делать не будем.
-
Начните расчёт нажатием ОК.
Наиболее важные результаты приведены в нижеследующей таблице, причём в 10 версии SPSS они уже выводятся в новой табличной форме.
Omnibus Tests of Model Coefficients (Универсальный критерий коэффициентов модели)
Chi-square (Хи-квадрат) | Df | Sig. (Значимость) | ||
Step 1 (ШаМ) 1 | Step (Шаг) | 18,789 | 1 | ,000 |
Block (Блок) | 18,789 | 1 | ,000 | |
Model (Модель) | 18,789 | 1 | ,000 |
Model Summary (Сводная таблица модели)
Step (Шаг) | -2 Log likelihood (-2 логарифмическое правдоподобие) | Сох & Snell R Square (R-квадрат Кокса и Шнела) | R Square Nadelkerkes (R-квадрат Наделькеркеса) |
1 | 43,394 | ,341 | ,456 |
Качество приближения регрессионной модели оценивается при помощи функции подобия. Мерой правдоподобия служит отрицательное удвоенное значение логарифма этой функции (-2LL). В качестве начального значения для -2LL применяется значение, которое получается для регрессионной модели, содержащей только константы. После добавления переменной влияния tzell значение -2LL равно 43,394; это значение на 18,789 меньше, чем начальное. Подобное снижение величины означает улучшение; разность обозначается как величина хи-квадрат и является очень значимой.
Это означает, что начальная модель после добавления переменной tzell претерпела значительное улучшение. Если при наличии некоторого количества независимых переменных анализ производится не при помощи метода вложения, а пошаговым образом, то получающиеся изменения отображаются в разделах "Блок" и "Шаг". При этом, если Вы производили ввод переменных в блочной форме, то показатель в разделе "Блок" приобретает особое значение.
Два других выведенных показателя, названные именами Кокса & Шела и Наделькеркеса, являются мерами определённости. Они также как и при линейной регрессии указывают на ту часть дисперсии, которую можно объяснить с помощью логистической регрессии. Мера определённости по Коксу и Шелу имеет тот недостаток, что значение равное 1 является теоретически не достижимым; этот недостаток устранен благодаря модификации данной меры по методу Наделькеркеса. Часть дисперсии, объяснимой с помощью логистической регрессии, в данном примере составляет 45,6 %.
Далее приводится классификационная таблица, в которой наблюдаемые показатели принадлежности к группе (1 = болен, 2 = здоров) противопоставляются предсказанным на основе рассчитанной модели.
Classification Table (Классификационная таблица) а
Observed (Наблюдаемый показатель) | Predicted (Спрогнозировано) | ||||
GRUPPE (Группа) | Percentage Correct (Процентный показатель верных показателей) | ||||
Krank (болен) | Gesund (здоров) | ||||
Шаг 1 | GRUPPE (Группа) | Krank (болен) | 18 | 6 | 75,0 |
| Gesund (здоров) | 4 | 17 | 81,0 | ||
| Overall Percentage (Суммарный процентный показатель) |
| 77,8 | |||
a. The cut value is ,500 (Разделительное значение равно ,500)
Из таблицы можно сделать вывод о том, что из общего числа больных, равного 24, тестом были признаны таковыми только 18 (в медицинской диагностике в таких случаях говорят о "строго положительных" результатах). Остальных 6 называют "ложно отрицательными"; они были признаны тестом здоровыми, хотя и являются больными. Из общего числа здоровых, равного 21, тестом были признаны таковыми только 17 ("строго отрицательные"), 4 признаны больными, хотя они и являются здоровыми ("ложно положительные"). В общем, правильно были распознаны 35 случаев из 45, это составляет 77,8 %.
В заключении выводятся результаты о рассчитанных коэффициентах и проверке их значимости:
Variables in the Equation (Переменные в уравнении)
|
| В (Коэф-фициент регрессии В) | S.E. (Стандарт- ная ошибка) | Wald (Вальд) | df | Sig. (Значи-мость) | Ехр (В) |
Step 1 (Шаг 1)а | TZELL | ,278 | ,082 | 11,599 | 1 | ,001 | 1,321 |
| Constant (Константа) | -19,005 | 5,587 | 11,571 | 1 | ,001 | ,000 |
a. Variable(s) entered on step 1: TZELL (Переменные, введенные на шаге 1: TZELL)
Проверка значимости отличия коэффициентов от нуля, проводится при помощи статистики Вальда, использующей распределение хи-квадрат, которая представляет собой квадрат отношения соответствующего коэффициента к его стандартной ошибке.
В приведенном примере получились сверх значимые коэффициенты а = -19,005 bt = 0,278. При помощи этих двух значений коэффициентов мы можем для каждого значения Т-типизации рассчитать вероятность р. К примеру, для некоего обследуемого со значением Т-типизации 72 получим
z= - 19,005+ 0,278x72= 1,018
и таким образом
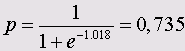
Рассчитанная вероятность р всегда указывает на исполнение предсказании, которое соответствует большей из двух кодировок зависимых переменных, в данном случае — на исполнение предсказания "здоров". Следовательно, рассматриваемый человек является здоровым с вероятностью 0,735.
Рассчитанная вероятность для всех случаев и связанная с ней принадлежность к группе кодировка 1 для болен и 2 для здоров) добавлены к файлу под именами рге_1 и pgr_l.
Теперь подключим к нашему анализу тест LAI. Дополнительно к переменной tzell теперь в поле ковариат поместите и переменную lai.
Расчёт выдаст сначала заметно снизившееся значение -2LL (хи-квадрат = 25,668) и следующую классификационную таблицу. Доля правильно спрогнозированных диагнозов незначительно выросла (с 77,8 % до 80,0 %).
Classification Table (Классификационная таблица)а
|
Observed (Наблюдаемый показатель) |
Predicted (Спрогнозировано) |
||||
|
Группа |
Percentage Correct (Процентный показатель верных показателей) |
||||
| Krank (болен) | Gesund (здоров) | ||||
|
Шаг 1 |
GRUPPE (Группа) | Krank (болен) |
20 |
4 |
83,3 |
| Gesund (здоров) |
5 |
16 |
76,2 |
||
| Overall Percentage (Суммарный процентный показатель) |
80,0 |
||||
а. The cut value is ,500 (Разделительное значение равно ,500)
Количество ложно отрицательных диагнозов снизилось на 2, а количество ложно положительных повысилось на 1. Для коэффициентов получим:
Variables in the Equation (Переменные в уравнении)
|
| В (Коэф0 фициент регрессии В) | S.E. Стандартная ошибка) | Wald (Вальд) | df | Sig. (Значи0 мость) | Ехр (В) |
Stepl (UJarlf | TZELL | ,201 | ,094 | 4,574 | 1 | 0,32 | 1,222 |
LAI | 2,205 | ,877 | 6,324 | 1 | ,012 | 9,074 | |
Constant (Константа) | -14,645 | 6,328 | 5,356 | 1 | ,021 | ,000 |
a. Variable(s) entered on step 1: TZELL, LAI. (Переменные, вводимые на шаге 1: TZELL, LAI)
Для обследуемого с типизированным числом Т-клеток равным 72 получилась вероятность оказаться здоровым р = 0,735. Если в дополнении к этому и тест LAI отрицателен (кодировка 1), то эта же вероятность рассчитывается следующим образом:

Вероятность, оказаться здоровым, при наличии данных уже двух диагностических методов значительно возросла.
Ещё один пример из области медицины, теперь уже с большим количеством независимых переменных, должен помочь нам разобраться в пошаговом методе анализа. Кроме того, в состав независимых переменных будет включена категориальная переменная.
Для данного примера в некоторой клинике со специальными автоматизированными методиками лечения были накоплены данные о пациентах с тяжёлыми (или даже смертельными) повреждениями лёгких. Из большого количества переменных были выбраны следующие:
Имя переменной | Расшифровка |
out | Исход (0 = скончался, 1 = выздоровел) |
alter (возраст) | Возраст |
bzeit | Время проведения искусственного дыхания в часах |
kob | Концентрация кислорода в воздушной массе для искусственного |
дыхания | |
адд | Интенсивность искусственного дыхания |
gesch (пол) | Пол (1 = мужской, 2 = женский) |
gr | Рост |
ursache (причина) | Причина повреждения лёгких (1 = несчастный случай, 2 = воспаление лёгких, 3 = прочее) |
Наряду с переменной out (исход), имеются переменные, при первом же взгляде на которые можно понять, что они с ней связаны. Причина повреждения лёгких является категориальной переменной, которая перед проведением анализа должна быть преобразована в несколько дихотомических переменных (к примеру, несчастный случай: да — нет).
Вопрос, на который нам предстоит найти ответ, звучит так: какое влияние на вероятность выздоровления оказывают отобранные переменные.
-
Откройте файл lunge.sav.
-
После выбора соответствующего меню в диалоговом окне Logistic Regression (Логистическая регрессия) переменной out присвойте статус независимой переменной, а всем остальным (кроме пг) присвойте статус ковариат. Здесь, как и при множественной линейной регрессии, ввод ковариат Вы можете производить по блокам.
Из-за вовлечения в анализ большого количества переменных компьютер должен решить, какие из них в конечном случае будут отобраны для использовании в уравнении вероятности. Поэтому здесь должен быть выбран не метод вложения, который включает в расчёт все переменные, а один из пошаговых методов.
Метод прямой селекции начинается с использования одних лишь констант на стартовом этапе , а затем последовательно подключаются переменные, которые демонстрируют сильную корреляцию с зависимыми переменными. Далее опять следует проверка того, какие переменные должны быть исключены, причём в качестве критерия проверки выбирается либо статистика Вальдовского (Wald), либо функция правдоподобия, либо один из вариантов, называемых "условной статистикой" (которые, однако, не рекомендуются). Метод обратной селекции сначала берёт в расчёт все переменные, а затем в обратном порядке происходит исключение малозначимых переменных.
-
Выберите в качестве метода Forward: LR (Прямой:LR) и щёлкните на кнопке Categorical... (Категориальные), чтобы поместить переменную ursache в поле, предусмотренное для категориальных ковариат.
Количество образовываемых "фиктивных" дихотомических переменных должно быть всегда на 1 меньше, чем число количество заданных категорий. Категория, оказавшаяся лишней, называется эталонной категорией и, в соответствии с предварительными установками, является последней категорией. При помощи поля контрастов Contrast) Вы можете управлять особенностями вовлечения в анализ образованных Фиктивных переменных; при контрасте равном Deviation (Отклонение) все категории кроме эталонной будут проверяются относительно суммарного эффекта.
-
Установите контраст Deviation (Отклонение) и при помощи щелчка на Continue (Далее) вернитесь в исходное диалоговое окно.
-
Начните расчёт нажатием ОК.
Вы можете проследить, какие переменные вовлекаются в анализ и как улучшается вероятность прогноза после вовлечения каждой новой переменной. На завершающей стати анализа присутствуют четыре переменные, а именно: возраст, время проведения искусственного дыхания, рост и концентрация кислорода в воздушной массе для искусственного дыхания.
Точность исполнения прогноза, которая достигается при использовании этих четыpex переменных, составляет 71,0 %; её можно увидеть в нижеследующей классификанионной таблице на стр 25.
Classification Table (Классификационная таблица)а
| Observed (Наблюдаемый показатель) | Predicted (Спрогнозировано) | ||||
| Outcome (Исход) | Percentage Correct (Процентный показатель верных прогнозов) | ||||
| gestorben (скончался) | ueberlebt (выздоровел) | ||||
|
Step 1 (Шаг)
|
Outcome (Исход) | gestorben (сконча-лся) | 29 | 34 | 46,0 |
| ueberlebt (выздоро- вел) | 14 | 54 | 79,4 | ||
| 63,4 | |||||
| Overall Percentage (Суммарный процентный показатель) | |||||
|
Step 2 Шаг 2)
|
Outcome (Исход) | gestorben (сконча- лся) | 32 | 31 | 50,8 |
| ueberlebt (выздоро- вел) | 16 | 52 | 76,5 | ||
| 64,1 | |||||
| Overall Percentage (Суммарный процентный показатель) | |||||
| StepS (Шаг 3) | Outcome (Исход) | gestorben (сконча- лся) | 33 | 30 | 52,4 |
| ueberlebt (выздоро- вел) | 19 | 49 | 72,1 | ||
| Overall Percentage (Суммарный процентный показатель) | 62,6 | ||||
| Step 4 (Шаг 4) | Outcome (Исход) | gestorben (сконча-лся) | 37 | 26 | 58,7 |
| ueberlebt (выздоро- вел) | 12 | 56 | 82,4 | ||
| 71,0 | |||||
| Overall Percentage (Суммарный процентный показатель) | |||||
a. The cut value is ,500 (Разделительное значение равно ,500)
Прогноз оправдался для 58,7 % умерших пациентов и для 82,4 % выздоровевших. Значения коэффициента Ь. и константы а для расчёта вероятности (выздоровления) находятся в следующей таблице:
Variables in the Equation (Переменные в уравнении)
В Коэф-фициент регрессии В) | S.E. (Стандар-тная ошибка) | Wald (Валь-довский) | df | Sig. (Значи- мость) | Ехр (В) | ||
Шаг 1а | BZEIT | -,081 | ,028 | 8,482 | 1 | ' ,004 | ,922 |
Конста- нта | 1,104 | ,385 | 8,205 | 1 | ,004 | 3,017 | |
Шаг 2b | GR | ,038 | ,017 | 5,109 | 1 | ,024 | 1,039 |
BZEIT | -,073 | ,028 | L 6,688 | 1 | ,010 | ,930 | |
Конста- нта | -5,460 | 2,924 | L 3,487 | 1 | ,062 | ,004 | |
Шаг 3c | КОВ | -2,678 | 1,264 | 4,489 | 1 | ,034 | ,069 |
GR | ,037 | ,017 | 4,622 | 1 | ,032 | 1,038 | |
BZEIT | -,077 | ,029 | 6,866 | 1 | ,009 | ,926 | |
Конста- нта | -2,995 | 3,192 | ,880 | 1 | ,348 | ,050 | |
Шаг 4d | ALTER (возраст) | -.037 | ,017 | 4,653 | 1 | ,031 | ,963 |
КОВ | -3,028 | 1,302 | 5,410 | 1 | ,020 | ,048 | |
GR | ,044 | ,017 | 6,650 | 1 | ,010 | 1,045 | |
BZEIT | -,062 | ,029 | 4,639 | 1 | ,031 | ,940 | |
Конста- нта | -2,884 | 3,079 | ,877 | 1 | ,349 | ,056 |
a. Variable(s) entered on step 1: BZEIT. (Переменные, вводимые на шаге 1: BZEIT.)
b. Variable(s) entered on step 2: GR. (Переменные, вводимые на шаге 2: GR.)
с. Variable(s) entered on step 3: КОВ. (Переменные, вводимые на шаге 3: КОВ.)
d. Variable(s) entered on step 4: ALTER. (Переменные, вводимые на шаге 4: ALTER.)
Если мы рассмотрим случай с 30-тилешим пациентом, с ростом 180 см, которому делали искусственное дыхание в течении 10 часов при концентрации кислорода в смеси равной 0,7, то исходя из соотношения
z= - 2,884- 0,037x30- 0,062x10+ 0,044x180- 3,028x0,7= 1,12В получим вероятность выздоровления
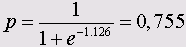
следовательно, вероятность выздоровления пациента равна 0,755
21.gif
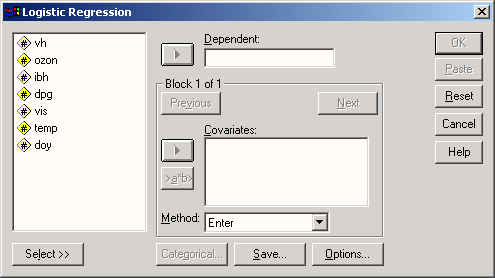
22.gif
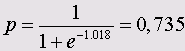
23.gif

16.5 Мультиномиальная логистическая регрессия
16.5 Мультиномиальная логистическая регрессия
Этот метод является вариантом логистической регрессии, при которой зависимая переменная не является дихотомической, как при бинарной логистической регрессии, а имеет больше двух категорий. В то время как, при бинарной логистической регрессии независимая переменная может иметь интервальную шкалу, то мультиномиальная логистическая регрессия пригодна только для категориальных независимых переменных, причём имеет значение, относятся ли они к шкале наименований или к порядковой шкале. Конечно же, не исключается возможность задания в качестве ковариат переменных, имеющих интервальную шкалу.
Начиная с 10 версии SPSS для независимых переменных, относящихся к порядковой шкале предусмотрен метод порядковой регрессии (см. гл. 16.6), который в данном случае является предпочтительным.
Для представления метода мольтиномиальной логистической регрессии был сначала взят простой пример с одной независимой переменной. Данные для этого примера "ыли взяты из ALLBUS (общий социологический опрос населения) 1998 года.
-
Откройте файл polein.sav, и при помощи выбора меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты)
достройте частотные таблицы для четырёх переменных, находящихся в этом файле:
Alter (Возраст)
| Frequency (Частота) | Percent (Процент) | Valid Percent (Действи- тельный процент) | Cumulative Percent (Совокупный процент) | |
Valid (Действи- тельное значение) | bis 45 Jahre (До 45 лет) | 1306 | 50,1 | 50,1 | 50,1 |
ueber 45 Jahre (Свыше 45 лет) | 1301 | 49,9 | 49,9 | 100,0 | |
Total (Сумма) | 2607 | 100,0 | 100,0 |
| |
Politische Links-Rechts-Einschaetzung (Политическая принадлежность к левым или правым)
| Frequency (Частота) | Percent (Процент) | Valid Percent (Действи- тельный процент) | Cumulative Percent (Совокупный процент) | |
Valid (Действи- тельное значение) | eher links (Скорее левый) | 740 | 28,4 | 28,4 | 28,4 |
Mitte (Центрист) | 1212 | 46,5 | 46,5 | 74,9 | |
eher rechts (Скорее правый) | 655 | 25,1 | 25,1 | 100,0 | |
Total (Сумма) | 2607 | 100,0 | 100,0 |
| |
Schicht (Прослойка)
Frequency (Частота) | Percent (Процент) | Valid Percent (Действи- тельный процент) | Cumulative Percent (Совокупный процент) | ||
Valid (Действи- тельное | Unterschicht (Нижняя прослойка) | 879 | 33,7 | 33,7 | 33,7 |
значение) | Mittelschicht (Средняя прослойка) | 1477 | 56,7 | 56,7 | 90,4 |
| Oberschicht (Верхняя прослойка) | 251 | 9,6 | 9,6 | 100,0 |
| Total (Сумма) | 2607 | 100,0 | 100,0 |
|
Schulbildung (Школьное образование)
Frequency (Частота) | Percent (Процент) | Valid Percent (Действи- тельный процент) | Cumulative Percent (Совокупный процент) | ||
Valid (Действи- тельное значение) | Hauptschule (Неполное среднее) | 1499 | 57,5 | 57,5 | 57,5 |
Mittlere Reife (Среднее) | 610 | 23,4 | 23,4 | 80,9 | |
Abitur (Атестат зрелости) | 498 | 19,1 | 19,1 | 100,0 | |
Total (Сумма) | 2607 | 100,0 | 100,0 |
| |
Мы хотим рассмотреть переменную polire (Политическая принадлежность к левым или правым) как зависимую переменную, а три остальные — как независимые переменные (факторы). В первом примере в качестве независимой переменной мы возьмем только переменную "Alter" (Возраст). Прежде всего построим таблицу сопряженности для этих двух переменных.
-
Выберите в меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
Переменной alter присвойте статус строчной переменной, a polire — столбцовой переменной, и через выключатель Cells... (Ячейки) активируйте вывод процентных показателей для ячеек.
Alter * Politische Links-Rechts-Einschfltzung Crosstabulation
(Возраст * Политическая принадлежность к левым или правым - таблица сопряженности)
| Politische Links-Rechts-Einschfltzung (Политическая принадлежность к левым или правым) | Total (Сумма) | ||||
eher links (Скорее левый) | Mitte (Цент- рист) | eher rechts (Скорее правый) | ||||
Alter (Воз-раст) | bis 45 Jahre (До 45 лет) | Count (Коли- чество) | 446 | 615 | 245 | 1306 |
| % of Total (% от возраста) | 34,2% | 47,1% | 18,8% | 100,0% | ||
ueber 45 Jahre (Свыше 45 лет) | Count % of Total (Коли- чество) | 294 | 597 | 410 | 1301 | |
| (% от возраста) | 22,6% | 45,9% | 31,5% | 100,0% | ||
Total (Сум- ма) | Count (Коли- чество) | 740 | 1212 | 655 | 2607 | |
| % of Total (% от возраста) | 28,4% | 46,5% | 25,1% | 100,0% | ||
Для младшей возрастной категории политическое самоопределение имеет тенденцию склонения симпатий к левым партиям, а для старшей — скорее к правым. Рассмотрим простую мультиномиальную логистическую модель, которая отражает взаимосвязь между политическим самоопределением и возрастом.
Так как политическое самоопределение, как зависимая переменная, включает три категории, то для определения вероятностей отнесения респондентов к этим трем категориям можно сформировать два недублированных логита, причём последняя категория "eher rechts" (скорее правый) будет использоваться как эталонная:
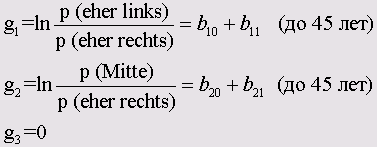
Нахождение коэффициентов b10, b11, b20 и b21 (называемых параметрическими оценками) и является основной задачей мультиномиальной логистической регрессии. Первая цифра индекса указывает на номер логита, а вторая на порядковый номер коэффициента в данном логите, причём цифра 0 на второй позиции индекса означает константу, за которой далее следует ровно столько коэффициентов, сколько независимых переменных (факторов) взято в рассмотрение. Коэффициентам последней (эталонной) категории присваивается значение 0.
Переменная Alter (Возраст), как единственная независимая переменная, имеет две категории, одна из которых рассматривается как эталонная, ее коэффициенты принимаются равными 0.
-
Выберите в меню Analyze (Анализ) Regression ...(Регрессия) Multinomial Logistic... (Мультиномиальная логистическая)
Откроется диалоговое окно Multinomial Logistic Regression (Мультиномиальная логистическая регрессия).
-
Переменную polire поместите в поле для зависимых переменных, а переменную alter (возраст) в поле для факторов и нажмите выключатель Statistics (Статистики).
Откроется диалоговое окно Multinomial Logistic Regression: Statistics (Мультиномиальная логистическая регрессия: Статистики)
-
Оставьте активированным вывод параметрических оценок с доверительным интервалом соответствующим 95 % и покиньте это диалоговое окно нажатием Далее и ОК.
Рис. 16.17: Диалоговое окно Multinomial Logistic Regression (Множественная логистическая регрессия)
Рис. 16.18: Диалоговое окно Multinomial Logistic Regression: Statistics (Множественная логистическая регрессия: Статистики)
Содержание таблицы результатов расчёта, выглядит следующим образом. Для не дублирующих категорий она содержит параметрические оценки, стандартную ошибку, проверку значимости при помощи статистики Вальда, значение экспоненциальной функции от параметрической оценки и его доверительный интервал.
Parameter Estimates (Оценки параметров)
Politische Links-Rechts-Einschaetzung (Политическая принадлежность к левым или правым) | В | Std. Error (Станда- ртная ошибка) | Wald (Вальд) | df (Сте-пень сво- боды) | Sig. (Значи- мость) | Ехр(В) | 95% Confidence Interval for Ехр(В) (95 % довери- тельный интервал для Ехр(В)) | ||
Lower Bound (Нижний предел) | Upper Bound (Верхний предел) | ||||||||
eher links (Скорее левый) | Intercept (Постоян- ное слага- емое) | -,333 | ,076 | 18,938 | 1 | ,000 |
|
|
|
[ALTER= 1,00] | ,932 | ,110 | 71,353 | 1 | ,000 | 2,539 | 2,045 | 3,151 | |
[ALTER= 2,00] | Оа | 0 |
| 0 |
| , |
|
| |
Mitte (Цен-трист) | Intercept (Постоян- ное слага-емое) | ,376 | ,064 | 34,320 | 1 | ,000 |
|
|
|
[ALTER= 1,00] | ,545 | ,099 | 30,198 | 1 | ,000 | 1,724 | 1,420 | 2,094 | |
rALTER= 2,00] | 0" | 0 |
| 0 |
|
|
|
| |
a. This parameter is set to zero because it is redundant (Данный параметр обнуляется, т.к. он является дублирующим)
Из таблицы можно взять следующие значения для b-коэффициентов:
b10 =-0,333
b11 (до 45 лет) = 0,932
b20 = 0,376
b21 (до 45 лет) = 0,545 1
Таким образом, для возрастной группы до 45 лет получим
g1 = -0,333 + 0,932 = 0,599
g2 = -0,376 + 0,545 = 0,921
и следовательно
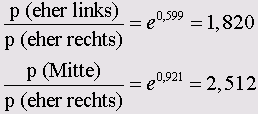
Для дублирующего логита по правилам вычисления логарифма справедливо
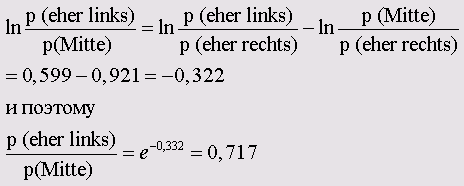
К примеру, в возрастной категории до 45 лет вероятность быть более склонным к тевым течениям в 1,820 раз выше вероятности склонности к правым течениям. Такой же расчёт можно произвести и для другой возрастной категории; в данном случае будут отсутствовать коэффициенты b11 и b21, т.к. они приравниваются к нулю.
Следует отметить, что прямое определение вероятности для трёх категорий политической самооценки, интересней, чем соотношение этих вероятностей между собой. Для каждой i-ой категории зависимых переменных эта вероятность может быть вычислена по следующей формуле:
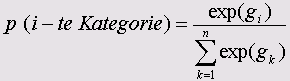
Здесь для большей удобочитаемости экспоненциальная функция обозначена как ехр. n указывает на число категорий (здесь n=3).
Для возрастной группы до 45 лет для трёх категорий политической самооценки получатся следующие вероятности:
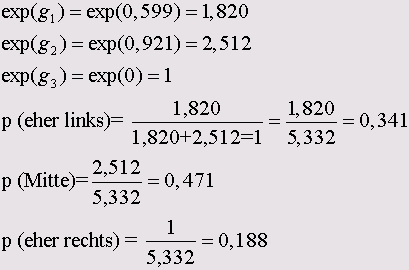
Стало быть, для отдельного человека, принадлежащего к возрастной группе до 45 лет вероятность склонения политической самооценки в сторону левых составляет, 0,341 или 34,1 %, в сторону центристов 47,1 % и в сторону правых 18,8 %. Внимательный читатель может заметить, что эти числа соответствуют процентным показателям таблицы сопряженности для возраста и политической самооценки. Таким образом, в случае наличия лишь одной независимой переменной легко удостовериться в правдоподобности расчётов, производимых при мультиномиальной логистической регрессии.
Для возрастной группы свыше 45 лет расчёты будут выглядеть следующим образом:
g1 = - 0,333 + 0 = - 0,333
g2 = 0,376 + 0 = 0,376
gз=0
ехр (g1) - ехр (-0,333) = 0,717
ехр (g2). ехр (0,376) = 1,456
ехр (g3) = ехр (0) = 1
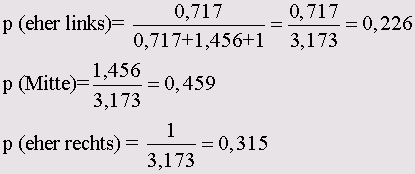
Если выразить полученные показатели в процентах, то и здесь так же наблюдается полное согласование с соответствующими процентными показателями таблицы сопряженности.
Следует отметить, что только в случае наличия лишь одной независимой переменной, как в приведённом примере, проведение расчёта с применением столь громоздкого метода, как многозначная логистическая регрессия, является достаточно бессмысленным — все соотношения могут быть выяснены проще, при помощи таблиц сопряженности. Поэтому мы введем в рассмотрение ещё одну дополнительную переменную — переменную schule (образование).
-
В диалоговом окне Multinomial Logistic Regression (Мультиномиальная логистическая регрессия) поместите переменную schule вместе с переменной alter в поле факторов.
-
В диалоговом окне Multinomial Logistic Regression: Statistics (Мультиномиальная логистическая регрессия: Статистики) активируйте дополнительные опции Cell probabilities (Вероятность по ячейкам) и Likelihood ratio test (Тест отношения правдоподобия) и начните расчёт вновь.
Таблица теста коэффициентов правдоподобия содержит изменения функции правдоподобия для случая, когда исключается соответствующий главный действующий фактор; эти изменения выражаются через соответствующие значения теста %2 (хи-квадрат). Выдаваемый уровень значимости р < 0,001 указывает на то, что оба фактора (возраст и школьное образование) оказывают очень значимое влияние на зависимую переменную (политическая самооценка).
Model Fitting Information (Информация о приближении, обеспечиваемой моделью)
Model (Модель) | -2 Log likelihood (-2 логарифми- ческое правдопо- добие) | Chi-square (Хи-квадрат) | df (степень свободы) | Sig. (Значи- мость) |
Intercept Only (Только постоянное слагаемое) | 252,208 | |||
Final (Оконча- тельно) | 93,429 | 158,779 | 6 | ,000 |
Likelihood Ratio Tests (Тест отношения правдоподобия)
(Результат) | -2 Log Likelihood of Reduced Model (-2 логарифми-ческое правдоподобие для сокращённой модели) | Chi-square (Хи-квадрат) | df (Степень свободы) | Sig. (Значи- мость) |
Intercept (Постоянное слагаемое) | 93,429 | ,000 | 0 | • |
ALTER (Возраст) | 171,496 | 78,067 | 2 | ,000 |
SCHULE (Образо- вание) | 178,489 | 85,060 | 4 | ,000 |
The chi-square statistic is the difference in -2 tog-likelihoods between the final model :-~d a reduced model. The reduced model is formed by omitting an effect from the final model. The null hypothesis is that all parameters of that effect are 0 (Статистика хи-квадрат отображает различие -2 логарифмического правдоподобия между окончательной моделью и усеченной моделью. Суть расчёта усеченной модели сводится к тому, что из окончательной модели исключается один фактор влияния.
Нулевая гипотеза соответствует обнулению всех параметров параметрических оценок данного фактора влияния).
Таблица (b — коэффициентов) выглядит следующим образом.
Parameter Estimates (Оценки параметров) | |||||||||
Politische Links-Rechts-Einschaetzung Политическая принадлежность к левым пли правым) | В | Std. Error (Стан- дартная ошибка) | Wald (Вальд) | df (Сте-пень сво-боды) | Sig. (Значи- мость) | Exp (В) | 95% Confidence Interval for Exp(B) (95 % довери- тельный интервал для Ехр(В)) | ||
Lower Bound (Ниж-ний пре-дел) | Upper Bound (Верх-ний пре-дел) | ||||||||
eher links (Ско- рее левый) | (Посто-янное слага-емое) | -,129 | ,137 | ,8feO | 1 | ,345 |
|
|
|
[ALTER= 1,00] | ,952 | ,117 | 66,600 | 1 | ,000 | 2,591 | 2,061 | 3,256 | |
ALTER= 2,00] | Oa | 0 |
| 0 |
| , | , |
| |
SCHULE= 1,00] | -,179 | ,142 | ,592 | 1 | ,207 | ,836 | ,632 | 1,104 | |
SHULE= 2,00] | -,480 | ,158 | 9,249 | 1 | ,002 | ,619 | ,454 | ,843 | |
[SHULE= 3,00] | 0" | 0 | l | 0 |
| , | , |
| |
Mine (Цент-рист) | (Постоян-ное слага-емое) | -,236 | ,137 | 2,982 | 1 | ,084 |
|
|
|
[ALTER= 1,00] | ,766 | ,106 | 52,174 | 1 | ,000 | 2,152 | 1,748 | 2,939 | |
[ALTER= 2,00] | Oa | 0 |
| 0 | , |
|
|
| |
[SCHULE= 1,00] | ,802 | ,141 | 32,539 | 1 | ,000 | 2,231 | 1,693 | 2,939 | |
[SHULE= 2,00] | ,149 | ,155 | ,922 | 1 | ,337 | 1,161 | ,856 | 1,574 | |
[SHULE= 3,00] | Oa | 0 | , | 0 | , | , | , | , | |
a. This parameter is set to zero because it is redundant (Данный параметр обнуляется, так как он является дублирующим)
В качестве примера определим вероятности для политической самооценки отдельного человека, принадлежащего к возрастной группе свыше 45 лет с неполным средним образованием. Для этого по аналогии с предыдущим примером произведём следующие вычисления:
g1 = - 0,129 + 0 - 0,179= - 0,308
g2 = - 0,236 + 0 + 0,802 = 0,566
gз= 0
exp (g1) = 0,735
exp (g2) = 1,761
exp (g3) - 1
Если перевести данные результаты в процентные показатели, то они будут означать, что среди граждан в возрасте свыше 45 лет с неполным средним образованием 21,0 % симпатизируют левым политическим течениям, 28,6 % правым, а 50,4 % остаются по центру.
Нет необходимости вычислять процентные показатели вероятностей самостоятельно. Вы можете взять их из следующей таблицы, отображающей наблюдаемые и прогнозируемые частоты:
Observed and Predicted Frequencies (Наблюдаемые и прогнозируемые частоты) | |||||||
Schulb-ildung (Образо- вание) | Alter (Возраст) | Politische Links-Rechts-Einschfltzung (Политическая левая или правая принадлежность) | Frequency (Частота) | Percentage (Процент) | |||
Observed (Наблю-даемая) | Predicted (Прогно-зируемая) | Pearson Residual (Остаток Пирсона) | Observed (Набл-юдаемый) | Predicted (Прогно-зируемый) | |||
Haupt- schule (Непол-ное среднее) | bis 45 Jahre (До 45 лет) | eher links (Скорее левый) | 143 | 157,488 | -1,365 | 25,8% | 28,4% |
Mitte (Центрист) | 312 | 313,760 | -,151 | 56,3% | 56,6% | ||
eher rechts (Скорее правый) | 99 | 82,752 | 1,937 | 17,9% | 14,9% | ||
ueber 45 Jahre(Свыше 45 лет) | eher links (Скорее левый) | 213 | 198,512 | 1,157 | 22,5% | 21,0% | |
Mitte (Центрист) | 478 | 476,240 | ,115 | 50,6% | 50,4% | ||
eher rechts (Скорее правый) | 254 | 270,248 | -1,170 | 26,9% | 28,6% | ||
Mifflere Reife (Сред-нее) | bis 45 Jahre (до 45 лет) | eher links (Скорее левый) | 129 | 131,561 | -,271 | 31,5% | 32,2% |
Mitte (Центрист) | 192 | 184,113 | ,784 | 46,9% | 45,0% | ||
eher rechts (Скорее правый) | 88 | 99,326 | -,628 | 21,5% | 22.8% | ||
ueber 45 Jahre(Свыше 45 лет) | eher links (Скорее левый) | 47 | 44,439 | ,435 | 23,4% | 22.1% | |
Mitte (Центрист) | 67 | 74,887 | -1,151 | 33,3% | 37,3% | ||
eher rechts (Скорее правый) | 87 | 81,674 | ,765 | 43,3% | 40,6% | ||
Abitur (Аттестат зрелости) | bis 45 Jahre (до 45 лет) | eher links (Скорее левый) | 174 | 156,952 | 1,848 | 50,7% | 45,8% |
Mitte (Центрист) | 111 | 117,127 | -,698 | 32,4% | 34,1% | ||
eher rechts (Скорее правый) | 58 | 68,922 | -1,472 | 16,9% | 20,1% | ||
ueber 45 Jahre(Свыше 45 лет) | eher links (Скорее левый) | 34 | 51,048 | -2,914 | 21,9% | 32,9% | |
Mitte (Центрист) | 52 | 45,873 | 1,078 | 33,5% | 29,6% | ||
eher rechts (Скорее правый) | 69 | 58,078 | 1,812 | 44,5% | 37,5% | ||
The percentages are based on total observed frequencies in each subpopulation (Процентные показатели основываются на наблюдаемых суммарных частотах для каждой частичной совокупности).
Теперь вы можете видеть, что наблюдаемые и прогнозированные значения оказались рассогласованными. Это произошло потому, что теперь в модель входят только главные факторы влияния, а не взаимодействия.
-
Чтобы это изменить, в диалоговом окне Multinomial Logistic Regression (Мультиномиальная логистическая регрессия) задействуйте выключатель Model (Модель).
Откроется диалоговое окно Multinomial Logistic Regression: Model (Мультиномиальная логистическая регрессия: Модель).
Вы можете включить в расчёт все главные факторы влияния и взаимодействия, если вместо предварительно установленной по умолчанию опции Main effects (Основные эффекты) активируете опцию Full factorial (Полнофакторная модель). При помощи опции Custom (Пользовательский режим), Вы можете отобрать включаемые в расчёт факторы влияния.
-
Активируйте опцию Full factorial (Полнофакторная модель) и начните расчёт вновь.
В таблице оценки параметра теперь находятся и взаимодействия. Если Вы обратите внимание на наблюдаемые и ожидаемые частоты, то заметите, что теперь они совпадают.
Рис. 16.19: Диалоговое окно Multinomial Logistic Regression: Model (Множественная логистическая регрессия: Модель)
-
Постройте самостоятельно ещё одну логистическую регрессию, в которой Вы можете взять .переменную schicht (Принадлежность к прослойке) в качестве третьего фактора.
25.gif
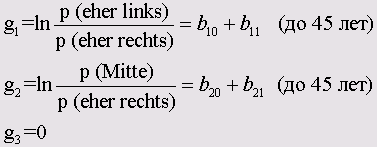
26.gif
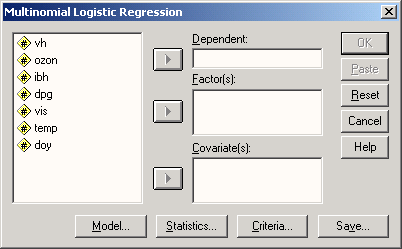
27.gif
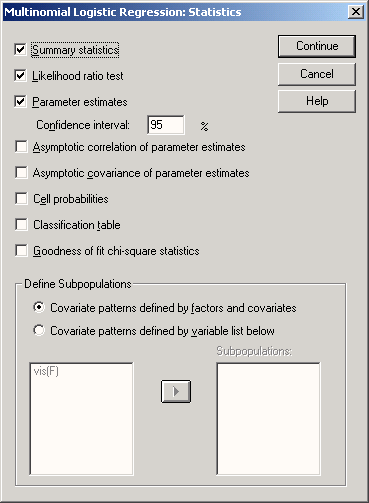
28.gif
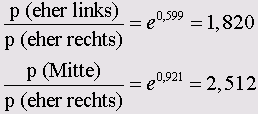
29.gif
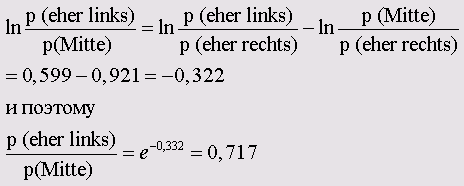
30.gif
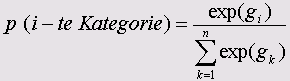
31.gif
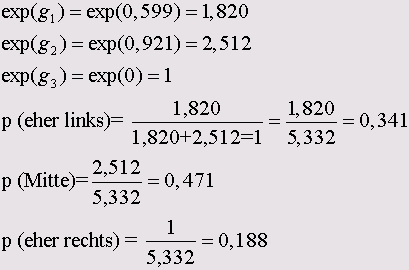
32.gif
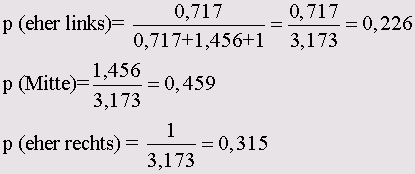
33.gif
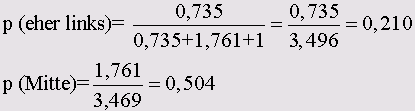
35.gif
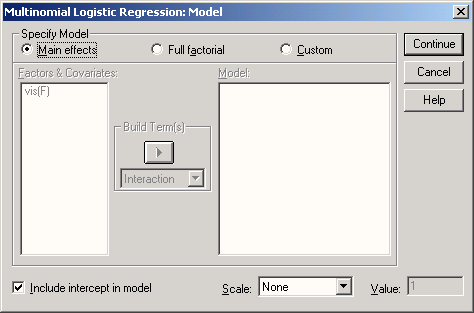
16.6 Порядковая регрессия
16.6 Порядковая регрессия
В то время как, мультиномиальная регрессия, представленная в разделе 16.5, предназначена для зависимой переменной, относящейся к номинальной шкале, то порядковая регрессия предназначена для целевой переменной, принадлежащей к порядковой шкале. Независимые переменные и здесь должны быть категориальными (то есть иметь номинальную или порядковую шкалу), однако в качестве ковариат допускается применение переменных с интервальной шкалой.
Мы изучим данный метод при помощи примера из области психологии. В главе 19.3 будет рассматриваться "Анкета о специфике лечения психических заболеваний в больнице Фрайбурга", которая дает представление о работе с пациентами на основании 35 отдельных пунктов. К примеру, восприимчивость пациента к целенаправленным лечебным действиям выясняется при помощи пункта "Разработать план и затем приступить к его воплощению", причём ответ даётся в соответствии с пятибалльной шкалой: от "абсолютно не верно" (кодировка 1) до "абсолютно верно" (кодировка 5).
Эта типичная порядковая переменная должна быть исследована в зависимости от возраста, пола, продолжительности болезни и образования. Значения приведенных переменных были собраны в отношении 85 пациентов и находятся в файле plan.sav.
-
Откройте файл plan.sav.
-
Выберите в меню Analyze... (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты) и постройте частотные таблицы для всех переменных.
Alter (Возраст)
Freq-uency (Часто-та) | Percent (Про-цент) | valid Percent (Действи- тельный процент) | uumuiative percent (Совокупный процент) | ||
Valid (Действи-тельное значение) | bis 40 Jahrejflo 45 лет) | 29 | 34,1 | 34,1 | 34,1 |
41-55 Jahre (41-55 лет) | 29 | 34,1 | 34,1 | 68,2 | |
ueber 55 Jahre (Свыше 55 лет) | 27 | 31,8 | 31,8 | 100,0 | |
Total (Сумма) | 85 | 100,0 | 100,0 | |||
Geschlecht (Пол)
Frequ-ency (Часто-та) | Percent (Про-цент) | Valid Percent (Действи- тельный процент) | Cumulative Percent (Совокупный процент | ||
Valid (Действи-тельное значение) | maennlich (Мужской) | 44 | 51,8 | 51,8 | 51,8 |
weiblich (Женский) | 41 | 48,2 | 48,2 | 100,0 | |
Total (Сумма) | 85 | 100,0 | 100,0 |
Krankheitsdauer (Продолжительность болезни)
Frequ-ency (Часто-та) | Percent (Про-цент) | Valid Percent (Действи- тельный процент) | Cumu-lative Percent (Сово-купный процент) | ||
Valid | bis 5 Jahre {До 5 лет) | 24 | 28,2 | 28,2 | 28,2 |
(Действи- | 6-10 Jahre (6-1 Олег) | 16 | 18,8 | 18,8 | 47,1 |
тельное | 11-20 Jahre (11-20 лет) | 32 | 37,6 | 37,6 | 84,7 |
значение) | ueber 20 Jahre (Свыше 20 лет) | 13 | 15,3 | 15,3 | 100,0 |
Total (Сумма) | 85 | 100,0 | 100,0 |
Schulbildung (Образование)
Freq-uency (Часто- та) | Percent (Про-цент) | Valid Percent (Действи- тельный процент) | Cumu-lative Percent (Сово-купный процент) | ||
Valid (Действи-тельное значение) | Haupt-schule (неполное среднее) | 53 | 62,4 | 62,4 | 62,4 |
Mittlere Reife (среднее) | 18 | 21,2 | 21,2 | 83,5 | |
Abitur (аттестат зрелости) | 14 | 16,5 | 16,5 | 100,0 | |
Total (Сумма) | 85 | 100,0 | 100,0 |
Einen Plan machen und danach handeln (Разработать план и затем приступить к его воплощению)
Freq-uency (Часто-та) | Percent (Про-цент) | Valid Percent (Действи-тельный процент) | Cumu-lative Percent (Сово-купный процент) | ||
Valid (Действи-тельное значе- ние) | gar nicht (абсолютно не верно) | 24 | 28,2 | 28,2 | 28,2 |
Wenig (слабо) | 18 | 21,2 | 21,2 | 49,4 | |
mittelmaessig (посред- ственно) | 18 | 21,2 | 21,2 | 70,6 | |
ziemlich(достаточно) | 16 | 18,8 | 18,8 | 89,4 | |
sehr stark (абсолютно верно) | 9 | 10,6 | 10,6 | 100,0 | |
(Сумма) | 85 | 100,0 | 100,0 |
-
Если Вы с помощью меню Analyze...(Анализ) Correlate (Корреляция) Bivariate... (Парная)
произведёте расчёт ранговой корреляции по Спирману между пунктом "Составить план и затем приступить к его воплощению" и другими переменными (с использованием синтаксических приемов, описанных в главе 26.3), то получите следующий результат:
Correlations (Корреляции)
Einen Plan machen und danach handeln (Разработать план и затем приступить к его воплощению) | |||
Spearman's rho (p Спирмана) | Alter (Возраст) | Correlation Coefficient (Корре-ляционный коэффициент) | -,376** |
Sig. (2-tailed) (Значимость (2-сторонняя)) | ,000 | ||
N | 85 | ||
Geschlecht (Пол) | Correlation Coefficient (Корре-ляционный коэффициент) | ,298" | |
Sig. (2-tailed) (Значимость (2-сторонняя)) | ,006 | ||
N | 85 | ||
Krankheitsda uer (Продолжи- тельность болезни) | Correlation Coefficient (Корре-ляционный коэффициент) | -,260* | |
Sig. (2-tailed) (Значимость (2-сторонняя)) | ,016 | ||
N | 85 | ||
Schulbildung (Образование) | Correlation Coefficient (Корре-ляционный коэффициент) | ,314** | |
Sig. (2-tailed) (Значимость (2-сторонняя)) | ,003 | ||
N | 85 |
**. Correlation is significant at the .01 level (2-tailed) (Корреляция является значимой на уровне 0,01 (2 - сторонняя)).
*. Correlation is significant at the .05 level (2-tailed) (Корреляция является значимой на уровне 0,01 (2 - сторонняя)).
Стало быть, существует значимая, хоть и не очень большая корреляция. Если учесть принятое кодирование переменных, то можно заметить, что женщины более склонны сначала составить план действий, а затем приступать к лечению, чем мужчины. Кроме того, более молодые пациенты, пациенты с непродолжительным периодом болезни и пациенты, имеющие высшее образование, более активно занимаются своим лечением.
Попытаемся теперь изучить одновременное влияние возраста, пола, продолжительности болезни и образования на целевую переменную "Разработать план и затем приступить к его воплощению". Подходящим методом для этого является порядковая регрессия.
-
Выберите в меню Analyze (Анализ) Regression (Регрессия) Ordinal... (Порядковая)
Откроется диалоговое окно Ordinal Regression (Порядковая регрессия).
Рис. 16.20: Диалоговое окно Ordinal Regression (Порядковая регрессия)
-
Переменной plan (план) присвойте статус зависимой переменной, а переменным alter (возраст), g, kdauer (продолжительность болезни) и schule (образование) — статус факторов.
-
В поле Covariate(s) (Ковариаты) вы можете внести ковариаты, относящиеся к интервальной шкале. Однако, в нашем примере таковые отсутствуют.
-
Нажмите кнопку Options... (Опции).
Наряду с параметрами, которые управляют итерационным процессом (предварительные установки для них мы оставляем без изменения), можно выбрать одну из пяти связующих функций, смысл которых будет пояснен далее. Функцией, установленной по умолчанию, является Logit (Логит); эта связь, как правило, оказывается лучшей.
-
Щёлкните на кнопке Output... (Вывод). Откроется диалоговое окно Ordinal Regression:Output (Порядковая регрессия: Вывод).
Здесь Вы получаете возможность управлять данными, выводимыми в окне просмотра и создавать новые переменные.
-
В разделе Display (Показать) оставьте предварительные установки Goodness of Jit statistics (Статистика критерия согласия), Summary statistics (Отчётная статистика) и Parameter estimates (Параметрические оценки). В разделе Saved variables (Сохранённые переменные) активируйте опции Estimated response probabilities (Оценочные вероятности отклика), Predicted category (Прогнозируемая категория) и Predicted category probability (Вероятность прогнозируемой категории).
-
Теперь нажмите кнопку Location... (Положение)
Здесь у Вас появляется возможность выбора между моделью, которая содержит только главные факторы влияния и, в случае необходимости, — ковариаты, а также моделью, которую Вы можете подобрать самостоятельно (Custom). В последнем случае у Вас появляется возможность учесть также все мыслимые взаимодействия. В данном случае, сначала мы хотим учесть только главные эффекты, что соответствует предварительной установке.
-
Посредством кнопки Scale... (Шкала) можно ввести, так называемые, компоненты шкалы. Как правило, это не является необходимым, и мы от них откажемся.
-
Начните расчёт нажатием ОК.
Рис. 16.21. Диалоговое окно Ordinal Regression: Output (Порядковая регрессия: Вывод)
Отображение результатов в окне просмотра начинается с вывода предостережения. В 66,2% всех ячеек, которые образовываются из комбинаций факторов и зависимых переменных, частота равна нулю. При этом не учитываются те комбинации факторов, которые повторяются. Вы можете включить в список выдачи наблюдаемые и ожидаемые частоты, а также их остатки, если после нажатия кнопки Output... (Вывод) активируете опцию Cell infonnation (Информация по ячейкам).
Warnings (Предостережения)

Далее следует таблица, содержащая абсолютные и выраженные в процентах частоты различных категорий зависимых переменных и факторов.
Case Processing Summary (Сводная таблица обработки наблюдений)
N (Коли-чество) | Marginal Percentage (Предельный процент) | ||
Einen Plan machen und danach handeln (Разработать план и затем приступать к лечению) | gar nicht (Абсолютно не верно) | 24 | 28,2% |
wenig (Слабо) | 18 | 21,2% | |
mittelmaessig (Посредственно) | 18 | 21,2% | |
ziemlich (Достаточно) | 16 | 18,8% | |
sehr stark (Абсолютно верно) | 9 | 10,6% | |
Alter (Возраст) | bis 40 Jahre (До 45 лет) | 29 | 34,1% |
41-55 Jahre (41-55 лет) | 29 | 34,1% | |
ueber 55 Jahre (Свыше 55 лет) | 27 | 31,8% | |
Geschlecht (Пол) | maennlich (Мужской) | 44 | 51,8% |
weiblich (Женский) | 41 | 48,2% | |
Krankheitsdauer (Продолжительность болезни) | bis 5 Jahre (До 5 лет) | 24 | 28,2% |
6-10 Jahre (6-10 лет) | 16 | 18,8% | |
(6-10 лет) | 32 | 37,6% | |
11-20 Jahre (11 -20 лет) | 13 | 15,3% | |
Schulbildung (Образование) | Hauptschule (Неполное среднее) | 53 | 62,4% |
Mittlere Reife (Среднее) | 18 | 21,2% | |
Abitur (Аттестат зрелости) | 14 | 16,5% | |
Valid (Действительное значение) | 85 | 100,0% | |
Missing (Пропущенное значение) | 0 | ||
Tola (Сумма) | 85 | ||
В качестве оценки значимости вклада отдельных независимых переменных в улучшение прогнозов, получаемых с помощью модели также, как и при бинарной логистической регрессии, служит отрицательное значение 2LL (Удвоенное значение логарифма функции правдоподобия). Разность между начальным значением ("Только постоянное слагаемое") и конечным значением ("Окончательно") указывается в виде значения теста хи-квадрат. которому соотнесен соответствующий уровень значимости. В приведенном примере наблюдается очень значимое улучшение (р < 0,001).
Model Fitting Information (Информация о приближении модели)
Model (Модель) | -2 Log likelihood (-2 логарифми-ческое правдоподобие) | Chi-Square (Хи-квадрат) | df (Степень свободы) | Sig. (Значи-мость) |
Intercept Only (Только постоянное слагаемое) | 207,180 | |||
Final (Окончательно) | 170,408 | 36,772 | 8 | ,000 |
Link function: Logit (Связывающая функция: Логит). | ||||
Для проверки, будут ли наблюдаемые частоты по ячейкам значимо отличаться от ожидаемых частот, рассчитанных на основе модели, выполняется хи-квадрат тест по Пирсону. Его результатом, для данного примера, является не значимая разность значений (р = 0,190), что говорит о достижении высокой степени приближения. Однако, следует обратить внимание на то, что из-за большого количества пустых ячеек применение теста хи-квадрат становится проблематичным.
Goodness of fit (Критерий согласия)
Chi-Square (Хи-квадрат) | df (Степень свободы) | Sig. (Значимость) | |
Pearson (Пирсон) | 158,733 | 144 | ,190 |
Deviance (Отклонение) | 127,454 | 144 | ,835 |
Link function: Logit (Связывающая функция: Логит).
Из трёх мер согласия приведенных ниже, мера, вычисленная по методу Нагелькерке (Nagelkerke) является мерой определённости, которая указывает на процентную долю дисперсии, объяснимой при помощи порядковой регрессии, (см. разд. 16.4). В приведенном примере оценка дисперсии составляет 36,7 %.
Pseudo R-Square (Псевдо R-квадрат)
Сох and Snell (Кокс и Шелл) | ,351 |
Nagelkerke (Нагелькерке) | ,367 |
McFadden (МакФадден) | ,138 |
Linkfunction: Logit (Связывающая функция: Логит).
Результатом анализа являются оценки параметров регрессии приведенные в нижеследующей таблице.
Parameter Estimates (Оценки параметров регрессии) | ||||||||
| Esti-mate (Оце-нка) | Std. Error (Стандар-тная ошибка) | Wald (Валь-дов-ский) | df (Сте-пень сво-боды) | Sig. (Значи-мость) | 95% Confidence Interval (95 % довери- тельный интервал) | ||
Lower Bound | Upper Bound | |||||||
Threshold (Порог) | [PLAN = 1] | -,220 | ,968 | ,052 | 1 | ,820 | -2,118 | 1,677 |
[PLAN = 2] | ,981 | ,988 | ,986 | 1 | ,321 | -,955 | 2,918 | |
[PLAN = 3] | 2,253 | 1,013 | 4,949 | 1 | ,026 | ,268 | 4,238 | |
[PLAN = 4] | 3,907 | 1,048 | 13,905 | 1 | ,000 | 1,853 | 5,960 | |
Location (Поло-жение) | [G=1] | 2,145 | ,540 | 15,787 | 1 | ,000 | 1,087 | 3,204 |
[G=2] | 1,357 | ,529 | 6,574 | 1 | ,010 | ,320 | 2,394 | |
[ALTER =1] | Oa | , | , | 0 | , | f | ( | |
[ALTER =2] | -1,091 | ,433 | 6,355 | 1 | ,012 | -1,939 | -,243 | |
[ALTER =3] | Oa | , | , | 0 | , | f | j | |
[KDAUER =1] | 1,811 | ,740 | 5,990 | 1 | ,014 | ,361 | 3,261 | |
JKDAUER =2] | 1,486 | ,782 | 3,606 | 1 | ,058 | -4.772E-02 | 3,019 | |
IKDAUER =3] | 1,340 | ,678 | 1 3,905 | 1 | ,048 | 1.101E-02 | 2,669 | |
[KDAUER =4] | Oa | , | , | 0 | , | ( | , | |
[SCHULE =1] | -1,183 | ,618 | 3,665 | 1 | ,056 | -2,394 | 2.807E-02 | |
[SCHULE =2] | -,659 | ,700 | ,886 | 1 | ,347 | -2,031 | ,713 | |
rSCHULE =31 | Oa |
|
| 0 |
|
|
| |
Link function: Logit (Связывающая функция: Логит).
a. This parameter is set to zero because it is redundant (Этот параметр приравнен к нулю, так как является дублирующим). !
Каждой категории зависимых переменных и каждой категории факторов сопоставлена оценка параметра регрессии, причём оценки для соответствующих категорий высших порядков являются дублирующими и поэтому приравнены к нулю. Оценки параметров регрессии для зависимой переменной являются пороговыми оценками, которые для факторов называются оценками положения.
Оценки положения дают возможность толковать влияние факторов и указывают на степень этого влияния. Поэтому, прежде чем будет продемонстрирована точная математическая связь между факторами влияния и зависимой переменной, можно констатировать следующее:
-
Из таблицы можно узнать, какие из факторов вообще оказывают значимое влияние на зависимую переменную. Такими факторами являются возраст, пол и продолжительность болезни, в то время как образование находится на самой границы значимости, до перехода этой границы осталось совсем не много.
-
Положительные оценки означают, что соответствующая категория действует в качестве высшей категории зависимой переменной; отрицательные оценки указывают на действие в качестве низших категорий зависимых переменных.
Принадлежность к младшим возрастным группам является причиной более единодушного одобрения предложения: "Разработать план лечения и затем приступать к его воплощению", все мужчины менее склонны к такому предложению, небольшая продолжительность болезни, а также высокое или низкое образование ведут к снижению степени одобрения. Это соответствует результатам корреляционного анализа.
Математическое значение оценок параметров регрессии заключается в том, что на них основе могут быть вычислены кумулятивные (суммарные) вероятности для категорий независимых переменных. Покажем это на конкретном примере.
Для этого возьмем в редакторе данных первого пациента и рассчитаем совокупную вероятность для случая, когда он отмечает одну из первых двух категорий ("gar nicht" (абсолютно не верно) или "wenig" (слабо)) для зависимой переменной.
Первый пациент является мужчиной средней возрастной группы с большой продолжительностью болезни и неполным средним образованием. Учитывая все эти сведения, можно ожидать высокую вероятность того, что больной проявит слабую готовность планомерно лечить свою болезнь.
На первом шаге расчёта мы должны сложить оценки положения, соответствующие отдельным категориям:
alter = 2 | 1,347 |
g = 1 | -1,091 |
Kdauer = 4 | 0,000 |
Schule = 1 | -1,183 |
Сумма | -0,917 |
Эту сумму нам теперь нужно отнять от пороговой величины второй категории зависимой переменной (plan = 2):
0,981 - (-0,917) = 0,981 + 0,917 = 1,898
Как можно заметить по значению, которое превосходит единицу, этот показатель пока ещё не является искомой совокупной вероятностью того, что больной отметит одну из первых двух категорий. Значение этого показателя соответствует связующей функции, приведенной к этой вероятности. В нашем примере мы выбрали в качестве связующей логит-функцию, установленную по умолчанию, так что для искомой вероятности справедливо следующее выражение:
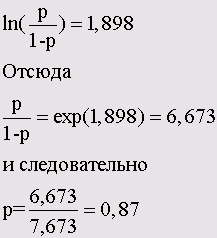
Таким образом, вероятность того, что первый пациент отметит одну из первых двух категорий, составляет р = 0,87 или 87 %. Фактически пациент отметил категорию 1.
Чтобы успокоить пользователей программы, следует сказать, что Вы можете избежать этих сложных расчётов. В диалоговом окне Ordinal Regression:Output (Порядковая регрессия: Вывод) мы активировали опцию сохранения некоторых переменных, которые теперь можем просмотреть.
Пять переменных est1_1-est5_1 соответствуют вероятностям для пяти категорий зависимой переменной. Если мы возьмем первого пациента, то достаточно сложить вероятности для первых двух категорий:
0,67 + 0,20 = 0,87
Это соответствует тому значению, которое мы рассчитали для совокупной вероятности второй категории. В переменной рге_1 сохранен номер категории, которой соответствует самая высокая вероятность, названная "прогнозируемой категорией". Переменная рср_1 ещё раз дает вероятность выбора этой категории.
Связующая логит-функция выбранная нами для этого примера, принадлежит к набору из пяти функций, приведенных ниже.
Функция | Форма | Применение |
Logit (Логит) | In (р/(1-р)) | Равномерно распределённые категории |
Complementary log-log (Сопряженный двойной логарифм) | ln(-ln(1-p)) | Высшие категории представлены сильнее |
Negative log-log (Отрицательный двойной логарифм) | -ln(-ln(p)) | Низшие категории представлены сильнее |
Probit (Пробит) | Инверсия стандартного комулятивного нормального распределения | Нормально распределённые частоты |
Cauchit (Коши) | tan(7t(p-0.5)) | Появление пиковых значений |
В качестве меры качества прогнозирования можно использовать ранговую корреляцию по Спирману между фактически наблюдаемой категорией (переменная plan) и прогнозируемой категорией (переменная рге_1). Для приведенного примера (связующая функция — логит) получим г = 0,611; для других связующих функций получаются более низкие значения.
Лучшую модель можно получить, если в диалоговом окне Ordinal Regression: Location (Порядковая регрессия: Положение) наряду с главными эффектами включить и взаимодействия. После активирования опции Custom (Пользовательский режим) в вашем распоряжении появляется вспомогательное меню, при помощи которого вместе с главным эффектом Вы сможете включить в модель и различные виды взаимодействия.
-
Активируйте опцию Custom (Пользовательский режим) и сперва выберите в появившемся списке Main effects (Главные эффекты).
-
При помоши транспортной кнопки перенесите все факторы в поле Location model: (Определение положения для модели).
-
Затем отметьте в разворачивающемся меню Interaction (Взаимодействие) и повторно перенесите все факторы в поле Location model: (Определение положения для модели). Будет выбрано взаимодействие четвёртого уровня. При помоши опции All 2-way (Все дважды) Вы можете задать взаимодействие второго уровня, при помощи опции АН З-way (Все трижды) — взаимодействие третьего уровня и т.д.
Теперь прогноз будет лучше; в случае применения для данного примера взаимодействия четвёртого уровня ранговая корреляция между наблюдаемой и прогнозируемой категориями возрастает с 0,611 до 0,739. При этом, конечно же, возрастает и количество параметрических оценок.
36.gif
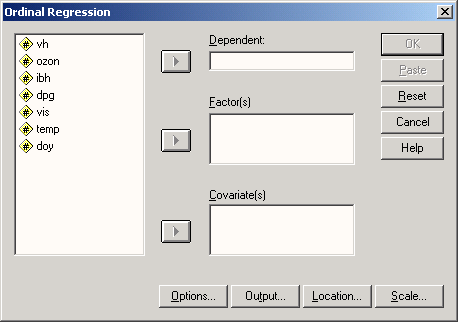
37.gif
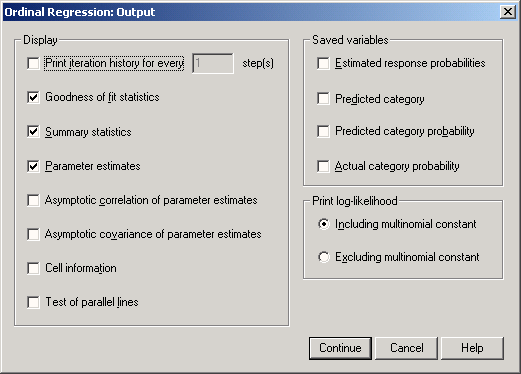
38.gif

39.gif
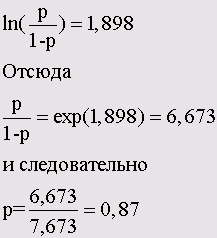
16.7 Пробит-анализ
16.7 Пробит-анализ
Этот метод известен также под именем "Дозаторный анализ кривых воздействия" и находит применение преимущественно в области токсикологии. В большинстве случаев речь идёт о том, как на заданное количество индивидуумов воздействуют различные дозировки некоторого вещества (к примеру, некоторого токсичного вещества).
Классический пример, который вошёл и в справочник по SPSS, исследует действие средства, предназначенного для уничтожения насекомых. При этом производится подсчёт, сколько насекомых из заранее известного количества погибли при воздействии определённых доз вещества. Особенный интерес в данном случае представляет дозировка, при которой уничтожается половина имеющихся насекомых.
Оставим животных в покое и обратимся, в виде исключения, к одному специально придуманному примеру. Шеф секретной службы некоторой вымышленной страны пожелал узнать, сколько денег он должен предложить гражданам соседнего государства, чтобы они доставляли ему некоторую тайную информацию. Для этой цели через своего посредника он предлагает первой группе 1000 долларов и отмечает, сколько человек соглашаются на его предложение вести шпионскую деятельность. Второй группе он предлагает 2000 долларов и вновь отмечает себе количество попаданий в цель. Он продолжает предлагать деньги и дальше, действуя таким пошаговым образом и доходит до суммы 10000 долларов. При этом исследованиям подвергаются две различные категории людей. К первой категории относятся люди, которые недовольны своим материальным положением, ко второй — люди, удовлетворенные своим материальным положением.
Для обеих категорий шеф секретной службы желает выяснить, сколько он должен предложить денег, чтобы достичь желаемой доли положительных ответов. К примеру, его интересует сумма, которую он должен заплатить, чтобы на его предложение согласилась половина опрашиваемой группы.
Для обеих категорий удовлетворенности материальным положением (доволен — недоволен) в нижеследующей таблице представлены долларовые суммы в порядке возрастания, количество вовлечённых в эксперимент людей (nges) и количество фактически завербованных шпионов (п).
группа | доллар | количество вовлечённых в эксперимент людей | количество фактически завербованных шпионов |
недоволен | 1000 | 59 | 8 |
недоволен | 2000 | 56 | 22 |
недоволен | 3000 | 53 | 28 |
недоволен | 4000 | 49 | 30 |
недоволен | 5000 | 51 | 35 |
недоволен | 6000 | 43 | 34 |
недоволен | 7000 | 40 | 36 |
недоволен | 8000 | 45 | 41 |
недоволен | 9000 | 40 | 38 |
недоволен | 10000 | 35 | 34 |
доволен | 1000 | 61 | 1 |
доволен | 2000 | 45 | 13 |
доволен | 3000 | 52 | 21 |
доволен | 4000 | 45 | 22 |
доволен | 5000 | 46 | 26 |
доволен | 6000 | 38 | 27 |
доволен | 7000 | 45 | 35 |
доволен | 8000 | 42 | 33 |
доволен | 9000 | 37 | 32 |
доволен | 10000 | 36 | 33 |
Эта информация построчно хранится в файле dollar.sav (переменные: gruppe, dollar, nges, n).
-
Откройте файл dollar.sav.
-
Выберите в меню Analyze (Анализ) Regression (Регрессия) Pmbit... (Пробит)
Откроется диалоговое окно Probit Analysis (Пробит-анализ).
Рис. 16.22: Диалоговое окно Probit Analysis (Пробит-анализ)
-
Поочерёдно перенесите переменные п в поле частоты отклика, переменную nges в поле наблюдаемого общего количества, переменную gruppe в поле факторов и переменную dollar в поле ковариат.
-
При помощи соответствующей кнопки для факторной переменной необходимо определить область принадлежности; для нашего примера она равна целым числам: 1 и 2.
-
Стандартным подходом при проведении пробит-анализа стало логарифмическое преобразование значений ковариат (при помощи десятичного логарифма); задайте и Вы это преобразование.
-
Оставьте установку обычной пробит-модели и щёлкните на кнопке опций. Дополнительно к установленным статистикам активируйте тест параллельности, который является уместным при анализе разнообразных групп.
-
Начните расчёт нажатием ОК.
Результирующие данные выводятся в старой табличной форме и являются довольно обширными. На одном из первых шагов определяются так называемые "пробиты". Они представляют собой стандартные значения, которые отвечают площади под частью кривой стандартной нормального распределения, соответствующей отношению частоты положительных ответов к общей частоте. Так, в первой группе, которой предлагалось по 1000 долларов, это предложение приняли 8 человек из 59, что соответствует относительной доле, равной
р=8/59= 0,1356
Это значение интерпретируется как часть площади под кривой стандартного нормального распределения (которая, как известно, суммарно нормирована к 1). По соответствующей статистической таблице можно установить, что стандартное значение равно -1,10. Это значение является пробитом к дозировке 1000 долларов.
Упомянутые пробиты для обеих групп в зависимости от логарифма дозировки представлены на одной диаграмме, которую вы можете увидеть в окне просмотра:
Для обеих групп график является практически линейным, что является предпосылкой для дальнейших рассуждений. В противном случае дополнительно следовало было бы рассматривать ход процесса воздействия на основе исходных значений (то есть без логарифмического преобразования).
Рис. 16.23: Отклики, трансформированные пробитом
Для обеих кривых определяется уравнение регрессионных прямых, причём для обеих прямых вычисляется общий угол наклона:
Regression Coeff. | Standard Error | Coeff./S.E. | ||||
DOLLAR | 2,78749 | ,17640 | 15,80205 | |||
Intercept | Standard Error | Intercept/S.E. | GRUPPE | |||
| -9 ,59552 | ,63415 | -15, 13130 | 1 | |||
| 2 | ||||||
| -9 ,99490 | ,64731 | -15,44060 | ||||
| Pearson Goodness -of -Fit Chi Square=10,043 DF = 17 P = ,902 | ||||||
Parallelism Test Chi Square = ,164 DF = 1 P = ,686 | ||||||
При тесте на качество согласия большое значение р (как в рассматриваемом примере) указывает на лучшее приближение. Второй тест по критерию хи-квадрат проясняет вопрос, действительно ли обе прямые могут рассматриваться как параллельные. Параллельности прямых соответствует незначимый результат теста (как в рассматриваемом случае).
Если мы рассмотрим уравнение регрессии для первой группы, то получим следующее уравнение, прогнозирующее значение пробита:
Probit= 2,78749xlog(Dollar)- 9,59552
Для значения 1000 долларов получим
Probit= 2,78749x3- 9,59552= - 1,2331
Если мы вновь обратимся к статистической таблице, содержащей значения стандартной кривой нормального распределения, то полученному стандартизированному значению в данном случае соответствует площадь 0,10878. Это значение используется для того, чтобы определить ожидаемую частоту отклика:
59x0,10878= 6,418
Полученные результаты сведены в следующую таблицу:
Number of Observed Expected | |||||||||||
GRUPPE | DOLLAR | Subjects Responses Responses Residual | Prob | ||||||||
1 | 3 | , 00 | 59 | ,0 | 8 | ,0 | 6,418 | 1 | ,582 | ,10878 | |
1 | 3 | ,30 | 56 | ,0 | 22, | 0 | 19 | ,422 | 2 | ,578 | ,34681 |
1 | 3 | ,48 | 53 | ,0 | 28, | 0 | 28 | ,546 | - | ,546 | ,53860 |
1 | 3 | , 60 | 49 | ,0 | 30, | 0 | 32 | , 923 | - | 2, 923 | , 67191 |
1 | 3 | ,70 | 51 | ,0 | 35, | 0 | 38 | , 902 | - | 3, 902 | ,76279 |
1 | 3 | ,78 | 43 | ,0 | 34, | 0 | 35 | ,491 | - | 1,491 | ,82537 |
1 | 3 | , 85 | 40 | ,0 | 36, | 0 | 34 | ,768 | 1 | ,232 | ,86921 |
1 | 3 | , 90 | 45 | ,0 | 41, | 0 | 40 | ,522 | , | 478 | , 90048 |
1 | 3 | , 95 | 40 | ,0 | 38, | 0 | 36 | ,928 | 1 | ,072 | , 92319 |
1 | 4 | ,00 | 35 | ,0 | 34, | 0 | 32 | ,899 | 1 | ,101 | , 93996 |
2 | 3 | ,00 | 61 | ,0 | 1, | 0 | 3, | 129 | - | 2,129 | ,05129 |
2 | 3 | ,30 | 45 | ,0 | 13, | 0 | 9, | 621 | 3 | ,379 | ,21380 |
2 | 3 | ,48 | 52 | ,0 | 21, | 0 | 19 | ,820 | 1 | ,180 | ,38115 |
2 | 3 | ,60 | 45 | ,0 | 22, | 0 | 23 | ,322 | - | 1,322 | ,51826 |
2 | 3 | ,70 | 46 | ,0 | 26, | 0 | 28 | ,703 | - | 2,703 | ,62397 |
2 | 3 | ,78 | 38 | ,0 | 27, | 0 | 26 | ,761 | , | 239 | ,70425 |
2 | 3 | ,85 | 45 | ,0 | 35, | 0 | 34 | ,436 | , | 564 | ,76524 |
2 | 3 | ,90 | 42 | ,0 | 33, | 0 | 34 | ,100 | - | 1,100 | ,81190 |
2 | 3 | ,95 | 37 | ,0 | 32, | 0 | 31 | ,373 | f | 627 | ,84791 |
2 | 4 | ,00 | 36 | /o | 33, | 0 | 31 | ,535 | 1 | ,465 | ,87597 |
Сразу же после этой таблицы для заданных вероятностей ( вероятности здесь следует понимать, как отношение частоты желательного отклика к общему числу испытуемых) выводятся значения необходимых дозировок (в нашем случае: денежная сумма в долларах) и их 95%-ый доверительный интервал. Ниже приводится таблица значений для первой группы:
95% Confidence Limits | |||
Prob | DOLLAR | Lower | Upper |
,01 | 405,30868 | 289,59056 | 529,15509 |
,02 | 507,66784 | 373,66257 | 647,93485 |
,03 | 585,63448 | 439,14578 | 736,94514 |
, 04 | 652,08194 | 495,79196 | 811,99633 |
,05 | 711,65439 | 547,15681 | 878,74346 |
,06 | 766,62851 | 594,99562 | 939,94335 |
, 07 | 818,31336 | 640,32303 | 997,17444 |
,08 | 867,54082 | 683,78664 | 1051,43643 |
,09 | 914,87813 | 725,82978 | 1103,40905 |
,10 | 960,73191 | 766,77131 | 1153,57841 |
, 15 | 1176,35221 | 961,74200 | 1387,62679 |
,20 | 1381,73708 | 1150,43739 | 1608,52696 |
,25 | 1586,29202 | 1340,43221 | 1827,40833 |
,30 | 1795,67203 | 1536,35222 | 2050,97344 |
,35 | 2014,28728 | 1741,83765 | 2284,49983 |
,40 | 2246,29254 | 1960,31730 | 2533,03836 |
,45 | 2496,16365 | 2195,45599 | 2802,13038 |
,50 | 2769,19498 | 2451,53866 | 3098,44683 |
,55 | 3072,09057 | 2733,92871 | 3430,56245 |
, 60 | 3413,82108 | 3049,73874 | 3810,08632 |
,65 | 3807,02441 | 3408,93562 | 4253,51516 |
, 70 | 4270,51303 | 3826,32195 | 4785,56534 |
,75 | 4834,19240 | 4325,40532 | 5445,75782 |
,80 | 5549,85527 | 4946,81830 | 6303,01441 |
,85 | 6518,83063 | 5769, 66817 | 7493,47901 |
, 90 | 7981,87380 | 6980,17468 | 9345,15098 |
, 91 | 8381,92608 | 7305,70121 | 9861,25890 |
,92 | 8839,28528 | 7675,37386 | 10455, 92397 |
, 93 | 9371,03216 | 8102,08907 | 11153,16983 |
,94 | 10002,81198 | 8605,11895 | 11989,28434 |
,95 | 10775,51263 | 9215,02568 | 13022,52271 |
, 96 | 11759, 93430 | 9984,40147 | 14354,56418 |
, 97 | 13094,24400 | 11015,11467 | 16185,74513 |
,98 | 15105,23259 | 12545,80989 | 18995,72850 |
, 99 | 18920,00171 | 15388,14261 | 24468,76250 |
Для того, чтобы переманить на свою сторону половину группы граждан чужой страны, недовольных своим финансовым положением (Prob = 0,5), начальник секретной службы должен предложить каждому по 2769 долларов, причём с 95%-ой вероятностью эта сумма колеблется от 2452 до 3098 долларов. Для группы довольных финансовым положением (для которой распечатка данных здесь не приведена) придётся заплатить больше: 3852 доллара, с 95%-ым доверительным интервалом эта сумма колеблется от 3437 до 4296 долларов.
Отношение этих двух значений медиан составит:
2769/3852= 0,719
Это соотношение отображается в небольшой статистической сводке:
Estimates of Relative Median Potency | |||
95% | Confidence | Limits | |
GRUPPE 1 VS. 2 | Estimate ,7190 | Lower ,60280 | Upper ,84419 |
Если Вы в диалоговом окне выберите не пробит, а логит-модель, то отношение частоты положительных откликов к общему количеству опрашиваемых р заменяется выражением
40.gif
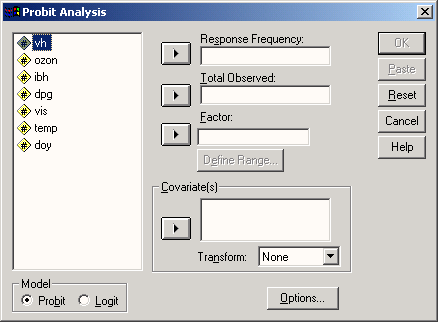
41.gif
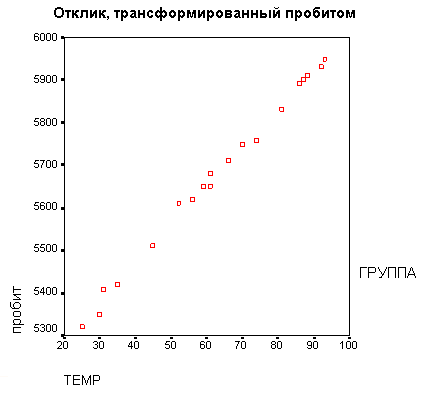
42.gif

16.8 Приближение с помощью кривых
16.8 Приближение с помощью кривых
При помощи этого пункта меню можно строить графики реального течения наблюдаемых процессов и приближать их при помощи аппроксимационных кривых. Для этого в ваше распоряжение предоставляется, в общей сложности, одиннадцать различных типов кривых. В большинстве случаев речь здесь будет идти о временных рядах.
В качестве примера рассмотрим изменение зарплаты в Федеративной республике Германии с 1950 года по 1988, описываемое так называемым индексом действительной зарплаты. Его можно получить при помощи соотнесения текущего годового уровня зарплаты к уровню к 1980 году, для которого значение индекса принимается равным 100.
Год | Индекс действительной зарплаты |
1950 | 28,6 |
1960 | 46,9 |
1965 | 63,0 |
1970 | 80,4 |
1975 | 87,9 |
1980 | 100,0 |
1981 | 98,2 |
1982 | 96,5 |
1983 | 96,0 |
1984 | 96,9 |
1985 | 98,0 |
1986 | 101,2 |
1987 | 104,5 |
1988 | 107,6 |
Эти данные находятся в файле lohasav. В файле также находится и ещё одна, третья, переменная, которая отражает разность между текущим значением года и 1949 годом. Эта переменная принимает значения от 1 до 39 и указывает на количество лет, прошедших с 1949 года.
-
Откройте файл lohn.sav.
-
Выберите в меню Analyze (Анализ) Regression (Регрессия) Curve Estimation...(Подгонка кривых)
Рис. 16.24: Диалоговое окно Curve Estimation (Подгонка кривых)
Откроется диалоговое окно Curve Estimation (Подгонка кривых), в котором можно выбрать одну из одиннадцати различных моделей.
Предлагаемым моделям соответствуют следующие формулы:
| Молель | Формула |
Линейная |
у= b0+ b1хX |
Логарифмическая | у= b0+ b1х ln(х) |
Обратная | |
Квадратичная | у= b0+ b1хX + b2хX2 |
Кубическая | у= b0+ b1хХ + b2хX2 + b3хX3 |
Степенная | y= b0хXb1 |
Показательная (комбинированная) | y= b0 * b1 |
S | у= е^(b0+b1xX) |
Логистическая | |
Рост | у= е^(b0+b1xX) |
Экспоненциальная | y=b0 х е^(b1xt) |
Для логистической модели необходимо предварительно задать параметр и, который задается непосредственно в диалоговом окне Curve Estimation (Подгонка кривых) в качестве верхнего предела. Задачей программы является определение коэффициентов b0, b1, b2 и b3.
В поле для меток наблюдений (Case labels) можете указать некоторую переменную для описания данного наблюдения, которая затем будет появляться в режиме выбора точек (см. гл. 22.8.1) на построенном графике (см. рис. 16.25).
-
Перенесите переменную lohn в поле для зависимых переменных, а переменную anz в поле для независимых переменных.
-
Произведём оценку при помощи квадратичной функции; деактивируйте линейную модель и отметьте вместо неё квадратичную модель.
Активирование опции Time (Время) имеет смысл только тогда, когда анализируемые переменные представлены в виде временных рядов с одинаковыми интервалами.
-
Затем щёлкните на кнопке Save (Сохранение) и в появившемся диалоговом окне выберите опцию, с помощью которой прогнозируемые значения переменной будут сохранены в исходном файле данных.
-
Вернувшись в первое диалоговое окно, начните расчёт нажатием ОК.
Вывод результатов производится в старой табличной форме. Самыми важными показателями являются:
Independent: ANZ
Dependent Mth Rsq d.f. F Sigf b0 b1 b2
LOHN QUA ,979 11 251,10 ,000 22,5918 3,0615 -,0242
Эта таблица содержит значения коэффициентов а, b1, и b2. К данным исходного файла была добавлена переменная fit_1, которая содержит прогнозируемые значения, найденные на основе рассчитанных коэффициентов. Далее в окне просмотра появляется график, на котором отображаются кривые, соответствующие изменению наблюдаемых и спрогнозированных значений.
Приближение с помощью выбранной кривой, как кажется, удалось довольно не плохо. В противном случае можно было бы применить и другие модели, для использования которых, конечно же, не помешал бы некоторый опыт в области подобных криволинейных приближений.
Рис 16.25: Наблюдаемая и оценочная кривая
43.gif

45.gif
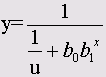
46.gif

16.9 Взвешенное оценивание (оценка с весами)
16.9 Взвешенное оценивание (оценка с весами)
В линейном регрессионном анализе, рассмотренном до настоящего времени, все наблюдения входят в модель равнозначно. При этом, исходной предпосылкой является тот факт, что все наблюдения должны иметь одинаковую дисперсию.
Если это условие не выполняется и дисперсия увеличивается с ростом значения независимой переменной, то отдельные точки можно взвесить так, чтобы наблюдения с большой дисперсией имели меньшее влияние.
В качестве примера рассмотрим тест, проверяющий знания детей в области географии. Дети в возрасте от 3 до 14 лет должны были в течение двух минут назвать как можно больше городов Германии. Результаты теста сведены в нижеследующей таблице, причём количество детей в каждой возрастной группе варьируется от двух до пяти:
Возраст | Количество названных городов |
3 | 2, 1, 0, 4 |
4 | 4, 2, 6 |
5 | 3, 8, 4, 7 |
6 | 3, 8, 9, 5 |
7 | 6, 10 |
8 | 7, 14, 10 |
9 | 9, 16, 10 |
10 | 9, 16, 15, 9 |
11 | 18, 12 |
12 | 22, 11, 14, 16 |
13 | 14, 21 |
14 | 20, 15, 23, 14, 26 |
Эти данные для сорока детей в общей сложности хранятся в переменных alter (возраст) и staedte (города), которые содержатся в файле snamen.sav.
-
Откройте файл snamen.sav.
-
Выберите в меню Graphs (Графики) Scatterplot... (Диаграмма рассеяния)
Рис. 16.26: Диаграмма рассеяния
-
Отметьте и постройте простую диаграмму рассеяния с переменной alter по оси абсцисс и переменной staedte пo оси ординат.
Вы увидите, что с ростом возраста растёт не только количество названных городов, но и рассеяние, то есть дисперсия, становится больше.
-
В соответствии с описанием из главы 16.1 проведите линейный регрессионный анализ, причём переменной staedte присвойте статус зависимой переменной, а переменной alter — независимой переменной.
-
Вы получите следующие результаты:
Model Summary (Сводная таблица по модели)
Model (Модель) | R | R Square (R-квадрат) | Adjusted R Square (Смещенный R-квадрат) | Std. Error of the Estimate (Стандартная ошибка оценки) |
1
| ,879а | ,772 | ,766 | 3,1623 |
a. Predictors: (Conslant), Alter (Bлияющие переменные: (Константа), возраст)
Coefficients (Коэффициенты) а | ||||||
Model (Модель) | Unstandardized Coefficients (He стандарти-зированные коэф-фициенты) | Standardized Coefficients (Стандарти-зированные коэф-фициенты) | Т | Sig. (Значи-мость) | ||
В | Std. Error (Станда-ртная ошибка) | /3 (Beta) | ||||
1 a. Dep | (Constant) (Koнстанта) | -2,722 | 1,273 |
| -2,138 | ,039 |
Alter (Возраст) endent Variable | 1,569 (Зависим | ,138 ая перемен-ная) | ,879 | 11,357 | ,000 | |
Коэффициент корреляции равен 0,879, а мера определённости 0,772.
В данном примере мы имеем дело с группами случаев, разделёнными по годам возраста, для которых независимая переменная имеет всегда одно и то же значение. Исходя из значений зависимой переменной сопоставленных каждому случаю, можно определить дисперсию; обратное значение этой дисперсии применяется обычно в качестве весового фактора для соответствующего случая.
Если подобной группировки данных нет, то пытаются выявить такую связь между дисперсией и переменной, чтобы степень дисперсии была пропорциональна значению данной переменной. При поиске так называемых весовых переменных речь идет о независимой переменной или, если их много, — об одной из независимых переменных. В приведенном примере такой переменной, очевидно, является независимая переменная alter, по которой и можно проследить изменение дисперсии.
Целью анализа сначала является определение наилучшей возможной степени р. а затем подсчёт веса для каждого случая, причём вес для значения переменной х определяется как
1/хp
-
Выберите в меню Analyze (Анализ) Regression.. .(Регрессия) Weight Estimation... (Взвешенное оценивание)
Откроется диалоговое окно Weight Estimation (Взвешенное оценивание).
Рис. 16.27: Диалоговое окно Weight Estimation (Весовая цепка)
-
Перенесите переменную staedte в поле зависимых переменных, а переменную alter в поля для независимых и для весовых переменных. Согласно с установками по умолчанию оптимальная степень вычисляется в пределе от —2 до 2 с шагом 0,5; измените шаг на 0,2.
-
Щёлкните на кнопке опций и в появившемся диалоговом окне активируйте опцию Save best weight as new variable (Сохранить лучший вес, как новую переменную).
Результаты расчёта, вывод которых производится в старой табличной форме, выглядят следующим образом:
Source variable | . . ALTER | Dependent variable. . STAEDTE | |
Log- likelihood | Function =-116,950816 | POWERvalue= -2,000 | |
log- likelihood | Function =-115,170919 | POWERvalue=-1,800 | |
Log- likelihood | Function =-113,434617 | POWERvalue=-1,600 | |
Log- likelihood | Function =-111,746484 | POWERvalue=-1,400 | |
Log- likelihood | Function =-110,111706 | POWERvalue=-1,200 | |
Log- likelihood | Function =-108,536154 | POWERvalue=-1,000 | |
Log- likelihood | Function =-107,026465 | POWERvalue=-,800 | |
Log- likelihood | Function =-105,590111 | POWERvalue=-,600 | |
Log- likelihood | Function =-104,235463 | POWERvalue=-,400 | |
Log- likelihood | Function =-102,971835 | POWERvalue=-,200 | |
Log- likelihood | Function =-101,809499 | POWERvalue=,000 | |
Log- likelihood | Function =-100,759655 | POWERvalue=,200 | |
Log- likelihood | Function =-99,834344 | POWERvalue=,400 | |
Log- likelihood | Function =-99,046284 | POWERvalue=,600 | |
Log- likelihood | Function =-98,408623 | POWERvalue=,800 | |
Log- likelihood | Function =-97,934594 | POWERvalue=1,000 | |
Log- likelihood | Function =-97,637078 | POWERvalue=1,200 | |
Log- likelihood | Function =-97,528092 | POWERvalue=1,400 | |
Log- likelihood | Function =-97,618231 | POWERvalue=1,600 | |
Log- likelihood | Function =-97,916114 | POWERvalue=1,800 | |
Log- likelihood | Function =-98,427890 | POWERvalue=2,000 | |
The Value ofPOWER MaximizingLog-likelihood Function =1,400 | |||
Source variable | ALTER | POWERvalue=:1,400 | |
Dependent variable. . STAEDTE | |||
Multiple R, 90081 | |||
R Square,81146 | |||
Adjusted R Square ,80650 | |||
Standard Error ,68669 | |||
| Analysis of Variance : |
|
|
| DF Sum of Squares | Mean Square |
|
Regression Residuals | 1 77,121477 38 17,918483 | 77,121477 ,471539 |
|
P = 163,55269 | Signif F = ,0000 |
|
|
------- | - — — Variables in the Equation — | - - - - - | - - - |
Variable | В SE В Beta | Т | Sig Т |
ALTER (Constant) | 1,569996 ,122764 ,900813 -2,728584 ,840793 | 12,789 -3,245 | ,0000 ,0025 |
Log-likelihood | Function = -97,528092 |
|
|
The following | new variables are being created: |
|
|
Name | Label |
|
|
WGT_1 | Weight for STAEDTE from WLS, MOD_ | 1 ALTER** | -1,400 |
Оптимальная степень оценивается при помощи логарифма функции правдоподобия; в данном случае максимальное значение получается при значении степени равном 1,4. Это значение используется для определения веса для каждого случая. К примеру, для трёхлетнего ребёнка вес равен
1/(31,4)=0,2148
Весовые показатели были добавлены в исходный файл под переменной с именем wgt_1. Затем повторно был выполнен расчёт регрессии. Корреляционный коэффициент при этом возрос до 0,90081, а мера определённости до 0,81146. Хотя эти изменения, а также изменение рассчитанных коэффициентов регрессии и констант незначительны, зато стала намного меньше соответствующая им стандартная ошибка.
47.gif
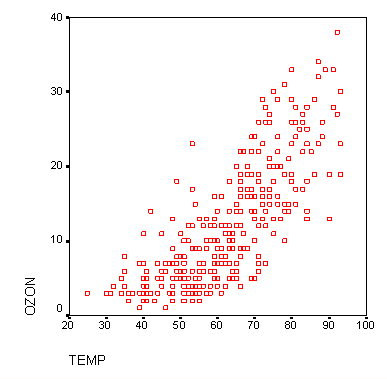
48.gif
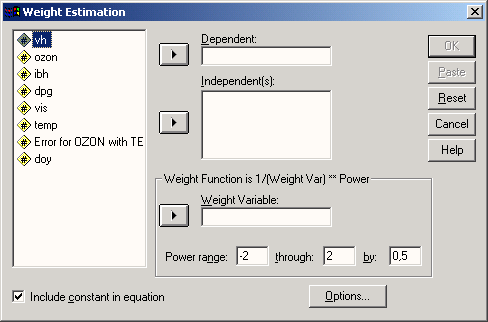
Глава 17. Дисперсионный анализ
Глава 17. Дисперсионный анализ
1. Дисперсионный анализ
Дисперсионный анализ
С помощью дисперсионного анализа исследуют влияние одной или нескольких независимых переменных на одну зависимую переменную (одномерный анализ) или на несколько зависимых переменных (многомерный анализ). В обычном случае независимые переменные принимают только дискретные значения (и относятся к номинальной или порядковой шкале); в этой ситуации также говорят о факторном анализе. Если же независимые переменные принадлежат к интервальной шкале или к шкале отношений, то их называют ковариациями, а соответствующий анализ — ковариационным.
В рамках дисперсионного анализа SPSS предлагает множество возможностей, в которых, однако, не всегда легко разобраться, в особенности для новичка. Даже учебники по SPSS напрямую не способствуют облегчению освоения имеющихся возможностей. Во-первых, нужно отметить, что в принципе дисперсионный анализ может выполняться в рамках двух подходов:
-
при помощи традиционного "классического" метода по Фишеру (Fisher) и
-
при помощи нового метода "обобщенной линейной модели".
Первый подход сводится к разложению по методу наименьших квадратов (МНК); в однофакторном случае совокупная дисперсия всех наблюдаемых значений раскладывается на дисперсию внутри отдельных групп и дисперсию между группами. В основе обобщенной линейной модели напротив, лежит, корреляционный или регрессионный анализ.
До 6 версии SPSS обобщенная линейная модель была реализована на основе процедуры MANOVA, управление которой могло происходить как через диалоговое окно, так и при помощи командного синтаксиса. В 7-ой версии эта процедура была заменена на процедуру GLM; при этом процедура MANOVA осталась, как и прежде, доступной через командный синтаксис.
Главным отличием между GLM и MANOVA является то, что в MANOVA используется, так называемая, "full rank linear model" (линейная модель полного ранга), а в GLM, так называемая, "поп full rank linear model" (линейная модель неполного ранга). Более подробную информацию по этому вопросу можно найти в специальной литературе, к примеру, в книге Р. Е. Кирка (R. E. Kirk) (см. список литературы). В GLM предлагаются ещё и дополнительные расширения, самым важным из которых, конечно же, является тест для сравнения средних значений отдельных слоев (подпопуляций), который выполняется после проведения дисперсионного анализа. Слои или подпопуляций определяются различными уровнями величины фактора, положенного в основу классификации. В то же время, MANOVA включает ряд дополнительных видов анализа (регрессионный анализ, дискриминантный анализ, канонический анализ, анализ главных компонентов и т.д.), которых нет в GLM.
В дальнейшем мы ограничимся рассмотрением только наиболее часто употребительных видов дисперсионного анализа. При этом будет проведено различие между, одномерными и многомерным дисперсионным анализом (в зависимости от количества зависимых переменных), а также выделен случай, когда факторы (независимые переменные) включают повторные измерения.
После открытия соответствующего файла (к примеру, varana.sav), дисперсионный анализ может быть вызван посредством выбора меню Analyze (Анализ) General Linear Model (Общая линейная модель)
Откроется вспомогательное меню (см. рис. 17.1)
Все без исключения возможности, предлагаемые в диалоговом окне, предполагают проведение расчётов на основе общей линейной модели. Если перечислять по очереди, то с помощью данного меню можно провести одномерный дисперсионный анализ (Univariate...), многомерный дисперсионный анализ (Multivariate...), многомерный дисперсионный анализ с учетом повторных измерений (Repeated Measures...). И, наконец, в данном меню имеется один пункт для расчёта компонентов дисперсии (Variance Components...) (см. гл. 17.4).
Возможно также проведение дисперсионного анализа по традиционному "классическому" методу Фишера. Однако такой анализ выполним только за счёт использования программного синтаксиса (процедура ANOVA). Этому методу посвящен отдельный раздел (см. гл. 17.1.2).
Рис. 17.1: Вспомогательное меню General Linear Model (Общая линейная модель)
В рамках данной книги нет возможности полностью рассмотреть все, что предлагается пользователю SPSS для проведения дисперсионного анализа, поэтому с помо-:лью нескольких примеров мы попытаемся сделать общий обзор и изложить вводные замечания для основных ситуаций. К основным ситуациям относятся:
-
одномерный анализ,
-
ковариационный анализ и
-
многомерный анализ.
Для одномерного анализа будут рассмотрены варианты без повторных измерений и с повторными измерениями. Последний раздел главы посвящен расчёту компонентов дисперсии.
1.gif
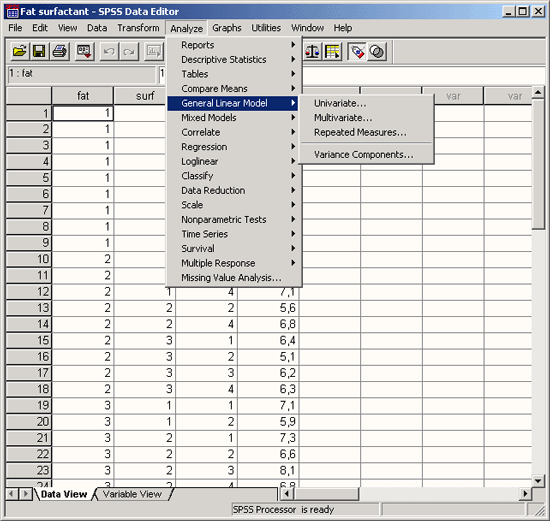
17.1 Одномерный дисперсионный анализ
17.1 Одномерный дисперсионный анализ
Однофакторный дисперсионный анализ (без и с повторными измерениями) уже рассматривался в главе 13, поэтому мы сразу обратимся к многофакторному дисперсионному анализу.
Так как дисперсионный анализ очень часто находит применение в области психологии, то первым примером и будет пример из этой области. В четыре различных момента времени 27 испытуемых были подвергнуты тесту на внимательность. Причём для каждого испытуемого регистрировался пол и возраст. Собранные значения представлены в следующей сводной таблице.
С | А | M1 | М2 | М3 | М4 | С | А | М1 | М2 | МЗ | М4 |
1 | 1 | 16 | 18 | 21 | 20 | 1 | 3 | 8 | 11 | 12 | 12 |
1 | 1 | 17 | 19 | 18 | 22 | 2 | 1 | 17 | 18 | 20 | 21 |
1 | 1 | 15 | 15 | 17 | 18 | 2 | 1 | 15 | 15 | 18 | 17 |
1 | 1 | 16 | 17 | 18 | 19 | 2 | 1 | 16 | 17 | 17 | 18 |
1 | 2 | 15 | 16 | 20 | 18 | 2 | 2 | 15 | 18 | 19 | 21 |
1 | 2 | 16 | 19 | 18 | 20 | 2 | 2 | 17 | 20 | 21 | 22 |
1 | 2 | 13 | 14 | 16 | 17 | 2 | 2 | 14 | 16 | 17 | 20 |
1 | 2 | 14 | 14 | 15 | 17 | 2 | 2 | 14 | 14 | 16 | 18 |
1 | 2 | 15 | 16 | 16 | 18 | 2 | 3 | 12 | 11 | 14 | 15 |
1 | 3 | 13 | 14 | 15 | 16 | 2 | 3 | 10 | 12 | 13 | 14 |
1 | 3 | 14 | 17 | 16 | 19 | 2 | 2 | 10 | 10 | 11 | 13 |
1 | 3 | 13 | 13 | 15 | 16 | 2 | 3 | 9 | 10 | 12 | 11 |
1 | 3 | 10 | 11 | 11 | 11 | 2 | 3 | 10 | 9 | 12 | 13 |
1 | 3 | 9 | 10 | 10 | 13 |
Полу (G) соответствуют коды: 1 для мужского и 2 для женского; возраст (А) представлен тремя возрастными группами. Испытуемым в возрасте до 30 лет соответствует код 1, испытуемым в возрасте от 31 до 50 лет — код 2 и испытуемым в возрасте свыше 50 лет — код 3. Четыре показателя внимательности соответствуют переменным М1-М4.
При помощи этого примера мы рассмотрим, во-первых, одномерный дисперсионный анализ без повторных измерений и, во-вторых, одномерный дисперсионный анализ с повторными измерениями. Одномерный дисперсионный анализ без повторных измерений может быть проведен как при помощи общей линейной модели, так и при помощи классического метода Фишера.
17.1.1 Одномерный дисперсионный анализ (общий многофакторный)
17.1.1 Одномерный дисперсионный анализ (общий многофакторный)
Исследуем влияние пола и возраста на результирующую величину показателя внимательности (M1). Здесь мы имеем дело с двумя факторами, из которых один (пол) разделён на две категории, а второй (возраст) на три. Комбинации этих двух факторов образуют в общей сложности шесть групп испытуемых (называемых также ячейками). Число наблюдений, относящихся к отдельным ячейкам является не одинаковым, а наоборот различным.
-
Откройте файл varana.sav.
-
Выберите в меню Analyze (Анализ) General Linear Model (Общая линейная модель) Univariate... (Одномерная) Откроется диалоговое окно Univariate (Одномерная) (см. рис. 17.2).
-
Перенесите переменную ml в поле зависимых переменных, а переменные geschl (пол) и alter (возраст) в поле фиксированных факторов.
Понятия "фиксированные" и "случайные" факторы требуют дополнительного объяснения. Фиксированными факторами или факторами с фиксированными эффектами называются такие факторы, которые охватывают все возможные классификационные слои одной независимой переменной, к примеру, пол мужской — женский или образование начальное — среднее — высшее. Однако, если слои (подпопуляции) фактора выбирается случайным образом из бесконечного множества возможных подпопуляции факторов, называемого генеральной популяцией, то говорят о факторах со случайными эффектами. В этом случае является уместным компонентный анализ, то есть расчёт так называемых компонентов дисперсии (см. гл. 17.4).
-
Щёлкните по кнопке Model... (Модель)
Откроется диалоговое окно Univariate: Model (Одномерная: Модель) (см. рис. 17.3).
Рис. 17.2: Диалоговое окно Univariate (Одномерная)
Рис. 17.3: Диалоговое окно Univariate: Model (Одномерная: Модель)
Модель дисперсионного анализа — это математическое соотношение, в котором каждая переменная представлена в виде суммы среднего значения и ошибки. Что касается выбора конкретной формы модели, то по умолчанию установлена полнофакторная модель Full factorial). В этой модели среднее значение каждого наблюдения представлено в виде генерального среднего и суммы вклада всех главных "эффектов" (факторов влияния), помимо которых производится также расчёт всех взаимодействий между факторами. Альтернативой является возможность выбора отдельных взаимодействий факторов влияния, которая осуществляется посредством активирования опции Custom (Пользовательский режим). Таким же образом должны быть отобраны и взаимодействия с ковариациями.
Для формирования сумм квадратов для МНК существует четыре различных подхода (четыре типа, обозначенных с помощью римских чисел I, II, III и IV), по умолчанию установлен тип III.
-
Оставьте в этом окне все установки по умолчанию и покиньте диалоговое окно нажатием кнопки Continue (Далее).
-
Щёлкните на выключателе Options... (Опции)
Откроется диалоговое окно Univariate: Options (Одномерная: Опции) (см. рис. 17.4)
-
Перенесите OVERALL (В целом) и обе переменные geschl (пол) и alter (возраст) в поле Display means for (Показать средние значения для); в этом случае в качестве результатов будут выведены средние значения и стандартная ошибка для совокупной выборки (OVERALL) и для всех слоев по обоим факторам. Средние значения для комбинаций взаимодействия на этом этапе рассчитываются только для неполнофакторных моделей.
-
Затем активируйте Descriptive Statistics (Дескриптивные статистики); благодаря выбору этой опции выводятся среднее значение, стандартные отклонения и количество наблюдений во всех ячейках.
-
Активируйте затем опцию Homogeneity tests (Тесты на однородность). Таким образом активируется проверка однородности дисперсии. Покиньте диалоговое окно нажатием Continue (Далее).
-
При помощи выключателя Plots... (Диаграммы) откройте диалоговое окно Univariate: Profile Plots (Одномерная: Профильные диаграммы) (см. рис. 17.5).
Рис. 17.4: Диалоговое окно Univariate: Options (Одномерная: Опции)
Рис. 17.5: Диалоговое окно Univariate: Profile Plots (Одномерная: Профильные диаграммы)
В случае профильных диаграмм речь идёт о графическом представлении средних значений слоев выбранных факторов в виде линейчатых диаграмм. При этом слои второго фактора соответственно могут быть использованы для отображения второй линии. Таким образом можно наглядно изобразить взаимодействия между двумя факторами.
-
Поместите переменную alter (возраст) в поле Horizontal Axis (Горизонтальная ось), а переменную geschl (пол) в поле Separate Lines (Отдельные линии). В принципе можно указывать дополнительную переменную и в поле Separate Plots (Отдельные графики); тогда для отдельных слоев этой переменной будут построены отдельные диаграммы.
-
Щёлкните на выключателе Add (Добавить) и покиньте диалоговое окно нажатием Continue (Далее).
-
В заключение щёлкните на выключателе Post Hoc... (Дополнительный тест). Откроется диалоговое окно Univariate: Post Hoc Multiple Comparisons for Observed Means (Одномерная: Дополнительно — множественные сравнения для наблюдаемых средних значений).
У Вас появится возможность выбрать один или несколько из восемнадцати тестов, необходимых для проведения дополнительного сравнения отдельных слоев выбранных факторов. Конечно же, это имеет смысл только для факторов с более чем двумя слоями.
-
Поместите переменную alter (возраст) в поле Post Hoc Tests for (Дополнительные тесты для).
-
Активируйте тест Шеффе (Scheffe). Теперь диалоговое окно выглядит так, как изображено на рисунке 17.6.
-
Покиньте диалоговое окно нажатием Continue (Далее).
-
Далее Вы имеете возможность определить контрасты и для каждого наблюдения сохранить некоторые статистические характеристики, как новые переменные. Мы от этого откажемся. Начните расчёт нажатием ОК.
В окне сначала появляется сводная таблица, озаглавленная "Межсубъектные факторы". Затем следует вывод средних значений, стандартных отклонений и количества наблюдений для отдельных ячеек, а также результаты теста на однородность.
Рис. 17.6: Диалоговое окно Univariate: Post Hoc Multiple Comparisons for Observed Means (Одномерная: Дополнительно — многократные сравнения для наблюдаемых средних значений)
Between-Subjects Factors (Межсубъектные факторы)
Value Label (Метка значения) | N | ||
GESCHL (Пол) | 1 | maennlich (Мужской) | 15 |
2 | weiblich (Женский) | 12 | |
ALTER (Возраст) | 1 | bis 30 Jahre (До 30 лет) | 7 |
2 | 31 - 50 Jahre (31 - 50 лет) | 9 | |
3 | ueber 50 Jahre (Свыше 50 лет) | 11 |
Descriptive Statistics (Дескриптивные статистики)
Dependent Variable: М1 (Зависимая переменная: М1) | ||||
GESCHL ' (Пол) | ALTER (Возраст) | Mean (Среднее значение) | Std. Deviation (Стандартное отклонение) | N |
maennlich (Мужской) | bis 30 Jahre (До 30 лет) | 16,00 | ,82 | 4 |
31 - 50 Jahre (31 - 50 лет) | 14,60 | 1,14 | 5 | |
ueber 50 Jahre (Свыше 50 лет) | 11,7 | 2,48 | 6 | |
Total (Сумма) | 13,60 | 2,69 | 15 | |
weiblich (Женский) | bis 30 Jahre (До 30 лет) | 16,00 | 1,00 | 3 |
31 - 50 Jahre (31 - 50 лет) | 15,00 | 1,41 | 4 | |
ueber 50 Jahre (Свыше 50 лет) | 10,20 | 1,10 | 5 | |
Total (Сумма) | 13,25 | 2,93 | 12 | |
Total (Сумма) | bis 30 Jahre (До 30 лет) | 16,00 | ,82 | 7 |
31 - 50 Jahre (31 - 50 лет) | 14,78 | 1,20 | 9 | |
ueber 50 Jahre (Свыше 50 лет) | 10,73 | 1,95 | 11 | |
Levene's Test of Equality of Error Variances a (Тест Левене на равенство дисперсии ошибок)
Dependent Variable: М1 (Зависимая переменная: М1)
F | df1 | df2 | Sig(Значимость) |
4,177 | 5 | 21 | ,009 |
Tests the null hypothesis that the error variance of the dependent variable is equal across groups (Проверяет нулевую гипотезу о том, что дисперсия ошибок зависимых переменных одинакова для всех групп).
a. Design: Intercept+GESCHL+ALTER+GESCHL * ALTER (Компоновка: Отрезок + Пол + Возраст + Пол*Возраст)
К сожалению, тест Левене на равенство дисперсий показывает, значимый результат со значением вероятности ошибки р = 0,009. Это означает, что отсутствует однородность дисперсий между группами, которая наряду с нормальным распределением значений выборки, является основной предпосылкой для возможности проведения дисперсионного анализа.
Традиционная схема дисперсионного анализа (еще раз отметим: проводимого на основе общей линейной модели) показывает незначимое влияние пола (р = 0,761), очень значимое влияние возраста (р = 0,001) и незначимое взаимодействие между обоими переменными (р = 0,611).
Tests of Between-Subjects Effects (Тест межсубъектных эффектов)
Dependent Variable: M1 (Зависимая переменная: М1)
Source (Источник) | Type III Sum of Squares (Сумма квадратов III типа) | Df | Mean Square (Среднее значение квадрата) | F | Sig. (Значи-мость) |
Corrected Model (Подпра- вленная модель) | 145,833a | 5 | 29,167 | 12,049 | ,000 |
Intercept (Отрезок) | 4916,763 | 1 | 4916,763 | 2031,187 | ,000 |
GESCHLJOonl | ,229 | 1 | ,229 | ,095 | ,761 |
ALTER (Возраст) | 144,273 | 2 | 72,137 | 29,801 | ,000 |
GESCHL * ALTER (Пол'Возраст) | 2,446 | 2 | 1,223 | ,505 | ,611 |
Error (Ошибка) | 50,833 | 21 | 2,421 | ||
Total (Сумма) | 5077,000 | 27 | |||
Corrected Total | 196,667 | 26 |
a R Squared = ,742 (Adjusted R Squared = ,680) (R-квадрат = 0,742 (смещённый R-квадрат = 0,680))
В случае отсутствия однородности дисперсии границу значимости рекомендуется устанавливать равной не р = 0,05, а р =0,01. Значимое влияние возраста проявляется в любом случае.
Если вы сравните эти результаты с результатами, полученными при методе Фишера (Fisher) (см. гл. 17.1.2), то заметите незначительное отклонение значения р для фактора влияния пол (geschlecht). Далее следует вывод дескриптивных статистик для совокупной выборки и для отдельных слоев факторов.
1. Grand Mean (Общее среднее значение)
| Dependent Variable: М1 (Зависимая переменная: М1) | |||
Mean (Среднее значение) | Std. Error (Стандартная ошибка) | 95% Confidence Interval (95 % доверительный интервал) | |
Lower Bound (Нижний предел) | Upper Bound (Верхний предел) | ||
13,828 | ,307 | 13,190 | 14,466 |
2. GESCHL (Пол)
| Dependent Variable: М1 (Зависимая переменная: М1) | ||||
GESCHL (Пол) | Mean (Среднее значение) | Std. Error (Стандартная ошибка) | 95% Confidence Interval (95 % доверительный интервал) | |
Lower Bound (Нижний предел) | Upper Bound (Верхний предел) | |||
maennlich (Мужской) | 13,922 | ,407 | 13,075 | 14,769 |
weiblich (Женский) | 13,733 | ,459 | 12,779 | 14,688 |
3. ALTER (Возраст)
| Dependent Variable: М1 (Зависимая переменная: М1) | ||||
ALTER (Возраст) | Mean (Среднее значение) | Std. Error (Стандартная ошибка) | 95% Confidence Interval (95 % доверительный интервал) | |
Lower Bound (Нижний предел) | Upper Bound (Верхний предел) | |||
bis 30 Jahre (До 30 лет} | 16,000 | ,594 | 14,764 | 17,236 |
31 - 50 Jahre (31 - 50 лет) | 14,800 | ,522 | 13,715 | 15,885 |
ueber 50 Jahre (Свыше 50 лет) | 10,683 | ,471 | 9,704 | 11,663 |
Затем следует вывод результатов теста Шеффе по сравнению отдельных возрастных групп. На основании частично дублированных результатов, можно сделать вывод, что самая старшая возрастная группа очень значимо отличается от двух других:
Multiple Comparisons (Множественные сравнения)
| Dependent Variable: M1 (Зависимая переменная: М1) Scheffe (Шеффе) | ||||||
(I) ALTER (Возраст) | (J) ALTER (Возраст) | Mean Difference (I-J) (Средняя разность) | Std. Error (Стандар -тная ошибка) | Sig. (Значи-мость) | 95% Confidence Interval (95 % доверительный интервал) | |
Lower Bound (Нижний предел) | Upper Bound (Верхний предел) | |||||
bis 30 Jahre (До 30 лет) | 31 -50 Jahre (31 -50 лет) | 1,22 | ,784 | ,317 | -.84 | 3,29 |
ueber 50 Jahre (Свыше 50 лет) | 5,27* | ,752 | ,000 | 3,29 | 7,25 | |
31 -50 Jahre (31 -50 лет) | bis 30 Jahre (До 30 лет) | -1,22 | ,784 | ,317 | -3,29 | ,84 |
ueber 50 Jahre (Свыше 50 лет) | 4,05* | ,699 | ,000 | 2,21 | 5,89 | |
ueber 50 Jahre (Свыше 50 лет) | bis 30 Jahre (До 30 лет) | -5,27* | ,752 | ,000 | -7,25 | -3,29 |
31 -50 Jahre (31 -50 лет) | -4,05* | ,699 | ,000 | -5,89 | -2,21 | |
Based on observed means (Основываясь на наблюдаемых средних значениях). * The mean difference is significant at the ,05 level (Усреднённая разность является значимой на уровне 0,05).
Этот факт подтверждается ещё раз при выводе результатов для рассматриваемых "однородных подгрупп" в другой форме.
М1
| Scheffe аbс (Шеффе) | |||
ALTER | N | Subset (Подгруппа) | |
1 | 2 | ||
ueber 50 Jahre (Свыше 50 лет) | 11 | 10,73 | |
31 - 50 Jahre (31 - 50 лет) | 9 | 14,78 | |
bis 30 Jahre (До 30 лет) | 7 | 16,00 | |
Sig. (Значимость) | 1,000 | ,283 | |
Means for groups in homogeneous subsets are displayed (Выводятся средние значения для групп в однородных подгруппах).
Based on Type III Sum of Squares (На основе суммы квадратов III типа).
The error term is Mean Square(Error) = 2,421 (Слагаемое ошибки равно среднему значению квадрата (ошибки) = 2,421).
a. Uses Harmonic Mean Sample Size = 8,699 (Используя среднегармонический размер выборок = 8,699).
b. The group sizes are unequal (Размеры групп не одинаковы). The harmonic mean of the group sizes is used (Используется среднее гармоническое размера групп). Туре I error levels are not guaranteed (Уровень ошибки для I типа не гарантируется).
с. Alpha = ,05
Завершает вывод результатов профильная диаграмма, в которой представлена линейчатая диаграмма возраста отдельно для каждого пола:
Вид графиков для обоих полов почти одинаков, что свидетельствует о незначимом взаимодействии между двумя факторами. Кроме того, наглядно проявляется незначимость различия между двумя полами.
2.gif
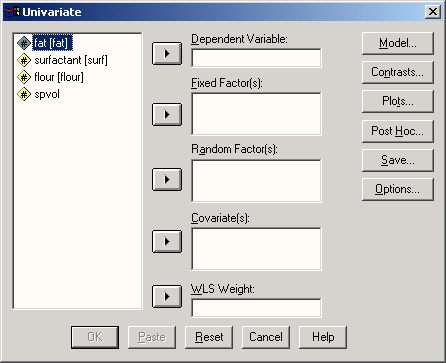
3.gif
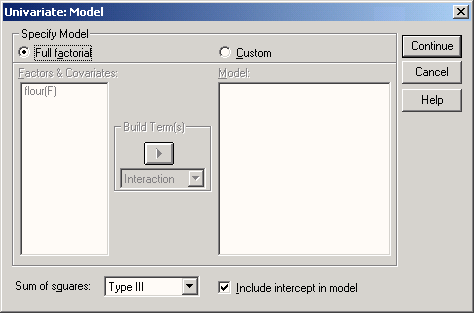
4.gif
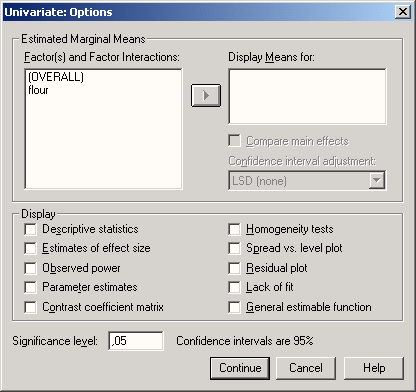
5.gif
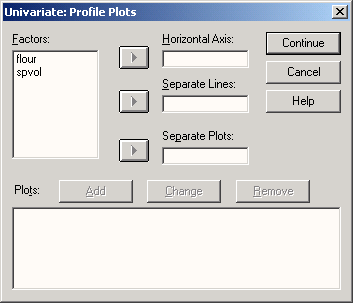
6.gif

7.gif
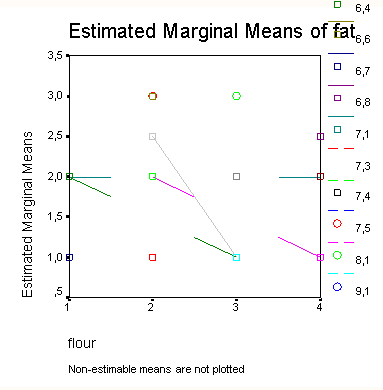
17.1.2 Одномерный дисперсионный анализ по методу Фишера (Fisher)
17.1.2 Одномерный дисперсионный анализ по методу Фишера (Fisher)
Проанализируем теперь пример, приведенный в разделе 17.1.1, при помощи традиционного "классического" метода Фишера. Так как, начиная с 8.0 версии программы, этот вид анализа уже не выводится в диалоговое окно, то нам придётся воспользоваться программным синтаксисом (процедура AN OVA).
-
Откройте файл varana.sav.
-
Выберите в меню File (Файл) New (Новый) Syntax (Синтаксис) Наберите следующую команду в поле редактора синтаксиса:
ANOVA VARIABLES=ml BY geschl (1,2) alter (1,3)
/STATISTICS MCA MEAN
/METHOD EXPERIM.
SPSS предлагает три метода для разложения квадратов отклонения в МНК для случая, когда объемы отдельных ячеек (количества наблюдений, относящихся к данной ячейке) не равны. При такой "несбалансированной компоновке", которая часто появляется при "непланируемых" (не экспериментальных) исследованиях, без дальнейшей обработки нельзя к общей сумме прибавлять суммы квадратов отдельных эффектов. Вы можете выбрать один из следующих методов обработки:
-
UNIQUE: Вклад каждого из факторов влияния рассматривается одновременно; каждый из них рассчитывается при условии сохранения постоянного значения всех остальных. Так как в этом случае можно сделать неявное предположение о возможном существовании причинной связи между факторами, то этот вариант следует выбирать тогда, когда не должно проводиться весовое сравнение значения отдельных факторов. Этот метод устанавливается по умолчанию.
-
HIERARCHICAL: Очерёдность расчёта эффектов определяется очерёдностью выбранных факторов. Этот метод следует применять тогда, когда можно заранее предположить иерархическую упорядоченность факторов.
-
EXPERIMENTAL: Эффекты обрабатываются в следующей последовательности: эффекты ковариаций, главные эффекты, взаимодействия в порядке возрастания. При расчёте одного эффекта производится вычисление всех предшествующих эффектов и эффектов, находящихся на том же уровне.
При одинаковых объемах ячеек ("ортогональная компоновка") все три метода дают одинаковые результаты.
При помощи вспомогательной команды STATISTICS можно организовать вывод следующих данных:
-
Mean: Выводятся средние значения и количество наблюдений для совокупной популяции, отдельных слоев фактора и каждой ячейки. Удивительно, но если вы выбираете метод UNIQUE для разложения суммы квадратов в МНК, то эта опция становится недоступной.
-
MCA (Множественный классификационный анализ): С помощью специальных коэффициентов (называемых т) (Eta) и Р (Beta)) отображается сила связи между отдельным фактором и зависимой переменной. Это является уместным, если не наблюдается ни каких значимых взаимодействий. Вывод результатов МСА недоступен при выборе метода UNIQUE.
-
Запустите команду ANOVA на исполнение щелчком на знаке Run Current (Запустить синтаксис).
После обычной сводной таблицы обрабатываемых наблюдений, сначала выводятся средние значения и частоты (соответствующие результаты вывода здесь не приводятся). Затем следует сводка дисперсионного анализа с суммами квадратов, степенями свободы, средними значениями сумм квадратов и т.д.:
ANOVA a | |||||||
| Experimental Method (Экспериментальный метод) | ||||||
Sum of Squares (Сумма квадра-тов) | df (Степень свободы) | Mean Square (Среднее значение квадрата) | F | Sig. (Значи-мость) | |||
М1 | Main Effects (Главные эффекты) | (Combined) (Объеди-нённо) | 143,388 | 3 | 47,796 | 19,745 | ,000 |
GESCHL (Пол) | ,458 | 1 | ,458 | ,189 | ,668 | ||
ALTER (Возраст) | 142,571 | 2 | 71,285 | 29,449 | ,000 | ||
2-Way Interacti-ons (2-сторонние взаимо-действия) | GESCHL * ALTER (Пол' Возраст) | 2,446 | 2 | 1,223 | ,505 | ,611 | |
Model (Модель) | 145,833 | 5 | 29,167 | 12,049 | ,000 | ||
Residual (Остатки) | 50,883 | 21 | 2,421 |
|
| ||
Total (Сумма) | 196,667 | 26 | 7,564 |
|
| ||
а М1 by GESCHL, ALTER (М1/по полу, возрасту)
Вероятность ошибки р, соответствующая тестовому значению F-критерия, выводится в правой колонке под заголовком "Sig." ("Значимость"). Ее величина свидетельствует о глобальной значимости для главных эффектов (р < 0,001). Данное значение основано только на факторе Alter (Возраст) (р < 0,001), но не на факторе Geschlecht (Пол) (р = 0,668). Взаимодействия в данном случае не наблюдаются (р = 0,611). Результаты очень близки к результатам расчёта при помощи общей линейной модели (см. гл. 17.1.1).
Результаты МСА выглядят следующим образом:
MCA a (Множественный классификационный анализ) | |||||||
| N | Predicted Mean (Прогнозируемое среднее значение) | Deviation (Отклонение) | ||||
Unadjusted (Несме-щенное) | Adjusted for Factors (Смещенное по факторам) | Unad-justed (Несме-щенное) | Adjusted for Factors (Смещенное по факторам) | ||||
М1 | GESCHL (Пол) | maennlich (Мужской) | 15 | 13,60 | 13,56 | ,16 | ,12 |
weiblich (Женский) | 12 | 13,25 | 13,30 | -,19 | -.15 | ||
ALTER (Возраст) | bis 30 Jahre (До 30 лет) | 7 | 16,00 | 16,00 | 2,56 | 2,55 | |
31 - 50 Jahre (31 -50 лет) | 9 | 14,78 | 14,78 | 1,33 | 1,33 | ||
ueber 50 Jahre (Свыше 50 лет) | 11 | 10,73 | 10,73 | -2,72 | -2,71 | ||
a Ml by GESCHL, ALTER (M1/no полу, возрасту)
Factor Summary a (сводные данные для факторов) | ||
Eta (Эта) | Beta (Бета) | |
Adjusted for Factors (Смещено по факторам) | ||
М1 GESCHL (Пол) | ,064 | ,048 |
ALTER (Возраст) | ,853 | ,852 |
а М1 by GESCHL, ALTER (М1/по полу, возрасту) | ||
Model Goodness of Fit (Критерий согласия для модели)
R | R Squared (R-квадрат) | |
М1 by GESCHL, ALTER (М1/по полу, возрасту) | ,854 | ,729 |
Оба коэффициента n (Eta) являются мерой силы связи (корреляции) между соответствующим фактором и зависимыми переменными, относящейся сюда же коэффициент (i (Beta) имеет частную природу и характеризует силу связи при отсутствии влияний со стороны других факторов. Значительное отличие коэффициентов Eta и Beta друг от друга (которое в данном случае не наблюдается) указывает на наличие взаимосвязи между факторами. И, наконец, величина "R Squared" ("R-квадрат") указывает на ту степень отклонения от совокупной дисперсии, которая может быть объяснена главными эффектами.
17.1.3 Одномерный дисперсионный анализ с повторным измерением
17.1.3 Одномерный дисперсионный анализ с повторным измерением
Исследуем вопрос следующего характера: наблюдаются ли в течение четырёх моментов времени значимые изменения показаний теста на внимательность. При этом необходимо учесть влияние двух факторов: пола и возраста.
В общем, в нашем распоряжении имеется три фактора: пол с двумя категориями, возраст с тремя категориями и время с четырьмя категориями. Это приводит к необходимости выполнения трёхфакторного дисперсионного анализа, в котором третий фактор (время) является фактором с повторным измерением. Этот фактор будет представлен не при помощи отдельных групп испытуемых, а при помощи значений переменных ml-m4.
-
Откройте файл varana.sav.
-
Выберите в меню Analyze (Анализ) General Linear Model (Общая линейная модель) Repeated Measures... (Повторные измерения)
-
Как уже было изложено в главе 13.4, отроется диалоговое окно Repeated Measures Define Factors(s) (Повторные измерения: Определение фактора(ов)).
-
Вместо установленного по умолчанию имени фактора factorl введите новое имя: zeit (время).
-
В поле Number of Levels (Количество слоев) введите значение 4. Щёлкните на Add (Добавить), и, если больше цет никаких факторов с повторными измерениями, покиньте диалоговое окно посредством нажатия кнопки Define (Определить).
Появится диалоговое окно Repeated Measures (Повторные измерения) (см. рис. 17.7).
-
Здесь, в первую очередь, последовательно перенесите четыре переменные повторных измерений ml-m4 в поле для внутрисубъектных переменных (Within-Subjects Variables).
-
Затем, переменные geschl (пол) и alter (возраст) перенесите в поле для межсубъектных факторов (Between-Subjects Factor(s)).
-
В диалоговом окне Options (Опции) активируйте вывод средних для трёх факторов: geschl (пол), alter (возраст) и zeit (время), в поле отображаемых результатов (Display) активируйте вывод дескриптивных статистик и, помимо этого, сделайте запрос на тест однородности.
Рис. 17.7: Диалоговое окно Repeated Measures (Повторные измерения)
-
Начните расчёт нажатием ОК.
На экране появятся довольно обширные результаты расчёта. Их расшифровка может оказаться довольно проблематичной для новичка. Поэтому ниже будет рассмотрена только та часть результатов, которая является важной для поиска ответа на вопрос: какой из трёх факторов — пол, возраст или время, оказывает значимое влияние и какие взаимодействия между этими факторами являются значимыми.
Сначала даётся сводная таблица для внутрисубъектных (время) и межсубъектных (пол и возраст) факторов. Затем выводятся дескриптивные статистики (среднее значение, стандартное отклонение, количество наблюдений) для отдельных ячеек, то есть характеристики переменных ml-m4 отдельно для пола и возрастных групп. Вывод этих показателей в книге не приводится.
Далее следуют результаты расчёта для фактора "Zeit" ("Время") и для взаимодействий с этим фактором, в основу которых положен метод общей линейной модели. Для этого были определены различные тестовые величины, которые выводятся под наименованиями: "Pillai's Trace" (След Пиллая), "Wilks' Lambda" (Лямбда Уилкса), "Hotelling's Trace" (След Хоттелинга) и "Roy's Largest Root" (Максимальный характеристический корень по методу Роя). С помощью надлежащих преобразований по этим тестовым величинам восстанавливается рампределения значение F, по которому затем определяется значение р, приводимое в колонке "Значимость" (Sig). Следует отметить, что след Пиллая ("Pillai's Trace") является наиболее сильным и устойчивым (робастным) тестом.
Результаты первых трёх тестов являются практически идентичными. Обнаружено очень значимое влияние временного фактора, а вот взаимодействия других факторов со временем, напротив, оказались не значимыми.
Одни и те же расчёты, то есть проверка временного фактора и взаимодействий со временем, производятся также при помощи традиционного "классического" метода Фишера. Соответствующие результаты можно взять из строки "Предполагается сферичность" во второй из нижеследующих таблиц, которая наряду с ними содержит ещё три варианта проверок.
Multivariate Tests c (Многомерные тесты)
Effect (Эффект) | Value (Значе-ние) | F | Hypothesis df (Гипотеза df) | Error df (Ошибка df) | Sig. (Зна-чимость) | |
ZEIT (Время) | Pillai's Trace (След Лиллая) | ,955] | 133,367" | 3,000 | 19,000 | ,000 |
Wilks' Lambda (Лямбда Уилкса) | ,045 | 133,367" | 3,000 | 19,000 | ,000 | |
Hotelling's Trace (След Хоттелинга) | 21,058 | 133,367а | 3,000 | 19,000 | ,000 | |
Roy's Largest Root (Макси-мальный характе-ристический корень по методу Роя) | 21,058 | 133,367е | 3,000 | 19,000 | ,000 | |
ZEIT*GESCHL (Время'Пол) | Pillai's Trace (След Пиллая) | ,106 | ,752" | 3,000 | 19,000 | ,535 |
Wilks1 Lambda (Лямбда Уилкса) | ,894 | ,752а | 3,000 | 19,000 | ,535 | |
Hotelling's Trace (След Хоттелинга) | ,119 | ,752а | 3,000 | 19,000 | ,535 | |
Roy's Largest Root (Макси-мальный характе-ристический корень по методу Роя) | ,119 | ,752" | 3,000 | 19,000 | ,535 | |
ZEIT * ALTER (Время* Возраст) | Pillai's Trace (След Пиллая | ,293 | 1,145 | 6,000 | 40,000 | ,355 |
Лямбда Уилкса) | ,710 | 1,183а | 6,000 | 38,000 | ,336 | |
Hotelling's Trace (След Хоттелинга) | ,404 | 1,213 | 6,000 | 36,000 | ,322 | |
Roy's Largest Root (Макси-мальный характе-ристический корень по методу Роя) | ,394 | 2,625" | 3,000 | 20,000 | ,079 | |
ZEIT * GESCHL * ALTER (Время'Пол* Возраст) | Pillai's Trace (След Пиллая) | ,406 | 1,699 | 6,000 | 40,000 | ,146 |
Wilks1 Lambda (Лямбда Уилкса) | ,622 | 1,699а | 6,000 | 38,000 | ,148 | |
Hotelling's Trace (След Хоттелинга) | ,564 | 1,691 | 6,000 | 36,000 | ,151 | |
Roy's Largest Root (Макси-мальный характе-ристический корень по методу Роя) | ,468 | 3,118Ь | 3,000 | 20,000 | ,049 | |
a, b, с — см. след. стр. | ||||||
Tests of Within-Subjects Effects (Тест внутрисубъектных эффектов)
Measure: MEASURE_1 (Мера: MEASURE_1 )
Source Источник) | Type III Sum of Squares (Сумма квадратов III типа) | df | Чеап Square (Среднее значение квадрата) | F | Sig. (Значи-мость) | |
ZEIT Время) | Sphericity Assumed (Предполагается сферичность) | 185,661 | 3 | 61,887 | 83,028 | ,000 |
Greenhouse-Geisser (Гринхауз-"айссер) | 185,661 | 2,577 | 72,055 | 83,028 | ,000 | |
Huynh-Feldt (Гин-Фельд) | 185,661 | 3,000 | 61,887 | 83,028 | ,000 | |
Lower-bound (Нижний предел) | 185,661 | 1,000 | 185,661 | 83,028 | ,000 | |
ZEIT* GESCHL Время * Пол) | Sphericity Assumed (Предполагается сферичность) | 1,520 | 3 | ,507 | ,680 | ,568 |
Greenhouse-Geisser (Гринхауз-"айссер) | 1,520 | 2,577 | ,590 | ,680 | ,547 | |
Huynh-Feldt (Гин-Фельд1 | 1,520 | 3,000 | ,507 | ,680 | ,568 | |
.ower-bound (Нижний предел) | 1,520 | 1,000 | 1,520 | ,680 | ,419 | |
ZEIT* ALTER (Время * Возраст) | Sphericity Assumed ^Предполагается сферичность) | 4,190 | 6 | ,698 | ,937 | ,475 |
Greenhouse-Geisser (Гринхауз-Гайссер) | 4,190 | 5,153 | ,813 | ,937 | ,467 | |
Huynh-Feldt (Гин-Фельд) | 4,190 | 6,000 | ,698 | ,937 | ,475 | |
Lower-bound (Нижний предел) | 4,190 | 2,000 | 2,095 | ,937 | ,408 | |
ZEIT* GESCHL* ALTER Время * Пол* Зозраст) | Sphericity Assumed (Предполагается сферичность) | 6,557 | 6 | 1,093 | 1,466 | ,204 |
Greenhouse-Geisser (Гринхауз-Гайссер^ | 6,557 | 5,153 | 1,272 | 1,466 | ,215 | |
Huynh-Feldt (Гин-Фельд) | 6,557 | 6,000 | 1,093 | 1,466 | ,204 | |
Lower-bound (Нижний предел) | 6,557 | 2.00C | 3,278 | 1,466 | ,254 | |
Error (ZEIT) (Ошибка (Время)) | Sphericity Assumed (Предполагается сферичность) | 46,958 | 63 | ,745 |
|
|
Greenhouse-Geisser (Гринхауз-Гайссер) | 46,958 | 54,110 | ,868 |
|
| |
Huynh-Feldt (Гин-Фельд) | 46,95f | 63,000 | ,745 |
|
| |
Lower-bound (Нижний предел) | 46,958 | 21.00C | 2,236 |
|
| |
a Exact statistic (Точная статистика)
b The statistic is an upper bound on F that yields a lower bound on the significance level (Статистической характеристикой является верхний придел значения Е-распределе-ния, который указывает на нижний предел уровня значимости).
c Design: Intercept+GESCHL+ALTER+GESCHL * ALTER (Компоновка: Отрезок + Пол + Возраст + Пол * Возраст )
Within Subjects Design: ZEIT (Компоновка внутри субъектов: Время)
Полученные результаты близки к результатам расчётов по общей линейной модели. Тест Левене на равенство дисперсий демонстрирует однородность дисперсии для моментов времени со второго по четвёртый и неоднородность дисперсии (р = 0,009) для первого момента (см. гл. 17.1.1).
Levene's Test of Equality of Error Variances a (Тест Левене на равенство дисперсии ошибок)
F | df1 | df2 | Sig. (Значимость) | |
М1 | 4,177 | 5 | 21 | ,009 |
М2 | ,878 | 5 | 21 | ,513 |
МЗ | 1,751 | 5 | 21 | ,167 |
М4 | 2,022 | 5 | 21 | ,117 |
Tests the null hypothesis that the error variance of the dependent variable is equal across groups (Проверяется нулевая гипотеза о том, что дисперсия ошибки независимых переменных остаётся постоянной для всех групп). a. Design: Intercept+GESCHL+ALTER+GESCHL * ALTER (Компоновка: Отрезок + Пол + Возраст + Пол * Возраст ) Within Subjects Design: ZEIT (Компоновка внутри субъектов: Время)
Далее идут расчёты для обоих факторов (пол и возраст), для которых не производятся повторные измерения, а также для их взаимодействия.
Tests of Between-Subjects Effects (Тест межсубъектных эффектов)
Measure: MEASURE_1 (Мера: MEASURE_1)
Transformed Variable: Average (Трансформированная переменная: Среднее значение)
Source (Источник) | Type III Sum of Squares (Сумма квадратов III типа) | Df | Mean Square (Среднее значение квадрата) | F | Sig. (Значимость) |
Intercept (Отрезок) | 25080,367 | 1 | 25080,367 | 2029,299 | ,000 |
GESCHL (Пол) | ,738 | 1 | ,738 | ,060 | ,809 |
ALTER (Возраст) | 667,147 | 2 | 333,573 | 26,990 | ,000 |
GESCHL * ALTER (Пол * Возраст) | 33,571 | 2 | 16,785 | 1,358 | ,279 |
Error (Ошибка) | 259,542 | 21 | 12,359 |
Получается незначимое влияние пола (р = 0,809), очень значимое влияние возраста (р < 0,001) и незначимое взаимодействие (р = 0,279). Под заголовком "Оцененные пределы средних" (Estimated Marginal Means) выводится информация о средних значениях и стандартных отклонениях для отдельных слоев факторов:
1. GESCHL (Пол)
| Measure: MEASURE_1 (Мера: MEASURE_1) | ||||
GESCHL (Пол) | Mean (Среднее значение) | Std. Error (Стандартная ошибка) | 95% Confidence Interval (95 % доверительный интервал) | |
Lower Bound (Нижний предел) | Upper Bound (Верхний предел) | |||
maennlich (Мужской) | 15,700 | ,460 | 14,743 | 16,657 |
weiblich (Женский) | 15,531 | ,519 | 14,452 | 16,609 |
2. ALTER (Возраст)
| Measure: MEASURE 1 (Мера: MEASURE 1) | ||||
ALTER (Возраст) | Mean (Среднее значение) | Std. Error (Стандартная ошибка) | 95% Confidence Interval (95 % доверительный интервал) | |
Lower Bound (Нижний предел) | Upper Bound (Верхний предел) | |||
bis 30 Jahre (До 30 лет) | 17,646 | ,671 | 16,250 | 19,042 |
31 - 50 Jahre (31 - 50 nejr) | 16,988 | ,590 | 15,761 | 18,214 |
ueber 50 Jahre (Свыше 50 лет) | 12,213 | ,532 | 11,106 | 13,319 |
3. ZEIT (Время)
| Measure: MEASURE_1 (Мера: MEASURE_1) | ||||
ZEIT (Время) | Mean (Среднее значение | Std. Error (Стандартная ошибка; | 95% Confidence Interval (95 % доверительный интервал) | |
Lower Bound (Нижний предел) | Upper Bound (Верхний предел) | |||
1 | 13,828 | ,307 | 13,190 | 14,466 |
2 | 14,964 | ,405 | 14,121 | 15,807 |
3 | 16,275 | ,386 | 15,472 | 17,078 |
4 | 17,394 | ,400 | 16,562 | 18,227 |
Для факторов, для которых не производятся повторные измерения (межсубъектные эффекты), можно вновь провести дополнительные тесты (Post Hoc), но, к сожалению, их нельзя применить для факторов, для которых производятся повторные измерения.
8.gif
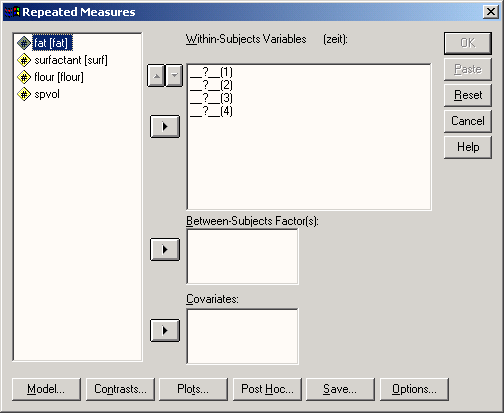
17.2 Ковариационный анализ
17.2 Ковариационный анализ
Если в дисперсионном анализе используется независимая переменная, относящаяся к интервальной шкале или к шкале отношений (метрической), то говорят не о факторе, а о ковариации. Поясним значение такой "контрольной переменной" на следующем примере.
Двадцать испытуемых с избыточным весом (11 мужчин и 9 женщин) изъявили желание похудеть и для этого взялись следовать определённой диете. Одиннадцать испытуемых дополнительно вступили в некоторое общество для желающих похудеть, в котором процесс похудения подстегивается при помощи специальных стимулирующих лекций и других мотивирующих методов. Для всех тестируемых были сняты показатели роста (в см) и веса (в кг) до и после прохождения курса. Далее при помощи расчета индекса Брока (Вгоса) фактический вес был отнесен к нормальному весу, где нормальный вес в килограммах мы можем получить, если от роста, взятого в сантиметрах, отнимем 100:

Так индекс Брока, равный 100 процентам означает нормальный вес, превышающий 100 процентов — избыточный вес.
-
Откройте файл gewicht.sav.
Переменная beh указывает на группу (1 = диета, 2 = диета + общество для желающих похудеть), а переменная g указывает на пол (1 = мужской, 2 = женский). К остальным переменным, участвующими в расчётах, относятся: gr (Рост), gew (Вес до лечения), gewl (Вес в конце лечения), ЬгосаО (Индекс Брока до лечения), brocaab (Уменьшение индекса Брока). Последняя переменная должна служить мерой эффективности диеты.
Мы хотим провести двухфакторный дисперсионный анализ с использованием переменных beh и g в качестве независимых переменных (факторов) и переменной brocaab в качестве зависимой переменной.
-
Выберите в меню Analyze (Анализ) General Linear Model (Общая линейная модель) Univariate... (Одномерная)
-
В появившемся диалоговом окне переменной brocaab присвойте статус зависимой переменной, а переменным beh и g — статус постоянных факторов.
-
После прохождения кнопки Options... (Опции) активируйте вывод оценки пределов средних для факторов beh и g.
-
Начните расчёт нажатием ОК.
Для группы, члены которой дополнительно вступили в общество для желающих похудеть, средний показатель снижения индекса Брока равен 11,558, в то время как для группы, члены которой худеют только при помощи одной диеты, снижение в среднем составляет 5,178. Дисперсионный анализ дает следующие результаты:
Tests of Between-Subjects Effects (Тесты межсубъектных эффектов)
Dependent Variable: BROCAAB (Зависимая переменная: BROCAAB)
Source (Источник) | Type III Sum of Squares (Сумма квадратов III типа) | Df | Mean Square (Средний квадрат) | F | Sig. (Значи-мость) |
Corrected Model (Подправленная модель) | 209,636" | 3 | 69,879 | 12,836 | ,000 |
Intercept (Отрезок) | 1371,877 | 1 | 1371,877 | 252,002 | ,000 |
ВЕН | 199,414 | 1 | 199,414 | 36,631 | ,000 |
G | 1.998E-03 | 1 | 1.998E-03 | ,000 | ,985 |
BEH*G | 3,026 | 1 | 3,026 | ,556 | ,467 |
Error (Ошибка) | 87,103 | 16 | 5,444 | ||
Total (Сумма) | 1805,668 | 20 | |||
Corrected Total (Подправленная суммарная вариация) | 296,738 | 19 |
a R Squared = ,706 (Adjusted R Squared = ,651) (R - квадрат = ,706 (смещённый R-квадрат = ,651))
Получается очень значимая разница между двумя группами (р < 0,001): то есть, членство в обществе оказывает очень значимое воздействие на процесс снижения веса.
Если рассмотреть результаты поподробнее, то можно заметить, что начальное значения индекса Брока для группы, дополнительно входящей в общество похудения, значительно выше (132,0 против 113,1). Таким образом, шансы потери веса в этой группе с самого начала выше, чем в другой. Поэтому было бы уместно включить в анализ начальное значение индекса Брока (переменную brоса0) в качестве контрольной переменной, то есть ковариации.
-
Откройте вновь диалоговое окно Univariate (Одномерная) и поместите дополнительно переменную brоса0 в поле ковариации.
-
Начните расчёт нажатием ОХ.
Результат ковариационного анализа будет выглядеть следующим образом:
Tests of Between-Subjects Effects (Тесты межсубъектных эффектов)
Dependent Variable: BROCAAB (Зависимая переменная: BROCAAB)
Source (Источник)
| Type III Sum of Squares (Сумма квадратов III типа)
| df
| Mean Square (Средний квадрат) | F | Sig. (Значи-мость) |
| Corrected ModelПодправленная модель) | 231,170a | 4 | 57,842 | 13,273 | ,000 |
| Intercept (Отрезок) | 8.568 | 1 | 8,568 | 1,966 | ,181 |
| BRACAO | 21,734 | 1 | 21,734 | 4,987 | ,041 |
| ВЕН | 11.077 | 1 | 11,077 | 2, 542 | ,132 |
G | 3.830 | 1 | 3,830 |
,879 | ,363 |
ВЕН *G | 4.644 | 1 | 4,644 | 1,066 | ,318 |
Error (Ошибка) | 65.368 | 15 | 4,358 | ||
Total (Сумма) | 1805,668 | 20 | |||
Corrected Total (Подправленная суммарная вариация) | 296,738 | 19 |
a R Squared = ,780 (Adjusted R Squared = ,721) (R - квадрат = ,780 (смещённый R-квадрат = ,721))
В результате, как и ожидалось, обнаружилось сильное влияние ковариации brоса0 (р = 0,041). Это ведёт к тому, что в обеих группах пропадает значимый эффект (р = 0,132). Из-за сильно отличающихся исходных показателей, доказательство значимого воздействия дополнительного членства в обществе для желающих похудеть является невозможным.
17.3 Многомерный дисперсионный анализ
17.3 Многомерный дисперсионный анализ
Многомерный дисперсионный анализ применяется тогда, когда в одном дисперсионном анализе необходимо одновременно исследовать влияние факторов и возможных ковариации (независимых переменных) на несколько зависимых переменных. Такой многомерный дисперсионный анализ следует предпочесть одномерному тогда (и только тогда), когда зависимые переменные не являются независимыми друг от друга, а наоборот коррелируют между собой.
Если Вы откроете данные из исследования гипертонии (файл hyper.sav) и рассчитаете корреляции между исходными значениями систолического и диастолического давлений, уровнями холестерина и сахара в крови (переменные rrs0, rrd0, cho10 и bz0), то вы заметите, что эти переменные, хотя и не сильно, но всегда значимо коррелируют между собой.
Если Вы хотите узнать, значимо ли отличаются перечисленные переменные для четырёх заданных возрастных групп (переменная ak), то вместо четырёх отдельных одномерных однофакторных дисперсионных анализов Вы должны провести один многомерный однофакторный анализ.
-
Откройте файл hyper.sav.
-
Выберите в меню Analyze (Анализ) General Linear Model (Общая линейная модель) Multivariate... (Многомерная)
Откроется диалоговое окно Multivariate (Многомерная) (см. рис. 17.8).
Поместите переменные rs0, rrd0, cho10, и bz0 в поле. предусмотренное для зависимых переменных, а переменной ak присвойте статус постоянного фактора.
Под выключателями Contrasts... (Контрасты), Model... (Модель) и Options... (Опции) Вы найдёте множество разнообразных возможностей для задания контрастов, выбора различных вариантов моделей или организации вывода всевозможных дополнительных результатов расчёта; к примеру, здесь можно активировать тесты проверки дисперсии на однородность.
Уже было указано на невозможность в рамках этой книги представить все имеющиеся возможности по отдельности. Чтобы рассмотреть все эти возможности Вам придётся обратиться к оригинальному учебнику по SPSS; опытному же пользователю для понимания будет достаточно просто посмотреть на пункты, имеющиеся в диалоговом окне. В крайнем случае, можно воспользоваться справкой.
-
Оставьте все установки по умолчанию и начните расчёт нажатием ОК.
Рис. 17.8: Диалоговое окно Multivariate (Многомерная)
Появятся довольно обширные результаты расчёта. Важным для нас является в первую очередь глобальный многомерный тест на предмет выявления значимых различий "где-нибудь" между возрастными группами:
Multivariate Tests c (Многомерные тесты)
Effect (Эффект ) | Value (Зна-чение) | F | Hypo-thesis df (Гипо-теза df) | Error df (Ошибка df) | Sig. (Значи-мость) | |
Inte-rcept Отре-зок) | Pillai's Trace (След Пиллая) | ,996 | 9252, 061а | 4,000 | 167,000 | ,000 |
Wilks' Lambda (Лямбда Уилкса) | ,004 | 9252,061 а | 4,000 | 167,000 | ,000 | |
Hotelling's Trace (След Хоттелинга) | 221,606 | 9252, 061а | 4,000 | 167,000 | ,000 | |
Roy's Largest Root 'Макси-мальный характе-ристический корень по методу Роя) | 221,606 | 9252,061 а | 4,000 | 167,000 | ,000 | |
АК | Dillai's Trace (След Пиллая) | ,178 | 2,661 | 12,00ol | 507,00o' | ,002 |
Wilks' Lambda (Лямбда Уилкса) | ,827 | 2,740 | 12,000 | 442,132 | ,001 | |
Hotelling's Trace (След Хоттелинга) | ,203 | ,805 | 12,000 | 197,000 | ,001 | |
Roy's Largest Root (Макси-мальный характе-ристический корень по методу Роя) | ,169 | 7,159Ь | 4,000 | 167,000 | ,000 | |
a. Exact statistic (Точная статистика)
b. The statistic is an upper bound on F that yields a lower bound on the significance level (Статистической характеристикой является верхний придел значения F-распределе-ния, который указывает на нижний предел уровня значимости).
с Design: Intercept+AK (Компоновка: Отрезок + АК)
Здесь производится расчёт величин, традиционных для общей линейной модели. Они уже представлены в главе 17.1.3. Основываясь на критерии "След Пиллая" ("Pillai's Trace"), следует отклонить нулевую гипотезу о том, что между четырьмя возрастными группами не наблюдается различий ни для одной из зависимых переменных (значение р = 0,002).
Для проверки, какие из четырёх зависимых переменных в чем-то различаются между собой, были проведены одномерные тесты. Результаты этих тестов полностью соответствуют результатам отдельного одномерного дисперсионного анализа для каждой зависимой переменной.
Мы здесь воздержимся от подробной расшифровки довольно большой таблицы "Тесты межсубъектных эффектов". Отметим только, что для систолического и диастолического давлений, уровней холестерина и сахара в крови получаются следующие значения вероятности ошибки р: 0,153, 0,002, 0,267 и 0,688 соответственно. Причиной суммарной значимости, поучающейся в результате многомерного теста, являются прежде всего значимые различия для диастолического давления.
Для опытных статистиков, хорошо знакомых с тонкостями многомерных методов, SPSS может предложить избыточное количество разнообразных возможностей в области дисперсионного анализа. В первую очередь можно использовать разнообразные возможности процедуры MANOVA, доступной отныне только через командный синтаксис. Эта процедура позволяет проводить простой и множественный регрессионный анализ, дискриминантный анализ, канонический анализ, анализ главных компонентов и др. Однако сложность работы с заданием параметров может составить некоторые затруднения для менее опытных пользователей. Поэтому в данной книге мы ограничились рассмотрением наиболее часто применяемых компоновок дисперсионного анализа.
10.gif
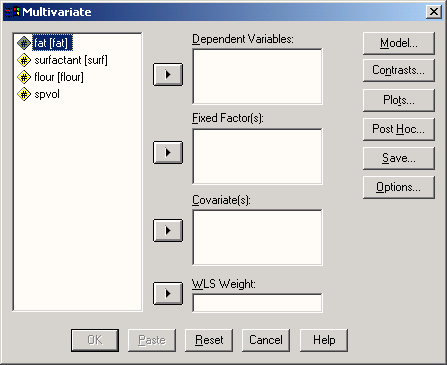
17.4 Компоненты дисперсии
17.4 Компоненты дисперсии
Расчёт компонентов дисперсии в общей линейной модели производится при наличии факторов со случайными эффектами. Факторами со случайными эффектами являются те факторы, слои которых были случайно выбраны из популяции (совокупности) многих возможных слоев факторов.
Проанализируем длину листьев растений растущих на одной клумбе. Для этого вырвем произвольно три растения, листья которых мы и будем измерять.
Растения | Длина листьев (см) | Растения | Длина листьев (см) | |
1 | 9,5 | 2 | 9,0 | |
1 | 9,8 | 2 | 9,5 | |
1 | 8,7 | 3 | 8,0 | |
1 | 8,8 | 3 | 7,8 | |
1 | 8,9 | 3 | 9,0 | |
1 | 10,0 | 3 | 8,7 | |
2 | 11,0 | 3 | 8,9 | |
2 | 10,5 | |||
Так как из большого количества растений мы произвольно взяли для исследований только три, то здесь можно говорить о факторе со случайными эффектами. Это следует учитывать, если при помощи некоего метода дисперсионного анализа нужно будет установить, зависит ли длина листьев от конкретного растения или насколько велика та часть дисперсии, причиной которой является неоднородность растений. Эти вопросы можно прояснить при помощи расчёта компонентов дисперсии.
-
Откройте файл pflanze.sav.
-
Выберите в меню Analyze (Анализ) General Linear Model (Общая линейная модель) Variance Components... (Компоненты дисперсии)
Откроется диалоговое окно Variance Components (Компоненты дисперсии).
-
Поместите laenge (длина) в поле для зависимой переменной, a pflanze (растение) в поле для случайных факторов.
-
Пройдя через кнопку Model... (Модель) вы можете выбрать, будете ли вы рассчитывать полнофакторную модель (установка по умолчанию) или включите в расчёт только некоторые факторы. При наличии только одного фактора, как в приведенном примере, можно говорить, конечно же, только о полнофакторной модели.
-
Выключатель Options... (Опции) предоставляет возможность выбора между четырьмя методами оценки компонентов дисперсии. Лучшим методом считается метод MINQUE (Minimum norm quadratic unbiased estimator) (Минимум нормы квадратической несмещённой оценки); поэтому он и установлен по умолчанию.
-
При помощи выключателя Save... (Сохранить) вы можете сохранить некоторые результаты в файле.
-
Оставьте это окно без изменений и начните расчёт нажатием ОК.
Рис. 17.9: Диалоговое окно Variance Components (Компоненты дисперсии)
В окне просмотра появятся оценки компонентов дисперсии.
Factor Level Information (Информация о слоях фактора)
N | ||
PFLANZE (Растение) | 1,00 | 6 |
2,00 | 4 | |
3,00 | 5 |
Dependent Variable: LAENGE (Зависимая переменная: Длина)
Variance Estimates (Оценки дисперсии)
Component (Компоненты) | Estimate (Оценка) |
Var(PFLANZE) (Переменная (Растение)) | ,471 |
Var(Error) (Переменная (Ошибка)) | ,438 |
Dependent Variable: LAENGE (Зависимая переменная: Длина) Method: Minimum Norm Quadratic Unbiased Estimation (Weight = 1 for Random Effects and Residual) (Метод: Минимум нормы квадратичной несмещённой оценки (Вес = 1 для случайных эффектов и остатков))
На основе этих результатов можно найти процентную долю дисперсии, получающуюся из-за наличия разных растений:
0,471/(0,471+0,438)=51,8%
Приведём ещё один несколько усложненный пример из учебника SPSS. На некоторой фирме, работающей в области электроники, в 36 различных печах при различных температурах (550 и 600 градусов по Фаренгейту) измеряют выносливость (в минутах) определенных радиоэлектронных комплектующих. Один инженер предполагает, что не все печи создают одинаковые условия для тестирования комплектующих. Чтобы это проверить, он случайно выбирает три печи и для каждой печи делает по три измерения выносливости комплектующих для каждой из температур.
Данные находятся в файле ofen.sav в переменных of en (печь), temp (температура) и zeit (время). Переменная ofen (печь) соответствует фактору со случайными эффектами, так как из 36 печей три были выбраны случайно. Температура также является фактором со случайными эффектами, так как температуры 550 и 600 градусов были выбраны из бесконечного множества возможных температур.
Так как вполне возможно, что в разных печах действуют различные температурные режимы, предположим, что температурный фактор является вложенным в фактор печей — т.н. ("гнездовая компоновка'").
-
Откройте файл ofen.sav.
-
Откройте так, как было изложено ранее, диалоговое окно Variance Components (Компоненты дисперсии).
-
Переменную zeit (время) поместите в поле зависимых переменных, а переменные ofen (печь) и temp (температура) в поле случайных факторов.
Мы должны здесь также учесть и вложенность фактора temp (температура) в фактор ofen (печь). Это можно осуществить только при помощи программного синтаксиса.
-
Щёлкните по выключателю Paste (Внести) для того, чтобы перенести синтаксис данной команды в редактор синтаксиса.
В редакторе будет показан следующий синтаксис:
VARCOMP
zeit BY ofen temp
/RANDOM = ofen temp
/METHOD = MINQUE (1)
/DESIGN
/INTERCEPT = INCLUDE .
-
Дополните вспомогательную команду DESIGN следующим образом:
VARCOMP
zeit BY ofen temp
/RANDOM = ofen temp
/METHOD = MINQUE (1)
/DESIGN = ofen temp(ofen)
/INTERCEPT = INCLUDE .
-
Запустите команду на исполнение при помощи кнопки Run Current. В окне просмотра появятся следующие оценки дисперсии:
Variance Estimates (Оценки дисперсии)
Component (Компонент) | Estimate (Оценка) |
Var(OFEN) (Переменная (Печь)) | 29,287 |
Var(TEMP(OFEN)) (Переменная Температура (Печь)) | 1525,889 |
Var(Error) (Переменная (Ошибка)) | 69,778 |
Dependent Variable: ZEIT (Зависимая переменная: Время) Method: Minimum Norm Quadratic Unbiased Estimation (Weight = 1 for Random Effects and Residual) (Метод: Минимум нормы квадратичной несмещённой оценки (Вес = 1 для случайных эффектов и остатков))
Из таблицы можно узнать, что доля дисперсии объясняемая наличием разных печей очень незначительна:
[29, 287/(29,287 + 1525,889 + 69,778)]*100 = 1,8%
До этого момента мы рассматривали только модели со случайными эффектами. Модели, содержащие как случайные, так и постоянные эффекты, получили название "смешанных" моделей.
И, наконец, следует указать на то, что методы MINQUE и ANOVA иногда могут выдавать негативные оценки компонентов дисперсии, что собственно противоречит самому определению дисперсии. Это может происходить потому, что количество наблюдений слишком мало, некоторые значения отсутствуют или выбран неподходящий метод оценки.
11.gif
Глава 18. Дискриминантный анализ
Глава 18. Дискриминантный анализ
1. Дискриминантный анализ
Дискриминантный анализ
С помощью дискриминантного анализа на основании некоторых признаков (независимых переменных) индивидуум может быть причислен к одной из двух (или к одной из нескольких) заданных заранее групп.
Такая постановка задачи, в особенности в случае двух заранее заданных групп, очень сильно напоминает постановку задачи для метода логистической регрессии (см. гл. 16.4). Ядром дискриминантного анализа является построение так называемой дискриминантной функции
d = b1х1+b2х2+... + bnхn+а ,
где x1 и хn — значения переменных, соответствующих рассматриваемым случаям, константы b1-bn и a — коэффициенты, которые и предстоит оценить с помощью дискриминантного анализа. Целью является определение таких коэффициентов, чтобы по значениям дискриминантной функции можно было с максимальной четкостью провести разделение по группам.
18.1 Пример из области медицины
18.1 Пример из области медицины
Обратимся ещё раз к примеру, который уже приводился при рассмотрении логистической регрессии. В этом примере приводятся выборочные данные о пациентах с нарушениями работы легких. Эти данные хранятся в файле lunge.sav. Приведем ещё раз переменные, которые в данном случае будут применяться при дискриминантом анализе:
Имя переменной | Значение |
out | Исход (0 = скончался, 1 = выжил) |
alter | Возраст |
bzeit | Время проведения искусственного дыхания в часах |
kob | Концентрация кислорода в смеси для искусственного дыхания |
адд | Интенсивность искусственного дыхания |
geschl | Пол (1 = мужской, 2 = женский) |
gr | Рост |
Переменная out делит пациентов на две группы; при помощи остальных переменных предстоит прогнозировать принадлежность к одной из групп.
-
Откройте файл lunge.sav.
-
Выберите в меню Analyze (Анализ) Classify (Классифицировать) Discriminant... (Дискриминантный анализ)
Откроется диалоговое окно Discriminant Analysis (Дискриминантный анализ).
Рис. 18.1: Диалоговое окно Discriminant Analysis (Дискриминантный анализ).
-
Поместите переменную out в поле, предназначенное для групповых переменных.
-
После щелчка по выключателю Define Range... (Определить промежуток) введите минимальное и максимальное значения этой переменной: 0 и 1.
-
Переменным agg, alter, bzeit, gcschl, gr и kob присвойте статус независимых переменных. Для начала оставим установленный по умолчанию метод: Enter independents together (Одновременный учет всех независимых переменных), при котором в анализе одновременно будут участвовать все независимые переменные.
-
После щелчка по выключателю Statistics... (Статистики) активируйте опции: Means (Средние значения), Univariate ANOVAs (Одномерные тесты ANOVA), Unstandardized Function Coefficients (Нестандартизированные коэффициенты функции) и Within-groop Correlation Matrice (Корреляционная матрица внутри группы).
-
Через выключатель Classify (Классифицировать) сделайте дополнительно запрос на вывод диаграмм по отдельным группам (Separate-groups Plots), результатов для отдельных наблюдений (Casewise results) и сводной таблицы (Summary table). При выводе результатов для отдельных наблюдений ограничимся первыми двадцатью, поместив этот предел в соответствующую позицию диалогового окна.
Довольно полезный график для объединенных групп, который был реализован в ранних версиях SPSS, и сейчас можно активировать в диалоговом окне, однако вместо графика в окне отображения результатов будет появляться предупреждение о том, что такая гистограмма в анализах более не доступна.
-
При помощи выключателя Save... (Сохранить) активируйте сохранение значения дискриминантной функции в дополнительной переменной (Discriminant Scores).
-
Начните расчёт нажатием ОК.
После вводного обзора действительных и пропущенных значений приводятся средние значения, стандартные отклонения, количество наблюдений для каждой группы в отдельности и суммарные показатели для обеих групп.
Переменная geschl является при этом дихотомической переменной, принадлежащей к номинальной шкале с кодировками: 1 (мужской пол) и 2 (женский пол). Средние значения пола для обоих групп по исходу Легения, кажущиеся на первый взгляд бесполезными, равны 1,63492 и 1,45588; если бы вместо этого переменные были закодированы при помощи 0 и 1, то оба средних значения равнялись бы 0,63492 и 0,45588 соответственно. Для таких дихотомических переменных, кодированных при помощи 0 и 1, среднее значение указывает на долю наблюдений с кодировкой 1. Это означает, что для группы "скончался" доля женщин в процентном отношении составляет 63,492, а для группы "выжил" 45,588.
Group Statistics (Статистики для групп) | |||||
Outcome (Исход) | Mean (Среднее значение) | Std. Deviation (Стандартное отклонение) | Valid N (listwise) (Действительные значения (по списку)) | ||
Unwe-ighted (Не взвешено) | Weig-hted (Взве-шено) | ||||
gesto-rben (Скон-чался) | Aggressivitaet der Beatmung (Интенси-вность искус-ственного дыхания) | 15,90013 | 10,90013 | 63 | 63,000 |
ALTER (Возраст) | 31,92063 | 13,82529 | 63 | 63,000 | |
Beatmungszeit in Std. (Время проведения искус-ственного дыхания в часах) | 15,36508 | 10,50085 | 63 | 63,000 | |
Geschlecht (Пол) | 1,63492 | ,48532 | 63 | 63,000 | |
Koerper-groesse (Рост) | 165,1429 | 15,55931 | 63 | 63,000 | |
Sauerstoff-Konzentration (Концент-рация кислорода в смеси для искус-ственного дыхания) | ,85952 | ,14807 | 63 | 63,000 | |
ueberlebt (Выжил) | Aggressivitaet der Beatmung (Интенси-вность искус-ственного дыхания) | 11,69699 | 8,16057 | 68 | 68,000 |
ALTER (Возраст) | 27,97059 | 10,86411 | 68 | 68,000 | |
Beatmungszeit in Std. (Время проведения искус-ственного дыхания в часах) | 10,79412 | 5,10065 | 68 | 68,000 | |
Geschlecht (TlonJ | 1,45588 | ,50175 | 68 | 68,000 | |
Koerpe-rgroesse (Рост) | 172,0588 | 11,01137 | 68 | 68,000 | |
Sauerstoff-Konzentration (Концентрация кислорода в смеси для искус-ственного дыхания) | ,80338 | ,15493 | 68 | 68,000 | |
Total | Aggressivitaet der Beatmung (Интенси-вность искус-ственного дыхания) | 13,51843 | 9,72600 | 131 | 131,000 |
ALTER (Воз_раст) | 29,87023 | 12,48654 | 131 | 131,000 | |
Beatmungszeit in Std. (Время проведения искус-ственного дыхания в часах) | 12,99237 | 8,44120 | 131 | 131,000 | |
Geschlecht (Пол) | 1,54198 | ,50015 | 131 | 131,000 | |
Koerpe-rgroesse (Рост) | 168,7328 | 13,78339 | 131 | 131,000 | |
Sauerstoff-Konzentration (Конце-нтрация кислорода в смеси для искус-ственного дыхания) | ,83038 | ,15369 | 131 | 131,000 | |
Затем проводится тест, насколько значимо различаются между собой переменные в обеих группах; наряду с тестовой величиной, в качестве которой служит Лямбда Уилкса ("Wilks-Lambda"), применяется также и простой дисперсионный анализ. Для всех переменных (кроме возраста, для которого однако также просматривается сильная тенденция к значимости) получается значимое различие между обеими группами:
Tests of Equality of Group Means (Тест равенства групповых средних значений)
Wilks Lambda (Лямбда Уилкса) | F | df1 | df2 | Sig. (Значи-мость) | |
Aggressivitaet der Beatmung (Интенсивность искусственного дыхания) | ,962 | 5,116 | 1 | 129 | ,025 |
ALTER (Возраст) | ,975 | 3,331 | 1 | 129 | ,070 |
Beatmungszeit in Std. (Время проведения искусственного дыхания в часах) | ,926 | 10,273 | 1 | 129 | ,002 |
Geschlecht (Пол) | ,968 | 4,297 | 1 | 129 | ,040 |
Koerpergroesse (Рост) | ,937 | 8,722 | 1 | 129 | ,004 |
Sauerstoff-Konzentration (Концентрация кислорода в смеси для искусственного дыхания) | ,966 | 4,481 | 1 | 129 | ,036 |
Далее следует корреляционная матрица между всеми переменными, в которой приводятся коэффициенты, осредненные для обеих групп:
Pooled Within-Groims Matrices (Объединённые внутригрупповые матрицы)
Aggres-sivitaet der Beat-mung (Интен-сивность искус-ственного дыхания) | ALTER (Воз-раст) | Beatmun-gszeit in Std. (Время прове-дения искус-ственного дыхания в часах) | Gesc-hlecht (Пол) | Koerper-groesse (Рост) | Saue-rstoff- Konzen-tration (Концен-трация кисл-орода в смеси для искус-ственного дыхания) | ||
Corre-lation (Корре-пяция) | Aggres-sivitaet der Beatmung (Интен-сивность искус-ственного дыхания) | 1,000 | -,072 | -,058 | ,141 | -,042 | ,285 |
ALTER (Возраст) | -,072 | 1,000 | ,093 | -,040 | ,277 | -.119 | |
Beatmu-ngszeit in Std. (Время прове-дения искус-ственного дыхания в часах) | -,058 | ,093 | 1,000 | ,069 | -,126 | -,089 | |
Geschlecht (Пол) | .141 | -0,40 | ,069 | 1,000 | -,481 | -,066 | |
Koerpe-rgroesse (Рост) | -,042 | ,277 | -,126 | -,481 | 1,000 | ,000 | |
Sauer-stoff-Konze-ntration (Конце-нтрация кисло-рода в смеси для искус-ственного дыхания) | ,285 | -,119 | -,089 | -,066 | ,000 | 1,000 | |
Следующими шагами являются расчёт и анализ коэффициентов дискриминантной функции. Значения этой функции должны как можно отчётливей разделять обе группы. Мерой удачности этого разделения служит корреляционный коэффициент между рассчитанными значениями дискриминантной функции и показателем принадлежности к группе:
Eigenvalues (Собственные значения)
Function (Функция) | Eigenvalue (Собственное значение) | % of Variance (% дисперсии) | Cumulative % (Сово-купный %) | Canonical Correlation (Канони-ческая корреляция) |
1 | ,256" | 100,0 | 100,0 | ,452 |
a. First 1 canonical discriminant functions were used in the analysis (В этом анализе используются первые 1 канонические дискриминантные функции).
Wilks' Lambda (Лямбда Уилкса)
Test of Function(s) (Тест функции (и)) | Wilks' Lambda (Лямбда Уилкса) | Chi-square (Хи-квадрат) | df | Sig. (Значимость) |
1 | ,796 | 28,733 | 6 | ,000 |
Судя по значению коэффициента, равному 0,452, корреляция абсолютно не удовлетворительная. При помощи Лямбда Уилкса производится тест на то, значимо ли в обеих группах отличаются друг от друга средние значения дискриминантной функции; в приводимом примере, значение р < 0,001, указывает на очень значимое различие.
Значение, выводимое под именем "Eigenvalue" (Собственное значение), соответствует отношению суммы квадратов между группами к сумме квадратов внутри групп. Эти две суммы Вы сможете получить, если проведете дисперсионный анализ значений дискриминантной функции (переменная dis1_1) по фактору out (см. гл. 13.3). Большие собственные значения (в данном случае такого, к сожалению, не наблюдается) указывают на "хорошие" (удачно подобранные) дискриминантные функции.
Следующая таблица дает представление о том, как сильно отдельные переменные, применяемые в дискриминантной функции, коррелируют со стандартизированными значениями этой дискриминантной функции. При этом корреляционные коэффициенты были рассчитаны в обеих группах по отдельности и затем усреднены:
Standardized Canonical Discriminant Function Coefficients
(Стандартизиро-ванные канонические коэффициенты дискриминантной функции) | |
Function (Функция) | |
1 | |
Aggressivitaet der Beatmung (Интенсивность искусственного дыхания) | ,316 |
ALTER (Возраст) | ,494 |
Beatmungszeit in Std. (Время проведения искусственного дыхания в часах| | ,491 |
Geschlecht (Пол) | ,066 |
Koerpergroesse (Рост) | -,544 |
Sauerstoff-Konzentration (Концентрация кислорода в смеси для искусственного дыхания) | ,385 |
Structure Matrix
(Структурная матрица) | |
Function (Функция) | |
1 | |
Beatmungszeit in Std. (Время проведения искусственного дыхания в часах) | ,558 |
Koerpergroesse (Рост) | -,514 |
Aggressivitaet der Beatmung (Интенсивность искусственного дыхания) | ,393 |
Sauerstoff-Konzentration (Концентрация кислорода в смеси для искусственного дыхания) | ,368 |
Geschlecht (Пол) | ,361 |
ALTER (Возраст) | ,318 |
Pooled within-groups correlations between discriminating variables and standardized canonical discriminant functions (Объединённые корреляции внутри групп между диск-риминантными переменными и стандартизированными каноническими дискриминант-ными функциями).
Variables ordered by absolute size of correlation within function (Переменные расположены в соответствии с абсолютными корреляционными величинами внутри функции).
И в заключение, приводятся сами коэффициенты дискриминантной функции:
Canonical Discriminant Function Coefficients
(Канонические коэффициенты дискриминантной функции) | |
Function (Функция) | |
1 | |
Aggressivitaet der Beatmung (Интенсивность искусственного дыхания) | ,033 |
ALTER (Возраст) | ,040 |
Beatmungszeit in Std. (Время проведения искусственного дыхания в часах) | ,060 |
Geschlecht (Пол) | ,133 |
Koerpergroesse (Рост) | -,041 |
Sauerstoff-Konzentration (Концентрация кислорода в смеси для искусственного дыхания) | 2,539 |
(Constant) | 2,121 |
Unstandardized coefficients (Нестандартизированные коэффициенты)
Здесь речь идёт о нестандартизированных коэффициентах — это множители при заданных значениях переменных, входящих в дискриминантную функцию. Стандартизированные коэффициенты, которые приводились ранее, основаны на стандартизированных значениях переменных, получаемых с помощью z-преобразования.
Далее приводятся средние значения дискриминантной функции в обеих группах:
Functions at Group Centroids
(Функции групповых центроидов) | |
Outcome (Исход) | Function (функция) |
1 | |
gestorben (Скончался) | ,522 |
ueberlebt (Выжил) | -,483 |
Unstandardized canonical discriminant functions evaluated at group means (Heстандартизированные канонические дискриминантные функции, которые оцениваются по групповым средним значениям).
Далее следует таблица, в которой построчно для каждого наблюдения приводится информация о значении дискриминантной функции и определяется принадлежность к одной из двух групп. Мы здесь ограничились первыми двадцатью наблюдениями.
Группа, к которой фактически принадлежит наблюдение, отображается в колонке с именем "Actual Group" (Фактическая группа). В следующих трёх колонках содержится информация о прогнозе принадлежности к группе, сделанном на основании значения дискриминантной функции. Сначала приводится прогнозируемая принадлежность к группе; если она не соответствует фактической принадлежности, то в колонке "Predicted Group" (Прогнозируемая группа) отображаются две звёздочки (**).
Casewise Statistics
(Статистики для наблюдений) | |||||||||||
| Case Number (Поряд-ковый номер случая) | Actual Group (Факти-ческая груп-па) | Highest Group (Старшая группа) | Second Highest Group (Вторая по старшинству группа) | Discri-minant Scores (Значе-ния дискри-ми- нант-ности) | ||||||
Predic-ted Group (Прогно-зируе-мая груп-па) | P(D>d G=g) | P(G=g | D=d) | Squared Maha-lanobis Distance to Centroid (Квадрат рас-стояния Махапа-нобиса до центро-ида) | Group (Груп-па) | P(G=g |D=d) | Squared Maha-lanobis Distance to Centroid (Квадрат рас-стояния Маха-ланобиса до центро-ида) | Function 1 (Фун-кция 1) | ||||
р | df | 1 | |||||||||
Origi-nal (Перво-нача-льно) | 1 | 0 | 1" | ,727 | 1 | ,702 | ,122 | 0 | ,298 | 1,834 | -.833 |
2 | 1 | 0" | ,116 | 1 | ,889 | 2,464 | 1 | ,111 | 6,631 | 2,092 | |
3 | 0 | 1" | ,842 | 1 | ,576 | ,040 | 0 | ,424 | ,650 | -,284 | |
4 | 1 | 1 | ,310 | 1 | ,821 | 1,032 | 0 | ,179 | 4,085 | -1,499 | |
5 | 1 | 1 | ,495 | 1 | ,767 | ,465 | 0 | ,233 | 2,846 | -1,165 | |
6 | 1 | 1 | ,453 | 1 | ,779 | ,563 | 0 | ,221 | 3,081 | -1,234 | |
7 | 0 | 1" | ,635 | 1 | ,728 | ,225 | 0 | ,272 | 2,189 | -,958 | |
8 | 1 | 1 | ,549 | 1 | ,752 | ,359 | 0 | ,248 | 2,575 | -1,083 | |
9 | 1 | 1 | ,880 | 1 | ,587 | ,023 | 0 | ,413 | ,729 | -,332 | |
10 | 0 | 1" | ,952 | 1 | ,609 | ,004 | 0 | ,391 | ,893 | -,423 | |
11 | 0 | 0 | ,026 | 1 | ,940 | 4,980 | 1 | ,060 | 10,477 | 2,753 | |
12 | 1 | 0" | ,618 | 1 | ,501 | ,249 | 1 | ,499 | ,256 | ,023 | |
13 | 0 | 0 | ,930 | 1 | ,603 | ,008 | 1 | ,397 | ,841 | ,434 | |
14 | 1 | 1 | ,817 | 1 | ,676 | ,053 | 0 | ,324 | 1,528 | -,714 | |
15 | 1 | 1 | ,958 | 1 | ,611 | ,003 | 0 | ,389 | ,908 | -,431 | |
16 | 0 | 1" | ,685 | 1 | ,524 | ,165 | 0 | ,476 | ,359 | -,077 | |
17 | 1 | 1 | ,388 | 1 | ,798 | ,745 | 0 | ,202 | 3,492 | -1,347 | |
18 | 0 | 1" | ,763 | 1 | ,550 | ,091 | 0 | ,450 | ,496 | -,182 | |
19 | 1 | 1 | ,748 | 1 | ,696 | ,103 | 0 | ,304 | 1,760 | -,805 | |
20 | 0 | 0 | ,308 | 1 | ,822 | 1,037 | 1 | ,178 | 4,095 | 1,540 | |
** Мisciassiriea case (Неправильно классифицированное наблюдение;
Далее выводятся две вероятности. Вторая из этих двух вероятностей, обозначенная P(G=g|D=d), является мерой принадлежности к одной из двух групп. Это вероятность того, что некоторой наблюдение принадлежит к прогнозированной группе, которая рассчитывается на основе подстановки в дискриминантную функцию значений набора переменных, соответствующих данному наблюдению. Вероятность того, что данный наблюдение принадлежит к другой группе получается вычитанием меры принадлежности из 1. Она приводится в колонке с названием "Second Highest Group" (Вторая по старшинству группа). Если мы рассмотрим первый наблюдение, то здесь вероятность того, что данный пациент выживет, рассчитанная на основании значении исходных переменных, равна 0,702 (в действительности он скончался).
Первую из двух рассмотренных вероятностей, получившую название Р (D>d|G=g), называют ещё и условной вероятностью. Это вероятность того, что пациент, принадлежащий к прогнозируемой группе, действительно имеет значения параметров, соответствующие дискриминантной функции или некоторые другие крайние значения.
В другой колонке приводится квадрат расстояния Махаланобиса до центроида (среднего значения группы значений дискриминантной функции). В правой колонке таблицы приводится соответствующее значение дискриминантной функции. Распределение значения дискриминантной функции отдельно по группам изображается на двух отдельных гистограммах.
Можно заметить, что значения дискриминантной функции для первой группы (скончался) смещены вправо, а значения второй группы (выжил) — влево, что однако свидетельствует об очень сильном смешении.
В завершении приводится классификационная таблица с указанием достигнутой точности прогнозирования. Значение этой точности равно 68,7 %, что является неудовлетворительным:
Рис. 18.2: Распределение значений дискриминантной функции для группы «скончался»
Рис. 18.3: Распределение значений дискриминантной функции для группы «выжил»
Classification Results 3
(Классификационные результаты) | |||||
Outcome (Исход) | Predicted Group Membership (Предсказанная принадлежность к одной из групп) | Total (Сум-ма) | |||
gestorben (Сконча-лся) | ueberlebt (Выжил) | ||||
Original Перво-начально) | Count (Колич-ество) | gestorben (сконча-лся | 38 | 25 | 63 |
ueberlebt (Выжил) | 16 | 52 | 68 | ||
% | gestorben (сконча-лся | 60,3 | 39,7 | 100,0 | |
ueberlebt (Выжил) | 23,5 | 76,5 | 100,0 | ||
а. 68,7% of original grouped cases correctly classified (68,7 % первоначально сгруппированных наблюдений были классифицированы корректно).
При применении метода логарифмической регрессии (см. гл. 16.4) результат получился немного лучше (доля корректного прогноза 70,99 %).
Для случая, когда пациенту мужского пола, 25 лет, ростом 184 см искусственное дыхание делали на протяжении 5 часов, при концентрации кислорода равной 0,7 и интенсивности соответствующей значению 10, получается следующее значение дискриминантной функции
d = 2,121 + 0,033*10 + 0,04*25 + 0,06*5 + 0,133*1-0,041*184 + 2,539*0,7 = -1,883
Опираясь на распределение значений дискриминантной функции, этого пациента можно отнести к группе выживших.
При выполнении дискриминантного анализа, как и для других многомерных процедур, можно применять и пошаговый образ действий, который как раз и рекомендуется при наличии большого количества независимых переменных. Этот метод похож на многомерный регрессионный анализ, однако переменные при проведении дискриминантного анализа выбираются по другим критериям.
Рассчитаем ещё раз наш пример, но уже с применением пошагового метода.
-
В исходном диалоговом окне дискриминантного анализа активируйте опцию Use stepwse method (Использовать пошаговый метод).
-
Щёлкните на кнопке Method... (Метод)
Откроется диалоговое окно Discriminant Analysis: Step-wise Method (Дискриминантаый анализ: Пошаговый метод).
-
Выберите метод, при помощи которого будет отобрана та переменная, которая увеличивает расстояние Махаланобиса (Mahalanobis) между двумя группами. Эта дистанционная мера базируется на евклидовых расстояниях между нормализованными значениями выборок с учётом корреляции соответствующих переменных.
-
Чтобы искусственно не раздувать объём выводимых результатов, в этот раз через кнопку Classify... (Классифицировать), активируйте опцию Summary table (Сводная таблица).
В рассматриваемом случае мы отказываемся от графического представления результатов. В анализ по очереди будут включены переменные: bzeit, gr, alter и kob; это те же самые переменные, которые использовались при применении метода логистической регрессии. По заключительной классификационной таблице можно сделать вывод о том, что в результате отбрасывания неподходящих переменных доля попаданий слегка выросла. Значение надежности прогноза составило 70,2 %.
Для проведения дискриминантного анализа Вы можете использовать и пример с двумя диагностическими тестами для обнаружения карциномы мочевого пузыря, рассмотренный в главе 16.4. Здесь можно получить более чёткое разделение двух групп (здоров — болен). Точность прогнозирования здесь составляет 82,2 %.
1.gif
2.gif
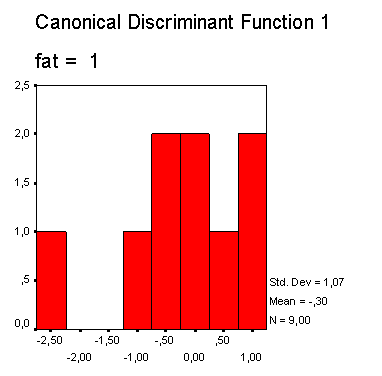
3.gif
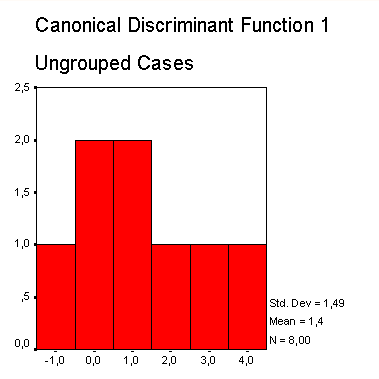
18.2 Пример из области социологии
18.2 Пример из области социологии
В своём исследовании "Культурный прорыв. Изменение ценностей в западном мире" (см. дополнительную литературу) Рональд Инглехарт (Ronald Inglehart) приводит тезис, что в более зрелых возрастных группах значимо большее количество человек высказались в пользу материальных ценностей (см. гл. 8.4.2). Среди младших поколений, согласно Инглехарту, растёт доля постматериалистов. Склонность опрошенных к постматериалистическим ценностям зависит от их образования и профессиональной квалификации. Чем выше образование и профессиональная квалификация, тем выше склонность к постматериалистическим ценностям. Значение имеет также и социально-экономический статус отца; согласно мнению Инглехарта, чем он выше, тем значительней доля постматериалистов. При помощи дискриминантного анализа мы проверим эту теорему смены ценностей, сформулированную американским политологом.
-
Откройте в редакторе данных файл postmat.sav.
Переменные, которые вы сможете найти в этом файле, приводятся в нижеследующей таблице.
Имя переменной | Значение |
ingMnd | Индекс Инглехарта |
Ценности: | |
1 Постматериалисты | |
2 Постматериалисты смешанного типа | |
3 Материалисты смешанного типа | |
4 Материалисты | |
5 Не могу дать ответ | |
6 Нет данных | |
statpaps | Социально-экономический статус отца (индекс) |
Значения: | |
1 Низкий | |
5 Высокий | |
8 Формируется в данный момент (отсутствующее значение) | |
9 Безработный, в заключении, умер, пенсионер и т.д. (отсутствующее | |
значение) | |
schule | Уровень образования опрашиваемых |
Значения: | |
1 Без образования | |
2 Начальная школа | |
3 Незаконченное среднее | |
4 Среднее | |
alter | Возраст опрашиваемых |
Значения: | |
1 18 до 29 лет | |
2 30 до 44 лет | |
3 45 до 59 лет | |
4 60 до 74 лет | |
5 75 до 88 лет | |
6 89 и старше | |
9 Не указан (отсутствующее значение) | |
ausbild | Профессиональное образование опрашиваемых Значения: 0 Образование отсутствует (отсутствующее значение) 1 Краткосрочное образование 2 Ученик 3 Мастер/техник 4 Высшее образование |
Прежде чем преступить к дискриминантному анализу, преобразуем сначала переменную ingl_ind к дихотомическому типу. Значения признаков: 1 ("Постматериалисты") и 2 ("Постматериалисты смешанного типа") должны бить включены в новое значение признака 1 ("Постматериалистические типы") переменной ingMnd, а значения признаков: 3 ("Материалисты смешанного типа") и 4 ("Материалисты") в новое значение признака 2-"Материалистические типы".
-
Для этого в редакторе синтаксиса введите следующие команды:
RECODE ingl_ind (1,2 = 1) (3,4 = 2)
INTO ingl_dic. VARIABLE LABELS
ingl_dic = "Inglehart-Index, dichotom".
VALUE LABELS
ingl_dic 1 "Postmat. Typen"
2 "Materialist.Typen".
EXECUTE.
-
Вы можете также загрузить в редактор синтаксиса и файл ingledic.sps, в котором находятся эти команды.
-
Пометьте команды и запустите программу щелчком на кнопке Run Current (Выполнить текущие команды).
В редакторе данных появится новая переменная ingl_dic. Теперь проведите дискриминантный анализ.
-
Выберите в меню опции Analyze (Анализ) Classify (Классифицировать) Discriminant... (Дискриминантный анализ)
-
Переменную ingl_dic поместите в поле групповых переменных.
-
Щёлкните на выключателе Define Range... (Определить область) и в качестве минимального значения введите 1, а в качестве максимального значения 2.
-
Переменные statpaps, schule, alter и ausbild поместите в список Independents (Независимые переменные). Оставьте метод ввода переменных Enter independents together (Независимые переменные вводить одновременно), установленный по умолчанию.
Диалоговое окно Discriminant Analysis (Дискриминантный анализ) должно теперь выглядеть так, как показано на рисунке 18.4.
Рис. 18.4: Диалоговое окно Discriminant Analysis (Дискриминантный анализ).
-
Щёлкните по выключателю Statistics... (Статистики)
Откроется диалоговое окно Discriminant Analysis: Statistics (Дискриминантный анализ: Статистики) (см. рис. 18.5).
Рис. 18.5: Диалоговое окно Discriminant Analysis: Statistics (Дискриминантный анализ: Статистики)
-
Активируйте опции: Means (Средние значения), Univariate ANOVAs (Одномерные тесты AN OVA), Unstandardized Func-tion Coefficients (He стандартизированные коэффициенты функции) и Within-groops Correlation Matrice (Корреляционная матрица внутри группы).
-
Подтвердите нажатием Continue (Далее).
-
Щёлкните на выключателе Classify... (Классифицировать). Откроется диалоговое окно Discriminant Analysis: Classification (Дискриминантный анализ: Классификация) (см. рис. 18.6).
Рис. 18.6: Диалоговое окно Discriminant Analysis: Classification (Дискриминантный анализ: Классификация)
-
Сделайте здесь запрос на Summary table (Сводную таблицу).
-
Щёлкните на выключателе Save... (Сохранить). Откроется диалоговое окно Discriminant Analysis: Save (Дискриминантный анализ: Сохранить) (см. рис. 18.7).
Рис. 18.7: Диалоговое окно Discriminant Analysis: Save (Дискриминантный анализ: Сохранить)
Видно, что в 10 версии появилась возможность сохранения информации о модели в так называемом, XML-файле (см. примечания к рис. 16.3).
-
Активируйте вывод Predicted group membership (Прогнозируемой принадлежности к группе), Discriminant scores (Значений дисриминантной функции) и Probabilities of group membership (Вероятностей принадлежности к группе).
-
Подтвердите нажатием Continue (Далее) и затем ОК.
В окне просмотра появится сначала обзор действительных и пропущенных значений:
Analysis Case Processing Summary (Анализ обработанных наблюдений)
Unweighted Cases (He взвешенные случаи) | N | Percent (Процент) | |
Valid (Действительные) | 2200 | 71,9 | |
Excluded (Исключенные) | Missing or out-of-range group codes (Отсутствующие или находящиеся за пределами допустимой области кодировки принадлежности к группе) | 19 | ,6 |
At least one missing discriminating variable (По меньшей мере одна отсутствующая дискриминационная переменная) | 816 | 26,7 | |
Both missing or out-of-range group codes and at least one missing discriminating variable (Обе кодировки принадлежности к группе отсутствуют или находятся за пределами допустимой области, или по меньшей мере одна отсутствующая дискриминационная переменная) | 23 | ,8 | |
Total (Общее количество исключённых) | 858 | 28,1 | |
Total (Общее количество случаев) | 3058 | 100,0 |
В общей сложности 858 наблюдений из 3058, находящихся в файле postmat.sav, были исключены из анализа из-за отсутствия значения переменной ingl_dic или отсутствия значений одной из дискриминационных переменных. Таким образом анализ проводился для 2200 наблюдений. Далее приводятся средние значения, стандартные отклонения и количество наблюдений для всех переменных из обеих групп и для каждой группы в отдельности.
По средним значениям уже заметно, что для постматериалистических типов характерны: более высокий социально-экономический статус отца (2,8148 по сравнению с 2,3904), более высокое образование (2,9853 по сравнению с 2,5248) и принадлежность к младшей возрастной группе (2,1842 по сравнению с 2,8151).
Group Statistics
(Статистики для групп) | |||||
INGL_DIC (Индекс Ингпехарта, дихото-мический) |
| Mean (сред-нее значе-ние) | Std. Deviation (Станда-ртное отклоне-ние) | Valid N (listwise) (Действительные значения (по списку)) | |
Unwei-ghted (Не взвеше-нные) | Weigh-ted (Взвеше-нные) | ||||
1,00 (Пост-материа-листический тип) | SES-lndex des Vaters (социально-экономи-ческий статус отца) | 2,8148 | 1,1718 | 1091 | 1091,000 |
Schulabschluss (Образование) | 2,9853 | ,8194 | 1091 | 1091,000 | |
ALTER, BEFRAGTE<R>, KATEGORISIERT (Возраст, опрошен-ного(ой), разбит на категории) | 2,1842 | 1,0887 | 1091 | 1091,000 | |
Berufsaus-bildung (Профес-сиональное образо-вание) | 2,1888 | 1,1562 | 1091 | 1091,000 | |
2,00 (Материа-листический тип) | SES-lndex des Vaters (социально-экономи-ческий статус отца) | 2,3904 | 1,0407 | 1109 | 1109,000 |
Scnulabschluss (Образование) | 2,5248 | ,7627 | 1109 | 1109,000 | |
ALTER, BEFRAGTE<R>, KATEGORISIERT (Возраст ,опрошен-ного(ой), разбит на категории) | 2,8151 | 1,2111 | 1109 | 1109,000 | |
Berufsa-usbildung (Профес-сиональное образование) | 1,8792 | 1,0249 | 1109 | 1109,000 | |
Total (Сумма) | SES-lndex des Vaters (социально-экономи-ческий статус отца) | 2,6009 | 1,1275 | 2200 | 2200,000 |
Schulabschluss (Образование) | 2,7532 | ,8240 | 2200 | 2200,000 | |
ALTER, BEFRAGTE<R>, KATEGORI-SIERT (Возраст, опрошен-ного(ой), разбит на категории) | 2,5023 | 1,1942 | 2200 | 2200,000 | |
Berufsa-usbildung (Профес-сиональное образование) | 2,0327 | 1,1027 | 2200 | 2200,000 | |
Затем проводится тест на значимость различия между переменными, относящимися к обеим группам, то есть выясняется присутствуют ли в них разделяющие (дискриминирующие) особенности, позволяющие судить об отношении к одной из двух групп (постматериалисты — материалисты).
Tests of Equality of Group Means (Тест равенства групповых средних значений)
Wilks1 Lambda (Лямбда Уилкса) | F | df1 | df2 | Sig. (Значимость) | |
SES-lndex des Vaters (социально-экономический статус отца) | ,965 | 80,746 | 1 | 2198 | ,000 |
Schulabschluss (Образование) | ,922 | 186,281 | 1 | 2198 | ,000 |
ALTER, BEFRAGTE<R>, KATEGORISIERT (Возраст, опрошенного(ых), разбит на категории) | ,930 | 164,951 | 1 | 2198 | ,000 |
Berufsausbildung (Профессиональное образование) | ,980 | 44,222 | 1 | 2198 | ,000 |
Как следует из колонки значимости, по всем переменным наблюдается значительное различие между группами (р < 0,001).
Далее приводится корреляционная матрица между всеми переменными, причём коэффициенты были рассчитаны для обеих групп:
Pooled Within-Groups Matrices (Объединённые матрицы внутри групп)
SES-lndex des Vaters (социально- экономи-ческий статус отца) | Schulab-schluss (Образо-вание) | ALTER, BEFRAG -TE<R>, KATEGO-RISIERT (Возраст, опрошен-ного(ой), разбит на категории) | Berufsau-sbildung (Профес- сиона-льное образо-вание) | ||
Corre-lation (Корре-ляция) | SES-lndex des Vaters (социально-экономи-ческий статус отца) | 1,000 | ,327 | -,033 | ,137 |
Schula-bschluss (Образо-вание) | ,327 | 1,000 | -,275 | ,377 | |
ALTER, BEFRA-GTE<R>, KATEGO-RISIERT (Возраст, опрошен-ного(ых), разбит на категории) | -,033 | -,275 | 1,000 | ,018 | |
Berufsa-usbildung (Профес-сиональное образо-вание) | ,137 | ,377 | ,018 | 1,000 | |
Прежде всего, здесь очень заметна корреляция между переменными schule и statpas и между переменными ausbild и schule. Чем выше социально-экономический статус отца, тем выше школьное образование опрашиваемого; чем выше его школьное образование, тем выше и профессиональное образование.
Далее следует анализ коэффициентов дискриминантной функции. Корреляционный коэффициент между рассчитанными значениями дискриминантной функции и реальной принадлежностью к группе, равный 0,353, является неудовлетворительным:
Eigenvalues (Собственные значения)
Function (Функция) | Eigenvalue (Собствен-ное значение) | % of Variance (% диспе-рсии) | Cumulative % (Сово-купный %) | Canonical Correlation (Канони-ческая корре-ляция) |
1 | ,142а | 100,0 | 100,0 | ,353 |
a. First 1 canonical discriminant functions were used in the analysis (Первые 1 канонические дискриминантные функции будут применяться в анализе).
Wilks' Lambda (Лямбда Уилкса)
Test of Function(s) Wilks' Lambda (Тест функции (и)) (Лямбда Уилкса) | Chi-square (Хи-квадрат) | df | Sig. (Значимость) |
1 ,875 | 292,431 | 4 | ,000 |
Тест, проведенный с помощью критерия "Лямбда Уилкса" (k), на предмет, значимо ли различаются между собой средние значения дискриминантной функции в обеих группах, показал очень значимый результат (значение р < 0,001).
Затем приводятся стандартизированные коэффициенты дискриминантной функции и их корреляция с используемыми переменными:
Standardized Canonical Discriminant Function Coefficients
(Стандартизиро-ванные канонические коэффициенты дискриминантной функции) | |
Function (Функция) | |
1 | |
SES-lndex des Vaters (социально-экономический статус отца) | ,321 |
Schulabschluss (Образование) | ,434 |
ALTER, BEFRAGTE<R>, KATEGORISIERT (Возраст, опрошенного(ой), разбит на категории) | -,599 |
Berufsausbildung (Профессиональное образование) | ,179 |
Structure Matrix
(Структурная матрица) | |
Function (Функция) | |
1 | |
Schulabschluss (Образование) | ,771 |
ALTER, BEFRAGTE<R>, KATEGORISIERT (Возраст, опрошенного(ой), разбит на категории) | -,726 |
SES-lndex des Vaters (социально-экономический статус отца) | ,508 |
Berufsausbildung (Профессиональное образование) | ,376 |
Pooled within-groups correlations between discriminating variables and standardized canonical discriminant functions (Объединённые корреляции внутри групп между дискриминантными переменными и стандартизированными каноническими дискриминант-ными функциями)
Variables ordered by absolute size of correlation within function (Переменные расположены соответственно величине их абсолютных корреляционных показателей).
После этого приводятся нестандартизированные коэффициенты дискриминантной функции и средние значения дискриминантной функции в обеих группах:
Canonical Discriminant Function Coefficients
(Канонические коэффициенты дискриминантной функции) | |
Function (Функция) | |
1 | |
SES-lndex des Vaters (социально-экономический статус отца) | ,290 |
Schulabschluss (Образование) | ,549 |
ALTER, BEFRAGTE<R>, KATEGORISIERT (Возраст, опрошенного(ой), разбит на категории) | -,520 |
Berufsausbildung (Профессиональное образование) | ,164 |
(Constant) (Постоянно) | -1,297 |
Unstandardized coefficients (нестандартизированные коеффициенты)
Functions at Group Centroids (Функции для групповых центроидов)
INGL DIC | Function (Функция) |
| 1 | |
1 ,00 (Постматериалистический тип) | ,380 |
2,00 (Материалистический тип) | -.374 |
Unstandardized canonical discriminant functions evaluated at group means (Нестандартизированные канонические дискриминантные функции, оценка которых происходит относительно средних значений групп).
В данном случае мы отказались от вывода очень длинной таблицы, в которой для каждого наблюдения построчно, приводится информация о значении дискриминантной функции и принадлежности к одной из двух групп.
В заключении приводится классификационная таблица с указанием точности попадания прогнозов:
Classification Resultsа
(Классификационные результаты) | |||||
INGL_DIC (Индекс Инглехарта, дихото-мический) | Predicted Group Membership (Прогнозируемая принадлежность к группе) | Total (Сум-ма) | |||
1,00 (Постматери-алисти-ческий тип) | 2,00 (Материа-листи-ческий тип) | ||||
Original (Перво-начально) | Count (Коли-чество) | 1 ,00 (Пост-материа-листи-ческий тип) | 710 | 381 | 1091 |
2,00 (Материа-листический тип) | 410 | 699 | 1109 | ||
Ungrouped cases (He сгруп-пирован-ные наблю-дения) | 7 | 12 | 19 | ||
% | 1 ,00 (Постматериа-листический тип) | 65,1 | 34,9 | 100,0 | |
2,00 (Материа-листи-ческий тип) | 37,0 | 63,0 | 100,0 | ||
Ungrouped cases (He сгруп-пирован-ные наблю-дения) | 36,8 | 63,2 | 100,0 | ||
а. 64,0% of original grouped cases correctly classified (64 % наблюдений, первоначально разнесённых по группам, были классифицированы корректно).
Правая колонка таблицы ("Total" (Сумма)) указывает на общее количество наблюдений, которые фактически относятся к соответствующим группам. К группе постматериалистических типов относится 1091 наблюдение, а к группе материалистических типов 1109. Обе колонки, объединенные общим наименованием ("Predicted Group Membership" (Прогнозируемая принадлежность к группе)), указывают на фактическое количество наблюдений, относящихся к каждой из групп. Первая колонка указывает на количество наблюдений, которые были отнесены к первой группе. Из 1091 постматериалистическйх наблюдений корректно определены были 710, это соответствует 65,1 % всех наблюдений. 381 наблюдение было по ошибке отнесено ко 2 группе, что соответствует 34,9 % всех наблюдений. Из 1109 материалистических наблюдений по ошибке к группе 1 были отнесены 410, что соответствует 37,0 %. 699 наблюдений были корректно отнесены к группе 2, что составило 63 %. Строка "Ungrouped cases" (Несгруппированные наблюдения) содержит наблюдения, которые не соответствуют ни одной из групп. Хотя эти наблюдения и не учитываются при расчёте дискриминантной функции, значение функции для них всё равно вычисляется. Из 19 наблюдений, для которых отсутствуют данные о принадлежности к какой-либо группе, 7 были отнесены к постматериалистическим типам, а 12 к материалистическим. В строке под таблицей приводится итоговый результат. 64 % наблюдений были классифицированы корректно. Так как даже при чисто случайном отнесении некоторого наблюдения к одной из двух имеющихся групп, корректность классификации данного наблюдения составила бы 50 %, то 64 %-ную точность прогноза следует рассматривать как довольно умеренный результат. Такой неудовлетворительный результат можно попытаться объяснить тем, что в обе группы входили смешанные типы, которые тяжелее классифицировать, нежели чистые типы. Проверим это предположение путём повторного проведения расчёта, но уже с учётом только чистых типов.
-
Выберите в меню Data (Данные) Select Cases... (Выбрать наблюдения)
-
Щёлкните на опции If condition is satisfied (Если выполняется условие) и затем на выключателе If... (Если).
-
В редакторе условий введите следующее условие:
ing1_ind = 1 OR ing1_ind = 4
-
Подтвердите нажатием Continue (Далее) и затем ОК.
-
В диалоговом окне Discriminant Analysis (Дискриминантный анализ) переменную ingl_ind (не ingl_dic!) поместите в поле для групповых переменных. В качестве границ области изменения задать значения 1 и 4.
-
В список независимых переменных поместите переменные statpaps, schule, alter и ausbild.
-
Дополнительные установки под выключателями Statistics... (Статистики), Classify... (Классифицировать) и Save... (Сохранить) произведите так, как было описано ранее.
Вы получите следующую классификационную таблицу:
Classification Results
(Результаты классификации) | |||||
INGLEHART-INDEX (Индекс Инглехарта, дихото-мический) | Predicted Group Membership (Прогнозируемая принадлежность к группе | Total (Сумма) | |||
POSTMATE-RIALISTEN (Постмате-риалисты) | MATERI-ALISTEN (Матери-алисты) | ||||
Original (Перво-начально) | Count (Коли-чество) | POSTMATE-RIALISTEN (Постмате-риалисты) | 409 | 109 | 518 |
MATERI-ALISTEN (Матери-алисты) | 133 | 297 | 430 | ||
% | POSTMATE-RIALISTEN (Постмате-риалисты) | 79,0 | 21,0 | 100,0 | |
MATERI-ALISTEN (Матери-алисты) | 30,9 | 69,1 | 100,0 | ||
а. 74,5% of original grouped cases correctly classified (74,5 % наблюдений, первоначально разнесённых по группам, были классифицированы корректно).
К группе постматериалистов относится 518 наблюдений. 409 наблюдений (79 %) были спрогнозированы корректно, а 109 (21,0 %) по ошибке отнесены к группе 4 ("чистые материалисты"). В группе чистых материалистов насчитывается 403 наблюдения. 297 наблюдений (69,1 %) были определены корректно, а 133 (30,9 %) по ошибке были отнесены к группе 1 ("чистые постматериалисты"). Конечным результатом является корректная идентификация наблюдений, равная 74,5 %. Этот показатель значительно выше предыдущего и может быть расценен как приемлемый.
4.gif
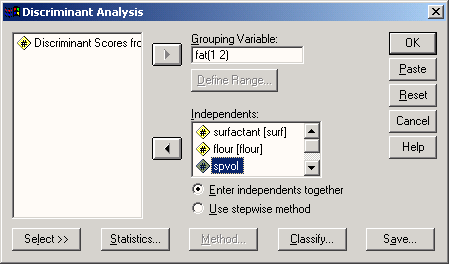
5.gif
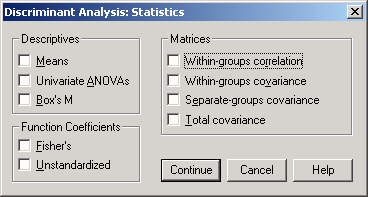
6.gif
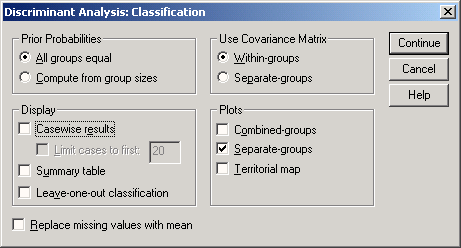
7.gif
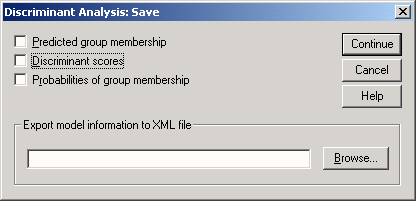
18.3 Пример из области биологии
18.3 Пример из области биологии
Дискриминантный анализ очень часто применяется для обработки данных из области биологии. В следующем типичном примере для некоторого количества индивидуумов принадлежность к группе уже известна, на основании чего и строится дискриминантная функция. Далее она используется для того, чтобы оценить принадлежность к определенной группе тех индивидуумов, для которых она ещё не известна.
В файле vogel.sav хранятся данные о половой принадлежности, длине крыла, длине клюва, размере головы, длине лап и весе 245 птиц определённого вида. Причём пол смогли определить только для 51 особи. Кодировка пола соответствует 1 = мужской и 2 = женский; отсутствие данных кодируется 9.
Если для перечисленных параметров Вы рассчитаете средние значения для самцов и самок, то для самок получите более высокие показатели. Исходя из этого, при помощи дискриминантного анализа можно попытаться определить пол тех особей, для которых этого нельзя было сделать ранее.
-
Откройте файл vogel.sav.
-
В диалоговом окне Discriminant Analysis (Дискриминантный анализ) переменной geschl (Пол) присвойте статус групповой переменной с пределами от 1 до 2, а переменным fluegel (Длина крыла), schnl (Длина клюва), kopfl (Размер головы), fuss (Длина лап) и gew (Вес) — статус независимых переменных. Выберите пошаговый метод.
-
В диалоговом окне Discriminant Analysis: Classify (Дискриминантный анализ: Классифицировать) активируйте Casewise results (Результаты для отдельных наблюдений) с ограничением в 40 наблюдений и Summary table (Сводная таблица).
-
Через выключатель Save... (Сохранить) при помощи активирования опций Predicted group membership (Прогнозируемая принадлежности к группе) и Probabilities of group membership (Вероятности принадлежности к группе) затребуйте генерирование соответствующих переменных.
Из всех результатов, приводимых в окне просмотра, в книге рассматриваются только статистики для каждого наблюдения. По классификационной таблице видно, что для 51 наблюдения с заранее известным полом 44 раза, т.е. в 86,3 % наблюдений, пол был спрогнозирован верно (см. следующую таблицу).
Если мы рассмотрим наблюдение 8, то здесь пол известен — женский и в результате прогноза получается женский пол, а вот для наблюдения 30 пол известен как мужской, но прогнозируется как женский. Наблюдения с нераспознанным полом приводятся в таблице как "ungrouped" (не группированные).
Для наблюдения 1, для которого пол оказался неизвестным, он прогнозируется как женский. Значение вероятности прогнозирования, 0,990, указывается в колонке "P(G=g | D=d)" под заголовком "Highest Group" (Старшая группа). Менее достоверным является прогноз пола для наблюдения 10, здесь вероятность прогнозирования составляет только 0,721.
Casewise Statistics
(Статистики для наблюдений) | ||||||||||||
Case Number (Номер случая) | Actual Group (Факти-ческая группа) | Highest Group (Старшая группа) | Second Highest Group (Вторая по старшинству группа) | Discri-minant Scores (Значе-ния диск-рими- нантной фун-кции) | ||||||||
Predicted Group (Прог-нози- руемая группа) | P(D>d | e=g) | P(G=9 I D=d) | Squared Ma-hala-nobis Distance to Cent-raid (Квадрат рас-стояния Маха-ланобиса до цент-роида) | Group (Груп-па) | P(G=g |D=d) | Squared Ма-halanobis Distance to Centraid (Квадрат рас-стояния Маха-ланобиса до центро-ида) | Fun-ction 1 (Фун-кция 1 ) | |||||
P | df | |||||||||||
Original (Пер- вона- чаль -но) | 1 | ungrouped (не груп-пирова-нный) | 2 | ,222 | 1 | ,990 | 1,489 | 1 | ,010 | 10,679 | 2,304 | |
2 | ungrouped (не груп-пирова-нный) | 2 | ,063 | 1 | ,997 | 3,453 | 1 | ,003 | 15,254 | 2,942 | ||
3 | ungrouped (не груп-пирова-нный) | 2 | ,064 | 1 | ,997 | 3,433 | 1 | ,003 | 15,213 | 2,937 | ||
4 | ungrouped (не груп-пирова-нный) | 2 | ,245 | 1 | ,989 | 1,353 | 1 | ,011 | 10,307 | 2,247 | ||
5 | ungrouped (не груп-пирова-нный) | 2 | ,126 | 1 | ,995 | 2,338 | 1 | ,005 | 12,792 | 2,613 | ||
6 | ungrouped (не груп-пирова-нный) | 2 | ,319 | 1 | ,984 | ,995 | 1 | ,016 | 9,271 | 2,081 | ||
7 | ungrouped (не груп-пирова-нный) | 2 | ,485 | 1 | ,971 | ,489 | 1 | ,029 | 7,543 | 1,783 | ||
8 | 2 | 2 | ,102 | 1 | ,996 | 2,673 | 1 | ,004 | 13,561 | 2,719 | ||
9 | ungrouped (не груп-пирова-нный) | 2 | ,387 | 1 | ,980 | ,748 | 1 | ,020 | 8,482 | 1,949 | ||
10 | ungrouped (не группирова-нный) | 2 | ,576 | 1 | ,721 | ,313 | 1 | ,279 | 2,213 | ,524 | ||
11 | ungrouped (не груп-пирова-нный) | 2 | ,651 | 1 | ,954 | ,205 | 1 | ,046 | 6,248 | 1,536 | ||
12 | ungrouped (не груп-пирова-нный) | 2 | ,140 | 1 | ,994 | 2,177 | 1 | ,006 | 12,411 | 2,559 | ||
13 | ungrouped (не груп-пирова-нный) | 2 | ,435 | 1 | ,976 | ,609 | 1 | ,024 | 7,995 | 1,864 | ||
14 | ungrouped (не группиро-ванный) | 2 | ,471 | 1 | ,973 | ,519 | 1 | ,027 | 7,662 | 1,804 | ||
15 | ungrouped (не группиро-ванный) | 2 | ,764 | 1 | ,938 | ,090 | 1 | ,062 | 5,510 | 1,384 | ||
16 | ungrouped (не группиро-ванный) | 2 | ,481 | 1 | ,972 | ,497 | 1 | ,028 | 7,576 | 1,789 | ||
17 | ungrouped (не груп-пирова-нный) | 2 | ,172 | 1 | ,993 | 1,868 | 1 | ,007 | 11,658 | 2,451 | ||
18 | 2 | 2 | ,399 | 1 | ,979 | ,712 | 1 | ,021 | 8,359 | 1,928 | ||
19 | ungrouped (не груп-пирова-нный) | 2 | ,705 | 1 | ,946 | ,143 | 1 | ,054 | 5,884 | 1,462 | ||
20 | 2 | 2 | ,969 | 1 | ,898 | ,002 | 1 | ,102 | 4,355 | 1,123 | ||
21 | 2 | 2 | ,249 | 1 | ,989 | 1,328 | 1 | ,011 | 10,238 | _ 2,236 | ||
22 | ungrouped (не груп-пиров-анный) | 2 | ,121 | 1 | ,995 | 2,407 | 1 | ,005 | 12,953 | 2,636 | ||
23 | 2 | 2 | ,071 | 1 | ,997 | 3,263 | 1 | ,003 | 14,853 | 2,890 | ||
24 | ungrouped (не груп-пирова-нный) | 2 | ,367 | 1 | ,981 | ,815 | 1 | ,019 | 8,704 | 1,987 | ||
25 | ungrouped (не груп-пиров-анный) | 2 | ,880 | 1 | ,857 | ,023 | 1 | ,143 | 3,598 | ,933 | ||
26 | ungrouped (не груп-пирова-нный) | 2 | ,537 | 1 | ,966 | ,382 | 1 | ,034 | 7,103 | 1,702 | ||
27 | ungrouped (не группиро-ванный) | 1 | ,640 | 1 | ,955 | ,218 | 2 | ,045 | 6,323 | -1,431 | ||
28 | 2 | 2 | ,744 | 1 | ,806 | ,107 | 1 | ,194 | 2,960 | ,757 | ||
29 | ungrouped (не груп-пирова-нный) | 2 | ,969 | 1 | ,883 | ,001 | 1 | ,117 | 4,035 | 1,045 | ||
30 | 1 | 2" | ,625 | 1 | ,749 | ,239 | 1 | ,251 | 2,428 | ,595 | ||
| 31 | ungrouped (не груп-пирова-нный) | 2 | ,646 | 1 | ,760 | ,211 | 1 | ,240 | 2,521 | ,624 | |
32 | 2 | 2 | ,173 | 1 | ,993 | 1,860 | 1 | ,007 | 11,636 | 2,448 | ||
33 | 1 | 2" | ,504 | 1 | ,970 | ,447 | 1 | ,030 | 7,378 | 1,753 | ||
34 | ungrouped (не груп-пирова-нный) | 2 | ,544 | 1 | ,966 | ,368 | 1 | ,034 | 7,046 | 1,691 | ||
35 | ungrouped (не груп-пирова-нный) | 2 | ,618 | 1 | ,958 | ,248 | 1 | ,042 | 6,480 | 1,582 | ||
36 | ungrouped (не груп-пирова-нный) | 2 | ,727 | 1 | ,943 | ,122 | 1 | ,057 | 5,744 | 1,433 | ||
37 | 2 | 2 | ,458 | 1 | ,974 | ,551 | 1 | ,026 | 7,781 | 1,826 | ||
38 | 2 | 2 | ,362 | 1 | ,981 | ,829 | 1 | ,019 | 8,750 | 1,995 | ||
39 | 2 | 2 | ,814 | 1 | ,929 | ,055 | 1 | ,071 | 5,211 | 1,319 | ||
40 | ungrouped (не груп-пирова-нный) | 2 | ,812 | 1 | ,930 | ,057 | 1 | ,070 | 5,222 | 1,322 | ||
** Misclassified case (** - Неверно классифицированный случай)
Для того, чтобы хотя бы частично сократить количество ошибочных значений для переменной пола, при анализе вы можете применять прогнозируемую групповую принадлежность только в тех случаях, для которых вероятность прогнозирования принимает некоторое минимально допустимое значение, к примеру, 0,9.
IF (dis_1 = 1 and disl_1 >= 0,9)
geschl=1
. IF (dis_1 = 2 and dis2_1 >= 0,9)
geschl=2.
EXECUTE.
Таким образом, в используемом примере можно присвоить половой показатель ещё 90-а птицам. Если вы снизите минимально допустимое значение вероятности прогнозирования, то это число станет ещё больше.
К файлу были добавлены три новые переменные:
dis_1: Прогнозируемая группа
disl_1: Вероятность принадлежности к группе 1
dis2_1: Вероятность принадлежности к группе 2.
18.4 Пример из области биологии (три группы)
18.4 Пример из области биологии (три группы)
В предыдущих примерах дискриминантный анализ всегда проводился при наличии лишь двух групп. В этой главе рассматривается пример, в котором групповая переменная имеет больше двух категорий, а именно три.
В файле kaefer.sav содержатся данные о длине и ширине грудной клетки трёх видов жуков (обозначенных как А, В и С). Если вы проведёте однофакторный дисперсионный анализ с последующими дополнительными тестами (Post-hoc-Tests), то увидите, что три разновидности жуков очень значимо различаются между собой как по длине, так и по ширине, поэтому вполне можно предположить, что этих жуков можно классифицировать между упомянутыми видами на основании их длины и ширины посредством дискриминантного анализа.
-
Откройте файл kaefer.sav.
Вы увидите, что 17 жуков из 30 не отнесены ни к иной из групп; поэтому классификация жуков по группам должна быть произведена при помощи дискриминантного анализа.
-
В диалоговом окне Discriminant Analysis (Дискриминантный анализ) переменной kaefer (Жук) присвойте статус групповой переменной с пределами от 1 до 3, а переменным laenge (Длина) и breite (Ширина) статус независимых переменных. Оставьте активной установку по умолчанию Enter independents together (Независимые переменные вводить одновременно).
-
В диалоговом окне Discriminant Analysis: Statistics (Дискриминантный анализ: Статистики) в разделе Descriptives (Дискриптивние статистики) активируйте опции: Means (Средние значения), Univariate ANOVAs (Одномерные тесты ANOVA) и в разделе Function Coefficients (Коэффициенты функции) опцию Unstandardized (He стандартизированные).
-
В диалоговом окне Discriminant Analysis: Classify (Дискриминантный анализ: Классифицировать) сделайте запрос на Case-wise results (Результаты для отдельных наблюдений) и Summary table (Сводную таблицу) и в разделе Plots (Графики) активируйте опцию Territorial map (Территориальная карта). Эта опция служит для построения классификационной диаграммы, так называемой территориальной карты (Territorial map). Построение этой диаграммы типично для случая с более чем двумя группами.
-
В заключение, в диалоговом окне Discriminant Analysis: Save (Дискриминантный анализ: Сохранить), активируйте все опции, находящиеся там, с целью создания соответствующих переменных в исходном файле.
Из всей гаммы приводимых результатов расчёта мы рассмотрим только самые важные. Из групповых статистик можно узнать, что в семейство А входят самые большие, а в семейство В самые маленькие жуки.
Group Statistics
(Статистики для групп) | |||||
KAEFEP (Жук) | Mean (Сред-нее значе-ние) | Std. Deviation (Станда-ртное отклоне-ние) | Valid N (listwise) (Действительные значения (по списку)) | ||
Unweighted (Не взвеше-нное) | Weighted (Взвеше-нное) | ||||
1 (Семейство А) | LAENGE (Длина) | 1 ,6226 | 5.968Е-02 | 42 | 42,000 |
BREITE (Ширина) | 1 ,2607 | 4J54E-02 | 42 | 42,000 | |
2 Семейство В) | LAENGE (Длина) | 1 ,3089 | 7.634Е-02 | 45 | 45,000 |
BREITE (Ширина) | 1,0122 | 4.415Е-02 | 45 | 45,000 | |
3 Семейство С) | LAENGE (Длина) | 1,4788 | 6.029Е-02 | 26 | 26,000 |
BREITE (Ширина) | 1,1192 | 5.114Е-02 | 26 | 26,000 | |
Total | LAENGE (Длина) | 1,4646 | ,1535 | 113 | 113,000 |
BREITE (Ширина) | 1,1292 | ,1191 | 113 | 113,000 | |
Статистика Лямбда Уилкса (>i) свидетельствует о том, что жуки очень значимо делятся на группы как по длине, так и по ширине.
Tests of Equality of Group Means (Тест на равенство средних значений групп)
Wilks' Lambda (Лямбда Уилкса) | F | df1 | df2 | Sig. (Значимость) | |
LAENGE (Длина) | ,187 | 239,154 | 2 | 110 | ,000 |
BREITE (Ширина) | ,153 | 303,326 | 2 | 110 | ,000 |
Если насчитывается более двух классификационных групп, то можно образовать больше одной дискриминантной функции; при трёх группах, как в приведенном примере, их будет две. Следующая таблица свидетельствует о том, что обе дискриминантные функции дают значимые результаты для разделения между группами и, следовательно, могут быть использованы соответствующим образом. Однако, первая функция дает вероятность прогноза 98,7 %, а вторая только 1,3 %.
Eigenvalues (Собственные значения)
Function (Функция) | Eigenvalue (Собствен-ные значение) | % of Variance (% диспер-сии) | Cumulative % (Совокуп-ный %) | Canonical Correlation (Канони-ческая корре-ляция) |
1 | 6,040а | 98,7 | 98,7 | ,296 |
2 | ,078а | 1,3 | 100,0 | ,269 |
a. First 2 canonical discriminant functions were used in the analysis (В этом анализе используются первые 2 канонические дискриминантные функции).
Wilks' Lambda (Лямбда Уилкса)
Test of Function(s) (Тест функции (й)) | Wilks1 Lambda (Лямбда Уилкса) | Chi-square (Хи-квадрат) | df | Sig. (Значимость) |
1 through 2 (1 до 2) | ,132 | 221,900 | 4 | ,000 |
2 | ,928 | 8,202 | 1 | ,004 |
Затребованные нестандартизированные коэффициенты функций приводятся в следующей таблице.
Canonical Discriminant Function Coefficients
(Канонические коэффициенты дискриминантных функций) | ||
Function (Функция) | ||
1 | 2 | |
LAENGE (Длина) | 5,831 | 18,769 |
BREITE (Ширина) | 14,891 | -23,659 |
(Constant) (Константа) | -25,355 | -,773 |
Unstandardized coefficients (Нестандартизированные коэффициенты)
Мы здесь опускаем вывод статистик для каждого отдельного случая. В результате расчетов Вы получаете соответствующие номера групп и вероятность прогнозирования под заголовком P(G = g|D = d). Прогнозирование осуществлено и для 17 неклассифицированных случаев.
На территориальной карте показано разделение на области, которые означают принадлежность к группе. При этом в пределах границ соответствующей области вероятность отнесения к данной группе выше, чем для других групп. На границах областей вероятности для граничащих групп одинаковы.
Значения обеих дискриминантных функций, на основе которых построена эта территориальная карта, Вы можете увидеть в редакторе данных под именами двух вновь созданных переменных: dis1_1 и dis2_1.
В заключение приводится обзор результатов классификации. По ним Вы можете заметить, что прогноз для групп А и В практически полностью был сделан верно и корректно классифицированы, в общей сложности, 91,2 % всех случаев.
Classification Results a
(Результаты Классификации) | ||||||
FUND (Семе-йство) | Predicted Group Membership | Total (Сум-ма) | ||||
1 (Семей-ство А) | 2 (Семей-ство В) | 3 (Семей-ство С) | ||||
Original (Перво-нача-льно) | Count (Коли-чество) | 1 (Семейство А) | 41 | 0 | 1 | 42 |
2 (Семейство В) | 0 | 43 | 2 | 45 | ||
3 (Семейство С) | 4 | 3 | 19 | 26 | ||
Ungrouped cases (He груп-пирован-ные случаи) | 7 | 6 | 4 | 17 | ||
% | 1 (Семейство А) | 97,6 | ,0 | 2,4 | 100,0 | |
2 (Семейство В) | ,0 | 95,6 | 4,4 | 100,0 | ||
3 (Семейство С) | 15,4 | 11,5 | 73,1 | 100,0 | ||
Ungrouped cases (He груп-пирован-ные случаи) | 41,2 | 35,3 | 23,5 | 100,0 | ||
а. 91,2% of original grouped cases correctly classified (91,2 % первоначально сгруппированных случаев были классифицированы корректно).
Символы, используемые втерриториальной карте | ||
Символ | Группа | Метка |
1 2 3 | 1 2 3 | Семейство А Семейство В Семейство С |
Маркировка | Центроиды групп | |
Наряду с уже упоминавшимися значениями обеих дискриминантных функции в редакторе данных были созданы: переменная dis_1, содержащая значение прогнозируемой группы и переменные disl_2, dis2_2 и dis3_2, которые содержат прогнозируемые вероятности отнесения к одной из трёх групп. Группа, которой соответствует наибольшая вероятность прогнозирования и есть прогнозируемая группа.
8.gif

Глава 19. Факторный анализ
Глава 19. Факторный анализ
1. Факторный анализ
Факторный анализ
Факторный анализ это процедура, с помощью которой большое число переменных, относящихся к имеющимся наблюдениям сводит к меньшему количеству независимых влияющих величин, называемых факторами. При этом в один фактор объединяются переменные, сильно коррелирующие между собой. Переменные из разных факторов слабо коррелируют между собой. Таким образом, целью факторного анализа является нахождение таких комплексных факторов, которые как можно более полно объясняют наблюдаемые связи между переменными, имеющимися в наличии.
19.1 Порядок выполнения факторного анализа
19.1 Порядок выполнения факторного анализа
На первом шаге процедуры факторного анализа происходит стандартизация заданных значений переменных (z-преобразование); затем при помощи стандартизированных значений рассчитывают корреляционные коэффициенты Пирсона между рассматриваемыми переменными.
Исходным элементом для дальнейших расчётов является корреляционная матрица. Для понимания отдельных шагов этих расчётов потребуются хорошие знания, прежде всего, в области операций над матрицами; интересующимся подробностями советуем обратиться к специальной литературе. Для построенной корреляционной матрицы определяются, так называемые, собственные значения и соответствующие им собственные векторы, для определения которых используются оценочные значения диагональных элементов матрицы (так называемые относительные дисперсии простых факторов).
Собственные значения сортируются в порядке убывания, для чего обычно отбирается столько факторов, сколько имеется собственных значений, превосходящих по величине единицу. Собственные векторы, соответствующие этим собственным значениям, образуют факторы; элементы собственных векторов получили название факторной нагрузки. Их можно понимать как коэффициенты корреляции между соответствующими переменными и факторами. Для решения такой задачи определения факторов были разработаны многочисленные методы, наиболее часто употребляемым из которых является метод определения главных факторов (компонентов).
Описанные выше шаги расчёта ещё не дают однозначного решения задачи определения факторов. Основываясь на геометрическом представлении рассматриваемой задачи, поиск однозначного решения называют задачей вращения факторов. И здесь имеется большое количество методов, наиболее часто употребляемым из которых является ортогональное вращение по так называемому методу варимакса. Факторные нагрузки повёрнутой матрицы могут рассматриваться как результат выполнения процедуры факторного анализа. Кроме того на основании значений этих нагрузок необходимо попытаться дать толкование отдельным факторам.
Если факторы найдены и истолкованы, то на последнем шаге факторного анализа, отдельным наблюдениям можно присвоить значения этих факторов, так называемые факторные значения. Таким образом для каждого наблюдения значения большого количества переменных можно перевести в значения небольшого количества факторов.
19.2 Пример из области социологии
19.2 Пример из области социологии
Изложенный метод будет проиллюстрирован на примере анкеты, составленной в Институте Социологии Университета Марбург. На основе этой анкеты на двух гессенских металлургических предприятиях было произведено исследование отношения к иностранцам. Опрашиваемым предложили высказать свое отношение к следующим пятнадцати положениям:
1. Необходимо улучшить интеграцию иностранцев.
2. Необходимо мягче относиться к беженцам.
3. Деньги Германии должны быть потрачены на нужды страны.
4. Германия — это не служба социальной помощи для всего мира.
5. Необходимо стараться налаживать хорошие отношения друг с другом.
6. Права беженцев следует ограничить.
7. Немцы станут меньшинством.
8. Право беженцев необходимо охранять во всей Европе.
9. Враждебность к иностранцам наносит вред экономике Германии.
10. Сначала необходимо создать нормальные жилищные условия для немцев.
11. Мы ведь тоже практически везде являемся иностранцами.
12. Мультикультура означает мультикриминал.
13. В лодке нет свободных мест.
14. Иностранцы вон.
15. Интеграция иностранцев — это убийство нации.
Оценки ставились по семибальной шкале: от полного несогласия (1) до полного согласия (7). Результаты опроса для 90 человек хранятся в файле ausland.sav в переменных а1-а15.
-
Откройте файл ausland.sav. В файле Вы заметите несколько дополнительных переменных, о которых мы расскажем позже.
-
Выберите в меню Analyze (Анализ) Data Reduction (Сокращение объема данных) Factor... (Факторный анализ)
Откроется диалоговое окно Factor Analysis (Факторный анализ) (см. рис. 19.1).
Рис. 19.1: Диалоговое окно Factor Analysis (Факторный анализ)
-
Переменные a1-a15 поместите в поле тестируемых переменных и ознакомьтесь с возможностями, предлагаемыми различными кнопками этого диалогового меню.
-
После щелчка по кнопке Descriptive Statistics (Дескриптивные статистики) оставьте вывод первичных результатов, которые включают в себя первичные относительные дисперсии простых факторов, собственные значения и процентные доли объяснённой дисперсии. Довольно часто бывает необходим также вывод одномерных статистик и корреляционных коэффициентов.
С помощью кнопки Extraction... (Отбор) Вы можете выбрать метод отбора; оставьте здесь анализ главных компонентов, установленный по умолчанию. Количество отобранных в этом случае факторов приравнивается к числу собственных значений, превосходящих единицу. У Вас также есть возможность собственноручно указать это количество. Так как неповёрнутое факторное решение, предоставляет малозначимую информацию, предотвратите его вывод щелчком на соответствующей опции.
Выключатель Rotation... (Вращение) позволяет выбрать метод вращения. Активируйте метод варимакса и оставьте активированным вывод повёрнутой матрицы факторов. Далее вы можете организовать вывод факторных нагрузок в графическом виде, в котором первые три фактора будут представлены в трёхмерном пространстве; в случае наличия только двух факторов в слое приводится только одно изображение.
Если Вы хотите найти значения факторов и сохранить их в виде дополнительных переменных задействуйте выключатель Scores... (Значения) и отметьте Save as variables (Сохранить как переменные). По умолчанию установлен регрессионный метод. Выключатель Options... (Опции) предназначен для обработки пропущенных значений. Здесь обеспечивается возможность заменить пропущенные значения средними значениями соответствующих переменных.
-
Для проведения расчётов щёлкните на ОК.
-
В окне обзора появятся результаты. Сначала приводятся первичные статистики:
Total Variance Explained
(Объяснённая суммарная дисперсия) | ||||||
Compo-nent (Компо-ненты) | Initial Eigenvalues (Первичные собственные значения) | Rotation Sums of Squared Loadings (Повёрнутые суммы квадратов нагрузок) | ||||
Total (Сумма) | % of Variance (% диспе-рсии) | Cumulative % (Сово-купный %) | Total (Сум-ма) | % of Variance (% дис-персии) | Cumu-lative % (Сово-купный %) | |
1 | 5,146 | 34,308 | 34,308 | 3,466 | 23,105 | 23,105 |
2 | 1,945 | 12,970 | 47,278 | 2,536 | 16,907 | 40,013 |
3 | 1,415 | 9,433 | 56,711 | 2,505 | 16,698 | 56,711 |
4 | ,990 | 6,601 | 63,312 | |||
5 | ,936 | 6,238 | 69,550 | |||
6 | ,760 | 5,068 | 74,617 | |||
7 | ,693 | 4,622 | 79,240 | |||
8 | ,612 | 4,083 | 83,323 | |||
9 | ,529 | 3,529 | 86,852 | |||
10 | ,473 | 3,151 | 90,004 | |||
11 | ,433 | 2,889 | 92,893 | |||
12 | ,339 | 2,262 | 95,1555 | |||
13 | ,301 | 2,007 | 97,161 | |||
14 | ,245 | 1,635 | 98,797 | |||
15 | ,181 | 1,203 | 100,000 | |||
Extraction Method: Principal Component Analysis (Метод отбора: Анализ главных компонентов).
По таблице можно увидеть, что три собственных фактора имеют значения превосходящие единицу. Следовательно для анализа отобрано только три фактора. Первый фактор объясняет 34,308 % суммарной дисперсии, второй фактор 12,97 % и третий фактор 9,433 %. Так как мы запретили вывод неповернутой матрицы факторов, то далее приводится повёрнутая матрица (см. следующую таблицу).
При факторном анализе постоянно появляются сообщения об ошибках, — так нам жаловался один пользователь, — например 2,56Е-02 и т.п. Действительно такой формат вывода в глазах непосвященного пользователя очень портит картину всей таблицы. Это, так называемый, Е-формат, знакомый всем программистам по языку Фортран (Fortran), где буква Е соответствует 10 в некоторой степени; для числа 2,5Е-02 можно было бы записать и 0,0256. Во втором примере (гл. 19.3) мы покажем Вам, как выходить из такой ситуации.
Rotated Component Matrix a
| (Повёрнутая матрица компонентов) | |||
Component (Компонент) | |||
1 | 2 | 3 | |
А1 | -,466 | ,628 | -,191 |
А2 | -,141 | ,657 | ,215 |
A3 | ,327 | -,153 | ,711 |
А4 | ,533 | -,106 | ,394 |
А5 | -,362 | ,783 | 4.52Е-02 |
А6 | -1.2Е-02 | -3.8Е-02 | ,763 |
А7 | ,525 | 3.58Е-02 | ,543 |
А8 | -,117 | ,719 | -,267 |
А9 | 2.56Е-02 | ,551 | -8.8Е-02 |
А10 | ,252 | -9.5Е-02 | ,685 |
А11 | ,125 | ,392 | -,292 |
А12 | ,802 | -,199 | ,108 |
А13 | ,685 | -,110 | ,465 |
А14 | ,837 | -,144 | -2.5Е-02 |
А15 | ,725 | -4.8Е-02 | ,144 |
Extraction Method: Principal Component Analysis ((Метод отбора: Анализ главных компонентов).
Rotation Method: Varimax with Kaiser Normalization (Метод вращения: Варимакс с нормализацией Кайзера),
a. Rotation converged in 8 iterations (Вращение осуществлено за 8 итераций).
Здесь начинается самая интересная часть факторного анализа: Вы должны попытаться объяснить отобранные факторы. Для этого возьмите в руки карандаш и в каждой строке повёрнутой факторной матрицы отметьте ту факторную нагрузку, которая имеет наибольшее абсолютное значение.
Как уже было сказано, эти факторные нагрузки следует понимать как корреляционные коэффициенты между переменными и факторами. Так переменная a1 сильнее всего коррелирует с фактором 2, а именно, величина корреляции составляет 0,628, переменная а2 также сильнее всего коррелирует с фактором 2 (0,657), переменная же а3 коррелирует сильнее всего с фактором 3 (0,711) и т.д. В большинстве случаев включение отдельной переменной в один фактор, осуществляемое на основе коэффициентов корреляции, является однозначным. В исключительных случаях, к примеру, как в ситуации с переменной а7, переменная может относиться к двум факторам одновременно. Могут быть также и переменные, в нашем примере a11, которыми нельзя нагрузить ни один из отобранных факторов.
Если поступить так, как изложено выше, то варианты мнений, указанные вначале рассмотрения примера, можно отнести в следующем порядке к трём факторам:
-
Фактор 1:
Германия — это не служба социальной помощи для всего мира.
Немцы станут меньшинством.
Мультикультура означает мультикриминал.
В лодке нет свободных мест.
Иностранцы вон.
Интеграция иностранцев — это убийство нации.
-
Фактор 2
Необходимо улучшить интеграцию иностранцев.
Необходимо мягче относиться к беженцам.
Необходимо стараться налаживать хорошие отношения друг с другом.
Права беженцев необходимо охранять во всей Европе.
Враждебность к иностранцам наносит вред экономике Германии.
Мы ведь тоже практически везде являемся иностранцами.
-
Фактор 3
Деньги Германии должны быть потрачены на нужды страны.
Права беженцев следует ограничить.
Немцы станут меньшинством.
Сначала необходимо создать нормальные жилищные условия для немцев.
Из-за равных по величине нагрузок, как для фактора 3, так и для фактора 1, положение "Немцы станут меньшинством" включено в оба фактора. Теперь мы подошли к последнему и решающему шагу факторного анализа: необходимо обнаружить и описать смысловую связь факторов. В рассматриваемом примере это можно сделать без особых усилий.
Первый фактор, и это очевидно, собрал все положения, враждебно настроенные по отношению к иностранцам. На основании позитивных корреляционных коэффициентов участвующих переменных с фактором и принимая во внимание полярность значений переменных (большое значение означает полное согласие) большое значение фактора означает высокую враждебность к иностранцам.
Во второй фактор входят те положения, которые указывают на дружелюбное отношение к иностранцам. Большое значение фактора означает здесь доброжелательное отношение к иностранцам.
Во второй фактор вошли точки зрения, соответствующие осторожному отношению к иностранцам; в противоположность к первому фактору это не враждебные точки зрения, а по большей части социальные страхи (деньги, жильё в первую очередь для немцев и т.д.). Большое значение фактора указывает здесь на высокую степень социального сомнения.
В соответствии с порядком изложения эти три фактора можно кратко охарактеризовать при помощи следующих выражений: Враждебная позиция, Доброжелательная позиция и Социальные страхи. Однако столь явно, как в приведенном примере факторы удаётся объяснить не всегда. Если нет возможности провести вербальное объяснение факторов, то факторный анализ можно считать неудавшимся.
Значения факторов
Поскольку мы пожелали произвести расчёт значений факторов, то в соответствии с тремя отобранными факторам были сгенерированы три новые переменные, на-
званные fac1_1, fac2_1 и fac3_1, которые содержат вычисленные значения факторов. Если Вы просмотрите текущий файл после поведения факторного анализа, то сможете увидеть имеющие нормализованные значения факторов. По каждому из отобранных фактору для каждого опрошенного было рассчитано специальное факторное значение. Факторное значение, как правило, лежит в пределах —3 до +3.
Рассмотрим факторную переменную fac1_1. Она включает следующие элементарные переменные: а4, а12, а13, а14 и а15. В качестве метки для этого фактора мы выбрали выражение: "Враждебная позиция". Большое положительное значение фактора означает одобрение элементарных переменных, то есть положений, входящих в этот фактор. Одобрение элементарных переменных, относящихся к первому фактору, тождественно ярко выраженным расистским взглядам. Для подтверждения этого факта рассмотрим два примера. Наблюдение 4 характеризуется очень низким факторным значением в переменной fac1_1. Оно равно —2,00455. В данном случае можно сделать заключение о том, что здесь не наблюдается расистская направленность или она очень слаба. Соответственно этому ведут себя и отдельные значения элементарных переменных (а4 = 2, а13 = 1, а14 = 1, а15 = 1). Наблюдение 17, в отличие от наблюдения 4, характеризуется очень высоким положительным значением фактора, который равен 3,14801. Основываясь на этом значении, мы можем исходить из того, что здесь явно заметна экстремально-расистская позиция. Соответственно этому ведут себя и отдельные значения элементарных переменных (а4 = 7, а13 = 7, а14 = 7, а15 = 7).
Рассмотрим факторную переменную fac2_1. К ней относятся элементарные переменные: a1, a2, а5, а8, а9 и a11. В качестве метки для этого фактора мы выбрали выражение: "Доброжелательная позиция". Большое положительное значение фактора означает полное согласие. Полное согласие соответствует дружелюбному отношению к иностранцам. И здесь рассмотрим два выборочных примера. Наблюдение 17 характеризуется очень малым значением фактора, которое составляет —3,32632. Основываясь на значении этого фактора можно сделать вывод, что едва ли в этом случае присутствует доброжелательное отношение к иностранцам. Соответственным образом ведут себя и отдельные значения элементарных переменных (a1 = 1, а2 = 1, а5 = 1, а8 = 2, а9 = 4, a11 = 6). В наблюдении 17 и следовало ожидать низкого значения фактора, так как здесь наблюдается высокое положительное факторное значение для факторной переменной fac1_1. В таком случае говорят, что существует отчётливая консистенция. По сравнению с предыдущим наблюдением, наблюдение 6 характеризуется очень высоким положительным значением факторной переменной fac2_1. Оно равно 1,23438. Исходя из значения фактора, можно сделать вывод, что существует сильное дружелюбное отношение к иностранцам. Соответственным образом ведут себя и отдельные значения элементарных переменных (a1 = 7, а2 = 7, а5 = 7, а8 = 7, а9 = 7, a11 = 7).
В заключение рассмотрим факторную переменную fac3_1. К ней относятся элементарные переменные аЗ, а6, а7 и а10. В качестве метки для этого фактора мы выбрали выражение: "Социальные страхи". Большое положительное значение фактора означает одобрение элементарных переменных. Одобрение элементарных переменных тождественно ярко выраженным социальным страхам. Рассмотрим для доказательства этого факта два примера. Наблюдение 5 характеризуется очень низким значением факторной переменной fac3_1. Оно равно —1,66369. В этом случае наблюдаются очень слабые социальные страхи и едва ли на основании социальных страхов можно наблюдать враждебное отношение к иностранцам. Соответственно этому ведут себя и отдельные значения элементарных переменных (аЗ = 5, аб = 2, а7 = 2, а 10 = 1). Наблюдение 43 в отличие от наблюдения 5 характеризуется очень высоким положительным факторным значением. Оно равно 1,93125. В этом случае наблюдаются очень сильные социальные страхи. Соответственным образом ведут себя и отдельные значения элементарных переменных (аЗ = 7, аб = 7, а7 = 7, а 10 = 7). В файле ausland.sav находятся ещё несколько дополнительных переменных, а именно:
| Удовлетворённость собственным местом в экономических отношениях (1 = да, 2 = нет) |
| Год рождения (1 = 1935-1949, 2 = 1941-1950, 3 = 1951-1960, 4 = 1961-1970) |
| Пол (1 = мужской, 2 = женский) |
| Социально-политическая активность (1 = да, 2 = нет) |
| Занимаемая должность (1 = рабочий, 2 = специалист, 3 = служащий) |
Эти переменные можно использовать для того, чтобы устанавливать связи для факторных значений. Самым распространённым методом для этого является разбиение факторных значений на четыре группы процентилей (см. гл. 8.6.2). Покажем это на примере первого факторного значения (переменная facl_l).
-
Выберите в меню Transform (Трансформировать) Rank Cases... (Создать иерархию наблюдений)
Откроется диалоговое окно Rank Cases (Создать иерархию наблюдений).
-
Переменную fac1_1 перенесите в список тестируемых переменных.
-
Щёлкните на выключателе Rank Types... (Типы иерархии), деактивируйте установленную по умолчанию опцию Rank (Ранг) и активируйте опцию Fractional rank as % (Дробный ранг как процентили). Оставьте установленное по умолчанию количество групп равное 4.
-
Подтвердите свой выбор нажатием на Continue (Далее) и затем на ОК.
Будет создана переменная nfac1_1, которая содержит значения 1 до 4 с примерно равномерной частотой.
-
Перейдите в редактор данных и измените имя переменной nfac1_1 на более удобное имя ausfeind, в поле метки наберите Враждебное отношение и значениям присвойте следующие метки: 1 = отсутствует, 2 = слабое, 3 = сильное и 4 = очень сильное. Теперь создадим таблицу сопряженности для новой переменной и переменной stellung (Занимаемая должность).
-
Выберите в меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
-
В диалоговом окне Crosstabs (Таблицы сопряженности) переменную stellung поместите в поле строк, а переменную ausfeind в поле столбцов и через выключатель Cells... (Ячейки) сделайте дополнительно запрос на вывод процентных значений по строкам.
В окне просмотра появится следующая таблица сопряженности.
berufliche Stellung * fremdenfeindliche Einstellung Crosstabulation
(Занимаемая должность * Враждебное отношение Таблица сопряженности ) | |||||||
| fremdenfeindliche Einstellung (Враждебное отношение) | Total (Сум-ма) | |||||
keine (отсу-тствует) | swach (сла- бое) | stark (силь-ное) | sehr stark (очень силь- ное) | ||||
beru-fliche Ste- llung (Зани-маемая дол-жность) | Arbe- iter (Рабо-чий) | Count (Коли-чество) | 6 | 7 | 7 | 11 | 31 |
% within berufliche Stellung (% от Зани-маемой долж-ности) | 19,4% | 22,6% | 22,6% | 35,5% | 100,0% | ||
Facha-rbeiter (Специ-алист) | Count (Коли-чество) | 5 | 7 | 7 | 8 | 27 | |
% within beru-fliche Stellung (% от Зани-маемой долж-ности) | 18,5% | 25,9% | 25,9% | 29,6% | 100,0% | ||
Anges-tellte (Служа-щий) | Count (Коли-чество) | 10 | 9 | 8 | 3 | 30 | |
% within beru-fliche Stellung (% от Зани-маемой долж-ности) | 33,3% | 30,0% | 26,7% | 10,0% | 100,0% | ||
Total (сумма) |
| Count (Коли-чество) | 21 | 23 | 22 | 22 | 88 |
% within beru-fliche Stellung (% от Зани-маемой долж-ности) | 23,9% | 26,1% | 25,0% | 25,0% | 100,0% | ||
Враждебное отношение к иностранцам у рабочих и специалистов выражено ярче, чем у служащих. Однако тест по критерию Хи-квадрат демонстрирует о незначимом различии.
Попытайтесь найти связи между другими факторными значениями и переменными.
1.gif
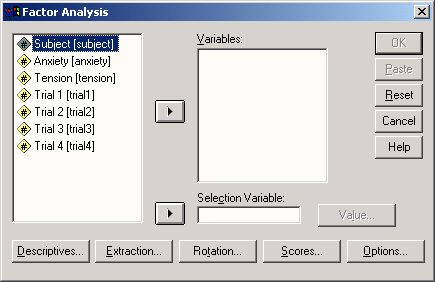
19.3 Пример из области психологии
19.3 Пример из области психологии
В анкете изучения вариантов поведения при заболевании по пунктам описываются возможные варианты поведения, дающие объяснение отношения больных к их болезни. На основании пятибалльной шкалы, балы которой соответствуют выражениям: абсолютно не подходит (1) —- незначительно (2) — умеренно (3) — довольно значительно (4) — и очень сильно (5), психолог должен понять, насколько сильно указанная ситуация подходит их пациенту. Помимо этого, посредством факторного анализа необходимо будет ещё определить, можно ли пункты анкеты логически связать с факторами, которые дают объяснение возможной типологии отношения к болезни. Сначала рассмотрим пункты стандартной анкеты:
1. Искать информацию о заболевании и лечении
2. Не желать признать случившееся
3. Занижать значение и важность болезни
4. Размышлять и мечтать о своём
5. Винить самого себя
6. Считать виноватыми других
7. Предпринимать активные действия для решения проблемы
8. Составить план и затем приступить к действиям
9. С нетерпением и раздражённо на всё реагировать
10. Выносить все эмоции наружу
П. Подавлять эмоции, проявлять самообладание
12. Искать улучшение настроения в употреблении алкоголя или успокаивающих средств
13. Больше себе позволять
14. Пытаться интенсивней жить
15. Решиться на борьбу с болезнью
16. Жалеть себя
17. Подбадривать себя
18. Пытаться достичь успеха и самоутверждения
19. Пытаться отвлечься
20. Искать уединения
21. Принимать болезнь как судьбу
22. Впасть в бесконечные размышления
23. Искать утешения в религии
24. Пытаться найти какой-либо смысл в болезни
25. Утешать себя тем, что другим ещё хуже
26. Ссылаться на судьбу
27. Точно следовать указаниям врача
28. Надеяться на врачей
29. Не доверять врачам, перепроверять диагноз, искать других врачей
30. Желать делать добро другим
31. Изображать напускное веселье
32. Принимать помощь от других
33. Позволять о себе заботиться
34. Отдаляться от других людей
35. Пытаться припомнить личный опыт и методы борьбы с подобными ударами судьбы
Результаты для 160 пациентов хранятся в файле fkv.sav в переменных fl-f35.
-
Откройте файл fkv.sav
-
Выберите в меню Analyze (Анализ) Data Reduction (Сокращение объема данных) Factor... (Факторный анализ)
Откроется диалоговое окно Factor Analysis (Факторный анализ) (см. рис. 19.1). Поместите переменные П-О5 в поле тестируемых переменных.
-
Щёлкните на выключателе Descriptives... (Дескриптивные статистики). Откроется диалоговое окно Factor Analysis: Descriptives (Факторный анализ: Дескриптивные статистики), как представлено на рисунке 19.2. Оставьте установленную по умолчанию опцию вывода Initial solution (Первичного решения).
-
Щёлкните на выключателе Extraction... (Извлечение), оставьте установку Principal components (Анализ главных компонентов). В отличие от первого примера факторного анализа, здесь количество факторов сознательно ограничим пятью. Если бы мы не сделали такого ограничения, то в соответствии с начальными установками было бы создано одиннадцать факторов, количество, которое очень тяжело поддаётся обзору.
Рис. 19.2: Диалоговое окно Factor Analysis: Descriptives (Факторный анализ: Дескриптивные статистики)
-
Щёлкните поэтому на опции Number of factors (Количество факторов) и введите число 5. Щелчком на соответствующей опции деактивируйте вывод неповёрнутых значений факторов. Активируйте опцию Scree plot (Точечная диаграмма). Точечная диаграмма графически представляет собственные значения факторов, упорядоченные по величине.
Диалоговое окно Factor Analysis:Extraction < Факторный анализ: Извлечение) должно теперь выглядеть так, как представлено на рисунке 19.3.
Рис. 19.3: Диалоговое окно Factor Analysis: Extraction (Факторный анализ: Отбор)
-
Подтвердите произведенные установки нажатием Continue (Далее). Щёлкните на выключателе Rotation... (Вращение) и выберите метод варимакса. Если вы желаете наряду с выводом повёрнутой матрицы факторов, установленным по умолчанию, получить факторные нагрузки в графическом виде, то щёлкните на опции Loading plot(s) (Диаграммы нагрузок). Диалоговое окно Factor Analysis:Rotation (Факторный анализ: Вращение) должно теперь выглядеть так, как изображено на рисунке 19.4.
-
Подтвердите нажатием кнопки Continue (Далее). Щёлкните по выключателю Scores... (Значения) и активируйте Save as variables (Сохранить как переменные), чтобы рассчитанные значения факторов сохранить в виде дополнительных переменных. Диалоговое окно Factor AnalysisiFactor Scores (Факторный анализ: Значения факторов) выглядит теперь так, как изображено на рисунке 19.5.
Рис. 19.4: Диалоговое окно Factor Analysis:Rotation (Факторный анализ: Вращение)
-
В заключение, с помощью кнопки Options... (Опции) Вы получите возможность, организовать вывод коэффициентов, отсортированных по размеру. В отличие от первого примера факторного анализа, здесь мы воспользуемся предлагаемой сортировкой.
-
Поэтому активируйте опцию Sorted by size (Сортированные по размеру).
Рис. 19.5: Диалоговое окно Factor Analysis:Factor Scores (Факторный анализ: Значения факторов)
Теперь мы запретим вывод малых факторных нагрузок и для этого установим граничное значение выводимых нагрузок равным 0,4. Достоинство этого шага состоит в том, что устраняется непривлекательное отображение малых значений в Е-формате (см. раздел 19.2).
-
Активируйте опцию Suppress absolute values less then: (He выводить абсолютные значения меньшие, чем:) и введите предельное значение 0,4.
Диалоговое окно Factor Analysis:0ptions (Факторный анализ: Опции) выглядит теперь так, как изображено на рисунке 19.6.
-
Для проведения факторного анализа подтвердите произведенные установки нажатием Continue (Далее) и в главном диалоговом окне ОК.
Рассмотрит результаты расчёта, которые появились в окне просмотра. Сначала приводятся первичные статистики.
Рис. 19.6: Диалоговое окно Factor Analysis:Options (Факторный анализ: Опции)
Total Variance Explained
(Объяснённая совокупная дисперсия) | ||||||
Component (Компо-ненты) | initial eigenvalues (Первичные собственные значения) | Kotation Sums of Squared Loadings (Повёрнутая сумма квадратов нагрузок) | ||||
Total (Сумма) | % of Variance (% дис-персии) | Cumulative % (Совокупный процент) | Total (Сумма) | % of Variance (% дис-персии) | Cumulative % (Совокупный процент) | |
1 | 5,0226 | 14,359 | 14,359 | 4,388 | 12,538 | 12,538 |
2 | 3,937 | 11,250 | 25,609 | 3,972 | 11,349 | 23,887 |
3 | 2,356 | 6,731 | 32,340 | 2,396 | 6,845 | 30,732 |
4 | 2,073 | 5924 | 38,264 | 2,257 | 6,447 | 37,179 |
5 | 1,706 | 4,873 | 43,138 | 2,085 | 5,958 | 43,138 |
6 | 1,478 | 4,222 | 47,359 |
|
|
|
7 | 1,319 | 3,768 | 51, 127 |
|
|
|
8 | 1,258 | 3,595 | 54, 722 |
|
|
|
9 | 1,228 | 3,508 | 58, 230 |
|
|
|
10 | 1,082 | 3,092 | 61,322 |
|
|
|
11 | 1,029 | 2,941 | 64,263 |
|
|
|
12 | ,942 | 2,692 | 66. 955 |
|
|
|
13 | ,890 | 2,542 | 69, 497 |
|
|
|
14 | ,878 | 2,508 | 72, 005 |
|
|
|
15 | ,823 | 2,353 | 74, 358 |
|
|
|
16 | ,737 | 2,104 | 76, 462 |
|
|
|
17 | ,704 | 2,011 | 78, 473 |
|
|
|
18 | ,664 | 1,898 | 80, 371 |
|
|
|
19 | ,652 | 1,862 | 82, 232 |
|
|
|
20 | ,618 | 1,766 | 83, 998 |
|
|
|
21 | ,572 | 1,634 | 85, 632 |
|
|
|
22 | ,516 | 1,474 | 87, 106 |
|
|
|
23 | ,473 | 1,352 | 88, 458 |
|
|
|
24 | ,466 | 1,331 | 89, 788 |
|
|
|
25 | ,459 | 1,310 | 91,099 |
|
|
|
26 | ,432 | 1,234 | 92, 332 |
|
|
|
27 | ,417 | 1,192 | 93, 524 |
|
|
|
28 | ,388 | 1,108 | 94, 632 |
|
|
|
29 | ,345 | ,985 | 95,617 |
|
|
|
30 | ,324 | ,927 | 96, 544 |
|
|
|
31 | ,287 | ,821 | 97, 365 |
|
|
|
32 | ,259 | ,740 | 98, 105 |
|
|
|
33 | ,240 | ,684 | 98, 789 |
|
|
|
34 | ,223 | ,638 | 99, 427 |
|
|
|
35 | ,201 | ,573 | 100,000 |
|
|
|
Extraction Method: Principal Component Analysis (Метод отбора: Анализ главных компонентов).
Насчитывается одиннадцать собственных значений, превосходящих единицу, что означало бы отбор одиннадцати факторов, если бы Вы не изменили установку по умолчанию Eigenvalues over: 1 (Собственные значения, превосходящие единицу) и не ограничили бы количество рассматриваемых факторов пятью. После точечной диаграммы, которую мы объясним позже, следует вывод повёрнутой факторной матрицы:
Rotated Component Matrix a
(Повёрнутая матрица компонентов) | |||||
Component (Компоненты) | |||||
1 | 2 | 3 | 4 | 5 | |
F5 | ,683 | ||||
F16 | ,683 | ||||
F22 | ,620 | ||||
F9 | ,581 | ||||
F26 | ,580 | ||||
F6 | ,544 | ||||
F35 | ,515 | ||||
F33 | ,491 | ||||
F12 | ,488 | ||||
F34 | ,458 | ||||
F4 | ,447 | ||||
F7 | ,710 | ||||
F8 | ,690 | ||||
F17 | ,654 | ||||
F14 | ,621 | ||||
F15 | ,597 | ||||
F18 | ,589 | ||||
F19 | ,572 | ||||
F1 | ,563 | ||||
F13 | ,510 | ||||
F20 | |||||
F28 | ,816 | ||||
F27 | ,765 | ||||
F31 | -,493 | ||||
F29 | |||||
F21 | ,683 | ||||
F25 | ,592 | ||||
F30 | ,522 | ||||
F23 | ,426 | ,469 | |||
F24 | ,404 | ||||
F3 | ,677 | ||||
F2 | ,457 | ,567 | |||
F10 | -,564 | ||||
F11 | ,403 | ||||
F32 | |||||
Extraction Method: Principal Component Analysis (Метод отбора: Анализ главных компонентов).
Rotation Method: Varimax with Kaiser Normalization (Метод вращения: варимакс с нормализацией Кайзера).
a. Rotation converged in 6 iterations (Вращение получено за б итераций).
Здесь мы опять подходим к самой интересной части факторного анализа — толкованию факторов. Факторные нагрузки пяти факторов в блочном виде расположены по диагонали матрицы. Переменные, находящиеся внутри одного блока, отсортированы в порядке убывания факторных нагрузок, причём был запрещен вывод факторных нагрузок, меньших 0,4. Высказывания f5, f16, f22, f9, f26, f6, f35, f33, f12, f34 и f4 принадлежат первому фактору, высказывания f7, f8, f17, f14, f15, f18, f19, f1, f1З и f10 второму и т.д. Высказывание f5 своим значением 0,683 нагружает сильнее всего первый фактор, высказывание f7 — второй фактор (со значением 0,710), высказывание f28 — третий фактор (со значением 0,816) и т.д.
Для того, чтобы отдельные высказывания отнести к определенному фактору, при выводе отсортированных значений Вам уже не нужно маркировать их карандашом, так как сопоставление в этом случае будет произведено автоматически. Несмотря на то, что представление данных в таком виде значительно удобнее, всё же здесь существует один серьёзный недостаток: сопоставление высказывания некоторому фактору рассматривается как единственно верное решение, без проверки, не имеет ли данное высказывание примерно такую же нагрузку и для какого-либо другого фактора. Рассмотрим, к примеру, пунктf23. Пункт f23 нагружает фактор 1 значением 0,426, а фактор 4 значением 0,469. Для обеспечения корректности в этом случае следует иметь дело с обоими факторами. Если нельзя чётко объяснить принадлежность одного из многих высказываний одному-единственному фактору, то факторный анализ следует считать неудавшимся. Аналогично, Вы не должны забывать об этой проблеме при выводе сортированных данных. Кроме того, факторный анализ считается неудавшимся и тогда, когда нельзя однозначно интерпретировать факторы. Поэтому далее мы попытаемся интерпретировать факторы из рассматриваемого примера.
-
Фактор 1:
Винить самого себя
Жалеть себя
Впасть в бесконечные размышления
С нетерпением и раздражённо на всё реагировать
Жаловаться на судьбу
Считать виноватыми других
Пытаться припомнить личный опыт и методы борьбы с подобными ударами судьбы
Искать улучшение настроения в употреблении алкоголя или успокаивающих средств
Размышлять и мечтать о своём
-
Фактор 2:
Предпринимать активные действия для решения проблемы
Составить план и затем приступить к действиям
Подбадривать себя
Пытаться интенсивней жить
Решиться на борьбу с болезнью
Пытаться достичь успеха и самоутверждения
Пытаться отвлечься
Искать информацию о заболевании и лечении
-
Фактор 3:
Надеяться на врачей
Точно следовать указаниям врача
Изображать наигранное веселье
-
Фактор 4:
Принимать болезнь как судьбу
Утешать себя тем, что другим ещё хуже
Желать делать добро другим
Искать утешения в религии
Пытаться найти какой-либо смысл в болезни
-
Фактор 5:
Занижать значение и важность болезни Не желать признать случившееся Выносить все эмоции наружу Подавлять эмоции, самообладание
В этом примере, также как и в предыдущем случае, можно без особых усилий истолковать содержание этих факторов.
Первый фактор собрал все пункты, описывающие депрессивное отношение к тяжёлой болезни. Эти пункты описывают состояние подавленности, удручённости и сомнений; здесь речь идёт о потере желания жить и попытке спрятаться за алкоголем и психотропными средствами. Обозначим фактор 1 меткой "Депрессивный подход".
Второй фактор собрал все пункты, описывающие активный подход к борьбе с болезнью. Эти пункты описывают состояние пробуждения желания жить, которое проявляется в рациональном подходе к борьбе с болезнью (Поиск информации), в нежелании позволить болезни ввести себя в угнетённое состояние (Пытаться отвлечься). Фактору 2 присвоим следующую метку: "Активное действие, направленное на решение проблемы".
Третий фактор собрал все пункты, основывающиеся на отношении врач-пациент. Следует обратить внимание на то, что высказывание f31 отрицательно нагружает этот фактор, то есть о наигранном веселье скорее всего речь не идёт. Для краткой характеристики этого фактора можно было бы выбрать выражение: "Надеяться на врачей".
Фактор 4 собрал все высказывания, указывающие на фаталистический или религиозно-направленный поиск смысла происходящего. В качестве краткой характеристики здесь можно было бы выбрать выражение: "Религиозность и поиск смысла".
В факторе 5 собрались все пункты, характеризующие состояние, в котором опрашиваемый не склонен признавать болезнь путём занижения её важности или нежелания осознавать реальность, а также душевной отчуждённости (Подавлять эмоции). Здесь следует обратить внимание на то, что пункт f10 (Выносить все эмоции наружу) нагружает фактор отрицательным значением, то есть эмоции скорее не выносятся наружу. В качестве краткой характеристики этого фактора можно было бы выбрать выражение: "Недооценка и психологическая отрешённость".
Точечная диаграмма
Займёмся теперь анализом точечной диаграммы, представленной на рисунке 19.7.
Точечная диаграмма может нам помочь определить количество учитываемых факторов. Как Вам уже известно, согласно установке по умолчанию, SPSS учитывает в результирующей модели все те факторы, собственное значение которых превосходит единицу. В нашем примере это было бы одиннадцать факторов.
Количество учитываемых факторов вы можете задать сами, что мы и сделали ранее. В качестве вспомогательного средства для определения задаваемого числа факторов может послужить специальная точечная диаграмма. Слово Screeplot, употребляемое для обозначения этой диаграммы состоит из двух частей: английского слова scree, что означает щебень и слова plot, что в английском соответствует графическому представлению. Такая диаграмма служит для того, чтобы маловажные факторы — щебень — можно было отделить от самых значимых факторов. Эти значимые факторы на графике образовывают в своего рода склон, то есть ту часть линии, которая характеризуется крутым подъёмом. В приведенной диаграмме такой крутой подъём наблюдается
в области первых пяти факторов. Пять факторов мы и положили в основу модели в самом начале анализа. Если посмотреть на график, то можно заметить что склон, то есть область значимых факторов, наблюдается выше пятого фактора (пятый, четвёртый, третий, второй ...), а ниже пятого фактора (шестой, седьмой, восьмой ...) расположился щебень, область незначимых факторов. Вы можете самостоятельно провести расчет с использованием модели, включающей различное число факторов; в рассмотренном примере было бы уместным произвести сравнение моделей с учётом четырёх, пяти и шести факторов.
Рис. 19.7: Точечная диаграмма
2.gif
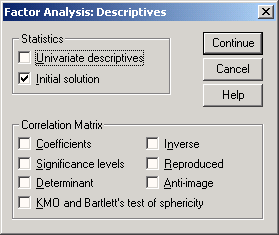
3.gif
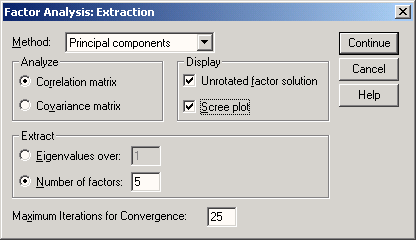
4.gif
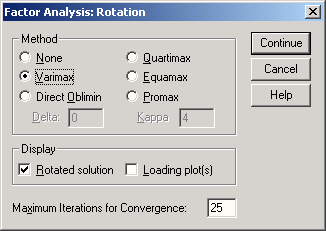
5.gif

6.gif

7.gif
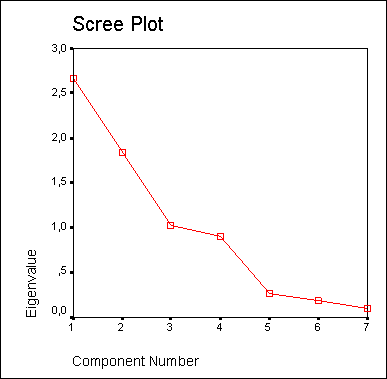
19.4 Задача вращения
19.4 Задача вращения
Рассмотрим поподробнее задачу вращения. Используем для этого приводившийся в разделе 19.2 пример опроса, исследующего отношение к иностранцам.
-
Откройте файл ausland.sav.
-
Выберите в меню Analyze (Анализ) Data Reduction (Сокращение объема данных) Factor... (Факторный анализ)
-
В диалоговом окне Factor Analysis (Факторный анализ) поместите переменные al-а!5 в поле тестируемых переменных.
-
С помощью кнопки Extraction... (Извлечение) укажите требуемое число создаваемых факторов равное двум, чтобы получить легко интерпретируемый двумерный пример.
-
Через выключатель Rotation... (Вращение) активируйте опцию Loading plot(s) (Диаграмма нагрузок), но для модели вращения оставьте установленную по умолчанию опцию None (Отсутствует).
-
В результате мы оставляем вывод так называемой компонентной диаграммы.
Рис. 19.8: Компонентная диаграмма без вращения
На этой диаграмме в графическом виде представлены факторные нагрузки обоих факторов. Для интерпретации факторов было бы оптимально, если бы точки лежали ближе к осям и подальше от точки начала отсчёта; тогда каждая переменная имела бы значительную нагрузку для одного фактора и незначительную для другого. Этого можно достичь поворотом осей против часовой стрелки, причём ортогональность системы координат (прямой угол между осями) должна сохраниться. В данном двумерном примере это вращение можно представить себе довольно наглядно, математически же подобный поворот можно произвести также и в и—мерном пространстве (то есть при наличии произвольного количества факторов).
Альтернативой прямоугольному (ортогональному) вращению является косоугольное вращение. В этом случае после вращения оси не сохраняют прямой угол по отношению друг к другу. В то время как при прямоугольном вращении корреляция между факторами отсутствует, то при косоугольном вращении этот принцип нарушается — факторы могут коррелировать между собой.
SPSS предлагает в общей сложности пять методов вращения: три метода для ортогонального вращения, один для косоугольного и еще один, который является комбинацией двух видов вращения. Эти методы Вы можете активировать через выключатель Rotation... (Вращение) в диалоговом окне Factor Analysis: Rotation (Факторный анализ: Вращение).
-
Varimax: Ортогональное вращение, при котором происходит минимизация количества переменных с высокой факторной нагрузкой. Этот метод является наиболее часто применяемым, поскольку он облегчает интерпретацию факторов.
-
Quartimax: Ортогональное вращение, при котором происходит минимизация количества факторов, необходимых для объяснения переменной. Этот метод используется редко и вообще не рекомендуется для применения.
-
Equamax: Ортогональное вращение; компромисс между предыдущими методами.
-
Direct oblimin: Косоугольное вращение.
-
Рrоmах: Комбинация ортогонального и косоугольного видов вращений.
Обычно для ортогонального вращения применяют метод варимакса, а для косоугольного — Direct oblimin. При помощи компонентной диаграммы отследим действие вращения, осуществленного с использованием метода варимакса.
-
В диалоговом окне Factor Analysis: Rotation (Факторный анализ: Вращение) вместо опции None (Отсутствует) активируйте опцию Varimax (Ba-римакс).
-
Рассмотрите изменённую компонентную диаграмму.
Рис. 19.9: Компонентная диаграмма после вращения
На диаграмме стало заметно смещение факторных нагрузок в сторону главных осей.
Факторный анализ является самым излюбленным приёмом практических статистиков, служащим для сокращения количества переменных. Наиболее интересной частью факторного анализа является толкование получающихся факторов, над которым, правда, придётся поразмыслить и применить весь имеющийся опыт.
8.gif
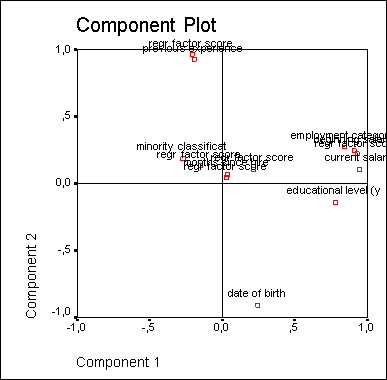
9.gif

Глава 20. Кластерный анализ
Глава 20. Кластерный анализ
1. Кластерный анализ
Кластерный анализ
В результате кластерного анализа при помощи предварительно заданных переменных формируются группы наблюдений. Под наблюдениями здесь понимаются отдельные личности (респонденты) или любые другие объекты. Члены одной группы (одного кластера) должны обладать схожими проявлениями переменных, а члены разных групп различными.
Наряду с кластеризацией наблюдений в SPSS предусмотрена кластеризация переменных. Здесь на основе заданных наблюдений образовываются группы переменных. Так как в принципе то же самое делает и факторный анализ (см. гл. 19), то в этой главе мы ограничимся рассмотрением только кластеризации наблюдений.
20.1 Принцип кластерного анализа
20.1 Принцип кластерного анализа
Для рассмотрения принципа кластерного анализа выберем сначала очень простой пример.
-
Откройте файл bier.sav, который содержит некоторые данные о 17 сортах пива (см. рис. 20.1).
Рис. 20.1: Данные файла bier.sav в редакторе данных
Переменная herkunft (производитель) указывает на страну-производителя пива, где США закодированы с помощью единицы. Расходы (kosten) приведены в долларах США для ёмкости равной 12 унциям для жидкости (примерно одна треть литра); калорийность указана для одинакового количества пива. Содержание алкоголя приводится в процентах.
Возьмём переменные kalorien (калории) и kosten (расходы) и представим их при помощи простой диаграммы рассеяния.
-
Выберите в меню Graphs (Графики) Scalier... (Диаграмма рассеяния)
-
Переменную kalorien (калории) поместите в поле оси х, а переменную kosten (расходы) в поле оси у, и для обозначения наблюдения используйте переменную bier (пиво).
-
Через кнопку Options... (Опции) активируйте опцию Display Chart with case labels (Показывать график с метками наблюдений).
Вы получите диаграмму рассеяния, представленную на рисунке 20.2.
Вы увидите четыре отдельных отчётливых группировки точек, три из них в нижней половине диаграммы и одну в верхнем правом углу. Следовательно, переменные kalorien (калории) и kosten (расходы), явно распадаются на четыре различных кластера по сортам пива.
Сорта пива, которые по значениям двух рассмотренных переменных похожи друг на друга, принадлежат к одному кластеру; сорта пива, находящиеся в различных кластерах, не похожи друг на друга. Решающим критерием для определения схожести и различия двух сортов пива является расстояние между точками на диаграмме рассеяния, соответствующими этим сортам.
Самой распространенной мерой для определения расстояния между двумя точками на плоскости, образованной координатными осями х и у, является евклидова мера:
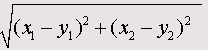
где x1:, и хn — координаты первой точки, у: и уг — координаты второй точки.
Рис. 20.2: Диаграмма рассеяния переменных kalorien (калории) и kosten (расходы)
В соответствии с этой формулой расстояние между сортами пива Budweisei Heineken составляет:
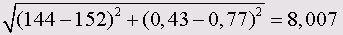
Это расстояние лишь незначительно превосходит то, которое получилось бы, если бы для расчета была взята только одна переменная — kalorien (калории):
|144 - 152 | = 8
Данный эффект можно объяснить тем, что уровни значений переменных kalorien (калории) и kosten (расходы) очень сильно отличаются друг от друга: у переменной kosten (расходы) значения меньше 1, а у переменной kalorien (калории) больше 100. Согласно формуле евклидовой меры, переменная, имеющая большие значения, практически полностью доминирует над переменной с малыми значениями.
Решением этой проблемы является рассмотренное в главе 19.1 z-преобразование (стандартизация) значений переменных. Стандартизация приводит значения всех преобразованных переменных к единому диапазону значений, а именно от —3 до +3.
Если Вы произведёте такое преобразование для переменных kalorien (калории) и kosten (расходы), то для пива Budweiser получите стандартизованные значения равные 0,400 и —0,469 соответственно, а для пива Heineken стандартизированные значения 0,649 и 1,848 соответственно.
Тогда расстояние между двумя сортами пива получится равным
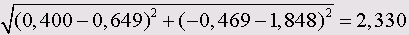
Таким образом, при помощи диаграммы рассеяния для двух переменных: kalorien (калории) и kosten (расходы), мы провели самый простой кластерный анализ. Мы выбрали такой вид графического представления, с помощью которого можно было бы отчётливо распознать группирование в кластеры (четыре в нашем случае).
К сожалению, столь отчётливая картина отношений между переменными, как в приведенном примере, встречается очень редко. Во-первых, структуры кластеров, если вообще таковые имеются, не так чётко разделены, особенно при наличии большого количества наблюдений. Скорее наоборот, кластеры размыты и даже проникают друг в друга. Во-вторых, как правило, кластерный анализ проводится не с двумя, а с намного большим количеством переменных.
При кластерном анализе с тремя переменными можно ввести ещё одну ось — ось z и рассматривать размещение наблюдений, а также проводить расчёт расстояния по формуле евклидовой меры в трёхмерном пространстве.
При наличии более трёх переменных определение расстояния между двумя точками х и у в любом n-мерном пространстве для математиков не представляет особого труда. Формула Евклида в таких случаях приобретает следующий вид:
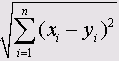
Наряду с евклидовой мерой расстояния, SPSS предлагает и другие дистанционные меры, а также меры подобия. Так что кластерный анализ можно проводить не только с переменными, относящимися к интервальной шкале, как в приведенном случае, но и с дихотомическими переменными, к примеру. В таком ситуации применяется уже другие дистанционные меры и меры подобия (см. разд. 20.3).
При проведении кластерного анализа отдельные кластеры могут формироваться при помощи пошагового слияния, для которого существует ряд различных методов (см. разд. 20.4). Важную роль играют иерархические и партиционные методы, причём последние применяются в подавляющем большинстве случаев. Оба эти метода можно задействовать, если пройти через меню Analyze (Анализ) Classify (Классифицировать)
Они помещены в этом меню под именами Hierarchical Cluster... (Иерархический кластер) и K-Means Cluster... (Кластерный анализ методом к-средних).
Рассмотрим сначала иерархический кластерный анализ, причём начнём с простого примера с 17 сортами пива.
1.gif
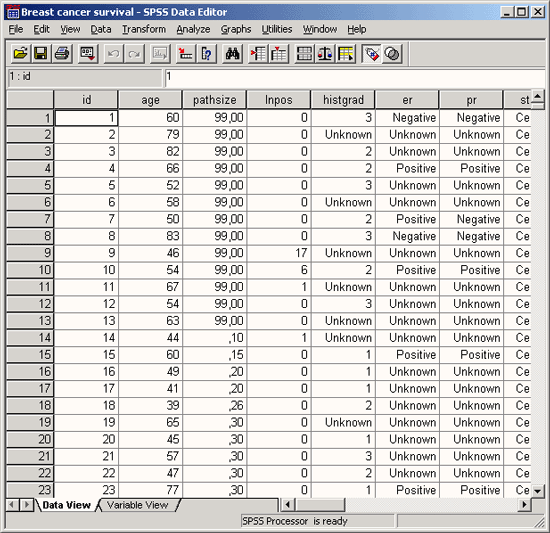
2.gif
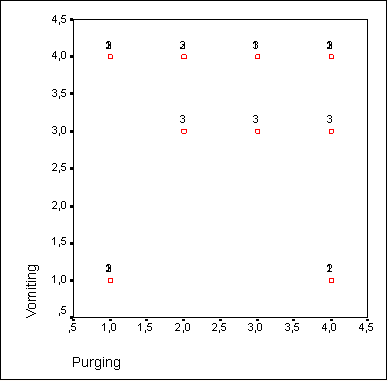
6.gif
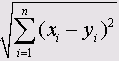
20.2 Иерархический кластерный анализ
20.2 Иерархический кластерный анализ
В иерархических методах каждое наблюдение образовывает сначала свой отдельный кластер. На первом шаге два соседних кластера объединяются в один; этот процесс может продолжаться до тех пор, пока не останутся только два кластера. В методе, который в SPSS установлен по умолчанию (Between-groups linkage (Связь между группами)), расстояние между кластерами является средним значением всех расстояний между всеми возможными парами точек из обоих кластеров.
20.2.1 Иерархический кластерный анализ с двумя переменными
20.2.1 Иерархический кластерный анализ с двумя переменными
Соберём заданные 17 сортов пива в кластеры при помощи параметров kalorien (калории) и kosten (расходы).
-
Выберите в меню Analyze (Анализ) Classify (Классифицировать) Hierarchical Cluster... (Иерархический кластерный анализ)
Вы увидите диалоговое окно Hierarchical Cluster Analysis (Иерархический кластерный анализ) (см. рис. 20.3).
-
Переменные каlorien (калории) и kosten (расходы) поместите в поле тестируемых переменных, а текстовую переменную bier (пиво) в поле с именем Label cases by: (Наименования (метки) наблюдений:).
-
Щелчком по выключателю Statistics... (Статистики) откройте диалоговое окно Hierarchical Cluster Analysis: Statistics (Иерархический кластерный анализ: Статистики) и наряду с выводом последовательности слияния (Agglomeration schedule) активируйте вывод показателя принадлежности к кластеру для каждого наблюдения. Хотя на основании графического представления на диаграмме рассеяния (см. рис. 20.2) и ожидается результат в виде четырёх кластеров, но не можем быть полностью уверены в достижении этого результата. Поэтому, для верности активируйте Range of solutions: (Область решений) и введите числа 2 и 5 в качестве границ области.
-
Вернувшись в главное диалоговое окно, щёлкните по выключателю Plots... (Диаграммы). Активируйте опцию вывода древовидной диаграммы (Dendrogram) и посредством опции None (Нет) отмените вывод накопительной диаграммы.
Рис. 20.3: Диалоговое окно Hierarchical Cluster Analysis (Иерархический кластерный анализ)
-
С помощью кнопки Method... (Метод) Вы получаете возможность выбрать метод образования кластеров, а также метод расчета дистанционной меры и меры подобия соответственно.
SPSS предлагает, в общей сложности, семь различных методов объединения, которые будут рассмотрены в главе 20.4. Метод Between-groups linkage (Связь между группами) устанавливается по умолчанию.
Дистанционные меры и меры подобия зависят от вида переменных, участвующих в анализе, то есть выбор меры зависит от типа переменной и шкалы, к которой она относится: интервальная переменная, частоты или бинарные (дихотомические) данные. В рассматриваемом примере фигурируют данные, относящиеся к интервальной шкале, для которых по умолчанию в качестве дистанционной меры устанавливается квадрат евклидового расстояния (Squared Euclidean distance). Некоторые дистанционные меры и меры подобия будут рассмотрены в главе 20.3.
-
Оставьте предварительные установки и в поле Transform Values (Преобразовывать значения) установите z-преобразование (стандартизацию) значений; необходимость этой опции была уже рассмотрена в главе 20.1. Другие предлагаемые возможности стандартизации играют скорее второстепенную роль.
-
Вернитесь назад в главное диалоговое окно и начните расчёт нажатием ОК.
После обычной обшей статистической сводки итогов по наблюдениям, в окне просмотра сначала приводится обзор принадлежности, из которого можно выяснить очерёдность построения кластеров, а также их оптимальное количество. По двум колонкам, расположенным под общей шапкой Cluster Combined (Объединение в кластеры), можно увидеть, что на первом шаге были объединены наблюдения 5 и 12 (т.е. Heineken и Becks); эти две марки максимально похожи друг на друга и отдалены друг от друга очень малое расстояние. Эти два наблюдения образовывают кластер с номером 5, в то время как кластер 12 в обзорной таблице больше не появляется. На следующем шаге происходит объединение наблюдений 10 и 17 (Coors Light и Schlitz Light), затем 2 и 3 (Lowenbrau и Michelob) и т.д.
Agglomeration Schedule
(Порядок агломерации) | ||||||
Stage (Шаг) | Cluster Combined (Объединение в кластеры) | Coefficients (Коэффициенты) | Stage Cluster First Appears (Шаг, на котором кластер появляется впервые) | Next Stage (Следу-ющий шаг) | ||
Cluster 1 (Кластер 1 ) | Cluster 2 (Кластер 2) | Cluster 1 (Кластер 1 ) | Cluster 2 (Кластер 2) | |||
1 | 5 | 12 | 8.508Е-03 | 0 | 0 | 9 |
2 | 10 | 17 | 2.880Е-02 | 0 | 0 | 4 |
3 | 2 | 3 | 4.273Е-02 | 0 | 0 | 13 |
4 | 8 | 10 | 6.432Е-02 | 0 | 2 | 7 |
5 | 7 | 13 | 8.040Е-02 | 0 | 0 | 8 |
6 | 1 | 15 | ,117 | 0 | 0 | 8 |
7 | 8 | 9 | ,206 | 4 | 0 | 14 |
8 | 1 | 7 | ,219 | 6 | 5 | 12 |
9 | 5 | 11 | ,233 | 1 | 0 | 11 |
10 | 14 | 16 | ,313 | 0 | 0 | 14 |
11 | 4 | 5 | ,487 | 0 | 9 | 16 |
12 | 1 | 6 | ,534 | 8 | 0 | 13 |
13 | 1 | 2 | ,820 | 12 | 3 | 15 |
14 | 8 | 14 | 1,205 | 7 | 70 | 15 |
15 | 1 | 8 | 4,017 | 13 | 14 | 16 |
16 | 1 | 4 | 6,753 | 15 | 11 | 0 |
Для определения, какое количество кластеров следовало бы считать оптимальным, решающее значение имеет показатель, выводимый под заголовком "коэффициент". По этим коэффициентом подразумевается расстояние между двумя кластерами, определенное на основании выбранной дистанционной меры с учётом предусмотренного преобразования значений. В нашем случае это квадрат евклидового расстояния, определенный с использованием стандартизованных значений. На этом этапе, где эта мера расстояния между двумя кластерами увеличивается скачкообразно, процесс объединения в новые кластеры необходимо остановить, так как в противном случае были бы объединены уже кластеры, находящиеся на относительно большом расстоянии друг от друга.
В приведенном примере — это скачок с 1,205 до 4,017. Это означает, что после образования трёх кластеров мы больше не должны производить никаких последующих объединений, а результат с тремя кластерами является оптимальным. Визуально же мы ожидали результат с четырьмя кластерами. Оптимальным считается число кластеров равное разности количества наблюдений (здесь: 17) и количества шагов, после которого коэффициент увеличивается скачкообразно (здесь: 14).
В пояснении нуждаются ещё и три последние колонки вышеприведенной таблицы, отражающей порядок агломерации; для этого в качестве примера мы рассмотрим строку, соответствующую 14 шагу. Здесь объединяются кластеры 8 и 14. Перед этим кластер 8 уже участвовал в объединениях на шагах 4 и 7, последний раз, стало быть, на шаге 7. Строго говоря, название колонки Stage Cluster First Appears (Шаг, на котором кластер появляется впервые) можно считать ошибочным и вместо этого её следовало назвать Cluster Last Appears (Последнее появление кластера). Кластер 14 последний раз участвовал в объединении кластеров на шаге 10. Новый кластер 8 затем примет участие в объединении кластеров на шаге 15 (колонка: Next Stage (Следующий шаг)).
Далее по отдельности для результатов расчёта содержащих 5, 4, 3 и 2 кластеров, приводится таблица с информацией о принадлежности каждого наблюдения к кластеру.
Cluster Membership (Принадлежность к кластеру)
Case (Случай) | 5 Clusters (5 кластеров) | 4 Clusters (4 кластера) | 3 Clusters (3 кластера) | 2 Clusters (2 кластера) |
1:Budweiser | 1 | 1 | 1 | 1 |
2:Lowenbrau | 2 | 1 | 1 | 1 |
3:Michelob | 2 | 1 | 1 | 1 |
4:Kronenbourg | 3 | 2 | 2 | 2 |
5:Heineken | 3 | 2 | 2 | 2 |
6:Schmidts | 1 | 1 | 1 | 1 |
7:Pabst Blue Ribbon | 1 | 1 | 1 | 1 |
8:Miller Light | 4 | 3 | 3 | 1 |
9:Budweiser Light | 4 | 3 | 3 | 1 |
10:Coors Light | 4 | 3 | 3 | 1 |
11:Dos Equis | 3 | 2 | 2 | 2 |
12:Becks | 3 | 2 | 2 | 2 |
13:Rolling Rock | 1 | 1 | 1 | 1 |
14:Pabst Extra Light | 5 | 4 | 3 | 1 |
15:Tuborg | 1 | 1 | 1 | 1 |
16:OlympiaGold Light | 5 | 4 | 3 | 1 |
17:Schlitz Light | 4 | 3 | 3 | 1 |
Таблица показывает, что два наблюдения 14 и 16 (Pabst Extra Light и Olympia Gold Light) при переходе к 3-х кластерному решению были включены в кластеры, соседствующие на диаграмме рассеяния; эти марки пива при оптимальном кластерном решении рассматриваются как принадлежащие к одному кластеру. Если посмотреть на 2-х кластерное решение, то оно группирует наблюдения 4, 5, 11 и 12 (Kronenbourg, Heineken, Dos Equis, Becks), то есть марки верхних правых кластеров диаграммы рассеяния; это марки иностранного производства.
В заключение приводится затребованная нами дендрограмма, которая визуализирует процесс слияния, приведенный в обзорной таблице порядка агломерации. Она идентифицирует объединённые кластеры и значения коэффициентов на каждом шаге. При этом отображаются не исходные значения коэффициентов, а значения приведенные к шкале от 0 до 25. Кластеры, получающиеся в результате слияния, отображаются горизонтальными пунктирными линиями.
******HIERARCHICAL CLUSTER ANALYSIS*** Dendrogram usinc ( Average Linkage (Between Groups) | |
Rescaled Distantce | Cluster Combine |
CASE | 0 5 10 15 20 25 |
Label | Hum +---- + ---- + ---- + _--_-- + ------ + |
Heineken | 5 |
Becks | 12 - - |
Dos Equis | 11--------------------------------- |
Krcnenbourg | 4 -- |
LcMBribrau | 2 ---- |
Michelcb | 3 - - |
Pabst Blue Ribbon | 7 ------------------------------ |
Rolling Rode | 13 -- - |
Budweiser | 4 --------------- |
Tuborg | 15 - - |
Schmdts | 6 ---------------------- |
Coors Light | 10 - |
Schlitz Light | 17 - |
Miller Light | 8 - - - - - |
Budweiser Light | 9 ------------------- |
Pabst Extra Light | 14 ------------------- |
Olynpia Gold Light | 16 - ------------------- |
В то время как дендрограмма годится только для графического представления процесса слияния, по диаграмме накопления можно проследить деление кластеров. Так как начиная с 7 версии SPSS графическое представление диаграммы накопления оставляет желать лучшего, мы отказались от активирования ее вывода.
Для вводного рассмотрения мы выбрали довольно простой пример, включающий только две переменных. В этом случае конфигурация кластеров поддается представлению в графическом виде.
7.gif

20.2.2 Иерархический кластерный анализ с более чем двумя переменными
20.2.2 Иерархический кластерный анализ с более чем двумя переменными
Рассмотрим пример из области кадровой политики некоего предприятия. 18 претендентов прошли 10 различных тестов в кадровом отделе предприятия. Максимальная оценка, которую можно было получить на каждом из тестов, составляет 10 балов. Список тестов был следующим:
№ теста | Предмет теста |
1 | Память на числа |
2 | Математические задачи |
3 | Находчивость при прямом диалоге |
4 | Тест на составление алгоритмов |
5 | Уверенность во время выступления |
6 | Командный дух |
7 | Находчивость |
8 | Сотрудничество |
9 | Признание в коллективе |
10 | Сила убеждения |
Результаты теста хранятся в файле assess.sav в переменных t1-t10. В файле находится также и текстовая переменная для характеристики тестируемых. С использованием результатов теста соответствия, мы хотим провести кластерный анализ, целью которого является обнаружение групп кандидатов, близких по своим качествам.
-
Откройте файл assess.sav.
-
Выберите в меню Analyze (Анализ) Classify (Классифицировать) Hierarchical Cluster... (Иерархический кластерный анализ)
-
В диалоговом окне Hierarchical Cluster Analysis (Иерархический кластерный анализ) переменные tl-tlO поместите в поле тестируемых переменных, а текстовую переменную name (имя) используйте для обозначения (маркировки) наблюдений.
-
Для начала должно быть достаточно вывода обзорной таблицы порядка агломерации; не делайте больше запроса на какие-либо данные и деактивируйте вывод диаграмм. Так как все переменные в этом примере имеют одинаковые пределы значений, стандартизация переменных является излишней.
Обзорная таблица порядка агломерации выглядит следующим образом:
Agglomeration Schedule
(Порядок агломерации) | ||||||
Stage (Шаг) | Cluster Combined (Объединение в кластеры) | Coefficients (Коэф-фициенты) | Stage Cluster First Appears (Шаг, на котором кластер появляется впервые) | Next Stage (Следую-щий шаг) | ||
Cluster 1 (Кластер 1) | Cluster 2 (Кластер 2) | Cluster 1 (Кластер 1) | Cluster 2 (Кластер 2) | |||
1 | 1 | 4 | ,000 | 0 | 0 | 6 |
1 | 14 | 18 | 2,000 | 0 | 0 | 4 |
3 | 12 | 15 | 2,000 | 0 | 0 | 6 |
4 | 9 | 14 | 2,000 | 0 | 2 | 8 |
5 | 2 | 10 | 2,000 | 0 | 0 | 13 |
6 | 1 | 12 | 3,000 | 1 | 3 | 15 |
7 | 13 | 16 | 4,000 | 0 | 0 | 12 |
8 | 9 | 11 | 4,000 | 4 | 0 | 11 |
9 | 5 | 7 | 5,000 | 0 | 0 | 14 |
10 | 6 | 17 | 6,000 | 0 | 0 | 13 |
11 | 3 | 9 | 6,000 | 0 | 8 | 15 |
12 | 8 | 13 | 7,000 | 0 | 7 | 14 |
13 | 2 | 6 | 7,500 | 5 | 10 | 16 |
14 | 5 | 8 | 12,833 | 9 | 12 | 16 |
15 | 1 | 3 | 194,000 | 6 | 11 | 17 |
16 | 2 | 5 | 198,500 | 13 | 14 | 17 |
17 | 1 | 2 | 219,407 | 15 | 16 | 0 |
Значительный скачок коэффициента наблюдается после 14-го шага; как указанно в разделе 20.1, это означает, что для данных, включающих 18 наблюдений, оптимальным является решение с четырьмя кластерами. Авторы в этом месте добавляют следующее: данный пример является искусственным, и из дидактических соображений мы предварительно скомпоновали данные таким образом, чтобы получился однозначный результат. После определения оптимального количества кластеров организуем для каждого наблюдения вывод информации о принадлежности к кластеру.
-
Для этого вновь откройте диалоговое окно Hierarchical Cluster Analysis (Иерархический кластерный анализ) и щёлкните по выключателю Statistics... (Статистики). В разделе Cluster Membership (Принадлежность к кластеру) активируйте опцию Single solution (Одно решение) и укажите желаемое количество кластеров 4.
Информацию о принадлежности каждого наблюдения к определённому кластеру вы можете сохранить в новой переменной.
-
Пройдите выключатель Save... (Сохранить), активируйте опцию Single solution (Одно решение) и для указания желаемого количества кластеров введите 4. Теперь помимо таблицы порядка агломерации для каждого наблюдения будет выводиться и информация о принадлежности к кластеру.
Из следующей таблицы видно, что в первый кластер входят четыре человека, во второй кластер — опять четыре человека, в третий кластер — пять человек и в четвёртый кластер — снова пять человек. Неясно ещё, что означают эти четыре кластера, то есть о чём говорят результаты 10 тестов, соответственно относящиеся к этим кластерам. Разобраться в значении кластеров нам помогут кластерные профили; они представляют собой средние значения переменных, которые включены в анализ, распределённые по кластерной принадлежности.
Cluster Membership (Принадлежность к кластеру)
Case (Случай) | 4 Clusters (4 кластера) |
1:VolkerR | 1 |
2:Sigrid К | 2 |
3:Elmar M | 3 |
4:Peter В | 1 |
5:Otto R | 4 |
6:Elke M | 2 |
7:Sarah К | 4 |
8:PeterT | 4 |
9:Gudrun M | 3 |
10:Siglinde P | 2 |
1 1 :Werner W | 3 |
12:Achim Z | 1 |
13:DieterK | 4 |
14:Boris P | 3 |
15:Silke W | 1 |
16:ClaraT | 4 |
17:Manfred К | 2 |
18:Richard M | 3 |
Если Вы рассмотрите данные в редакторе данных, то заметите, что добавилась переменная clu4_l; эта переменная указывает на кластерную принадлежность каждого наблюдения и может быть использована для расчёта кластерного профиля.
-
Выберите в меню Analyze (Анализ) Compare Means (Сравнить средние значения) Means... (Средние значения)
Переменным t1-t10 присвойте статус зависимых переменных, а переменной clu4_1 статус независимой переменной, и начните расчёт. В качестве результатов расчёта выводятся средние значения и стандартные отклонения итогов десяти тестов для четырёх кластеров. Для удобства поместим средние значения в отдельную таблицу.
Кластер 1 | Кластер 2 | Кластер 3 | Кластер 4 | |
Память на числа | 10,00 | 10,00 | 4,20 | 4,80 |
Математические задачи | 10,00 | 10,00 | 4,80 | 4,40 |
Находчивость при прямом диалоге | 9,00 | 4,25 | 10,00 | 4,00 |
Тест на составление алгоритмов | 10,00 | 10,00 | 4,40 | 4,00 |
Уверенность во время выступления | 10,00 | 4,75 | 10,00 | 4,20 |
Командный дух | 9,50 | 4,50 | 4,40 | 10,00 |
Находчивость | 9,25 | 3,75 | 10,00 | 4,40 |
Сотрудничество | 9,75 | 4,25 | 4,00 | 10,00 |
Признание в коллективе | 10,00 | 4,25 | 3,80 | 10,00 |
Сила убеждения | 9,50 | 4,25 | 10,00 | 5,00 |
Тестируемые, входящие в первый кластер имеют очень хорошие показатели во всех тестах. Это те конкурсанты, которые наверняка прошли бы на завершающий отборочный тур. Во второй кластер включены те, кто имеет хорошие показатели по математическим тестам (память на числа, математические задачи, тест на составление алгоритмов), но со слабыми оценками в социальной компетентности и уверенности при выступлениях. В третий кластер вошли те, кто уверенно себя чувствует во время выступления, но имеют слабые показатели в математических тестах и социальной компетентности. В конце концов, в четвёртом кластере, собраны люди с высоким уровнем социальной компетентности, но со слабыми результатами в тестах на решение математических задач и на силу убеждения.
В примерах, подобных этому, перед проведением кластерного анализа рекомендуется сократить количество переменных. Подходящим методом для этого является факторный анализ (см. гл. 19), который большое количество переменных заменяет меньшим количеством факторов. Продемонстрируем данный процесс на следующем примере.
20.2.3 Иерархический кластерный анализ с предварительным факторным анализом
20.2.3 Иерархический кластерный анализ с предварительным факторным анализом
Рассмотрим пример из области географии. В 28 европейских странах в 1985 году были собраны следующие данные, выступающие здесь в качестве переменных:
Переменная | Значение |
land | Страна |
sb | Процент городского населения |
lem | Средняя продолжительность жизни мужчин |
lew | |
ks | Детская смертность на 1000 новорожденных |
so | Количество часов ясной погоды в году |
nt | Количество дней пасмурной погоды в году |
tjan | Средняя дневная температура в январе |
tjul | Средняя дневная температура в июле |
Эти данные вы увидите, если откроете файл europa.sav. Переменная land является текстовой переменной, предназначенной для обозначения страны.
Целью нашего кластерного анализа является нахождение стран с похожими свойствами. При самом общем рассмотрении переменных (от непосредственного указания стран мы здесь воздержимся) становится заметным, что данные, содержащиеся в файле связаны исключительно с ожидаемой продолжительностью жизни или с климатом. Лишь процентный показатель населения, проживающего в городах, не вписывается в эти рамки. Стало быть, сходства, которые возможно будут найдены между некоторыми странами, основываются на продолжительности жизни и климате этих стран.
Исходя из вышесказанного, в данном случае перед проведением кластерного анализа рекомендуется сократить количество переменных. Подходящим методом для этого является факторный анализ (см. гл. 19), который вы можете провести, выбрав в меню Analyze (Анализ) Data Reduction (Преобразование данных) Factor... (Факторный анализ)
Если Вы проведёте факторный анализ и примените, к примеру, вращение по методу варимакса, то получите два фактора. В первый фактор войдут переменные: lem. lew, ks и sb, а во второй фактор - переменные: so, nt, tjan и tjul. Первый фактор однозначно характеризует продолжительность жизни, причём высокое значение фактора означает высокую продолжительность жизни, а второй отражает климатические условия; здесь высокие значения означают тёплый и сухой климат. Вместе с тем, Вы наверняка заметили, что в первый фактор интегрирована и переменная sb, что очевидно указывает на высокую ожидаемую продолжительность жизни при высоких процентных долях городского населения. Вы можете рассчитать факторные значения для этих двух факторов и добавить их к файлу под именами fac1_1 и fac2_1. Чтобы Вам не пришлось самостоятельно проводить факторный анализ на этом этапе, указанные переменные уже включены в файл europa.sav. Вы можете видеть, к примеру, что высокой продолжительностью жизни обладают северные страны (высокие значения переменной fac1_1) или южные страны с тёплым и сухим климатом (высокие значения переменной fac2_1). Факторные значения можно вывести с помощью меню Analyze (Анализ) Reports (Отчёты) Case Summaries... (Итоги по наблюдениям)
Они выглядят следующим образом:
Case Summaries a (Итоги по наблюдениям)
LAND (Страна) | Lebenserwartung (Ожидаемая продолжительность жизни) | Klima (Климат) | |
1 | ALBA | -1,78349 | ,57155 |
2 | BELG | ,55235 | -,57937 |
3 | BULG | -,43016 | -,13263 |
4 | DAEN | ,97206 | -,23453 |
5 | DDR | ,26961 | -,3351 1 |
6 | DEUT | ,19121 | -,44413 |
7 | FINN | -,30226 | -1,28467 |
8 | FRAN | 1,05511 | 1,04870 |
9 | GRIE | ,12794 | 2,65654 |
10 | GROS | ,75443 | -,05221 |
11 | IRLA | ,16370 | -,66514 |
12 | ISLA | 1,75315 | -,97421 |
13 | ITAL | ,40984 | 1,68933 |
14 | JUGO | -2,63161 | -,44127 |
15 | LUXE | -.16469 | -,98618 |
16 | NIED | 1,31001 | -,29362 |
17 | NORW | ,96317 | -,46987 |
18 | OEST | -,20396 | -,31971 |
19 | POLE | -,65937 | -,92081 |
20 | PORT | -1,10510 | 1,59478 |
21 | RUMA | -1,32450 | ,09481 |
22 | SCHD | 1,22645 | -,20543 |
23 | SCHZ | , 56289 | -,45454 |
24 | SOWJ | -,67091 | -1,32517 |
25 | SPAN | , 83627 | 1,91193 |
26 | TSCH | -,59407 | -,40632 |
27 | TUER | -,52049 | 1,04424 |
28 | UNGA | -,75761 | -,08695 |
Total N | 28 | 28 | 28 |
a. Limited to first 100 cases (Ограничено первыми 100 наблюдениями).
Распределим эти 28 стран по кластерам при помощи двух факторов: ожидаемая продолжительность жизни и климат.
-
Выберите в меню Analyze (Анализ) Classify (Классифицировать) Hierarchical Cluster... (Иерархический кластерный анализ)
-
Переменные fac1_1 и fac2_1 поместите в поле тестируемых переменных, а переменную land (страна) — в поле с именем Label cases by: (Наименование (маркировка) наблюдений).
-
После прохождения выключателя Statistics... (Статистики), наряду с таблицей порядка агломерации сделайте запрос на вывод информации о принадлежности к кластеру для наблюдений. Активируйте Range of solutions: (Область решений) и введите граничные значения 2 и 5.
-
Для сохранения информации о принадлежности отдельных наблюдений к кластеру в виде дополнительных переменных, воспользуйтесь выключателем Save... (Сохранить). В соответствии с установками, произведенными в диалоговом окне статистики, активируйте и здесь Range of solutions: (Область решений) и введите граничные значения 2 и 5.
-
Деактивируйте вывод дендрограмм. Так как переменные, используемые в данном кластерном анализе, являются факторными значениями с одинаковыми областями допустимых значений, то стандартизация (z-преобразование) значений является излишней.
Agglomeration Schedule
(Порядок агломерации) | ||||||
Stage (Шаг) | Cluster Combined (Объединение в кластеры) | Coefficients (Коэф-фициенты) | Stage Cluster First Appears (Шаг, на котором кластер появляется впервые) | Next Stage (Следу-ющий шаг) | ||
Cluster 1 (Кластер 1) | Cluster 2 (Кластер 2) | Cluster 1 (Кластер 1) | Cluster 2 (Кластер 2) | |||
1 | 16 | 22 | 1,476 | 0 | 0 | 8 |
2 | 2 | 23 | 1,569 | 0 | 0 | 10 |
3 | 5 | 6 | 1,803 | 0 | 0 | 5 |
4 | 4 | 17 | 5,546 | 0 | 0 | 8 |
5 | 5 | 11 | 8,487 | 3 | 0 | 10 |
6 | 3 | 18 | 8,617 | 0 | 0 | 12 |
7 | 7 | 15 | ,108 | 0 | 0 | 15 |
8 | 4 | 16 | ,118 | 4 | 1 | 13 |
9 | 26 | 28 | ,129 | 0 | 0 | 12 |
10 | 2 | 5 | ,148 | 2 | 5 | 18 |
11 | 19 | 24 | ,164 | 0 | 0 | 15 |
12 | 3 | 26 | ,183 | 6 | 9 | 20 |
13 | 4 | 10 | ,228 | 8 | 0 | 18 |
14 | 13 | 25 | ,231 | 0 | 0 | 19 |
15 | 7 | 19 | ,254 | 7 | 11 | 20 |
16 | 1 | 21 | ,438 | 0 | 0 | 22 |
17 | 20 | 27 | ,645 | 0 | 0 | 22 |
18 | 2 | 4 | ,648 | 10 | 13 | 21 |
19 | 8 | 13 | ,810 | 0 | 14 | 23 |
20 | 3 | 7 | ,939 | 12 | 15 | 24 |
21 | 2 | 12 | 1,665 | 18 | 0 | 24 |
22 | 1 | 20 | 1,793 | 16 | 17 | 25 |
23 | 8 | 9 | 1,839 | 19 | 0 | 27 |
24 | 2 | 3 | 2,229 | 21 | 20 | 26 |
25 | 1 | 14 | 4,220 | 22 | 0 | 26 |
26 | 1 | 2 | 5,925 | 25 | 24 | 27 |
27 | 1 | 8 | 6,957 | 26 | 23 | 0 |
Сначала приводятся самые важные результаты. В таблице порядка агломерации Вы можете проследить последовательность образования кластеров; объяснения по этому поводу приводились в разделе 20.1. Скачкообразное изменение коэффициентов наблюдается при значениях 2,229 и 4,220; это означает, что после образования четырёх кластеров больше не должно происходит ни каких объединений и решение с четырьмя кластерами является оптимальным.
Принадлежность наблюдений к кластерам можно взять из нижеследующей таблицы, которая содержит также и информацию о принадлежности к кластерам для других вариантов решения (пять, три и два кластера).
Если Вы посмотрите на четырёхкластернное решение на нижеследующей таблице, то заметите, к примеру, что к третьему кластеру относятся следующие страны: Франция, Греция, Италия и Испания. Это страны с высокой продолжительностью жизни и тёплым климатом и поэтому не зря они являются предпочтительными для отдыха.
Cluster Membership (Принадлежность к кластеру)
Case (Случай) | 5 Clusters (5 кластеров) | 4 Clusters (4 кластера) | 3 Clusters (3 кластера) | 2 Clusters (2 кластера) |
1:ALBA | 1 | 1 | 1 | 1 |
2:BELG | 2 | 2 | 2 | 1 |
3:BULG | 3 | 2 | 2 | 1 |
4:DAEN 5:DEUT | 2 | 2 | 2 | 1 |
6:DDR | 2 | 2 | 2 | 1 |
7:FINN | 3 | 2 | -3 | 2 |
8:FRAN | 4 | 3 | -3 | 2 |
9:GRIE | 4 | 2 | 2 | 1 |
10:iGROS | 2 | 2 | 1 | |
11:IRLA | 2 | 2 | 2 | 1 |
12:ISLA | 2 | 3 | о | 2 |
13:ITAL | 4 | 4 | 1 | 1 |
14:JUGO | 5 | 2 | 2 | 1 |
1 5:LUXE | 3 | 2 | 2 | 1 |
16:NIED | 2 | 2 | 1 | |
17:NORW | 2 | 2 | 2 | 1 |
18:OEST | 3 | 2 | 2 | 1 |
19:POLE | 3 | 2 1 | 1 | 1 |
20:PORT | 1 | 1 | 1 | 1 |
21:RUMA | 1 | 2 | 1 | |
22:SCHD 23:SCHZ | 2 | 2 | 2 | 1 |
24:SOWJ | 3 | 1 | i | 2 |
!25:SPAN | 4 | 1 | ||
26:TSCH | 3 | 1 | 1 | 1 |
27:TUER 28:UNGA | 1 | 2 | 1 | 1 |
20.3 Меры расстояния и меры сходства
20.3 Меры расстояния и меры сходства
Основой кластеризации (образования групп) наблюдений является дистанционная матрица и матрица подобия наблюдений. Так как расстояние (дистанция) также применяется и для оценки подобия, то разница между этими двумя матрицами не велика. В зависимости от того, к какой шкале измерений относятся переменные, участвующие в анализе, SPSS предлагает различные дистанционные меры и меры подобия.
20.3.1 Переменные, относящиеся к интервальной шкале (метрические переменные)
20.3.1 Переменные, относящиеся к интервальной шкале (метрические переменные)
Для переменных такого рода на выбор предлагается восемь различных мер расстояния и мер сходства, которые мы и рассмотрим далее. Примером расчёта послужат два наблюдения из файла assess.sav (см. гл. 20.3), для которых расстояние и подобие должны быть рассчитаны с использованием переменных t3 и t4:
t3 | t4 | |
Отто P. | 5 | 4 |
Эльке М. | 4 | 10 |
Евклидова дистанция (расстояние)
Евклидова дистанция между двумя точками х и у — это наименьшее расстояние между ними. В двух- или трёхмерном случае — это прямая, соединяющая данные точки. Общей формулой для n-мерного случая (л переменных) является: 1
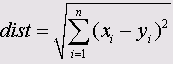
Сокращение dist, как и в следующей формуле, соответствует слову дистанция. Для ! приведенного примера получим
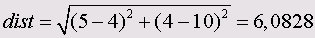
Квадрат евклидового расстояния
Этот вариант устанавливается по умолчанию. Благодаря возведению в квадрат при расчёте лучше учитываются большие разности. Эта мера должна всегда использоваться при построении кластеров при помощи центроидного и медианного методов, а также метода Варда (Ward-Method) (см. разд. 20.5).
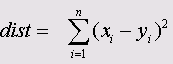
Для приведенного примера имеем cfot=(5-4)2 + (4-10)2 =37
Косинус
Как и для корреляционных коэффициентов Пирсона, область значений этой меры находится между -1 и +1.
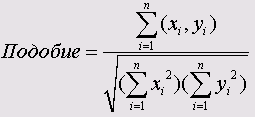
Для приведенного примера имеем
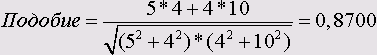
Корреляция Пирсона
Если кластеризация наблюдений осуществляется только на основании двух переменных, то корреляционный коэффициент Пирсона (см. разд. 15.1) со значениями находящимися в пределах от -1 до +1 не годится для использования в качестве меры подобия; он будет давать только значения -1 или +1.
Чебышев (Chebychev)
Разностью двух наблюдений является абсолютное значение максимальной разности последовательных пар переменных, соответствующих этим наблюдениям.
В приведенном примере абсолютная разность значений первой переменной равна 1, а второй переменной — 6. Поэтому разность Чебышева равна 6.
Блок (Block)
Эта дистанционная мера, называемая также дистанцией Манхэттена или в шутку — дистанцией таксиста, определяется суммой абсолютных разностей пар значений. Для двумерного пространства это не прямолинейное евклидова расстояние между двумя точками, а путь, который должен преодолеть Манхэттенский таксист, чтобы проехать от одного дома к другому по улицам, пересекающимся под прямым углом.
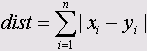
Для нашего примера имеем dfst = |5-4| + |4-10| = 7
Минковский (Minkowski)
Расстояние Минковского равно корню r-ой степени из суммы абсолютных разностей пар значений взятых в r-ой степени:
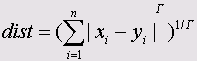
В SPSS при расчете этого расстояния допускается применение только квадратного корня, в то время как степень разности значений можно выбрать в пределах от 1 до 4. Если эту степень взять равной 2, то получим евклидово расстояние.
Пользовательская мера
Это обобщенный вариант расстояния Минковского. Это расстояние, называемое также степенным расстоянием, равно корню r-ой степени из суммы абсолютных разностей пар значений взятой в р-ой степени:

Здесь как для корня, так и для степени суммы можно выбирать значения от 1 до 4.
8.gif
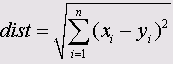
10.gif
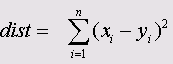
11.gif
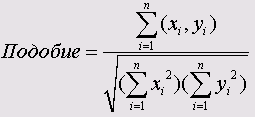
12.gif
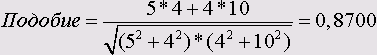
13.gif
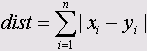
14.gif
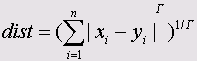
15.gif

20.3.2 Частоты
20.3.2 Частоты
В качестве примера возьмём файл laender.sav, в котором значения переменных отображают частоты. В файле находится текстовая переменная land (федеральная земля) и три переменные cdu, spd и andere (другие). Для шестнадцати земель Федеративной Республики Германия в 1994 году эти переменные отображают количество мест в земельном парламенте, принадлежащих двум основным партиям — CDU и SPD, а также места, относящиеся к другим партиям.
-
Откройте файл laender.sav.
-
На основании трёх переменных cdu, spd и andere проведите иерархический кластерный анализ, текстовую переменную land примените для обозначения наблюдений.
-
Через выключатель Method... (Метод) активируйте опцию Counts (Частоты). У Вас появится возможность выбора между двумя дистанционными мерами.
Мера хи-квадрат
Для того, чтобы найти расстояние между двумя наблюдениями, сравнивают частоты выпадения переменных, относящихся к этим наблюдениям. В качестве примера рассмотрим две федеративные земли: Хессен и Тюринген:
CDU | SPD | Andere (Другие) | |
Хессен | 46 | 46 | 18 |
| Тюринген | 43 | 21 | 25 |
Для такой таблицы долей присутствия разных партий подходит статистика хи-квадрат (см. разд. 11.3.1). Квадратный корень из значения хи-квадрат будет применяться в качестве дистанционной меры.
В приведенном примере значение хи-квадрат получилось равным 8,447 значит дистанционная мера равна 2,9064.
Мера фи-квадрат
Эта мера представляет собой попытку нормализации меры хи-квадрат. Для этого она делится на квадратный корень общей суммы частот.
В рассматриваемом примере сумма частот для двух земель Хессен и Тюринген равна 199, так что мера фи-квадрат получается равной 0,2060.
Если Вы в качестве дистанционной меры выберите меру хи-квадрат, то получите результат, в котором оптимальным решением окажется решение с пятью кластерами. Два самых больших кластера образовываются землями, в которых CDU или SPD имеют большинство мест, один кластер — землями Бранденбург и Бремен, в управлении которых относительно велико представительство других партий, один кластер образует Бавария, в связи с абсолютно доминирующей ролью CDU и один кластер — Саксония, тоже в связи с доминирующей ролью CDU, но с некоторой долей других партий, которая больше доли SPD.
20.3.3 Бинарные переменные
20.3.3 Бинарные переменные
Здесь, как правило, речь идёт о переменных, которые указывают на факт осуществления некоторого события или выполнения определённого критерия. В файле данных это обстоятельство должно быть закодировано при помощи двух численных значений, причём в соответствии с установками по умолчанию, SPSS для кодировки осуществления события ожидает цифру 1.
Если сопоставить друг с другом две переменные, то все возможные сочетания наблюдений дают четыре различные частоты, которые называются а, Ь, с, d и имеют следующий смысл:
| Переменная 2 | |||
| сбылось | не сбылось | ||
Переменная 1 | Сбылось | а | b |
| Не сбылось | с | d | |
На основании этих частот, можно рассчитать множество различных дистанционных мер, 27 из которых применяются в SPSS. Двадцать разновидностей мер, называемых мерами подобия, рассмотрены в разделе 15.4. Остальные приводятся ниже.
Квадрат евклидовою расстояния
Бинарное евклидово расстояние, возведенное в квадрат, представляет собой количество наблюдений, для которых, по крайней мере, один из критериев присутствует и один отсутствует. Эта мера является установкой по умолчанию.
dist= b + с
Евклидово расстояние
Бинарное евклидово расстояние представляет собой корень из числа наблюдений, для которых, по крайней мере, один из критериев присутствует и один отсутствует.
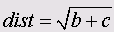
Разность длин
Эта мера имеет минимальное значение равное 0 и не имеет верхнего придела.

Образцовая разность
Образцовая разность может принимать значения от 0 до 1.
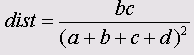
Дисперсия
Дисперсия имеет минимальное значение равное 0 и не имеет верхнего придела.

Форма
У этой дистанционной меры нет ни нижнего ни верхнего предела
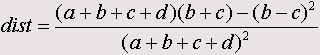
Мера Ланса и Уильямса (Lance and Williams)
Эта мера может принимать значения от 0 до 1.

Приведенные меры отличаются друг от друга присутствием в соответствующей формуле различных наборов из четырёх частот: а, b, с и d
Так, для евклидовой меры в расчёт включают только те наблюдения, для которых имеется один признак и отсутствует другой, а в других дистанционных формулах учитываются все частоты. Исключением является дистанционная мера по Лансу и Уильямсу, в которой в расчет не берутся те наблюдения, для которых отсутствуют оба признака.
На какой мере Вы остановите свой выбор, зависит от того, какую роль вы отводите частотам а, b, с и d.
17.gif

18.gif
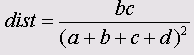
19.gif

20.gif
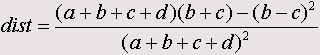
20.4 Методы объединения
20.4 Методы объединения
SPSS предлагает, в общей сложности, семь методов объединения. Из них метод Связь между группами (Between-groups linkage) устанавливается по умолчанию.
Связь между группами
Дистанция между кластерами равна среднему значению дистанций между всеми возможными парами наблюдений, причём один наблюдения берётся из одного кластера, а другой из другого. Информация, необходимая для расчёта дистанции, находится на основании всех теоретически возможных пар наблюдений. По этой причине данный метод и устанавливается по умолчанию.
Связь внутри групп
Это вариант связи между группами, а именно, здесь дистанция между двумя кластерами рассчитывается на основании всех возможных пар наблюдений, принадлежащих обоим кластеров, причём учитываются также и пары наблюдений, образующиеся внутри кластеров.
Близлежащий сосед
Дистанция между двумя кластерами определяется, как расстояние между парой значений наблюдений, расположенных друг к другу ближе всего, причём каждое наблюдение берётся из своего кластера.
Дальний сосед
Дистанция между двумя кластерами определяется как расстояние между самыми удалёнными друг от друга значениями наблюдений, причём каждое наблюдение берётся из своего кластера.
Центроидная кластеризация
В обоих кластерах рассчитываются средние значения переменных относящихся к ним наблюдений. Затем расстояние между двумя кластерами рассчитывается как дистанция между двумя осредненными наблюдениями.
Медианная кластеризация
Этот метод похож на центроидную кластеризацию. Однако в предидущем методе центроид нового кластера получается как взвешенное среднее центроидов обоих исходных кластеров, причём количества наблюдений исходных кластеров образовывают весовой коэффициент. В медианном же методе оба исходных кластера берутся с одинаковым весом.
Метод Варда (Ward-Method)
Сначала в обоих кластерах для всех имеющихся наблюдений производится расчёт средних значений отдельных переменных. Затем вычисляются квадраты евклидовых расстояний от отдельных наблюдений каждого кластера до этого кластерного среднего значения. Эти дистанции суммируются. Потом в один новый кластер объединяются те кластера, при объединении которых получается наименьший прирост общей суммы дистанций. Так как некоторые из предлагаемых методов имеют явные недостатки (Близлежащий сосед, Дальний сосед), а другие очень мало наглядны и плохо поддаются последующему анализу, рекомендуется применять устанавливаемый по умолчанию и наиболее понятный метод Between-groups linkage (Связь между группами).
20.5 Кластерный анализ при большом количестве наблюдений (Кластерный анализ методом к-средних)
20.5 Кластерный анализ при большом количестве наблюдений (Кластерный анализ методом к-средних)
Иерархические методы объединения, хотя и точны, но трудоёмки: на каждом шаге необходимо выстраивать дистанционную матрицу для всех текущих кластеров. Расчётное время растёт пропорционально третьей степени количества наблюдений, что при наличии нескольких тысяч наблюдений может утомить и серьёзные вычислительные машины.
Поэтому при наличии большого количества наблюдений применяют другие методы. Недостаток этих методов заключается в том, что здесь необходимо заранее задавать количество кластеров, а не так как в иерархическом анализе, получить это в качестве результата Эту проблему можно преодолеть проведением иерархического анализа со случайно отобранной выборкой наблюдений и, таким образом, определить оптимальное количество кластеров. Если количество кластеров указать предварительно, то появляется следующая проблема: определение начальных значений центров кластеров. Их также можно взять из предварительно проведённого иерархического анализа, в котором для каждого наблюдения рассчитывают средние значения переменных, использовавшихся при анализе, а потом в определённой форме сохраняют их в некотором файле. Этот файл может быть затем прочитан методом, который применяется для обработки больших количеств наблюдений. Если нет желания проходить весь этот длинный путь, то можно воспользоваться методом, предлагаемым для данного наблюдения программой SPSS. Если количество кластеров k, которое необходимо получить в результате объединения, задано заранее, то первые k наблюдений, содержащихся в файле, используются как первые кластеры. На последующих шагах кластерный центр заменяется наблюдением, если наименьшее расстояние от него до кластерного центра больше расстояния между двумя ближайшими кластерами. По этому правилу заменяется тот кластерный центр, который находится ближе всего к данному наблюдению. Таким образом получается новый набор исходных кластерных центров. Для завершения шага процедуры рассчитывается новое положение центров кластеров, а наблюдения перераспределяются между кластерами с изменённым центрами. Этот итерационный процесс продолжается до тех пор, пока кластерные центры не перестанут изменять свое положение или пока не будет достигнуто максимальное число итераций.
В качестве примера расчёта по этому алгоритму, рассмотрим выборку из результатов исследований Института социологии Марбургского Университета им. Филипса, в котором проводился опрос 1000 студентов относительно использования ими компьютера и их отношения к современным информационным и телекоммуникационным технологиям. В разделе "Пользование компьютерными программами" были представлены следующие вопросы с различным количеством подпунктов, на которые необходимо было ответить в соответствии с пятибальной шкалой (от отлично до абсолютно не использую):
1. Насколько свободно вы можете работать в следующих приложениях?
Обработка текста, Графические программы, обработка звука или видео, монтаж Базы данных и табличные расчёты
2. Насколько хорошо вы владеете следующими языками программирования?
BASIC, Paskal ,С, Машинные языки, Программирование для Интернета(к примеру, HTML), Java
3. Насколько хорошо Вы можете работать в следующих операционных системах?
DOS , Windows ,UNIX
4. Насколько хорошо Вы разбираетесь в следующих возможностях Интернета?
E-mail, группы новостей, почтовая рассылка, Путешествие по всемирной сети Интернет, Chat, IRC, ICQ, Предложение собственных услуг(к примеру, домашней страницы)
5. Насколько хорошо Вы разбираетесь в играх?
Как часто Вы играете в компьютерные игры, Насколько хорошо Вы ориентируетесь в сценах компьютерных игр?
Ответы на эти вопросы хранятся в переменных vla-v5b в файле computer.sav. В этом файле также находятся и другие переменные, использовавшиеся при исследовании (пол, возраст, место жительства, профессия). На основании вопросов об использовании программных продуктов попытаемся определить группы (кластеры) пользователей. Для начала рекомендуется сократить количество переменных при помощи факторного анализа, как описано в разделе 20.2.3.
-
Откройте файл computer.sav
-
Выберите в меню Analyze (Анализ) Data Reduction (Преобразование данных) Factor... (Факторный анализ)
-
Переменные vla-v5b внесите в список целевых переменных.
-
Через выключатель Extraction... (Отбор) деактивируйте вывод неповёрнутого факторного решения.
-
Через выключатель Rotation... (Вращение) для осуществления вращения активируйте метод варимакса.
-
Минуя выключатель Options... (Опции) в разделе Coefficient Display Format (Формат отображения коэффициентов) (подразумеваются факторные нагрузки) активируйте Sorted by Size (Отсортированные по размеру). Затем активируйте опцию Suppress absolute values less then: (He выводить абсолютные значения меньше чем:) и введите значение ,40.
-
В заключение щёлкните по выключателю Scores... (Значения), чтобы значения факторов сохранить в виде новых переменных.
В результате расчёта было отобрано четыре фактора и добавлено в файл четыре переменные от (fac1_1 до fac4_1), которые и отображают эти четыре фактора. Среди результатов присутствует повёрнутая факторная матрица (см. следующую таблицу).
Факторная матрица красноречиво демонстрирует, что отобранные факторы могут быть расположены в следующей смысловой последовательности (по убыванию значимости):
-
Приложение
-
Программирование
-
Использование Интернета
-
Игры
Rotated Component Matrix
(Повёрнутая матрица компонентов) | ||||
Component (Компонент) | ||||
1 | 2 | 3 | 4 | |
Textverarbeitung (Обработка текста) | ,848 | |||
Windows | ,840 | |||
DOS | ,653 | |||
WWW | ,619 | |||
Datenbanken (Базы данных и табличные расчёты) | ,611 | |||
Multimedia (Мультимедиа) | ,535 | |||
С | ,771 | |||
Maschinensprache (Машинные языки) | ,741 | |||
PASCAL | ,729 | |||
BASIC | ,612 | |||
Java | ,606 | ,474 | ||
UNIX | ,587 | ,504 | ||
Chat | ,699 | |||
eigene Dienste (Предложение собственных услуг ) | ,696 | |||
Internetsprachen (Программирование для Интернет) | ,468 | ,670 | ||
,584 | ,609 | |||
ICQ | ,601 | |||
Szene (Сцены компьютерных игр) | ,881 | |||
Intensitaet (Интенсивность) | ,850 | |||
Extraction Method: Principal Component Analysis (Метод отбора: Анализ главных компонентов).
Rotation Method: Varimax with Kaiser Normalization (Метод вращения: варимакс с нормализацией Кайзера).
a. Rotation converged in 11 iterations (Вращение осуществлено за 11 итераций).
Теперь используем сохранённые нами значения этих четырёх факторов для проведения кластерного анализа для студентов. Так как количество наблюдений равное 1085 слишком велико для иерархического кластерного анализа, выберем метод анализа кластерных центров.
-
Присвойте переменным fac1_1-fac4_1 метки: "Приложения", "Программирование", "Использование Интернет" и "Игры" соответственно.
-
Выберите в меню Analyze (Анализ) Classify (Классифицировать) K-Means Cluster... (Кластерный анализ методом к-средних)
Откроется диалоговое окно K-Means Cluster Analysis (Кластерный анализ методом к-средних).
Рис. 20.4: Диалоговое окно K-Means Cluster Analysis (Анализ кластерных центров)
-
Переменные от fac1_1 до fac4_1 поместите в поле тестируемых переменных. Теперь Вы подошли к тому месту, где нужно указывать количество кластеров. Подходящим вариантом было бы сперва провести иерархический кластерный анализ для произвольно выбранных наблюдений и получившееся количество кластеров принять за оптимальное. Вы, конечно же, можете провести и несколько опытных, пробных расчётов с различным количеством кластеров и после этого определиться с подходящим вариантом решения.
-
Мы остановимся на четырёх кластерах; введите это значение в поле Number of Clusters (Количество кластеров).
-
Через выключатель Iterate... (Итерации) укажите число итераций равное 99; установленное по умолчанию количество итераций равное 10, оказалось бы недостаточным.
-
Щёлкните по выключателю Save... (Сохранить), чтобы при помощи дополнительных переменных зафиксировать принадлежность наблюдений к кластеру.
-
Щёлкните на ОК, чтобы начать расчёт.
Сначала приводятся первичные кластерные центры и обобщённые данные итерационного процесса (30 итераций); затем выводятся окончательные кластерные центры и информация о количестве наблюдений.
Final Cluster Centers
(Кластерные центры окончательного решения) | ||||
Cluster (Кластер) | ||||
1 | 2 | 3 | 4 | |
Приложение | -,15219 | -,62362 | -,23459 | 1,16856 |
Программирование | -2,91321 | ,232223 | ,23371 | ,05918 |
Использование Интернет | -1,71057 | ,7232 | -.02994 | ,25268 |
Игры | ,04717 | ,51053 | -1,51014 | ,26081 |
При оценке кластерных центров следует в первую очередь обратить внимание на то, что здесь речь идёт о средних значениях факторов, которые находятся в пределах примерно от -3 до +3. К тому же, надо помнить, что в соответствии с кодировкой ответов (1 = отлично, 5 = абсолютно не использую) большое отрицательное значение фактора означает его большую степень его проявления, то есть сигнализирует о высокой компетентности, и наоборот, большое положительное значение фактора подразумевает низкую степень его проявления.
Если учесть всё вышесказанное, то наши четыре кластера можно интерпретировать следующим образом:
Кластер1: Программисты, Интернет-эксперты
Кластер2: Пользователи стандартного программного обеспечения
КластерЗ: Игроки
Кластер4: Начинающие пользователи
В заключение выводятся показатели количества наблюдений, относящихся к каждому из кластеров. Группа пользователей (кластер 2) наиболее многочисленна.
Number of Cases in each Cluster
(Количество наблюдений в каждом кластере) | ||
Cluster (Кластер) | 1 | 63,000 |
2 | 488,000 | |
3 | 221,000 | |
4 | 313,000 | |
Valid (Действительные) | 1085,000 | |
Missing (Отсутствующие) | ,000 | |
К исходному файлу была добавлена переменная qc1_1, отражающая принадлежность к определённому кластеру. Эту переменную можно использовать для обнаружения возможных связей между кластерной принадлежностью и полом, возрастом, профессией и происхождением (западные земли Германии, восточные земли Германии, зарубежные страны).
Наряду с количеством кластеров можно так же, как было упомянуто в начале главы, задать и первичные кластерные центры. Для этого их необходимо определённым образом ввести в файл данных SPSS. Изучим процесс создания такого файла на рассмотренном примере,
-
После щёлка в диалоговом окне K-Means Cluster Analysis (Кластерный анализ методом k-средних) по выключателю Centers» (Центры), диалоговое окно примет расширенный вид (см. рис. 20.5).
-
Активируйте Read initial from (Читать первичные значения из) и щёлкните на выключателе File... (Файл). Откроется диалоговое окно K-Means Cluster Analysis: Read initial from (Кластерный анализ методом К-средних: Читать первичные значения из).
-
Откройте файл zentren.sav.
Файл содержит
-
количественную переменную с именем cluster_
-
одну строку для каждого кластера
-
первичные значения для каждой кластерной переменной.
То, как выглядит этот файл в редакторе данных, Вы можете увидеть на рисунке 20.6. Аналогично тому, как Вы смогли считать из файла первичные кластерные центры, при помощи выключателя Write final as (Сохранить окончательные результаты как), Вы можете сохранить окончательные кластерные центры в отдельном файле для дальнейших расчётов.
Рис. 20.5: Диалоговое окно K-Means Cluster Analysis (Анализ кластерных центров)
Рис. 20.6: Файл с первичными кластерными центрами
Мы надеемся, что при помощи приведенных примеров нам удалось пробудить у Вас интерес к кластерному анализу и облегчить понимание интереснейших статистических методов.
22.gif
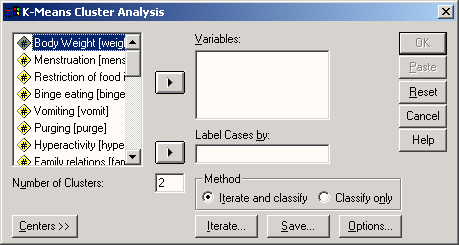
23.gif

24.gif
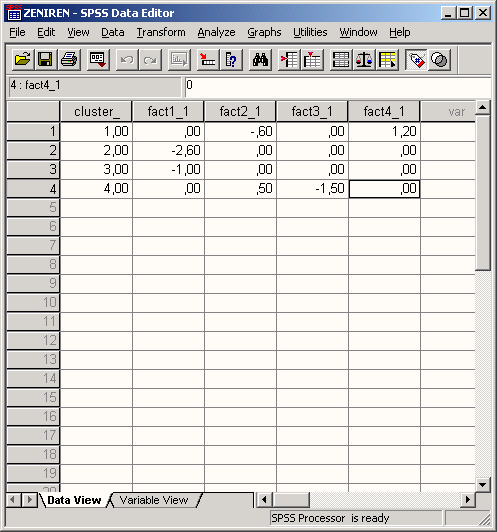
Глава 21. Анализ пригодности
Глава 21. Анализ пригодности
1. Анализ пригодности
Анализ пригодности
Анализ пригодности (а также: анализ вопросов или анализ заданий) помогает подбирать вопросы (задания) для тестов. При помощи разнообразных критериев а результате такого такой анализа устанавливается, какие задания подходят для определённого теста, а какие нет.
Для этой цели некоторой совокупности (выборке) респондентов предлагают предварительный вариант теста со всеми предполагаемыми заданиями и проводят анализ этих заданий. При помощи этого анализа исключают неподходящие задания, а оставшиеся включают в итоговую форму теста. Тест составленный таким образом должен рассматриваться не как статистический проверочный метод (к примеру, t-тест или U-тест), а как метод исследования личностных признаков.
Более подробную информацию о построении и анализе тестов Вы сможете найти в книге Линерта (Lienert) (см. список литературы). Линерт подразделяет тесты в зависимости от вида исследуемого личностного признака, а именно выделяются тест уровня образованности, тест способностей и личностный тест. Тестовое задание состоит преимущественно из двух частей: проблемы или вопроса и варианта решения проблемы или ответа.
Следует понимать разницу между заданиями, для которых считается правильным только один ответ, а другие — неправильными, и заданиями со ступенчатым ответом. Примерами пунктов, построенными по принципу верно — не верно могут служить следующие пункты:
-
Покупаете ли вы дорогую одежду (да — нет)?
-
Является ли кит представителем семейства млекопитающих (верно — неверно)? Возможны также и задания с множественными ответами:
-
Кем по национальности был Альфред Нобель (немец — швейцарец — швед — австриец — датчанин)?
Задания со ступенчатым вариантом ответа построены иначе. Исследуемый личностный признак оценивается не при помощи ответа верно — не верно, а при помощи ответов, указывающих на силу проявления признака, к примеру:
-
Я теряю самообладание (никогда — редко — иногда — часто).
Для оценки таких ответов каждому варианту ответа присваивается некоторый количественный показатель (как правило, 1, 2, 3 ...).
21.1 Задания типа верно — не верно
21.1 Задания типа верно — не верно
В качестве примера, который мы хотим обработать при помощи SPSS, рассмотрим личностный тест, с помощью которого определяется степень любопытства опрашиваемых.
№ | Вопрос | Правильный ответ |
1 | У Вас много книг? | Да |
2 | Ходите ли Вы за покупками всё время в одни и те же магазины? | Нет |
3 | Считаете ли Вы, что космонавтику развивать необходимо? | Да |
4 | Вас не интересует, почему на вашего соседа одели наручники? | Нет |
5 | Можете ли Вы долго заниматься чем-нибудь одним? | Да |
6 | Регулярно ли Вы смотрите новости? | Да |
7 | Знаете ли Вы, сколько человек живёт в городе, в котором проживаете Вы? | Да |
8 | Ходите ли Вы на работу всегда одной и той же дорогой? | Нет |
9 | Становится ли Вам иногда скучно? | Нет |
10 | Хотели бы Вы полететь на Луну? | Да |
11 | Читаете ли Вы ежедневные газеты регулярно? | Да |
12 | Спрашивали ли Вы уже себя, как будет выглядеть мир через сто лет? | Да |
13 | Замечаете ли вы иногда, что недовольны тем, что Вы можете и знаете? | Да |
14 | Предоставите ли Вы себя для научных экспериментов? | Да |
15 | Интересует ли Вас, сколько зарабатывает ваш сосед? | Да |
16 | Бездельничаете ли Вы во время отпуска? | Нет |
17 | Приятней ли Вам находиться в кругу большого количества друзей, нежели с одним другом? | Да |
18 | Случается ли с вами часто так, что Вы не знаете с чего начать? | Да |
Здесь речь идёт о вопросах, на которые следует давать строго определенные ответы: верно или не верно. Ответ верно соответствует наличию любопытства. Такое же самое значение можно присвоить и ответу не верно; при разработке теста, в него рекомендуется включать и такие вопросы, значимым ответом на которые является отрицательный. Это всегда возможно при соответствующей формулировке.
Если следовать Линерту, то для оценки пригодности отдельных пунктов следует применять нижеследующие два критерия:
Индекс сложности
В простейшем случае он представляет собой долю правильных ответов на данный вопрос, взятую в процентах от общего количества ответов. Для вопросов с несколькими возможными ответами и ступенчатыми ответами существуют модифицированные формулы. Удивительно, но для сложных вопросов индекс сложности принимает малые значения, а для лёгких большие. Вопросы с низким и высоким индексом сложности считаются не желательными.
Коэффициент избирательности
Коэффициентом избирательности, который является важным критерием для оценки применимости вопроса, служит корреляционный коэффициент между ответом на вопрос и суммарным показателем теста. В качестве суммарного показателя теста берётся сумма всех ответов. Это означает, что все правильные ответы должны иметь одинаковый знак! К сожалению, этому важному обстоятельству в справочниках уделяется не достаточно внимания. Для приведенного примера это означает, что пункты 2, 4, 8, 9 и 16 перед анализом должны быть подвергнуты перекодировке.
Для определения корреляционного коэффициента Линерт предлагает различные варианты, так, к примеру, двухрядная поточечная корреляция между заданием с ответом верно — не верно и значением масштаба или ранговая корреляция между заданием со ступенчатым ответом и значением масштаба. Как ни странно: SPSS всегда использует коэффициенты Пирсона.
Непригодные для применения пункты обычно отбираются посредством сравнения индексов сложности и избирательности. Самым простым способом является отбор сначала тех вопросов, которые обладают индексом сложности ниже 20 или выше 80, а затем из списка оставшихся вопросов исключаются те, которые имеют самые низкие коэффициенты избирательности. Линерт предлагает рассчитывать ещё и дополнительные показатели вопросов, такие как: индекс однородности, индекс пригодности, селекционный показатель и (если имеется так называемый внешний критерий) коэффициенты действительности.
Коэффициент пригодности
Коэффициент пригодности является важным критерием для оценки результата теста. Он является мерой точности, с которой проводится тестирование некоторого признака. SPSS предлагает для этой цели множество методов; по умолчанию устанавливается альфа Кронбаха (Cronbach's Alpha) со значением, модуль которого находится между 0 и 1. Обработаем наш пример при помощи SPSS.
-
Откройте файл nuegier.sav.
Помните о том, что вопросы 2, 4, 8, 9 и 16 должны быть перекодированы; их кодовые числа необходимо поменять местами (1 станет 2, 2 станет 1).
-
Это можно сделать при помощи метода, рассмотренного в главе 8, посредством выбора меню Transform (Трансформировать) Recode (Перекодировать) Into same Variables... (В те же переменные)
Можно было бы также воспользоваться и синтаксисом. Для этого необходимо было бы записать следующие инструкции:
RECODE item2, item4, item8, item9, item16 (1=2) (2=1). EXECUTE.
-
После перекодировки выберите в меню Analyze (Анализ) Scale (Масштабировать) Reliability Analysis... (Анализ пригодности) Откроется диалоговое окно Reliability Analysis (Анализ пригодности).
-
Переменные iteml-itemlS поместите в поле пунктов (Items:). Затем из числа предлагаемых методов расчёта коэффициентов пригодности необходимо выбрать подходящий:
Рис. 21.1: Диалоговое окно Reliability Analysis (Анализ пригодности)
-
Alpha (Альфа): Альфа Кронбаха (при дихотомических пунктах используется формула Кудера-Ричардсона 20 (Kuder-Richardson- Formula 20))
-
Split-half (Расщепление на две половины): Определение пригодности с расщеплением на две половины по Спирману-Брауну (Spearman-Brown)
-
Guttman (Гуттман): Определение нижней границы пригодности Гуттмана
-
Parallel (Парралельно): Оценка максимального правдоподобия пригодности теста при условии наличия одинаковых дисперсий пунктов
-
Strict parallel (Строго параллельно): Оценка максимального правдоподобия пригодности теста при условии наличия одинаковых средних значений пунктов и одинаковых дисперсий пунктов.
-
Оставьте предварительную установку Alpha (Альфа) и щёлкните на выключателе Statistics...(Статистики). Откроется диалоговое окно Reliability AnalysisStatistics (Анализ пригодности: Статистики).
Вы можете произвести следующие виды расчётов:
-
Descriptives for (Дескриптивные (описательные) статистики для) Item (Пункт): Среднее значение и стандартное отклонение для каждого пункта анкеты или вопроса Scale (Шкала): Среднее значение, дисперсия и стандартное отклонение для значения масштаба
Рис. 21.2: Диалоговое окно Reliability Analysis'.Statistics (Анализ пригодности: Статистики)
Scale if item deleted (Масштабировать, если пункт удалён): Когда при расчёте значения масштаба этот пункт (вопрос) не учитывается, для каждого такого Пункта (ответа на вопрос анкеты), выводятся: среднее значение и дисперсия значения шкалы, корреляция пункта со значением масштаба (то есть избирательность) и альфа Кохрана.
-
Summaries (Итоги, общие сведения)
Means (Средние значения): Различные виды статистик для средних значений пунктов
Variances (Дисперсия): Различные виды статистик для дисперсий пунктов
Covariances (Ковариации): Различные виды статистик для ковариаций между пунктами
Correlations (Корреляции): Различные виды статистик для корреляций между пунктами.
-
Inter-Item (Между пунктами)
Correlations (Корреляции): Корреляционная матрица Covariances (Ковариации): Ковариационная матрица
-
ANOVA-ТаЫе (Таблица ANOVA)
F test (F тест): Двухфакторный дисперсионный анализ (факторы: наблюдения, пункты) с повторным измерением и одним значением в каждой ячейке Friedman chi-square (Хи-квадрат Фридмана): тест Хи-квадрат Фридмана и коэффициент согласования Кендала (при наличии переменных, относящихся к порядковой шкале)
Cochran chi-square (Хи-квадрат Кохрана): Q Кохрана (при наличии дихотомических переменных).
Далее ещё имеются:
-
Hottelling's T-square (Т-квадрат Хоттелинга): Тест Хоттелинга для проверки утверждения, что средние значения пунктов равны между собой.
-
Tukey's test ofadditivity (Критерий аддитивности Тьюки): Тест Тьюки на аддитивность пунктов.
В случае установки опции Intraclass correlation coefficient (Корреляционный коэффициент внутри класса) речь идёт о расчёте корреляционного коэффициента внутри класса (ICC); информацию по этому поводу Вы найдёте в разделе 15.5.
-
Здесь ограничьтесь активизацией опции Scale if item deleted (Масштабировать, если пункт удалён) и щёлкните на Continue (Далее).
-
Начните расчёт нажатием ОК.
В окне просмотра появятся результаты расчёта. И в 10 версии вывод этих результатов ещё не производится в новой табличной форме.
RЕLIАВILIТУ ANALYSIS SCALE (ALPHA) | ||||
Item-total | Statistics | |||
Scale Mean if Item Deleted | Scale Variance if Item Deleted | Corrected Item-Total Correlation | Alpha if Item Deleted | |
ITEM1 | 24,9333 | 13,5126 | ,5410 | ,7664 |
ITEM2 | 25,0667 | 14,4092 | ,2679 | ,7862 |
ITEM3 | 25,1000 | 13,5414 | ,5097 | ,7684 |
ITEM4 | 25,4333 | 16,0471 - | -,1676 | ,8052 |
ITEMS | 25,2000 | 13,6828 | ,4907 | ,7701 |
ITEM6 | 25,1667 | 14,5575 | ,2358 | ,7883 |
ITEM7 | 25,5000 | 15,2931 | ,1738 | ,7887 |
ITEMS | 24,8000 | 15,1310 | ,1154 | ,7942 |
ITEM9 | 25,2000 | 13,8897 | ,4304 | ,7745 |
ITEM10 | 24,8667 | 13,8437 | ,4732 | ,7717 |
ITEM11 | 25,3667 | 14,2402 | ,4223 | ,7760 |
ITEM12 | 25,0667 | 13,3057 | ,5763 | ,7633 |
ITEM13 | 25,0000 | 13,2414 | ,6017 | ,7615 |
ITEM14 | 24,9667 | 13,8954 | ,4196 | ,7752 |
ITEM15 | 25,0000 | 13,3103 | ,5813 | ,7630 |
ITEM16 | 25,0333 | 14,0333 | ,3713 | ,7787 |
ITEM17 | 24,9667 | 15,3437 | ,0283 | ,8023 |
ITEM18 | 24,9667 | 13,9644 | ,4000 | ,7766 |
Reliability Coefficients | ||||
N of Cases =30,0 | N of Items= 18 | |||
Alpha =,7887 | ||||
Коэффициент пригодности, равный 0,7887, является очень высоким. В колонке с названием Corrected Item-Total Correlation (Откорректированный пункт — суммарная корреляция) находятся коэффициенты избирательности. Основываясь на значении этих коэффициентов, пункты 4 и 17 можно считать непригодными для дальнейшего использования, да и пункт 8 должен быть исключён.
-
Мы уже говорили о необходимости проведения расчета индекса сложности. Для расчёта индекса сложности выберите в меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты)
Процентный показатель частоты появления правильного ответа (кодировка 1) является индексом сложности соответствующего пункта. Все индексы сложности собраны в нижеследующей таблице.
Пункт | Индекс сложности | Пункт | Индекс сложности |
1 | 36,7 | 10 | 30,0 |
2 | 50,0 | 11 | 80,0 |
3 | 53,3 | 12 | 50,0 |
4 | 86,7 | 13 | 43,3 |
5 | 63,3 | 14 | 40,0 |
6 | 60,0 | 15 | 43,3 |
7 | 93,3 | 16 | 46,7 |
8 | 23,3 | 17 | 40,0 |
9 | 63,3 | 18 | 40,0 |
Если следовать рекомендации, сформулированной в начале раздела и исключать пункты с индексом сложности меньшим 20 и большим 80, то помимо пунктов 4, 8 и 17 необходимо исключить из списка и пункт 7.
Если вновь провести анализ пунктов с оставшимися четырнадцатью пунктами, то коэффициент пригодности получится равным 0,8297. Благодаря исключению неподходящих пунктов он стал ещё выше.
1.gif
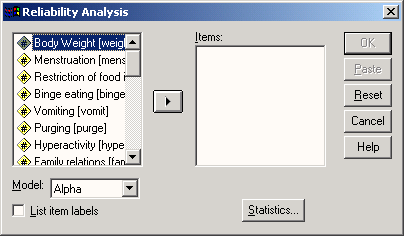
2.gif
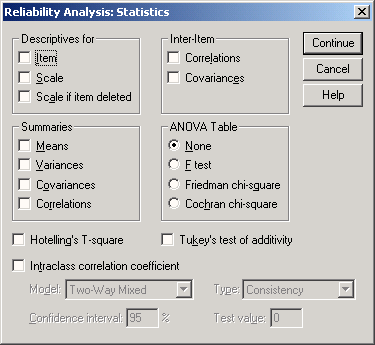
21.2 Задания со ступенчатыми ответами
21.2 Задания со ступенчатыми ответами
В разделе 19.3 была представлена анкета исследования Фрайбургского университета, посвященного отношению респондентов к болезни. Эта анкета охватывает в общей сложности 35 пунктов, отображающих при помощи кодировок 1 = "абсолютно нет" до 5 = "очень сильно" ситуацию, характеризующую то, как пациенты склонны бороться с поразившим их недугом. Пункты были подвергнуты факторному анализу; один из пяти результирующих факторов мы назвали: "Активное действие, направленное на решение проблемы".
В этот фактор вошли следующие переменные:
11 | Искать информацию о заболевании и лечении |
17 | Предпринимать активные действия для решения проблемы |
f8 | Составить план лечения и затем приступить к его реализации |
f13 | Больше себе позволять |
f14 | Пытаться интенсивней жить |
f15 | Решиться на борьбу с болезнью |
f17 | Подбадривать себя |
f18 | Пытаться достичь успеха и самоутверждения |
f19 | Пытаться отвлечься |
110 | Искать уединения |
Эти пункты можно собрать в один тест, который для каждого пациента будет давать некоторое значение на шкале уровня активности его действий. При помощи теста пригодности проверим также реальную пригодность этих пунктов. Так как все пункты имеют положительную кодировку в направлении активного образа действия, в перекодировке, как в разд. 19.1, нет необходимости.
-
Откройте файл fkv.sav.
-
Выберите в меню Analyze (Анализ) Scale (Масштабировать) Reliability Analysis... (Анализ пригодности)
-
Переменные f1, f7, f8, f1З, f14, f15, f17, f18, f19 и f20 поместите в поле, предназначенное для пунктов (вопросов анкеты).
-
Через выключатель Statistics...(Статистики) в группе Descriptives for (Дескриптивные статистики для) активируйте опцию Scale if Item deleted (Масштабировать, если пункт удалён).
В окне просмотра появятся следующие результаты.
RELIABILITY ANALYSIS-SCALE (ALPHA) | |||
Item-total | Statistics | ||
Scale Scale Mean Variance if Item if Item Deleted Deleted | Corrected Item-Total Correlation | Alpha if Item Deleted | |
F1 30,2750 45,5214 | ,4514 | ,8059 | |
F7 30,3937 43,9761 | ,5534 | ,7944 | |
F8 31,0812 43,8990 | ,5453 | ,7953 | |
F13 31,1125 46,1885 | ,4592 | ,8046 | |
F14 30,4250 45,8057 | ,4857 | ,8019 | |
F15 30,2937 45,1899 | ,4351 | ,8084 | |
F17 30,4312 43,4418 | ,6558 | ,7840 | |
F18 30,7000 44,3245 | ,5701 | ,7929 | |
F19 30,5750 46,7491 | ,4632 | ,8042 | |
F20 30,7687 48,2166 | ,3679 | ,8131 | |
Reliability Coefficients | |||
N of Cases = 160,0 | N of Items =10 | ||
Alpha = ,8170 | |||
В колонке Corrected Item-Total Correlation (Откорректированный пункт — суммарная корреляция) приводятся коэффициенты избирательности, а внизу таблицы можно увидеть коэффициент пригодности. В нашем случае он является довольно высоким — значение равно 0,817. На основании получившихся коэффициентов избирательности нет повода для исключения каких-либо пунктов; после любого такого исключения, в рассматриваемом случае, коэффициент пригодности снижался бы, как показано в колонке Alfa if Item Deleted (Альфа, если пункт удалён).
Пригодность всех пунктов не является сюрпризом, т.к., за исключением пункта 20 (который к тому же имеет и наименьшую избирательность), все пункты обладают достаточными факторными нагрузками (> 0,4). Как показывает нижеследующая таблица, большие факторные нагрузки говорят о высоких коэффициентах избирательности.
Избирательность | Факторная нагрузка | |
f1 | 0,6558 | 0,654 |
f7 | 0,5701 | 0,589 |
f8 | 0,5534 | 0,710 |
f13 | 0,5453 | 0,690 |
f14 | 0,4857 | 0,621 |
f15 | 0,4632 | 0,572 |
f17 | 0,4592 | 0,510 |
f18 | 0,4514 | 0,563 |
f19 | 0,4351 | 0,597 |
f20 | 0,3679 | <0,400 |
Что же касается расчёта индекса сложности, то в данном примере он довольно проблематичен; пожалуй, к правильному ответу можно отнести только кодировки 4 и 5.
Глава 22. Стандартные графики
Глава 22. Стандартные графики
1. Стандартные графики
Стандартные графики
Одним из достоинств SPSS для Windows является наличие большого количества разнообразных графиков, которые могу быть построены как при помощи процедур меню графиков, так и из разнообразных процедур меню статистик. Что касается последнего меню, то для выяснения специальных возможностей графического представления Вы можете обратиться к главам: 6 (частотный анализ), 10 (предварительное исследование данных), И (таблицы сопряженности), 16 (регрессионный анализ), 20 (анализ выживания) и 24 (многомерное масштабирование). В главе 4 (Краткий обзор SPSS для Windows) уже были рассмотрены некоторые вопросы построения и редактирования графиков.
Каждый созданный график появляется в окне просмотра вместе с другими таблицами. Для построения графика, как правило, оказывается достаточным после выбора типа графика указать необходимые переменные, на основании которых он и будет построен по ранее заданной схеме. Если же у Вас появилось желание отредактировать график по своему вкусу, то для этого необходимо дважды щёлкнуть на какой-либо точке в пределах графика. После этого у Вас появится множество возможностей для дополнительного редактирования.
Начиная с 8-ой версии в SPSS наряду с традиционными стандартными графиками существует возможность создавать и интерактивные графики. Стандартные графики строятся при помощи многочисленных процедур статистического меню или меню графиков, составные компоненты которых и соответственно их возможности нисколько не изменились. Однако, в меню графиков добавилась ещё одна позиция — Interactive (Интерактивно), которая открывает ещё одно собственное меню, служащее для построения так называемых интерактивных графиков. Интерактивные графики дают довольно широкую палитру новых возможностей.
Наряду с удобными глобальными возможностями менять отдельные стилевые элементы графиков и преобразовывать переменные, используемые для построении графика, отныне при помощи интерактивных графиков становится также возможным одновременное построение нескольких графиков для отдельных категорий дополнительных переменных.
Чтобы последовательно изложить эти новые возможности интерактивных графиков, процедуры построения графиков в SPSS должны быть рассмотрены в двух отдельных главах. В текущей главе рассматриваются исключительно традиционные стандартные графики; новые интерактивные графики будут представлены в следующей главе (гл. 23). Обратимся теперь к стандартным графикам.
Разобраться в многочисленных графиках, создаваемых при помощи меню графиков составляет трудность пожалуй только для новичка, поэтому мы не будем здесь рассматривать все имеющиеся тонкости. Однако мы попытаемся дать обзор графиков при помощи типичных практических примеров. При этом в окно просмотра будет выводиться установленный по умолчанию базовый вид графиков, правда, с необходимыми для нас заголовками, подзаголовками и сносками. Возможные изменения (штриховки, цвет, виды линий, виды диаграмм, изменение типа и размера шрифта и т.д.) будут рассмотрены в разделе 22.16.
При разработке графического представления диаграмм можно заметить, что в принципе на практике существуют две различные исходные ситуации. Наиболее часто встречается ситуация, когда дополнительно к результатам статистического анализа, хранящимся в файле данных SPSS, необходимо построить и графическое представление этих результатов. К примеру, у Вас появилось желание представить частоты четырёх возрастных групп из исследования гипертонии (файл hyper.sav) в виде линейчатой диаграммы. В этом случае компьютер сам при помощи соответствующих расчётов находит частоты, необходимые для построения столбцов диаграммы.
Совсем другую ситуацию можно наблюдать, если перед нами находятся уже подсчитанные и обработанные данные. Такой случай возникает, если бы, к примеру, Вы взяли из газеты информацию о ежедневной добыче нефти стран, входящих в ОРЕС, и захотели бы представить эти данные в виде линейчатой диаграммы. При наличии таких готовых данных, очень часто приходится поразмыслить над тем, как их представить в файле.
-
Если Вы щёлкните в списке меню на Graphs (Графики), то увидите меню с вариантами графиков.
Различные виды графиков будут по отдельности рассмотрены в разделах 22.1 по 22.14.
Перед рассмотрением графиков необходимо остановиться ещё раз на одном важном моменте. Установки по умолчанию задают различные цвета, в которые окрашиваются элементов графиков (к примеру, маркеры, сегменты) и линии, что облегчает понимание диаграммы и улучшает презентабельность. Если же Вы хотите напечатать график на принтере или представить его в других формах, то в большинстве подобных случаев использовать цветные графики не рекомендуется. В таких случаях разные поверхности Вы можете обозначить при помощи различных штриховок, а разные линии при помощи различных видов линий.
-
Эти свойства вы сможете изменить, если выберите в меню Edit (Правка) Options... (Параметры) и в диалоговом окне Options (Параметры) щёлкните на Charts (Диаграммы).
-
В разделе Fill Patterns and Line Styles (Заливка узором и стиль линий) вместо опции Cycle through colors, then patterns (Сначала просмотреть цвета, затем узоры) активируйте опцию Cycle through patterns (Просмотреть узоры).
В рассматриваемых далее методах построения графиков через выключатель Titles... (Заголовки) Вы можете присвоить диаграмме своё название, через выключатель Options... (Параметры) выбрать метод обработки пропущенных значений и в поле Template (Шаблон) при помощи активирования Use chart specifications from: (Установки диаграммы взять из:) загрузить установки для построения графика из других файлов.
22.1 Столбчатые диаграммы
22.1 Столбчатые диаграммы
Столбчатые диаграммы применяются, как правило, в следующих ситуациях:
-
Отображение частот переменных, относящихся к номинальной или порядковой шкале
Рис. 22.1: Меню с вариантами графиков
-
Отображение средних значений, сумм или других показателей последовательных переменных (т.е. переменных, принадлежащих к интервальной шкале или к шкале отношений), отображение переменных, сгруппированных по категориям переменных с номинальной или порядковой шкалой или временной зависимости.
-
Для построения столбчатой диаграммы, после открытия соответствующего файла SPSS, выберите в меню Graphs (Графики) Ваг... (Столбчатые)
Откроется диалоговое окно Bar Charts (Столбчатые диаграммы) (см. рис. 22.2).
Вы можете выбрать между простой, кластеризованной (кластерной) и состыкованной столбчатыми диаграммами. Данные, отображаемые в этих диаграммах, могут быть заданы как категории одной переменной, как разные переменные или как значения отдельных наблюдений.
Рис. 22.2: Диалоговое окно Bar Charts (Столбчатые диаграммы)
1.gif
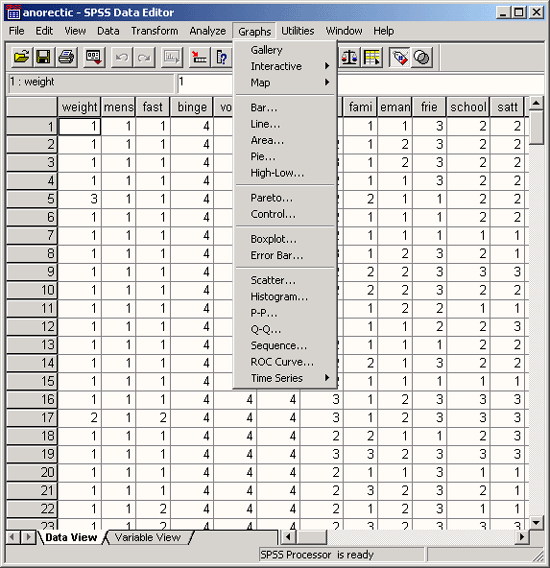
2.gif
22.1.1 Простые столбчатые диаграммы
22.1.1 Простые столбчатые диаграммы
-
Откройте файл с данными об исследовании гипертонии (файл hyper.sav).
Мы хотим построить столбчатую диаграмму для процентных показателей частот четырёх возрастных групп (переменная ak).
-
Щёлкните на области Simple (Простая) и оставьте предварительную установку Summaries for groups of cases (Обработка категорий одной переменной).
-
Щёлкните по кнопке Define (Определить); откроется соответствующее диалоговое окно.
-
В поле Category Axis: (Ось категорий) введите переменную ak, активируйте % of cases (% наблюдений) и, пройдя выключатель Titles... (Заголовок), введите заголовок для диаграммы.
-
Щёлкните на ОК.
Рис. 22.3: Диалоговое окно Define Simple Bar: Summaries for groups of cases (Простая столбчатая диаграмма: Обработка категорий одной переменной)
Будет построен график, показанный на рисунке 22.4.
Теперь представим в графическом виде изменение среднего значения уровня сахара в крови (переменные bz0, bz1, bz6 и bz12), взятого из того же файла (hyper.sav).
-
В этот раз в диалоговом окне Ваг Charts (Столбчатые диаграммы) активируйте Summaries of separate variables (Обработка отдельных переменных); после нажатия выключателя Define (Определить) откроется соответствующее диалоговое окно (см. рис. 22.5).
-
В поле Bars Represent (Значения столбцов) по очереди внесите переменные bz0, bz1, bz6 и bz12 и оставьте установленную по умолчанию функцию Mean of values (Средние значения).
-
Пройдя выключатель Titles... (Заголовок), введите заголовок диаграммы.
-
Щёлкните на ОК.
Рис. 22.4: Простая столбчатая диаграмма (Категории одной переменной)
Будет построен график, приведенный на рисунке 22.6.
Следует отметить тот недостаток, что в этой диаграмме не полностью приведены метки значений и на вертикальной оси показана только ограниченная область от 103,5 до 106,0, из-за чего по ошибке можно сделать неверное заключение о сильном изменении уровня сахара. Вы можете подкорректировать эти ошибки в редакторе диаграмм.
Рис. 22.5: Диалоговое окно Define Simple Bar: Summaries of separate variables (Построение простой столбчатой диаграммы: Обработка отдельных переменных)
-
Если Вы хотите выбрать функцию отличную от установленной по умолчанию Mean of values (Средние значения), щёлкните на одной из переменных в списке и затем на выключателе Change Summary...(Изменить метод обработки).
Откроется диалоговое окно с перечнем функций (см. рис. 22.7).
Это диалоговое окно появляется только для столбчатой, линейной, круговой диаграмм и диаграммы с областями, причём не каждая из находящихся здесь функций пригодна для всех видов диаграмм. Если для имеющихся данных Вы хотите отобразить медианы или другие процентили (сравните с гл. 6), то активируйте опцию Values are grouped midpoints (Значения являются сгруппированными средними точками).
В следующем примере рассматривается вопрос отображения готовых данных. Допустим, Вы взяли из некоторой газеты данные по 1993 году о добыче нефти в семи странах, входящих в ОРЕС и являющихся ведущими в этой отрасли.
Рис. 22.6: Простая столбчатая диаграмма (Отдельные переменные)
Страна | Млн.баррель/день |
Саудовская- Аравия | 8,0 |
Иран | 3,3 |
Венесуэла | 2,3 |
Объединённые Арабские Эмираты | 2,2 |
Нигерия | 1,8 |
Кувейт | 1,6 |
Ливия | 1,4 |
Представим эти данные в форме столбчатой диаграммы.
-
Откройте файл oel.sav.
-
В диалоговом окне Bar Charts (Столбчатые диаграммы) активируйте опцию Values of individual cases (Значения отдельных наблюдений).
После нажатия выключателя Define (Определить) откроется соответствующее диалоговое окно.
-
В поле Bars Represent (Значения столбцов) внесите переменную barrel; в группе Category Labels (Метки категорий) активируйте Variable: (Переменная) и внесите переменную land.
Рис. 22.7: Диалоговое окно Summary Function (Обрабатывающая функция).
Рис. 22.8: Диалоговое окно Define Simple Bar: Values of individual cases (Построение простой столбчатой диаграммы: Значения отдельных случаев)
-
Пройдя выключатель Titles... (Заголовок), введите заголовок диаграммы и щёлкните на ОК.
График будет выглядеть так, как на рисунке 22.9.
Рис. 22.9: Простая столбчатая диаграмма (Значения отдельных случаев)
3.gif
4.gif
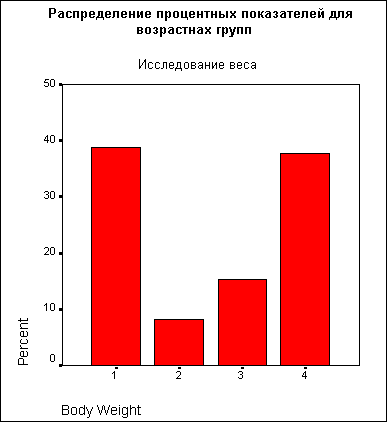
5.gif
6.gif
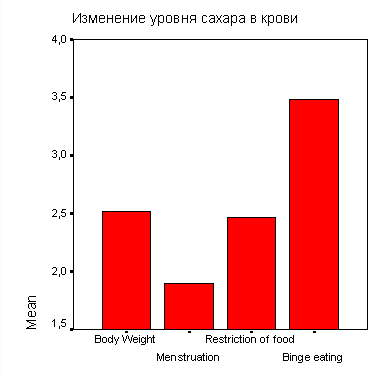
7.gif

8.gif
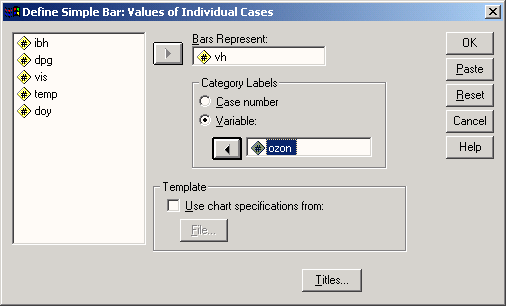
9.gif

22.1.2 Кластеризованные столбчатые диаграммы
22.1.2 Кластеризованные столбчатые диаграммы
Теперь в целях обработки данных, полученных в ходе исследования гипертонии (файл hyper.sav), отдельно для двух методик лечения (переменная med с двумя своими значениями, равными 1 и 2) в графическом виде должны быть представлены частотные показатели четырёх возрастных групп (переменная ak) в процентном выражении.
-
Откройте файл hyper.sav.
-
В диалоговом окне Bar Charts (Столбчатые диаграммы) щёлкните на области Clustered (Кластеризованная); активируйте опцию, устанавливаемую по умолчанию, Summaries for groups of cases (Обработка категорий одной переменной).
-
Щёлкните на кнопке Define (Определить); откроется главное диалоговое окно, изображённое на рисунке 22.10.
Рис. 22.10: Диалоговое окно Define Clustered Bar: Summaries for groups of cases (Построение группированной диаграммы: Обработка категорий одной переменной)
-
В поле Category Axis: (Ось категорий) введите переменную ak, в поле Define Clusters by: (Создать группы при помощи:) введите переменную med. Активируйте % of cases (% наблюдений).
-
Пройдя выключатель Titles... (Заголовок), введите заголовок для диаграммы и начните построение диаграммы щелчком на ОК (см. рис. 22.11).
В качестве примера графического представления готовых данных рассмотрим доли I рынка принадлежащие самым крупным изготовителям компьютеров в 1991 и 1992 годах:
Изготовитель | Доля рынка, % | |
1991 | 1992 | |
IBM | 16,3 | 12,4 |
Apple | 11,2 | 11,9 |
Compaq | 6,0 | 6,6 |
NEC | 6,4 | 5,1 |
Dell | 1,7 | 3,5 |
Эти данные построчно сохранены в переменных firma (изготовитель), jahr (год) и anteil (доля) в файле pc.sav.
-
Откройте файл pc.sav и просмотрите его содержимое в редакторе данных.
-
В диалоговом окне Bar Charts (Столбчатые диаграммы) щёлкните на области Clustered (Кластеризованная) и активируйте устанавливаемую по умолчанию опцию Summaries for groups of cases (Обработка категорий одной переменной).
-
После щелчка на выключателе Define (Определить) в открывшемся диалоговом окне в поле Category Axis: (Ось категорий) введите переменную firma, а в поле Define Clusters by: (Определить группы по:) — переменную jahr. В группе Bars Represent (Значения столбцов) активируйте Other summary function (Другая обрабатывающая функция) и в появившееся поле введите переменную anteil; функцию Mean of values (Средние значения) можете оставить.
-
Пройдя выключатель Titles... (Заголовок), введите подходящий заголовок и начните построение диаграммы щелчком на ОК.
Рис. 22.11: Группированная столбчатая диаграмма
Рис. 22,12: Группированная столбчатая диаграмма
10.gif
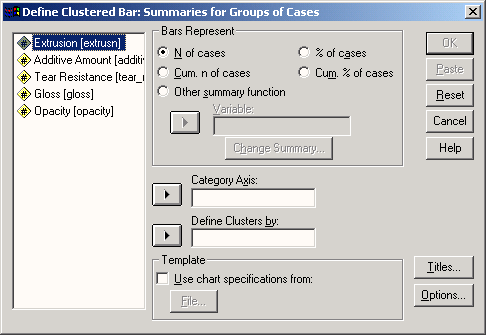
11.gif
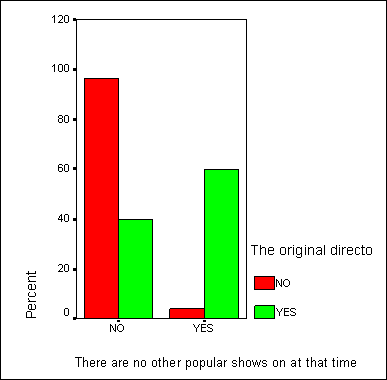
12.gif
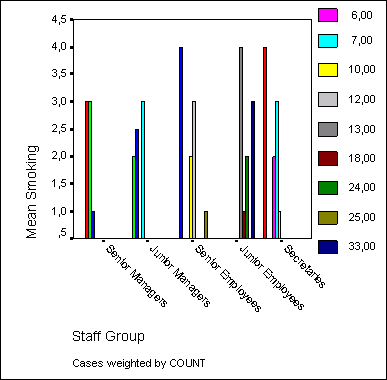
22.1.3 Состыкованные диаграммы
22.1.3 Состыкованные диаграммы
Как правило, состыкованная столбчатая диаграмма применяется тогда, когда столбцы отражают частоты, которые должны быть разделены при помощи некоторой внешней переменной. В таком случае, и обзор суммарных частот предоставляется пользователю иначе, нежели в виде кластеризованной столбчатой диаграммы.
-
Откройте файл studium.sav, содержащий данные опроса студентов.
Мы хотим отобразить в графическом виде распределение частот, отражающих психологическое состояние студентов (переменная psyche), отдельно для каждого пола (переменная sex).
-
В диалоговом окне Bar Charts (Столбчатые диаграммы) щёлкните на области Stacked (Состыкованная) и активируйте опцию, устанавливаемую по умолчанию, Summaries for groups of cases (Обработка категорий одной переменной). Щелчком по кнопке Define (Определить) откройте соответствующее диалоговое окно.
-
В поле Category Axis: (Ось категорий) введите переменную psyche, а в поле Define Stacks by: (Создать штабели при помощи:) введите переменную sex. Оставьте установку по умолчанию N of cases (Количество наблюдений).
-
Пройдя выключатель Titles... (Заголовок), введите подходящий заголовок.
В данном примере имеются пропущенные значения, которые в соответствии с установками по умолчанию будут обрабатываться как отдельные категории.
-
Для того, чтобы запретить это действие щёлкните на выключателе Options... (Параметры) и уберите отметку для опции Display groups defined by missing values (Пропущенные значения отображать как категории).
-
Вернувшись в диалоговое окно Define Stacked Bar: Summaries for groups of cases (Построение состыкованной диаграммы: Обработка категорий одной переменной) щелчком на ОК начните построение диаграммы (см. рис. 22.11).
В следующем примере рассматривается графическое представление уже имеющихся (готовых) данных. Приведенная ниже таблица содержит показатели рождаемости в западных и восточных землях Германии, начиная с 1985 по 1992 год:
Рис. 22.13: Диалоговое окно Define Stacked Bar: Summaries for groups of cases (Построение штабельной диаграммы: Обработка категорий одной переменной)
Рис. 22.14: Штабельная столбчатая диаграмма
Гол | Количество | |
Запал | Восток | |
1985 | 586.155 | 227.648 |
1986 | 635.963 | 222.229 |
1987 | 642.010 | 225.959 |
1988 | 677.259 | 215.734 |
1989 | 681.537 | 198.922 |
1990 | 727.199 | 178.476 |
1991 | 722.250 | 107.769 |
1992 | 718.730 | 87.030 |
-
Откройте файл geburten.sav и просмотрите его содержимое в редакторе данных.
Эти данные построчно сохранены в переменных jahr (год), wo и anz (количество). Переменная wo при помощи кодировок 1 и 2 указывает на принадлежность к Западной или Восточной Германии.
-
В диалоговом окне Bar Charts (Столбчатые диаграммы) щёлкните на области Stacked (Состыкованная) и активируйте опцию Summaries for groups of cases (Обработка категорий одной переменной), устанавливаемую по умолчанию.
-
После щелчка на выключателе Define (Определить) в открывшемся диалоговом окне в поле Category Axis: (Ось категорий) введите переменную jahr, а в поле Define Stacks by: (Создать штабели при помощи:) — переменную wo. В группе Bars Represent (Значения столбцов) активируйте Other summary function (Другая обрабатывающая функция) и в появившееся поле введите переменную anz; вместо установленной по умолчанию функции Mean of values (Средние значения), пройдя выключатель Change Summary...(Изменить метод обработки) отметьте функцию суммы (Sum of values).
-
С помощью кнопки Titles... (Заголовок), введите подходящий заголовок и начните построение диаграммы щелчком на ОК.
13.gif
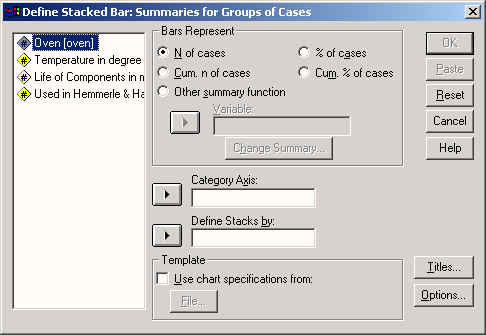
14.gif

22.10 Диаграммы Парето
22.10 Диаграммы Парето
Диаграмма Парето представляет собой столбчатую диаграмму, в которой столбцы располагаются в порядке убывания, а дополнительная кривая может указывать на совокупную частоту для представленных категорий. При этом при суммировании отдельных столбцов по заданному правилу должна получаться некоторая итоговая величина, имеющая определенный смысл.
-
Чтобы построить диаграмму Парето, после открытия необходимого Вам файла SPSS, выберите в меню Graphs (Графики) Pareto... (Парето)
Откроется соответствующее диалоговое окно.
Вы можете построить простую или состыкованную диаграмму Парето, причём и здесь существует три варианта представления данных.
Для иллюстрации процесса построения этих диаграмм достаточно одного примера. В следующей таблице приведены данные текущих расходов семей западной Германии в 1992 году.
Рис. 22.55: Диалоговое окно Pareto Charts (Диаграммы Парето)
Статья расходов | Расколы (/миллиарды DM) |
Квартира | 302,5 |
Одежда | 116,2 |
Аренда | 247,7 |
Электричество | 55,6 |
Бытовые расходы | 137,4 |
Здоровье | 78,8 |
Проезд | 253,5 |
Отдых | 147,9 |
Прочее | 108,5 |
-
Откройте файл privver.sav, в котором построчно в переменных zweck (статья) и dm сохранены эти данные.
-
В диалоговом окне Pareto Charts (Диаграммы Парето) щёлкните на области Simple (Простая) и оставьте опцию Counts or sums for groups of cases (Частоты или суммы категорий одной переменной), установленную по умолчанию,.
-
Нажатием выключателя Define (Определить) откройте следующее диалоговое окно.
-
В поле Category Axis: (Ось категорий) введите переменную zweck. В группе Bars Represent (Значения столбцов) поставьте маркер рядом с опцией варианта выбора Sums of variable: (Суммы переменных) и переведите переменную dm в появившееся поле. Отображение совокупной (кумулятивной) кривой устанавливается по умолчанию.
Рис. 22.56: Диалоговое окно Define Simple Pareto: Counts or Sums for Groups of Cases (Построение простой диаграммы Парето: Частоты или суммы категорий одной переменной)
-
С помощью выключателя Titles... (Заголовок), введите подходящий заголовок.
-
Щелчком на ОК начните построение диаграммы (см. рис. 22.57).
Из-за отображения кумулятивной (совокупной) кривой некоторые столбцы пришлось опустить довольно низко. В подобных случаях намного удобнее запретить отображение совокупной кривой. График без совокупной кривой Вы можете видеть на рисунке 22.58.
57.gif
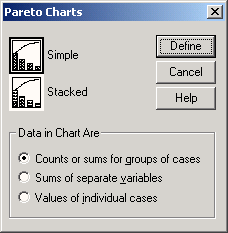
58.gif

22.11 Контрольные карты
22.11 Контрольные карты
С помощью построения контрольных карт при наличии временной зависимости Вы можете проверить, лежат ли средние значения переменных в пределах области рассеяния, объясняемой действием случайных факторов, или же они выходят за пределы этой области. В общем случае подразделение данных может происходить не только по временным интервалам, а и посредством других подгрупп.
-
После открытия необходимого Вам файла SPSS выберите в меню Graphs (Графики) Control... (Контроль)
Откроется диалоговое окно Control Charts (Контрольные карты).
Рис. 22.57: Диаграмма Парето (с кумулятивной кривой)
Рис. 22.58: Диаграмма Парето (без совокупной кривой)
Существует четыре разновидности контрольных карт и две возможности представления данных. Поэтому число возможных контрольных карт довольно велико и не может быть полностью рассмотрено в рамках этой книги. С одной стороны речь идёт об анализе средних значений, а с другой об анализе относительных частот переменных, относящихся к номинальной шкале.
Для рассмотрения этих диаграмм нам будет достаточно одного типичного примера. В этом примере необходимо проверить качество изделий, которые были произведены шестью станками за определённый промежуток времени. К примеру, необходимо произвести контроль длины этих изделий. Измерения длины изделий (в см) были произведены на шести станках для двенадцати промежутков времени и помещены в следующую сводную таблицу.
Рис. 22.59: Диалоговое окно Control Charts (Контрольные карты)
Интервал | Станок 1 | Станок 2 | Станок 3 | Станок 4 | Станок 5 | Станок 6 |
1 | 24,07 | 24,11 | 24,17 | 24,02 | 24,07 | 23,95 |
2 | 23,98 | 24,09 | 24,03 | 24,18 | 24,10 | 24,20 |
3 | 24,14 | 23,99 | 23,93 | 24,06 | 24,04 | 24,10 |
4 | 23,96 | 24,10 | 23,97 | 23,90 | 24,00 | 23,91 |
5 | 23,98 | 24,02 | 24,00 | 24,05 | 23,84 | 23,95 |
6 | 24,01 | 23,95 | 23,97 | 23,83 | 24,12 | 24,02 |
7 | 23,98 | 24,05 | 24,16 | 24,07 | 23,90 | 24,00 |
8 | 24,07 | 24,12 | 24,07 | 24,14 | 23,99 | 23,96 |
9 | 24,11 | 24,16 | 24,22 | 24,12 | 24,00 | 24,05 |
10 | 24,05 | 24,04 | 23,90 | 24,10 | 24,10 | 23,97 |
11 | 24,00 | 24,08 | 23,97 | 23,87 | 23,92 | 24,06 |
12 | 24,07 | 24,01 | 23,89 | 24,04 | 23,92 | 24,09 |
-
Откройте файл werk.sav.
-
В диалоговом окне Control Charts (Контрольные карты) щёлкните на области X-Bar, R, s. Поставьте маркер рядом с опцией Cases are subgroups (Наблюдения используются в качестве подгрупп).
-
Щелчком по выключателю Define (Определить) откройте соответствующее диалоговое окно (см. рис. 22.60).
-
В поле Subgroups Labeled by: (Метки подгрупп:) введите переменную zeit (время), а в поле Samples (Образцы) переменные ml, m2, m3, m4, т5 и тб.
-
Оставьте устанавливаемую по умолчанию функцию X-Bar and range (Х-горизонталь диапазон) и щелчком на ОХ начните построение диаграммы (см. рис. 22.61).
На втором графике, который помещается в окне просмотра, будет отображено изменение стандартного отклонения.
Рис. 22.60: Диалоговое окно X-Bar, R, s: Cases Are Subgroups (Х-горизонталь, R, s: Случаи в качестве подгрупп)
Рис. 22.61: Контрольная карта
59.gif
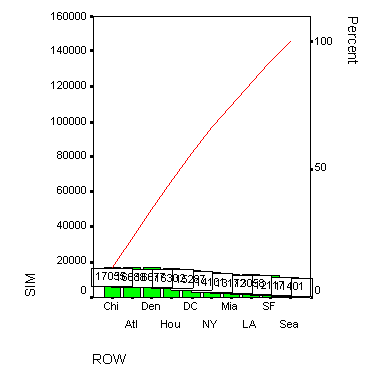
60.gif
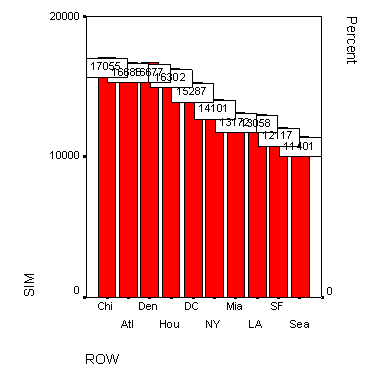
61.gif
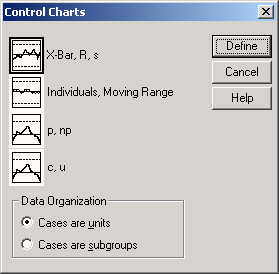
62.gif
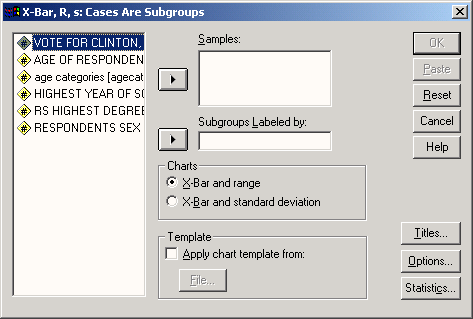
63.gif
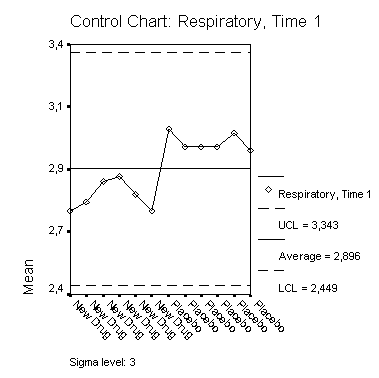
22.12 Диаграммы нормального распределения
22.12 Диаграммы нормального распределения
При проведении практически всех статистических тестов важную роль играет вопрос, подчиняются ли анализируемые данные нормальному распределению (для сравнения см. разд. 5.1.2). Проверку нормального распределения можно производить визуально, при помощи гистограммы (для пояснения см. разд. 22.9), однако лучше это осуществлять с использованием специального статистического теста, к примеру, теста Колмогорова-Смирнова (для получения подробной информации см. разд. 14.5). Ещё одну возможность анализа нормального распределения предоставляют диаграммы нормального распределения, которые в SPSS подразделяются на два вида:
-
Р-Р- нормальный вероятностный график
-
Q-Q-нормальный вероятностный график
В первом случае (Р-Р) в форме диаграммы рассеяния на графике отображается зависимость ожидаемых совокупных частот от фактических совокупных частот, а во втором случае (Q-Q) зависимость ожидаемой частоты от наблюдаемой частоты.
Построение диаграмм нормального распределения типа Q-Q можно производить и в рамках предварительного исследования данных. В таком варианте они уже были рассмотрены ранее (для получения подробной информации см. разд. 10.4.1). Поэтому здесь мы приведём пример, касающийся только диаграммы нормального распределения типа Р-Р.
-
Откройте файл hyper.sav и выберите в меню Graphs (Графики) Р-Р... (Р-Р-диаграммы) Откроется диалоговое окно Р-Р Plots (Р-Р-диаграммы).
Рис. 22.62: Диалоговое окно Р-Р Plots (Р-Р-диаграммы)
Вы видите, что тест на нормальное распределение устанавливается по умолчанию. Наряду с этим Вы можете производить тестирование на предмет наличия ещё двенадцати видов распределения, к примеру, на наличие распределения Вайбула (Weibull), Лапласа (Laplace), Хи-квадрат (%2) и /-распределения Стьюдента (Student). Вы можете просмотреть все предлагаемые типы распределений в ниспадающем меню.
-
Мы хотим проверить на предмет нормального распределения переменную а (Alter — возраст); для этого перенесите эту переменную в поле тестируемых переменных.
В диалоговом окне присутствуют также и различные возможности преобразования данных, в состав которых входят: пересчет в натуральные логарифмы, z-преобразование (перевод к стандартизованному виду) и два вида преобразований, применяемых для временных последовательностей.
Для подсчёта ожидаемых значений, подчиняющихся нормальному распределению, на выбор предлагаются четыре различных метода. Если количество значений, полученных в результате наблюдений, обозначить буквой п, а ранговые показатели этих значений буквой г (г = 1, ..., п), то формулы, соответствующие указанным методам, будут выглядеть следующим образом:
Blom (Блом): | (r-3/8) / (n+1/4) |
Rankit (Ранговое преобразование): | (r-1/2) / n |
Tukey (Тьюки): | (r-1/З) / (n+1/З) |
Van der Waerden (Ван дер Верден): | r / (n+1) |
Формула Блома (Blom) устанавливается по умолчанию. Далее Вам предоставляется возможность выбора одного из четырёх различных методов для обозначения одинаковых значений (так называемых связок).
Среднее значение: | Равным значениям присваивается средний ранг |
Максимум: | Равным значениям присваивается ранг, высший из двух |
Минимум: | Равным значениям присваивается ранг, низший из двух |
Связи разрывать произвольно | Если в первых трёх методах для дельнейшего анализа используется только один элемент данных, то в этом методе может использоваться столько элементов, сколько значений имеется в наличии. |
-
Оставьте предварительные установки и подтвердите построение диаграммы нажатием ОК.
Будут построены две диаграммы. На первой, простой Р-Р-диаграмме отображается зависимость ожидаемых совокупных частот от фактических совокупных частот, рассчитанная при помощи формулы рангового преобразования Блома (Blom). На второй диаграмме, Р-Р-диаграмме без тренда, отображается разность между фактическими и ожидаемыми совокупными (кумулятивными) частотами в зависимости от фактических совокупных частот.
Рис. 22.63: Диаграмма нормального распределения типа Р-Р
Рис. 22.64: Диаграмма нормального распределения типа Р-Р с исключённым трендом
64.gif
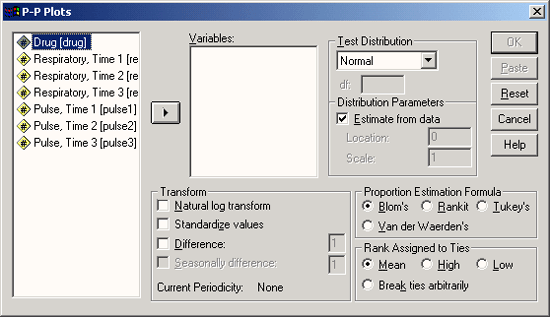
65.gif
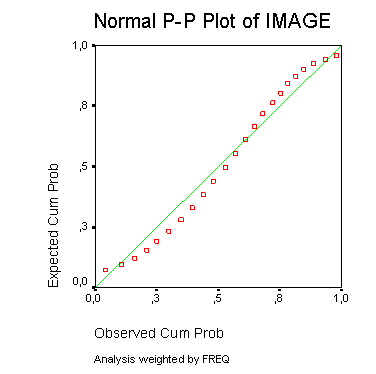
66.gif
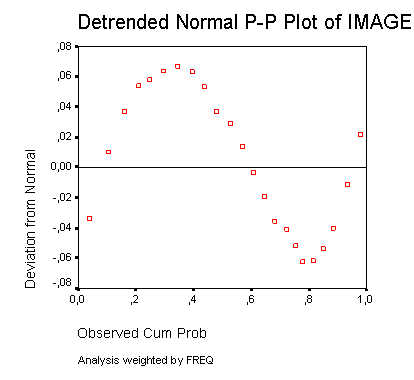
22.13 Кривые ROC
22.13 Кривые ROC
Понятие кривых ROC (Receiver Operating Characteristic — функциональные характеристики приемника) взято из методологии анализа качества приёма сигнала (Signal Detection Analysis). Теория, стоящая за этим анализом, Theorie of Signal Detectability (TSD — "Теория определимости сигнала"), хотя и происходит первоначально из электроники и электротехники, но может также быть применена в области медицины, для анализа взаимодействия чувствительности и представительности диагностического теста. Поясним это при помощи примера.
В разделе 16.4 (Бинарная логистическая регрессия) было показано, каким образом при помощи переменных, соответствующих результатам Т-типизации клеток, которые относятся к интервальной шкале, может быть спрогнозировано появление карциномы мочевого пузыря. Если вы посмотрите на обе группы (больных и здоровых), то заметите, что здоровые демонстрируют более высокие значения Т-типизации ячеек, а больные скорее более низкие значения. Поэтому можно попытаться найти граничное значение Т-типизации ячеек, которое будет чётко разделять обе группы больных и здоровых.
Это и было достигнуто при помощи метода бинарной логистической регрессии. Пройдём ещё раз тот путь, который мы проходили в главе 16.4.
-
Откройте файл hkarz.sav.
-
Выберите в меню Analyze... (Анализ) Regression. ..(Регрессия) Binary logistic... (Бинарная логистическая)
-
В диалоговом окне Logistic Regression (Логистическая регрессия) переменную gruppe (группа) поместите в поле зависимых переменных, а переменную tzell — в поле ковариций. Результаты теста LAI мы сначала не будем использовать в расчёте. При помощи выключателя Save... (Сохранить) организуйте сохранение прогнозируемой принадлежности к группе в виде дополнительной переменной. Начните расчёт нажатием ОК.
К исходному файлу данных добавилась переменная pgr_1. Если Вы построите таблицу сопряженности между переменной gruppe (группа) в качестве строчной переменной и переменной pgr_1 в качестве столбцовой переменной, то получите следующий результат (для сравнения см. рис. 16.7):
GRUPPE * Predicted group Crosstabulation
(GRUPPE * Прогнозируемая группа таблица сопряженности) | ||||
Count (Количество) | ||||
Predicted group (Прогнозируемая группа) | Total (Сумма) | |||
krank (Болен) | gesund (Здоров) | |||
GRUPPE | krank (Болен) | 18 | 6 | 24 |
gesund (Здоров) | 4 | 17 | 21 | |
Total (Сумма) | 22 | 23 | 45 | |
Среди 24 фактически больных 18 были верно расценены как больные (Rightly Positive (Верно положительный), RP), а 6 не верно отнесены к группе здоровых (Wrong Negative (Ложно отрицательный), WN). Из 21 фактически здорового человека 17 были верно отнесены к группе здоровых (Rightly Negative (Верно отрицательный), RN) и 4 не верно расценены больными (Wrong Positive (Ложно положительный), WP).
В качестве чувствительности теста выступает доля верно положительных предсказаний в суммарном количестве больных.

Эта величина характеризует способность теста как можно точнее отфильтровывать пациентов с сомнительным наличием болезни.
Под представительностью теста понимают долю верно отрицательных среди здоровых пациентов:

Эта величина характеризует способность теста обнаруживать исключительно пациентов с сомнительным наличием болезни. Для приведенного примера имеем
Чувствительность =18/(18 + 6) = 0,750
Представительность = 17/(17 + 4) = 0,810
-
Если при помощи меню Data (Данные) Sort Cases... (Сортировать наблюдения)
вы отсортируйте данные по переменной tzcll, то заметите, что все наблюдения со значениями, лежащими ниже 66,5, отнесены к категории болен, а все наблюдения со значениями, находящимися выше 66,5, отнесены к категории здоров.
-
Если Вы сместите граничное значение вниз или вверх и вновь рассчитаете чувствительность и специфичность, то результаты изменятся таким образом, что повышение чувствительности будет идти за счёт представительности, а повышение представительности за счёт чувствительности. Эту зависимость можно анализировать при помощи кривой ROC.
-
Выберите в меню Graphs (Графики) ROC Curve... (Кривая ROC)
Откроется диалоговое окно ROC Curve (Кривая ROC)
-
Переменной tzell присвойте статус тестируемой переменной, а переменной gruppe — статус переменной состояния. Под значением Value of State Variable: (Значение переменной состояния) понимается положительное значение, т.е. кодировка, соответствующая состоянию "болен". Введите в это поле 1. В группе Display (Показать) активируйте все имеющиеся опции.
-
Щелчком по кнопке Options... (Параметры) откройте диалоговое окно ROC Curve: Options (Кривая ROC: Опции) (см. рис. 22.66).
-
Активируйте опцию Smaller test result indicates more positive test (Меньший результат теста означает более положительный результат), так как в данном примере состоянию "болен" соответствует тенденция к уменьшению значений тестируемых переменных по сравнению с состоянием "здоров".
Результаты анализа, отображаемые в окне просмотра, приводятся ниже.
Case Processing Summary (Обработанные наблюдения)
GRUPPE b | Valid N (listwise) (Действительные случаи (в соответствии со списком)) |
Positive a (Положительные) | 24 |
Negative (Отрицательные) | 21 |
Smaller values of the test result variable(s) indicate stronger evidence for a positive actual state (Низкие значения переменной(ых) указывают на скорее положительный результат теста).
a. The positive actual state is krank (Положительный результат теста соответствует состоянию болен).
b. The test result variable(s): TZELL has at least one tie between the positive actual state group and the negative actual state group (Результирующая переменная (переменные) теста: TZELL имеет по крайней мере одну связку между положительной и отрицательной группами).
Рис. 22.65: Диалоговое окно ROC Curve (Кривая ROC)
Рис. 22.66: Диалоговое окно ROC Curve: Options (Кривая ROC: Опции)
Area Under the Curve (Площадь под кривой)
| Test Result Variable(s): TZELL (Переменная(ые) результата теста: TZELL) | ||||
Area (Площадь) | Std. Error (Стандартная ошибка) | Asymptotic Sig.a (Асимптотическ ая значимость) | Asymptotic 95% Confidence Interval (Асимптотический 95 % доверительный интервал) | |
Lower Bound (Нижняя граница) | Upper Bound (Верхняя граница) | |||
,849 | ,059 | ,000 | ,734 | ,964 |
The test result variable(s): TZELL has at least one tie between the positive actual state group and the negative actual state group (Результирующая переменная(ые) теста: TZELL имеет по крайней мере одну связку между положительной и отрицательной группами). Statistics may be biased (Статистики могут быть искажены (сдвинуты)).
a. Under the nonparametric assumption (В соответствии с непараметрическим предположением)
b. Null hypothesis: true area = 0.5 (Нулевая гипотеза: истинное значение площади = 0,5)
Coordinates of the Curve (Координаты кривой)
Test Result Variable(s): TZELL (Результирующая переменная(ые) теста: TZELL)
Positive if Less Than or Equal Toa (Положительно, если меньше или равно) | Sensitivity (Чувствительность) | 1 - Specificity (1-Представительность) |
47,5000 | ,000 | ,000 |
52,0000 | ,042 | ,000 |
56,5000 | ,083 | ,000 |
58,0000 | ,125 | ,000 |
59,7500 | ,167 | ,000 |
61,0500 | ,208 | ,000 |
61,3000 | ,208 | ,048 |
61,7500 | ,292 | ,048 |
62,2500 | ,417 | ,048 |
62,0000 | ,458 | ,095 |
63,7500 | ,500 | ,095 |
64,7500 | ,542 | ,143 |
64,5000 | ,542 | ,190 |
65,7500 | ,625 | ,190 |
67,2500 | ,750 | ,190 |
68,7500 | ,792 | ,190 |
69,2500 | ,833 | ,190 |
69,7500 | ,833 | ,238 |
70,5000 | ,833 | ,333 |
71,2500 | ,958 | ,381 |
71,7500 | ,958 | ,476 |
72,2500 | ,958 | ,524 |
72,7500 | ,958 | ,571 |
73,2500 | ,958 | ,667 |
73,7500 | 1,000 | ,714 |
74,5000 | 1,000 | ,762 |
75,5000 | 1,000 | ,810 |
76,5000 | 1,000 | ,857 |
77,7500 | 1,000 | ,952 |
79,5000 | 1,000 | 1,000 |
The test result variable(s): TZELL has at least one tie between the positive actual state group and the negative actual state group (Результирующая переменная(ые) теста: TZELL имеет по крайней мере одну связь между положительной и отрицательной группами),
a. The smallest cutoff value is the minimum observed test value minus 1, and the largest cutoff value is the maximum observed test value plus 1. All the other cutoff values are the averages of two consecutive ordered observed test values.(Минимальное разделяющее значение равно минимальному наблюдаемому значению теста минус 1, максимальное разделительное значение равно максимальному наблюдаемому значению теста плюс 1. Все остальные разделительные значения являются средними значениями двух соседних наблюдаемых значений теста.)
С помощью кривой ROC чувствительность и комплиментарное значения представительности приводятся к единице. Диагностируемое значение с нулевой степенью прогнозирования изображается здесь линией, наклоненной под углом 45 градусов (диагональю). Чем больше выгнута кривая ROC, тем более точным является прогнозирование результатов теста. Индикатором этого свойства служит площадь под кривой ROC, которая для теста с нулевой степенью прогнозирования равна 0,5, а для случая с максимальной степенью прогнозирования — 1. Для рассматриваемого примера получилось значение равное 0,849, причём 95 % доверительный интервал соответствует значениям площади, принадлежащим диапазону от 0,734 до 0,964.
В следующей таблице Вы можете увидеть чувствительность и представительность для различных граничных значений. Для граничного значения 67,5 Вы вновь встретите уже рассчитанные нами показатели.
69.gif
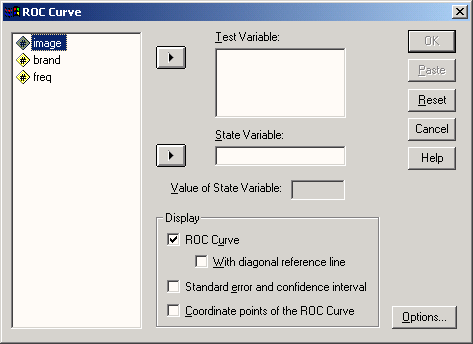
70.gif
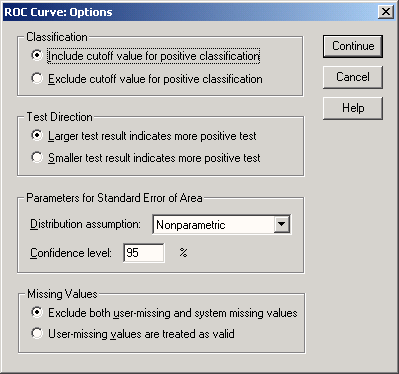
71.gif
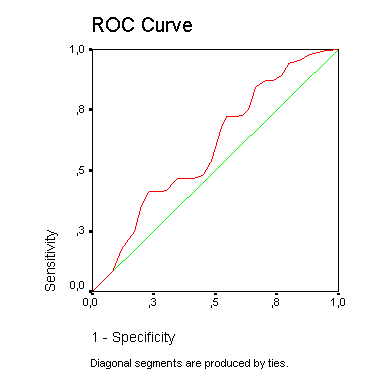
22.14 Временные диаграммы и графики последовательностей
22.14 Временные диаграммы и графики последовательностей
-
Посторонние временных рядов и графиков последовательностей происходит посредством выбора меню Graphs (Графики) Time Series... (Временной ряд) и Graphs (Графики) Sequence... (Последовательность)
соответственно. В связи с тем, что в модулях SPSS, рассматриваемых в этой книге, отсутствует анализ временных рядов, мы не будем подробно останавливаться на этой диаграмме. Информацию по этому вопросу Вы можете найти в книге этих же авторов: 'SPSS. Методы исследования рынка и мнений".
22.15 Основы редактирования графиков
22.15 Основы редактирования графиков
Для того, чтобы разобраться во всех возможностях, которые SPSS для Windows предоставляет для редактирования графиков, наверняка потребуется некоторое время.
Построение графиков происходит при помощи большого количества процедур меню статистик и из меню графиков. Все графики, построенные таким образом, попадают сразу в окно просмотра. Отсутствует промежуточное сохранение, существовавшее вплоть до 6-ой версии SPSS.
Даже при построении Ваших первых графиков (теперь в SPSS они, как правило, называются диаграммами) можно не беспокоиться об их внешнем виде, поскольку в силу вступают соответствующие установки по умолчанию. Если Вы к тому же добавили некоторые наименования (заголовок, подзаголовок, сноски), то такой вид уже будет вполне достаточен для того, чтобы графики можно было использовать в большинстве практических ситуаций.
Если Вы хотите придать графикам более наглядный и презентабельный вид или же существует необходимость произвести определённые корректировки (к примеру, если метки переменных слишком длинны), то график следует перенести в редактор диаграмм. Для этого в окне просмотра дважды щёлкните в любом месте в области диаграммы.
В редакторе диаграмм Вы сможете производить над графиком следующие действия:
-
корректировать (или изменить)
-
сохранить график в каком-либо другом графическом формате
-
сохранить как образец для других графиков и
-
копировать в буфер обмена Windows.
Обзор всего многообразия возможностей дополнительной обработки, которые предлагает Вам редактор диаграмм, приводится в разделе 22.16. В разделе 22.17 рассматриваются три типичных примера редактирования.
22.16 Редактор диаграмм
22.16 Редактор диаграмм
Для того, чтобы график можно было изменить (доработать, редактировать), он должен быть помещён в редактор диаграмм. Это происходит после двойного щелчка на какой-либо точке в области диаграммы, находящейся в окне просмотра. Тогда редактор диаграмм будет выглядеть так, как на рис. 22.67.
В верху редактора диаграмм присутствуют меню и две панели инструментов. Если Вы пройдётесь курсором по кнопкам панелей инструментов, не нажимая их, то сможете увидеть краткое описание кнопок. При помощи кнопок верхней панели инструментов, Вы можете получить информацию о диалоговых полях, которые Вы заполняли в последних построенных диаграммах, перейти в редактор данных, в нём перейти к нужному Вам наблюдению; а также получить информацию об отдельных переменных.
Кнопки, стоящие во второй панели инструментов, преимущественно служат для вызова форматирующих меню и будут рассмотрены в соответствующем разделе. Статистические, графические меню и меню помощи уже известны, и поэтому здесь они рассматриваться не будут.
Рис. 22.67: Редактор диаграмм
-
File (Файл): При помощи меню File (Файл) построенную диаграмму Вы можете сохранить, вывести на печать или скопировать свойства с некоторого графика-образца.
-
Edit (Правка): При помощи меню Edit (Правка) Вы можете скопировать график в буфер обмена или изменить установки графика.
-
View (Вид): В меню View (Вид) Вы можете включить или выключить строку состояния и управлять панелями инструментов.
-
Gallery (Галерея): При помощи меню Gallery (Галерея) Вы можете выбрать другой тип графика для отображения ваших данных. Причём в списке Вы увидите некоторые дополнительные типы графиков, которые ещё не были рассмотрены, к примеру, смешанные диаграммы, диаграммы связывающих линий и разделённые круговые диаграммы.
-
Chart (Диаграммы): Меню Chart (Диаграммы) служит для изменения внешнего вида диаграммы и элементов ее описания.
Пункты меню Options... (Параметры), Axis... (Оси) и Bar Spacing... (Расстояние между столбцами) являются специфическими для текущего типа диаграммы. После выбора этих опций открываются соответствующие диалоговые окна, содержание которых говорит само за себя.
-
Series (Ряды): При помощи меню Series (Ряды) можно менять представление данных, то есть столбцы на линии или другие виды графического представления.
-
Format (Формат): Если Вы щёлкните на этой кнопке, то получите список меню, представленный на рис. 22.68.
Большинство пунктов этого меню выведены на вторую панель инструментов. Вместо того, чтобы открывать меню, вы можете просто щёлкнуть на кнопке с соответствующим символом на панели инструментов.
 Point Id (Выделение точек)
Point Id (Выделение точек)При помощи этой кнопки Вы можете менять режимы отображения точек на диаграмме рассеяния (для сравнения см. разд. 22.8.1)
 Fill Pattern (Заливка узором)
Fill Pattern (Заливка узором)Откроется диалоговое меню, в котором Вы можете выбрать необходимый рисунок из восьми образцов заливки для окрашивания замкнутых контуров, таких как: столбцы, области под линиями и области заднего плана.
Нужный объект выделяется щелчком на его поле. После этого на углах объекта должны появиться маркеры коррекции.
Вы выбираете необходимый тип заливки и щелчком на кнопке Apply (Применить) присваиваете его выбранному объекту.
Заливка белого цвета является прозрачной. Этот вид заливки следует выбирать тогда, когда некоторая последовательность данных должна быть показана на фоне другой последовательности.
Рис. 22.68: Меню Format (Формат)
 Color (Цвет)
Color (Цвет)Для изменения цвета объекта графика (элемента представления данных или текста) выделите данный объект и выберите этот пункт меню. Откроется палитра с шестнадцатью различными цветами. Кому этого не достаточно, может открыть ещё одну дополнительную значительно более обширную палитру.
Выбором опций Fill (Заливка) и Border (Рамка) происходит переключение между возможностью изменить цвет объекта или рамки (контура) выделенного объекта.
Выберите одну из двух имеющихся опций. При помощи Apply (Применить) цвет будет перенесён на выделенный объект.
Чтобы расширить имеющуюся палитру цветов, щёлкните на кнопке Edit (Правка); после этого Вы сможете создать дополнительные или пользовательские цвета.
Если текущей палитре должен быть присвоен статус палитры по умолчанию, то щёлкните на выключателе Save as Default (Сохранить как палитру по умолчанию).
 Marker (Маркер)
Marker (Маркер)Эта кнопка открывает палитру из 28-ми различных маркеров для обозначения положения точки данных на линейчатых диаграммах, диаграммах с областями и диаграммах рассеяния. Вы можете также установить один из четырёх предустановленных размеров маркеров.
Для изменения вида представления точек или рядов данных выделите сначала нужный элемент при помощи щелчка на графике. После этого на выделенном объекте появятся чёрные маркеры коррекции.
В группе Style (Стиль) выберите необходимую маркировку.
В группе Size (Размер) активируйте одну из опций предустановленных размеров маркеров. На экране разница между размерами отображаемых маркеров не значительна, но при печати она будет довольно хорошо заметна.
При помощи Apply (Применить) присвойте выделенному ряду данных маркеры с выбранными свойствами. Если Вы нажмёте кнопку Apply All (Применить для всех), то выбранный тип маркировки будет присвоен всем последовательностям данных.
Если изменения должны коснуться только размера маркеров, но не стиля маркировки, то следует деактивировать опцию Apply style (Применить стиль).
Если изменения должны коснуться только стиля представления маркеров, но не размера, то следует деактивировать опцию Apply size (Применить размер).
Маркеры на линейчатых диаграммах и диаграммах с областями становятся видимыми только в том случае, если их вывод будет задан в диалоговом окне Interpolation (Интерполяция). Это диалоговое окно вызывается из меню Format (Формат). Маркеры не могут быть заданы для изображения точек гистограмм и столбчатых диаграмм.
 Line Style (Линии)
Line Style (Линии)Здесь на выбор предлагаются четыре типа линий и четыре предустановленные толщины для этих линий.
На графике щелчком необходимо выделить линию, которую необходимо изменить. После этого на объекте появятся маркеры коррекции.
В группе Style (Стиль) выберите тип линии.
В группе Weight (Толщина) присвойте необходим} ю то.глину выбранному типу линии.
После щелчка на кнопке Apply (Применить) выбранная конфигурация линии будет присвоена активному объекту. Эта кнопка остаётся неактивной, если выделены данные, которые не могут быть представлены на графике при помощи линии или элемента, содержащего линии (рамки, оси).
 Bar Style (Столбцы)
Bar Style (Столбцы)Эта опция служит для изменения представления столбцов в графиках, содержащих столбцы. Некоторые типы столбцов не могут применяться для гистограмм.
Программа предлагает в Ваше распоряжение несколько типов столбцов. Если выбраны столбцы с тенью (Drop shadow) или с ЗD-эффектами (3D-effect), то для этих типов столбцов дополнительно ещё может устанавливаться и толщина (Depth). Эта опция управляет толщиной сторон и верхнего торца столбца. Толщина при этом указывается в процентах от ширины столбца. При положительных значениях параметра Depth (Толщина) эффект строится начиная с правой стороны столбца, как показано на рисунках соответствующих опций, а при отрицательных значениях — с левой стороны столбца.
Если Вы нажмёте кнопку Apply All (Применить для всех), то установленные свойства будут применены ко всем столбцам. Эта кнопка становится активной только тогда, когда в редакторе диаграмм находится столбчатая диаграмма или интервальная столбчатая диаграмма.
 Bar Label Style (Метки столбцов)
Bar Label Style (Метки столбцов)Программа предлагает три варианта идентификации столбцов при помощи числовых значений.
Если выбран один из стилей оформления числового значения (кроме None), то на каждом столбце появляется числовое значение, соответствующее высоте этого столбца. Для столбчатой диаграммы с областями метки столбцов указываются сверху и снизу каждого столбца. Три опции представленные в диалоговом окне Bar Label Styles (Метки столбцов) определяют внешний вид метки на столбце. Если Вы применяете тёмные цвета или узоры, в таком случае рекомендуется выбирать опцию Framed (В рамке), числовое значение в рамке будет лучше читаться.
Если Вы нажмёте кнопку Apply All (Применить для всех), то установленные свойства метки будут применены ко всем столбцам. Эта кнопка становится активной только тогда, когда в редакторе диаграмм находится столбчатая диаграмма, интервальная столбчатая диаграмма или гистограмма.
 Interpolation (Интерполяция)
Interpolation (Интерполяция)В данном диалоговом окне задаются различные возможности и методы для соединения точек данных.
Эта опция может применяться для диаграмм с областями, линейчатых диаграмм, линейчатых диаграмм разностей, для последовательностей средних значений в диаграммах величины ошибки, для заключительных показателей на диаграммах максимальных и минимальных значений, а также в диаграммах рассеяния (исключая 3D-диаграммы рассеяния).
На графике щелчком выделите линию или последовательность данных. После этого на каждом объекте появятся маркеры коррекции.
В группе Line Interpolation (Вид интерполяционной линии) выберите один из методов соединения точек при помощи некоторой кривой. Если SPSS должна рассчитать регрессионную прямую для диаграммы рассеяния, выберите в меню Chart (Диаграммы) пункт Options (Параметры).
Если Вы нажмёте кнопку Apply All (Применить для всех), интерполяция будет применена ко всем последовательностям данных. При помощи Apply (Применить) интерполяция будет применена только к объектам, выделенным в данный момент. Если Вы выделили данные, которые не могут быть отображены на графике при помощи линии, кнопка Apply (Применить) становится неактивной.
Если активировать опцию Display markers (показать маркеры), то для каждой точки выделенной кривой будет отображена маркировка. Тип маркера может быть выбран при помощи опции Marker (Маркер), находящейся в меню Format (Формат).
Существуют следующие виды интерполяции:
-
None (Отсутствует): при выборе этой опции соединение между точками отсутствует.
-
Straight (Прямая): точки последовательно соединяются прямой линией в том порядке, в котором они находятся в файле данных.
-
В списке Steps (Шаги) Вы можете выбрать один из альтернативных методов построения ступенчатой интерполяции. Эти методы соответствуют шаговым функциям, в которых точки данных соединяются с левых сторон, в центрах или с правых сторон шагов, в зависимости от того была ли выбрана опция Left step (Левый шаг), Center step (Центральный шаг) или Right step (Правый шаг). Шаги между собой соединяются вертикальными отрезками.
-
В списке Jump (Прыжок) может быть выбран один из методов скачкообразной интерполяции. Скачкообразные методы строятся точно так же, как и пошаговые, но в них отсутствуют вертикальные соединения. В зависимости от выбора Left jump (Прыжок слева) Center jump (Прыжок по центру) или Right jump (Прыжок справа) точки данных будут лежать с левой стороны, по середине или с правой стороны горизонтальных отрезков.
-
В списке Spline (Сплайн) может быть выбран один из методов соединения точек данных при помощи кривой.
— при выборе опции Spline (Сплайн) для соединения точек данных между собой строятся кубические сплайны.
— при выборе опции 3rd-order Lagrange (Лагранж 3-го порядка) осуществляется интерполяция, при которой кривая аппроксимируется полиномом третье! о порядка, который строится на основе четырёх последовательных точек данных.
— при выборе опции 5rd-order Lagrange (Лагранж 5-го порядка) осуществляется интерполяция, при которой кривая аппроксимируется полиномом пятого порядка, который строится на основе шести последовательных точек данных.
 Text (Текст)
Text (Текст)
Эта опция предоставляет возможность изменить шрифт и размер текстовых элементов.
Сначала одним щелчком выделяют текст на графике. После этого на тексте появляются метки коррекции.
В группе Font (Шрифт) выбирают необходимый тип шрифта, а в группе Size (Размер) необходимый размер. Размер шрифта (кегль) выражается в точках.
После щелчка на кнопке Apply (Применить) выбранные свойства будут перенесены на выделенный объект. Эта кнопка становится активной только тогда, когда выделен текстовый объект.
 3D-Rotation (ЗО-врашение)
3D-Rotation (ЗО-врашение)Это один из двух методов, с использованием которых можно вращать ЗD-диаграмму рассеяния. При помощи переключателей на левой стороне диалогового окна диаграмму можно вращать вперёд или назад относительно осей X, Y и Z.
Рисунки на переключателях указывают на ось и направление вращения. Вы можете вращать систему координат при помощи коротких щелчков на соответствующих переключателях или удерживая нажатой кнопку мыши. Вращение, задаваемое таким образом, отображается на упрощенной схеме, где изображены три оси; эта схема находится в центре диалогового окна.
Если активирована опция Show tripod (Показать треножник), то будет показан треножник, линии которого проходят через центр области построения диаграммы параллельно осям. Активирование треножника особенно рекомендуется тогда, когда необходимо проследить вращение осей при выключенном обрамлении трехмерного графика.
Вращение выделенной диаграммы происходит при помощи кнопки Apply (Применить).
График будет повёрнут только тогда, когда к нему будет применено заданное вращение. В течении операции вращения применение каких-либо других команд становится невозможным.
 Swap Axes (Смена осей)
Swap Axes (Смена осей)При помощи этой опции в двумерном графике можно поменять местами вертикальную и горизонтальную оси.
 Explode Slice (Выдвинуть сегмент)
Explode Slice (Выдвинуть сегмент)Чтобы выдвинуть сегмент круговой диаграммы, выделите его и нажмите эту кнопку.
 Break Lines at Missing (Разорвать линию в месте отсутствующего значения)
Break Lines at Missing (Разорвать линию в месте отсутствующего значения)Разрыв линии на линейной диаграмме при наличии отсутствующего значения.
 Chart options (Параметры графика)
Chart options (Параметры графика)Здесь Вам предлагается выбор дополнительных параметров для столбчатых и линейчатых диаграмм, а также диаграмм с областями. В случае линейчатых диаграмм, Вы также можете разделить линии по категориям.
При активировании опции Change scale to 100 % (Перевести масштаб в проценты) точки данных столбчатых диаграмм и частотных диаграмм с областями переводятся в процентные показатели и отображаются как процентные доли. Если редактируемая диаграмма является столбчатой, то столбцы будут автоматически штабелированы. Если на редактируемой диаграмме столбец или область отображает только один ряд данных, то эта опция остаётся недосягаемой. Эта опция также неприменима в случае, если диаграмма отображает функцию накопительной суммы.
В группе Line Options (Параметры линии) предлагаются ещё две возможности обработки линейных диаграмм.
-
Опция Connect markers within categories (Соединить маркеры внутри категорий) соединяет маркеры, которые принадлежат к одним и тем же категориям, но лежат на разных кривых. Эта опция может применяться для диаграмм, на которых представлены как минимум две кривые. Она не влияет на текущий статус интерполяции или маркировки кривых.
-
Опция Display projection (Показать проекцию) позволяет выделить некоторую про-екцируемую категорию. Категории, находящиеся справа от проецируемой категории отображаются иначе.
Если на диаграмме в виде столбцов представлены по меньшей мере два ряда данных, то при помощи группы Ваг Туре (Тип столбцов), её можно преобразовать в кластеризованную или состыкованную диаграмму. Если активирована опция Change scale to 100 % (Перевести масштаб в проценты), то группа Ваг Туре (Тип столбцов) становится недоступной.
 Set/exit spin mode (Включить/выключить режим вращения)
Set/exit spin mode (Включить/выключить режим вращения)И эта кнопка делает возможным непосредственное вращение ЗD-диаграммы рассеяния в окне редактора диаграмм; но здесь в процессе вращения диаграмма претерпевает некоторые упрощения.
Вращать диаграмму вперёд и назад относительно осей X, Y и Z можно при помощи кнопок с соответствующими символами в левой части диалогового окна.
Символы на клопах вращения указывают на оси и направление вращения. Вы можете вращать область координат пошагово при помощи коротких щелчков или беспрерывно, удерживая кнопку мыши нажатой. Производимое таким образом вращение, отображается при помощи системы трех осей в центре окна редактора диаграмм.
72.gif
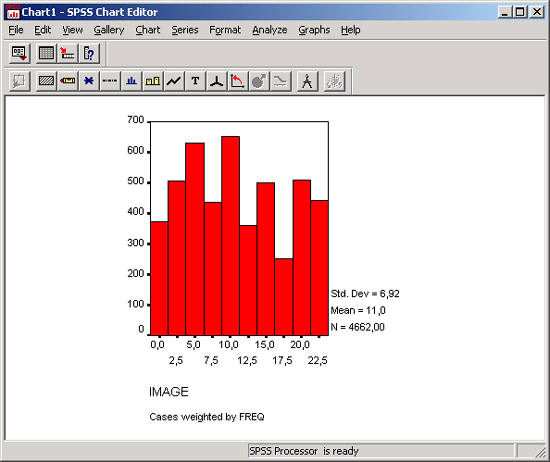
75.gif

22.17 Примеры редактирования графиков
22.17 Примеры редактирования графиков
Некоторые примеры редактирования графиков уже приводились в главах 4, 6 и 11. В этой главе мы рассмотрим ещё три дополнительных примера.
22.17.1 Пример первый: изменение наименования осей
22.17.1 Пример первый: изменение наименования осей
-
Откройте в окне просмотра результатов файл balken.spo, в котором хранится график, изображённый на рис. 22.43.
Здесь необходимо изменить наименование вертикальной оси.
-
Двойным щелком перенесите график в редактор диаграмм и щелчком выделите наименование вертикальной оси.
-
После этого выберите в меню Chart (Диаграмма) Axis... (Ось)
В появляющемся окне Вам предлагается множество разнообразных возможностей редактирования оси.
-
Измените название оси на "Холестерин, исходный показатель" и покиньте диалоговое окно нажатием ОК.
В результате Вы увидите отредактированный график, который после закрытия редактора диаграмм будет отображён и в окне просмотра результатов.
22.17.2 Пример второй: редактирование круговой диаграммы
22.17.2 Пример второй: редактирование круговой диаграммы
-
Откройте файл kreis.spo, в котором хранится круговая диаграмма, представленная на рис. 22.30. Эта диаграмма пока ещё не показывает результаты голосования в процентах.
-
Двойным щелком перенесите график в редактор диаграмм.
-
Щёлкните дважды на названии одной из представленных партий (к примеру, SPD или CDU).
-
Откроется диалоговое окно Pie Options (Параметры круговой диаграммы) (см. рис. 22.69).
-
Поставьте маркер в поле Percents (Проценты) и щёлкните на кнопке Format... (Формат).
Откроется диалоговое окно Pie Options: Label Format (Параметры круговой диаграммы: Формат метки), представленное на рисунке 22.70.
Здесь Вам предоставляется возможность указать место нахождения численного значения переменной.
-
В группе Display Frame Around (Показать круговую рамку) активируйте опцию Outside labels (Метка снаружи).
-
Подтвердите нажатием Continue (Далее) и затем на ОК. Вы получите диаграмму, изображённую на рисунке 22.71.
Рис. 22.69: Диалоговое окно Pie Options (Параметры круговой диаграммы)
89.gif
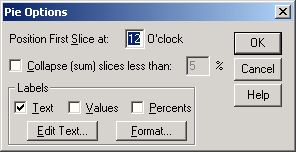
22.17.3 Пример третий: нанесение регрессионных линий
22.17.3 Пример третий: нанесение регрессионных линий
-
В окне просмотра результатов откройте файл streumat.spo, в котором находится матричная диаграмма рассеяния, изображённая на рис. 22.50, и двойным щелком перенесите её в редактор диаграмм.
-
В списке меню редактора диаграмм выберите Chart (Диаграмма) Options... (Параметры)
Рис. 22.70: Диалоговое окно Pie Options: Label Format (Параметры круговой диаграммы: Формат метки)
Рис. 22.71: Результаты голосования на местных выборах в земле Гессен 1993.
Откроется диалоговое окно Scatterplot Options (Параметры диаграммы рассеяния) (см. рис. 22.72).
-
В группе Fit Line (Приближённая линия) активируйте опцию Total (Обобщённая).
-
Щёлкните на выключателе Fit Options... (Параметры приближения). Откроется диалоговое окно Scatterplot Options: Fit Line (Параметры диаграммы рассеяния: Приближённая линия).
-
Щёлкните на области Linear regression (Линейная регрессия) и в группе Regression Prediction Line(s) (Линия(и) для оценки качества регрессии) отметьте опцию Mean (Среднее значение); таким образом для регрессионной прямой Вы получите 95 % доверительный интервал.
-
Покиньте диалоговое окно нажатием Continue (Далее) и затем ОК.
Теперь на рассматриваемой диаграмме рассеяния присутствуют регрессионные прямые и соответствующие им доверительные интервалы.
Рис. 22.72: Диалоговое окно Scatterplot Options (Параметры диаграммы рассеяния)
Рис. 22.73: Диалоговое окно Scatterplot Options: Fit Line (Параметры диаграммы рассеяния: Приближённая линия)
В корректировке нуждаются ещё названия переменных.
-
Дважды щёлкните на тексте в левом верхнем диагональном элементе.
-
В появившемся диалоговом окне Scatterplot Matrix Scale Axes (Оси матричной диаграммы рассеяния) в группе Individual Axes (Отельные оси) отметьте редактируемый текст и щёлкните на выключателе Edit... (Правка).
Откроется диалоговое окно Scatterplot Matrix Scale Axes: Edit Selected Axis (Оси матричной диаграммы рассеяния: Редактирование выделенной оси).
-
Наберите в диалоговом окне более короткий текст, к примеру, "ожидаемая продолжительность жизни" (Lebenserwartung) и подтвердите нажатием Continue (Далее).
-
Поступите также и с двумя другими диагональными элементами матричной диаграммы рассеяния.
-
Закончите редактирование графика нажатием ОК (см. рис. 22.74).
Всё многообразие возможностей для корректировки графиков, предлагаемых программой, при помощи нескольких приведенных примеров можно рассмотреть только в самых общих чертах. Эти примеры, по меньшей мере, должны были послужить Вам мотивацией для самостоятельного проведения дальнейших опытов, в ходе которых можно выяснить и другие возможности приведения графиков к более презентабельному виду.
Рис. 22.74: Матричная диаграмма рассеяния с регрессионными прямыми и доверительными интервалами
90.gif
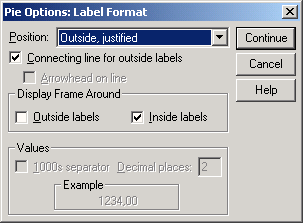
91.gif
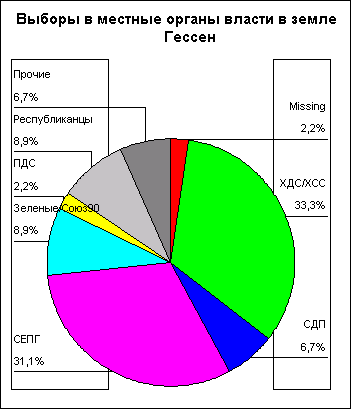
92.gif
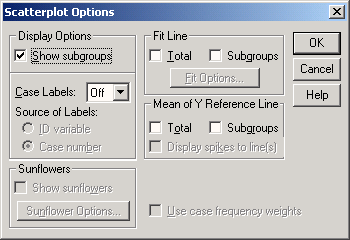
93.gif
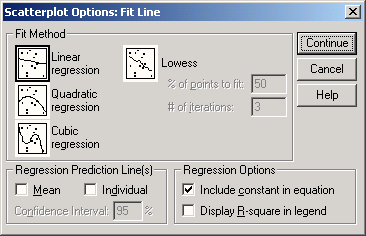
94.gif
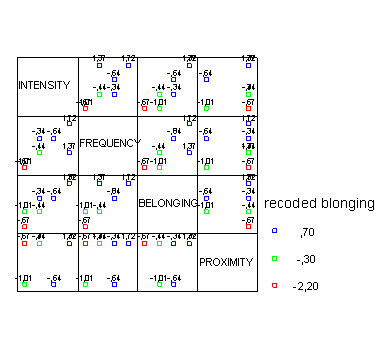
22.2 Линейчатые диаграммы
22.2 Линейчатые диаграммы
Линейчатую диаграмму вместо столбчатой следует выбирать тогда, когда необходимо отобразить большое количество столбцов, а также тогда, когда столбцы располагаются в определённой последовательности. Как правило, это временная последовательность.
Рис. 22.15: Штабельная столбчатая диаграмма
-
Для построения линейной диаграммы после открытия соответствующего файла SPSS выберите в меню: Graphs (Графики) Line... (Линейчатые)
Откроется диалоговое окно Line Charts (Линейчатые диаграммы) (см. рис. 22.16).
Вы можете построить простую, сложную и связанную линейные диаграммы. Как и для столбчатых диаграмм данные, отображаемые в этих диаграммах, могут быть заданы как категории одной переменной, как разные переменные или как значения отдельных наблюдений.
Рис. 22.16: Диалоговое окно Line Charts (Линейчатые диаграммы)
15.gif
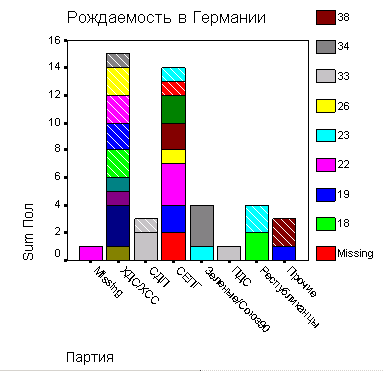
16.gif
22.2.1 Простые линейчатые диаграммы
22.2.1 Простые линейчатые диаграммы
В файле buecher.sav хранится информация о развитии книгопечатания в Германии с 1962 по 1991 год.
-
Откройте файл buecher.sav и просмотрите его содержимое в редакторе данных.
-
В диалоговом окне Line Charts (Линейчатые диаграммы) щёлкните на области Simple (Простая) и оставьте, опцию Summaries for groups of cases (Обработка категорий одной переменной), устанавливаемую по умолчанию.
-
После щелчка по выключателю Define (Определить) откроется соответствующее диалоговое окно.
-
В поле Category Axis: (Ось категорий) введите переменную jahr (год). В группе Line Represent (Значения линий) активируйте Other summary function (Другая обрабатывающая функция) и в появившееся поле введите переменную anz (количество). Вместо установленной по умолчанию функции Mean of values (Средние значения), пройдя выключатель Change Summary...(Изменить метод обработки), отметьте функцию суммы значений (Sum of values) (которая в данном случае, правда, дает тот же эффект).
-
С помощью выключателя Titles... (Заголовок), введите подходящий заголовок.
-
Начните построение диаграммы щелчком на ОК.
Рис. 22.17: Диалоговое окно Define Simple Line: Summaries for Groups of Cases (Построение простой линейчатой диаграммы: Обработка категорий одной переменной)
Рис. 22.18: Линейчатая диаграмма
17.gif
18.gif

22.2.2 Сложные линейчатые диаграммы
22.2.2 Сложные линейчатые диаграммы
Следующая таблица демонстрирует тенденцию нарушения законов по охране окружающей среды в Западной Германии с 1985 по 1992 год:
Гол | Нарушения | ||
UA | CV | UB | |
1985 | 2.750 | 8.562 | 901 |
1986 | 3.682 | 9.294 | 1.161 |
1987 | 5.390 | 10.529 | 1.311 |
1988 | 6.748 | 1 1 .968 | 1.671 |
1989 | 8.559 | 1 1 .827 | 1.590 |
1990 | 8.157 | 9.942 | 1.525 |
1991 | 9.724 | 9.601 | 1.457 |
1992 | 12.453 | 8.687 | 1.573 |
Где
UA — Переработка мусора, наносящая вред окружающей среде
GV — Загрязнение воды
UB — Использование запрещённого промышленного оборудования
Эти данные построчно сохранены в переменных jahr (год), ua, gv и ub в файле umwelt.sav.
-
Откройте файл umwelt.sav и просмотрите его содержимое в редакторе данных.
-
В диалоговом окне Line Charts (Линейчатые диаграммы) щёлкните на области Multiple (Сложная) и активируйте опцию Summaries of separate variables (Обработка отдельных переменных).
-
После щелчка по выключателю Define (Определить) откроется соответствующее диалоговое окно (см. рис. 22.19).
-
В поле Category Axis: (Ось категорий) введите переменную jahr. В поле Line Represent (Значения линий) по очереди введите переменные ua, gv и ub; вместо установленной по умолчанию функции Mean of values (Средние значения), с помощью выключателя Change Summary...(Изменить метод обработки), отметьте функцию суммы значений (Sum of values).
-
После щелчка по выключателю Titles... (Заголовок), введите подходящий заголовок и начните построение диаграммы щелчком на ОК.
Рис. 22.19: Диалоговое окно Define Multiple Line: Summaries of Separate Variables (Построение сложной линейчатой диаграммы: Обработка отдельных переменных)
19.gif
22.2.3 Связанные линейчатые диаграммы
22.2.3 Связанные линейчатые диаграммы
Это разновидность сложной линейчатой диаграммы, в котором точки данных обозначены разными символами и соединены вертикальной связью.
-
Воспользуйтесь примером из предыдущего раздела и в диалоговом окне Line Charts (Линейчатые диаграммы) щёлкните на области Drop-line (Связанные линии).
-
Во всём остальном поступите так же, как и в предыдущем разделе.
Рис. 22.20: Сложная линейчатая диаграмма
Построенная нами диаграмма будет соответствовать приведенной на рисунке 22.21.
20.gif
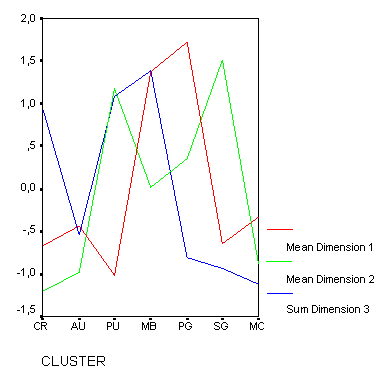
22.3 Диаграммы с областями
22.3 Диаграммы с областями
Диаграммы с областями являются разновидностью линейчатой диаграммы, в которой области, находящиеся под линиями, закрашиваются благодаря чему график выглядит более наглядным.
-
Для построения диаграммы с областями, после открытия необходимого файла SPSS, выберите в меню Graphs (Графики) Area... (С областями)
Откроется диалоговое окно Area Charts (Диаграммы с областями) Вы можете построить простую или состыкованную диаграмму с областями. И здесь данные, отображаемые в этих диаграммах, могут быть заданы как категории одной переменной, как разные переменные или как значения отдельных наблюдений.
Рис. 22.21: Связанная линейчатая диаграмма
Рис. 22.22: Диалоговое окно Area Charts (Диаграммы с областями)
21.gif
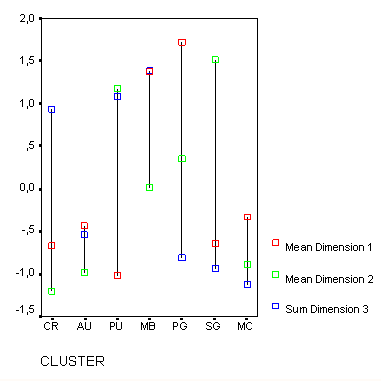
22.gif

22.3.1 Простая диаграмма с областями
22.3.1 Простая диаграмма с областями
Следующая таблица содержит информацию о производстве велосипедов с 1986 по 1992 год. Производственные показатели разбиты дополнительно на сбыт внутри страны и экспорт.
Год | Штук (млн.) | ||
Производство | Внутри страны | Экспорт | |
1986 | 4,00 | 3,14 | 0,86 |
1987 | 3,74 | 3,01 | 0,73 |
1988 | 3,88 | 3,14 | 0,74 |
1989 | 4,40 | 3,67 | 0,73 |
1990 | 4,81 | 4,08 | 0,73 |
1991 | 4,91 | 4,35 | 0,56 |
1992 | 4,55 | 4,10 | 0,45 |
Эти данные построчно сохранены в переменных jahr (год), gesamt (общий объем производства), inland (внутри страны) и export (экспорт) в файле fahrrad.sav.
-
Откройте файл fahrrad.sav и просмотрите его содержимое в окне редактора данных.
Сначала данные о совокупном производстве представим в виде простой диаграммы с областями.
-
В диалоговом окне Area Charts (Диаграммы с областями) щёлкните на области Simple (Простая) и оставьте опцию Summaries for groups of cases (Обработка категорий одной переменной), устанавливаемую по умолчанию.
-
После щелчка по выключателю Define (Определить) откроется главное диалоговое окно (см. рис. 22.23).
-
В поле Category Axis: (Ось категорий) введите переменную jahr и в группе Area Represents (Значения областей) установите маркер возле Other summary function (Другая обрабатывающая функция). В появившееся поле введите переменную gesamt и оставьте функцию Mean of values (Средние значения), устанавливаемую по умолчанию.
-
С помощью выключателя Titles... (Заголовок), введите подходящий заголовок и начните построение диаграммы щелчком на ОК.
Рис. 22.23: Диалоговое окно Define Simple Area: Summaries for Groups of Cases (Построение простой диаграммы с областями: Обработка категорий одной переменной)
Рис. 22.24: Диаграмма с областями
Следует отметить то, что начальной точкой отсчёта вертикальной оси является не ноль, а значение 3,6.
23.gif
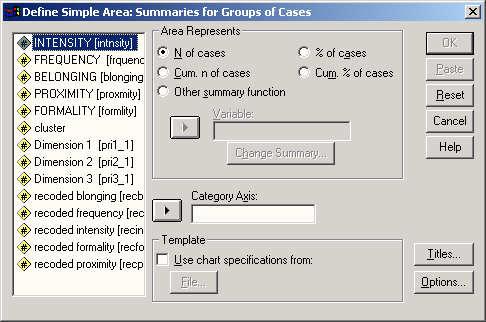
24.gif
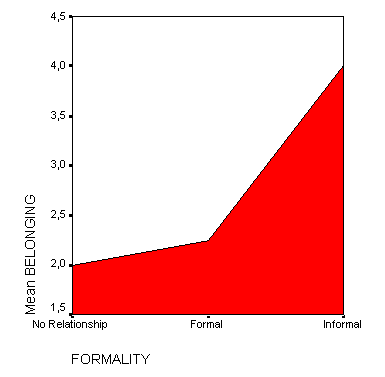
22.3.2 Состыкованные диаграммы с областями
22.3.2 Состыкованные диаграммы с областями
Этот вид диаграмм следует применять только тогда, когда штабелируемые области дают не лишенный смысла эффект суммирования. Мы ещё раз обратимся к примеру, рассмотренному в предыдущем разделе, но теперь совокупную производительность разделим на продукцию, реализуемую внутри страны и экспорт.
-
В диалоговом окне Area Charts (Диаграммы с областями) щёлкните на области Stacked (Состыкованная) и отметьте опцию Summaries of separate variables (Обработка отдельных переменных).
-
После щелчка по выключателю Define (Определить) откроется соответствующее диалоговое окно.
-
В поле Category Axis: (Ось категорий) введите переменную jahr, а в поле Areas Represent (Значения областей) введите обе переменные inland и export и оставьте функцию Sum of values (Сумма значений), устанавливаемую по умолчанию.
-
Минуя выключатель Titles... (Заголовок), введите подходящий заголовок и начните построение диаграммы щелчком на ОК.
Рис. 22.25: Диалоговое окно Define Stacked Area: Summaries of Separate Variables (Построение штабельной диаграммы с областями: Обработка отдельных переменных)
Рис. 22.26: Штабельная диаграмма с областями.
25.gif
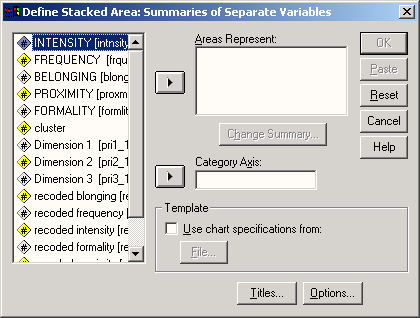
26.gif
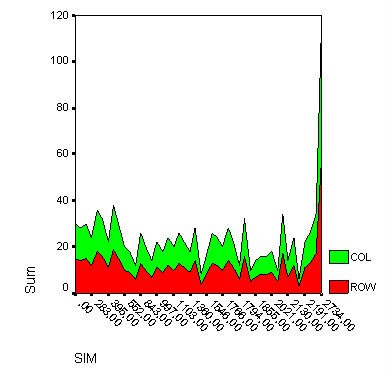
22.4 Круговые диаграммы
22.4 Круговые диаграммы
Представление данных в виде круговых диаграмм стоит выбирать тогда, когда частоты или значения переменных можно, не нарушая здравого смысла, сложить вместе и эта сумма будет соответствовать ста процентам.
Отобразим при помощи круговой диаграммы частоты категорий переменной psyche (психологическое состояние студентов) из файла studium.sav.
-
Откройте файл studium.sav и выберите в меню Graphs (Графики) Pie... (Круговые) Откроется диалоговое окно Pie Charts (Круговые диаграммы).
-
Оставьте опцию Summaries for groups of cases (Обработка категорий одной переменной), установленную по умолчанию и щелчком на кнопке Define (Определить) откройте следующее диалоговое окно.
Рис. 22.27: Диалоговое окно пе Charts (Круговые диаграммы)
Рис. 22.28: Диалоговое окно Define Pie: Summaries for Groups of Cases (Построение круговой диаграммы: Обработка категорий одной переменной)
-
В поле Define slices by: (Создать сектора при помощи:) введите переменную psyche.
-
Щёлкните на выключателе Options... (Параметры) и уберите маркер с опции Display groups defined by missing values (Пропущенные значения отображать как категории).
-
С помощью выключателя Titles... (Заголовок), введите подходящий заголовок и начните построение диаграммы щелчком на ОК (см. рис. 22.29).
Типичным примером применения круговой диаграммы является отображение процентных показателей голосов избирателей, проголосовавших за те или иные партии.
На местных выборах земли Гессен в 1993 году получилось следующее распределение голосов в процентах:
Партия | ДОЛЯ ГОЛОСОВ (%) |
SPD | 36,4 |
CDU | 32,0 |
Gruene (Зелёные) | 11,0 |
Republikaner (Республиканцы) | 8,3 |
FPD | 5,1 |
Прочие | 7,2 |
Этот пример является примером с уже имеющимися (готовыми) данными.
Рис. 22.29: Круговая диаграмма
-
Откройте файл kommunal.sav, в котором в переменных р и рг построчно находятся необходимые для нас данные.
-
В диалоговом окне Pie Charts (Круговые диаграммы) опять оставьте опцию Summa-ries for groups of cases (Обработка категорий одной переменной), установленную по умолчанию.
-
После щелчка по выключателю Define (Определить) в поле Define slices by: (Создать сектора при помощи:) введите переменную р. Поставьте маркер возле Other summary function (Другая обрабатывающая функция) и в появившееся поле введите переменную рг. Используйте установленную по умолчанию опцию Sum of values (Сумма значений).
-
С помощью выключателя Titles... (Заголовок), введите подходящий заголовок и начните построение диаграммы щелчком на ОК (см. рис. 22.30).
В главе 22.17 мы придадим этой диаграмме более презентабельный вид.
27.gif
28.gif
29.gif
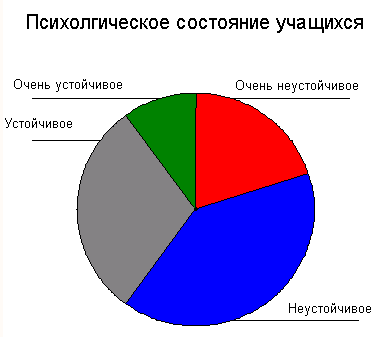
22.5 Диаграммы максимальных и минимальных значений
22.5 Диаграммы максимальных и минимальных значений
Если вы посмотрите на поведение биржевых котировок акций, то заметите, что для фиксированного промежутка времени, к примеру, для одного дня, существует три важнейших характеристики: максимальное и минимальное значения, а также значение в конце промежутка, при закрытии биржи. Такой и подобные ему процессы могут быть представлены при помощи диаграммы максимальных и минимальных значений, которая на биржевом сленге иногда называется потолок-пол-закрытие.
-
После открытия необходимого Вам файла SPSS выберите в меню Graphs (Графики) High-Low... (Максимум-минимум)
После этого откроется соответствующее диалоговое окно.
Существует пять видов диаграмм максимума-минимума, данные для которых, как и для предыдущих графиков, могут интерпретироваться тремя различными способами.
22.5.1 Простые биржевые диаграммы — потолок-пол-закрытие
22.5.1 Простые биржевые диаграммы - потолок-пол-закрытие
Предположите, что вы располагаете некоторыми акциями и фиксировали их котировки в течение десяти дней:
Рис. 22.30: Круговая диаграмма
Рис. 22.31: Диалоговое окно Higli-Low Charts (Диаграммы максимума-минимума)
День | Максимальная котировка | Минимальная котировка | Окончательная котировка |
1 | 164,35 | 161,48 | 162,33 |
2 | 166,12 | 163,03 | 164,12 |
3 | 167,84 | 164,75 | 165,97 |
4 | 167,79 | 163,93 | 166,13 |
5 | 171,14 | / 168,04 | 170,94 |
6 | 175,33 | 171,44 | 171,99 |
7 | 174,88 | 172,93 | 173,01 |
8 | 173,20 | 170,50 | 171,82 |
9 | 169,54 | 166,43 | 167,28 |
10 | 168,24 | 165,14 | 166,43 |
Эти данные построчно сохранены в четырёх переменных tag (день), hoch (максимум), tief (минимум) и ende (окончательная котировка) в файле aktien.sav.
-
Откройте файл aktien.sav и в диалоговом окне High-Low Charts (Диаграммы максимума-минимума) щёлкните на области Simple High-Low-Close (Простая диаграмма — потолок-пол-закрытие).
-
Установите метку возле опции Summaries of separate variables (Обработка отдельных переменных) и нажатием выключателя Define (Определить) откройте следующее диалоговое окно (см. рис. 22.32).
-
В поле Category Axis: (Ось категорий) введите переменную tag и в соответствующие поля введите переменные hoch (High), tief (Low) и ende (Close). Оставьте установленную по умолчанию функцию Mean of values (Средние значения).
-
С помощью выключателя Titles... (Заголовок), введите подходящий заголовок.
-
Начните построение диаграммы щелчком на ОК.
Рис. 22.32: Диалоговое окно Define Simple High-Low-Close: Summaries of Separate Variables (Построение простой диаграммы — потолок-пол-закрытие: Обработка отдельных переменных)
Рис. 22.33: Простая диаграмма — потолок-пол-закрытие
30.gif
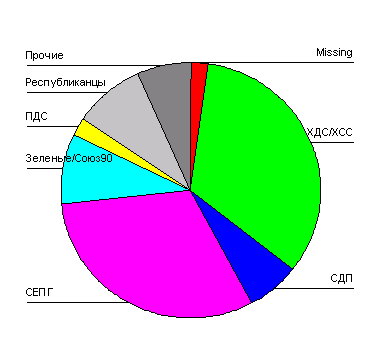
31.gif
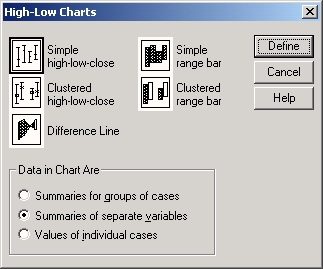
32.gif
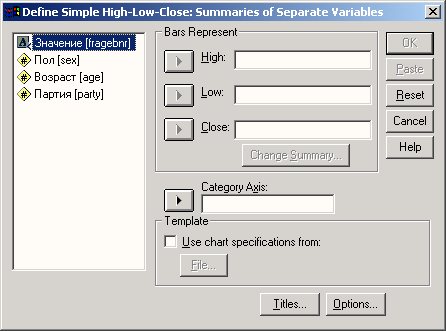
33.gif
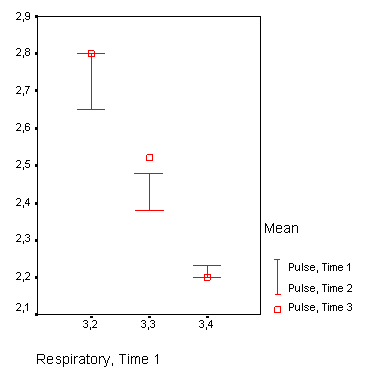
22.5.2 Кластеризованные диаграммы — максимум-минимум-закрытие
22.5.2 Кластеризованные диаграммы - максимум-минимум-закрытие
При помощи этого метода осуществляется возможность представить несколько процессов потолок-пол-закрытие в одной диаграмме. Для реализации этой возможности в диалоговом окне High-Low Charts (Диаграммы максимума-минимума) щёлкните на области Clustered high-low-close (Кластеризованная диаграмма — максимум-минимум-закрытие).
22.5.3 Линейчатые диаграммы разностей
22.5.3 Линейчатые диаграммы разностей
При помощи этой диаграммы может быть представлено взаимное изменение значений двух переменных, причём обе результирующие кривые могут пересекаться. Это пересечение как раз и может быть очень наглядно представлено с помощью линейчатых диаграмм разностей.
Нижеследующая таблица содержит данные о развитии рынка образования в Германии с 1985 по 1992 год.
Год | Количество учебных мест | |
| Предложение | Спрос | |
1985 | 719.110 | 755.994 |
1986 | 715.880 | 730.980 |
1987 | 690.287 | 679.622 |
1988 | 665.964 | 628.793 |
1989 | 668.649 | 602.014 |
1990 | 659.435 | 559.531 |
1991 | 668.000 | 550.671 |
1992 | 721.756 | 608.121 |
-
Откройте файл lehre.sav, в котором в переменными jahr (год), angeb (предложение) и nachf (спрос) хранятся необходимые нам данные.
-
В диалоговом окне High-Low Charts (Диаграммы максимума-минимума) щёлкните на области Difference Line (Линия разностей). Установите метку возле опции Summaries of separate variables (Обработка отдельных переменных).
-
Нажатием выключателя Define (Определить) откройте следующее диалоговое окно (см. рис. 22.34).
-
В поле Category Axis: (Ось категорий) введите переменную jahr и в группе Differenced Pair Represents (Значения разностных пар) в поля 1 и 2 введите переменные angeb и nachf. Активируйте функцию суммы (Sum of values) с помощью кнопки Change Summary (Сменить процедуру обработки).
-
С помощью выключателя Titles... (Заголовок), введите подходящий заголовок.
-
Начните построение диаграммы щелчком на ОК.
Рис. 22.34: Диалоговое окно Define Difference Line: Summaries of Separate Variables (Построение линейчатой диаграммы разностей: Обработка отдельных переменных).
Рис. 22.35: Линейчатая диаграмма разностей
34.gif
35.gif

22.5.4 Простые интервальные столбцы
22.5.4 Простые интервальные столбцы
Этот вид диаграммы является разновидностью простой диаграммы — потолок-пол-закрытие, в которой, однако, отображается только максимальное и минимальное значения, а окончательное отсутствует.
В качестве примера рассмотрим ситуацию, когда Вы, предположим, на протяжении десяти дней фиксировали свою максимальную и минимальную температуры:
День | Температура(°С) | |
Минимум | Максимум | |
14 марта 1994 | 2,4 | 11,3 |
15 марта 1994 | 2,6 | 11,5 |
16 марта 1994 | 3,7 | 12,4 |
17 марта 1994 | 6,2 | 14,8 |
18 марта 1994 | 6,2 | 14,8 |
19 марта 1994 | 1,9 | 9,7 |
20 марта 1994 | 4,3 | 11,3 |
21 марта 1994 | 7,6 | 13,4 |
22 марта 1994 | 7,0 | 12,9 |
23 марта 1994 | 6,3 | 11,0 |
Эти данные построчно сохранены в трёх переменных (tag (день), train (минимальная температура), tmax (максимальная температура)) в файле celsius.sav.
-
Откройте файл celsius.sav и в диалоговом окне High-Low Charts (Диаграммы максимума-минимума) щёлкните на области Simple range bar (Простые интервальные столбцы).
-
Установите метку возле опции Summaries of separate variables (Обработка отдельных переменных).
-
Нажатием выключателя Define (Определить) откройте следующее диалоговое окно (см. рис. 22.36).
-
В поле Category Axis: (Ось категорий) введите переменную tag и в группе Bar Pair Represents (Значения пары столбцов) введите переменные tmin и tmax в поля 1 и
2. Установленную по умолчанию функцию Mean of values (Средние значения) можете оставить.
-
С помощью выключателя Titles... (Заголовок), введите подходящий заголовок и начните построение диаграммы щелчком на ОК.
22.5.5 Кластеризованные интервальные столбцы
22.5.5 Кластеризованные интервальные столбцы
В одной диаграмме при помощи интервальных столбцов могут быть представлены и изменения нескольких переменных.
-
Для этого в диалоговом окне High-Low Charts (Диаграммы максимума-минимума) щёлкните на области Clustered range bar (Кластеризованные интервальные столбцы).
Рис. 22.36: Диалоговое окно Define Simple Range Bar: Summaries of Separate Variables (Построение диаграммы с простыми интервальными столбцами: Обработка отдельных переменных)
36.gif
22.6 Коробчатые диаграммы
22.6 Коробчатые диаграммы
Метод, при помощи которого, можно отобразить медиану и оба квартиля, минимальные и максимальные значения, а также пропущенные и экстремальные значения, уже рассматривался в главе 10.4.1. Эти диаграммы могут быть построены в ходе предварительного исследования данных или через меню графиков.
-
После открытия необходимого Вам файла SPSS выберите в меню Graphs (Графики) Boxplot... (Коробчатые диаграммы) Откроется диалоговое окно Boxplot (Коробчатая диаграмма) (см. рис. 22.38).
-
Вы можете выбрать простую или.кластеризованную диаграмму, причём данные могут быть представлены в виде категорий одной переменной или в виде разных переменных.
Рис. 22.37: Простые интервальные столбцы
Рис. 22.38: Диалоговое окно Boxplot (Коробчатая диаграмма)
37.gif

38.gif
22.6.1 Простые коробчатые диаграммы
22.6.1 Простые коробчатые диаграммы
В рамках исследования гипертонии (файл hyper.sav) мы хотим для четырёх разных возрастных категорий (переменная ak) отобразить исходные показатели систолического кровяного давления (переменная rrs0).
-
Откройте файл hyper.sav.
-
В диалоговом окне Boxplot (Коробчатая диаграмма) щёлкните на области Simple (Простая) и оставьте опцию Summaries for groups of cases (Обработка категорий одной переменной), устанавливаемую по умолчанию.
-
Щелчком по выключателю Define (Определить) откройте главное диалоговое окно, в котором в поле Category Axis: (Ось категорий) введите переменную ak, а в поле Variable: (Переменная) переменную rrs0. Если Вы введёте какую-либо переменную в поле Label Cases by: (Метки наблюдений), то её метки значений будут использованы для обозначения пропущенных и экстремальных значений.
-
Начните построение диаграммы щелчком на ОК (см. рис. 22.39).
Если необходимо отобразить изменение систолического давления с течением времени, то для этого следует выбрать переменные rrs0, rrs1, rrs6 и rrs12.
-
Щёлкните вновь на области Simple (Простая), но теперь поставьте маркер возле опции Summaries of separate variables (Обработка отдельных переменных).
-
Щелчком по выключателю Define (Определить) откройте следующее диалоговое окно, в котором в поле Boxes Represent (Значения коробок) по очереди введите переменные rrs0, rrs1, rrs6 и rrs12.
-
Вновь начните построение диаграммы щелчком на ОК (см. рис. 22.40).
На этой диаграмме метки отображаются не полностью, поэтому их ещё необходимо доработать.
Рис. 22.39: Коробчатая диаграмма (категории одной переменной)
Рис. 22.40: Коробчатая диаграмма (разные переменные)
39.gif

40.gif
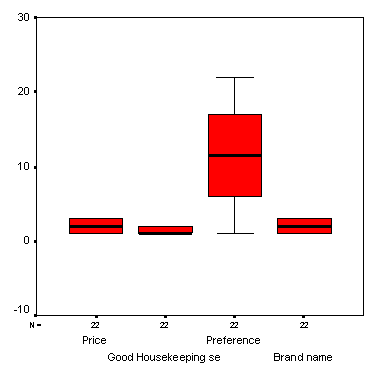
22.6.2 Кластеризованные коробчатые диаграммы
22.6.2 Кластеризованные коробчатые диаграммы
Вы можете использовать в данной диаграмме ещё одну переменную, тогда коробчатые диаграммы будут сгруппированы по категориям этой переменной.
-
Для этого в диалоговом окне Boxplot (Коробчатая диаграмма) щёлкните на области Clustered (Кластеризованная).
22.7 Столбики ошибок
22.7 Столбики ошибок
Если при помощи коробчатой диаграммы представляются медиана и оба квартиля, то диаграмма столбцов по величинам ошибки служит для отображения средних значений и характеристик рассеяния (стандартное отклонение, стандартная ошибка или доверительный интервал — по выбору).
-
После открытия необходимого Вам файла SPSS выберите в меню Graphs (Графики) Error Bar... (Столбики ошибок)
Откроется диалоговое окно Error Bar (Столбики ошибок).
Также как и для коробчатых диаграмм, Вы можете выбрать простую или кластеризованную диаграмму столбцов по величинам ошибки, причём данные могут быть представлены в виде отдельных категорий одной переменной или в виде разных переменных.
Рис. 22.41: Диалоговое окно Error Bar (Столбцы по величинам ошибки)
41.gif
22.7.1 Простая диаграмма величины ошибки
22.7.1 Простая диаграмма величины ошибки
В рамках исследования гипертонии (файл hyper.sav) для четырёх разных возрастных категорий (переменная ak) мы хотим отобразить исходные показатели уровня холестерина (переменная chol0).
-
Откройте файл hyper.sav.
-
В диалоговом окне Error Bar (Столбики ошибок) щёлкните на области Simple (Простая) и оставьте опцию Summaries for groups of cases (Обработка категорий одной переменной), устанавливаемую по умолчанию.
-
Щелчком по выключателю Define (Определить) откройте соответствующее диалоговое окно (см. рис. 22.42).
-
В поле Category Axis: (Ось категорий) введите переменную ak, а в поле Variable: (Переменная) переменную chol0.
В группе Bars Represent (Значения столбцов) Вам предлагаются на выбор следующие варианты:
-
Доверительный интервал для среднего значения (по умолчанию равен 95 %)
Рис. 22.42: Диалоговое окно Define Simple Error Bar: Summaries for Groups of Cases (Построение простой диаграммы величины ошибки: Обработка категорий одной переменной)
-
Стандартная ошибка (предустановленный множитель равен 2)
-
Стандартное отклонение (предустановленный множитель равен 2)
-
Выберите отображение простого стандартного отклонения (множитель равен 2).
-
С помощью выключателя Titles... (Заголовок), введите подходящий заголовок и начните построение диаграммы щелчком на ОК.
Если необходимо отобразить изменение уровня холестерина с течением времени, то для построения графика необходимо использовать переменные chol0, chol1, chol6 и chol12.
Рис. 22.43: Простая диаграмма величины ошибки (категории одной переменной)
-
В диалоговом окне Error Bar (Столбики ошибок) вновь щёлкните на области Simple (Простая), но теперь поставьте маркер возле опции Summaries of separate variables (Обработка отдельных переменных).
-
Щелчком по выключателю Define (Определить) откройте следующее диалоговое окно, в котором по очереди введите переменные chol0, chol1, chol6 и chol12 в поле Error Bars (Значения столбцов ошибок). В этом случае выберите отображение 95 % -го доверительного интервала (который является установкой по умолчанию).
-
С помощью выключателя Titles... (Заголовок), введите подходящий заголовок и начните построение диаграммы щелчком на ОК (см. рис. 22.44).
Рис. 22.44: Простая диаграмма величины ошибки (разные переменные)
Метки значений на горизонтальной оси необходимо будет ещё подкорректировать.
42.gif

43.gif
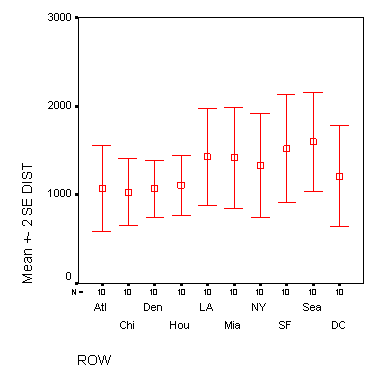
44.gif
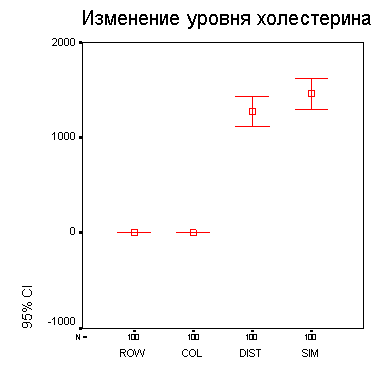
22.7.2 Кластеризованная величина ошибки
22.7.2 Кластеризованная величина ошибки
Диаграммы величины ошибки можно объединять в группы при помощи дополнительных переменных.
-
Для этого в диалоговом окне Error Bar (Величина ошибки) щёлкните на области Clustered (Кластеризованная).
22.8 Диаграмма рассеяния
22.8 Диаграмма рассеяния
Диаграмма рассеяния в графическом виде отображает отношения между двумя переменными, которые как минимум относятся к интервальной шкале. Пример диаграммы рассеяния уже был представлен в главе 15.
-
Чтобы построить диаграмму рассеяния, после открытия необходимого Вам файла SPSS выберите в меню Graphs (Графики) Scatter... (Рассеяние)
Откроется диалоговое окно Scatterplot (Диаграмма рассеяния).
Имеются различные возможности построения диаграмм рассеяния. Для нижеследующих примеров взят файл europa.sav (можно сравнить с гл. 20), который содержит данные некоторых признаков для 28 европейских стран.
Рис. 22.45: Диалоговое окно Scatterplot (Диаграмма рассеяния)
45.gif

22.8.1 Простая диаграмма рассеяния
22.8.1 Простая диаграмма рассеяния
-
Откроите файл europa.sav.
-
В диалоговом окне Scatterplot (Диаграмма рассеяния) щёлкните на области Simple (Простая).
-
Щелчком по выключателю Define (Определить) откройте соответствующее диалоговое окно (см. рис. 22.46).
Мы хотим отобразить ожидаемую продолжительность жизни мужчин (переменная lem) в зависимости от урбанизации (процентного показателя доли городского населения, переменная sb).
-
Переменную lem из списка исходных переменных перенесите в поле оси Y, а переменную sb — в поле оси X.
Если Вы поместите какую-нибудь переменную в поле Set Markers by: (Установить маркеры для:), то согласно принадлежности к этой переменной отдельные точки значений на диаграмме будут представлены окрашенными в другой цвет или помечены при помощи какого-либо отличительного маркировочного символа.
-
Поместите переменную land в поле, предусмотренное для описания наблюдений (Label Cases by: (Метки наблюдений)). Значение этой переменной, соответствующее в приведенном примере сокращённому названию страны, будет размещено в диаграмме рассеяния вблизи соответствующей точки данных.
Рис. 22.46: Диалоговое окно Simple Scatterplot (Простая диаграмма рассеяния)
-
Для этой цели щёлкните по выключателю Options... (Параметры) и в появившемся диалоговом окне активируйте опцию Display chart with case labels (Показать график с метками наблюдений).
-
Пройдя выключатель Titles... (Заголовок), введите подходящий заголовок и начните построение диаграммы щелчком на ОК.
Рис. 22.47: Простая диаграмма рассеяния с метками случаев
Большое количество меток наблюдений приводит к снижению наглядности графика, поэтому можно рекомендовать оставить их только для избранных точек.
В качестве альтернативы на вооружение можно взять обозначение метками только наиболее характерных точек.
-
Для этого постройте диаграмму заново.
-
Через выключатель параметров уберите маркер опции Display chart with case labels (Показать график с метками наблюдений).
Теперь метки на графике присутствовать не будут.
-
Двойным щелчком поместите график в редактор диаграмм.
-
Одним щелчком по символу выбора точек
 перейдите в режим выбора точек. Теперь при помощи курсора для выделения точек, Вы можете выбрать отдельные точки на диаграмме рассеяния и обозначить их метками.
перейдите в режим выбора точек. Теперь при помощи курсора для выделения точек, Вы можете выбрать отдельные точки на диаграмме рассеяния и обозначить их метками.
Если несколько точек находятся очень близко друг к другу, то будет показан список меток, из которого Вы сможете выбрать необходимую метку.
Рис. 22.48: Простая диаграмма зассеяния с выборочными метками случаев
Численные показатели для любой точки, находящейся на диаграмме рассеяния также можно просмотреть в редакторе данных .
-
Для этого при помощи курсора для выделения точек выберите нужную точку и в списке команд щёлкните на кнопке перехода в редактор данных:

Вы увидите редактор данных. Изменения данных, вносимые в редакторе данных, естественно непосредственно не влияют на уже построенную диаграмму рассеяния.
В главе 22.17 мы покажем, как на одной диаграмме рассеяния можно отобразить четыре разных регрессионных линии (к примеру, регрессионные прямые).
46.gif

47.gif
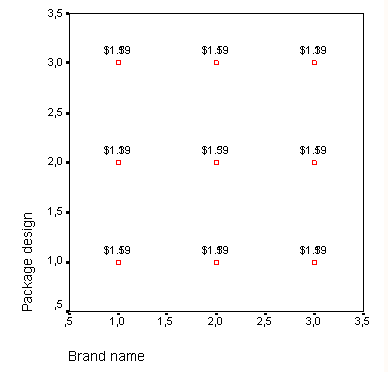
49.gif
22.8.2 Матричные диаграммы рассеяния
22.8.2 Матричные диаграммы рассеяния
Этот метод применяется для отображения нескольких диаграмм рассеяния на одном графике.
-
В диалоговом окне Scatterplot (Диаграмма рассеяния) щёлкните на области Matrix (Матрица).
-
Щелчком на выключателе Define (Определить) откройте соответствующее диалоговое окно.
Переменные lem (ожидаемая продолжительность жизни мужчин), so (количество часов солнечной погоды в году) и nt (количество пасмурных дней в году) мы хотим попарно связать друг с другом.
-
Для этого переменные lem, so и nt поочерёдно перенесите в поле, предусмотренное для матричных переменных.
-
Начните построение диаграммы щелчком на ОК.
Число строк и столбцов в матричной диаграмме соответствует количеству переменных. Каждая ячейка является диаграммой рассеяния для одной пары переменных. Диагональные ячейки содержат метки переменных, находящихся в соответствующих ячейках матрицы (в данном примере метки являются слишком длинными).
Рис. 22.49: Диалоговое окно Scatterplot Matrix (Матричная диаграмма рассеяния)
Рис. 22.50: Матричная диаграмма рассеяния
Первая диагональная ячейка содержит метку переменной km. Это означает, что для всех диаграмм первой строки эта переменная находится со стороны вертикальной оси (оси Y). Какая из переменных при этом откладывается по горизонтальной оси (ось X), следует узнавать из следующих диагональных ячеек. Такие же правила справедливы и для последующих строк.
К примеру, в центральном поле первой строки представлена взаимосвязь средней ожидаемой продолжительности жизни (по вертикали) и количества часов солнечной погоды (по горизонтали). Явно заметна обратная зависимость.
И в матричных диаграммах рассеяния можно задать маркировку для некоторой переменной, организовать вывод меток наблюдений, а также отображение любой другой необходимой информации; можно так же организовать построение различных линий регрессии (для сравнения см. разд. 22.17).
51.gif

52.gif
22.8.3 Наложенные диаграммы рассеяния
22.8.3 Наложенные диаграммы рассеяния
В одном графике можно представить несколько диаграмм рассеяния.
-
Для этого в диалоговом окне Scatterplot (Диаграмма рассеяния) щёлкните на области Overlay (Наложение) и затем на кнопке Define (Определить).
В появившемся диалоговом окне могут быть заданы соответствующие X-Y-пары переменных, которые должны быть представлены вместе. Значения, принадлежащие соответствующей паре, на диаграмме будут отмечены одной определённой маркировкой.
Этот метод имеет смысл применять только тогда, когда речь идёт о переменных с одними и теми же областями значений.
22.8.4 Трёхмерные диаграммы рассеяния
22.8.4 Трёхмерные диаграммы рассеяния
Эти диаграммы строятся на основании значений трёх переменных и поэтому включают три оси.
По оси у откладывается высоту положения точки
По оси х откладывается горизонтальное положение каждой точки
По оси z откладывается глубина положения каждой точки.
Отобразим переменную lem (средняя ожидаемая продолжительность жизни мужчин) на оси у, переменную sb (процентный показатель городского населения) на оси х и переменную so (количество часов солнечной погоды в году) на оси г.
-
В диалоговом окне Scatterplot (Диаграмма рассеяния) щёлкните на области 3D (3-х мерная).
-
Щелчком по выключателю Define (Определить) откройте соответствующее диалоговое окно (см. рис. 22.51).
-
Перенесите поочерёдно переменные lem, sb и so из списка исходных переменных в поля принадлежащие осям у, х и z-
-
Начните построение диаграммы щелчком на ОК.
Рис. 22.51: Диалоговое окно 3-D Scanerplot ( Трёхмерная диаграмма рассеяния)
Очень длинные наименования осей при построении рисунка 22.52 были откорректированы.
И здесь Вы бы могли отметить маркировкой значения одной из переменных, а также указать наименования наблюдений и при помощи выключателя Titles... (Заголовок) дать диаграмме подходящее название.
Рис. 22.52: Трёхмерная диаграмма рассеяния
53.gif

54.gif

22.9 Гистограммы
22.9 Гистограммы
Гистограмма уже несколько раз рассматривалась в предыдущих главах.
-
Чтобы построить гистограмму, после открытия необходимого Вам файла SPSS (к примеру, файла hyper.sav), выберите в меню Graphs (Графики) Histogram... (Гистограмма)
Откроется диалоговое окно Histogram (Гистограмма) (см. рис. 22.53).
С помощью гистограммы можно наглядно отобразить распределение переменных, относящихся по меньшей мере к интервальной шкале.
-
Откройте файл hyper.sav.
-
Поместите переменную chol0 в поле переменных и активируйте вывод кривой нормального распределения.
-
Начните построение гистограммы щелчком на ОК.
Рис. 22.53: Диалоговое окно Histogram (Гистограмма)
Рис. 22.54: Гистограмма с кривой нормального распределения
Чтобы выяснить, значимо ли отличается получившееся распределение от нормального, Вы не должны полагаться только на внешний вид гистограммы, а проверить его при помощи специального статистического теста. Для этого в SPSS реализован тест Колмогорова-Смирнова (см. разд. 14.5), который в данном случае указывает на незначимое отклонение от нормального распределения (значение р = 0,616).
55.gif

56.gif

Глава 23. Интерактивные графики
Глава 23. Интерактивные графики
1. Интерактивные графики
Интерактивные графики
Начиная с 8-ой версии, SPSS предоставляет в распоряжение пользователя так называемые интерактивные графики, которые располагают множеством новых возможностей по сравнению с прежними графиками, теперь уже получившими название стандартных.
Диаграммы, которые можно построить с помощью интерактивного графического интерфейса, включают следующие виды:
-
столбчатые диаграммы
-
линейчатые диаграммы
-
круговые диаграммы
-
коробчатые диаграммы
-
диаграммы величины ошибки
-
гистограммы
-
диаграммы рассеяния
Эти виды диаграмм будут рассмотрены в разделах 23.1 по 23.7. В разделах 23.8 будет показан ещё один подход к работе с интерактивными графиками, а в разделе 23.9 будут даны несколько советов по корректировке уже построенных диаграмм.
23.1 Столбчатые диаграммы
23.1 Столбчатые диаграммы
Возможности, которые SPSS предлагает для построения этого вида диаграмм, проиллюстрируем с использованием нескольких переменных, содержащихся в файле pcalltag.sav. В этом файле находятся ограниченный набор из многочисленных переменных, полученных в ходе исследования на тему "Компьютер в повседневной жизни", проведенного в Институте Социологии Магдебургского Университета им. Филиппса.
23.1.1 Простая столбчатая диаграмма: отображение частот
23.1.1 Простая столбчатая диаграмма: отображение частот
Один из вопросов цитируемого исследования звучал так: В какое время суток Вы предпочитаете работать за компьютером? "Частотные показатели" ответов на отдельные категории этого вопроса должны быть представлены в графическом виде.
-
Откройте файл pcalltag.sav.
-
Выберите в меню Graphs (Графики) Interactive (Интерактивно) Ваг... (Столбчатые)
Откроется диалоговое окно Create Bar Chart (Создание столбчатой диаграммы).
Это диалоговое окно имеет строение, типичное для диалогов построения интерактивных графиков. Оно разбито на пять регистрационных карт, первая из которых Assign Variables (Присвоить переменные) открывается сразу после открытия окна. Эта карта состоит из списка переменных, пяти полей для ввода переменных, двух кнопок с символами в верхней части регистрационной карты, соответствующих двум возможностям построения диаграммы и трёх выключателей.
В зависимости от установок, активированных на данный момент времени, переменные в списке могут быть отсортированы в алфавитном порядке или по типу переменных. Если Вы хотите изменить этот порядок, щёлкните правой кнопкой мыши на одной из переменных и в появившемся меню выберите желаемый тип сортировки.
В этом же меню Вы можете указать, должны ли переменные в исходном списке быть представлены при помощи своих имён или при помощи меток. Так как метки переменных ввиду своей большой длины, как правило, не могут быть полностью отображены в списке переменных, мы рекомендуем, оставить представление переменных в виде их имён.
Переменные, находящиеся в списке переменных, можно разделить на два типа: категориальные и метрические. Эти два типа переменных идентифицируются при помощи двух разных символов, устанавливаемых в начале имени. Категориальными переменными являются переменные, относящиеся к номинальной или порядковой шкале. После активирования необходимой переменной и щелчка правой кнопкой мыши может быть изменён и её тип.
В данном примере категориальными являются переменные: arbeit (облегчение рабочих процессов), besitz (обладание компьютером), fachgr (группы специальностей), freund (трудность завязывания знакомств), gcsclil (пол), internet (использование Интернета), pczeit (время суток, когда используется компьютер) и uebstaat (пусть компьютерными технологиями занимается государство). К метрическим переменным относятся: compstd (количество часов за компьютером в неделю), interstd (количество часов в Интернете в неделю) и semester (количество семестров). К ним добавляются ещё и системные переменные Scount (частота), Spct (процент) и Scase (наблюдение), которые используются для построения столбчатых диаграмм с абсолютными частотами, процентными показателями или диаграмм для отдельных наблюдений соответственно.
Рис. 23.1: Диалоговое окно Create Bar Chart (Создание столбчатой диаграммы)
Рис. 23.2: Меню диалогового окна Create Bar Chart (Создание столбчатой диаграммы)
Первые два из пяти имеющихся полей расположены в виде схематичной х-у-системы координат, причём в поле оси у сразу по умолчанию внесена системная переменная Scount (частота). Это означает, что если Вы оставите эту предварительную установку, то будет построена столбчатая диаграмма, отображающая абсолютные частоты. Обрабатываемая переменная должна быть помещена в поле оси х.
Во всех диалоговых окнах, рассмотренных нами ранее, для перемещения переменной из поля исходных переменных в какое-либо поле тестируемых переменных необходимо было выделить её щелчком мыши и воспользоваться кнопкой со стрелкой, указывающей направление перемещения. В диалоговых окнах для построения интерактивных графиков перенос переменной осуществляется при помощи техники перетаскивания. Если вы расположите указатель мыши над одной из переменных, он примет вид руки. Теперь удерживая нажатой кнопку мыши, перенесите эту переменную в необходимое поле.
-
Переместите таким образом в поле оси х переменную pczeit (время суток).
-
Подтвердите нажатием ОК. В результате этих действий будет построена простая столбчатая диаграмма с абсолютными частотами переменной время суток.
Подсказка Bars show counts (Столбцы указывают на частоты) кажется мешающей и даже лишней.
-
Вы можете запретить вывод подсказок, если деактивируете опцию Display Key (Показать подсказку), предоставляемую в регистрационной карте Assign Variables (Присвоить переменные) в группе Bars Represent (Значения столбцов). Тогда диаграмма будет выглядеть так. как на рисунке 23.4.
Во всех последующих примерах этой главы отображение подсказок будет деактивировано, без каких-либо дополнительных предупреждений. Построенная нами столбчатая диаграмма является диаграммой вертикального типа. Этот тип диаграмм устанавливается по умолчанию и считается традиционным.
Рис. 23.3: Престал столбчатая диаграмма с абсолютными частотами
Рис. 23.4: Простая столбчатая диаграмма с отключенной подсказкой
-
Если Вы желаете построить горизонтальную столбчатую диаграмму, воспользуйтесь кнопкой с соответствующим символом; эта кнопка находится в верхней части регистрационной карты.
Теперь вместо абсолютных частот отобразим на графике процентные показатели.
Для этого перетащите в поле оси у системную переменную $pct (процент) и вновь активируйте вывод вертикальной столбчатой диаграммы.
После рассмотрения представления абсолютных частот и процентных показателей при помощи простой столбчатой диаграммы, необходимо обратить внимание на то, как могут быть отображены средние значения, к примеру, медианы или другие показатели одной переменной в зависимости от другой, категориальной переменной.
Рис. 23.5: Горизонтальная, простая столбчатая диаграмма
1.gif

2.gif
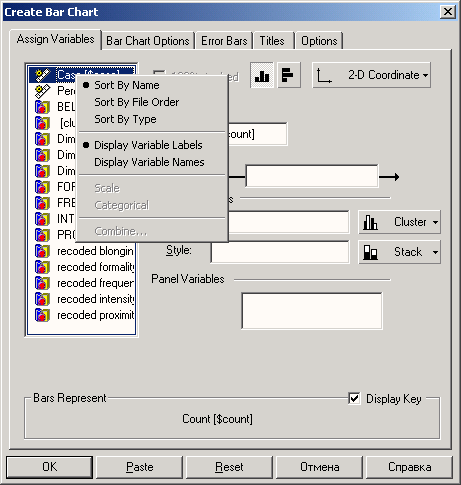
3.gif
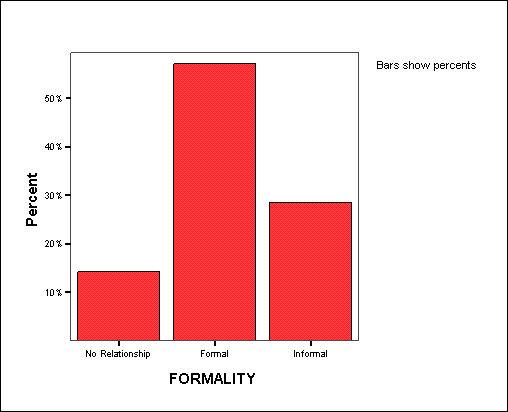
4.gif

5.gif
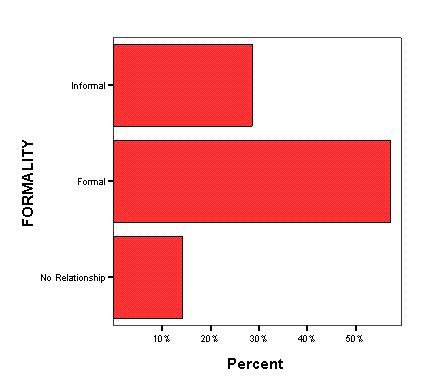
23.1.2 Простая столбчатая диаграмма: характеристики метрической переменной
23.1.2 Простая столбчатая диаграмма: характеристики метрической переменной
Переменная fachgr (труппы специальностей) описывает шесть разных групп специальностей, а переменная compstd (количество часов за компьютером в неделю) количество часов в неделе, которое студенты проводят за компьютером. Мы хотим на простой столбчатой диаграмме отобразить зависимость среднего количества часов, проводимых за компьютером, от профилирующей специальности.
-
В регистрационной карте Assign Variables (Присвоить переменные) диалогового окна Create Bar Chart (Создание столбчатой диаграммы) перенесите переменную fachgr к поле оси х, а переменную compstd — в поле оси у.
Внизу диалогового окна появится ниспадающее меню, в котором в Вашем распоряжении будут находиться тридцать различных статистических показателей для представления зависимой переменной (в данном случае compstd) .
-
Оставьте отображение средних значений, установленное по умолчанию, и подтвердите построение диаграммы нажатием ОК.
Рис. 23.6: Простая столбчатая диаграмма с процентными показателями
Рис. 23.7: Простая столбчатая диаграмма средних значений
Займёмся теперь расшифровкой отдельных элементов регистрационных карт.
-
Щёлкните сначала на выключателе 2О-системы координат. Откроется меню для добавления ещё одной координаты (ЗD-координата) и для создания ЗО-эффек-тов.
-
Активируйте ЗО-эффект.
-
Щёлкните по закладке Bar Chart Options (Параметры столбчатой диаграммы); откроется соответствующая регистрационная карта (см. рис. 23.8).
Вы можете выбрать вид изображения столбцов и в группе Bar Labels (Метки столбцов) активировать опции Count (Количество) и Value (Значение). Если в группе Bar Baseline (Базовая линия столбцов) Вы активируете опцию Custom (Пользовательский режим), то столбцы будут изображаться начиная с указанного Вами значения. При активизации ЗD-эффектов, Вы сможете выбрать квадратную и круглую форму представления основания столбцов.
-
Выберите первый из трёх видов столбцов с квадратной формой основания, активируйте метки Count (Количество) и Value (значение) и оставьте автоматическое построение базовой линии (см. рис. 23.9).
На регистрационной карте Error Bars (Столбцы по величинам ошибки) для столбцов можно организовать указание доверительных интервалов, стандартных отклонений и стандартных ошибок. Как величину доверительного интервала, так и множитель стандартной ошибки и стандартного отклонения здесь можно регулировать пошаговым образом.
Существует три формы столбцов ошибок и четыре различных направления прорисовки этих столбцов.
-
Из режима ЗD-эффектов перейдите к 2О-системе координат, откройте регистрационную карту Error Bars (Столбцы по величинам ошибки) и активируйте опцию Display Error Bars (Показать столбцы ошибок). Активируйте вывод простой стандартной ошибки и оставьте без изменения все остальные установки по умолчанию.
Рис. 23.8: Регистрационная карта Bar Chart Options (Параметры столбчатой диаграммы)
Рис. 23.9: Столбчатая диаграмма с 3D-эффектом и обозначением столбцов
-
Если в регистрационной карте Bar Chart Options (Параметры столбчатой диаграммы) ещё активированы опции группы Bar Labels (Метки столбцов), деактивируйте их.
В регистрационной карте Titles... (Заголовки) Вы можете указать заголовок, подзаголовок и комментарии. В регистрационной карте Options (Параметры) наряду со стандартным форматом, устанавливаемым по умолчанию, для столбчатых диаграмм могут быть установлены ещё шесть дополнительных форматов. Попробуйте самостоятельно все возможности, предоставляемые SPSS. Для отображения диаграмм на мониторе, конечно же, больше подходят те опции, которые позволяют изобразить график в наиболее подходящем цветовом варианте. Для повышения разнообразия оттенков при печати на принтере в распоряжение пользователя предоставляется опция Grayscale (Оттенки серого), которая применяется и при публикации интерактивных графиков в этой книге.
Следующий пример должен помочь нам лучше разобраться в значении различных типов переменных. Переменная polgrund (политическая позиция), к примеру, так же, как и переменная uebstaat (пусть компьютерными технологиями занимается государство) является категориальной. Первая переменная при помощи кодировок 1 = скорее левый, 2 = центрист и 3 = скорее правый указывает на политическую приверженность, а вторая переменная при помощи кодировок от 1 = согласен до 5 = не согласен выражает отношение к позиции: "Пусть компьютерными технологиями занимается государство".
-
Поместите переменную polgrund (политическая позиция) в поле оси х, а переменную uebstaat (пусть компьютерными технологиями занимается государство) в поле оси у. Внизу диалогового окна появится информация, что столбцами теперь уже может быть присвоены величины моды, то есть наиболее часто встречающегося значения (категориальной) переменной uebstaat. Мы же хотим отобразить среднее значение этой переменной.
-
Правой кнопкой мыши щёлкните на переменной uebstaat, находящейся в поле оси у и в появившемся меню присвойте ей статус метрической переменной (Scale).
Рис. 23.10: Регистрационная карта Error Bars (Столбцы по величинам ошибки)
Рис. 23.11: Столбчатая диаграмма с указанием стандартной ошибки
-
В списке, появившемся внизу окна, оставите опцию по умолчанию, а именно Means (Отображение средних значений) и подтвердите построение диаграммы нажатием ОК. Вы заметите, что созданная столбчатая диаграмма демонстрирует только незначительные различия средних значений. Для более ясного отображения различий необходимо перекомпоновать шкалу значений.
-
Дважды щёлкните на графике и затем правой кнопкой мыши на наименовании вертикальной оси. В появившемся меню активируйте Scale Axis... (Масштабировать ось); откроется диалоговое окно Scale Axis (Масштабировать ось) (см. рис. 23.12).
-
Установите значение минимума равным 2,8, а цену деления (Tick Interval) равную 0,2.
Точно таким же образом Вы можете масштабировать любую столбчатую диаграмму, чтобы в конечном итоге получить довольно заметные различия столбцов. Однако это имеет смысл делать только тогда, когда эти различия являются значимыми. Как показала проверка при помощи Н-теста по Крускалу и Уоллису, респонденты с левыми политическими взглядами чаще соглашались с точкой зрения: "Пусть компьютерными технологиям;: занимается государство", чем респонденты с правыми политическими взглядами, именно такие значимые различия мы и наблюдаем в данном примере построения интерактивной диаграммы.
К сожалению, в данной диаграмме респонденты, полностью разделяющие левые политические взгляды, изображаются самым коротким столбцом, что может быть объявлено кодировкой (1 = согласен).
6.gif
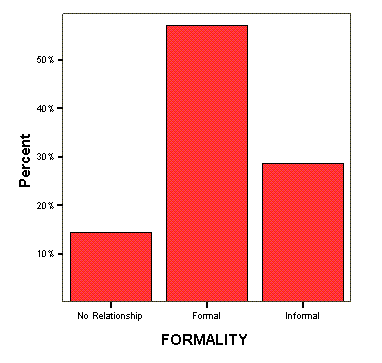
7.gif
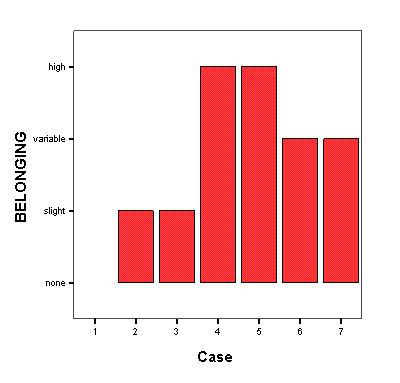
8.gif
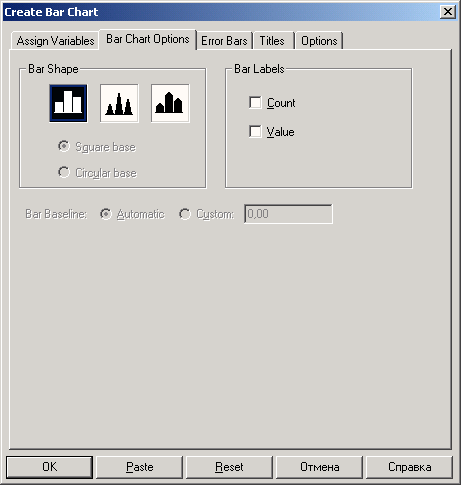
9.gif
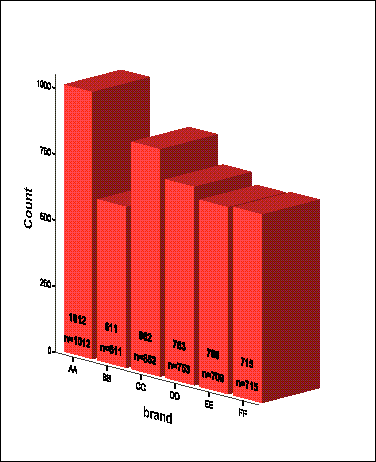
10.gif
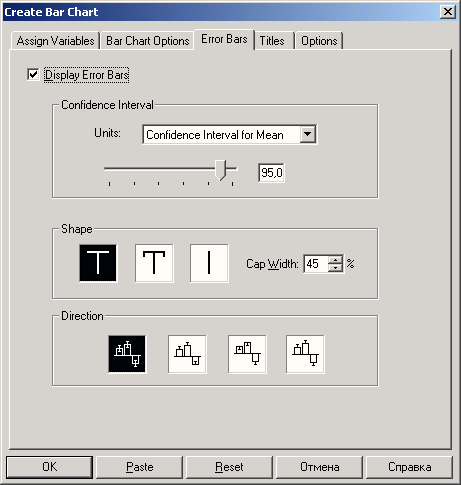
11.gif

23.1.3 Группированная столбчатая диаграмма
23.1.3 Группированная столбчатая диаграмма
Рассмотрим теперь как частоты различных ответов на вопрос: "В какое время с; -ток Вы предпочитаете работать за компьютером?" зависят от пола респондентов. Для этого имеются четыре возможности.
Рис. 23.12: Диалоговое окно Scale Axis (Масштабировать ось)
Рис. 23.13: Простая столбчатая диаграмма с коррекцией оси
-
Нажмите выключатель 2-D Coordinate (2-D координаты) и в появившемся меню активируйте опцию 3-D Coordinate (3-D координата). Откроется ещё одно поле (поле оси z) (см. рис. 23.14).
-
Переменную pczeit (время суток) поместите в поле оси х, переменную geschl (пол) в поле оси г, а системную переменную Spct (процент) в поле оси у.
-
Подтвердите построение нажатием ОК.
Этот тип отображения столбцов применять не рекомендуется, т.к. столбцы относящиеся к женщинам частично скрыты.
Следующие два варианта построения диаграммы получаются благодаря введению легенды, отражающей принадлежность столбцов при помощи цвета и узора.
-
Активируйте вновь двумерное представление диаграммы и перенесите переменную geschl (пол) в поле Color (Цвет) группы Legend Variables (Переменные легенды). Обращайте внимание на то, чтобы соседний выключатель был установлен в положение Cluster (Группа).
При отображении графика в цвете заметно, что женщины более склонны к работе за компьютером в утренние и послеобеденные часы, а мужчины напротив вечером и ночью.
-
Теперь переменную geschl (пол) поместите в поле Style (Стиль) группы Legend Variables (Переменные легенды) и обратите внимание на то, чтобы соседний выключатель был установлен в положение Cluster (Группа) (см. рис. 23.17).
Ещё одна возможность построения графика выражается указанием полевых переменных.
-
Поместите переменную geschl (пол) в поле Panel Variables (Переменные полей) (см. рис. 23.18).
Указание переменной в качестве разделителя полей имеет смысл в том случае, если она имеет насколько категорий. Можно вносить также и несколько полевых переменных.
Рис. 23.14: Диалоговое окно построения столбчатой диаграммы в трёхмерной системе координат
Рис. 23.15: Группированная столбчатая диаграмма в трёхмерной системе координат
Рис. 23.16: Группированная столбчатая диаграмма с переменной в качестве легенды (различные цвета)
Рис. 23.17: Группированная столбчатая диаграмма с переменной в качестве легенды (различная штриховка)
Рис. 23.18: Столбчатая диаграмма, группированная при помощи полевой переменной
12.gif

13.gif
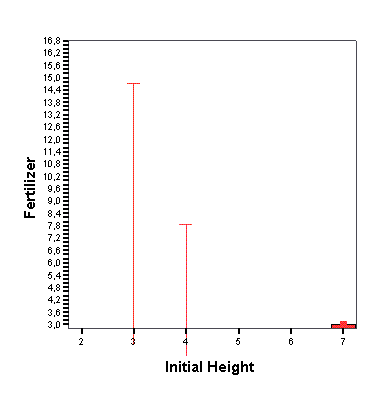
14.gif
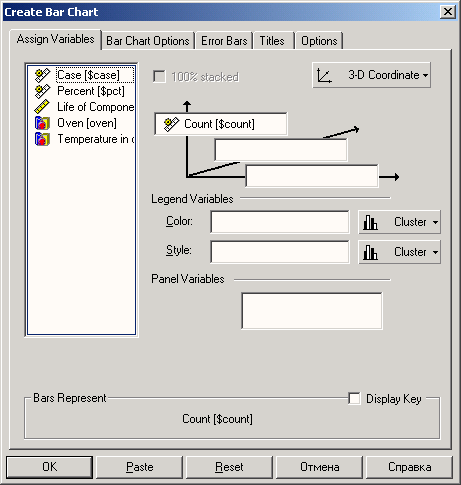
15.gif
16.gif

17.gif
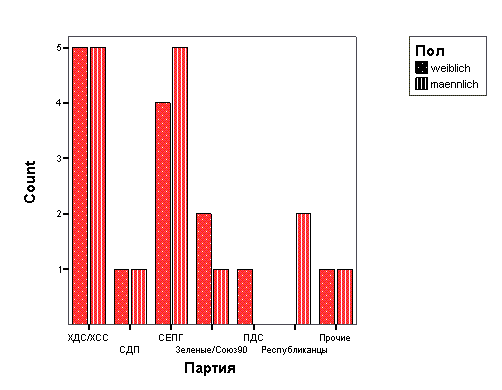
18.gif
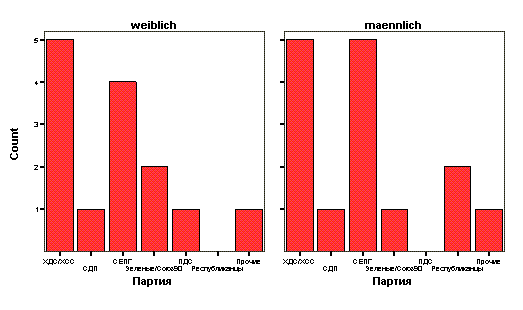
23.1.4 Штабельная столбчатая диаграмма
23.1.4 Штабельная столбчатая диаграмма
Вместо группированной столбчатой диаграммы вы можете построить штабельную столбчатую диаграмму. Для этого переключатель, находящийся рядом с полем Color (Цвет) или Style (Стиль), установите в положение Stack (Штабельная).
Группированная диаграмма с рисунка 23.17 при установке режима Stack (Штабельная) выглядит так, как изображено на рисунке 23.19.
23.10 Коррекция интерактивных графиков
23.10 Коррекция интерактивных графиков
Для того, чтобы получить больше информации об интересующих Вас данных или приукрасить диаграммы перед презентацией, Вы можете их многогранно откорректировать.
Некоторые виды корректировок мы Вам уже представляли. К ним относятся:
-
отключение подсказок (разд. 23.5),
-
изменение шкалы оси (разд. 23.1.2, 23.5),
-
отделение сегмента круговой диаграммы (разд. 23.4.1),
-
варианты обозначения наблюдений на диаграмме рассеяния (разд. 23.8),
-
отключение обозначений наблюдений на диаграмме рассеяния (разд. 23.8).
Чтобы получить возможность модифицировать построенную диаграмму, Вы должны сначала дважды щёлкнуть на области ее построения. Тогда перед Вами появятся практически необозримые возможности корректировки диаграммы.
Мы объясним ещё нескольких принципиальных моментов на уже рассмотренных нами примерах. Данные для примеров взяты из знакомого уже нам файла pcalltag.sav.
-
Откройте файл pcalltag.sav.
-
Выберите в меню Graphs (Графики) Interactive (Интерактивно) Ваr... (Столбчатые)
-
В диалоговом окне Create Bar Chart (Создание столбчатой диаграммы) переместите переменную fachgr (группы специальностей) в поле оси х, а системную переменную Spct (процент) — в поле оси у.
-
В регистрационной карте Titles... (Заголовки) дайте диаграмме название: "Частотные показатели по специальностям" и в качестве поясняющей подписи введите "Институт социологии 1998".
-
В регистрационной карте Options (Параметры) активируйте отображение столбцов в сером цвете (Grayscale).
-
Подтвердите установки нажатием ОК.
В окне просмотра появится соответствующая столбчатая диаграмма. Откорректируем построенную диаграмму, а именно
-
уберём подсказку,
-
разместим по центру заголовок и пояснение, а также изменим шрифт.
-
Щёлкните дважды на диаграмме, чтобы получить возможность её редактировать.
Диаграмма осталась в окне просмотра, но изменились пункты меню, находящиеся под строкой меню. Слева и сверху появились дополнительные панели инструментов; значение кнопок этих панелей Вы узнаете, если с остановками пройдётесь по ним курсором.
Теперь при помощи правой кнопки мыши вы можете активировать для корректировки любой элемент диаграммы, после чего появляется соответствующее контекстное меню. В этом меню Вам предоставляются обширные возможности для коррекции элементов.
-
Щёлкните правой кнопкой мыши на подсказке: "Столбцы указывают на процентные показатели" и в появившемся меню выберите опцию Hide Key (Спрятать подсказку).
-
При помощи левой кнопки выделите мыши заголовок диаграммы и, не отпуская кнопку, передвиньте его немного вправо, таким образом, чтобы он оказался по центру диаграммы.
-
Теперь правой кнопкой мыши щёлкните на заголовке.
-
В контекстном меню выберите опцию Text... (Текст).
Рис. 23.57: Простая столбчатая диаграмма с заголовком и подсказкой
-
В диалоговом окне Text (Текст) в поле Font (Шрифт) активируйте опцию Times New Roman, в поле Font Style (Начертание) опцию Bold Italic (Жирный курсив) и в поле Size (Размер) установите значение 14. Подтвердите нажатием ОК.
-
Переместите заголовок при помощи левой кнопки мыши немного влево.
-
Таким же образом расположите по центру и пояснение, находящееся в нижней части диаграммы, установите курсивное начертание и размер 9.
-
Дважды щёлкните на любой точке за пределами диаграммы. Панели инструментов исчезнут и график вернётся к нормальному виду (см. рис. 23.58) .
На следующем примере мы покажем, как на графике построить координатную сетку и добавить необходимый текст. Вновь построим простую линейчатую диаграмму, отображающую тенденцию потребления пива, рассмотренную в разд. 23.2.1 .
-
Откройте файл bierjahr.sav.
-
Выберите в меню Graphs (Графики) Interactive (Интерактивно) Line... (Линейчатые)
-
Перенесите переменную jahr (год) в поле оси х, а переменную bier (пиво) в поле оси у.
-
Подтвердите нажатием ОК. В окне просмотра появится такая же диаграмма, как на рисунке 23.20.
-
Дважды ввод щёлкните на этом графике и сначала отключите подсказку, если она ещё присутствует.
-
Щёлкните правой кнопкой мыши на какой-либо точке графика.
-
В появившемся контекстном меню выберите опцию Grid Lines... (Линии сетки). Откроется диалоговое окно Grid Lines (Линии сетки), в которое входят две регистрационные карты.
-
В карте, открытой по умолчанию, Bier-verbrauch je Einwohner (Liter) активируйте опции Display Grid lines (Показать сетку) и At major ticks only (Только на главных делениях).
-
Откройте регистрационную карту Jahr (Год) и активируйте опции Display Grid lines (Показать сетку) и At major and minor ticks (Главные и вспомогательные деления).
-
Подтвердите построение нажатием ОК.
Рис. 23.58: Откорректированная простая столбчатая диаграмма
На диаграмме появится координатная сетка, которая облегчит сопоставление точек построенной кривой цифровыми значениями, откладываемыми по осям.
Теперь добавим в диаграмму текст.
-
Щёлкните левой кнопкой мыши на значке левой панели инструментов, обозначенном маленькой (прописной) буквой а. Затем опять же левой кнопкой мыши щёлкните в какой-нибудь точке на свободном пространстве в диаграмме, начиная с которой вы хотели бы вводить текст. Наберите в двух строках текст: "Снижение потребления пива в Германии".
Линейчатая диаграмма, изменённая таким образом, будет отображена в окне просмотра.
Рис. 23.59: Линейчатая диаграмма с координатной сеткой и дополнительным текстом
Остальные возможности модифицирования графиков, испробуйте, пожалуйста, самостоятельно; отправляйтесь в путешествие на поиски открытий!
57.gif
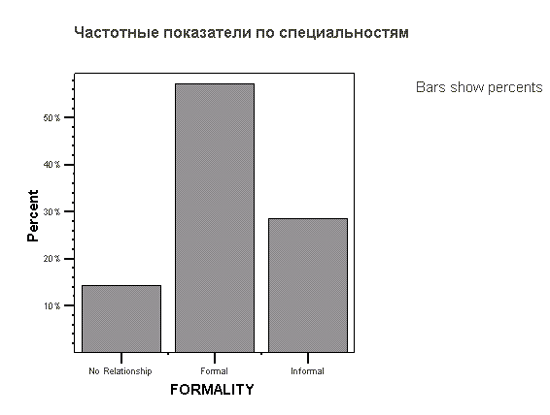
58.gif

59.gif

23.11 Построение диаграммы поданным сводной таблицы
23.11 Построение диаграммы по данным сводной таблицы
Данные, находящиеся в сводной таблице результатов разнообразных статистических расчетов, могут быть непосредственно отображены в графическом виде. Порядок действий рассмотрим на простом примере.
-
Откройте файл pcalltag.sav и посредством выбора меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты) постройте частотную таблицу переменной pczeit (время суток): Tageszeit (Время суток)
|
| Frequency (Частота) | Percent (Процент) | Valid Percent (Действи-тельный процент) | Cumulative Percent (Совоку-пный процент) |
Valid (Действитель ные значения) | vormittags (первая половина) | 118 | 9,6, | 11,1 | 11,1 |
nachmittags (вторая половина) | 331 | 26,9 | 31,3 | 42,4 | |
abends (вечер) | 524 | 42,6 | 49,5 | 91,9 | |
nachts (ночь) | 86 | 7,0 | 8,1 | 100,0 | |
Total (Сумма) | 1059 | 86,2 | 100,0 |
| |
Missing (Отсутству-ющие значения) | Nichtnutzer (Неисполь-зующие) | 65 | 5,3 |
|
|
System (Системные значения) | 105 | 8,5 |
|
| |
Total (Сумма) | 170 | 13,8 |
|
| |
Total (Сумма) |
| 1229 | 100,0 |
|
|
Мы хотим представить процентные показатели действительных наблюдений в виде столбчатой диаграммы. Для этого:
-
Щёлкните дважды на таблице и выделите действительные процентные показатели для четырёх категорий времени суток.
-
Щёлкните правой кнопкой мыши на выделенной области и в контекстном меню выберите опцию Create Graph (Построить график). Затем выберите вид диаграммы, в нашем случае это Ваг (Столбчатая).
-
С другими возможностями техники "Из таблицы в график" поэкспериментируйте, пожалуйста, самостоятельно.
Рис. 23.60: Столбчатая диаграмма, построенная на основании данных сводной таблицы
60.gif
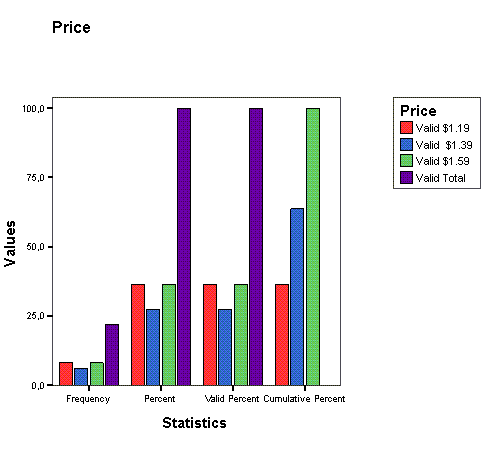
23.2 Линейчатые диаграммы
23.2 Линейчатые диаграммы
Отображение информации в виде линейчатой диаграммы, как правило, выбирается в том случае, если необходимо отобразить изменение показателей с течением времени. При этом делается различие между отображением одной переменной (простая линейчатая диаграмма) и разбиением одной переменной при помощи некоторой категориальной переменной (сложная линейчатая диаграмма).
23.2.1 Простые линейчатые диаграммы
Немецкие пивовары в последнее время стали жаловаться на снижение уровня потребления пива. Представим развитие потребления пива в графическом виде.
-
Откройте файл bierjahr.sav. Файл содержит две переменные jahr (год) и bier (пиво). В первой переменной хранится информация о годовых показателях потребления пива с 1970 по 1997 год, во второй переменной среднее потребление пива на одного человека в литрах.
-
Выберите в меню Graphs (Графики) Interactive (Интерактивно) Line... (Линейчатые)
Откроется диалоговое окно Create Line (Создание линейчатой диаграммы), содержащее пять регистрационных карт. В первую очередь, как обычно, открывается регистрационная карта Assign Variables (Присвоить переменные).
-
Перенесите переменную jahr (год) в поле оси х, а переменную bier (пиво) в поле оси у.
Рис. 23.19: Штабельная столбчатая диаграмма (различная штриховка)
Имейте в виду, что в данном примере каждому году соответствует только одно значение зависимой переменной (bier (пиво)); в общем случае же каждому значению независимых переменных Вы можете поставить в соответствие сколько угодно значений зависимых переменных, которые затем обрабатываются, например, вычисляется среднее значение. Это значение и отображается на диаграмме. Подобный пример будет рассматриваться дальше.
-
В данном примере всё же оставьте установку по умолчанию Means (Среднее значение) и подтвердите построение нажатием ОК.
Рис. 23.20: Диалоговое окно Create Line (Создание линейчатой диаграммы)
Обратите внимание на то, что шкала потребления пива начинается не с нулевой отметки, из-за чего снижение потребления очень сильно бросается в глаза. Для большей наглядности Вы можете дополнительно отметить маркерами значения, соответствующие отдельно взятым годам.
-
Для этого перейдите на регистрационную карту Dots and Lines (Точки и линии) и в группе Display (Показать) активируйте опцию Dots (Точки).
Вы можете также произвести эти установки, если с самого начала выберите меню Graphs (Графики) Interactive (Интерактивно) Dot... (Точки) и в регистрационной карте Dots and Lines (Точки и линии) активируете опцию Lines (Линии) (см. рис. 23.22).
Рис. 23.21: Простая линейчатаядиаграмма
Кривую на диаграмме вы можете представить и в виде ленты.
-
На регистрационной карте Assign Variables (Присвоить переменные) поставьте переключатель в положение 3-D Effect (3-D эффект); опцию Dots (Точки) необходимо в данном случае деактивировать.
Отображение линии в виде ленты Вы также можете организовать при помощи меню Graphs (Графики) Interactive (Интерактивно) Ribbon... (Лента) (см. рис. 23.23).
Рис. 23.22: Простая линейчатая диаграмма с отображением отдельных точек
Рис. 23.23: Простая линейчатая диаграмма с 3-D эффектом (лента)
В заключении обзора линейчатых диаграмм мы приведём пример, в котором для диаграммы будут рассчитаны средние значения нескольких показателей. Некоторая фирма, занимающаяся производством минеральной воды, утверждает, что регулярное употребление воды производства этой фирмы ведёт к снижению уровня холестерина в крови. Для того, чтобы это доказать на протяжении 12 недель проводилось наблюдение за 18 добровольцами.
-
Откройте файл mineral.sav.
-
В файле находятся переменные woche (неделя) и chol (холестерин). Переменная woche (неделя) имеет значения от 0 до 12, которые указывают на номер на соответствующей недели, а в переменной chol (холестерин) хранится уровень холестерина. Значение уровня холестерина при переменной woche (неделя) равной 0 соответствует исходному уровню перед началом лечения. Каждую неделю у добровольцев измеряются 18 показателей уровня холестерина в крови.
Следует отметить, что такой вид представления данных для SPSS не считается традиционным. Для каждого последовательного измерения, как правило, должна образовываться новая переменная, для нашего примера, допустим, это были бы переменные chol0 до chol12, на основании которых можно было бы провести тест значимости для зависимых выборок. Этот факт указывает на значительное отличие рассматриваемого примера от структуры данных, обычно применяемой в SPSS.
-
В регистрационной карте Assign Variables (Присвоить переменные) поместите переменную woche (неделя) в поле оси х, а переменную chol (холестерин) — в поле оси у.
-
Активируйте регистрационную карту Error Bars (Столбцы по величинам ошибки) и организуйте вывод 95 %-го доверительного интервала.
Первые три недели действительно можно наблюдать значительное понижение уровня холестерина, но затем этот уровень вновь начинает расти.
Рис. 23.24: Простая линейчатая диаграмма с доверительным интервалом
19.gif
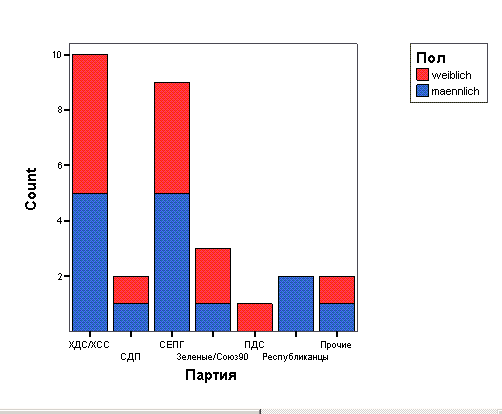
20.gif
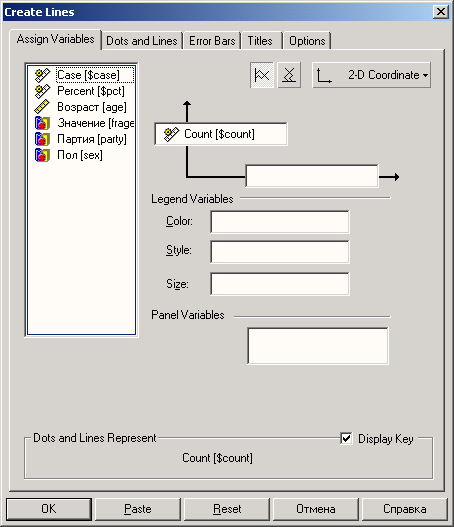
21.gif

22.gif

23.gif

24.gif
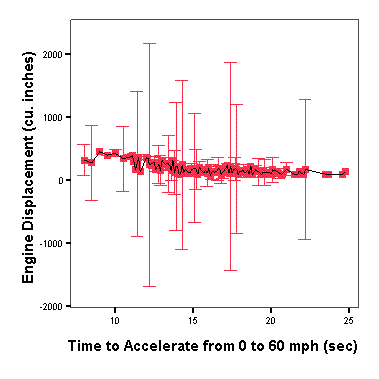
23.2.2 Сложные линейчатые диаграммы
23.2.2 Сложные линейчатые диаграммы
Сложная диаграмма получается при разбиении одной переменной на категории.
-
Откройте файл gaetraenk.sav.
В этом файле находятся данные с 1991 по 1997 годы о потреблении трёх видов напитков на одного человека. Переменная jahr указывает на год, перемен ная verb на потребление в литрах на одного человека, а переменная getraenk на вид напитка (1 = алкогольные; 2 = вода, соки; 3 = кофе, чай, молоко).
-
Перенесите переменную jahr в поле оси х, переменную verb в поле оси у, а переменную getraenk в поле Style (Стиль) группы переменных легенды.
-
При помощи соответствующего переключателя выберите отображение с 3D эффектом.
На диаграмме наблюдается снижение потребления алкогольных напитков, кофе, чая и молока и одновременно сильное повышение потребления воды и соков.
В регистрационной карте Dots and Lines (Точки и линии) Вы можете активировать отображение связывающих линий; тогда на сложной линейчатой диаграмме будут соединены между собой точки с одинаковой координатой х. Построение связывающих линий вы также можете организовать путём выбора меню Graphs (Графики) Interactive (Интерактивно) Drop-Line... (Связывающие линии) Теперь обратимся к диаграммам с областями.
Рис. 23.25: Сложная линейчатая диаграмма с 3D эффектом
25.gif
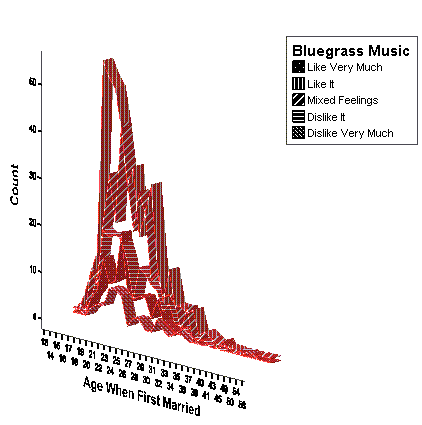
23.3 Площадные диаграммы
23.3 Площадные диаграммы
Если области, находящееся под линиями, закрашены, то в таком случае говорят о диаграммах с областями. Как правило, диаграммы такого рода выглядят, показательней.
Для объяснения площадных диаграмм должно быть достаточно одного простого примера. Вернёмся для этого к файлу bierjahr.sav, рассмотренному в разделе 23.2.1, который содержит данные о потреблении пива с 1970 по 1997 годы.
-
Откройте файл bierjahr.sav.
-
Выберите в меню Graphs (Графики) Interactive (Интерактивно) Area... (Области)
Откроется диалоговое окно Create Area Chart (Создание диаграммы с областями).
-
В исходной регистрационной карте поместите переменную jahr (год) в поле оси х, а переменную bier (пиво) в поле оси у.
-
Если Вы посмотрите в окне просмотра на получившуюся диаграмму, то заметите, что было бы целесообразней начинать отсчёт оси у не со значения 0, а со значения 130, к примеру.
-
Чтобы внести такую корректировку поступите так, как было описано в разделе 23.1.2. Щёлкните дважды на графике и затем правой кнопкой мыши на наименовании оси у. В появившемся меню активируйте Scale Axis... (Масштабировать ось). В диалоговом окне Scale Axis (Масштабировать ось) в группе Scale (Шкала) в поле Minimum (Минимум) введите значение 130, а в поле Maximum (Максимум) — значение 160, значение Tick Interval (Цена деления) установите равным 5.
Рис. 23.26: диалоговое окно Create Area Chart (Создание диаграммы с областями)
Рис. 23.27: Простая площадная диаграмма
-
Испытайте другие возможности самостоятельно, к примеру, постройте штабельную или группированную диаграмму с областями. Используйте для этого файл get-raenk.sav рассмотренный в разделе 23.2.2 .
26.gif
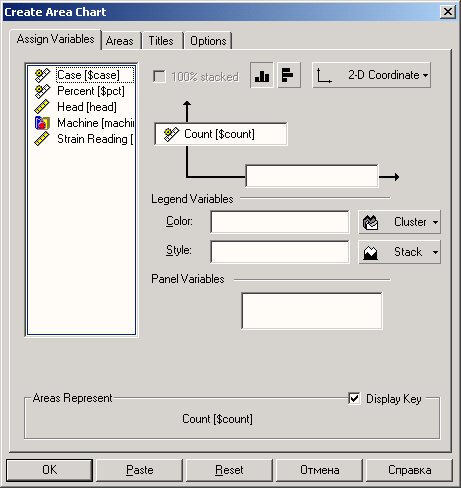
27.gif

23.4 Круговые диаграммы
23.4 Круговые диаграммы
Круговая диаграмма, как самый излюбленный способ представления категориальных переменных, выбирается тогда, кода количество категорий не велико. При помощи диаграмм этого вида можно отобразить абсолютные или процентные показатели частот категориальных переменных или слагаемые некоторой метрической переменной, если их можно с учётом категорий представить в виде некоторой общей суммы, имеющей определенный смысл, которая будет соответствовать ста процентам. В рамках интерактивных графиков SPSS предлагает простые, штабельные и разложенные круговые диаграммы.
23.4.1 Простые круговые диаграммы
23.4.1 Простые круговые диаграммы
В главе 23.1.1 был представлен файл pcalltag.sav. содержащий некоторые переменные из исследования на тему Компьютер в повседневной жизни. Представим переменную pczeit (В какое время суток Вы предпочитаете работать за компьютером?) в виде круговой диаграммы.
-
Откройте файл pcalltag.sav.
-
Выберите в меню Graphs (Графики) Interactive (Интерактивно) Pie... (Круговые) Simple... (Простая)
Откроется диалоговое окно Create Simple Pie Chart (Создание простой круговой диаграммы) с четырьмя регистрационными картами: Assign Variables (Присвоить переменные), Pies (Круги), Titles... (Заголовки) и Options (Параметры).
-
Перенесите переменную pczeit в поле Slice By (Сектора), а переменную Spct — в поле Slice Summary (Сумма частей).
Рис. 23.28: Диалоговое окно Create Simple Pie Chart (Создание простой круговой диаграммы)
Если вы будете использовать диаграмму для экранной презентации или печатать на цветном принтере, присвойте каждому сегменту свой цвет; если же Вы будете печатать диаграмму в чёрно-белых тонах, то лучше применить различные виды штриховок.
-
Откройте регистрационную карту Pies (Круги) и в группе Slice Labels (Метки секторов) активируйте опции Category (Категория) и Value (Значение). Оставьте установку по умолчанию All Outside (Все снаружи).
Благодаря активированию этих опций вокруг диаграммы будут приведены описания категорий, которые представляют собой метки переменных с соответствующими им процентными показателями.
Вы можете построить одновременно несколько диаграмм, находящихся рядом друг с другом или друг над другом, если зададите несколько полевых переменных. Мы хотим отобразить зависимость переменной polgrund (Политическая позиция) от переменных geschl (пол) и internet (Использование Интернета: да или нет).
Рис. 23.29: Простая круговая диаграмма
-
Перенесите переменную polgrund в поле Slice By (Сектора) и оставьте переменную Spct в поле Slice Summary (Сумма секторов).
-
Переменным geschl и internet присвойте статус полевых переменных и деактивируйте вывод наименований сегментов, который возможно ещё остался после построения предыдущего графика.
Между использующими Интернет (верхние круговые диаграммы) и не использующими (нижние круговые диаграммы) нет ни каких различий в отношении политических убеждений, но между полами различия существуют: учащихся с правыми убеждениями среди мужчин больше, чем среди женщин.
Для круговых диаграмм тоже можно применить трёхмерный эффект.
-
При помощи выключателя Reset (Сброс) деактивируйте все предыдущие установки.
-
Переменную fachgr (специальности) поместите в поле Slice By (Сектора). Переменной $pct присвойте статус обобщающей переменной и включите выключатель Style (Стиль).
-
Установите ЗО-режим при помощи соответствующего выключателя.
Рис. 23.30: Простые круговые диаграммы с влиянием полевых переменных
В результате этих действий Вы получите круговую диаграмму с трёхмерным эффектом. В качестве примера ещё одного способа обработки круговой диаграммы рассмотрим отделение сегмента, а именно, сегмента, соответствующего доле учащихся, которые специализируются в естественных науках.
-
Щёлкните дважды на 3D графике и затем правой кнопкой мыши — на интересующем нас сегменте.
-
В появившемся меню активируйте опцию Explode from Pie (Отделить от круга).
Рис. 23.31: Круговая диаграмма в трёхмерном исполнении с отделённым сектором
Последним примером простой круговой диаграммы будет отображение сумм некоторой метрической переменной в зависимости от категорий зависимой переменной.
-
Переменную pczeit (время суток) поместите в поле Slice By (Сектора) и активируйте выключатель Style (Стиль).
-
Переменной compst присвойте статус обобщающей. Она указывает на то, сколько часов в неделю студенты проводят за компьютером.
-
В поле Slice Represents Computer-Stunden pro Woche (Сектора соответствуют количеству часов в неделю, проведенных за компьютером) оставьте установленную по умолчанию опцию суммы.
-
В регистрационной карте Titles (Заголовки) укажите название диаграммы: "Время, проведённое за компьютером"
Рис. 23.32: Простая круговая диаграмма с представлением суммы
Из диаграммы можно сделать вывод о том, что студенты работают на компьютере в основном по вечерам и намного реже в первой половине дня и ночью.
28.gif
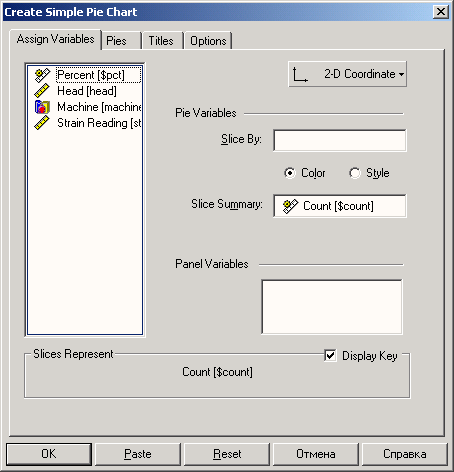
29.gif

30.gif
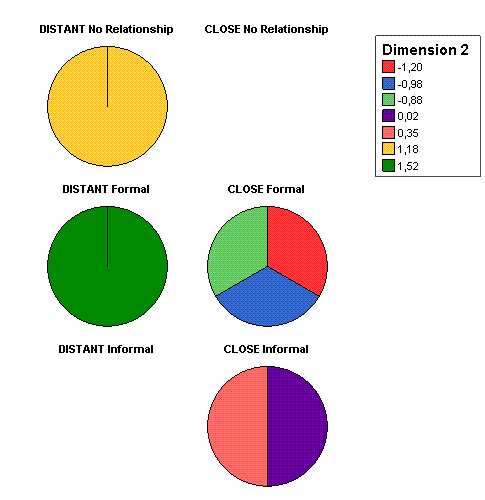
31.gif

32.gif
23.4.2 Штабельные круговые диаграммы
23.4.2 Штабельные круговые диаграммы
При помощи штабельной диаграммы отображение некоторой категориальной переменной может производиться по группам, обусловленным некоторой дополнительной переменной.
-
Выберите в меню Graphs (Графики) Interactive (Интерактивно) Pie... (Круговые) Clustered... (Группированная)
Откроется диалоговое окно Create Clustered Pie Chart (Создание группированной круговой диаграммы).
-
Переменную pczeit (время суток) поместите в поле Slice By (Сектора), а переменную geschl (пол) в поле Clustered by (Группировать при помощи), переменной $pct присвойте статус обобщающей переменной (Slice Summary) и включите выключатель Style (Стиль).
Рис. 23.33: Группированная круговая диаграмма
Эта диаграмма представляется не очень наглядной, поэтому для её изучения мы ограничимся приведенным примером.
33.gif

23.4.3 Рассыпанная круговая диаграмма (рассыпанные круги)
23.4.3 Рассыпанная круговая диаграмма (рассыпанные круги)
Круговые диаграммы могут быть разложены в двумерной х-у системе координат, по осям которой будут отображаться две дополнительные категориальные переменные. При активировании соответствующего символа можно добавить и третью переменную (r), что приведёт к построению трёхмерной диаграммы.
Мы хотим при помощи такой диаграммы представить реакцию на положение: "Я тяжело вхожу в дружеские отношения" (переменная freund) в зависимости от пола и использования сети Интернет (да — нет).
-
Выберите в меню Graphs (Графики) Interactive (Интерактивно) Pie... (Круговые) Plotted... (Рассыпанная)
Откроется диалоговое окно Create Plotted Pie Chart (Создание рассыпанной круговой диаграммы).
Рис. 23.34: Разделённая круговая диаграмма
-
Переменную internet (использование сети Интернет) поместите в поле оси у, переменную geschl (пол) в поле оси х, переменную freund (трудность завязывания знакомств) в поле Slice By (Сектора) и переменной Spct присвойте статус обобщающей переменной (Slice Summary). Активируйте опцию Style (Стиль).
Из построенной зависимости видно отсутствие разницы между пользователями сети Интернет и теми, кто ею не пользуется, а также незначительные отличия по половому признаку. Доля студентов, которые дали отрицательный ответ на поставленный вопрос, среди женщин выше, чем среди мужчин.
Трёхмерный вариант диаграммы с использованием ЗD-эффектов, который строится путём установки соответствующего выключателя в положение 3D Coordinate (Трехмерные координаты), будет не столь показательным и поэтому не рекомендуется для применения.
34.gif

23.5 Коробчатые диаграммы
23.5 Коробчатые диаграммы
Так называемые коробчатые диаграммы являются самыми удобными для отображения медианы, первого и третьего квартилей, минимального и максимального значений, а также аномальных и экстремальных значений.
В файле klin.sav хранятся некоторые медицинские показатели, описывающие состояние 981 пациента некоторой клиники. Постоим сначала две отдельные диаграммы уровня сахара в крови, разделённые по половому признаку.
-
Откройте файл klin.sav.
-
Выберите в меню Graphs (Графики) Interactive (Интерактивно) Boxplot... (Коробчатые) Откроется диалоговое окно Create Boxplot (Создание коробчатой диаграммы).
-
Переменную gluk поместите в поле оси у, а переменную geschl — в поле оси х.
Рис. 23.35: Диалоговое окно Create Boxplot (Создание коробчатой диаграммы)
Рис. 23.36: Коробчатая диаграмма с аномальными и экстремальными значениями
В коробчатых диаграммах аномальные значения обозначаются кружками, а экстремальные звёздочками. Аномальными считаются те значения, которые находятся за пределами коробки между отметками полуторной и тройной высоты этой коробки. Если маркировки аномальных и экстремальных значений Вам мешают и Вы захотите от них избавиться, то поступите следующим образом:
-
Откройте регистрационную карту Boxes (Коробки) и деактивируйте опцию маркировки аномальных и экстремальных значений. Вы заметите, что хотя метки аномальных и экстремальных значений теперь и отсутствуют, но шкала всё равно остаётся излишне растянутой до значения 600. Поэтому график необходимо ещё дополнительно доработать.
-
Щёлкните дважды на графике и затем правой кнопкой мыши — на вертикальной оси.
-
В появившемся меню активируйте опцию Scale Axis... (Масштабировать ось).
Откроется диалоговое окно Scale Axis — Blutzucker (Маштабировать ось — Уровень сахара).
-
Минимуму присвойте значение 0, максимуму 200 и возьмите цену деления 50.
-
Излишним представляется ещё и напоминания: Outliers are hidden (Показ аномальных значений отключён), а также Extreme are hidden (Показ экстремальных значений отключён). Щёлкните на этом тексте правой кнопкой мыши и в контекстном меню активируйте опцию Hide Key (Спрятать подсказку).
Коробчатые диаграммы могут быть сгруппированы при помощи некоторой дополнительной переменной, которая называется переменной легенды.
-
В поле оси х вместо переменной geschl поместите переменную altek, которая отображает шесть возрастных категорий, а переменную geschl поместите в поле Style (Стиль) группы переменных легенды Legend Variables (Переменные легенды).
-
Произведите описанные выше действия над шкалой получившегося графика.
Рис. 23.37: Коробчатая диаграмма с отключённым режимом демонстрации аномальных и экстремальных значений
Рис. 23.38: Коробчатая диаграмма с одной переменной легенды
Ещё одной разновидностью группировки при помощи дополнительной переменной, является группировка при помощи полевой переменной.
-
Теперь переменной geschl вместо статуса переменной легенды присвойте статус полевой переменной. И здесь также дополнительно откорректируйте маштаб оси.
Рис. 23.39: Коробчатая диаграмма с одной полевой переменной
Ещё одну возможность добавления дополнительной переменной в диаграмму открывает активирование режима 3D Coordinate (Третья координата). Но этот вариант представления данных является очень непоказательным.
В заключение продемонстрируем ещё коробчатую диаграмму с ЗD-эффектом.
-
При помощи выключателя Reset (Сброс) дёак-тивируйте все установки.
-
Переменную chol (холестерин) поместите в поле оси у, а переменную alterk (возрастные группы) — в поле оси х.
-
Активируйте опцию 3D-Effect (Трехмерный эффект), деактивируйте отображение аномальных и экстремальных значений и в регистрационной карте Boxes (Коробки) активируйте опцию Display count labels (Показать метки частот).
-
В построенном графике подкорректируйте шкалу путём установки минимального значения равным 0 и максимального значения равным 400. Мешающую подсказку Вы можете убрать щелчком правой кнопки мыши с последующим выбором опции Hide Key (Спрятать подсказку).
Рис. 23.40: Коробчатая диаграмма с применением трехмерного эффекта и указанием частот
35.gif
36.gif
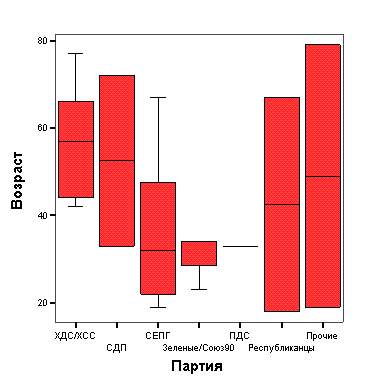
37.gif
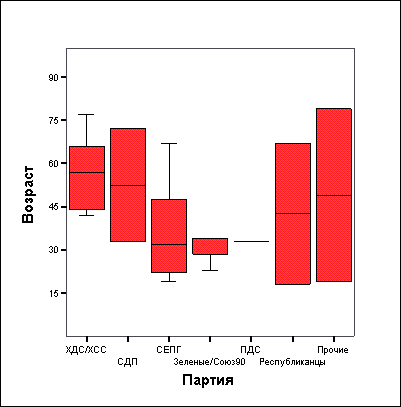
38.gif
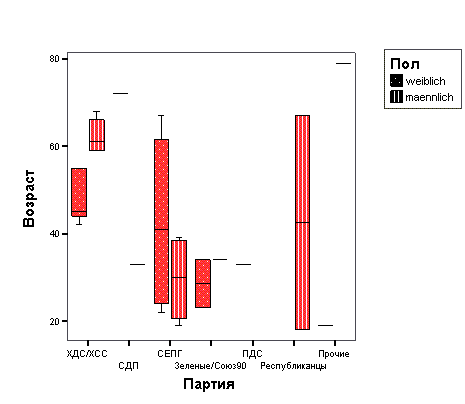
39.gif

40.gif

23.6 Столбчатые диаграммы величины ошибки
23.6 Столбчатые диаграммы величины ошибки
Если коробчатые диаграммы служат для графического представления показателей переменных, которые не подчиняются нормальному распределению (медиана, квартили), то диаграммы величины ошибки служат для отображения значений нормально распределённых переменных (среднее значение, стандартное отклонение, стандартная ошибка). Похожие столбцы, применяемые для отображения ошибок уже были рассмотрены в разделе 23.1 (см. рис. 23.10). Там они рассматривались при объяснении построения столбчатых диаграмм.
Для объяснения примера построения интерактивной диаграммы величины ошибки возьмём файл klin.sav, упоминавшийся в разделе 23.5. В этом файле среди множества переменных, описывающих состояние довольно большого коллектива пациентов, хранятся переменные gr (рост) и alterk (шесть возрастных групп). Мы хотим построить график среднего значения и стандартного отклонения роста в зависимости от этих возрастных групп.
-
Откройте файл klin.sav.
-
Выберите в меню Graphs (Графики) Interactive (Интерактивно) Error Bar... (Величина ошибки)
Откроется диалоговое окно Create Error Bar Chart (Создание столбчатой диаграммы величины ошибки).
-
Переменную alterk (шесть возрастных групп) поместите в поле оси х, а переменную gr (рост) в поле оси у.
По собственному усмотрению, дополнительно к выводу среднему значения, Вы можете организовать отображение доверительного интервала, стандартного отклонения или стандартной ошибки среднего значения, причём процентный показатель для доверительного интервала или множитель для стандартного отклонения и стандартной ошибки можно устанавливать плавно, в бесступенчатом режиме (см. рис. 23.41).
Рис.23.41: Диалоговое окно Create Error Bar Chart (Создание столбчатой диаграммы величины ошибки)
-
Активируйте отображение стандартного отклонения (множитель 1,0).
-
Откройте регистрационную карту Error Bars (Столбды по величинам ошибки) и в области Bar Labels (Метки столбцов) активируйте режимы обозначения столбцов Mean (Среднее значение) и Count (Количество).
И для столбчатой диаграммы величины ошибки можно применять трехмерный эффект.
-
Для этого активируйте ЗD-эффект с помощью кнопки на верху открытого диалогового окна и в регистрационной карте Error Bars (Столбцы по величинам ошибки) деактивируйте режимы обозначения столбцов Mean (Среднее значение) и Count (Количество)
Группирующие переменные можно задавать различным образом.
-
Деактивируйте 3D-Effect (3D эффект).
-
Переменную geschl (пол) поместите в поле Style (Стиль) группы переменных легенды.
Рис. 23.42: Диаграмма величины ошибки
Рис. 23.43: Диаграмма величины ошибки с ЗD-эффектом
Рис. 23.44: Группированная диаграмма величины ошибки
Чтобы столбцы не пересекались, они отображаются с некоторым смещением.
41.gif
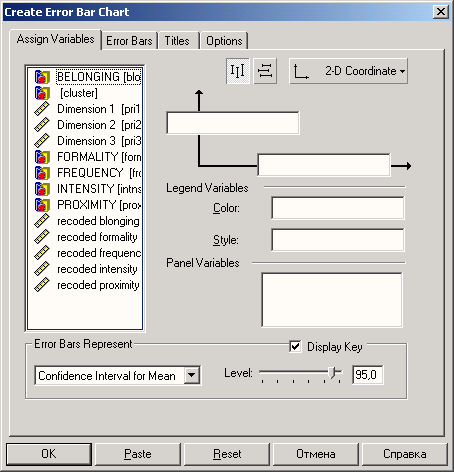
42.gif
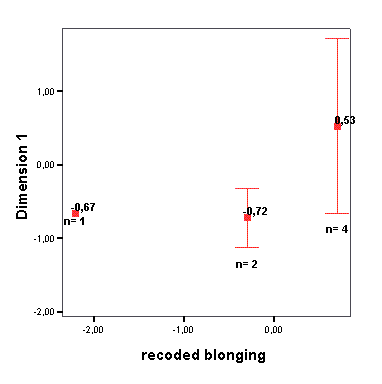
43.gif
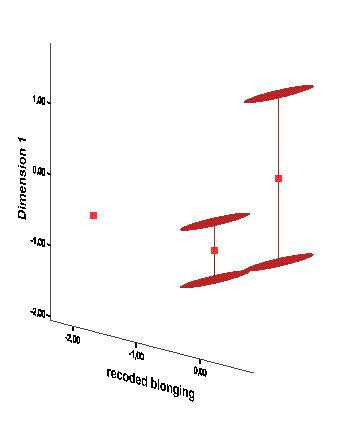
44.gif
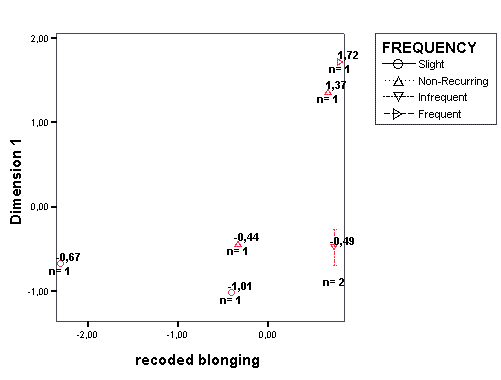
23.7 Гистограммы
23.7 Гистограммы
Гистограммы отображают распределение переменных, принадлежащих к интервальной шкале. При таком отображении значения переменной разделяются на интервалы, производится подсчёт частот попадания отдельных значений переменных в эти интервалы и после этого полученные показатели представляются в форме столбцов, расположенных в непосредственной близости друг к другу. В соответствии с установками по умолчанию, количество и ширина интервалов выбирается программой автоматически; при желании эти величины могут быть установлены пользователем.
Отобразим при помощи гистограммы распределение показателей роста (переменная gr) группы пациентов из файла klin.sav.
-
Откройте файл klin.sav.
-
Выберите в меню Graphs (Графики) Interactive (Интерактивно) Histogram... (Гистограмма) Откроется диалоговое окно Create Histogram (Создание гистограммы).
-
Поместите переменную gr (рост) в поле оси х. В поле оси у оставьте системную переменную Scount (количество), устанавливаемую по умолчанию.
-
Откройте регистрационную карту Histogram (Гистограмма). Активируйте опцию Normal curve (Кривая нормального распределения). Оставьте автоматическую генерацию количества интервалов и ширины интервала.
Группирующую переменную Вы можете ввести в диаграмму посредством активирования оси г.
-
При помощи соответствующего выключателя активируйте ЗD-систему координат и в поле оси z перенесите переменную geschl (пол).
Рис. 23.45: Диалоговое окно Create Histogram (Создание гистограммы)
В трёхмерной системе координат мы уже видим две гистограммы. Отображение кривой нормального распределения в этом случае невозможно.
Вы можете организовать вывод так называемой кумулятивной гистограммы; интервальные частотные показатели при этом будут суммироваться.
-
Деактивируйте поле оси z и активируйте опцию Cumulative histogram (Кумулятивная гистограмма) (см. рис. 23.48).
Рис. 23.46: Гистограмма с кривой нормального распределения
Рис.23.47: Группированная гистограмма
Рис. 23.48: Сводная гистограмма
Для того, чтобы решить, подчиняется ли рассматриваемая переменная нормальному распределению, недостаточно полагаться только на внешний вид гистограммы, а лучше провести более точный статистический тест. SPSS для этого предлагает тест Колмогорова-Смирнова (см. разд. 14.5); для нашего примера этот тест дает результат/> = 0,02, что говорит о значимом отклонении рассматриваемого распределения от нормального.
45.gif
46.gif
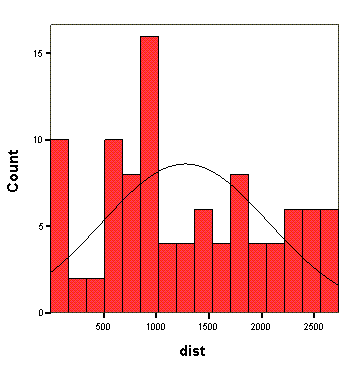
47.gif
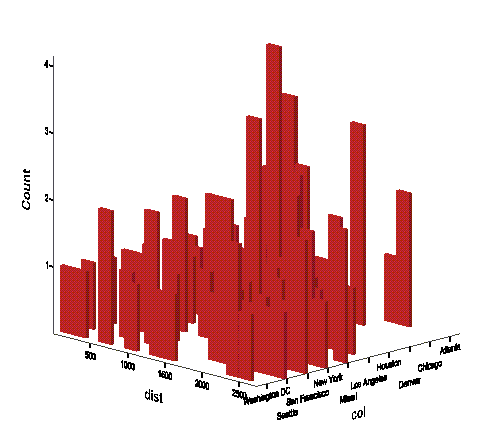
48.gif
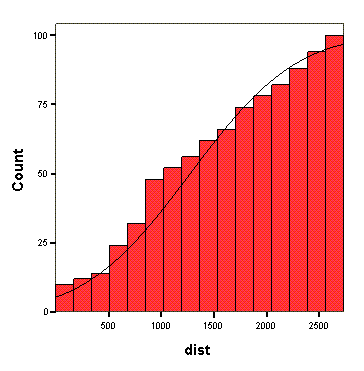
23.8 Диаграммы рассеяния
23.8 Диаграммы рассеяния
При помощи диаграмм рассеяния описываются отношения между двумя интервальными переменными, которые представляются в форме скопления точек. Возможны также и трёхмерные диаграммы рассеяния, но их, как правило, довольно тяжело интерпретировать.
В файле welt.sav сохранены несколько переменных, характеризующие 109 стран, к ним относятся: название страны, код региона, средняя ожидаемая продолжительность жизни мужчин и женщин, а также ежедневное потребление калорий.
Отобразим зависимость ожидаемой продолжительности жизни мужчин от ежедневного количества потребления калорий.
-
Откройте файл welt.sav.
-
Выберите в меню Graphs (Графики) Interactive (Интерактивно) Scatterplot... (Диаграмма рассеяния)
Откроется диалоговое окно Create Scatterplot (Создание диаграммы рассеяния).
-
Переменную kalorien (калории) поместите в поле оси х, а переменную lem (продолжительность жизни мужчин) в поле оси у.
-
Переменную land (страна) поместите в поле Label Cases By (Метки наблюдений) (см. рис. 23.50).
Отображение меток наблюдений на графике, правда, следует рекомендовать только при наличии относительно небольшого количества наблюдений, иначе многие метки будут накладываться друг на друга и, следовательно, станут нечитаемы. В качестве альтернативы отображения всех меток Вы можете выбрать тактику отображения меток выборочных наблюдений.
Рис. 23.49: Диалоговое окно Create Scatterploi (Создание диаграммы рассеяния)
Рис. 23.50: Диаграмма рассеяния
-
Чтобы сначала запретить отображение меток, дважды щёлкните на диаграмме и выберите в меню Formal (Формат) Graph Elements (Графические элементы) Cloud (Облако)
В диалоговом окне Cloud (Облако) перейдите на регистрационную карту Labels (Метки) и деактивируйте опцию Symbol Labels (Метки точек).
Чтобы теперь обозначить отдельные точки, щёлкайте на них правой кнопкой мыши и в появляющемся контекстном меню выбирайте опцию Symbol Label (Метка точки) (см. рис. 23.51). Пользуясь клавишей Shift, Вы можете также сразу выбрать интересующие Вас точки и за один шаг обозначить их меткой.
Страны, представленные в этом файле, разделены на шесть регионов. Теперь при помощи диаграммы рассеяния мы хотим отобразить зависимость продолжительности жизни от потребляемого количества калорий для всех стран, обозначив при этом страны, относящиеся к разным регионам при помощи отличительных маркеров.
-
Поместите дополнительно переменную region (регион) в поле Style (Стиль) области Legend Variables (Переменные легенды), но в этот раз не задавайте никакой переменной для обозначения наблюдений.
Вы можете легко распознать страны бедного региона Африка (внизу слева) и богатого региона OECD (вверху справа).
Теперь нанесём на диаграмму регрессионную прямую и соответвующий доверительный интервал.
-
Для этого откройте регистрационную карту Fit (Приближение).
-
В поле Method (Метод) активируйте опцию Regression (Регрессия) и в группе Prediction Lines (Линии прогноза) опцию Mean (Среднее значение). Оставьте 95%-й доверительный интервал, устанавливаемый по умолчанию.
Рис. 23.51: Опция Symbol Label (Метка точки)
Рис. 23.52: Диаграмма рассеяния с различными маркерами для обозначения точек
На диаграмме теперь присутствуют регрессионная прямая и линии, обозначающие границы доверительного интервала. Слегка мешает описание приведенной на диаграмме линейной регрессии и соответствующей меры определенности.
-
Щёлкните дважды на диаграмме и затем правой кнопкой мыши на этой вспомогательной информации. В контекстном меню выберите Hide Key (Спрятать подсказку).
Рис. 23.53: Диаграмма рассеяния с регрессионной прямой и доверительным интервалом
И в заключение, мы приведём пример построения диаграммы рассеяния в трёхмерном пространстве. В файле wasser.sav в виде переменных х, у и grw приведены данные измерения линии фунтовых вод города Штадталлендорф, находящегося на земле Гессен. Переменные х и у соответствуют координатам области размером 4x4 километра, в пределах которой проводились измерения уровня грунтовых вод (в метрах).
-
Откройте файл wasser.sav.
-
Посредством установки соответствующего выключателя в положение 3-D Coordinate (3-D координата) активируйте отображение поля оси г.
-
Переменную х поместите в поле оси х, перемененную grw — в поле оси z, а у переменную — в поле оси у.
-
Откройте регистрационную карту Fit (Приближение) и в поле Method (Метод) активируйте опцию Smoother (Сглаживание).
-
В регистрационной карте Titles... (Заголовки) укажите название диаграммы.
В окне просмотра будет показана диаграмма изображённая на рисунке 23.54.
Для трёхмерного режима существует возможность плавного вращения диаграммы. Благодаря такому вращению сглаженную поверхность можно оценить из разных точек просмотра.
-
Дважды щёлкните на диаграмме. Рядом с редактором диаграмм появится панель с двумя вращающимися колёсами, при помощи которых диаграмму можно вращать в двух направлениях.
Пример возможного вида диаграммы, полученной с помощью такого изменения точки просмотра, представлен на рисунке 23.55.
Рис. 23.54: Трёхмерная диаграмма рассеяния со сглаживанием
Рис. 23.55: Повёрнутая трёхмерная диаграмма рассеяния
С этой позиции диаграмма просматривается лучше, чем в предыдущем варианте.
49.gif
50.gif
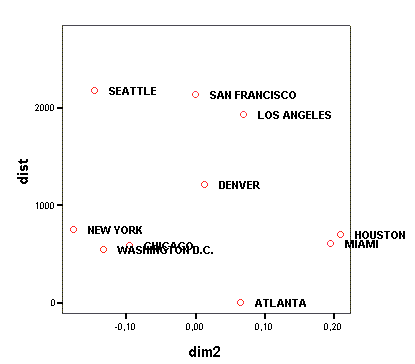
51.gif
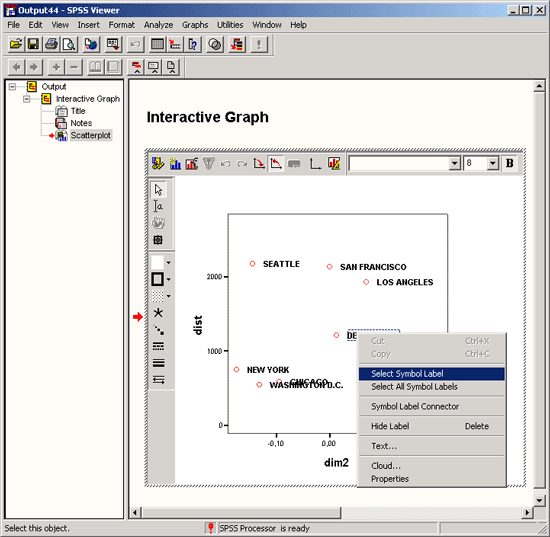
52.gif
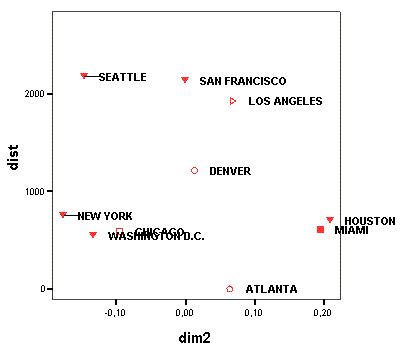
53.gif
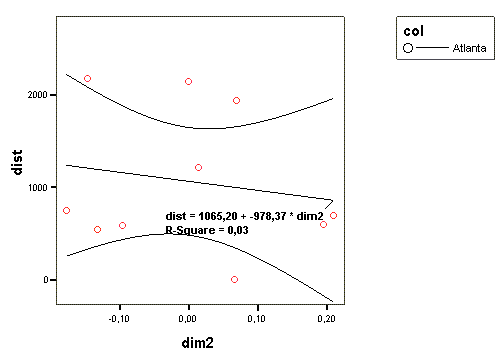
54.gif

55.gif

23.9 Интерактивные режимы работы с графиками
23.9 Интерактивные режимы работы с графиками
К построению интерактивных графиков можно подойти и с принципиально другой стороны. Мы покажем Вам этот отличительно другой принцип действий на примере и предоставим Вам возможность самостоятельно решать, нравится он вам или нет.
Построим простую столбчатую диаграмму для переменной pczeit (время суток) из файла pcalltag.sav (см. рис. 23.6).
-
Откройте файл pcalltag.sav.
-
Перейдите в окно просмотра и выберите в меню Insert (Вставить) Interactive 2-D Graph (Интерактивный 2-D график)
Точно также Вы можете выбрать и вставку 3-D графика. Будет активировано пустое поле для графика, окружённое слева и сверху панелями инструментов. Значение кнопок, имеющихся в этом окне, Вы сможете узнать, если пройдётесь по ним курсором.
-
Выберите в меню Insert (Вставить) Summary (Результат) Ваr (Столбцы) и затем Edit (Правка) Assign Variables (Присвоить переменные)
Откроется диалоговое окно Assign Graph Variables (Присвоение переменных для графика).
Рис. 23.56: Диалоговое окно Assign Graph Variables (Присвоение переменных для графика)
Переместите переменную pczeit (время суток) в поле оси х, а системную переменную Spct (процент) в поле оси у. В окне просмотра появится столбчатая диаграмма с соответствующими переменными. Таким же образом Вы можете построить, а затем откорректировать все диаграммы, рассмотренные в разделах с 23.1 по 23.8.
56.gif

Глава 24. Модуль Tables
Глава 24. Модуль Tables
1. Модуль Tables
Модуль Tables
Модуль Tables служит для создания таблиц, готовых к презентации. По сравнению с режимом построения частотных таблиц и таблиц сопряженности, а также таблиц средних значений, в этом модуле пользователю предоставляются более широкие возможности. После вызова меню Analyze (Анализ) Custom Tables (Настраиваемые таблицы) На выбор Вам будут предложены четыре вспомогательных меню:
-
основные таблицы,
-
общие таблицы,
-
таблицы множественных ответов,
-
частотные таблицы.
При помощи вспомогательного меню Basic Tables (Основные таблицы) можно создавать таблицы с простой компоновкой. Вспомогательное меню General Tables (Таблицы общего назначения) служит для организации вывода сложных таблиц; вспомогательное меню таблиц множественных ответов предназначено для обработки множественных ответов. Вспомогательное меню Tables of Frequencies (Таблицы частот) следует выбирать тогда, когда существуют одинаковые варианты ответов для большого количества вопросов, находящихся в анкете. В следующих разделах мы вкратце рассмотрим возможности, предлагаемые в этих четырёх вспомогательных меню для организации вывода информации в удобном для презентации виде.
24.1 Обрабатываемая анкета
24.1 Обрабатываемая анкета
Особенности модуля Tables изучим на примере исследования мнения членов профсоюзов в отношении организации мероприятий, проводимых 1-го Мая. Исследование проводилось в округе Марбург-Биденкопф. Из общей совокупности членов (примерно 27.000) всех профсоюзов, действующих в округе Марбург-Биденкопф, для исследования была произведена случайная выборка из членских карточек отдельных профсоюзных организаций (был взят каждый 56-й адрес членов различных профсоюзов). Таким образом, в общей сложности было отобрано 474 человека. Вернулась 271 заполненная анкета, что соответствует 57.2 % от общего количества.
Рассмотрим выбранную нами часть довольно обширной анкеты:
Институт политологии
Университет Марбург
Проект 1-е Мая
Анкета
v1 Как Вы проводите выходные дни? | |
Просмотр телепередач | [] |
Общение с друзьями | [] |
Приглашаю к себе гостей | [] |
Хобби | [] |
Общество по увлечениям | [] |
Семейные заботы | [] |
Слушаю радио/читаю | [] |
Кино/концерты/театр | [] |
То же, что и всегда/то одно то другое | [] |
Выбираюсь на природу/путешествую | [] |
Необходимые дела (дом, квартира, сад) | [] |
Помощь соседям | [] |
Спорт | [] |
Другое <то, чего нет в списке> | |
v2 Пол | |
Мужской | [] |
Женский | [] |
v3 Являетесь ли Вы активным членом какого-либо общества? | |
Спортивное общество (если да: 1) | [] |
Общество любителей животных | |
(голуби/дрессировка собак/верховая езда) (если да: 1) | [] |
Свободное время (культурная направленность) (и т.д.) Другое <указать> | [] |
v4 Если бы Вы могли выбирать, какое из следуюших предложений по проведению 1*го Мая понравилось бы Вам больше всего? <максимально две позиции> | |
Политические выступления | [] |
Шествия | [] |
Финал розыгрыша кубка | [] |
Музыкальные мероприятия/ярмарки | [] |
Просмотр игр высшей лиги по телевизору | [] |
Демонстрации | [] |
Исполнение рабочих обязанностей | [] |
Путешествие/пикник | [] |
Семейный праздник | [] |
Другое: | |
v5 Сохраняется ли еще актуальность 1-го Мая, как АНЯ трудяшихся? | |
Да (1) | [] |
нет (2) | [] |
не знаю (9) | [] |
v6 Можете ли вы припомнить, как в последние голы здесь, на месте, профсоюзами было организовано празднование 7-го Мая? |
|
Да (1) | [] |
нет (2) | [] |
не знаю (9) | [] |
v7 Если ля, какое мероприятие Вы можете припомнить? | |
Собрание | [] |
Шествие | [] |
Демонстрация | [] |
Выступления | [] |
Митинг | [] |
Праздник пива | [] |
Праздничные гуляния | [] |
Музыкальные концерты | [] |
Информационные стенды | [] |
Детский праздник | [] |
Другое: <указать> | |
v8 Принимали ли Вы когда-нибудь участие в первомайских мероприятиях? | |
Да (1) | [][] |
нет (2) | [] |
данные отсутствуют/не знаю (9) | [] |
v9 Если да, то в каком голу? | |
<Год> | |
19.. | [] |
v10 Как часто в течение последних 70 лег? <пожалуйста, укажите количество> | |
<всегда = 9> | [] |
v11 Что Вам понравилось? <максимально две позиции> | |
Речи (1) | [] |
Встретил много коллег (2) | [] |
Интересная программа (3) | [] |
Не помню (4) | [] |
Другое: <указать> (5) | [] |
v12 Если Вы не принимали участие в первомайских мероприятиях, то почему? | |
<максимально две позиции> | |
Скучные политические выступления (1) | [] |
Слишком много агитации (2) | [] |
Слишком мало общения (3) | [] |
Слишком много речей (4) | [] |
Слишком много общения (5) | [] |
Чувствуется принудительность праздника (6) | [] |
Слишком много традиционных профсоюзных мероприятий (7) | [] |
Не могу вспомнить (8) | [] |
Не знаю/данные отсутствуют (9) | [] |
v13 Считаете ли Вы, что политически важно, чтобы мероприятия 1-го Мая, как дня трудящихся, организовывали именно профсоюзы и этот подход следует сохранить? |
|
Да (1) | [] |
нет (2) | [] |
не знаю (9) | [] |
v14 Согласны ли Вы с утверждением, что 1-е Мая главным образом является праздником / высокопоставленных чиновников? | [] |
Да (1) | [] |
нет (2) | [] |
не знаю (9) | [] |
v15 Чем, по Вашему мнению, преимущественно занимаются профсоюзы в наши дни? | |
<максимально две позиции> | |
Ведут переговоры о тарифах (1) | [] |
35-часовая рабочая неделя/сокращение рабочего времени (2) | [] |
Защищают права наёмных рабочих (3) | [] |
Скандалами (4) | [] |
Образовательной работой (5) | [] |
Производственной работой/представляют интересы производства (6) | [] |
Не знаю/данные отсутствуют (7) | [] |
Другое: | |
v16 Чем, по Вашему мнению, в первую очередь должны заниматься профсоюзы в наши дни> <максимально две позиции> | [] |
Вести переговоры о тарифах (1) | [] |
Переходом на 35-часовую рабочую неделю/сокращением рабочего времени (2) | [] |
Защищать права наёмных рабочих (3) | [] |
Скандалами (4) | [] |
Образовательной работой (5) | [] |
Производственной работой (6) | [] |
Обеспечением сохранности рабочих мест (7) | [] |
Сокращением безработицы (8) | [] |
Образованием и защитой рабочих мест в восточной Германии (9) | [] |
Противостоять нарушениям социальной политики (10) | [] |
Заниматься организацией экологически безвредного производства (11) | [] |
Не знаю/данные отсутствуют (99) | [] |
v17 Членом какой профсоюзной организации Вы являетесь? | |
Профсоюз строителей (BSE) (1) | [] |
Профсоюзная организация Deutsche Post (Немецкая почта) (2) | [] |
Профсоюз полицейской службы (GdP) (3) | [] |
Профсоюз сферы образования (GEW) (4) | [] |
Профсоюз железнодорожников Германии (GdED) (5) | [] |
Торговля Банки Страхование (HBV) (6) | [] |
Профсоюз горнодобывающей промышленности (IG Bergbau) (7) | [] |
Профсоюз химической промышленности (IG Chemie Papier Keramik) (8) | [] |
Профсоюз деревообрабатывающей промышленности (IG Holz) (9) | [] |
Профсоюз кожевенной промышленности (IG Leder) (10) | [] |
Профсоюз средств массовой информации (IG Medien) (11) | [] |
Профсоюз металлургической промышленности (IG Metall) (12) | [] |
Профсоюз пищевой промышленности (NGG) (13) | [] |
Профсоюз сферы услуг (OTV) (14) | [] |
Профсоюз лёгкой промышленности (ТВ) (15) | [] |
Другой: | |
v18 С какого гола Вы являетесь членом профсоюза? | |
<19..> | [] |
v19 Ваш гол рождения | |
<19..> | [] |
v20 Какую должность Вы занимаете в данный момент? | |
Студент(ка)/Ученик(ца) (1) | [] |
Рабочий(ая) (2) | [] |
Помощник/ученик на производстве (3) | [] |
Мастер (4) | [] |
Служащий(ая) (5) | [] |
Ведущий специалист (6) | [] |
Высокая государственная должность (7) | [] |
Пенсионер(ка) (8) | [] |
Другое (9) | [] |
Безработный(ая) (10) | [] |
v21 Примерно, в каких пределах находится Ваш ежемесячный доход? | |
до 1.000 DM (1) | [] |
до 2.000 DM (2) | [] |
до 3.000 DM (3) | [] |
до 4.000 DM (4) | [] |
до 5.000 DM (5) | [] |
до 6.000 DM (6) | [] |
до 7.000 DM (7) | [] |
свыше 7.000 DM (8) | [] |
нет данных (9) | [] |
v22 Какая из партий в настояшее время наилучшим образом отражает Вашу позицию? | |
CDU/CSU (1) | [] |
SPD (2) | [] |
FDP (3) | [] |
Buendnis 90/Die Gruenen (Союз 90/Зепёные) (4) | [] |
Republikaner (Республиканцы) (5) | [] |
PDS/Linke Liste (Левые) (6) | [] |
Другая (7) | [] |
Ни одна из партий (8) | [] |
v23 Известно ли Вам когда и при каких обстоятельствах 1-е Мая стал законным выходным днем |
|
Примерно в 1900 (1) | [] |
Введён благодаря социалистическому интернационалу (2) | [] |
После 1-ой Мировой войны (3) | [] |
Примерно в 1919 (4) | [] |
Введён благодаря рабочим (5) | [] |
Учреждён нацистами/Гитлером (6) | [] |
В результате распоряжения нацистов/Гитлера (7) | [] |
Самый трагичный день для профсоюзов (8) | [] |
До 1900 (9) | [] |
Около 1933 (10) | [] |
После 2-ой Мировой войны (11) | [] |
Данные отсутствуют (99) | [] |
Для тех, кто не желает давать ответ на тот или иной вопрос, в некоторых вопросах анкеты, как правило, присутствует один из специальных вариантов ответов данные отсутствуют, не знаю или не знаю/данные отсутствуют. Этим ответам соответствует кодировка 9 или последовательность цифр 99. Несмотря на это, было очень много анкет, на которых и этот вариант ответа не был отмечен, поэтому остаётся неясно, отказался ли респондент отвечать или просто забыл. Во всех таких неясных случаях при вводе данных в файл для соответствующего вопроса проставлялась цифра 0. Следовательно, кодировка 0 означает отсутствующее значение; ему присваивалась метка "Данные отсутствуют". Количество отсутствующих данных уже учтено в таблицах, рассматриваемых в этой главе; в качестве альтернативы кодировку 0 Вы можете трактовать как отсутствующее значение.
Результаты опроса находятся в файле mai.sav.
-
Откройте сначала в редакторе данных файл mai.sav.
24.2 Основные таблицы
24.2 Основные таблицы
Один из вопросов анкеты относительно праздника 1-го Мая звучал следующим образом: Сохраняется ли ещё актуальность 1-го Мая, как дня трудящихся? (v5). Сравним для начала вид стандартных частотных таблиц, которые рассматривались ранее, с видом таблиц, которые строятся при помощи модуля Tables.
-
Выберите в меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты)
-
Переместите переменную v5 в поле целевых переменных и подтвердите свой выбор нажатием ОК.
Вы получите следующую таблицу:
Ist der 1.Mai als TdA noch zeitgemaess?
(Сохраняется ли ещё актуальность 1-го Мая, как дня трудящихся)
Frequericy (Частота) | Percent (Процент) | Valid Percent (Действи-тельный процент) | Cumu-lative Percent (Сово-купный процент) | ||
Valid (Действи-тельные значения) | fehlende Angabe (Данные отсут-ствуют) | 39 | 14,4 | 14,4 | 14,4 |
Ja (Да) | 152 | 56,8 | 56,8 | 71,2 | |
Nein (Нет) | 59 | 21,8 | 21,8 | 93,0 | |
Weiss nicht (He знаю) | 19 | 7,0 | 7,0 | 100,0 | |
Total (Сумма) | 271 | 100,0 | 100,0 |
Теперь выведите распределение частот переменной v5 при помощи модуля Tables.
-
Выберите в меню следующие опции Analyze (Анализ) Custom Tables (Настраиваемые таблицы) Basic Tables... (Основные таблицы) Откроется диалоговое окно изображённое на рисунке 24.1.
-
Перенесите переменную v5 из списка исходных переменных в список строчных переменных (Subgroups/Down) и подтвердите установки нажатием ОК.
Вы получите следующие результаты:
1st der 1 .Mai als TdA noch zeitgemaess? (Сохраняет ли ещё актуальность 1-е Мая, как день трудящихся?) | fehlende Anqabe (Данные отсутствуют) | 39 |
Ja (Да) | 154 | |
Nein (Нет) | 59 | |
Weiss nicht (He знаю) | 19 |
Модуль Tables отображает распределение частот в табличной форме. В соответствии с установками программы выводятся только абсолютные значения. О том, как можно дополнительно организовать отображение процентных показателей, мы ещё расскажем. Таблица начинается заголовком 1st der I.Mai als TdA (Tag der Arbeit) noch zeitgemaess? (Сохраняется ли ещё актуальность 1-го Мая, как дня трудящихся?). Этот заголовок является меткой переменной v5. Если метки переменной не существует, то в этом месте указывается её имя. Значения переменной v5 отображаются в виде соответствующих названий: fehlende Angabe (Данные отсутству ют), Ja (Да), Nein (Нет) и Weiss nicht (He знаю). Результаты опроса показывают, что ещё довольно большое количество членов профсоюзов (154) находят День трудящихся актуальным, хотя, как известно, активность участия в мероприятиях 1-го Мая с каждым годом снижается.
Рис. 24.1: Диалоговое окно Basic Tables (Основные таблицы)
1.gif

24.2.1 Применение нескольких строчных переменных
24.2.1 Применение нескольких строчных переменных
В Первомайском исследовании ставился так же вопрос о том, членом какого профсоюза является опрашиваемый (v17). Выведем дополнительно в окно просмотра результаты для переменной v!7.
Выберите в меню следующие опции Analyze (Анализ) Custom Tables (Пользовательские таблицы) Basic Tables... (Основные таблицы)
В диалоговом окне Basic Tables (Основные таблицы) поместите переменные v5 и v17 в список строчных переменных (Subgroups/Down).
Активируйте щелчком опцию Each separately (stacked) (Каждая отдельно (с наложением)).
Подтвердите свой выбор нажатием ОК. Вы получите следующие данные:
| ||
I1st der 1 .Mai als TdA noch zeitgemaess? (Сохраняет ли ещё актуальность 1-е Мая, как день трудящихся? | fehlende Anqabe (Данные отсутствуют) | 39 |
Ja (Да) | 154 | |
Nein (Нет) | 59 | |
Weiss nicht (He знаю) | 19 | |
Gewerkschaftsmitglied in (Член профсоюза): | fehlende Angabe (Данные отсутствуют) | 6 |
Профсоюз строителей (BSE) | 32 | |
Профсоюз Deutsche Post (Немецкая почта) | 13 | |
Профсоюз полицейской службы (GdP) | 6 | |
Профсоюз сферы образования (GEW) | 20 | |
Профсоюз железнодорожников Германии (GdED) | 11 | |
Торговля Банки Страхование (HBV) | 19 | |
Профсоюз химической промышленности (IG Chemie Papier Keramik) | 22 | |
Профсоюз деревообрабатывающей промышленности (IG Holz) | 1 | |
Профсоюз работников средств массовой информации (IG Medien) | 11 | |
Профсоюз металлургической промышленности (IG Metall) | 73 | |
Профсоюз пищевой промышленности (NGG) | 1 | |
Профсоюз сферы услуг (? TV) | 52 | |
Профсоюз лёгкой промышленности | 1 | |
Профсоюз Сад Земля Лес (GGLF) | 3 | |
По виду таблицы Вы можете заметить, что обе переменные внутри неё представлены отдельно друг от друга. В таких случаях говорят также и о штабельном представлении. По очереди выводятся стеки v5 и v!7. Если данные двух переменных выводятся в штабельной форме (с наложением), то две отдельные таблицы будут как бы склеены. При этом первая таблица (соответствующая v5) содержит уже знакомые нам данные.
24.2.2 Добавление второго измерения (столбцовые переменные)
24.2.2 Добавление второго измерения (столбцовые переменные)
До этого мы создавали только одномерные таблицы. Одномерная таблица отражает только основную информацию, и не даёт никакой информации, к примеру о том. ответили ли члены Профсоюза сферы образования (GEW) на вопрос, сохраняет ли ещё 1-е Мая актуальность, иначе, нежели члены Профсоюза металлургов (IG Metall). Для получения такой информации мы должны добавить к таблице ещё одно измерение. Для этого поступите следующим образом:
-
В диалоговом окне Basic Tables (Основные таблицы) поместите переменную v17 в список строчных переменных (Subgroups/Down), а переменную v5 — в список столбцовых переменных (Across).
Таблица, в состав которой входит как строчная, так и столбцовая переменные, называется также перекрёстной таблицей. Перекрёстная таблица является двумерной. Рассмотрим вкратце физические измерения одной таблицы: первое физическое измерение определяется строками. Число строк соответствует длине таблицы. Второе физическое измерение определяется столбцами. Число столбцов соответствует ширине таблицы. Существует также и ещё одна размерность таблицы: слои. Слои таблицы определяют её глубину. Трёхмерную таблицу можно получить путём использования слойных переменных, называемых также табличными переменными. В диалоговом окне Basic Tables (Основные таблицы) они должны быть помещены в подгруппу Separate Tables (Отдельные таблицы). К рассмотрению этой возможности мы ещё вернёмся в следующем разделе.
-
Для получения перекрёстной таблицы между переменными v17 и v5, подтвердите установки нажатием ОК. В окне просмотра появятся следующая информация:
Ist der 1 .Mai als TdA noch zeitgemaess? (Сохраняет ли ещё актуальность 1-е Мая, как день трудящихся?) | |||||
fehlende Angabe (Данные отсут-ствуют) | Ja (Да) | Nein (Нет) | Weiss nicht (He знаю) | ||
Gewerkscha-ftsmitglied in (Член профсоюза): | fehlende Angabe (Данные отсутствуют) | 5 | 1 | ||
Профсоюз строителей (BSE) | 2 | 25 | 3 | 2 | |
Профсоюз Deutsche Post (Немецкая почта) | 1 | 8 | 2 | 2 | |
Профсоюз полицейской службы (GdP) | 2 | 4 | |||
Профсоюз сферы образования (GEW) | 11 | 5 | 4 | ||
Профсоюз железно-дорожников Германии (GdED) | 1 | 7 | 3 | ||
Торговля Банки Страхование (HBV) | 1 | 13 | 5 | ||
Профсоюз химической промышленности (IG Chemie Papier Keramik) | 14 | 6 | 2 | ||
Профсоюз дерево-обрабатывающей промышленности (IG Holz) | 1 | ||||
Профсоюз работников средств массовой информации (IG Medien) | 2 | 5 | 4 | ||
Профсоюз метелургической промыш-ленности (IG Metall) | 4 | 44 | 17 | 8 | |
Профсоюз пищевой промышленности (NGG) | 1 | ||||
Профсоюз сферы услуг (? TV) | 10 | 28 | 9 | 5 | |
Профсоюз лёгкой промышле-нности | 1 | ||||
Профсоюз Сад Земля Лес (GGLF) | 3 | ||||
Заголовком столбцов служит метка переменной v5 (Ist der 1.Mai als TdA noch zeitgemaess? (Сохраняет ли ещё актуальность 1-е Мая, как день трудящихся?)). Возможные значения переменных образовывают соответствующие колонки (fehlende Angabe (Данные отсутствуют), Ja (Да), Nein (Нет) и Weiss nicht (He знаю)). Заголовком строк служит метка переменной v17 (Gewerkschaftsmitglied in (Член профсоюза)). Метки значений этой переменной образовывают соответствующие строки (Профсоюз строителей (BSE), Профсоюз Deutsche Post (Немецкая почта), Профсоюз полицейской службы (GdP) и т.д.). Из перекрёстной таблицы видно, что члены профсоюзов более интеллектуальных отраслей (GEW (Профсоюз сферы образования), IG-Medien (Профсоюз работников масс-медиа)) на вопрос, является ли ещё актуальным 1-е Мая, дают отрицательный ответ чаще, нежели члены профсоюзов классической индустрии, таких как Профсоюз металлургической промышленности (IG Metall) или Профсоюз сферы услуг (OTV). Бросается также в глаза тот факт, что ни один из членов молодого профсоюза работников полиции не считает 1-е Мая актуальным праздником. Конечно же, профсоюз полицейской службы играет во многих отношениях, особая роль.
Рассмотрим ещё один пример двумерной таблицы. В исследовании отношения к празднованию 1-го Мая были также заданы вопросы относительно занимаемой должности (v20) и ежемесячного дохода (v20). Мы хотим при помощи двумерной (перекрёстной) таблицы получить информацию о том, существует ли взаимосвязь между занимаемой должностью и доходом. Для этого поступите следующим образом:
-
В диалоговом окне Basic Tables (Основные таблицы) поместите переменную v20 в поле строчных переменных, а переменную v21 — в поле столбцовых переменных.
-
Подтвердите установки нажатием ОК.
Результаты опроса будут представлены в следующем виде:
| Nettoeinkommen (monatlich) (Чистыйдоход (в месяц)) | ||||||||
bis 1.000 DM (до 1.000 DM) | bis 2.000 DM (до 2.000 DM) | bis 3.000 DM (до 3.000 DM) | bis 4.000 DM (до 4.000 DM) | bis 5.000 DMfao 5.000 DM) | bis 6.000 DM (до 6.000 DM) | mehr als 7.000 DM (свыше 7.000 DM) | keine-Angaben (Данные отсут-ствуют) | ||
Berufs-position (Зани-маемая долж-ность) | Auszubil-dende(r)/ Lerting (Студент (ка)/ Ученик (ца)) | 5 | 3 |
|
|
|
|
|
|
Arbei-terln (Рабо-чий(ая)) | 3 | 18 | 23 |
|
|
|
| 3 | |
Fachar-beiterln/ Geselle (Помощ-ник/ ученик на произ-водстве) |
| 7 | 34 | 4 | 1 |
|
| 1 | |
Meister (Мастер) |
|
| 3 | 1 |
|
|
|
| |
Anges-tellte(r) (Служа- щий(ая)) | 1 | 19 | 27 | 10 | 3 | 1 |
| 5 | |
Leitende(r) Anges-tellte(r) (Ведущий специ-алист) |
| 2 | 1 | 3 |
|
| 1 | 1 | |
Beamte(r) (Государс-венная руково-дящая должность) | 1 | 3 | 6 | 11 | 5 | 3 | 1 | 1 | |
Rentn-erln/ Pensio- naerln (Пенсио-нер(ка)) | 5 | 20 | 6 | 3 | 1 |
|
| 7 | |
Hausfrau/ Hausmann (Домо-хозяйка(ин)) | 4 | 1 |
| 1 | 1 |
|
| 2 | |
Eiwerb-sunfeehg (Нетрудо-способен (а)) |
| 1 |
|
|
|
|
|
| |
Arteitslos (Безра-ботный(ая)) | 1 | 4 | 1 |
|
|
|
| 2 | |
Заголовком столбцов служит метка переменной v21 (Nettoeinkommen (monatlich) (Чистый доход (в месяц)). Значения переменной v21 образовывают соответствующие столбцы (bis1000 DM (до 1.000 DM), bis 2.000 DM (до 2.000 DM), ...). Заголовком строк является метка переменной v20 (Berufsposition (Занимаемая должность)). Метки значений этой переменной образовывают соответствующие строки (Auszubildende(r)/ Lerling (Студент(ка)/Ученик(ца)), Arbeiter(ln (Рабочий(ая)), ...). В перекрёстной таблице связь между занимаемой должностью и ежемесячным доходом заметна с первого взгляда. Так, например, ни один из учеников не зарабатывает больше 2.000 DM в месяц, рабочий не зарабатывает более 3.000 DM в месяц, а среди высокопоставленных государственных чиновников девять человек имеют месячный доход более 4.000 DM. Исходя из перекрёстной таблицы можно сделать вывод, что ежемесячный доход тем выше, чем выше занимаемая должность опрашиваемого. Конечно же, такая взаимосвязь, не является неожиданностью.
24.2.3 Добавление третьего измерения (табличные переменные)
24.2.3 Добавление третьего измерения (табличные переменные)
В исследовании отношения к празднованию 1-го Мая был также задан вопрос, как часто за последние десять лет опрашиваемый присутствовал на мероприятиях, посвящённых 1-му Мая, (v10). Эту переменную мы хотим скрестить с переменной v5, содержащей ответы на вопрос Ist der 1.Mai als TdA noch zeitgemaess? (Сохраняет ли ещё актуальность 1-е Мая, как день трудящихся?). В качестве третьего измерения добавим переменную v2 (Geschlecht (Пол)).
-
В диалоговом окне Basic Tables (Основные таблицы) перенесите переменную v10 в поле строчных переменных, переменную v5 в поле столбцовых переменных, а переменную v2 в поле табличных переменных (Separate Tables).
Диалоговое окно Basic Tables (Основные таблицы) должно теперь выглядеть так, как изображено на рисунке 24.2.
Рис. 24.2: Добавление третьего измерения
-
Подтвердите установки нажатием ОК. В окне просмотра сначала будет показана только таблица для первого слоя (Geschlecht weiblich (Женщины)). После двойного щелчка на этой таблице при помощи техники сводных таблиц Вы получите возможность сделать видимыми таблицы и для других слоев. Для этого откройте соответствующее ниспадающее меню. Вы получите две следующие таблицы.
Geschlecht weiblich (Женщины) | |||||
Ist der 1.Mai als TdA noch zeitgemaess? (Сохраняет ли ещё актуальность 1-е Мая, как день трудящихся?) | |||||
fehlende Angabe (Данные отсутствуют) | Ja (Да) | Nein (Нет) | Weiss nicht (He знаю) | ||
Wie oft in letzten 10 Jahren? (Как часто за последние десять лет?) (v8) | 0 | 1 | 19 | 13 | 6 |
1 | 5 | 1 | |||
2 | 1 | ||||
3 | 1 | 2 | |||
4 | 3 | ||||
5 | 1 | ||||
6 | 1 | ||||
7 | 2 | 1 | |||
8 | 1 | ||||
всегда | 5 | ||||
Geschlecht maenlich (Мужчины) | |||||
Ist der 1 .Mai als TdA noch zeitgemaess? (Сохраняет ли ещё актуальность 1-е Мая, как день трудящихся?) | |||||
fehlende Angabe (Данные отсутствуют) | Ja (Да) | Nein (Нет) | Weiss nicht (He знаю) | ||
Wie oft in letzten 10 Jahren? (Как часто за последние десять лет?) (v8) | 0 | 83 | . 32 | 12 | |
1 | 4 | 3 | 1 | ||
2 | 6 | ||||
3 | 6 | 1 | |||
4 | 3 | ||||
5 | 1 | ||||
6 | 4 | 3 | |||
7 | 1 | ||||
8 | 3 | ||||
всегда | 5 | 2 | |||
Обе таблицы выглядят как самостоятельные таблицы; метка Geschlecht (Пол) и признаки слойной переменной v2 (женщины, мужчины) расположены с левой стороны. Трёхмерная таблица показывает, что как среди мужчин, так и среди женщин, частота высказывания мнения, что 1-е Мая уже является не актуальным, растёт со снижением посещаемости первомайских мероприятий. Люди, не желающие идти на первомайские мероприятия, как правило, полагают, что 1-е Мая не является более актуальным. Значительных отличий между полами не наблюдается.
2.gif

24.2.4 Вложенные данные
24.2.4 Вложенные данные
Если в табличных измерениях (строки, столбцы, слои) применяется более одной переменной, то переменные могут выводиться с наложением или с вложением. Сравним сначала оба метода при помощи одномерной таблицы. Нам необходимо получить частотные распределения переменных v2 (Пол) и v8 (Принимали ли Вы когда-нибудь участие в первомайских мероприятиях?). Рассмотрим сначала уже знакомую нам штабельную форму вывода информации.
-
Для этого в диалоговом окне Basic Tables (Основные таблицы) переменные v2 и v8 поместите в список строчных переменных. Активируйте установку Each separately (stacked) (Каждая отдельно (с наложением)). Вы получите следующий вывод.
| ||
Geschlecht (Пол) | weiblich (женский) | 77 |
maennlich (мужской) | 194 | |
Teilnahme an gewerkschaftlichen Mai-Veranstaltung (Участие в Первомайских мероприятиях, организованных профсоюзами) | fehlende Angabe (Данные отсутствуют) | 3 |
Ja (Да) | 110 | |
Nein (Нет) | 156 | |
keine Angabe/weiss nicht (Данные отсутствуют/не знаю) | 2 | |
В качестве результата мы получили две таблицы, следующие по очереди: таблицу для переменной v2 и таблицу для переменной v8.
-
Повторите вывод информации с активированием переключателя All combinations (nested) (Все комбинации (с вложением)).
-
Подтвердите установки нажатием ОК. Результаты Вы получите в следующем виде:
Geschlecht (Пол) | weiblich (женский) | Teilnahme an gewerkschaftlichen Mai-Veranstaltung (Участие в Первомайских мероприятиях, организованных профсоюзами) | fehlende Angabe (Данные отсутствуют) | 1 |
Ja (Да) | 36 | |||
Nein (Нет) | 40 | |||
keine Angabe/weiss nicht (Данные отсутствуют/не знаю) | 2 | |||
maennlich (мужской) | Teilnahme an gewerkschaftlichen Mai-Veranstaltung (Участие в Первомайских мероприятиях, организованных профсоюзами) | fehlende Anqabe (Данные отсутствуют) | ||
Ja (Да) | 74 | |||
Nein (Нет) | 116 | |||
keine Angabe/weiss nicht (Данные отсутствуют/не знаю) | 2 |
Если переменные вложены друг в друга, как в рассматриваемом примере, то между ними существуют отношения главенства и подчинённости. Перечисление состава меток значений подчинённых переменных (в нашем примере переменной v8), входят во все описания главенствующей переменной (в нашем примере переменной v2).
Рассмотрим теперь оба метода: вложение и наложение для двумерной таблицы. Речь сначала пойдёт о двумерной таблице с двумя строчными переменными.
-
Перенесите в список строчных переменных переменные v20 (Какую должность Вы занимаете в данный момент?) и v21 (Приблизительно в каких пределах находится Ваш ежемесячный доход?), а переменную v2 (Пол) в список столбцовых переменных. Рассмотрим сначала штабельный вариант.
-
Активируйте для этого опцию Each separately (stacked) (Каждая отдельно (с наложением)). Вы получите результаты опроса в следующем виде:
| Geschlecht (Пол) | ||
weiblich (женский) | maennlich (мужской) | ||
Berufs-position (Занимаемая должность) | Auszubildende(r)/Lerlinq (Студент(кa)/ученик(цa)) | 4 | 4 |
Arbeiterln (Рабочий(ая)) | 12 | 35 | |
Facharbeiterln/Geselle (Помощник/ученик на производстве) | 2 | 45 | |
Meister (Мастер) |
| 4 | |
Angestellte(r) (Служащий(ая)) | 35 | 31 | |
Leitende(r) Anaestellte(r) (Ведущий специалист) | 1 | 7 | |
Beamte(r) (Государственная руководящая должность) | 10 | 21 | |
Rentnerln/Pensionaerln (Пенсионер(ка)) | 6 | 36 | |
Hausfrau/Hausmann Щомохозяйка(ин)) | 3 | 6 | |
Erwerbsunfaehig (Нетрудоспособен^)) | 1 |
| |
Arbeitslos (Безработный(ая)) | 3 | 5 | |
Nettoein kommen (monatlich) (Чистый доход (в месяц)) | bis 1.000 DMJflo 1.000 DM) | 11 | 9 |
bis 2.000 DM (до 2.000 DM) | 33 | 45 | |
bis 3.000 DM (до 3.000 DM) | 18 | 83 | |
bis 4.000 DM (до 4.000 DM) | 7 | 26 | |
bis 5.000 DM (до 5.000 DM) | 1 | 10 | |
bis 6.000 DM (до 6.000 DM) | 1 | 3 | |
mehr als 7.000 DM (свыше 7.000 DM) |
| 2 | |
keine Angaben (Данные отсутствуют) | 6 | 16 | |
В качестве результата мы получили две вертикально совмещённых перекрёстных таблицы, первая таблица для переменных v20 и v2, а вторая для переменных v21 и v2.
Geschlecht (Пол) | |||||
weiblich (женский) | maennlich (мужской) | ||||
Berufs position (Зани-маемая должность) | Auszubi ldende(r)/ Lerling (Студент(ка)/ Ученик(ца)) | Nettoein kommen (monatlich) (Чистый доход (в месяц)) | bis 1.000 DM (до 1.000 DM) | 2 | 3 |
bis 2.000 DM (до 2.000 DM) | 2 | 1 | |||
Arbeiterln (Рабо-чий(ая)) | Nettoein kommen (monatlich) (Чистый доход (в месяц)) | bis 1.000 DM (до 1.000 DM) | 3 |
| |
bis 2.000 DM (до 2.000 DM) | 7 | 11 | |||
bis 3.000 DM (до 3.000 DM) | 2 | 21 | |||
keine Angaben (Данные отсутствуют) |
| 3 | |||
Facharbe iterln/G eselle (Помощник/ учен ик на произво-дстве) | Nettoein kommen (monatlich) (Чистый доход (в месяц)) | bis 2.000 DM (до 2.000 DM) | 11 | 6 | |
bis 3.000 DM (до 3.000 DM) |
| 33 | |||
bis 4.000 DM (до 4.000 DM) |
| 4 | |||
bis 5.000 DM (до 5.000 DM) |
| 1 | |||
keine Angaben (Данные отсутствуют) |
| 1 | |||
Meister (Мастер) | Nettoein kommen (monatlich) (Чистый доход (в месяц)) | bis 3.000 DM (до 3.000 DM) |
| 3 | |
bis 4.000 DM (до 4.000 DM) |
| 1 | |||
Angestellte(r) (Служа-щий(ая)) | Nettoein kommen (monatlich) (Чистый доход (в месяц)) | bis 1.000 DM (до 1.000 DM) | 1 |
| |
bis 2.000 DM (до 2.000 DM) | 15 | 4 | |||
bis 3.000 DM (до 3.000 DM) | 12 | 15 | |||
bis 4.000 DM (до 4.000 DM) | 4 | 6 | |||
bis 5.000 DM (до 5.000 DM) |
| 3 | |||
bis 6.000 DM (до 6.000 DM) |
| 1 | |||
keine Angaben (Данные отсутствуют) | 3 | 2 | |||
Leitende(r) Angestellte(r) (Ведущий специалист) | Nettoein kommen (monatlich) (Чистый доход (в месяц)) | bis 2.000 DM (до 2.000 DM) | 1 | 1 | |
bis 3.000 DM (до 3.000 DM) |
| 1 | |||
bis 4.000 DM (до 4.000 DM) |
| 3 | |||
mehr als 7.000 DM (свыше 7.000 DM) |
| 1 | |||
keine Anqaben (Данные отсутствуют) |
| 1 | |||
-
Теперь выберите опцию All combinations (nested) (Все комбинации (с вложением)). Вариант с вложением будет выглядеть следующим образом:
Beamte(r) (Государственная руководящая должность) | Nettoeinkommen (monatlich) (Чистый доход (в месяц)) | bis 1 .000 DM (до 1 .000 DM) | 1 | |
bis 2.000 DM (до 2.000 DMJ | 2 | 1 | ||
bis 3.000 DM (до 3.000 DM) | 2 | 4 | ||
bis 4.000 DM (до 4.000 DMJ | 3 | 8 | ||
bis 5.000 DM (до 5.000 DM) | 1 | 4 | ||
bis 6.000 DM (до 6.000 DM) | 1 | 2 | ||
mehr als 7.000 DM (свыше 7.000 DM) | 1 | |||
keine Angaben (Данные отсутствуют) | 1 | |||
Rentnerln/ Pensionaerln (Пенсионер(ка)) | Nettoeinkommen (monatlich) (Чистый доход (в месяц)) | bis 1.000 DM (до 1.000 DM) | 3 | 2 |
bis 2.000 DM (до 2.000 DM) | 3 | 17 | ||
bis 3.000 DM (до 3.000 DM) | 6 | |||
bis 4.000 DM (до 4.000 DM) | 3 | |||
bis 5.000 DM (до 5.000 DM) | 1 | |||
keine Angaben (Данные отсутствуют) | 7 | |||
Hausfrau/ Hausmann (Домохозяй-ка(ин)) | Nettoeinkommen (monatlich) (Чистый доход (в месяц)) | bis 1.000 DM (до 1.000 DMJ | 1 | 3 |
bis 2.000 DM (до 2.000 DM) | 1 | |||
bis 4.000 DM (до 4.000 DM) | 1 | |||
bis 5.000 DM (до 5.000 DM) | 1 | |||
keine Anqaben (Данные отсутствуют) | 2 | |||
Erwerbsunfaehig (Нетрудо-способен(а)) | Nettoeinkommen (monatlich) (Чистый доход (в месяц)) | bis 2.000 DM (до 2.000 DM) | 1 | |
Arbeitslos (Безработный(ая)) | Nettoeinkommen (monatlich) (Чистый доход (в месяц)) | bis 1.000 DM (до 1.000 DM) | 1 | |
bis 2.000 DM (до 2.000 DM) | 1 | 3 | ||
bis 3.000 DM (до 3.000 DM) | 1 | |||
keine Angaben (Данные отсутствуют) | 1 | 1 | ||
Если переменные двумерной таблицы вложены одна в другую, то между ними существуют отношения главенства и подчинённости. Метки значений подчинённых переменных (в нашем примере: v21 — Nettoeinkommen (monatlich) (Чистый доход (в месяц))), выводятся для каждой комбинации меток значений переменных v20 и v2 (высокая государственная должность — женщины; высокая государственная должность — мужчины; пенсионер — женщины; пенсионер — мужчины и т.д.).
Рассмотрим теперь ещё несколько вариантов представления данных нашего примера. Теперь речь пойдёт о двумерной таблице с двумя столбцовыми переменными. Сначала изучим штабельный вариант.
-
Для этого переменную v20 поместите в поле строчных переменных, а переменные v21 и v2 в поле столбцовых переменных, и активируйте опцию Each separately (stacked) (Каждая отдельно (с наложением)). Результаты опроса будут выглядеть следующим образом (см. стр. 515):
| Nettoeinkommen (monatlich) (Чистый доход (в месяц)) | Geschlecht (Пол) | |||||||||
bis 1.000 DM (до 1.000 DM) | bis 2.000 DM (до 2.000 DM) | bis 3.000 DM (до 3.000 DM) | bis 4.000 DM (до 4.000 DM) | bis 5.000 DM (до 5.000 DM) | bis 6.000 DM (до 6.000 DM) | mehr als 7.000 DM (свыше 7.000 DM) | keine Angaben (Данные отсут ствуют) | weib-lich (жен-ский) | maen-nlich (муж-ской) | ||
Benjfs-position (Зани-маемая долж ность) | Auszubi-ldende(r)/ Lerling (Студент (ка)/ Учени-к(ца)) | 5 | 3 |
|
|
|
|
|
| 4 | 4 |
Arbe-iterln (Рабочий (ая)) | 3 | 18 | 23 |
|
|
|
| 3 | 12 | 35 | |
Fachar-beiterln/ Geselle (Помо-щник/ ученик на произ-водстве) |
| 7 | 34 | 4 | 1 |
|
| 1 | 2 | 45 | |
Meister (Мастер) |
|
| 3 | 1 |
|
|
|
|
| 4 | |
Anges-tellte(r) (Служа-щий (ая)) | 1 | 19 | 27 | 10 | 3 | 1 |
| 5 | 35 | 31 | |
Leite-nde(r) Anges-tellte(r) (Ведущий специа-лист) |
| 2 | 1 | 3 |
|
| 1 | 1 | 1 | 7 | |
Beamte(r) (Государ-ственная руково-дящая долж-ность) | 1 | 3 | 6 | 11 | 5 | 3 | 1 | 1 | 10 | 21 | |
Rentnerln/ Pensi-onaerln (Пенсио-нер(ка)) | 5 | 20 | 6 | 3 | 1 |
|
| 7 | 6 | 36 | |
Hau-sfrau/ Haus-mann (Домо-хозяйка(ин)) | 4 | 1 |
| 1 | 1 |
|
| 2 | 3 | 6 | |
Erwerb-sunfaehig (Нетрудо-спосо-бен(а)) |
| 1 |
|
|
|
|
|
| 1 |
| |
Arbeitslos (Без-работный (ая)) | 1 | 4 | 1 |
|
|
|
| 2 | 3 | 5 | |
Nettoeinkommen (monatlich) (Чистый доход (в месяц)) | ||||||||||||||||
bis 1.000 DM (до 1.000 DM) | bis 2.000 DM (до 2.000 DM) | bis 3.000 DM (до 3.000 DM) | bis 4.000 DM (до 4.000 DM) | bis 5.000 DM (до 5.000 DM) | bis 6.000 DM (до 6.000 DM) | mehr als 7.000 DM (свыше 7.000 DM) | keine Angaben (Данные отсут-ствуют) | |||||||||
(Поп) | (Пол) | (Пол) | (Пол) | (Пол) | (Пол) | (Пол) | (Пол) | |||||||||
ж | м | ж | м | ж | м | ж | м | ж | м | ж | м | ж | м | м | ||
Beruf-sposi-tion (Зани-маемая долж-ность) | Auszu-bildende (r)/ Lerling (Студент (ка)/ Ученик (ца)) | 2 | 3 | 2 | 1 |
|
|
|
|
|
|
|
|
|
|
|
Arbeiterln (Рабочий (ая) | 3 |
| 7 | 11 | 2 | 21 |
|
|
|
|
|
|
|
| 3 | |
Fachar-beiterln /Geselle (Помо-щник /ученик на произ-водстве) |
|
| 1 | 6 | 1 | 33 |
| 4 |
| 1 |
|
|
|
| 1 | |
Meister (Мастер) |
|
|
|
|
| 3 |
| 1 |
|
|
|
|
|
|
| |
Anges-tellte(r) (Служащий (ая)) | 1 |
| 15 | 4 | 12 | 15 | 4 | 6 |
| 3 |
| 1 |
| 3 | 2 | |
Leite-nde(r) Ange-stellte(r) (Ведущий специ-алист) |
|
| 1 | 1 |
| 1 |
| 3 |
|
|
|
| 1 |
| 1 | |
Beamte(r) (Государ-ственная руково-дящая должность) | 1 |
| 2 | 1 | 2 | 4 | 3 | 8 | 1 | 4 | 1 | 2 | 1 |
| 1 | |
Rent-nerln/ Pensio -naerln (Пенси онер (ка)) | 3 | 2 | 3 | 17 |
| 6 |
| 3 |
| 1 |
|
|
|
| 7 | |
Haus-frau/ Haus-mann (Дом-охозяйка (ин)) | 1 | 3 |
| 1 |
|
|
| 1 |
| 1 |
|
|
| 2 |
| |
Erwe-rbsunfa-ehig (Нетрудо-спос-обен) |
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
| |
Arbe-itslos (Безра-ботный)) |
| 1 | 1 | 3 | 1 |
|
|
|
|
|
|
|
| 1 | 1 | |
-
Если теперь Вы измените соответствующую установку на All combinations (nested) (Все комбинации (с вложением)), то данные будут представлены как показано на стр. 516.
В данном случае выводится перекрёстная таблица переменных v20 и v21. Переменная v2 является подчинённой. Метки значений переменной v2 (weiblich (женский), maennlich (мужской)) указываются для каждой комбинации переменных v20 и v21.
В целях экономии места мы откажемся от рассмотрения примеров трёхмерных таблиц. Если у Вас есть желание, то используя файл mai.sav, Вы можете поупражняться самостоятельно.
Зависимые и независимые переменные
Какие переменные использовать в качестве строчных, а какие в качестве столбцовых. Вы должны решать самостоятельно. Жёстких правил для этого не существует. Обычно независимую переменную используют в качестве столбцовой, а зависимую в качестве строчной переменной. Если же вы используете вложение при отображении данных, то зависимую переменную, как правило, следует располагать под независимыми.
24.2.5 Процентные показатели
24.2.5 Процентные показатели
Как вы наверняка заметили, в простых таблицах обычно приводятся только абсолютные показатели. Но в связи с тем, что зачастую бывает проще сравнивать данные, представленные в процентной форме, рассмотрим теперь возможность отображения процентных показателей.
Процентные показатели по столбцам
Представим сначала в процентной форме ответы на вопрос, является ли ещё 1-е Мая, как день трудящихся, актуальным праздником.
-
В диалоговом окне Basic Tables (Основные таблицы) переменную v5 перенесите в список строчных переменных.
-
Щёлкните на переключателе Statistics... (Статистики). Откроется диалоговое окно Basic Tables: Statistics (Основные таблицы: Статистики), изображённое на рисунке 24.3.
-
При помощи переключателя Add (Добавить) перенесите опции Count (Количество) и Col % (Столбцовый %) из списка Statistics (Статистики) в список Cell Statistics (Статистики в ячейках).
-
Подтвердите установки нажатием Continue (Далее) и затем на ОК. Вы получите результаты опроса в следующем виде:
Рис. 24.3: Диалоговое окно Basic Tables: Statistics (Основные таблицы: Статистики)
Count (Количество) | Col % (Столбцовый %) | ||
1st der 1 .Mai als TdA noch zeitgemaess? (Сохраняет ли ещё актуальность 1-е Мая, как день трудящихся?) | fehlende Angabe (Данные отсутствуют) | 39 | 14,4% |
Ja (Да) | 154 | 56,8% | |
Nein (Нет) | 59 | 21,8% | |
Weiss nicht (He знаю) | 19 | 7,0% |
В данной таблице приведены как абсолютные значения (Count (Количество)), так и процентные показатели, соответствующие числу допустимых значений (Col % (Столбцовый %)). Из результатов ясно видно, что, что 58 % опрошенных членов профсоюзов находят 1-е Мая актуальным, 21,8 % полагают, что День трудящихся уже отжил своё, а для 7 % вопрос оказался неразрешимым.
Приведём ещё один пример: мы хотим проверить, связан ли ответ на вопрос о том что, организация первомайских мероприятий профсоюзами является политически важным аспектом, который следует сохранить (v!3), с партийной ориентацией опрошенных (v22).
-
В диалоговом окне Basic Tables (Основные таблицы) переменную v!3 перенесите в список строчных переменных, а переменную v22 в список столбцовых переменных.
-
Щёлкните на переключателе Statistics... (Статистики) и перенесите опции Count (Количество) и Col % (Столбцовый %) в список Cell Statistics (Статистики в ячейках). Данные будут представлены в следующем виде (см. след, стр.):
Среди членов профсоюзов, отдающих свое предпочтение партиям CDU/CSU, 22,2 % полагают, что организация празднования 1-го Мая профсоюзами не важна с политической точки зрения, среди SPD-ориентированных членов профсоюзов эту позицию поддерживают только 4,4 %, среди приверженцев Союза 90/Зелёных (Buendbis 90/Die Gruenen) — 4,5 %, а среди сторонников республиканцев (Republikaner), данную точку зрения разделяют 22,2 %.
Приведём ещё один пример: в данном случае должны быть отображены показатели членства в профсоюзных организациях (v!7), причём в порядке снижения частот.
Перенесите переменную v17 в список строчных переменных.
-
Щёлкните на переключателе Statistics... (Статистики) и перенесите опции Count (Количество) и Col % (Столбцовый %) в список Cell Statistics (Статистики в ячейках).
-
В группе Sorting by Cell Count (Сортировка частотных показателей в ячейках) поставьте маркер возле опции Descending (По убыванию). Диалоговое окно Basic Tables: Statistics (Основные таблицы: Статистики) должно теперь выглядеть так, как на рисунке 24.4.
Рис. 24.4: Диалоговое окно Basic Tables: Statistics (Основные таблицы: Статистики)
Результаты опроса будут выглядеть следующим образом:
Count (Коли-чество) | Col % (Столб-цовый %) | ||
Gewerkschaftsm itglied in (Член профсоюза): | Профсоюз металлургической промышленности (IG Metall) | 73 | 26,9% |
Профсоюз сферы услуг (? TV) | 52 | 19,2% | |
Профсоюз строителей (BSE) | 32 | 11,8% | |
Профсоюз химической промышленности (IG Chemie Papier Keramik) | 22 | 8,1% | |
Профсоюз сферы образования (GEW) | 20 | 7,4% | |
Торговля Банки Страхование (HBV) | 19 | 7,0% | |
Профсоюз Deutsche Post (Немецкая почта) | 13 | 4,8% | |
Профсоюз железнодорожников Германии (GdED) | 11 | 4,1% | |
Профсоюз работников средств массовой информации (IG Medien) | 11 | 4,1% | |
fehlende Anqabe (Данные отсутствуют) | 6 | 2,2% | |
Профсоюз полицейской службы (GdP) | 6 | 2,2% | |
Профсоюз Сад Земля Лес (GGLF) | 3 | 1,1% | |
Профсоюз деревообрабатывающей промышленности (IG Holz) | 1 | ,4% | |
Профсоюз пищевой промышленности (NGG) | 1 | ,4% | |
Профсоюз лёгкой промышленности | 1 | .4% |
29 % опрошенных являются членами профсоюза металлургической промышленности (IG Metall), 19,2 % членами профсоюза сферы услуг (OTV), 11,8 % членами профсоюза профсоюз строителей (BSE), 8,1 % членами профсоюза химической промышленности (IG Chemie Papier Keramik), 7,4 % входят в GEW, и 7,0 % в профсоюз Торговля—Банки—Страхование (HBV). От 4 до 5 % являются членами профсоюза почтовой службы (DPG) (4,8 %), профсоюза железнодорожников Германии (GdED) (4,1 %) и профсоюза работников средств массовой информации (IG Medien) (4,1 %). И завершают список более мелкие профсоюзы, такие как профсоюз полицейской службы (GdP) (2,2 %), профсоюз Сад—Земля—Лес (GGLF) (1,1 %), профсоюз деревообрабатывающей промышленности (IG Holz) (0,4 %), профсоюз пищевой промышленности (NGG) (0,4 %) и профсоюз лёгкой промышленности (0,4 %).
Теперь, чтобы получить информацию о зависимости социального положения опрашиваемых от их пола, представим в перекрёстной таблице переменные v2 (Пол) v20 (Социальное положение).
-
Перенесите переменную v20 в список строчных переменных, а переменную v2 в список табличных переменных.
-
Затем щёлкните на переключателе Statistics... (Статистики) и перенесите опции Count (Количество) и Col % (Столбцовый %) в список Cell Statistics (Статистики в ячейках).
-
В группе Sorting by Cell Count (Сортировка частотных показателей) поставьте маркер возле опции Descending (По убыванию).
-
Подтвердите нажатием Continue (Далее) и затем ОК. В окне просмотра Вы увидите следующий вывод, причём вторая таблица станет видимой только после двойного щелчка по первой таблице и активирования в ниспадающем меню.
Geschlecht maenlich (Мужчины) | |||
Count (Коли-чество) | Col % (Столб-цовый % ! | ||
Berufsposition (Занимаемая должность) | Auszubildende(r)/Lerlinq (Студент(ка)/Ученик(ца)) | 31 | 16,0% |
Arbeiterln (Рабочий(ая)) | 35 | 18,0% | |
Facharbeiterln/Geselle (Помощник/ученик на производстве) | 45 | 23,2% | |
Meister (Мастер) | 36 | 18,6% | |
Angestellte(r) (Служащий(ая)) | 21 | 10,8% | |
Leitende(r) Angestellte(r) (Ведущий специалист) | 6 | 3,1% | |
Beamte(r) (Государственная руководящая должность) | 4 | 2,1% | |
Rentnerln/Pensionaerln (Пенсионер(ка)) | 7 | 3,6% | |
Hausfrau/Hausmann (Домохозяйка(ин)) | 5 | 2,6% | |
Erwerbsunfaehig (Нетрудоспособен(а)) | 4 | 2,1% | |
Arbeitslos (Безработный(ая)) | |||
Geschlecht weiblich (Женщины) | |||
Count (Коли-чество) | Col % (Столб-цовый %) | ||
Berufsposition (Занимаемая должность) | Auszubildende(r)/Lerlinq (Студент(ка)/Ученик(ца)) | 35 | 45,5% |
Arbeiterln (Рабочий(ая)) | 12 | 15,6% | |
Facharbeiterln/Geselle (Помощник/ученик на производстве) | 2 | 2,6% | |
Meister (Мастер) | 6 | 7,8% | |
Angestellte(r) (Служащий(ая)) | 10 | 13,0% | |
Leitende(r) Angestellte(r) (Ведущий специалист) | 3 | 3,9% | |
Beamte(r) (Государственная руководящая должность) | 4 | 5,2% | |
Rentnerln/Pensionaerln (Пенсионер(ка)) | 1 | 1,3% | |
Hausfrau/Hausmann (Домохозяйка(ин)) | 3 | 3,9% | |
Erwerbsunfaehig (Нетрудоспособен(а)) | |||
Arbeitslos (Безработный(ая)) | 1 | 1,3% | |
Метка переменной v2 (Geschlecht (Пол)) и её признаки (maenlich (мужской), weiblich (женский)) расположены в левом верхнем углу. Поскольку переменная v2 была применена в качестве переменной слоев, то мы получили столько отдельных таблиц, сколько значений у этой переменной, т.е. две. По результатам, отображаемым в таблицах, видно, что 45,5 % опрошенных женщин занимают должности служащих, в то время как служащими работают только 16 % мужчин. Такой высокий показатель должностей служащих среди женщин можно объяснить тем, что, во-первых, на этих должностях выполняется в основном офисная работа, а во-вторых, Марбург как университетский город (в городе расположен университет им. Филипса) является самым крупным работодателем в округе. Женщины оказались немного впереди и в отношении государственных руководящих должностей. В промышленном секторе в предложении и спросе на профессиональные должности явно заметно другое соотношение полов. В то время, как только одна женщина (1,3 %) занята на должности ведущего специалиста, среди мужчин такую должность занимают 7 человек (3,6 %). Ни одна женщина не занимает должности мастера, и только 25,6 % женщин работают как помощники, в то время как среди мужчин это уже 23,2 %. Из 80 мужчин, занятых на рабочих должностях (Arbeiter (Рабочий) и Facharbeiter/Geselle (Помощник/ученик на производстве)), 45 человек, т.е. больше половины, заняты на должности профессионального помощника, а из 14 женщин, занятых на рабочих должностях (Arbeiterln
(Рабочая) и Facharbeiterln/Geselle (Помощница/ученик на производстве)) это только 2 человека.
Строчные проценты
Создадим перекрёстную таблицу для переменных v!7 (Gewerkschaftsmitglied in (Член профсоюза)) и v2 (Geschlecht (Пол)), чтобы посмотреть какие из профсоюзных организаций привлекают женщин, а какие мужчин.
-
Перенесите переменную v!7 в список строчных переменных, а переменную v2 — в список табличных переменных.
-
Щёлкните на переключателе Statistics... (Статистики) и перенесите опции Count (Количество), Row % (Строчный %) и Col % (Столбцовый %) в список Cell Statistics (Статистики в ячейках).
-
В группе Sorting by Cell Count (Сортировка частотных показателей) поставьте маркер возле опции Descending (По убыванию). Вы получите следующую таблицу:
| Geschlecht (Пол) | ||||||
maennlich (мужской) | weiblich (женский) | ||||||
Count (Коли-чество) | Col % (Стол-цовый %) | Row % (Стро-чный %) | Count (Коли-чество) | Col % (Столб-цовый %) | Row % (Стро-чный %) | ||
Gewerksch aftsmitglied in (Член профсоюза): | Профсоюз металлургической промышленности (IG Metall) | 63 | 32,5% | 86,3% | 10 | 13,0% | 13,7% |
Профсоюз сферы услуг (OTV) | 26 | 18,6% | 69,2% | 16 | 20,8% | 30,8% | |
Профсоюз строителей (BSE) | 29 | 14,9% | 90,6% | 3 | 3,9% | 9,4% | |
Профсоюз химической промышленности (IG Chemie Papier Keramik) | 13 | 6,7% | 59,1% | 9 | 11,7% | 40,9% | |
Профсоюз сферы образования (GEW) | 13 | 6,7% | 65,0% | 7 | 9,1% | 35,0% | |
Торговля Банки Страхование (HBV) | 5 | 2,6% | 26,3% | 14 | 18,2% | 73,7% | |
Профсоюз Deutsche Post (Немецкая почта) | 7 | 3,6% | 53,8% | 6 | 7,8% | 46,2% | |
Профсоюз железнодорожников Германии (GdED) | 9 | 4,6% | 81,8% | 2 | 2,6% | 18,2% | |
Профсоюз работников средств массовой информации (IG Medien) | 7 | 3,6% | 63,6% | 4 | 5,2% | 36,4% | |
fehlende Angabe (Данные отсутствуют) | 3 | 1 ,5% | 50,0% | 3 | 3,9% | 50,0% | |
Профсоюз полицейской службы (GdP) | 4 | 2,1% | 66,7% | 2 | 2,6% | 33,0% | |
Профсоюз Сад Земля Лес (GGLF) | 3 | 1 ,5% | 100,0% |
|
|
| |
Профсоюз деревообрабатывающей промышленности (IG Holz) | 1 | ,5% | 100,0% | 1 | 1,3% | 100,0% | |
Профсоюз пищевой промышленности (NGG) |
|
|
|
|
|
| |
Профсоюз лёгкой промышленности | 1 | ,5% | 100,0% |
|
|
| |
Обратим сначала внимание на столбцовые проценты: среди членов профсоюзов мужского пола 32,5 % являются членами профсоюза металлургической промышленности (1G Metall), 18,6 % — профсоюза сферы услуг (OTV) и т.д. Среди всех членов профсоюзов женского пола, 13,7 % состоят в профсоюзе металлургической промышленности (IG Metall), 30,8 % — в профсоюзе сферы услуг (OTV) и т.д. Рассмотрим теперь строчные проценты: 86,3 % членов профсоюза металлургической промышленности (IG Metall) составляют мужчины и только 13,7 % женщины; 73,3 % профсоюза "Торговля—Банки—Страхование" (HBV) составляют женщины и только 26,3 % мужчины и т.д. Таким образом, профсоюз металлургической промышленности (IG Metall) привлекает в свои ряды в основном мужчин, а профсоюз "Торговля—Банки—Страхование" (HBV) — женщин.
Послойные проценты
Мы хотим проверить, существуют ли различия между полами (v2) в отношении ответа на вопрос Принимали ли Вы когда-нибудь участие в Первомайских мероприятиях? (v8).
-
Перенесите переменную v8 в список строчных переменных, а переменную v2 в список табличных переменных.
-
Щёлкните на переключателе Statistics... (Статистики).
-
Перенесите в список Cell Statistics (Статистики в ячейках) опции Count (Количество) и Layer % (Послойный %). В группе Sorting by Cell Count (Сортировка частотных показателей) активируйте опцию None (Отсутствует). Подтвердите установки нажатием Continue (Далее).
-
Затем щёлкните на переключателе Layout... (Компоновка). Откроется диалоговое окно Basic Tables: Layout (Основные таблицы: Компоновка), изображённое на рисунке 24.5.
-
В группе Statistics Labels (Метки статистик) активируйте опцию Down the lef side (С левой стороны). Такой порядок организации приведёт к тому, что будет выведена только одна таблица, в которой оба слоя будут примыкать друг к другу с боковых сторон.
-
Подтвердите свой выбор нажатием Continue (Далее) и затем ОК. В окне просмотра Вы увидите следующую таблицу:
Рис. 24.5: Диалоговое окно Basic Tables: Layout (Основные таблицы: Компоновка)
| Geschlecht (Пол) | ||||
weiblich (женский) | maennlich (мужской) | ||||
Count (Коли-чество) | Layer % (Посло-йный %) | Count (Коли-чество) | Layer % (Посло-йный %) | ||
Teilnahme an gewerkschaftlichen Mai-Veranstaltung (Участие в Первомайских мероприятиях, организованных профсоюзами) | fehlende Angabe (Данные отсутствуют) | 1 | 1,3% | 2 | 1,0% |
Ja (Да) | 36 | 46,8% | 74 | 38,1% | |
Nein (Нет) | 40 | 51,9% | 116 | 59,8% | |
Keine Angabe/weiss nicht (Данные отсутствуют/не знаю) |
|
| 2 | 1,0% | |
Сумма послойных процентных показателей одного слоя (weiblich (женский), maennlich (мужской)) равна 100 %. Рассмотрим результаты опроса: так, например, 46,8 % женщин уже хоть раз принимали участие в первомайских мероприятиях, а среди мужчин это делали только 38,1 %.
Табличные проценты
Проверим, существуют ли различия между полами (v2) в отношении ответа на вопрос v14 (Согласны ли Вы с утверждением, что 1-е Мая является праздником главным образом для высокопоставленных чиновников?).
-
Перенесите переменную v!4 в список строчных переменных, а переменную v2 в список табличных переменных.
-
Щёлкните на переключателе Statistics... (Статистики) и перенесите в список Cell Statistics (Статистики в ячейках) опции Count (Количество), Layer % (Послойный %) и Table % (Табличный %).
Вы получите следующие таблицы, причём вторая таблица появится только после двойного щелчка по первой таблице и активирования соответствующей позиции в ниспадающем меню.
Geschlecht weiblich (Женщины) | ||||
Count (Коли-чество) | Layer % (Посло-йный %) | Table % (Табли-чный %) | ||
1 . Mai = Fest fuer hauptamt. Funktionaere? (1-е Мая = праздник для высокопоставленных чиновников?) | fehlende Angabe (Данные отсутствуют) | 15 | 19,5% | 5,5% |
Ja (Да) | 17 | 22,1% | 6,3% | |
Nein (Нет) | 37 | 48,1% | 13,7% | |
Weiss nicht (He знаю) | 8 | 10,4% | 3,0% | |
Geschlecht maenlich (Мужчины) | ||||
Count (Коли-чество) | Layer % (Посло-йный %) | Table % (Табли-чный %) | ||
1 . Mai = Fest fuer hauptamt. Funktionaere? (1-е Мая = праздник для высокопоставленных чиновников?) | fehlende Angabe (Данные отсутствуют) | 25 | 12,9% | 9,2% |
Ja (Да) | 42 | 21 ,6% | 15,5% | |
Nein (Нет) | 110 | 56,7% | 40,6% | |
Weiss nicht (He знаю) | 17 | 8,8% | 6,3% | |
Сумма всех показателей табличных процентов равна 100 %. Так, 56,7 % мужчин ответили на поставленный вопрос "нет" (Layer % (Послойный %)), а среди женщин такой же ответ дали 48,1 %. Мужчины, ответившие на вопрос отрицательно (нет), составляют 40,6 % всех опрошенных (см. колонку Table % (Табличный %)).
3.gif
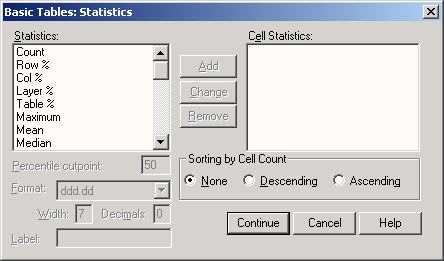
4.gif
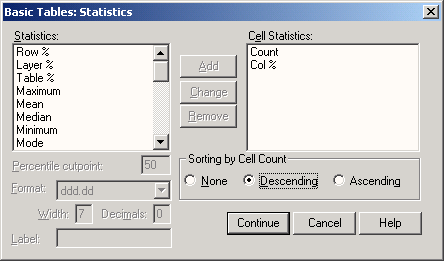
5.gif

24.2.6 Суммарные значения
24.2.6 Суммарные значения
При помощи опции подсчета суммарных значений можно составить объединённые показатели некоторого количества ячеек. Разберем сначала следующий пример: партийные предпочтения опрашиваемых (v22) необходимо представить в табличной форме с сортировкой по убыванию и учётом общего количества опрашиваемых.
-
Перенесите переменную v22 в список строчных переменных.
-
Щёлкните на переключателе Statistics... (Статистики) и перенесите опции Count (Количество) и Col % (Столбцовый %) в список Cell Statistics (Статистики в ячейках).
-
Активируйте опцию Descending (По убыванию) и подтвердите нажатием Continue (Далее).
-
Щёлкните на выключателе Totals... (Суммы). Вы увидите диалоговое окно Basic Tables: Totals (Основные таблицы: Суммы), изображённое на рисунке 24.6.
Рис. 24.6: Диалоговое окно Basic Tables: Totals (Основные таблицы: Суммы)
Если активирована опция Totals over each group variable (Суммы для каждой групповой переменной), для каждой групповой переменной будут выводиться суммарные значения всех статистик активированных через выключатель Statistics... (Статистики); если активирована опция Table-margin totals (Суммарные показатели таблицы), то суммарные значения активированных статистик будут рассчитываться и для всей таблицы.
-
Для нашего примера активируйте опцию Table-margin totals (Суммарные показатели таблицы). В окне просмотра появится таблица с результатами опроса.
| Count (Коли-чество) | Col % (Столб-цовый %) | |
Parteipraeferenz (Предпочитаемая партия) | SPD | 91 | 33,6% |
keine (Ни одна из партий) | 77 | 28,4% | |
fehlende Angabe (Данные отсутствуют) | 46 | 17,0% | |
Buendbis 90/Die Gruenen (Союз 90/Зелёные) | 22 | 8,1% | |
CDU/CSU | 18 | 6,6% | |
Republikaner (Республиканцы) | 9 | 3,3% | |
Andere (Другая) | 4 | 1,5% | |
FDP | 2 | ,7% | |
PDS/Linke Liste (Левые) | 2 | ,7% | |
Table-margin total (Суммарный показатель таблицы) | 271 | 100,0% | |
Результаты опроса показывают сильную поддержку профсоюзами немецкой социал-демократии. 33,6 % опрошенных полагают, что их интересы лучше всего выражает SPD и только 6,6 % такого мнения о CDU/CSU. Результирующие показатели приведены в строке Table-margin total (Суммарный табличный показатель). Всего был опрошен 271 человек (= 100 %}.
На втором этапе представим партийные предпочтения (v22) отдельно для каждого пола (v2). Вывод данных должен происходить с сортировкой частот по убыванию. И организуем так же вывод суммарных показателей для групповых переменных.
-
Перенесите переменную v22 в список строчных переменных, а переменную v2 — в список табличных переменных.
-
Щёлкните на переключателе Statistics... (Статистики) и перенесите опции Count (Количество) и Col % (Столбцовый %) в список Cell Statistics (Статистики в ячейках). Активируйте опцию Descending (По убыванию). Подтвердите нажатием Continue (Далее).
-
Щёлкните на выключателе Totals... (Суммы) и активируйте на этот раз опцию Totals over each group variable (Суммы для каждой групповой переменной). Опция Table-margin ratals (Суммарные показатели таблицы) должна быть деактивированна. Вы получите следующие таблицы, причём вторая и третья таблицы станут видимыми только после двойного щелчка на первой таблице и активирования соответствующей позиции в ниспадающем меню.
Geschlecnt maenlich (Мужчины) | |||
Count (Коли-чество) | Со! % (Столб-цовый %) | ||
Parteipraeferenz (Предпочитаемая партия) | SPD | 73 | 37,6% |
keine (Ни одна из партий) | 51 | 26,3% | |
fenlende Angabe (Данные отсутствуют) | 30 | 15,5% | |
Buendbis 90/Die Gruenen (Союз 90/Зепёные) | 13 | 6,7% | |
CDU/CSU | 16 | 8,2% | |
Republikaner (Республиканцы) | 7 | 3,6% | |
andere (Другая) | 2 | 1,0% | |
FDP | 2 | 1,0% | |
PDS/Linke Liste (Левые) | |||
Group Total (Суммарный показатель группы) | 194 | 100,0% | |
Geschlecht weiblich (Женщины) | |||
Count (Коли-чество) | Col % (Столб-цовый %) | ||
Parteipraeferenz (Предпочитаемая партия) | SPD | 18 | 23,4% |
keine (Ни одна из партий) | 26 | 33,8% | |
fenlende Angabe (Данные отсутствуют) | 16 | 20,8% | |
Buendbis 90/Die Gruenen (Союз 90/Зелёные) | 9 | 1 1 ,7% | |
CDU/CSU | 2 | 2,6% | |
Republikaner (Республиканцы) | 2 | 2,6% | |
andere (Другая) | 2,6% | ||
FDP | |||
PDS/Linke Liste (Левые) | 2 | 2,6% | |
Group Total (Суммарный показатель группы) | 77 | 100,0% | |
Group total (Суммарный показатель группы) | |||
Count (Коли-чество) | Col % (Столб-цовый %) | ||
Parteipraeferenz (Предпочитаемая партия) | SPD | 91 | 33,6% |
keine (Ни одна из партий) | 77 | 28,4% | |
fehlende Angabe (Данные отсутствуют) | 46 | 17,0% | |
Buendbis 90/Die Gruenen (Союз 90/Зелёные) | 22 | 8,1% | |
CDU/CSU | 18 | 6,6% | |
Republikaner (Республиканцы) | 9 | 3,3% | |
andere (Другая) | 4 | 1,5% | |
FDP | 2 | ,7% | |
PDS/Linke Liste (Левые) | 2 | ,7% | |
Group Total (Суммарный показатель группы) | 271 | 100,0% | |
В окне просмотра приводятся три самостоятельные таблицы. Для групповой переменной в соответствующей строке с меткой Group Total (Суммарный показатель группы) указываются соответствующие суммарные значения.
Из 194 мужчин 73 полагают, что их интересы лучше всего выражает SPD, это 37,6 %; среди 77 женщин сторонниками SPD чувствуют себя только 18 человек, что соответствует 23,4 %. Явно видно, что в процентном выражении значительно большее количество мужчин, чем женщин, ощущает, что их интересы представляет именно Социал-демократическая партия. Среди женщин же доля тех, кто в настоящее время не чувствует, что их интересы представляет хотя бы одна из партий, значительно выше, нежели среди мужчин (33,8 % против 26,3 %). Следует также отметить, что вообще довольно значительная доля опрошенных не ощущает, что их интересы представляет какая-либо из партий, это свидетельствует о неудовлетворённости работой партий.
Суммарные показатели пакетированных переменных
Рассмотрим на примере, как ведут себя суммарные показатели пакетированных или штабельных переменных.
-
В диалоговом окне Basic Tables (Основные таблицы) перенесите переменные v2 (Geschlecht (Пол)) и v6 (Erinnerung an 1. Mai (Воспоминания о празднике 1-е Мая)) в список строчных переменных.
-
Активируйте опцию Each separately (stacked) (Каждая отдельно (с наложением)).
-
Щёлкните на переключателе Statistics... (Статистики) и перенесите опции Count (Количество) и Col % (Столбцовый %) в список Cell Statistics (Статистики в ячейках). Подтвердите установки нажатием Continue (Далее).
-
Щёлкните на выключателе Totals... (Суммы) и активируйте опцию Totals over each group variable (Суммы для каждой групповой переменной). Вы получите следующую таблицу:
Count (Коли-чество) | Col % (Стол-бцовый %) | ||
Geschlecht (Пол) | weiblich (женский) | 77 | 28,4% |
maennlich (мужской) | 194 | 71 ,6% | |
Group Total (Суммарный показатель группы) | 271 | 100,0% | |
Erinnerung an 1 . Mai -feier im Ort (Воспоминания о местных мероприятиях, посвящённых 1-му Мая) | fehlende Angabe (Данные отсутствуют) | 48 | 17,7% |
Ja (Да) | 67 | 24,7% | |
Nein (Нет) | 143 | 52,8% | |
Weiss nicht (He знаю) | 13 | 4,8% | |
Group Total (Суммарный показатель группы) | 271 | 100,0% |
По таблице видно, что при наложении переменных каждая переменная рассматривается как группа. Сумма процентных показателей каждой из групп (v2 и v6) равна 100 % (Group Total (Суммарный показатель группы)).
Суммарные показатели вложенных переменных
Рассмотрим вышеприведенный пример с учётом вложения переменных.
-
В диалоговом окне Basic Tables (Основные таблицы) активируйте опцию АН combinations (nested) (Все комбинации (с вложением)).
-
В диалоговом окне Basic Tables: Totals (Основные таблицы: Суммы) активируйте дополнительно опцию Table-margin totals (Суммарные показатели таблицы). Вы получите следующую таблицу:
Count (Коли-чество) | Col % (Стол-бцовый %) | ||||
Gesc-hlecht (Пол) | Weib-lich (жен-ский) | Erinnerung an 1 . Mai -feier im Ort (Воспоми-нания о местных меро-приятиях, посвящённых 1-му Мая) | fehlende Angabe (Данные отсут-ствуют) | 18 | 6,6 |
Ja (Да) | 19 | 7,0% | |||
Nein (Нет) | 33 | 12,2% | |||
Weiss nicht (He знаю) | 7 | 2,6% | |||
Group Total (Сум-марный показатель группы) | 77 | 18,4% | |||
maen-nlich (муж-ской) | Erinnerung an 1 . Mai -feier im Ort (Воспоми-нания о местных меро-приятиях, посвящённых 1-му Мая) | fehlende Angabe (Данные отсут-ствуют) | 30 | 11,1% | |
Ja (Да) | 48 | 17,7% | |||
Nein (Нет) | 110 | 40,6% | |||
Weiss nicht (He знаю) | 6 | 2,2% | |||
Group Total (Суммарный показатель группы) | 194 | 71 ,6% | |||
Table-margin total (Сум-марный показатель таблицы) | 271 | 100,0% |
Таблица показывает, что для вложенных переменных сумма процентных показателей значений подчинённых переменных — в нашем примере подчиненной является переменная v6 - равна 100 % (28,4 % + 71,6 % = 100 %).
6.gif
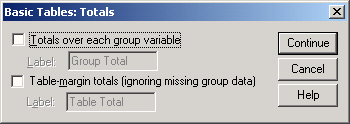
24.2.7 Средние значения и другие итоговые статистики
24.2.7 Средние значения и другие итоговые статистики
Организуем вывод итоговых статистик, таких как среднее значение и стандартное отклонение для переменных v)8 (С какого года Вы являетесь членом профсоюза? <19..>) и v!9 (Ваш год рождения? <19..>). Поскольку в опросе 1993 года относительно организации празднования 1-го Мая не были заданы вопросы: "Сколько лет вы уже являетесь членом профсоюза?" и "Сколько Вам лет?", мы сначала вычислим эти значения исходя их значений переменных v18 и v19. Для этого поступим следующим образом:
-
Выберите в меню Transform (Трансформировать) Compute... (Вычислить)
-
В качестве целевой переменной введите имя mitglied (членство).
-
В поле редактирования Numeric Expression (Числовое выражение) наберите 93-vl8. Диалоговое окно Compute Variable (Вычисление переменной) должно выглядеть теперь так, как на рисунке 24.7.
Рис. 24.7: Диалоговое окно Compute Variable (Вычисление переменной)
-
Подтвердите установки нажатием ОК.
Переменной mitglied (членство) теперь будет присвоено числовое значение, соответствующее продолжительности членства в профсоюзе. Вычислите теперь переменную alter (возраст).
-
Повторно выберите в меню опцию Transform (Трансформировать) Compute... (Вычислить)
-
В поле целевой переменной наберите имя alter (возраст). В поле редактирования Numeric Expression (Числовое выражение) введите 93-v19. Подтвердите установки нажатием ОК.
Переменной alter (возраст) теперь будет присвоено числовое значение, соответствующее возрасту опрашиваемого. Организуем сначала вывод статистик для переменной alter (возраст).
-
Выберите в меню Analyze (Анализ) Custom Tables (Пользовательские таблицы) Basic Tables... (Основные таблицы)
-
Переменную alter поместите в список Summaries (Итоги). Подтвердите нажатием ОК. В качестве простейшей итоговой таблицы вы получите следующую таблицу:
alter (возраст) | 44,17 |
Если Вы больше не будете требовать никаких дополнительных статистик, то по умолчанию будет выдаваться среднее значение обрабатываемой переменной. Средний возраст опрошенных составил 44,17 года. Теперь организуем вывод среднего значения переменной mitglied (членство).
-
Выберите в меню опции Analyze (Анализ) Custom Tables (Пользовательские таблицы) Basic Tables... (Основные таблицы) Переменная age должна ещё находиться в поле Summaries (Итоги).
-
В это же поле перенесите дополнительно переменную и подтвердите установки нажатием ОК. Вы получите следующую таблицу:
alter (возраст) | 44,17 |
mitglied (членство) | 18,42 |
Если в списке Summaries (Итоги) находится несколько переменных, то они будут отображаться друг под другом, так как в вышеприведенной таблице. Среднее арифметическое переменной mitglied (членство) равно 18,42 годам. Организуем теперь дополнительно и другие итоговые статистики, такие как минимальное значение, максимальное значение и стандартное отклонение.
-
Выберите в меню Analyze (Анализ) Custom Tables (Пользовательские таблицы) Basic Tables... (Основные таблицы)
В списке Summaries (Итоги) теперь должны стоять переменные alter (возраст) и mitglied (членство).
-
Щёлкните на переключателе Statistics... (Статистики).
-
Перенесите в поле Cell Statistics (Статистики в ячейках) статистики Mean (Среднее значение), Minimum (Минимум), Maximum (Максимум) и Std Deviation (Стандартное отклонение). Диалоговое окно Basic Tables: Statistics (Основные таблицы: Статистики) должно теперь выглядеть так, как на рисунке 24.8.
-
Подтвердите нажатием Continue (Далее) и затем ОК. Вы получите следующую таблицу:
Рис. 24.8: Диалоговое окно Basic Tables: Statistics (Основные таблицы: Статистики)
Mean (Среднее значение) | Minimum (Минимум) | Maximum (Максимум) | Std Deviation (Стандартное отклонение) | |
alter (возраст) | 44,17 | 18,00 | 90,00 | 14,42 |
mitglied (членство) | 18,42 | 1,00 | 63,00 | 13,00 |
Если Вы организовываете вывод нескольких итоговых статистик, то выбранные статистики приводятся в соседствующих колонках.
Подгруппы и итоговые статистики
Организуем вывод итоговых показателей переменных alter (возраст) и mitglied (членство) отдельно для каждого пола. В поле Summaries (Итоги) диалогового окна Basic Tables (Основные таблицы) должны теперь стоять переменные alter (возраст) и mitglied (членство).
-
Перенесите переменную v2 в список строчных переменных.
-
Щёлкните на переключателе Statistics... (Статистики).
-
Из списка Cell Statistics (Статистики в ячейках) удалите все статистики кроме Mean (Среднее значение). Подтвердите свой выбор нажатием Continue (Далее) и затем ОК. В окне просмотра Вы увидите следующую таблицу:
Geschlecht (Пол) | weiblich (женский) | alter (возраст) |
mitglied (членство) | ||
maennlich (мужской) | alter (возраст) | |
mitglied (членство) |
Средний возраст опрошенных женщин составляет 41,23 года, а средняя продолжительность членства в профсоюзных организациях 14,38 лет. Средний возраст мужчин равен 45,34 годам и мужчины являются членами профсоюзов в среднем 20,01 года. Стало быть, мужчины в среднем старше женщин и более длительный период являются членами профсоюзных организаций.
7.gif
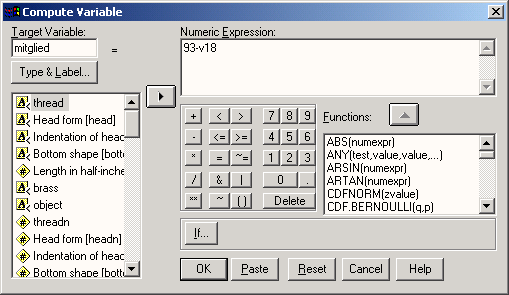
8.gif
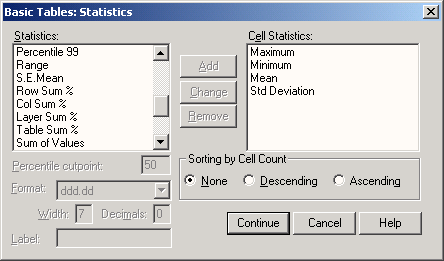
24.2.8 Возможности форматирования
24.2.8 Возможности форматирования
Отдельно для мужчин и женщин проанализируем членство в отдельно взятых профсоюзных организациях и продемонстрируем возможности переключателей Format... (Формат) и Titles... (Заголовки).
-
Для начала в диалоговом окне Basic Tables (Основные таблицы) щёлкните на кнопке Reset (Сброс).
-
Переменную v17 (Членом какой профсоюзной организации Вы являетесь?) поместите в поле строчных переменных, а переменную v2 (Пол) в список столбцовых переменных.
-
Щёлкните на переключателе Statistics... (Статистики) и перенесите опции Count (Количество) и Col % (Столбцовый %) в список Cell Statistics (Статистики в ячейках). Подтвердите свой выбор нажатием Continue Шалее).
-
Щёлкните на переключателе Format... (Формат). Откроется диалоговое окно Basic Tables: Format (Основные таблицы: Формат), как на рисунке 24.9.
Рис. 24.9: Диалоговое окно Basic Tables: Format (Основные таблицы: Формат)
Те, кто работал с более ранними версиями программы, заметят, что диалоговое окно сильно уменьшилось в размерах. В нём остались только опции отображения пустых ячеек и отсутствующих данных. В прежних версиях можно было повлиять на вид рамок, ширину столбцов и поля.
-
Оставьте предварительные установки, и покиньте диалоговое окно нажатием Continue (Далее).
-
Щёлкните на выключателе Titles... (Заголовки). Откроется диалоговое окно Basic Tables: Titles (Основные таблицы: Заголовки).
Рис. 24.10: Диалоговое окно Basic Tables: Titles (Основные таблицы: Заголовки)
Здесь в полях Title (Заголовок), Caption (Примечание) и Corner (Угол) Вы можете набрать любой текст. Заголовок будет центрирован по таблице, а примечание с выравниванием по левому краю будет приведено под таблицей. Текст, указанный в поле Corner (Угол), появится в верхнем левом углу таблицы; однако авторы этого нововведения вряд ли смогут похвастаться его успешностью.
-
В поле Title (Заголовок) наберите текст: "Членство в профсоюзе и пол", а в поле Caption (Примечание) Округ Марбург-Биденкопф.
-
Подтвердите установки нажатием Continue (Далее) и затем ОК. В окне просмотра будет показана следующая таблица:
| Geschlecht (Пол) | ||||
maennlich (мужской) | weiblich (женский) | ||||
Count (Коли-чество) | Col % (Стол-бцовый %) | Count (Коли-чество) | Col % (Стол-бцовый %) | ||
Gewe-rkschaf tsmitglied in (Член проф-союза): | fehlende Angabe (Данные отсутствуют) | 3 | 3,9 | 3 | 1,5 |
Профсоюз строителей (BSE) | 3 | 3,9 | 29 | 14,9 | |
Профсоюз Deutsche Post (Немецкая почта) | 6 | 7,8 | 7 | 3,6 | |
Профсоюз полицейской службы (GdP) | 2 | 2,6 | 4 | 2,1 | |
Профсоюз сферы образования (GEW) | 7 | 9,1 | 13 | 6,7 | |
Профсоюз железно-дорожников Германии (GdED) | 2 | 2,6 | 9 | 4,6 | |
Торговля Банки Страхование (HBV) | 14 | 18,2 | 5 | 2,6 | |
Профсоюз химической промышленности (IG Chemie Papier Keramik) | 9 | 11,7 | 13 | 6,7 | |
Профсоюз дерево-обрабатывающей промышленности (IG Holz) | 4 | 5,2 | 1 | ,5 | |
Профсоюз работников средств массовой информации (IG Medien) | 10 | 13,0 | 7 | 3,6 | |
Профсоюз металлургической промышленности (IG Metall) | 1 | 1,3 | 63 | 32,5 | |
Профсоюз пищевой промышленности (NGG) | 16 | 20,8 | 36 |
| |
Профсоюз сферы услуг (? TV) |
|
| 1 | 18,6 | |
Профсоюз лёгкой промышленности |
|
| 3 | ,5 | |
Профсоюз Сад Земля Лес (GGLF) |
|
|
| 1,5 | |
Kreis Marburg-Biedenkopf (Округ Марбург-Биденкопф)
Меньше стало и диалоговое окно заголовков; в ранних версиях можно было указывать также и желаемое выравнивание текста (по левому краю, по центру, по правому краю).
Судя по результатам опроса можно сказать, что почти треть опрошенных мужчин являются членами профсоюза металлургической промышленности (IG Metall). Большая часть опрошенных женщин входят в профсоюз сферы услуг (OTV) (20,8 %).
9.gif
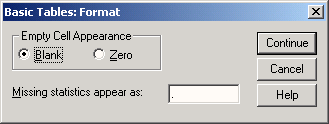
10.gif
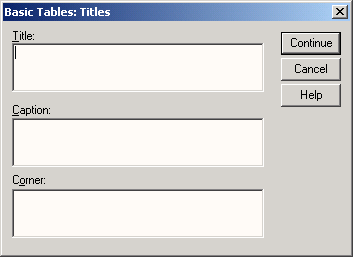
24.3 Общие таблицы
24.3 Общие таблицы
Вспомогательное меню General Tables... (Общие таблицы) предоставляет разнообразные возможности для компоновки таблиц. Если, например, в одной таблице необходимо отобразить различные статистики для нескольких переменных, то для этого имеется специальная опция. Изучим сначала построение общей таблицы на простом примере.
-
Выберите в меню Analyze (Анализ) Custom Tables (Пользовательские таблицы) General Tables... (Общие таблицы)
Откроется диалоговое окно General Tables (Общие таблицы), изображённое на рисунке 24.11.
Рис. 24.11: Диалоговое окно General Tables (Общие таблицы)
-
Перенесите переменную v2 в список строчных переменных и подтвердите свой выбор нажатием ОК.
Geschlechl (Пол) | weiblich (женский) | 77 |
maennlich (мужской) | 194 |
Здесь, так же как и в случае с простыми таблицами, добавлением переменной столбцов можно получить двумерную таблицу, а добавлением третьей переменной для слоев можно организовать трёхмерную таблицу.
Отличие этого вида таблиц от простых таблиц заключается в том, что здесь Вы можете задать различные ступени вложения. В то время как в простых таблицах для переменных таблицы Вы выбирали опцию stacked (с наложением) или nested (с вложением), в общих таблицах Вы можете выбрать необходимый режим отдельно для каждой переменной.
11.gif
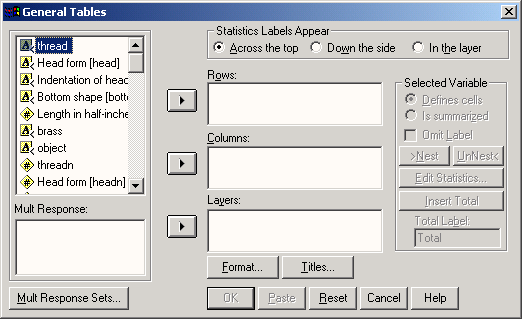
24.3.1 Пакетированные и вложенные переменные
24.3.1 Пакетированные и вложенные переменные
Мы хотим проверить, зависит ли в отношение к актуальности 1-го Мая, как дня трудящихся, от участия в профсоюзных первомайских мероприятиях и от мнения, что 1-е Мая является праздником только для высокопоставленных функционеров. Проверка будет происходить с разделением по половому признаку. Поступите следующим образом:
-
Перенесите переменные v2 и v5 в поле строчных переменных.
-
Выделите переменную v5 и щёлкните на выключателе >Nest (Вложить).
-
Перенесите переменные v8 и v!4 в поле столбцовых переменных. Диалоговое окно должно теперь выглядеть так, как на рисунке 24.12.
Рис. 24.12: Диалоговое окно General Tables (Общие таблицы)
Переменные v2 и v5 теперь будут вложены по строкам, а переменные v8 и v!4 будут пакетированы по столбцам.
-
Подтвердите сделанные установки нажатием ОК. Вы получите следующую таблицу:
Teilnahme an gewerkschaftlichen Mai-Veranstaltung (Участие в первомайских мероприятиях, организованных профсоюзами) | 1 . Mai = Fest fuer hauptamt. Funktionaere? (1-е Мая = праздник для высокопоставленных чиновников?) | ||||||||||
fehle-nde Angabe (Дан-ные отсут-ству-ют) | Ja (Да) | Nein (Нет) | Weiss nicht (Не знаю) | fehle-nde Angabe (Дан-ные отсу-тству-ют) | Ja (Да) | Nein (Нет) | Weiss nicht (Не знаю) | ||||
Geschl echt (Пол) | we-iblich (жен-ский) | Istder LMaials TdA noch zeitg-emaess? (Сох-раняет ли еще акту-альность 1-е Мая, как день трудя-щихся?) | fehlende Angabe (Данные отсут-ствуют) |
| 10 | 5 |
| 14 |
| 1 |
|
Jaffla) |
| 20 | 18 |
| 1 | 7 | 26 | 4 | |||
Nein (Нет) | 1 | 6 | 11 |
|
| 9 | 7 | 2 | |||
Weiss nicht (Не знаю) |
|
| 6 |
|
| 1 | 3 | 2 | |||
maen-nlich (муж-ской) | Istder LMaials TdA noch zeit-gemaess? (Сох-раняет ли еще акту-альность 1-е Мая, как день трудя-щихся?) | fehlende Angabe (Данные отсут-ствуют) |
| 17 | 7 |
| 24 |
|
|
| |
Ja (Да) | 2 | 42 | 71 | 1 | 1 | 20 | 87 | 8 | |||
Nein (Нет) |
| 14 | 27 |
|
| 19 | 19 | 3 | |||
Weiss nicht (Не знаю) |
| 1 | 11 | 1 |
| 3 | 4 | 6 | |||
Если Вы хотите отменить вложение переменной v5, выделите эту переменную и щёлкните на переключателе UnNest> (Без вложения).
12.gif
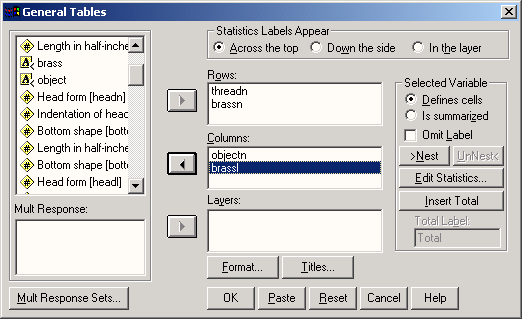
24.3.2 Статистики в ячейках
24.3.2 Статистики в ячейках
В отличие от простых таблиц, в общих таблицах вывод статистик в ячейках можно организовывать отдельно для каждой переменной.
Для демонстрации этой возможности приведём следующий пример:
-
Перенесите переменные v2 и v22 в поле строчных переменных.
-
Выделите переменную v2 и щёлкните на выключателе Edit Statistics... (Редактировать статистики).
Откроется диалоговое окно General Tables: Cell Statistics (Общие таблицы: Статистики в ячейках).
Рис. 24.13: Диалоговое окно General Tables: Cell Statistics (Общие таблицы: Статистики в ячейках)
-
Подтвердите предустановку (вывод статистики Count (Количество)) нажатием Continue (Далее).
-
Теперь выделите переменную v22 и ешё раз щёлкните на переключателе Edit Statistics... (Редактировать статистики). В диалоговом окне General Tables: Cell Statistics (Общие таблицы: Статистики в ячейках) выделите только Col % (Столбцовый %) и активируйте сортировку по убыванию.
-
Подтвердите установки нажатием Continue (Далее) и в главном диалоговом окне щёлкните на ОК. Вы получите следующую таблицу:
Geschlecht (Пол) | weiblich (женский) | Count (Количество) | 77 |
maennlich (мужской) | Count (Количество) | 194 | |
Parteipraeferenz (Предпочитаемая партия) | SPD | Col % (Столбцовый %) | 33,6% |
keine (Ни одна из партий) | Col % (Столбцовый %) | 28,4% | |
fehlende Angabe (Данные отсутствуют) | Col % (Столбцовый %) | 17,0% | |
Buendbis 90/Die Gruenen (Союз 90/Зелёные) | Col % (Столбцовый %) | 8,1% | |
CDU/CSU | Col % (Столбцовый %) | 6,6% | |
Republikaner (Республиканцы) | Col % (Столбцовый %) | 3,3% | |
andere (Другая) | Col % (Столбцовый %) | 1,5% | |
FDP | Col % (Столбцовый %) | ,7% | |
PDS/Linke Liste (Левые) | Col % (Столбцовый %) | ,7% |
Как уже упоминалось, возможность организовывать вывод статистик в отдельности для каждой из переменных, как это было сделано в вышеприведенной таблице, в простых таблицах отсутствует.
13.gif
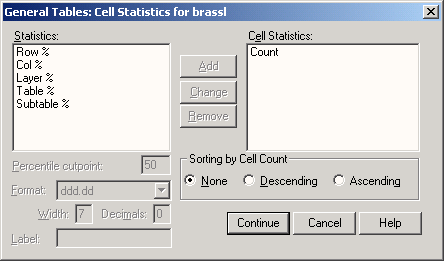
24.3.3 Суммарные показатели
24.3.3 Суммарные показатели
В общих таблицах, также как и в простых таблицах, Вы можете организовывать вывод суммарных статистик для переменных. Для этого необходимо выделить интересующую переменную и активировать опцию Is summarized (Подвести итог).
Организуем вывод итоговых статистик для переменных alter (возраст) и mitglied (членство) (см. гл. 24.2.7). Для этого поступите следующим образом:
-
Перенесите переменные alter (возраст) и mitglied (членство) в поле строчных переменных.
-
Выделите переменную mitglied (членство) и активируйте опцию Is summarized (Подвести итог). Повторите эти же действия и для переменной age (возраст).
-
Подтвердите установки нажатием ОК. Вы получите следующую таблицу:
mitqlied (членство) | 18,42 |
alter (возраст) | 44,17 |
Используя переключатель Edit Statistics... (Редактировать статистики), Вы можете добавить и другие статистики, такие как Minimum (Минимум), Maximum (Максимум) и Variance (Дисперсия).
24.4 Обработка множественных ответов
24.4 Обработка множественных ответов
В анкете относительно организации празднования 1-го Мая имеются вопросы с множественными ответами. К примеру возможно несколько вариантов ответов на вопрос: "Как Вы проводите выходные дни?" Здесь опрашиваемый может отметить более одного ответа, например, "Просмотр телепередач" и "Хобби". Для обработки множественных ответов в модуле Tables так же, как и в базовом модуле (см. гл. 12), существует два метода: метод множественных дихотомий и метод множественных категорий.
24.4.1 Дихотомический метод
24.4.1 Дихотомический метод
Для изучения этого метода возьмём вопрос: "Как Вы проводите выходные дни?" Переменные via no vlq представляют ответы на вопрос v1 (via соответствует ответу Просмотр телепередач, vlb Общение с друзьями и т.д.). Переменные при этом являются дихотомическими, то есть они могут иметь только два возможных значения: 1 соответствует ответу "Да", а 0 ответу "Нет/нет данных". Чтобы переменную vl обработать в табличной форме, необходимо сначала определить набор множественных ответов.
-
Для этого выберите в меню опцию Analyze (Анализ) Custom Tables (Пользовательские таблицы) Multiple Response Tables... (Таблицы множественных ответов)
Откроется диалоговое окно Multiple Response Tables (Таблицы множественных ответов) (см. рис. 24.14).
-
Щёлкните на выключателе Define Sets... (Определить наборы) для организации соответствующего набора ответов.
Откроется диалоговое окно Multiple Response Tables: Define Multiple Response Sets (Таблицы множественных ответов: Определение набора множественных ответов), как изображено на рисунке 24.15. Дихотомический метод установлен по умолчанию.
-
Перенесите переменные vla-vlq в список Variables in Set (Переменные набора).
Рис. 24.14: Диалоговое окно Multiple Response Tables (Таблицы множественных ответов)
-
В качестве счётной величины укажите 1 (Ответы — да).
-
Образовываемому набору переменных присвойте имя frei (свободный) и метку Freizeit (свободное время). Диалоговое окно должно теперь выглядеть так, как на рисунке 24.16.
-
Щёлкните на переключателе Add (Добавить), чтобы добавить переменную набора в поле наборов множественных ответов.
-
Подтвердите нажатием Save (Сохранить). Вы опять попадёте в главное диалоговое окно Multiple Response Tables (Таблицы множественных ответов).
В списке Multiple Response Sets (Наборы множественных ответов) теперь находится переменная Sfrei. SPSS автоматически помечает переменные наборов знаком $. Отобразим распределение частот переменной Sfrei в табличной форме.
Рис. 24. 15: Диалоговое окно Multiple Response Tables: Define Multiple Response Sets (Таблицы множественных ответов: Определение наборов множественных ответов)
Рис. 24.16: Заполненное диалоговое окно Multiple Response Tables: Define Multiple Response Sets (Таблицы множественных ответов: Определение наборов множественных ответов)
-
Для этого перенесите переменную Sfrei в поле строчных переменных и подтвердите нажатием ОК. Вы получите результаты опроса в следующем виде:
Free time (Свободное время) | Fernsehen (Просмотр телепередач) | 9 |
Geselligkeit (Общение с друзьями) | 52 | |
Stammtisch (Приглашаю к себе гостей) | 2 | |
Hobbies (Хобби) | 26 | |
Verein (Общество по увлечениям) | 18 | |
Familienleben (Семейные заботы) | 4 | |
Radio hoeren/Lesen (Слушаю радио/читаю) | 3 | |
Kino/Konzerte/Theater (Кино/концерты/театр) | 14 | |
das uebtiche/dies und das (To же, что и всегда/то одно то другое) | 163 | |
Ausflueg/Wanderung machen (Выбираюсь на природу/путешествую) | ||
wichtige Arbeiten verrichten (Необходимые дела (дом, квартира, сад) | 52 | |
Nachbarschaftshilfe (Помощь соседям) | 2 | |
Sport (Спорт) | 35 | |
Anderes 1 . Antwort (Другое 1 -и ответ) | 14 | |
Anderes 2. Antwort (Другое 2-й ответ) | 2 |
14.gif

15.gif
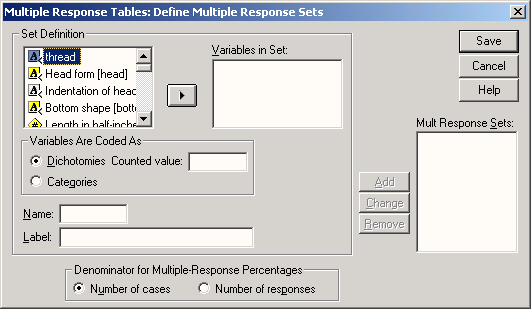
16.gif
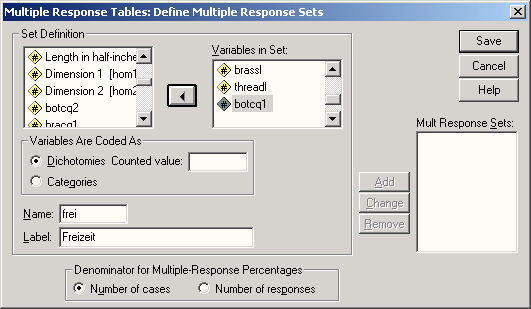
24.4.2 Категориальный метод
24.4.2 Категориальный метод
В категориальном методе при кодировке сначала определяется максимальное количество ответов. Затем образовывается такое же количество переменных.
С целью изучения особенностей этого метода, мы рассмотрим следующий пример: закодируем вопрос vl: "Как Вы проводите выходные дни?" не дихотомически, а категориально. В этом случае мы сначала подсчитываем максимальное количество отмеченных ответов. Мы исходим, например, из того, что каждый из респондентов отметил не более шести предлагаемых вариантов ответа. Тогда мы образовываем шесть переменных. Эти переменные имеют следующие метки значений: 1 — Просмотр телепередач, 2 — Общение с друзьями, 3 — Приглашаю к себе гостей, 4 — Хобби и т.д. В отличие от дихотомического метода мы обойдёмся меньшим количеством переменных, хотя они и не дихотомические, а имеют более двух категорий. Категориальный метод кодировки применяется прежде всего тогда, когда заранее задано максимальное число возможных ответов, как это было сделано при формулировке вопросов v4, vll, v!2 v!5 и vl6. При кодировке анкеты эти переменные были закодированы категориально. И в категориальном методе необходимо сначала определить набор множественных ответов. Для объяснения категориального метода на примере возьмём переменную v11: "Что Вам понравилось?"
-
В диалоговом окне Multiple Response Tables (Таблицы множественных ответов) щёлкните на переключателе Define Sets... (Определить наборы).
-
Перенесите переменные v11a и v11b в список Variables in Set (Переменные в наборе) и активизируйте вид кодировки Categories (Категории).
-
Присвойте переменной набора имя zusagen (согласие) и метку Gefallen (Одобрение).
-
Затем щёлкните на переключателе Add (Добавить) и подтвердите нажатием Save (Сохранить).
-
В главном диалоговом окне перенесите переменную Szusagen в поле строчных переменных.
Вы получите следующую таблицу:
Gefallen (Одобрение) | es wurde eine ansprecende Rede qehalten (была произнесена интересная речь) | 20 |
ich konnte viele Kolleqinnen und Kolleqen treffen (я встретил много коллег) | 26 | |
lebendiqe Proqrammqestaltunq (интересная программа) | 19 | |
weiss nicht mehr (уже не помню) | 14 | |
anderes (другое) | 3 | |
Geselligkeit, Gemeinschaftsqefuehl (общение, чувство сплочённости) | 7 | |
Solidaritaetskundgebunq (манифестация солидарности) | 4 | |
Darstellung von und Engagement fuer Arbeiterrechte (изложение прав трудящихся и помощь по защите этих прав) | 5 | |
Diskussionen, Gespraeche, Meinungsaustausch (дискуссии, беседы, обмен мнениями) | 6 | |
Kultur, Musik (культурные мероприятия, музыка) | 2 | |
Feiem, Essen, Trinken (праздничное застолье) | 3 | |
nichts besonderes (ничего особенного) | 6 | |
Familie dabei (прогулка с семьёй) | 2 | |
lokaler Bezugsrahmen/aktuelle Themen (обсуждение местных проблем/актуальные темы) | 3 | |
Работа с переменными наборов
Переменные наборов могут обрабатываться как обычные переменные. Выведем, к примеру, отдельно для каждого пола данные по переменной, которая характеризует варианты проведения свободного времени (переменная набора $frei).
-
Переменной $frei присвойте статус строчной переменной, а переменной v2 — статус столбцовой переменной. Вы получите следующую двумерную таблицу:
Geschlecht (Пол) | |||
weiblich (женский) | maennlich (мужской) | ||
Free time (Свободное время) | Femsehen (Просмотр телепередач) | 1 | 8 |
Geselliqkeit (Общение с друзьями) | 21 | 31 | |
Stammtisch (Приглашаю к себе гостей) | 2 | ||
Hobbies (Хобби) | 4 | 22 | |
Verein (Общество по увлечениям) | 4 | 14 | |
Familienleben (Семейные заботы) | 2 | 2 | |
Radio hoeren/Lesen (Слушаю радио/читаю) | 3 | ||
Kino/Konzerte/Th eater (Кино/концерты/театр) | 6 | 8 | |
das uebliche/dies und das (To же, что и всегда/то одно то другое) | 51 | 112 | |
Ausflueg/Wanderung machen (Выбираюсь на природу/путешествую) | 16 | 36 | |
wichtige Arbeiten verrichten (Необходимые дела (дом, квартира, сад) | 2 | ||
Nachbarschaftshilfe (Помощь соседям) | |||
Sport (Спорт) | 10 | 25 | |
Anderes 1 . Antwort (Другое 1 . ответ) | 3 | 11 | |
Процентные показатели для переменных наборов
На один вопрос с множественными ответами каждый опрашиваемый может дать несколько ответов. Как правило, общее количество ответов больше, нежели количество наблюдений (количество опрашиваемых). Вы можете выбрать, какой из этих показателей — количество наблюдений или количество ответов — будет далее использоваться в качестве основы расчётов. Поясним это на примере переменной $frei (Как Вы проводите выходные дни?).
-
В диалоговом окне Multiple Response Tables (Таблицы множественных ответов) переменную набора Sfrei поместите в список строчных переменных.
-
Щёлкните на переключателе Statistics... (Статистики). Откроется диалоговое окно Multiple Response Tables: Statistics (Таблицы множественных ответов: Статистики).
-
Активируйте дополнительно опции Column Percentages (Проценты по столбцам) и Totals (Суммы).
-
Подтвердите нажатием Continue (Далее) и затем на ОК. Вы получите следующую частотную таблицу:
Количество наблюдений, пригодных для проведения расчетов, и, следовательно, базис процентного соотношения равняется 256. Сумма процентных показателей превосходит значение 100 %, так что цифра 100,0 в строке Col % (Столбцовый %) кажется абсолютно бессмысленной.
Free time (Свободное время) | Femsehen (Просмотр телепередач) | Count (Количество) | 9 |
Col % (Столбцовый %) | 3,5 | ||
Geselligkeit (Общение с друзьями) | Count (Количество) | 52 | |
Col % (Столбцовый %) | 20,3 | ||
Stammtisch (Приглашаю к себе гостей) | Count (Количество) | 2 | |
Col % (Столбцовый %) | ,8 | ||
Hobbies (Хобби) | Count (Количество) | 26 | |
Col % (Столбцовый %) | 10,2 | ||
Verein (Общество по увлечениям) | Count (Количество) | 18 | |
Col % (Столбцовый %) | 7,0 | ||
Familienleben (Семейные заботы) | Count (Количество) | 105 | |
Col % (Столбцовый %) | 41,0 | ||
Radio hoeren/Lesen (Слушаю радио/читаю) | Count (Количество) | 4 | |
Col % (Столбцовый %) | 1,6 | ||
Kino/Konzerte/Th eater (Кино/концерты/театр) | Count (Количество) | 3 | |
Col % (Столбцовый %) | 1,2 | ||
das uebliche/dies und das (To же, что и всегда/то одно то другое) | Count (Количество) | 14 | |
Col % (Столбцовый %) | 5,5 | ||
Ausflueg/Wanderung machen (Выбираюсь на природу/путешествую) | Count (Количество) | 163 | |
Col % (Столбцовый %) | 63,7 | ||
wichtige Arbeiten verrichten (Необходимые дела (дом, квартира, сад) | Count (Количество) | 52 | |
Col % (Столбцовый %) | 20,3 | ||
Nachbarschaftshilfe (Помощь соседям) | Count (Количество) | 2 | |
Col % (Столбцовый %) | ,8 | ||
Sport (Спорт) | Count (Количество) | 35 | |
Col % (Столбцовый %) | 13,7 | ||
Anderes 1. Antwort (Другое 1-й ответ) | Count (Количество) | 14 | |
Col % (Столбцовый %) | 5,5 | ||
Anderes 2. Antwort (Другое 2-й ответ) | Count (Количество) | 2 | |
Col % (Столбцовый %) | ,8 | ||
Total (Сумма) | Count (Количество) | 256 | |
Col % (Столбцовый %) | 100,0 | ||
Рис. 24.17: Диалоговое окно Multiple Response Tables: Statistics (Таблицы множественных ответов: Статистики)
Если Вы хотите сравнивать показатели не относительно количества наблюдений, а относительно количества ответов, то поступите следующим образом.
-
В диалоговом окне Multiple Response Tables (Таблицы множественных ответов) воспользуйтесь переключателем Define Sets... (Определить наборы).
-
В диалоговом окне Multiple Response Tables: Define Multiple Response Sets (Таблицы множественных ответов: Организация наборов множественных ответов) в группе Denominator for Multiple-Response Percentages (Знаменатель для процентных показателей множественных ответов) вместо опции Number of Cases (Количество наблюдений), устанавливаемой по умолчанию, активируйте опцию Number of responses (Количество ответов).
-
Щёлкните на переключателе Save (Сохранить) и затем на ОК. Теперь частотная таблица будет отображена с изменёнными процентными показателями.
Free time (Свободное время) | Fernsehen (Просмотр телепередач) | Count (Количество) | 9 |
Col % (Столбцовый %) | 1,8 | ||
Geselligkeit (Общение с друзьями) | Count (Количество) | 52 | |
Col % (Столбцовый %) | 10,4 | ||
Stammtisch (Приглашаю к себе гостей) | Count (Количество) | 2 | |
Col % (Столбцовый %) | ,4 | ||
Hobbies (Хобби) | Count (Количество) | 26 | |
Col % (Столбцовый %) | 5,2 | ||
Verein (Общество по увлечениям) | Count (Количество) | 18 | |
Col % (Столбцовый %) | 3,6 | ||
Familienleben (Семейные заботы) | Count (Количество) | 105 | |
Col % (Столбцовый %) | 21,0 | ||
Radio hoeren/Lesen (Слушаю радио/читаю) | Count (Количество) | 4 | |
Col % (Столбцовый %) | ,8 | ||
Kino/Konzerte/Theater (Кино/концерты/театр) | Count (Количество) | 3 | |
Col % (Столбцовый %) | ,6 | ||
das uebliche/dies und das (To же, что и всегда/то одно то другое) | Count (Количество) | 14 | |
Col % (Столбцовый %) | 2,8 | ||
Ausflueg/Wanderung machen (Выбираюсь на природу/путешествую) | Count (Количество) | 163 | |
Col % (Столбцовый %) | 32,5 | ||
wichtige Arbeiten verrichten (Необходимые дела (дом, квартира, сад) | Count (Количество) | 52 | |
Col % (Столбцовый %) | 10,4 | ||
Nachbarschaftshilfe (Помощь соседям) | Count (Количество) | 2 | |
Col % (Столбцовый %) | ,4 | ||
Sport (Спорт) | Count (Количество) | 35 | |
Col % (Столбцовый %) | 7,0 | ||
Anderes 1. Antwort (Другое 1-й ответ) | Count (Количество) | 14 | |
Col % (Столбцовый %) | 2,8 | ||
Anderes 2. Antwort (Другое 2-й ответ) | Count (Количество) | 2 | |
Col % (Столбцовый %) | ,4 | ||
Total (Сумма) | Count (Количество) | 256 | |
Col % (Столбцовый %) | 51,1 | ||
В графе Total (Сумма) и здесь указывается количество действительных наблюдений; на этом месте хотелось бы видеть текущий опорный показатель вычисления процентных долей, то есть суммарное количество ответов. Если их сложить, то мы получим цифру 501. Сумма процентных показателей на этот раз равна 100 %.
Результирующий процентный показатель в строке Col % (Столбцовый %) равный 51,1, отражает в процентах долю суммарного количества наблюдений (256) в суммарном количестве ответов (501).
17.gif
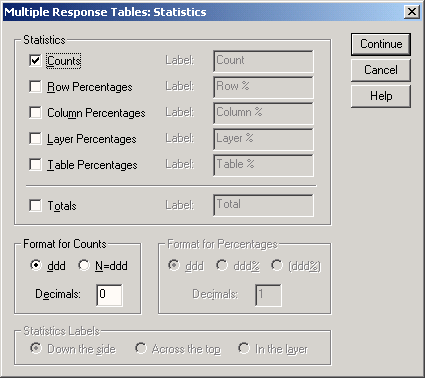
24.5 Таблицы частотных показателей
24.5 Таблицы частотных показателей
Таблицы частотных показателей имеет смысл применять в том случае, когда для большого количества вопросов одного исследования допускается использование одинаковых вариантов ответов. В опросе относительно организации празднования 1-го Мая таким свойством обладают переменные v5, v6, v8, v!3 и v!4. На вопросы, обуславливающие значения данных переменных, можно ответить да, нет и не знаю.
24.5.1 Примеры таблиц частотных показателей
24.5.1 Примеры таблиц частотных показателей
Рассмотрим для начала простейший случай частотной таблицы. Для этого Отразим частоты категорий переменной v5 (1st der l.Mai als TdA noch zeitgemaess? (Сохраняет ли ещё актуальность 1-е Мая, как день трудящихся?)).
-
Выберите в меню опции Analyze (Анализ) Custom Tables (Пользовательские таблицы) Tables of Frequencies... (Таблицы частот)
Откроется диалоговое окно Tables of Frequencies (Таблицы частот), изображённое на рисунке 24.18.
Рис. 24. 18: Диалоговое окно Tables of Frequencies (Таблицы частот)
-
Перенесите переменную v5 в список Frequencies for (Частоты для) и подтвердите свой выбор нажатием на ОК. Вы получите следующую таблицу:
1st der 1 .Mai als TdA noch zeitgemaess? (Сохраняет ли ещё актуальность 1-е Мая, как день трудящихся?) | |
Count (Количество) | |
fehlende Anqabe (Данные отсутствуют) | 39 |
Ja (Да) | 154 |
Nein (Нет) | 59 |
Weiss nicht (He знаю) | 19 |
Содержание данной частотной таблицы соответствует содержанию таблицы, которую Вы могли бы получить выбором меню Analyze (Анализ) Custom Tables (Пользовательские таблицы) Basic Tables... (Основные таблицы) с присвоением переменной v5 статуса строчной переменной.
Уникальные возможности вспомогательного меню Tables of Frequencies... (Таблицы частот) заключаются в одновременном представлении нескольких переменных с одинаковыми возможностями ответов. Отобразим одновременно показатели переменных v5, v6 и v8.
-
Выберите в меню Analyze (Анализ) Custom Tables (Пользовательские таблицы) Tables of Frequencies... (Таблицы частот)
-
Перенесите переменные v5, v6 и v8 в список Frequencies for (Частоты для) и подтвердите свой выбор нажатием на ОК. В окне просмотра результатов появится следующая таблица:
Istder t.MaialsTdA noch zeitgemaess? (Сохраняет ли ещё актуальность 1-е Мая, как день трудящихся?) | Erinnerung an 1 . Mai Feier im Ort (Воспоминания о праздновании 1-го Мая по месту жительства) | |
Count (Количество) | Count (Количество) | |
fehlende Angabe (Данные тсутствуют) | - 39 | 48 |
Ja (Да) | 154 | 67 |
Nein (Нет) | 59 | 143 |
Weiss nicht (He знаю) | 19 | 13 |
Если слова, входящие в заголовки столбцов, не помещаются в одной строке при заданной ширине столбцов, то они распределяются в нескольких строках.
18.gif

24.5.2 Процентные показатели суммарных значений
24.5.2 Процентные показатели суммарных значений
Процентные показатели суммарных значений могут выводиться и в частотных таблицах. Рассмотрим следующий пример: нам необходимо получить абсолютные значения, процентные показатели и суммарные значения переменных v8, v13 и v14.
-
Для этого выберите в меню Analyze (Анализ) Custom Tables (Пользовательские таблицы) Tables of Frequencies... (Таблицы частот)
-
Перенесите переменные v8, v!3 и v!4 в список Frequencies for (Частоты для).
-
Затем щёлкните на выключателе Statistics... (Статистики).
Откроется диалоговое окно Tables of Frequencies: Statistics (Таблицы частот: Статистики), изображённое на рисунке 24.19. В этом диалоговом окне по умолчанию установлена опция Count Display (Показывать количество).
-
Активируйте дополнительно выключатели Display (Показать) в группах Percent! (Проценты) и Totals (Суммы). Таблица результатов опроса будет выглядеть следующим образом:
Рис. 24.19: Диалоговое окно Tables of Frequencies: Statistics (Таблицы частот: Статистики)
| Teilnahme an gewerkschaftlichen Mai-Veranstaltung (Участие в первомайских мероприятиях, организованных профсоюзами) | Gestalt. 1 . Mai durch Gew. pol. wichtig? (Важно ли политически, чтобы мероприятия 1 -то Мая организовывали именно профсоюзы?) | 1 . Mai = Fest fuer hauptamt. Funktionaere? (1-е Мая = праздник для высокопоставленных чиновников?) | |||
Count (Коли-чество) | % | Count (Коли-чество) | % | Count (Коли-чество) | % | |
fehlende Angabe (Данные отсутствуют) | 3 | 1,1% | 2 | ,7% | 40 | 14,8% |
Ja (Да) | 110 | 40,6% | 221 | 81,5% | 59 | 21,8% |
Nein (Нет) | 156 | 57,6% | 29 | 10,7% | 147 | 54,2% |
keine Angaben/weiss nicht (Данные отсутствуют/не знаю) | 2 | ,7% | 19 | 7,0% | 25 | 9,2% |
Total (Сумма) | 271 | 100,0% | 271 | 100,0% | 271 | 100,0% |
В диалоговом окне Tables of Frequencies: Statistics (Таблицы частот: Статистики) Вы можете активировать и другие форматы отображения количества и процентов.
19.gif

24.5.3 Работа с подгруппами
24.5.3 Работа с подгруппами
Применение подгрупп возможно и в частотных таблицах. Для изучения этой возможности рассмотрим следующий пример: для каждого пола нам необходимо вывести данные по переменным v8 (Teilnahme an gewerkschaftlichen Mai-Veranstaltung (Участие в первомайских мероприятиях, организованных профсоюзами)) и v6 (Erinnerung an 1. Mai Feier im Ort (Воспоминания о праздновании 1-го Мая по месту жительства)).
-
Перенесите переменные v8 и v6 в список Frequencies for (Частоты для), а переменную v2 в список In Each Table (В каждой таблице). Диалоговое окно должно теперь выглядеть так, как показано на рисунке 24.20.
Рис. 24.20: Диалоговое окно Tables of Frequencies (Таблицы частот)
-
Подтвердите свой выбор нажатием на ОК. В окне просмотра будет показана следующая таблица:
| Geschlecht (Пол) | |||
weiblich (женский) | maennlich (м\ | ркской) | ||
Teilnahme an gewer-kscha-ftlichen Mai-Verans-taltung (Участие в первомайских мероприятиях, органи-зованных профсоюзами) | Erinnerung an 1 . Mai Feier im Ort (Воспо-минания о праздно-вании 1-го Мая по месту жительства | Teilnahme an gewerks-chaftlichen Mai-Veranstaltung (Участие в первомайских мероприятиях, органи-зованных профсоюзами) | Erinnerung an 1 . Mai Feier im Ort (Воспо-минания о праздно-вании 1-го Мая по месту жительства | |
Count (Коли-чество) | Count (Коли-чество) | Count (Коли-чество) | Count (Коли-чество) | |
fehlende Angabe (Данные отсу-тствуют) | 1 | 18 | 2 | 30 |
Ja(fla) | 36 | 19 | 74 | 48 |
Nein (Нет) | 40 | 33 | 116 | 110 |
keine Angaben/weiss nicht (Данные отсу-тствуют /не знаю) |
| 7 | 2 | 6 |
В диалоговом окне Tables of Frequencies (Таблицы частот) Вы можете сгруппировать подгруппы в одну таблицу (см. вышеприведенный пример) или разместить их в разных таблицах. Если вы хотите произвести группировку в разных таблицах, то группирующую переменную необходимо поместить в список Separate Tables (Отдельные таблицы). В первом и во втором вариантах группировки может быть организован вывод процентных показателей и суммарных значений.
Выведем отдельно для каждого пола значения переменных v13 и v14, но в этом случае, в отличие от первого примера, данные будут находиться в разных таблицах. В таблице также должны быть рассчитаны процентные показатели и суммарные значения. Для выполнения этого задания поступите следующим образом:
-
Перенесите переменные v13 и v14 в список Frequencies for (Частоты для), а переменную v2 — в список Separate Tables (Отдельные таблицы).
-
Затем сделайте щелчок на переключателе Statistics... (Статистики) и активируйте Percents Display (Показать проценты).
-
Подтвердите свой выбор нажатием Continue (Далее) и затем на ОК. В окне просмотра будут показаны следующие таблицы, причём вторая таблица появится только после двойного щелчка на первой таблице и активирования соответствующей позиции в ниспадающем меню.
Geschlecht maenlich (Женщины) | ||||
Gestalt. 1 . Mai durch Gew. pol. wichtig? (Важно ли политически, чтобы мероприятия 1-го Мая организовывали именно профсоюзы?) | 1. Mai = Fest fuer hauptamt. Funktionaere? (1-е Мая = праздник для высокопоставленных чиновников?) | |||
Count (Количество) | % | Count (Количество) | % | |
fehlende Angabe (Данные отсутствуют) | 15 | 5,5% | ||
Ja (Да) | 63 | 23,2% | 17 | 6,3% |
Nein (Нет) | 6 | 2,2% | 37 | 13,7% |
Weiss nicht (He знаю) | 8 | 3,0% | 8 | 3,0% |
Geschlecht maenlich (Мужчины) | ||||
Gestalt. 1 . Mai durch Gew. pol. wichtig? (Важно ли политически, чтобы мероприятия 1-го Мая организовывали именно профсоюзы?) | 1 . Mai = Fest fuer hauptamt. Funktionaere? (1-е Мая = праздник для высокопоставленных чиновников?) | |||
Count (Количество) | % | Count (Количество) | % | |
fehlende Angabe (Данные отсутствуют) | 2 | ,7% | 25 | 9,2% |
Ja (Да) | 158 | 58,3% | 42 | 15,5% |
Nein (Нет) | 23 | 8,5% | 110 | 40,6% |
Weiss nicht (He знаю) | 11 | 4,1% | 17 | 6,3% |
Возможно также и отображение большего количества подгрупп. Организуем вывод показателей переменных v5 и v8 отдельно для каждого пола (v2) и партийной ориентации (v22).
-
Перенесите переменные v5 и v8 в список Frequencies for (Частоты для), а переменные v2 и v22 — в список In Each Table (В каждой таблице).
Теперь Вы можете выбрать необходимый вариант представления: All combinations (nested) (Все комбинации (с вложением)) или Each separately (stacked) (Каждая отдельно (с наложением)). Если вы оставите установку по умолчанию All combinations (nested) (Все комбинации (с вложением)), то будет образована иерархия подгрупп; если вы активируете опцию Each separately (stacked) (Каждая отдельно (с наложением)), то переменные v5 и v8 сначала будут представлены отдельно для каждого пола, а затем отдельно для каждой партийной ориентации.
-
Активируйте опцию Each separately (stacked) (Каждая отдельно (с наложением)) и подтвердите нажатием ОК. Вы получите частотную таблицу с пакетированными подгруппами, которую в книге, к сожалению, полностью отобразить не получилось (см. след, стр.)
В соответствии с размещением в списке Subgroups (Подгруппы), сначала выводится распределение частот переменных v5 и v8 для подгруппы v2, а затем распределение частот переменных v5 и v8 для подгруппы v22.
Модуль Tables предоставляет большое количество различных возможностей для построения презентационных таблиц. После непродолжительных занятий для Вас не должно составить никакого труда, чтобы подобрать и построить необходимую таблицу.
20.gif

Глава 25. Экспортирование выходных данных
Глава 25. Экспортирование выходных данных
1. Экспортирование выходных данных
Экспортирование выходных данных
В этой главе мы бы хотели представить Вам важнейшие возможности экспорта основных таблиц и диаграмм в формате SPSS в другие приложения Windows, такие, как например Word.
Мы рассмотрим следующие темы:
-
Перенос статистических результатов в Word,
-
Перенос диаграмм в Word,
-
Экспортирование сводных таблиц и диаграмм как HTML-Документов.
25.1 Перенос статистических результатов в Word
25.1 Перенос статистических результатов в Word
В дальнейшем мы основываемся на том, что в Вашем распоряжении есть Word 97 или сравнимая с ним версия.
Рассмотрим следующий пример: Вы хотите перенести результаты расчета частотного распределения переменной partei из нашего импровизированного опроса За кого бы Вы проголосовали, если бы в воскресенье были выборы в Бундестаг? в текстовый документ Word. Там результаты должны документироваться и оцениваться. Действуйте следующим образом:
-
Запустите текстовый редактор Word.
-
Запустите SPSS, и загрузите файл wahl.sav в редактор данных.
-
В пунктах меню выберите: Analyze (Анализ,) Descriptive statistics (Описательные статистики) Frequencies... (Частоты)
Открывается диалоговое окно Frequencies... (Частоты).
-
Перенесите переменную partei в список целевых переменных.
-
Нажмите ОК. Результаты для частотного распределения появятся в окне просмотра.
-
Щёлкните правой кнопкой мыши на таблице частоты. Окно просмотра выглядит теперь таким образом, как показано на рисунке 25.1.
-
Выберите в вызванном меню опцию Copy Objects (Копировать объекты). В качестве альтернативного варианта, Вы можете выбрать пункты меню Edit (Редактировать) Copy Objects (Копировать объекты)
Рис. 25.1.Окно просмотра с вызванном меню копирования результатов
Статистические результаты, касающиеся частотного распределения будут скопированы в буфер обмена Windows. Буфер обмена является ячейкой памяти, где хранятся любые сведения, которые по желанию снова могут быть вызваны. Эти данные теряются при выходе из Windows, а также при записи новых сведений в буфер обмена. С помощью буфера обмена вышеназванные объекты могут быть перенесены из одной программы в другую. Таким образом, можно копировать статистические результаты из SPSS и переносить их после этого в документ Word. Попробуем это сделать.
-
С помощью панели задач переместитесь в Word.
Панель задач Windows 98 управляет работающими программами. Панель задач может быть вызвана нажатием кнопок <Alt> и <Таb.>. Каждая программа, которую Вы запускаете, имеет собственный символ на панели задач. Чтобы перейти к уже открытой программе, просто щёлкните на соответствующем символе в панели задач.
-
Выберите в строке меню Word опции Правка Вставить
Команда Вставить вставляет данные из буфера обмена в документ, начиная с текущей позиции курсора. Экран выглядит теперь как на рисунке 25.2.
-
Если Вы хотели бы увеличить или уменьшить таблицу, то щёлкните здесь левой кнопкой мыши. Таблица получает теперь так называемую управляющую рамку, как на рисунке 25.3.
Рис. 25.2. Таблица частотного распределения в документе Word
Рис. 25.3. Таблица частотного распределения с управляющей рамкой
Если Вы, например, щёлкните мышью внизу справа рамки, то Вы сможете увеличивать или уменьшать таблицу по диагонали. Для этого удерживайте нажатой левую кнопку мыши, и перемешайте мышь по полю. Отпустите кнопку мыши, когда достигните желаемого размера.
Вы также можете дальше работать с основными таблицами в Word, чтобы, например, изменять или добавлять заголовки.
-
Для этого щёлкните правой кнопкой мыши на таблице частоты. Раскрывается меню (см рисунок 25.4).
-
Выберите опцию Изменить рисунок
Таблица частоты откроется для редактирования (см рисунок 25.5). В Вашем распоряжении теперь находится дополнительная строка меню на нижней кромке экрана.
-
Испробуйте различные возможности. Например, измените заголовок таблицы Прогноз выборов 98.
-
Произведя желаемые изменения, просто щёлкните на переключатель Закрыть графику.
Задание для тренировки
-
Для тренировки перенесите частотное распределение переменных alter (возраст) и sex (пол) в Word.
Рис. 25.4. Вызванное меню в Word
Рис. 25.5. Таблица частотного распределения, открытая для редактирования в Word
1.gif

2.gif
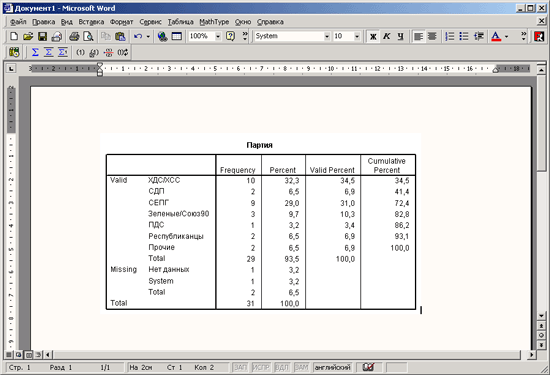
3.gif

4.gif

5.gif
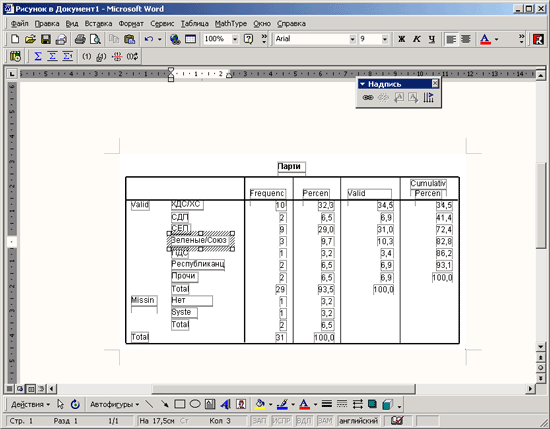
25.2 Перенос диаграмм в Word
25.2 Перенос диаграмм в Word
-
Запустите текстовый редактор Word.
-
Запустите SPSS, и загрузите файл btw98.spo в окно просмотра результатов (см. рисунок 25.6).
Мы хотим экспортировать эту диаграмму в Word.
-
Щёлкните левой кнопкой мыши на диаграмме.
-
Выберите опцию меню: Edit (Редактировать) Copy Objects (Копировать объекты)
Диаграмма будет скопирована в буфер обмена.
-
Нажмите кнопки <Alt> и <Таb>. Удерживать нажатой кнопку <Alt>, пока Вы но переместитесь в текстовый редактор.
-
Выберите из пунктов меню Word: Правка Вставить
Диаграмма будет перенесена в окно текстового документа (см рисунок 25.7). Здесь Вы можете дальше работать над диаграммой (см главу 25.1).
Рис. 25.6. Диаграмма в окне просмотра результатов
Рис. 25.7. Диаграмма в Word
6.gif

7.gif
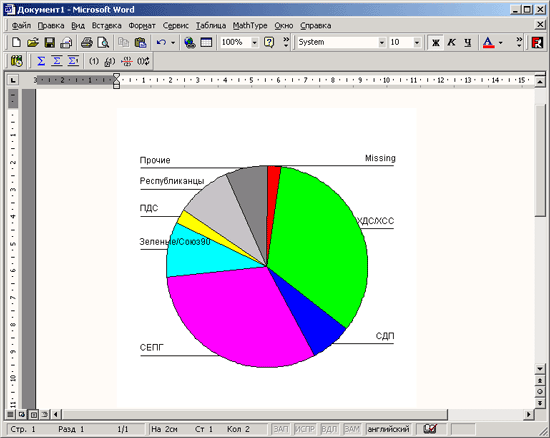
25.3 Экспорт сводных таблиц и диаграмм как HTML-документов
25.3 Экспорт сводных таблиц и диаграмм как HTML-документов
-
Запустите SPSS и загрузите файл studium.sav в редактор данных.
-
Постройте частотное распределение переменной semester.
Просмотрите полученные результаты в окне просмотра. Мы хотим экспортировать таблицы в HTML-формат, разместить их на Web-странице. Для этого нужно сделать следующее.
-
Щёлкните правой кнопкой мыши на частотной таблице "Количество семестров" (Anzahl der Semester).
Окно просмотра выглядит теперь, как изображено на рисунке 25.8.
-
Выберите опцию Export... (Экспортировать)
-
Открывается диалоговое окно Export Output (Экспортировать выходные данные) (см рисунок 25.9).
-
В поле File Name (Имя файла) введите, например, C:\SPSSBUCH\test.htm и подтвердите его выбор нажатием ОК.
-
Запустите программу-браузер, например, Microsoft Internet Explorer.
-
Введите в строке Path (Путь): file:///C:/SPSSBUCH/test.htm. Обратите внимание на то, что после слова file (файл) должны стоять три черты, наклоненных вправо.
Рис. 25.8. Таблица в окне просмотра с раскрытым общим меню
Рис. 25.9. Диалоговое окно Экспорт данных
Результаты построения частотного распределения переменной semester будут отныне показываться, как HTML-Документ (см. рис. 25.10).
Теперь мы хотим экспортировать еще и диаграмму.
-
Постройте для этого гистограмму переменной semester с нанесенной кривой нормального распределения.
-
В окне просмотра щёлкните правой кнопкой мыши на диаграмме, и выберите опцию Export... (Экспортировать). Откроется диалоговое окно Export Output (Экспортировать выходные данные).
-
Выберите в списке Export (Экспорт) опцию Output Document (Выходной документ).
-
И, наконец, щёлкните на переключателе Options... (Опции). Откроется диалоговое окно HTML Options (Опции HTML) (см. рисунок 25.11).
Рис. 25.10. Частотное распределение переменной semester в виде HTML-документа
-
В этом диалоговом окне щёлкните на переключателе Chart Options... (Опции для диаграммы)
Откроется диалоговое окно JPG Output Filter Setup (Установка выходного фильтра JPG) (см. рисунок 25.12).
-
Активируйте в области Resolution (Разрешение) опцию Screen (Экран) и подтвердите ввод ОК.
-
Возвратившись в диалоговое окно Export Output (Экспортировать выходные данные), введите имя файла C:\SPSSBUCH\histogramm.htm.
-
Запустите программу-браузер, например, Microsoft Internet Explorer.
-
Введите в строчку Path (Путь): file://C:/ SPSSBUCH/histogramm.htm. Обратите внимание на то, что после слова file (файл) должны стоять три черты, наклоненных вправо.
Рис. 25.11. Диалоговое окно HTML Options (HTML Опции)
Рис. 25.12. Диалоговое окно JPG Выход Фильтр Установка
Гистограмма с нанесенной кривой нормального распределения является отныне HTM L-Документом (см. рис. 25.13).
-
У Вас не должно возникнуть трудностей в дальнейшей самостоятельной работе с оставшимися опциями.
Рис. 25.13. Гистограмма в окне программы-браузера
8.gif
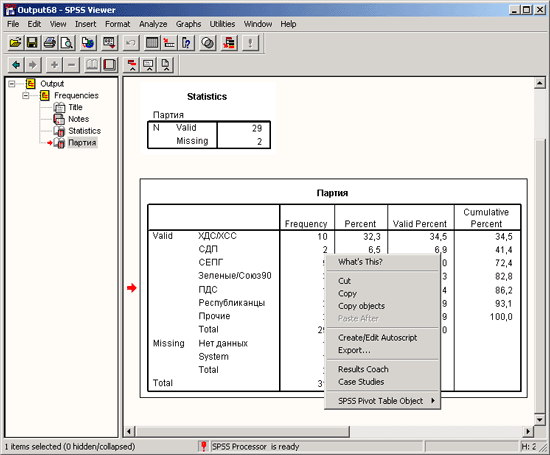
9.gif
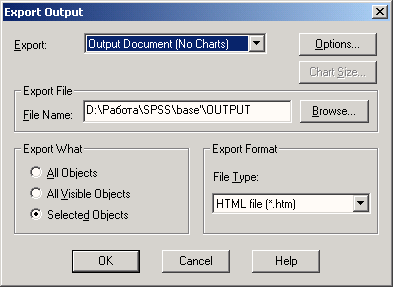
10.gif
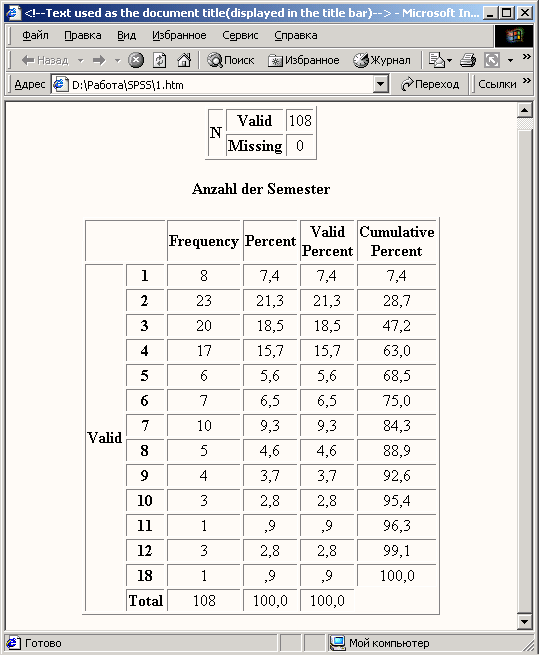
11.gif
12.gif
13.gif
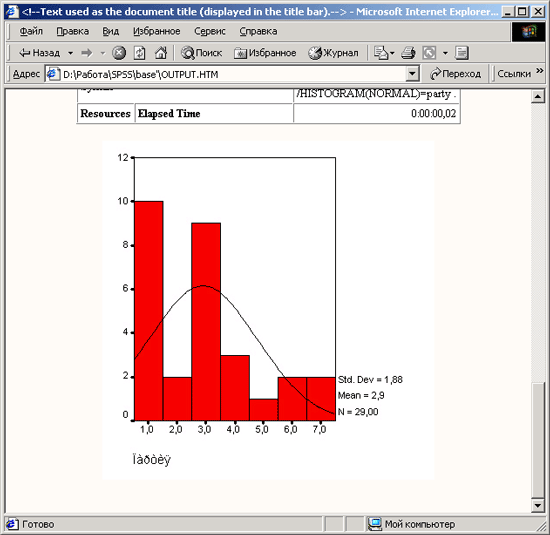
Глава 26. Программирование
Глава 26. Программирование
1. Программирование
Программирование
Пользователи, давно работающие с программой SPSS, в особенности, если им приходилось использовать ее на больших ЭВМ, уже привыкли давать описание данных и формулировать желаемый метод их обработки по строгим синтаксическим правилам в виде некоторой программы на языке SPSS.
Выгода такого подхода заключается в том, что пользователю не приходится постоянно пребывать в диалоговом режиме, а можно просто наблюдать, как компьютер выполняет единожды заданные команды. В связи с необходимостью написания команд и контроля командного синтаксиса, пользователь будет вынужден лучше продумывать свои шаги и, быть может, у него появится более чёткое понимание статистических методов используемых в программе.
Наверняка найдётся немало пользователей, охотно решающих свои проблемы в работе с SPSS именно таким методом. Но даже новички в SPSS, которые используют SPSS for Windows именно потому, что здесь есть возможность работы через диалоговые окна и не желают изучать синтаксис программы, также смогут почерпнуть для себя немало полезного, познакомившись с синтаксисом. Так, в области отбора и модификации данных, а также при выполнении некоторых статистических методов, имеются команды и опции, которые доступны только через синтаксис. Или, к примеру, имеется процедура MATRIX (Матрица), предназначенная для проведения операций с матрицами, которая может быть задействована исключительно при помощи соответствующего программного синтаксиса.
Конечно же, в рамках данной книги, которая как раз и направлена на изучение техники работы в Windows без привлечения синтаксиса программы, не получится дать подробное и полное описание синтаксиса SPSS.
Следующие разделы предназначены с одной стороны для тех пользователей, которые уже знакомы с синтаксисом программы, но с другой, возможно, послужат мотивацией к более подробному изучению данной темы для начинающих пользователей SPSS. В первом разделе будут представлены некоторые основные синтаксические правила. Второй раздел посвящён изучению работы с готовыми SPSS-программами для Windows, третий раздел — тому, как отдельные команды при помощи синтаксиса могут быть включены в диалоговый расчётный процесс, и наконец в четвёртом разделе будут рассмотрены два примера использования процедуры MATRIX (Матрица).
В пятом разделе речь пойдёт о том, как при помощи так называемых сценариев можно автоматизировать выполнение некоторых задач.
26.1 Основные синтаксические правила
26.1 Основные синтаксические правила
Элементы программного языка SPSS можно разделить на следующие категории:
-
Команда (инструкция): инструкция, управляющая процессом работы SPSS.
-
Вспомогательная команда: дополнительная инструкция к команде SPSS. В одну команду может входить несколько вспомогательных команд.
-
Спецификации: некоторые данные, дополняющие команду или вспомогательную команду. Спецификации могут содержать ключевые слова, цифры, арифметические операции, имена переменных и специальные разделительные знаки.
-
Ключевые слова: слова, применяемые в спецификациях, которым в SPSS предопределено некоторое значение.
Рассмотрим синтаксис теста Стьюдента для зависимых переменных:
T-TEST
PAIRS= chol0
WITH choll (PAIRED)
/CRITERIA=CIN(.95)
/MISSING=ANALYSIS.
Здесь T-TEST - команда. PAIRS, CRITERIA и MISSING - вспомогательные команды, после знака равенства в этих командах идут соответствующие спецификации. WITH, CIN и ANALYSIS являются ключевыми словами.
При написании и редактировании командного синтаксиса следует учесть следующие простые правила:
-
Каждая команда должна начинаться с новой строки и заканчиваться тачкой (.).
-
Вспомогательные команды отделяются друг от друга при помощи косой черты (/). Перед первой вспомогательной командой косая черта может не ставится.
-
Текст, взятый в одинарные кавычки (используемый для идентификации меток), должен находиться в одной строке.
-
Строка с программным синтаксисом не должна превышать 80 знаков.
В качестве десятичного разделительного знака в спецификациях должна применяться точка (.), независимо от установок операционной системы Windows.
При интерпретации команд синтаксиса компьютер на различает верхний и нижний регистры (кроме меток, заключённых в одинарные кавычки). Команда может занимать любое количество строк; ввод пробела или переход на новую строку разрешается в той точке, где разрешено применение одиночного пробела, то есть перед и после косой черты, скобок, арифметических операторов или между именами переменных.
В программных файлах, которые должны работать в операционном модуле, каждая команда должна начинаться с новой строки. Каждая последующая строка одной и той же команды должна начинаться как минимум с одинарного пробела; поэтому в конце команды точка может не ставиться. Синтаксис отдельных команд Вы можете просмотреть при помощи справочной системы (см. разд. 4.9).
26.2 Выполнение готовой программы для SPSS
26.2 Выполнение готовой программы для SPSS
В рамках эксперимента в области психологии пятнадцать мужчин были подвергнуты тестированию на предмет концентрации внимания (далее ТКВ — тест концентрации внимания). При этом вся совокупность респондентов была разбита на две группы: восемь человек вошли в экспериментальную группу и семь в контрольную. Группы компоновались таким образом, чтобы в начале эксперимента усреднённые показатели обеих
групп были примерно равны. Затем респондентам из экспериментальной группы было предложено выпить по три кружки пива, а респондентам контрольной группы пришлось довольствоваться минеральной водой. Через час в обеих группах был повторно проведен ТКВ.
Конечно же, предметом этого теста является изучение влияния алкоголя на функциональные способности человека. Предположим, что данные этого эксперимента мы обрабатывали на большой ЭВМ. Тогда существовало бы, как правило, два файла, один из которых в столбцах форме содержал данные (файл alko.dat), а второй программу 8Р85(файл alko.sps). Файлы выглядят следующим образом:
Файл данных
1 | 1 | 15 | 19 |
2 | 2 | 20 | 16 |
3 | 2 | 14 | 13 |
4 | 1 | 17 | 21 |
5 | 1 | 22 | 24 |
6 | 2 | 18 | 14 |
7 | 2 | 22 | 19 |
8 | 1 | 19 | 18 |
9 | 2 | 17 | 16 |
10 | 1 | 14 | 18 |
11 | 2 | 17 | 17 |
12 | 1 | 15 | 17 |
13 | 1 | 18 | 18 |
14 | 2 | 17 | 14 |
15 | 1 | 20 | 21 |
Программный файл SPSS
DATA LIST FILE='\spssbuch\alko.dat'
/g 4 kltl 6-7 klt2 9-10.
COMPUTE kltdiff=klt2-klt1.
VARIABLE LABELS g "Группа" /
klt1 "Тест на концентрацию внимания Проба 1" /
klt2 "Тест на концентрацию внимания Проба 2" /
kltdiff "Тест на концентрацию внимания Повышение" .
VARIABLE LABELS
g 1 "Экспериментальная группа"
2 "Контрольная группа".
NPAR TESTS K-S(NORMAL)=klt1,klt2,kltdiff.
TEMPORARY. SELECT IF g=1.
T-TEST PAIRS=klt1 WITH klt2.
TEMPORARY. SELECT IF g=2.
T-TEST PAIRS=klt1 WITH klt2.
T-TEST GROUPS=g(1,2)
/VARIABLES=klt1,klt2,kltdiff.
После проверки значений ТКВ на предмет наличия нормального распределения, в данной программе будут исследоваться следующие вопросы:
-
Являются ли различными показатели ТКВ обеих групп в первой и во второй пробах?
-
Различаются ли показатели ТКВ и их изменения между обеими группами?
Для выполнения этой программы в SPSS for Windows у Вас существует две возможности:
-
Можно запустить SPSS for Windows, загрузить программу в редактор синтаксиса и после маркировки соответствующего текста, выполнить ее, нажав кнопку со значком Run Current (Выполнить текущее задание).
-
Можно запустить программу в операционном модуле SPSS.
26.2.1 Запуск из редактора синтаксиса
26.2.1 Запуск из редактора синтаксиса
Рассматриваемая программа для SPSS находиться в файле alko.sps, имеющемся на приложенном компакт-диске; данные для этой программы можно найти в этой же директории в файле alko.dat.
Не будем вдаваться в подробности того, как были созданы эти ASCII-файлы. Возможно, они были скопированы с какой-нибудь большой ЭВМ или созданы с помощью одного из многочисленных текстовых редакторов, например, редактора, поставляемого с MS-DOS.
-
После запуска SPSS for Windows выберите в меню File (Файл) Open (Открыть) Syntax... (Синтаксис) Откроется диалоговое окно Open File (Открыть файл).
-
Выберите директорию прилагаемого диска и выделите файл alko.sps (см. рис. 26.1).
-
Подтвердите выбор нажатием кнопки Open (Открыть). Инструкции программного файла появятся в окне редактора синтаксиса. При необходимости здесь же их можно и отредактировать.
-
Выберите в меню Edit (Правка) Select All (Выделить всё)
-
Щелчком на выключателе Run Current (Выполнить текущее задание) запустите программу на исполнение. Результаты расчёта будут выведены в окно просмотра.
-
После выбора меню File (Файл) Save as... (Сохранить как) появится диалоговое окно, в котором Вы можете указать имя файла (с рекомендуемым расширением: .spo) для сохранения содержимого окна просмотра.
Рис. 26.1: диалоговое окно Open file (Открыть файл)
-
При выборе опции File (Файл) Print (Печать) Вы можете вывести содержимое окна просмотра на подключенный принтер.
-
При выходе из SPSS, после использования команды меню file (Файл) Close (Закрыть) на экране появится вопрос, не хотите ли вы сохранить рассчитанные данные в файле данных SPSS (рекомендуемое расширение: .sav).
1.gif

26.2.2 Операционный модуль
26.2.2 Операционный модуль
Ещё одну возможность запуска готовой SPSS-программы представляет операционный модуль. Выполнение программы происходит при этом не с помощью диалога с SPSS, a как бы на заднем плане (в фоновом режиме), причём во время расчёта Вы можете выполнять на компьютере и другие задачи.
Это очень удобно при выполнении ёмких процедур SPSS. Одной из таких процедур является, к примеру, кластерный анализ, в котором применяется иерархический метод (см. разд. 20.1) и необходимо обработать большое количество наблюдений.
Такое большое для кластерного анализа количество наблюдений (n=300) включает файл psych.sav, который наряду с номерами наблюдений содержит переменные а, Ь, и с, описывающие значения оценки состояния пациентов психиатрического отделения по соответствующим шкалам: на шкале А отображается уровень невротичности, на шкале В — адаптация к обществу и на шкале С — целенаправленность действий. Патологическими отклонениями считаются высокие значения по шкале А и В и низкие по шкале С. Попытаемся на основании этих трёх шкал разделить пациентов на группы.
-
Откройте файл psych.sav.
-
Выберите в меню Analyze (Анализ) Classify (Систематизировать) Hierarchical Cluster... (Иерархический кластер)
-
Перенесите переменные а, Ь, и с в поле тестируемых переменных.
-
Минуя выключатель Statistics (Статистики) установите область решений от 2 до 6 кластеров.
-
Через выключатель Method (Метод) активируйте стандартизацию значений (z-преобразование).
-
Деактивируйте вывод диаграмм.
Если Вы сейчас начнёте расчёт нажатием кнопки ОК, то программе для расчёта понадобится несколько минут. Мы произведём расчёт в операционном модуле, для чего нам сначала необходимо создать файл с соответствующим программным синтаксисом.
-
Для этого в диалоговом окне Hierarchical Cluster Analysis (Иерархический кластерный анализ) щёлкните на переключателе Paste (Вставить), после чего в редактор синтаксиса будут внесены следующие команды SPSS:
PROXIMITIES а Ьb с
/MATRIX OUT ("C:\TEMP\spssclus.tmp") /VIEW= CASE
/MEASURE= SEUCLID
/PRINT NONE
/STANDARDIZE= VARIABLE Z
. CLUSTER
/MATRIX IN ("C:\TEMP\spssclus.tmp") ' /METHOD BAVERAGE
/PRINT SCHEDULE CLUSTER(2,6)
/PLOTS NONE.
ERASE FILE= "C:\TEMP\spssclus.tmp".
-
Выбрав в меню File (Файл) Save as... (Сохранить как) Сохраните содержимое редактора синтаксиса, к примеру, в файле claSter.sps.
-
Завершите работу в редакторе синтаксиса выбором команды меню File (Файл) Close (Закрыть)
-
Из стартового меню рабочего стола запустите операционный модуль SPSS (SPSS 10.0 Production Facility) (см. рис. 26.2).
Рис. 26.2: Меню Start (Пуск) рабочего стола операционной системы Windows 2000
Откроется диалоговое окно операционного модуля SPSS (см. рис. 26.3).
Рис. 26.3: Диалоговое окно SPSS Production Facility (Операционный модуль SPSS)
-
Щёлкните на переключателе Add... (Добавить). Откроется диалоговое окно Attach SPSS Syntax File (Вложить файл синтаксиса SPSS).
-
Выделите, сохранённый Вами, файл cluster.sps.
-
Нажатием выключателя Open (Открыть) вернитесь в исходное диалоговое окно. Синтаксические файлы, открытые по ошибке, Вы можете удалить из диалогового окна при помощи выключателя Remove (Удалить). В поле Folder for output (Папка результатов) Вы можете указать место, куда должен быть помещён файл с результатами, рассчитанными операционным модулем.
-
Укажите, например, в качестве папки для результатов C:\SPSSBOOK.
-
Нажмите выключатель Edit (Править).
Рис. 26.4: Диалоговое окно Attach SPSS Syntax File (Вложить файл синтаксиса SPSS)
Откроется тестовый редактор, в котором Вы можете дополнительно отредактировать открытую SPSS-программу. В нашем примере при помощи команды GET следует указать ссылку на истинное расположение соответствующего файла данных. После ввода этой команды программа SPSS будет выглядеть следующим образом:
GET FILE='С:\SPSSBUCH\psych.sav'.
PROXIMITIES а b с
/MATRIX OUT ("С:\WIN95\TEMP\spssclus.tmp") /VIEW= CASE /MEASURE= SEOCLID
/PRINT NONE /STANDARDIZE:?
VARIABLE Z .
CLUSTER
/MATRIX IN ("C:\WIN95\TEMP\spssclus.tmp") /METHOD BAVERAGE
/PRINT SCHEDULE CLUSTER(2,6)
/PLOTS NONE.
ERASE FILE= "C:\WIN95\TEMP\spssclus.tmp".
-
Посредством выбора меню сохраните программу, изменённую в текстовом редакторе File (Файл) Save (Сохранить) и закройте окно редактора.
-
Теперь сохраните программу в форме операционной задачи. Для этого выберите в меню File (Файл) Save as... (Сохранить как)
Откроется диалоговое окно Save as Production Job (Сохранить как операционную задачу). Для файла операционной задачи предлагается расширение .spp (см. рис. 26.5).
-
Наберите имя файла C:\SPSSBOOK\clasjob.spp и покиньте диалоговое окно нажатием кнопки Save (Сохранить).
-
Вновь вернувшись в диалоговое окно SPSS Production Facility (Операционный модуль SPSS) выберите в меню Run (Выполнить) Production Job (Операционная задача)
Пока выполняется операционная задача, вы можете заняться другой работой. После окончания решения задачи Вы увидите, что результаты сохранены в формате файла окноа просмотра с расширением .spo под именем, соответствующим имени файла рассчитанной задачи.
Рис. 26.5: Диалоговое окно Save as Production Job (Сохранить как операционную задачу)
2.gif
3.gif
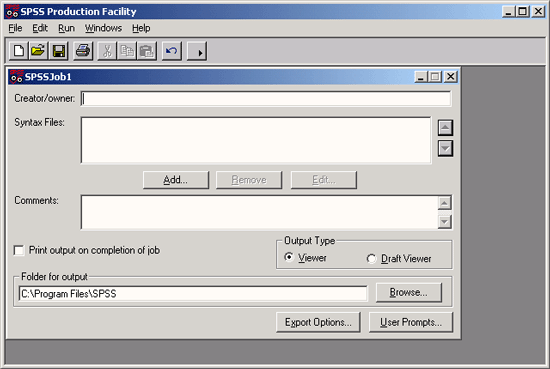
4.gif
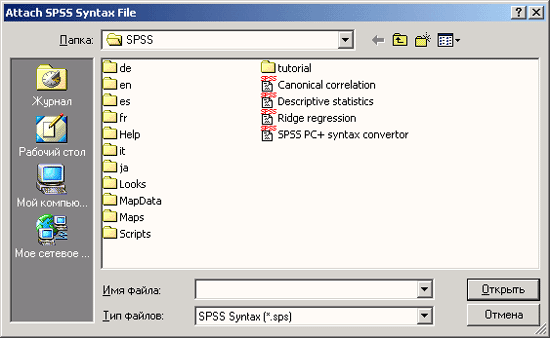
5.gif
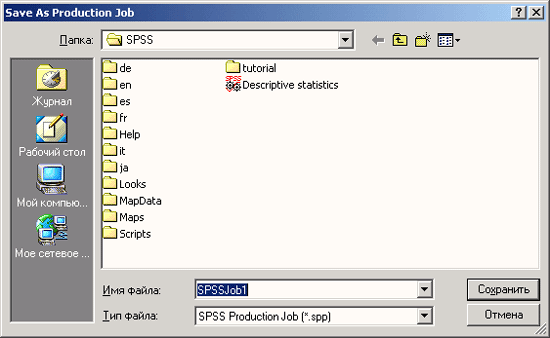
26.3 Объединение синтаксиса и диалогового режима
26.3 Объединение синтаксиса и диалогового режима
На нескольких примерах мы покажем то, как программный синтаксис можно с пользой внедрить в диалоговый режим SPSS. Во всех статистических процедурах, установки, произведенные в соответствующих диалоговых окнах, могут быть перенесены в редактор синтаксиса при помощи специального переключателя. При необходимости, Вы можете дополнительно отредактировать этот синтаксис для того, чтобы добиться выполнения некоторых задач, недоступных в режиме работы через диалоговые окна. Конечно же, для этого необходимо знать особенности подобных синтаксических возможностей.
В качестве первого примера рассмотрим тест Стьюдента для зависимых выборок. Тест Стьюдента для зависимых выборок был использован в разделе 13.2 при сравнения двух
переменных chol0 и chol1 из файла hyper.sav. Синтаксис, генерируемый программой после нажатия переключателя Paste (Вставить), выглядит следующим образом:
T-TEST
PAIRS= chol0 WITH
chol1 (PAIRED)
/CRITERIA=CIN(.95)
/MISSING=ANALYSIS.
Если Вы хотите сравнить между собой не только переменные chol0 и chol 1, а и попарно сравнить все четыре переменные chol0, chol1, cho!6 и chol 12, то в итоге при помощи данного диалогового окна Вам придётся произвести шесть операций парного сравнения. Это довольно утомительный процесс и, если было бы необходимо попарно сравнить еще большее количество переменных, то он отнял бы у Вас довольно много времени.
-
Программный синтаксис, отображаемый в редакторе синтаксиса, приведите к следующему виду
T-TEST
PAIRS= chol0, chol1, chol6, chol12
/CRITERIA=CIN(.95) /MISSING=ANALYSIS .
-
Начните расчёт
Попарно будут протестированы все переменные, перечисленные во вспомогательной команде PAIRS.
Похожий пример возьмём из раздела 15.2, где для этих четырёх переменных производится расчёт корреляционной матрицы Пирсона. Вы увидите следующий исходный синтаксис
CORRELATIONS
/VARIABLES=chol0 choll chol6 chol12
/PRINT=TWOTAIL SIG
/MISSING=PAIRWISE .
Если же Вы, допустим, желали бы рассчитать не совокупную корреляционную матрицу, а, например, проверить корреляции одной только переменной chol0 с переменными chol1, chol6 и chol 12, то Вам пришлось бы произвести три довольно объёмных расчёта. И в этом случае Вы можете очень эффективным способом отредактировать программный синтаксис, применив ключевое слово WITH:
CORRELATIONS
/VARIABLES=chol0 WITH chol1 chol6 chol12
/PRINT=TWOTAIL SIG
/MISSING=PAIRWISE .
Следующий пример касается трансформации данных, а именно, образования новых переменных при помощи некоторой формулы. С этой целью вновь вернёмся к файлу hyper.sav, точнее говоря — к переменным rrs0, rrs1, rrs6, rrs12, rrd0, rrd1, rrd6 и rrd12, отражающим состояние систолического и диастолического давлений в четыре различных момента времени. Образуем шесть новых переменных, которые будут отображать показатели трёх последующих моментов времени, выраженные в процентах от исходной величины (переменные rrs0 и rrd0). Для этого после выбора меню Transform (Трансформировать) Count (Подсчитать) необходимо задать в общей сложности шесть формул вида
prrs1=(rrs1/rrs0)*100
где prrs1 — в нашем примере, процентный показатель, соответствующий переменной rrs1, соотнесённой к исходной величине rrs0. Но если Вы будете в этом случае применять синтаксис, то, пожалуй, все можно сделать гораздо быстрее.
-
Выберите в меню File (Файл) New (Новый) Syntax... (Синтаксический)
-
В редакторе синтаксиса введите шесть следующих команд:
COMPOTE prrsl=rrs1/rrs0*100.
COMPOTE prrs6=rrs6/rrs0*100.
COMPOTE prrsl2=rrs12/rrs0*100
. COMPOTE prrdl=rrdl/rrd0*100.
COMPOTE prrd6=rrd6/rrd0*100.
COMPOTE prrdl2=rrd12/rrd0*100.
EXECOTE.
-
Затем щёлкните на Edit (Правка) Select All (Выделить всё)
-
Нажатием кнопки Run Current (Выполнить текущее задание) начните выполнение вышеуказанной последовательности команд.
Для использования в дальнейших расчётах у Вас появятся шесть новых переменных, которые будут отображать искомые процентные показатели. Если Вы посмотрите на шесть приведенных команд COMPUTE, то наверняка заметите, что все они построены по одному и тому же принципу. Меняются только числители и знаменатели, на месте которых необходимо подставлять соответствующие переменные. Абсолютно такую же последовательность команд COMPUTE можно создать при помощи команд DO REPEAT — END REPEAT. Введите в редакторе синтаксиса следующую структуру команд:
DO REPEAT p=prrs1,prrs6,prrs12,prrd1,prrd6,prrd12/
z=rrs1,rrs6,rrs12,rrd1,rrd6,rrd12/
a=rrs0,rrs0,rrs0,rrd0,rrd0,rrd0.
COMPOTE p=z/a*100.
END REPEAT .
Здесь р, z и а являются, так называемыми, переменными-заменителями для реальных переменных, используемых при вычислениях. Они обрабатываются слева направо согласно заданной команды COMPUTE. В рассмотренном примере затраты времени на ввод данных вряд ли стали меньше, но при наличии большего количества переменных в списках экономия времени будет уже ощутимой.
26.4 Программы операций над матрицами
26.4 Программы операций над матрицами
Между двумя командами SPSS: MATRIX и END MATRIX можно поместить программу, позволяющую выполнять операции над матрицами. Для изучения этой возможности рассмотрим два примера.
Пётр пошёл за покупками в магазин и принёс домой 2 литра молока, 10 яиц, 3 плитки шоколада и 5 стаканчиков йогурта, за что он заплатил в сумме 11,80 грн. На следующий день Юля купила 1 литер молока, 15 яиц, 2 плитки шоколада и 4 стаканчика йогурта за 10,01 грн. После этого Николай заплатил 15,07 грн за 3 литра молока, 12 яиц, 5 плиток шоколада и 3 стаканчика йогурта, и, в конце концов, Лене 2 литра молока, 20 яиц, 5 плиток шоколада и 5 стаканчиков йогурта обошлись в 15,74 грн. И никто из них не принёс при этом расчётный чек из магазина. Мама хочет узнать, сколько же стоит каждый продукт в отдельности. Пётр, который учится в пятом классе, предложил решение при помощи системы линейных уравнений:
2А | + | 10В | + | зс | + | 5D | 1180 |
А | + | 15В | + | 2С | + | 4D | 1001 |
ЗА | + | 12В | + | 5С | + | 3D | 1507 |
2А | + | 20В | + | 4С | + | 5D | 1574 |
Юля, ученица восьмого класса, привила эти уравнения к матричному виду:
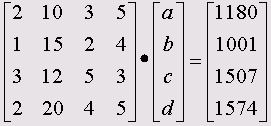
Николай записал эту матрицу в символьной форме:
АХ=С
и соответственно
X = А-1 С
Юля решает эту задачу в SPSS, для чего и пишет следующую программу:
MATRIX.
COMPUTE a={2 ,10 ,3,5;1,15,2,4;3,12,5,3;2,20,4,5}. COMPUTE с={1180,-1001,-1507;1574} . COMPUTE x=INV(a)*c.
PRINT x.
END MATRIX.
-
Чтобы выполнить эту программу выберите в меню File (Файл) Open (Открыть) Syntax... (Синтаксический)
-
Выберите тип файлов Syntax (*.sps) (Синтаксис). На прилагаемом учебном диске найдите файл sabine.sps. В окне редактора синтаксиса появится необходимая нам программа.
-
Выберите теперь Edit (Правка) Select All (Выделить всё)
-
Начните выполнение программы нажатием кнопки Run Current (Выполнить текущее задание).
В окне просмотра появятся результаты расчёта: х
119,0000000
26,0000000
134,0000000
56,0000000
Теперь видно, что один литр молока стоит 1,19 грн, одно яйцо 0,26 грн, одна плитка шоколада 1,34 грн и один стаканчик йогурта 0,56 грн. Для написания программ, использующих операции с матрицами, существует множество различных инструкций и функций. Для выяснения их смысла, обращайтесь, пожалуйста, к первоисточнику по SPSS.
В следующем примере мы хотим запрограммировать начальный этап факторного анализа, а именно, рассчитать собственные значения корреляционной матрицы.
-
Для этого примера используйте данные из файла ausland.sav, рассмотренного в гл. 19, и наберите в редакторе синтаксиса следующую SPSS-программу:
CORRELATIONS VARIABLES=A1
TO A15/MATRIX=OUT (*) .
MATRIX.
MGET FILE=*/TYPE=CORR.
CALL eigen(cr,evec,ewerte) .
PRINT ewerte.
END MATRIX.
-
Выберите в меню Edit (Правка) Select All (Выделить всё)
-
Начните выполнение программы нажатием кнопки со значком Run Current (Выполнить текущее задание).
После этого в окне просмотра будут показаны собственные значения; первые пять из них выглядят следующим образом:
EWERTE
5,146239283
1,945444977
1,414941459
,990117365
,935705222
Вычисленные собственные значения полностью соответствуют результатам, полученным в гл. 19.
6.gif
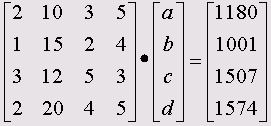
26.5 Сценарии
26.5 Сценарии
В SPSS интегрирован язык сценариев (Visual Basic), предоставляющий некоторые возможности для автоматизации вычислительных процессов. Степень использования сценариев зависит от уровня Ваших познаний и может быть разбита на три уровня:
1. Использование стандартных сценариев, имеющихся в SPSS: это может сделать каждый пользователь, так как в этом случае не требуется ни каких навыков программирования.
2. Модифицирование имеющихся сценариев: для этого необходимо располагать некоторыми базовыми знаниями.
3. Написание собственных сценариев: для этого необходимы навыки программирования на Visual Basic.
В этой книге мы ограничимся только те, что при помощи примера покажем применение сценариев, поставляемых вместе с SPSS. Изложение материала по написанию собственных сценариев и в особенности изучение языка Visual Basic, очень сильно увеличило бы объём данной вводной книги.
Кроме того, использование сценариев при работе с SPSS только начинает набирать обороты и сценарии поставляемые вместе с SPSS кажутся ещё не слишком продвинутыми. Однако, следить за сообщениями фирмы SPSS всё же полезно; время от времени в журнале для пользователей "SPSS direct" представляются новые сценарии, которые можно интегрировать в программу.
26.5.1 Применение сценария
26.5.1 Применение сценария
Для изучения принципа работы со сценариями должно быть достаточно рассмотрения только одного сценария, который в сводных таблицах меняет идентификатор Sig на р.
-
Откройте файл hyper, sav.
-
Выберите в меню Analyze (Анализ) Compare Means (Сравнить средние значения) Paired-Samples T Test... (Т-тест для спаренных выборок)
-
Переменным chol0 и chol1 присвойте статус спаренных переменных. Основные результаты теста отображены в следующей таблице:
Paired Samples Test
(Тест спаренных выборок) | |||||||||
| Paired Differences | t | Df | Sig. (2-sided) Значи-мость (двухсто ронняя)) | |||||
Mean (Сред- значе-ние) | Std. Deviation (Станда- ртное откло- нение) | Std. Error Mean (Стандар-тная ошибка среднего значения) | 95% Confidence Interval of the Difference (95 %-й доверительный интервал разности) | ||||||
Lower (Ниж-ний предел) | Upper (Верх-ний предел) | ||||||||
Pair1 (Пар а1) | Chole-sterin, Ausga- ngswert -Cholesterin, nach 1 Monat (Холе- стирин, исходный показатель -холе- стерин, спустя 1 месяц) | -1,93 | 26,09 | 1,98 | -5,83 | 1,98 | -,974 | 173 | ,332 |
-
В окне просмотра один раз щёлкните на сводной таблице.
-
Выберите в меню. Utilities (Утилиты) Run Script... (Выполнить сценарий) Откроется диалоговое окно Run Script (Выполнение сценария).
Рис. 26.6: Диалоговое окно Run Script (Выполнение сценария)
-
В директории PROGRAM F1LES\SPSS\SCRIPTS просмотрите список сценариев, предлагаемых в SPSS.
-
Выделите сценарий с именем Change sig to p.
-
И нажатием кнопки Run (Выполнить), пошлите его на исполнение. В окне просмотра появится изменённая сводная таблица.
Paired Samples Test
(Тест спаренных выборок) | |||||||||
| Paired Differences |
|
|
| |||||
|
| Std. Error | 95% Confidence Interval of the | ||||||
| Mean (Среднее значение) | Std. Deviation (Станда- ртное откло- нение) | Mean (Стандар-тная ошибка среднего значения) | Difference (95 %-й доверительный интервал разности) | t | Df | Р = | ||
Lower (Ниж- ний предел) | Upper (Верх- ний предел) | ||||||||
Pair 1 | Cholesterin, |
|
|
|
|
|
|
|
|
(Пар а1) | Ausga- ngswert -Choles- terin, nach 1 Monat |
|
|
|
|
|
|
|
|
| (Холе- стирин, | -1,93 | 26,09 | 1,98 | -5,83 | 1,98 | -,974 | 173 | ,332 |
| исходный |
|
|
|
|
|
|
|
|
| показатель - |
|
|
|
|
|
|
|
|
| холе- стерин, спустя 1 месяц) |
|
|
|
|
|
|
|
|
Действие остальных сценариев рассмотрите, пожалуйста, самостоятельно.
7.gif

26.5.2 Автоматические сценарии
26.5.2 Автоматические сценарии
Специальной формой сценариев являются, так называемые, автоматические сценарии. Если они активированы, то автоматически воздействуют на компоновку выводимых результатов некоторых процедур. Для изучения работы автоматических сценариев рассмотрим пример, в котором мы будем управлять компоновкой корреляционной матрицы.
-
Откройте файл hyper.sav.
-
Выберите в меню Edit (Правка) Options... (Параметры)
-
В диалоговом окне Options (Параметры) перейдите на регистрационную карту Scripts (Сценарии). Вам будет показан список автоматических сценариев, хранящихся в директории PROGRAM FILES\SPSS\SCRIPTS.
Рис. 26.7: Доступные автоматические сценарии
-
Выберите подходящий вид расчёта и просмотрите результаты действия этого авто-сценария.
8.gif
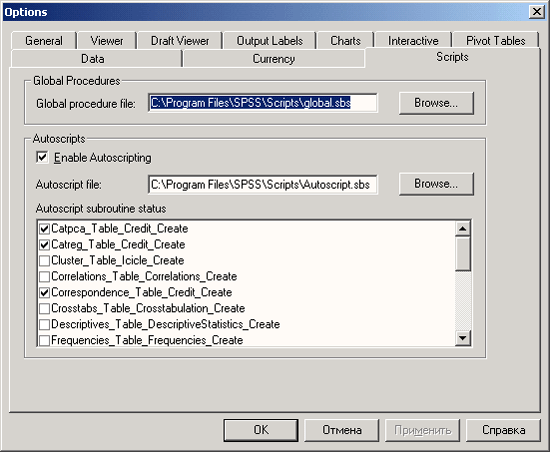
26.5.3 Редактор сценариев
26.5.3 Редактор сценариев
Если у вас появилось желание модифицировать имеющиеся сценарии или написать новые, воспользуйтесь редактором сценариев. Мы ограничимся только открытием и просмотром одного существующего сценария в редакторе сценариев.
-
Выберите в меню File (Файл) Open (Открыть) Script... (Сценарий)
Выберите тип файлов *.sbs (SPSS-сценарий) и выберите в директории PROGRAM FILES\SPSS\SCRIPTS сценарий, очищающий окно просмотра результатов или навигатор (то есть устраняющий примечания) (Clean navigator.sbs).
-
Выделите этот сценарий и подтвердите выбор нажатием Open (Открыть). Редактор сценариев будет выглядеть так, как изображено на рисунке 26.8.
Рис. 26.8: Редактор сценариев Просмотрите этот сценарий, чтобы иметь представление о языке сценариев.
9.gif
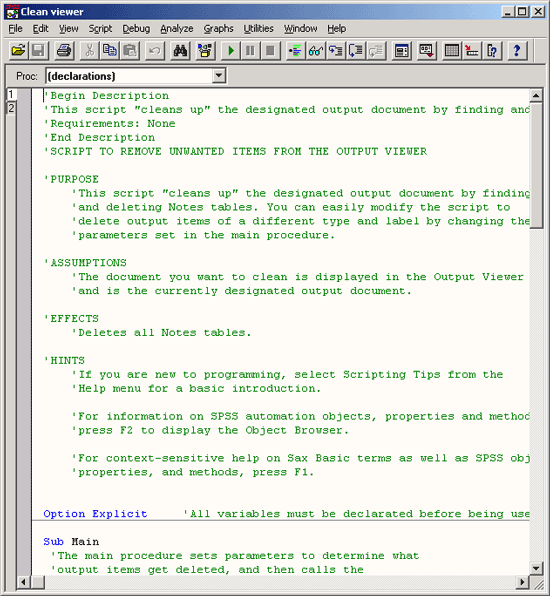
Глава 27. Нововведения в 11-ой версии SPSS
Глава 27. Нововведения в 11-ой версии SPSS
1. Использование программы SPSS в качестве ядра для современных маркетинговых исследований
Использование программы SPSS в качестве ядра для современных маркетинговых исследований
Новая, 11-ая версия SPSS появилась в мае этого года, разумеется в английской локализации. Разработчики пакета сочли, что пользовательский интерфейс в последней версии уже является достаточно совершенным, поэтому подавляющее большинство изменений в новой версии связаны с усовершенствованием или добавлением статистических процедур, которые более полно обеспечивают потребности пользователей в современных методах обработки информации, возникающей в результате маркетинговых исследований, а также исследований в области социологии и психологии.
Основное внимание уделено расширению функциональных возможностей специальных модулей SPSS, таких как SPSS Categories, SPSS Advanced Models и другие. Собственно расширение программного наполнения специальных модулей и делает новую версию программы, которая уже успела стать стандартом в области обработки данных, еще более привлекательной для пользователей с весьма широким диапазоном деловых и научных интересов.
Если раньше данная программа широко использовалась в таких «классических» областях науки и бизнеса, как биология, социология, психология, управление качеством производства, общие маркетинговые исследования и экономическое прогнозирование, то сейчас новую версию можно с успехом применять в таких актуальных специализированных областях, как маркетинг, основанный на использовании баз данных, Data Mining, Data Warehousing и другие. Особенного внимания заслуживает тот факт, что изменения, внесенные в модуль SPSS Regression Models, позволяют использовать SPSS при решении задач управления лояльностью клиентов (CRM). Отметим, что данная тема представляет собой один из наиболее популярных разделов современного практического маркетинга.
Отдельного упоминания заслуживает то факт, что большинство наиболее популярных статистических методов прогнозирования, включенных в модуль SPSS Regression Models, позволяют работать с большим объемом недоступной информации. В математике в таком случае говорят о повышении робастности метода, то есть его устойчивости по отношению к неопределенностям и существенным отклонениям от диапазона параметров, для которого разрабатывался метод. Такое повышение робастности весьма желательно в маркетинговых исследованиях и в социологии, где всегда присутствует большой объем отсутствующих или недостоверных данных. Небесполезно данное улучшение и в области управления качеством, где всегда существует компромисс между подробностью информации о производственном процессе и его усложнением.
Изменения коснулись и техники вычислений. Подобные изменения не сказываются на интерфейсе и прочих видимых функциональных особенностях программы, но однако они затрагивают вычислительное ядро, которое используется в ходе проведения конкретных расчетов. Здесь основное внимание было сосредоточено на повышении эффективности статистических алгоритмов, в некоторых случаях эффективность повысилась до 50 раз.
Эффективность одной из наиболее часто используемых статистических процедур, общей линейной модели (GLM), возросла в 10 раз, что несомненно скажется на обшей производительности при выполнении статистических исследований, особенно в области обработки больших массивов экспериментальных данных, которые возникают, например, в решении задач управления качеством, социологии и медицины.
В два раза выросла скорость выполнения самых массовых статистических процедур, таких как расчет дисперсии и вычисление средних. Можно смело сказать, что пользователь, который нуждается только в самых простых статистических методах, заметит именно двукратное повышение эффективности работы программы.
Особенно повышение быстродействия чувствительно в случае, когда речь идет о методах кластерного анализа, широко используемого в маркетинге, социологии, психологии и медицине, которые иногда требовали многочасовых расчетов даже на мощных компьютерах, для чего в предыдущих версиях SPSS был предусмотрен пакетный режим выполнения задач.
Следует отметить, что только одно столь существенное повышение производительности уже может быть основанием для выпуска новой версии программы. Снижение затрат времени, которое обеспечивает новая версия SPSS, позволяет более интенсивно использовать эту программу в практических маркетинговых исследованиях, анализировать большее количество вариантов, обрабатывать более широкие и представительные выборки. В результате издержки, связанные с исследованиями падают, а степень достоверности информации повышается.
Изменения, которые были внесены в изобразительную и презентационную части программы в основном затрагивают гибкость отображения результатов статистической обработки данных и включают несколько более показательных видов графиков. Например, при выводе информации о приближении данных с помощью выбранного метода аппроксимации, на графике приводится информация о том насколько хорошо полученное приближение. Такая дополнительная возможность может оказаться весьма полезной для не слишком опытных пользователей или пользователей не имеющих и не нуждающихся в глубокой математической подготовке. В целом изменения, которым подверглась графическая и презентационная часть программы направлены на упрощение работы и облегчение интерпретации результатов вычислений неподготовленными пользователями.
Рассматривая изменения, внесенные в техническую часть программы, необходимо упомянуть, что новая версия SPSS способна конвертировать базовые и переносимые файлы программы SAS (www.sas.com), своего наиболее мощного конкурента в области статистической обработки данных. Очень многие массивы общедоступной информации, имеющие отношения к маркетинговым исследованиям и социальной статистике, например данные по исследованию уровня жизни США и других стран (в том числе и России — знаменитый RLMS, www.unc.edu), проводимые американскими исследователями имеют формат переносимых файлов SAS.
Кроме того, следуя тенденции к превращению SPSS в мощное средство для проведения маркетинговых исследований и анализа разнородной информации, в 11-ой версии существенно расширено удобства доступа к различным форматам баз данных. В список поддерживаемых форматов теперь входят Sybase 11 и 12; Infomix 7.3+, 9.14: Infomix 2000 (9.20); UDB (DB2 6.1 и 7.1); SQL Server 2000; Oracle 8.06; Oracle! Releases 2 and 3 (8.1.6, 8.1.7). Улучшена связь с Microsoft Data Access pack. Более мощным стал язык запросов, появилась возможность на уровне запроса формировать и имена переменных и метки, что облегчает интерпретацию результатов и повышает их наглядность. Повысилась гибкость и функциональные возможности мобильных таблиц — это изменение затрагивает модуль SPSS Tables.
Если подытожить все вышесказанное, то можно сделать вывод, что переход конкретного пользователя на новую версию SPSS оправдан в том случае, когда этот пользователь нуждается в расширении своего арсенала методов статистической обработки данных, реализации наиболее современных тенденций в маркетинговых исследованиях, испытывает проблемы с полнотой информации, на основании которой необходимо сделать надежные и достоверные выводы, а также сталкивается с жесткими временными ограничениями, накладываемыми на процесс проведения исследований. Кроме того, работа с 11-ой версией SPSS снимает часть проблем, с которыми сталкиваются пользователи на начальных этапах освоения сложных методов статистического анализа, применяемого в широком спектре областей деятельности.
Переход к новой версии желателен, если пользователь собирается более широко применять современные методы анализа данных в ходе своей деятельность и уже имеет опыт использования аппарата математической статистики.
И, наконец, переход к новой версии не столь необходим, если в ходе деятельности пользователя возникает потребность в применении только самых простых статистических методах, а интерпретация результатов не вызывает особенных проблем. Кроме того, необходимо отметить, что предыдущая версия SPSS 10.1 имеет русскую локализацию, а выход локализованной 11-ой версии может стать весьма отдаленной перспективой.
2. Конкретные нововведения в SPSS 11
Конкретные нововведения в SPSS 11
Приведем краткий список конкретных изменений, внесенных в вычислительную часть программы.
Следуя намеченному выше плану, начнем с нововведений в специализированные модули программы.
-
В модуле Advanced Models добавлена новая статистическая процедура Linear mixed models (смешанные линейные модели), также известная как Heirarchical Linear Models (иерархические линейные модели), которая используется для получения наиболее точной прогнозирующей модели при работе с вложенной структурой данных. Гибкость этой модели позволяет существенно расширить применимость методов прогноза в решении задач экономического анализа и маркетинга: ANOVA фиксированными эффектами Model, Randomized Complete Blocks Design, Split-Plot Design, Purely Random Effects Model, Random Coefficient Model, Multilevel Analysis, модель безусловного линейного роста, модель линейного роста с a person-level covariate, Repeated Measures Analysis and Repeated Measures Analysis with time-dependent covariate. Кроме того, данная модель позволяет анализировать данные с повторными измерениями, включая неполные повторные измерения, когда объем информации изменяется от объекта к объекту.
-
Внедрена новая процедура Descriptive ratio statistics (Дескриптивные статистики отношений)
-
Использование медианы в качестве статистики при агрегировании данных, отсутствие данной возможности вызывало удивление у опытных пользователей SPSS.
-
Метод многомерной логистической регрессии теперь можно использовать для построения психологического профиля клиента при проведении маркетинговых исследований.
-
Улучшена масштабируемость и повышена производительность методов многомерной логистической регрессии (Multinomial Logistic Regression), иерархического Кластерного анализа (Hierarchical Cluster Analysis ). Скорость выполнения иерархического кластерного анализа возросла от 5 до 50 раз в зависимости от типа вычислений. А скорость выполнения мультиноминальной логистической регрессии и Общих Линейных Моделей (General Linear Models ) увеличилась в 10 раз
-
Процедуры MLR, PLUM, GLM и MIXED позволяют сохранять предсказываемые значения даже при наличии пропущенных значений. Данные процедуры также можно использовать для определения целевых групп клиентов в маркетинговых исследованиях.
-
Усовершенствована процедура категориальной регрессии (CATREG): возможность преобразования переменных, возможность обработки пропущенных значений, улучшение вывода таблиц и другие
-
Усовершенствована процедура преобразования данных с использованием монотонных и немонотонных сплайнов с назначаемой пользователем степенью и числом узлов
В технической и презентационной части программы произошли следующие изменения:
-
Для визуализации качества построенного приближения данных используется новый вид графиков
-
Для получения большего объема данных о корреляционных связях введена новая форма выходных таблиц
-
В выводимой информации появилась возможность использования длинных строк
-
Расширились возможности задания вариантов обработки пропущенных значений
-
Появились дополнительные возможности сохранения файлов данных
-
В OLAP-кубах появилась статистика процентного изменения.
-
Повышена защита данных путем шифрования при обмене между клиентом SPSS для Windows и сервером SPSS Server.
-
Усовершенствован конструктор чтения баз данных (Database Wizard).
-
Возможность делать выборку при импорте данных через ODBC.
-
Возможность доступа к данным только для чтения.
-
Не требуется login при доступе к данным MS Access.
-
Улучшена графика и возможности работы с таблицами в SPSS Viewer
Приложение. Обзор процедур SPSS
Приложение
Обзор процедур SPSS
В нижеследующей таблице приводятся команды SPSS, при помощи которых через синтаксис могут быть вызваны различные статистические процедуры, а также соответствующие им опции меню, необходимые при пользовании диалоговыми окнами SPSS for Windows. Кроме того, в таблице указывается, к какому модулю относится та или иная процедура:
В = Basemodule (Базовый модуль)
R = Regression Models (Регрессионные модели)
А = Advanced Models (Дополнительные модели)
В последней колонке указывается вариант представления результатов процедуры в окне просмотра: новый — с применением новой техники сводных таблиц или же старый соответствующий ещё традиционной форме листинга больших ЭВМ (SPSS classic).
Команда SPSS | Опция меню | Модуль | Вариант представ- ления |
AGGREGATE | Data (Данные) | В | новый |
Aggregate... (Группировать, Агрегировать данные) | |||
ALSCAL | Analyze (Анализ) | В | старый *) |
Scale (Масштабирование, Анализ шкал) | |||
Multidimensional Scaling... (Многомерное масштабирование, Многомерное шкалирование) | |||
CLUSTER | Analyze (Анализ) | В | новый |
Classify (Систематизировать, Классификация) | |||
Hierarchical Cluster... (Иерархический кластерный анализ, Иерархическая кластеризация) | |||
CNLR | Analyze (Анализ) | R | старый |
Regression (Регрессия) | |||
Nonlinear. . .(Нелинейная) | |||
CORRELATIONS | Analyze (Анализ) | В | новый |
Correlate (Корреляция, Корреляции) | |||
Bivariate... (Двумерная, Парные) | |||
COXREG | Analyze (Анализ) | А | старый *) |
Survival (Выживание, Выживаемость) | |||
Сох Regression... (Регрессия Кокса) | |||
Analyze (Анализ) | |||
Survival (Выживание, Выживаемость) | |||
Cox w/Time-Dep Cov... (Кокс с ковариациями, зависящими от времени, Кокс с ковариатами, зависящими от времени) | |||
CROSSTABS | Analyze (Анализ) | В | новый |
Descriptive Statistics (Дескриптивные статистики) | |||
Crosstabs... (Таблицы сопряженности) | |||
CURVEFIT | Analyze (Анализ) | В | старый |
Regression (Регрессия) | |||
Curve Estimation... (Оценка с помощью кривой. Подгонка кривых) | |||
DESCRIPTIVES | Analyze (Анализ) | В | новый |
Descriptive Statistics (Дескриптивные статистики) | |||
Descriptives... (Дескриптивные статистики) | |||
DISCRIMINANT | Analyze (Анализ) | в | новый |
Classify (Систематизировать, Классификация) | |||
Discriminant (Дискриминационный анализ, Дискриминантный анализ) | |||
EXAMINE | Analyze (Анализ) | в | новый |
Descriptive Statistics (Дескриптивные статистики) | |||
Explore... (Исследование данных. Исследовать) | |||
FACTOR | Analyze (Анализ) | в | новый |
Data Reduction (Упрощение данных, Снижение размерности) | |||
Factor... (Факторный анализ) | |||
FREQUENCIES | Analyze (Анализ) | в | новый |
Descriptive Statistics (Дескриптивные статистики) | |||
Frequencies... (Частоты) | |||
GENLOG | Analyze (Анализ) | А | старый *) |
Loglinear (Логлинейная, Логлинейныей анализ) | |||
General... (Общий) | |||
Analyze (Анализ) | |||
Loglinear (Логлинейная, Логлинейный анализ) | |||
Logit (Логит) | |||
GLM | Analyze (Анализ) | А | новый |
General Linear Model (Общая линейная модель) | |||
Multivariate... (Многомерная, ОЛМ-Многомерная) | |||
Analyze (Анализ) | А | ||
General Linear Model (Общая линейная модель) | |||
Repeated Measures... (ОЛМ-Повторные измерения) | |||
GRAPH | Graphs (Графики) | В | |
HILOGUNEAR | Analyze (Анализ) | А | старый |
Loglinear (Логлинейная, Логлинейный анализ) | |||
Model Selection... (Выбор модели, Подбор модели) | |||
IGRAPH | Graphs (Графики) | В | |
Interactive (Интерактивные) | |||
KM | Analyze (Анализ) | А | старый *) |
Survival (Выживание, Выживаемость) | |||
Kaplan-Meier... (Каплан-Майер, Каплан-Мейер) | |||
LOGISTIC | Analyze (Анализ) | R | старый |
REGRESSION | Regression (Регрессия) | ||
Binary Logistic... (Бинарная логистическая, Логистическая) | |||
MATRIX | Только через синтаксис программы | В | старый |
MEANS | Analyze (Анализ) | В | новый |
Compare Means (Сравнить средние значения, Сравнение средних) | |||
Means... (Средние значения, Среднее) | |||
MULT RESPONSE | : Analyze (Анализ) | В | старый |
Multiple Response (Множественные ответы) | |||
NLR | Analyze (Анализ) | R | старый |
Regression (Регрессия) | |||
Nonlinear. . .(Нелинейная) | |||
NOMREG | Analyze (Анализ) | R | новый |
Regression (Регрессия) | |||
Multinomial Logistic... (Многозначная логистическая, Мультиноминальнач регресссия) | |||
NONPAR CORR | Analyze (Анализ) | В | новый |
Correlate (Корреляция) | |||
Bivariate... (Двумерная, Парные) | |||
NPAR TESTS | Analyze (Анализ) | В | новый |
Nonparametric Tests (Непараметрические тесты, Нерараметрические критерии) | |||
OLAP CUBES | Analyze (Анализ) | В | новый |
Reports (Отчёты) | |||
OLAP Cubes... (OLAP кубы) | |||
ONEWAY | Analyze (Анализ) | В | новый |
Compare Means (Сравнить средние значения, Сравнение средних) | |||
One-Way ANOVA... (Однофакторный ANOVA, Однофакторный дисперсионный анализ) | |||
PARTIAL CORR | Analyze (Анализ) | В | старый |
Correlate (Корреляция, Корреляции) | |||
Partial (Частичная, Частные) | |||
PLUM | Analyze (Анализ) | А | новый |
Regression (Регрессия) | |||
Ordinal... (Порядковая) | |||
PROBIT | Analyze (Анализ) | R | старый |
Regression (Регрессия) | |||
Probit... (Пробит) | |||
PROXIMITIES | Analyze (Анализ) | В | новый |
Correlate (Корреляция, Корреляции) | |||
Distances... (Дистанции, Расстояния) | |||
QUICK CLUSTER | Analyze (Анализ) | В | новый |
Classify (Систематизировать, Классификация) | |||
K-Means Cluster... (Анализ кластерных центров, Кластеризация К-средним) | |||
RANK | Transform (Трансформация, Преобразовать) | В | новый |
Rank Cases... (Создать иерархию, Ранжирование наблюдений) | |||
REGRESSION | Analyze (Анализ) | В | новый |
Regression (Регрессия) | |||
Linear. . . (Линейная) | |||
RELIABILITY | Analyze (Анализ) | В | старый |
Scale... (Масштабирование, Анализ шкал) | |||
Reliability Analysis... (Анализ пригодности, Анализ надежности) | |||
REPORT | Analyze (Анализ) | В | старый *) |
Reports (Отчёты) | |||
Report Summaries in Rows... (Итоговый отчёт по строкам, Итоги по строкам) | |||
Analyze (Анализ) | |||
Reports (Отчёты) | |||
Report Summaries in Columns... (Итоговый отчёт по столбцам, Итоги по столбцам) | |||
SUMMARISE | Analyze (Анализ) | В | новый |
Reports (Отчёты) | |||
Case Summaries... (Итоговые показатели случаев, Итоги по наблюдениям) | |||
SURVIVAL | Analyze (Анализ) | А | старый *) |
Survival (Выживание, Выживаемость) | |||
Life Tables... (Таблицы жизни, Таблицы дожития) | |||
TABLES | Analyze (Анализ) | Tables | новый |
Custom Tables (Индивидуальные таблицы, Настраиваемые таблицы) | |||
T-TEST | Analyze (Анализ) Compare Means (Сравнить средние значения, Сравнение средних) Independent-Samples T Test... (Т-тест независимых выборок, Т-критерий для независимы Analyze (Анализ) Compare Means (Сравнить средние значения, Сравнение средних) Paired-Samples T Test... (Т-тест спаренных выборок, Т-критерий для парных выборок) | В | новый |
UNIANOVA | Analyze (Анализ) General Linear Model (Общая линейная модель) Univariate... (ОЛМ-Одномерная) | В | новый |
VARCOMP | Analyze (Анализ) General Linear Model (Общая линейная модель) Variance Components... (Компоненты дисперсии) | А | новый |
WLS | Analyze (Анализ) Regression (Регрессия) Weight Estimation... (Весовая оценка. Взвешенная) | R | старый |
2SLS | Analyze (Анализ) Regression (Регрессия) 2-Stage Least Squares... (2-х ступенчатые наименьшие квадраты, Двух этапный МНК ) | R | старый |
Процедуры, отмеченные знаком *), описываются в книге: "SPSS. Методы исследования рынка и мнений" .