8. Примитивы, использующие сплайны — Spline
Примитивы, использующие сплайны — Spline
Подпакет Spline вместе с уже описанным подпакетом NumericalMath'SplineFit' (сплайновая регрессия) обеспечивает представление данных с помощью сплайна. В подпакете Spline определена единственная функция Spline [points, type], которая создает графический примитив, представляющий сплайн-кривую типа type (Cubic, Bezier или CompoziteBezier — см. описание подпакета NumericalMath'SplineFit').
Среди ее опций важно отметить следующие (как и ранее, приведены значения, используемые по умолчанию): SplineDots->None, SplinePoints->25, Max-Bend->10.0 и SplineDivision->20.0.
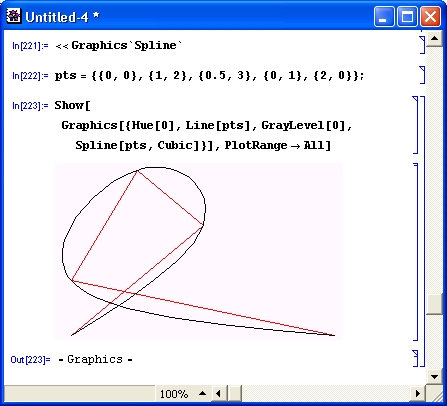
Рисунок 14.85 показывает задание массива из пяти точек на плоскости и соединение их отрезками прямых и кубическими сплайн-функциями. Хорошо видна аналогия сплайна с гибкой линейкой.
Сплайн-функции в данном случае применяются в порядке задания точек в списке pts. В этом случае возможно создание замкнутых линий (рис. 14.85 является наглядным примером этого).
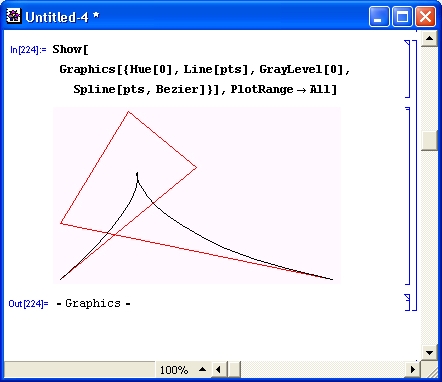
Следует отметить, что хотя сплайн-аппроксимация дает хорошие результаты при умеренном числе точек, при малом их числе и неудачном выборе типа сплайнов результат может оказаться неудовлетворительным. Рисунок 14.86 иллюстрирует такую ситуацию.
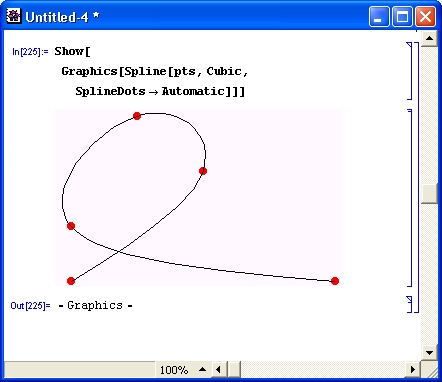
Рисунок 14.87 показывает возможность построения сплайн-функции вместе с точками, через которые она проходит.
Рис. 14.85. Пример интерполяции пяти точек отрезками прямой и сплайнами
Рис. 14.86. Пример срыва сплайн-интерполяции точек
Рис. 14.87. Построение исходных точек и проходящей через них сплайн-функции
Создание поверхностей вращения — SurfaceOfRevolution
Одна из задач компьютерной графики — создание поверхностей вращения. Средства для этого дает подпакет SurfaceOfRevolution. Они представлены следующими функциями:
- SurfaceOfRevolution [f, {x, xmin, xmax} ] — строит поверхность, образованную вращением кривой, описанной функцией f, при изменении х от xmin до xmax, в плоскости ху;
- SurfaceOfRevolution [{fx, f у}, {t, tmin, tmax} ] — строит поверхность, образованную вращением кривой, описываемой параметрически заданной на плоскости функцией {f x, f у}, в плоскости xz при изменении параметра t от tmin до tmax;
- SurfaceOfRevolution[{fx,fy,fz},{t,tmin,tmax}] — строит поверхность, образованную вращением кривой, описываемой параметрически заданной в пространстве функцией {fx, fy, fz}, в плоскости xz при изменении параметра t от tmin до tmax;
- SurfaceOfRevolution[f,{{x,xmin,xmax},{theta,thetamin,thetamax}}] — строит поверхность вращения кривой, описываемой функцией f, при угле theta, меняющимся от thetamin до thetamax.
Рисунок 14.88 дает простой пример построения поверхности, образованной линией cos(x) при изменении х от 0 до 4л, вращающейся вокруг оси xz. Построение задано функцией SurfaceOfRevolution [f, {x, xmin, xmax} ]. В этом случае линия вращается в пределах угла от 0 до 2-я, поэтому поверхность получается круговой.
Рис. 14.88. Фигура, образованная вращением линии cos(x)
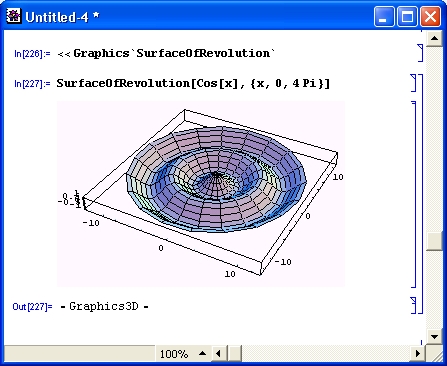
Следующий пример показывает ту же фигуру (рис. 14.89) в другом положении. Это достигается сменой угла обзора с помощью опции viewVertical.
Рис. 14.89. Фигура рис. 14.88 в другом положении
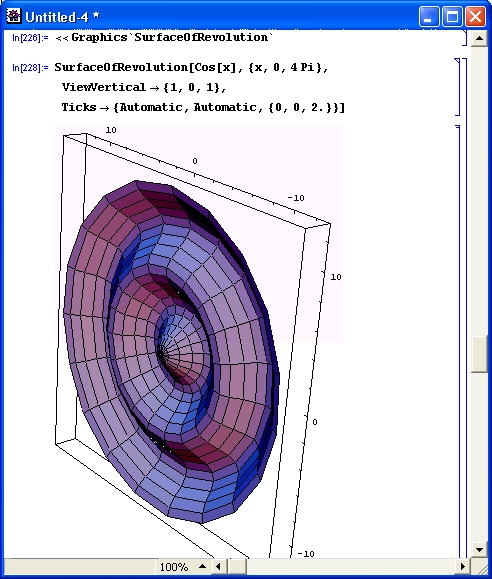
Пример применения функции SurfaceOfRevolutibn [ {fx, fy}, {t, tmin, tmax) ] представлен на рис. 14.90. Формируется этакое декоративное яйцо на подставке. Заменив в определении функции Cos [u] на Sin [u], можно получить изображение рюмки.
Рис. 14.90. Построение декоративного яйца на подставке
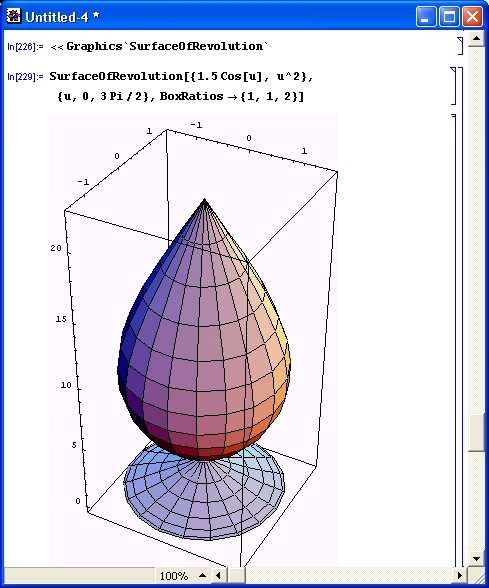
Рисунок 14.91 демонстрирует возможность построения объемной фигуры с вырезами. Все, что для этого надо, — удачно выбрать диапазон изменения угла вращения. Если он будет от 0 до 2л, то фигура будет сплошной, не содержащей вырезов.
Рис. 14.91. Построение яйца с вырезом
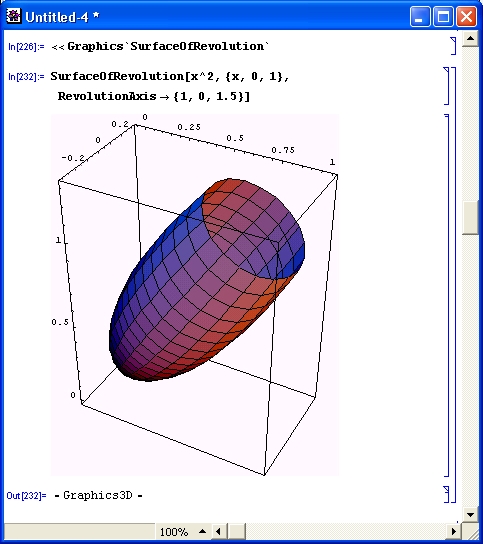
Для управления положением оси вращения служат следующие опции:
- RevolutionAxis->{x, z } — задает поворот вокруг оси, соединяющей начало координат с точкой {х, z} в плоскости xz\
- RevolutionAxis-> {х, у, z} — задает поворот вокруг оси, соединяющей начало координат с точкой {х, у, z}.
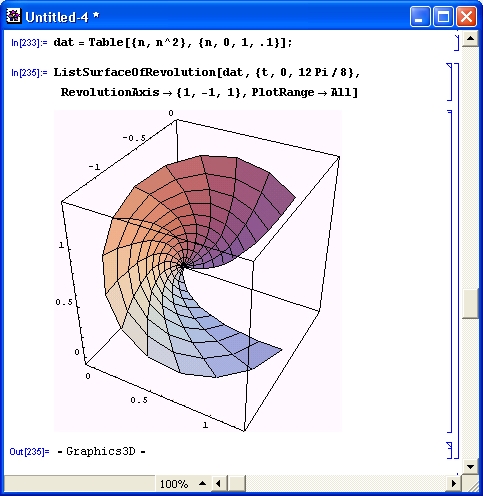
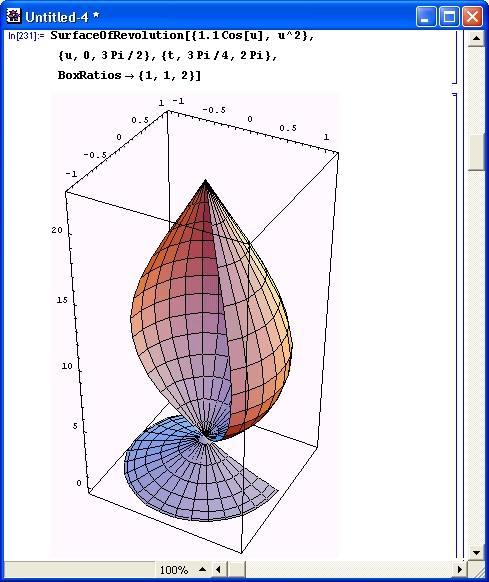
Рисунок 14.92 иллюстрирует применение опции RevolutionAxis->{x, у, z }.
Следующая функция позволяет построить фигуру вращения, образующая линия которой задается массивом точек:
- ListSurfaceOfRevolution [ {point1,point2,...} ] — создает поверхность вращения, заданную массивом точек pointl, point2, ...;
- ListSurfaceOfRevolution[{point1,point2,...}, {theta,thetamin,thetamax}] — создает поверхность вращения, заданную массивом точек, при угле вращения theta от thetamin до thetamax.
Рисунок 14.93 показывает задание массива точек с помощью функции Table и фигуру вращения, полученную при использовании функции ListSurfaceOf-Revolution во второй форме.
Рис. 14.92. Управление положением оси вращения
Рис. 14.93. Пример построения фигуры вращения с образующей, заданной массивом точек
Что еще есть в пакете расширения Graphics
Помимо уже рассмотренных подпакетов пакет расширения Graphics содержит подпакеты ThreeScript и Common. Подпакет ThreeScript содержит функцию преобразования трехмерных графических объектов в программный код формата 3-Script, например:
<<Graphics 'ThreeScript'
obj = Graphics3D[Polygon[0,0,0, 0,1,0, 0,1,1]]
• GraphicsSD •
ThreeScript[ "object.ts", obj]
object.ts
!!object.ts
% Graphics3D objects
boundingbox
0 0 0
0 1 1
viewpoint
1.3 -2.399999999999999 2.
ambientlight
000
lightsources
1. 0. 1.
1 0 0
1. 1. 1.
0 1 0
0. 1. 1.
0 0 1
polygon
0 0 0
0 1 0
0 1 1
Подпакет Common содержит просто перечень системных символов (точнее, слов), которые приняты во всех подпакетах пакета Graphics. Вот этот список: Horizontal, MaxArrowLength, ScaleFactor, ScaleFunction и Vertical.
В этом уроке мы научились:
- Выполнять анимацию графиков различного типа.
- Управлять цветами графиков.
- Строить стрелки на графиках.
- Строить графики комплекснозначных функций.
- Строить объемные контурные графики.
- Строить графики с окраской внутренних областей.
- Строить графики специальных типов.
- Строить графики неявных функций.
- Выводить обозначения кривых — легенды.
- Строить графики с множеством объектов.
- Строить параметрические трехмерные графики.
- Представлять поля на плоскости и в пространстве.
- Строить объемные многогранники — полиэдры.
- Создавать графические формы.
- Работать с примитивами, использующими сплайны.
- Создавать поверхности вращения.
gl14-85.jpg
gl14-86.jpg
gl14-87.jpg
gl14-88.jpg
gl14-89.jpg
gl14-90.jpg
gl14-91.jpg
gl14-92.jpg
gl14-93.jpg