Урок 12. Статистические расчеты
Урок 12. Статистические расчеты
1. Статистические расчеты
Статистические расчеты
- Статистические расчеты — пакет Statistics
- Построение гистограмм
- Статистика распределен и и
- Статистическая обработка данных
- Сглаживание данных
- Регрессия различного вида
В ядре системы Mathematica практически нет статистических функций. Зато пакет расширения Statistics дает сотни функций, охватывающих практически все разделы теоретической и прикладной статистики. Тем не менее, вопрос о привлечении универсальных математических систем к выполнению серьезных математических расчетов является спорным из-за существования множества специальных статистических компьютерных систем, таких как Statistica, StatGraphics и т. д.
Большинство специализированных статистических программ предлагают специальный интерфейс, базирующийся на обработке табличных данных большого объема, реализуют многовариантный расчет необходимых статистических параметров (например, регрессию сразу по десяткам формул) и отсев заведомо ошибочных данных. Поэтому при статистических расчетах применение подобных программ предпочтительно.
2. Статистические расчеты— пакет Statistics
Статистические расчеты— пакет Statistics
Учитывая ограниченный объем книги и приведенные выше обстоятельства, данный раздел не содержит исчерпывающего описания всех сотен функций расширения Statiatics, а лишь дает обзор этого пакета с описанием наиболее часто используемых средств статистики, относящихся к обработке данных. Это не слишком снижает ценность описания, поскольку функции статистики по большей части просты и имеют вполне очевидные (для специалистов) имена.
Пакет расширения Statistics содержит следующие подпакеты:
- Confidencelntervals — функции доверительных интервалов;
- ContinuousDistributions — функции непрерывных распределений;
- DataManipulation — манипуляции с данными;
- DataSmoothing — сглаживание данных;
- DescriptiveStatistics — статистика распределений;
- DiscreteDistributions — функции дискретных распределений;
- HypothesisTests — проверка статистических гипотез;
- LinearRegression — линейная регрессия;
- MultiDescriptiveStatistics — статистика многомерных распределений;
- MultinormalDistribution — функции многомерных нормальных распределений;
- NonlinearFit — нелинейная регрессия;
- NormalDistribution — функции нормального распределения;
- Common — данные общего характера.
Как и ранее, для работы каждого из подпакетов требуется его загрузка в память компьютера с помощью команды
<<Statistics`Имя_подпакета`
Имена подпакетов расширения статистики приведены выше.
Манипуляции с данными — DataManipulation
Статистические данные обычно бывают представлены в виде списков — как одномерных, так и двумерных (таблиц и матриц) и даже многомерных. Большая часть функций, обеспечивающих манипуляции с данными, сосредоточена в подпакете DataManipulation.
Данные могут вводиться в строках ввода или считываться из файлов с помощью функции ReadList. Для манипуляций с данными могут использоваться многие функции ядра системы, описанные ранее, — в частности, все функции обработки списков. Подпакет DataManipulation дает ряд удобных функций. Ниже представлена первая группа таких функций:
- Column [data, n] — возвращает n-й столбец списка data;
- Column [data, {nl, n2,...}] — возвращает список из столбцов ni списка данных;
- ColumnTake [data, spec] — возвращает столбцы списка data с данной спецификацией spec;
- ColumnDrop [data, spec] — удаляет столбцы списка data с данной спецификацией spec;
- Column Jo in [datal, data2,...] — объединяет столбцы списков datai;
- RowJoin [datal, data2,...] — объединяет строки списков datai;
- DropNonNumeric [data] — удаляет из списка data нечисловые элементы;
- DropNonNumericColumnfdata] — удаляет из списка data столбцы с нечисловыми элементами.
Примеры применения этих функций:
<<Statistics`DataManipulation `
data = {{а, 3}, {b, 6}, {с, 4}, {d, i},
{e, 5}, {i 4}}
{{a, 3}, {b, 6}, {c, 4}, {d, i}, {e, 5), {f, 4}}
col2 = Column[data, 2]
{3, 6, 4/i, 5, 4}
newdata = DropNonNumeric[col2]
{3, 6, 4, 5, 4}
Полезны также следующие функции подпакета:
- BooleanSelect [list, sel] — удаляет из list элементы, которые дают True при тестировании выражения sel;
- TakeWhile [list,pred] — удаляет из list все элементы, начиная с того, для которого pred дает True;
- LengthWhile [list,pred] — возвращает число элементов, которые были удалены после того, как pred дало значение True (отсчет с начала списка).
Примеры применения этих функций:
TakeWhile[col2, NumberQ]
(3,6, 4}
LengthWhile[col2, NumberQ]
3
Ряд функций служит для подготовки данных с целью построения гистограмм:
- Frequencies [list] — готовит данные для представления частотной гистограммы;
- QuantileForm[list] — дает отсортированные данные для представления квантилей;
- CumulativeSums [list] — дает кумулятивное суммирование данных списка.
Пример построения гистограммы по данным списка из двойных элементов с помощью функции Frequencies дан на рис. 12.1. Для построения графика при этом использована функция BarChart из пакета расширения Graphics.
Рис. 12.1. Пример построения гистограммы по данным функции Frequencies
Для подготовки гистограмм могут использоваться и следующие функции:
BinCounts[data,{min,max,dx}]
RangeCounts [data, {cl, c2,...} ]
CategoryCounts [data, {el, e2,...} ]
BinLists[data,{min,max,dx}]
RangeLists [data, {cl,c2,...} ]
CategoryLists [data, {el, e2,...} ]
С примерами их работы можно ознакомиться по справочной системе Mathenatica, содержащей полное описание данного подпакета.
Статистика распределений — DescriptiveStatistics
В подпакете DescriptiveStatistics сосредоточены наиболее важные функции по статистике распределений:
- CentralMoment (data, r) — возвращает центральный момент данных data порядка r;
- Mean [data] — возвращает среднее значение данных data;
- MeanDeviation [data] — возвращает среднее отклонение данных;
- Median [data] — возвращает центральное значение (медиану) данных;
- MedianDeviation [data] — возвращает абсолютное отклонение (от медианы) данных;
- Skewness [data] — возвращает коэффициент асимметрии данных;
- StandardDeviation [data] — возвращает стандартное отклонение данных;
- GeometricMean [data] — возвращает геометрическое среднее данных;
- HarmonicMean [data] — возвращает гармоническое среднее данных;
- RootMeanSquare [data] — возвращает среднеквадратичное значение данных;
- Quantile [data, q] — возвращает q-й квантиль;
- InterpolatingQuantile [data, q] — возвращает q-й квантиль, используя при вычислениях интерполяцию данных;
- VarianceData [data] — возвращает среднеквадратичное отклонение данных.
Мы не приводим определений этих функций, поскольку при символьных данных data их легко получить именно в том виде, который реализован в системе Mathematica:
ds={xl,x2,x3} {xl, x2, хЗ}
Mean[ds]
1/3 *(xl + x2 + x3)
MeanDeviation[ds]
1/3 (Abs[xl + — (-xl-x2-x3)] +
Abs[x2+ 1/3 (-xl-x2-x3) + Abs 1/3[-xl-x2-x3) +хЗ])
Median[ds]
x2
Variancefds]
1/2((x1+1/3(-xl + x2 - x3))2 + (x2 + 1/3 (-xl-x2-x3))2 + (— (-xl-x2-x3) + x3)2)
Skewness[ds]
(SQRT(3) ( (xl 4- -1 (-xl - x2 - x3))3 +
(x2+1/3 (-xl-x2-x3))3 + (1/3 (-xl -x2- x3) + x3))2 /
(x2+ 1/3 (-xl-x2-x3))2 +(1/3 (-xl-x2-x3) +х3)2 )^(3/2)
Следующие примеры поясняют действие этих функций при обработке численных данных:
<<Statistics'DescriptiveStatis tics'
data:={10.1,9.6,11,8.2,7.5,12,8.6,9}
CentralMoment[data,2]
1.9525
Mean[data]
9.5
MeanDeviation[data]
1.175
Median[data]
9.3
MedianDeviation[data]
0.95
Skewness[data]
0.374139
StandardDeviation[data]
1.4938
GeometricMean[data]
9.39935
HarmonicMean[data]
9.30131
RootMeanSquare[data]
9.60221
Quantile[data,1]
12
InterpolatingQuantile[data,1]
InterpolatingQuantile[
{10.1, 9.6, 11, 8.2, 7.5, 12, 8.6, 9), 1]
Variance[data]
2.23143
С рядом других, менее распространенных функций этого подпакета можно ознакомиться с помощью справочной системы. Там же даны примеры их применения.
Сглаживание данных — DataSmoothing
В подпакете DataSmoothing определены функции для сглаживания данных, имеющих большой случайный разброс. К таким данным обычно относятся результаты ряда физических экспериментов, например по энергии элементарных частиц, или сигналы, поступающие из космоса. Для того чтобы отсеять информацию из таких данных с большим уровнем шумов и применяется процедура сглаживания. Она может быть линейной (например, усреднение по ряду точек) или нелинейной.
Определены следующие функции сглаживания:
- MovingAverage [data, r] — сглаживание данных data методом усреднения для г точек;
- MovingMedian [data, r] — сглаживание данных data по медиане для г точек (опция RepeatedSmoothing->True используется для повторного сглаживания);
- LinearFilter [data, {c0, cl,..., сr-1} ] — линейная фильтрация (сj— весовые множители);
- ExponentialSmoothing [data, a] — экспоненциальное (нелинейное) сглаживание, параметр а задает степень сглаживания.
Ниже представлены результаты сглаживания символьных данных, выявляющие соотношения, используемые при сглаживании:
ds : = {xl, х2 , хЗ , х4 , х5}
MovingAverage[ds,3]
{1/3* (xl + x2 + x3), — (х2 + хЗ + х4), — (хЗ + х4 + х5)}
MovingMedian[ds,3]
{х2, хЗ, х4}
ExponentialSmoothing[ds, 0.2]
{xl, xl + 0.2 (-xl + x2) , xl+0.2 (-xl + x2) +0.2 (-xl-0.2 (-xl + x2) + x3) , xl+0.2(-xl+x2)+0.2 (-xl-0.2 (-xl + x2) +x3) +
0.2 (-xl-0.2 (-xl+x2) - 0.2 (-xl- 0.2 (-xl + x2) + x3) + x4) , xl+0.2(-xl + x2) +0.2(-xl-0.2(-xl + x2) +x3) + 0.2 (-xl- 0.2 (-xl+x2) -0.2(-xl-0.2(-xl + x2) + x3) + x4) + 0.2 (-xl- 0.2 (-xl+x2) - 0.2 (-xl- 0.2 (-xl+x2) + x3) -
0.2 (-xl-0.2 (-xl+x2) -0.2 (-xl-0.2 (-xl + x2) + x3) + x4) + x5)}
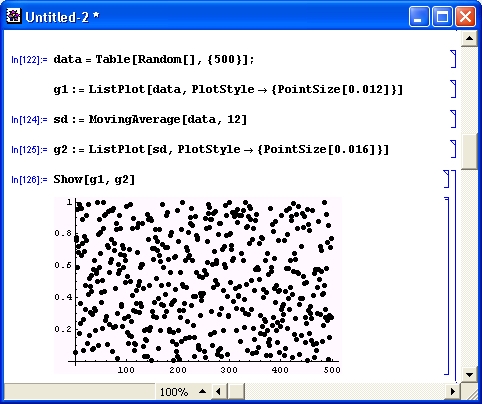
Применение сглаживания усреднением иллюстрирует рис. 12.2. На нем задан массив (таблица) из 500 случайных точек с равномерным распределением и создан графический объект из этих точек в виде кружков малого диаметра. Затем выполнена операция сглаживания (по 12 смежным точкам) и создан графический объект сглаженных точек в виде кружков большего диаметра. Для сопоставления оба объекта построены на одном графике функцией Show.
Рис. 12.2. Пример линейного сглаживания данных из 500 точек
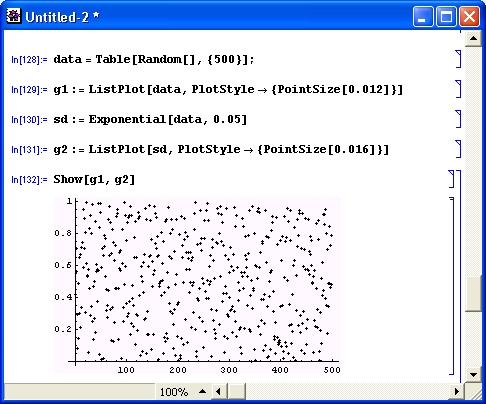
Нетрудно заметить, что сглаженные точки группируются вокруг среднего значения, равного 0.5, тогда как исходные точки разбросаны практически равномерно по всему полю рисунка. Эффективность нелинейного (экспоненциального) сглаживания демонстрирует рис. 12.3. Показанный на этом рисунке документ построен по тому же принципу, что и документ рис. 12.2.
Остальные функции сглаживания можно использовать аналогичным образом. Выбор метода сглаживания зависит от решаемых пользователем задач и остается за ним.
Рис. 12.3. Пример экспоненциального сглаживания
Другие подпакеты расширения Statistics
Подпакет NormalDistribution содержит хорошо известные функции нормального распределения вероятностей и родственные им функции следующих распределений:
- NormalDistribution [mu, sigma] — нормальное распределение;
- StudentTDistribution [r] — T-распределение Стьюдента;
- ChiSquareDistribution [r] — X 2 -распределение;
- FRatioDistribution [rl, r2] — F-распределение.
Для этих и многих других непрерывных распределений заданы также функции плотности распределения, среднего значения, среднеквадратичного отклонения, стандартного отклонения, вычисления коэффициента асимметрии и т. д. Целый ряд таких функций задан и в подпакете ContinuousDistributions для ряда функций непрерывного распределения. Мы не приводим их, поскольку они подобны функциям обработки списков, описанным выше.
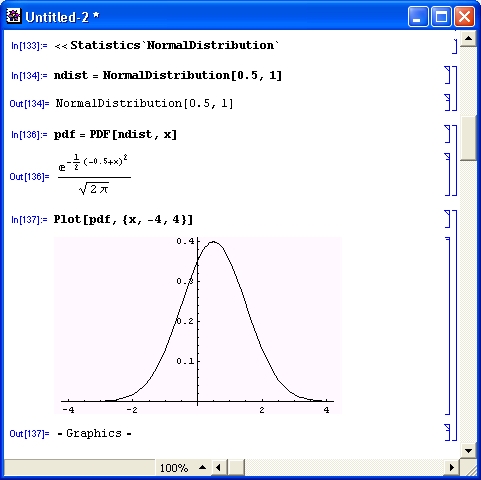
Рисунок 12.4 иллюстрирует получение выражения для плотности нормального распределения pdf и получение графика плотности этого распределения со смещенной вершиной.
Подпакет DiscreteDistributions содержит подобные функции для дискретного распределения вероятностей (Пуассона, биномиального, гипергеометрического и иных распределений). Таким образом, три упомянутых подпакета охватывают практически все имеющие применение законы распределения. Функции для оценки доверительных интервалов сосредоточены в подпакете Confidencelntervals.
Рис. 12.4. Пример работы с функцией нормального распределения
В подпакете HypothesisTests сосредоточено сравнительно небольшое число хорошо известных функций для выполнения тестов проверки статистических гипотез. Загрузка пакета и проведение теста на среднее значение показаны ниже:
<<Statistics` HypothesisTests`
datal = {34, 37, 44, 31, 41, 42, 38, 45, 42, 38};
MeanTest[datal, 34, KnownVariance -> 8]
QneSidedPValue -> 3.05394 x 10-9 ...
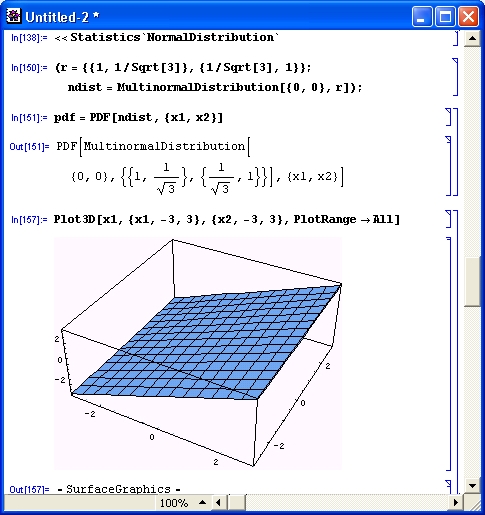
У специалистов в области статистики интерес вызовут подпакеты MultiDescriptive-Statistics и MultinormalDistribution с многочисленными функциями многомерных распределений. Они позволяют оценивать статистические характеристики объектов, описываемых функциями нескольких переменных. Рисунок 12.5 поясняет загрузку подпакета MultinormalDistribution, получение выражения для плотности нормального распределения по двум переменным xl и х2 и получение трехмерного графика для плотности такого распределения.
Подпакет Common используется остальными подпакетами пакет Statistics.
Рис. 12.5. Получение аналитического выражения и графика нормального распределения по двум переменным
gl12-1.jpg

gl12-2.jpg
gl12-3.jpg
gl12-4.jpg
gl12-5.jpg
3. Регрессия
Регрессия
Линейная регрессия общего вида — LinearRegression
В подпакете LinearRegression имеются расширенные функции для проведения линейной регрессии общего вида — в дополнение к включенной в ядро функции Fit. Прежде всего это функция Regress:
- Regress [data, { I, х, х^2 }, х] — осуществляет регрессию данных data, используя квадратичную модель;
- Regress [data, {I, x1, x2, xlx2 }, {x1, x2 }] — осуществляет регрессию, используя в ходе итераций зависимость между переменными x 1 и х 2 ;
- Regress [data, {f 1, f2,...}, vars] — осуществляет регрессию, используя модель линейной регрессии общего вида с уравнением регрессии, представляющим линейную комбинацию функций f i от переменных vars.
Данные могут быть представлены списком ординат {у1,у2,...} или списком
{{xll,xl2,...,yl}, {х21,х22,...,у2},...}.
Ниже приведены примеры использования функции Regress:
<<Statistics`LinearRegression`
data={{1,1.9},{2,2.95},{3,4.3},{4,4.8},{5,5}}
{{1, 1.9}, {2, 2.95}, {3, 4.3}, {4, 4.8}, (5, 5}}
(regress = Regress[data, {l,x, x^2}, x] Chop[regress, 10^(-6)])
[Parameter-Table->
| Estimate | SE | TStat | PValue | |
| 1 | 0.1 | 0.421613 | 0.237185 | 0.834595 |
| x | 1.89786 | 0.321297 | 5.90687 | 0.0274845' |
| X 2 | -0.182143 | 0.0525376 | -3.4669 | 0.0740731 |
RSquared->0.988994, AdjustedRSquared ->0.977988,
EstimatedVariance -> 0.0386429, ANOVATable ->
| Model | DF 2 | SumOfSq 6.94471 | MeanSq 3.47236 | FRatio 89.8577 | PValue 0.0110062, |
| Error | 2 | 0.0772857 | 0.0386429 | ||
| Total | 4 | 7.022 |
func = Fit[data, {l,x,.x^2}, x]
0.1 +1.89786x-0.182143x2
Options[Regress]
{RegressionReport -> SurnmaryReport, IncludeConstant -» True, BasisNames->Automatic, Weights->Automatic, Tolerance->Automatic, ConfidenceLevel->0.95}
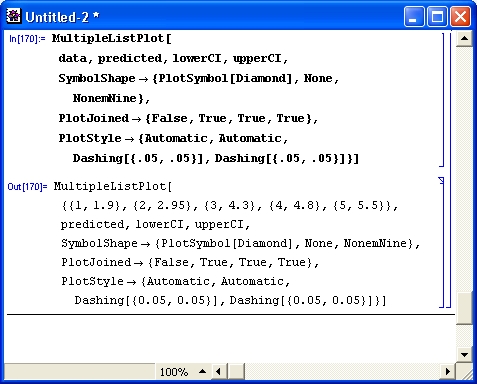
На рис. 12.6 показан еще один пример проведения регрессии, сопровождаемой графической визуализацией с помощью функции MultipleListPlot.
Риc. 12.6. Пример проведения регрессии с графической визуализацией
Пакет линейной регрессии содержит и ряд иных функций, с которыми можно ознакомиться с помощью справочной базы данных системы Mathematica. Напоминаем еще раз, что сама функция при линейной регрессии может быть нелинейна, она является линейной только относительно искомых коэффициентов регрессии.
Нелинейная регрессия — NonlinearFit
В подпакете NonlinearFit содержатся функции для выполнения нелинейной регрессии общего вида:
- NonlinearFit[data,model,variables,parameters] — выполняет регрессию по заданной модели (формуле) model с переменными variables и параметрами parameters для заданных данных data;
- NonlinearRegress[data,model,variables,parameters] —выполняет регрессию по заданной модели (формуле) model с переменными variables и параметрами parameters для заданных данных data с выдачей списка диагностики.
Данные могут быть представлены списком ординат {у1,у2,...} или списком {{x11,x12,..., yl}, {х21, х22,..., у2},...}. В ходе регрессии минимизируются заданные параметры, так что заданная модель регрессии приближает данные с минимальной среднеквадратичной погрешностью.
На рис. 12.7 показан пример выполнения логарифмической регрессии. При ней модель представлена выражением a*Log[b*x]. Результатом действия функции NonlinearFit является уравнение регрессии в виде этой модели с найденными значениями параметров а и Ь. Представлена также визуализация регрессии в виде графика функции-модели и исходных точек. Следует отметить, что реализация нелинейной регрессии разными методами может давать заметно различающиеся результаты, так что представленные результаты не являются абсолютно строгими.
Рис. 12.7. Пример логарифмической регрессии
Применение функции NonlinearRegress иллюстрирует следующий пример:
NonlinearRegress [data, a*Log[b*x] ,{x},{a,b}]
{BestFitParameters -> {a -> 0.665503, b -4 4. 11893},
ParameterCITable ->
Estimate Asymptotic SE CI
a 0.665503 0.0504167 {0.525524, 0.805482},
b 4.11893 0.806289 {1.88031, 6.35754}
EstimatedVariance -> 0 . 00558058,
DF SumOfSq MeanSq
Model 2 17.7425 8.87126
ANOVATable ->
Error 4 '0.0223223 0.00558058,
Uncorrected Total 6 17.7648
Corrected Total 5 0.994689
1. -0.972212 AsymptoticCorrelationMatrix ->
Curvature
Max Intrinsic 2 . 94314 x lO'16,
FitCurvatureTable -» }
Max Parameter-Effects 2.07792
95. % Confidence Region 0.379478
Как нетрудно заметить, в данном случае выдается отчет о проведении регрессии. Более детальные данные об опциях и обозначениях в отчетах нелинейной регрессии можно найти в справочной базе данных.
Полиномиальная регрессия — PolynomialFit
К сожалению, средства регрессии в Mathematica разбросаны по разным пакетам. Так, в подпакете PolynomialFit пакета NumericalMath определена функция для полиномиальной регрессии:
- PolynomialFit [data, n] — возвращает полином степени п, обеспечивающий наилучшее среднеквадратичное приближение для данных, представленных параметром data. Если data является списком ординат функции, то абсциссы формируются автоматически с шагом 1. Если data является списком координат {xi,yi}, то полином наилучшим образом приближает зависимости
Ниже представлен пример применения функции полиномиальной аппроксимации
<<NumericalMath`PolynomialFit`
р = PolynomialFit[{l,3.9,4.1,8.9,16,24.5,37,50},3]
FittingPolyncmial [ <> , 3]
p[5]
15.8727
Expand[p[x]]
2.35-1.44066x+0.659848x2 +0.0338384x3
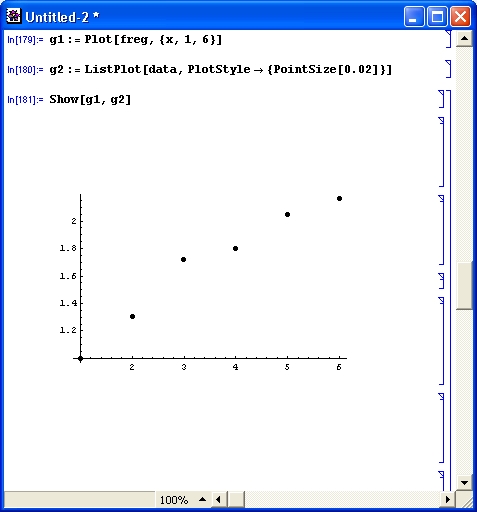
Другой пример с построением графиков исходных точек и аппроксимирующего полинома дан на рис. 12.8.
Рис. 12.8. Графики точек исходной зависимости и аппроксимирующего полинома
Нетрудно заметить, что точки исходной зависимости неплохо (но не точно) укладываются на график полинома.
Сплайны представляют собой набор полиномов невысокой степени, последовательно применяемых к наборам точек аппроксимирующей функции. Чаще всего используется кубическая сплайновая аппроксимация, при которой коэффициенты полиномов выбираются из условий равенства в стыкуемых точках не только значений функции, но также первой и второй производных. Это придает графику сплайна вид плавной кривой, точно проходящей через узловые точки и напоминающей изгибы гибкой линейки (spline в переводе — гибкая линейка).
Подпакет SplineFit пакета NumericalMath содержит функцию для проведения сплайн- регрессии, при которой сплайн-функция проходит максимально близко к аппроксимируемым точкам в смысле наилучшего среднеквадратичного приближения. Для этого используется функция SplineFit [data, type], которая возвращает сплайн функцию для данных data, используя сплайн-аппроксимацию типа type — по умолчанию это кубический сплайн Cube (другие типы — Bezier и CompositeBezier).
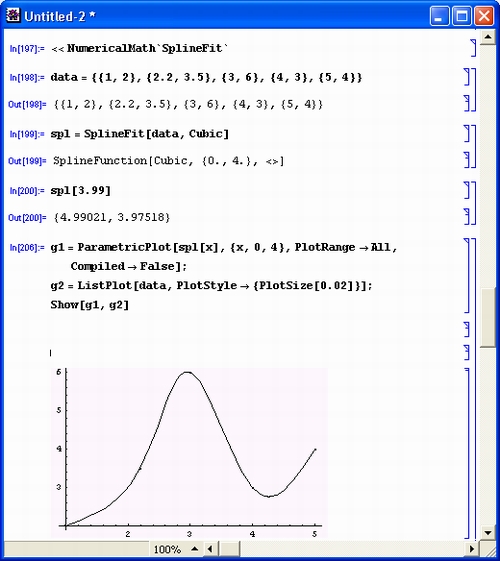
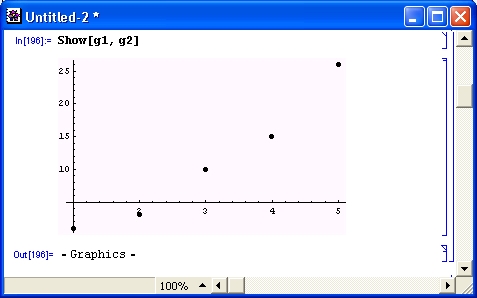
Рисунок 12.9 показывает пример сплайн- регрессии для обычной зависимости у(х), представленной пятью парами точек. На нем построены также графики аппроксимирующей функции и исходных точек.
Рис. 12.9. Пример сплайн- регрессии для зависимости у(х), заданной списком координат своих узловых точек
Рис. 12.10. Пример сплайн-интерполяции параметрически заданной функции
Специфика сплайн- регрессии по функции SplineFit заключается в преобразовании значений как xi, так и yi. Это позволяет представлять сплайнами в общем виде параметрически заданные функции, что поясняет рис. 12.10.
Тригонометрическая регрессия — TrigFit
Многие выражения содержат периодические тригонометрические функции, например sin(X) или cos(X). Помимо обычного спектрального представления выражений, подпакет TrigFit пакета NumericalMath имеет функции для тригонометрической регрессии:
- TrigFit [data, n, x] — дает тригонометрическую регрессию для данных data с использованием косинусов и синусов вплоть до cos(n x) и sin(n x) и с периодом 2л;
- TrigFit [data, n, {x,L}] — дает тригонометрическую регрессию для данных data с использованием косинусов и синусов вплоть до cos(2лuc/L) и sm(2лnx/L) и с периодом I;
- TrigFit [data, n, {x, x0, xl} ] — дает тригонометрическую регрессию для данных data с использованием косинусов и синусов вплоть до cos(2лn(x - х 0 )/ (x-x0)) и sin(2лn(x-x 0 )/(x 1 -x 0 )) и с периодом (x1-x0).
Примеры выполнения тригонометрической регрессии даны ниже:
<<Numerical Math'TrigFit'
data = Table[l+2Sin[x]+3Cos[2x],{x, 0, 2Pi-2Pi/7, 2Pi/7}];
TrigFit[data, 0, x]
1.
TrigFit[data, 1, {x, L}]
l.+ 0.Cos 2[лx/L]+ 2. Sin [2лx/L]
Fit[Transpose!{Range[0, 2Pi-2Pi/7, 2Pi/7], data}],
{1, Cos[x], Sin[x]}, x]
1. - 4.996xl(T16Cos[x] + 2. Sin[x]
TrigFit[data, 3, {x, x0, xl}];
Chop[%]
l. + 3.Cos [4л (x-x0)/(-x0+x1)]+2. Sin [2л (x-x0)/(-x0+x1)]
В этом уроке мы научились:
- Вычислять ортогональные многочлены.
- Выполнять статистические расчеты с помощью пакета Statistics.
- Строить гистограммы.
- Вычислять статистики распределений.
- Использовать статистическую обработку данных.
- Сглаживать данные.
- Выполнять регрессию различного вида.
gl12-10.jpg

gl12-6.jpg
gl12-7.jpg
gl12-8.jpg
gl12-9.jpg