Геометрические расчеты — пакет Geometry

 

В этом разделе описан пакет Geometry, содержащий ряд функций, полезных при выполнении геометрических расчетов. В основном это функции, относящиеся к построению регулярных полигонов на плоскости и полиэдров в пространстве. Кроме того, в пакете есть функции, задающие вращение фигур на плоскости и в пространстве.

Характеристики регулярных полигонов и полиэдров — Polytopes

Подпакет Polytopes содержит ряд функций для регулярных полигонов (многоугольников):

• NumberOfVertices [р] — число вершин углов полигона;
• NumberOfEdges [p] — число сторон полигона;
• NumberOf Faces [p] — число граней полигона;
• Vertices [р] — список координат вершин углов полигона;
• Area [р] — площадь полигона при длине каждой стороны, равной 1;
• InscribeciRadius [р]— радиус вписанной в полигон окружности;
• CircumscribedRadius [р] — радиус описывающей полигон окружности.

В этих функциях наименование полигона р может быть следующим (в скобках дано число сторон):

Digon (2)

Triangle (3)

Square (4)

Pentagon (5)

Hexagon (6)

Heptagon (7)

Octagon (8)

Nonagon (9)

Decagon (10,)

Undecagon (11)

Dodecagon (12)

На рис. 11.20 показаны примеры применения некоторых из этих функций и построение крупными точками вершин полигона — Пентагона (пятиугольника).

Для объемных фигур — полиэдров — имеются следующие функции:

• NumberOfVertices [р] — число вершин углов полиэдра;
• NumberOfEdges [р] — число сторон полиэдра;
• NumberOf Faces [р] — число граней полиэдра;
• Vertices [p] — список координат вершин углов полиэдра;
• Area [p] — площадь полиэдра при длине каждой стороны, равной 1;
• InscribedRadius [р] — радиус вписанной в полиэдр окружности;
• CircumscribedRadius [р] — радиус окружности, описывающей полиэдр;
• Volume [p] — объем полиэдра;
• Dual[p] — дуальный полиэдр;
• Schlafli[p] — символ полиэдра.

Рис. 11.20. Примеры работы с функциями полигонов

Здесь наименование полиэдра может быть следующим:

Tetrahedron (4)

Cube (6)

Octahedron (8)

Didecahedron (12)

Icosahedron (20)

Примеры применения функций полиэдров представлены ниже:

Volume[Octahedron]

(Корень из 2) /3

Vertices [Octahedron]

{{0, 0, 1.41421}, {1.41421, 0, 0}, {0, 1.41421, 0},

{0, 0, -1.41421}, {-1.41421, 0, 0}, {0, -1.41421, 0}}

Dual [Octahedron]

Cube

InscribedRadius [Octahedron]

1/(Корень из 6)

GircumscribedRadius [Octahedron]

1/(Корень из 2)

 

Вращение фигур на плоскости и в пространстве — Rotations

Для задания поворота плоских фигур на заданный угол в подпакете Rotations заданы следующие функции:

• RotationMatrix2D[theta] — дает матрицу для поворота на угол theta в двух измерениях;
• Rotate2D [vec, theta] — поворачивает вектор vec по часовой стрелке на угол theta;
• Rotate2D[vec,theta,{x,y}] — поворачивает вектор vec по часовой стрелке на угол theta относительно точки с координатами {х, у}.

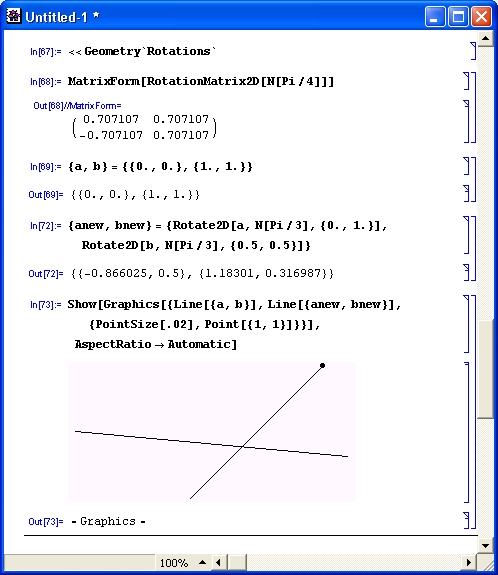
Рисунок 11.21 иллюстрирует работу с этими функциями.

Рис. 11.21. Работа с функциями поворота

Аналогичные функции существуют и для поворота трехмерных фигур:

• RotationMatrix3D [psi, theta,phi] — дает матрицу поворота на заданные углы в трехмерном пространстве;
• Rotate3D [vec, psi, theta, phi] — поворачивает вектор vec на заданные углы в трехмерном пространстве;
• Rotate3D [vec, psi, theta, phi,{x,y,z}]— поворачивает вектор vec на заданные углы в трехмерном пространстве относительно точки с координатами {х,у, z}.

Приведем пример вычисления матрицы трехмерного поворота:

RotationMatrix3D[Pi, Pi/2, Pi/6]

{{-(Корень из 3)/2,0,1/2 }},{1/2,0,(Корень из 3)/2},{ 0,1,0,}}