Урок 11. Математические пакеты расширения
Урок 11. Математические пакеты расширения
1. Математические пакеты расширения
Математические пакеты расширения
- Пакет алгебраических функций Algebra
- Пакет вычислительных функций Calculus
- Пакет дискретной математики DiscreteMath
- Геометрические расчеты — пакет Geometry
- Линейная алгебра — пакет LinearAlgebra
- Расширение в теории чисел — пакет NumberTheory
- Численные расчеты — пакет NumericalMath
Начиная с этого урока, мы переходим к изучению стандартных пакетов расширения (Standard Add-on Packages), которые встроены в системы Mathematica 3/4. Они не требуют отдельной инсталляции, но перед использованием их средств пакеты надо объявлять. Стандартные пакеты расширений содержат примерно столько же дополнительных средств, сколько их содержится в ядре, — то есть тоже порядка тысячи. Применение пакетов расширения особенно эффективно, если оно производится достаточно опытными пользователями.
Общие замечания по пакетам расширения
Пакеты расширения системы Mathematica (Add-ons) являются наборами файлов с расширением .т, написанными на языке программирования системы и объединенными под именами соответствующих пакетов. Пакеты добавляют в систему ряд функций, которые отсутствуют в ядре системы. Они могут модифицироваться и создаваться пользователями, что обеспечивает легкую адаптацию системы под задачи конкретного пользователя.
Применение пакетов имеет три основные особенности:
- необходимо предварительно объявлять загрузку пакета или отдельных его частей — подпакетов или функций;
- скорость вычислений для функций пакетов несколько ниже, чем для функций ядра;
- модификация функций пакетов пользователем может нарушить программную совместимость, что не позволит работать с ними в стандартной системе Mathematica и затруднит обмен документами.
В системе Mathematica 3 (и особенно в Mathematica 4) проведена тщательная оптимизация ядра, что позволило перенести часть апробированных функций из пакетов расширений в ядро системы и тем самым существенно повысить скорость их выполнения. Однако пакеты расширения по-прежнему относятся к важным средствам дополнения и модернизации системы. Некоторые функции вызываются из пакетов автоматически — они описаны ранее как средства ядра системы Mathematica 4.
Следует отметить, что систематизация пакетов расширения по содержащимся в них функциям не доведена до совершенства. Например, функции регрессии разбросаны по ряду пакетов расширения. По мере возможности этот недостаток в данной книге устранен.
2. Пакет алгебраических функций Algebra
Пакет алгебраических функций Algebra
Пакет расширения Algebra содержит ряд новых функций для работы с неравенствами, ограниченными полями и полиномами. Для доступа сразу ко всем функциям пакета используется команда «Algebra`.
Загрузка отдельных функций показана в примерах использования этого пакета, описанных ниже.
До сих пор мы сталкивались с решениями уравнений, представленных равенствами. Пакет Algebra дает важное дополнение в виде функций, обеспечивающих работу с неравенствами. Прежде всего это функция SemialgebraicCompo-nents [ineqs, vars], которая определят комплект решений неравенств ineqs по переменной vars.
Приведенные ниже примеры иллюстрируют работу данной функции:
<<Algebra`Algebraiclnequalities`
SemialgebraicComponents[{х (х^2 - 1) (х^3 - 2) > 1}, х]
{-3, 3}
SemialgebraicComponents[{х + у ^ 2 < 5, х/у > 1}, {х, у}]
SanialgebraicCarpanents[(x+у 2 < 5, — x/y>1}, {х, у}]
SemialgebraicComponents[{х ^ 2 + у ^ 2 < 5, х у > 0}, {х, у}]
{{-3/16,-3/16},{3/16,3/16}}
SemialgebraicComponents[{x ^ 2 + y ^ 2/4 + z ^ 2/9 > 1, х ^ 2 + (у - 1) ^ 2 + (2- 2) ^ 2 < 0}, {х, у, z}]
{}
Для решения неравенства служит функция InequalitySolve [expr, var], которая решает неравенство ехрг относительно переменной var.
Следующие примеры иллюстрируют применение данной функции:
<<Algebra` InequalitySolve`
InequalitySolve [х (х^2- 5) (х^2- 6) > 0, х]
-sqrt(6) <х<-sqrt(5) | | 0<х<sqrt(6)| | х>7sqrt(6)
InequalitySolve[x^2/Abs[х- 2] >= 0 && 1/х < х + 1, х]
-1/2(1-sqrt(5)<x<0| | 1/2(-1+sqrt(5)<x<2| | x>2
Функции для представления комплексных данных — Relm
Подпакет Relm обеспечивает переназначение функций комплексной переменно!! для более корректной их работы:
<<Algebra`ReIm`
Re[l/x+l/y]
Re[x]/(Im[x]2+Re[x]2 )+ Re[y]/( Iim[y]2+Re[y]2)
Re[(z + I)^3 + Exp[I z]]
E[mz] Cos[Re[z]] -2 (1+ Im[z])2Re[z] +
Re[z] (-(1+ Im[z])2+Re[z]2)
Im[x] ^= 0; RealValued[f, g]
{f, g)
Im[l/(l- I f[x] g[x])]
f [x] g[x]/(1+ f[x]2g[x]2 )
Im[Sin[a]]
Cos[Re[a]] Sinh[Tm[a]]
Операции в конечных полях — FiniteFields
Поле является алгебраическим понятием, которое может быть определено как множество, имеющее не менее двух элементов, над которыми заданы две бинарные ассоциативные и коммутативные операции — сложения и умножения. Кроме того, для существования поля нужны два особых элемента — нуль 0, задающий правило сложения а + 0 = а, и единица 1 для задания правила умножения а*1 = 1. Определено также понятие противоположного элемента -а, такого что а + (-а) = 0, и обратного элемента а-- 1 , такого что a- 1 а = 1. Поле характеризуется размером р и целым положительным целым d, называемым степенью расширения.
Пакет задает набор функций GF[p] [{k}], GF[p,l] [{k}], GF[p, {0,1}] [{k}], GF[p,d] HGF[p,ilist] [elist], действие которых иллюстрируют следующие примеры:
<<Algebra` FiniteFields`
GF[7][4] + GF[7][6]
{3}7
GF[3,4][1,2,1] GF[3,4][2,2,2,0]
{1, 1, 2, 0}3 GF[5,1][1] + GF[3,4][1,1,1]
{1, 1, 1, 0}3+ (1)5
Вряд ли подробное их описание заинтересует большинство читателей. Специалистов по полям не затруднит более детальное знакомство с этими функциями в разделе Add-ons справочной базы данных. Там же можно найти описание ряда других функций, относящихся к теории конечных полей.
Оценка интервалов изоляции корней полиномов — Rootlsolation
Следующие функции подпакета Rootlsotation позволяют оценивать интервалы изоляции для действительных и комплексных корней полиномов:
- CountRoots [poly, {x,ml,m2} ] — возвращает число корней полинома poly от переменной х в комплексном интервале {ml, m2 };
- RealRootsIntervals [poly] — возвращает разделенный интервал изоляции для вещественных корней полинома poly;
- RealRootsIntervals [polyl,poly2,...] — возвращает разделенные интервалы изоляции для вещественных корней нескольких полиномов;
- ComplexRootsIntervals [poly] — возвращает разделенный интервал изоляции для комплексных корней полинома;
- ComplexlRootsIntervals [polyl, poly2,...] — возвращает разделенные интервалы изоляции для комплексных корней нескольких полиномов;
- Contractlnterval [a,n] — возвращает интервал изоляции для числа а с точностью, задаваемой числом знаков результата п.
Применение этих функций поясняют следующие примеры:
<<Algebra`Rootlsolation`
f = (x^2- 1) (х^2- 3) (х^2- 5); CountRoots [f, {x, 1, 2}]
1
CountRoots[(х^2+2) х^4, {х, -I, 2 I}]
5
CountRoots[х^21- 1, {х, 0, 5 + 10*1}]
5
RealRootlntervals[f]
{{-4, -2}, {-2,.-1}, {-1, -1}, {1, 1}, {1, 2}, {2, 4}}
ComplexRootlntervals[f+5]
{{-1, 0}, {0, 1}, {-7-71, -7/4}, {-7, -7/4 + 7I},
{-7/4, -7I + 7/2}, {-7/4, -7/2 + 7I}}
ComplexRootlntervals[x^3, x^5+l]
{{{-2, 0}, {0, 0),
{-3-31, 0}, {-3, 31}, {-31, 3), {0, 3+31}}, {2, 1, 2, 2, 2, 2}}
Contractlnterval[Root[x^7- 1, 5], 5]
{ 58333/262144 + 511143I/ 524288+ 116665/524288+ 63893I/65536}
N[%]
{-0.222523+ 0.9749281, -0.222521 + 0.974931}
Если конечные поля — понятие достаточно экзотическое, то полиномы встреча- ются сплошь и рядом во многих математических и научно-технических расчетах. В пакете расширения Algebra определен ряд новых операций над полиномами. Начнем их рассмотрение с функции PolynomialExtendedGCD:
- PolynomialExtendedGCD [polyl, poly2 ] — возвращает наибольший общий делитель двух полиномов;
- PolynomialExtendedGCD[polyl,poly2,Modulus->p] —возвращает наи- больший общий делитель двух полиномов по модулю р.
Примеры применения этой функции приведены ниже:
<<Algebra"PolynomialExtendedGCD
PolynomialExtendedGCDlxл2 + 3 х + 2, Expand[(x + 1)(х + 2)], Modulus->7]
{2+ Зх+х2, (0, 1}}
PolynomialExtendedGCD[
Expand[ ((12+1) z^2 + 5 z + I) (I z + 3)], Expand[ ((9+1) z + (3+1)) ((31) z +9)]]
{-31+z,
{- 2261/3341+ 710I/3341( 35/3341- 3951/10023)+ (5959/20046- 20531/20046)z}}
Далее следует функция PolynomialPowerMod [polyl, n, (poly2, р} ], которая является существенно ускоренной версией функции PolynomialMod.
- степени ускорения свидетельствует следующий пример:
<<Algebra`PolynomialPowerMod`
Timing[PolynomialPowerMod[1 + х, 200, х^З + x^2 + 1, Prime[4750]]][[1]], Timing [ PolynomialMod [ (1 + x)^200, x^ + х^2 + 1, Prime [4750] ]][[1]]
{0. Second, 2.37 Second)
В данном случае вычисления по функции PolynomialPowerMod оказались вы- полненными менее чем за 0.01 с, что дает нулевой результат.
Еще одна функция в трех ее модификациях работает с симметричными полиномами:
- SymmetricReduction [ {xl,...,xn}, k] — возвращает симметричный полином степени k по переменным {х1,..., хn);
- SymmetricReduction [f, {xl,...,xn}] — возвращает часть полинома {p,q} по переменным {х1,...,хп}, где f=p+q, причем р есть симметричная часть, q — остаток;
- SymmetricReduction [f, {xl,...,xn}, {s1,..., sn} ] — возвращает часть полинома (p,q) попеременным {xl, ...,xn}, где элементарный симметричный полином представляет список {s1,..., sn}.
Следующий пример поясняет создание симметричного полинома 4-й степени по переменным {х,у, z,w,t}:
<<Algebra` SymmetricPolynomials`
SyiranetricPolynomial[{x, y, z, w, t}, 4]
twxy+ twxz+ twyz+txyz+wxyz
Действие других функций поясняют следующие примеры:
SynraetricReduction[(х + у)^2 + (х + z)^2 + (z + у)^2, {х, у, z}]
{2 (х+у+ z)2- 2 (xy+xz+yz), 0}
SymmetricReduction[х^5 + у^5 + z^4, {х, у, z}, {s1, s2, s3}]
{s15- 5s13s2 + 5s1s22+ 5sl2s3- 5s2s3, z4-z5}
Преобразование полиномов в схему Горнера — Horner
Подпакет Horner в системе Mathematica 4 реализует хорошо известную схему вычисления полиномов — схему Горнера. При ней операции возведения в степень заменяются операциями умножения. Для этого служит функция Horner:
- Horner [poly] — устанавливает полином poly в форму Горнера;
- Horner [poly, vars] — устанавливает полином ряда переменных vars в форму Горнера.
Примеры преобразования полиномов в схему Горнера:
<<NumericalMath`Horner`
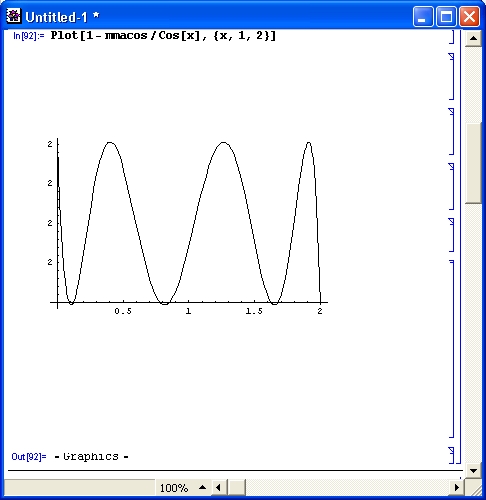
Horner[ 11 х^3 -4 х^2 + 7 х + 2 ]
2+ х (7 + х (-4 + 11х))
Horner[ а х^3 + bх^2 + с х + d, х ]
d+ х (с + х (b + ах))
Horner[ х^(1/3) + х + х^(3/2) ]
Схема Горнера может использоваться и для отношения полиномов:
Horner [polyl/poly2] и Horner [polyl/poly2, varsl,vars2] .
Эти функции можно использовать для улучшенного представления аппроксимации Паде, что демонстрирует следующий пример:
<<Calculus ` Fade`
approx = Padef Exp[Log[x] -х] , {х, 0, 3, 2}]]
Horner[ approx ]
Переход к схеме Горнера дает ряд преимуществ перед обычным вычислением полиномов: уменьшается время вычислений, повышается их точность, уменьшается вероятность расхождения численных методов, в которых используются полиномы. В системе Mathematica 3 подпакет Corner находился в пакете расширения NumberMath, что было не вполне логично.
3. Пакет вычислительных функций Calculus
Пакет вычислительных функций Calculus
Пакет расширения Calculus содержит представительный набор функций для решения дифференциальных уравнений, задания функций единичного скачка и импульса, выполнения операций с векторами, преобразований Фурье и Лапласа, выполнения спектрального анализа и синтеза, расширенного вычисления пределов и проведения аппроксимаций аналитических функций. Для открытия пакета используется команда Calculus`
Решение дифференциальных уравнений — DSolvelntegrals
Многие нелинейные дифференциальные уравнения не имеют общего решения. В под-пакете DSolvelntegrals определены функции, позволяющие найти решения в форме полного интеграла:
- Completelntegral [eqn, u [х, у,...], {х, у...} ] — создает полный интеграл для дифференциального уравнения, касательного к и [х, у,...];
- Differential Invariants [ {eqnsl, eqns2,...}, {u [х] , v [х] ,...}, х} — возвращает список дифференциальных инвариантов для простых переменных {u[x] ,v[x] ,...} и х;
- Differential Invariants [ {eqnsl, eqns2,...}, {u, v,...}, х} — возвращает список дифференциальных инвариантов для простых переменных {u, v,...} и х;
Применение этих функций поясняют следующие примеры:
<<Calculus`DSolvelntegrals`
Completelntegral[
Derivative[0, 1][u][х, у] == (u[x, у] +
x^2*Derivative[l, 0][u][x, y]^2)/y, u[x,y], {х,у}]
Completelntegral[-u[x, у] +
(2 + y)*Derivative[0, 1][u] [x, y] +
x*Derivative[l, 0][u][x, y] + 3*Derivative[l, 0][u][x, y]^2 == 0,
u[x,y], {x,y}, IntegralConstants->F]
Differentiallnvariants[
{U`[X] == -(U[X] (U[X] +V[X])),
V`-[x] == V[x] (u[x] +V[x])},{u, v}, x]
Дельта-функция Дирака — DiracDelta
В подпакете DiracDelta системы Mathematica 3 задано определение двух полезных функций Дирака:
- UnitStep [х] — возвращает функцию с единичным скачком при х = 0 (дает значение 0 при х < 0 и 1 при х > 1);
- DiracDelta [x] — возвращает дельта-функцию Дирака, которая является импульсом с единичной площадью, бесконечно малой шириной в точке х = 0 и бесконечно большой амплитудой.
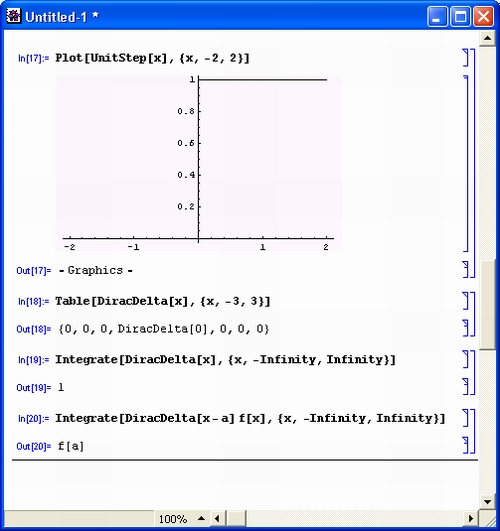
Рисунок 11.1 поясняет применение этих функций. Функция UnitStep имеет простую графическую иллюстрацию, тогда как построение графика функции DiracDelta в принципе невозможно — эта функция представляет собой линию бесконечно большой высоты в точке х - 0. Обратите внимание на то, что интеграл от функции Дирака при интегрировании от -°° до +°° равен 1.
Рис. 11.1. Робота с функцией единичного скачка и дельта-функцией Дирака
Обе описанные функции широко применяются при решении задач автоматического регулирования и при математическом моделировании систем и устройств. Поэтому в системе Mathematica 4 они перешли в разряд встроенных функций.
Улучшенное вычисление пределов — Limit
Подпакет Limit не создает новых функций. Он просто переопределяет встроенную функцию Limit, так что ограничимся примерами его применения:
<<Calculus` Limit`
Limit[Е^х^х/ Е^х^(2 х), x->Infinity]
0
Limit [Е^х^х— Е^х^ (2 х) , x->Infinity]
-бесконечность
Limit[E:x ExpIntegralE[2, ArcTan[E^x]- Pi/2] -E^x- x, x->Infinity]
1 - EulerGamma - I л
Limit[Zeta[l+x, v] - 1/x, x->0]
-PolyGamma[0, v] ,
Limit[x^0 PolyGamma[2,x], x->Infinity] .
0
Limit[x^2 PolyGamma[2,x], x->Infinity]
-1
Limit[x^3 PolyGamma[2,x], x->Infinity]
-бесконечность
Работа скорректированной функции наиболее эффективна при вычислении пределов от выражений, содержащих специальные математические функции, и пределов при х, стремящемся к бесконечности.
Рациональная аппроксимация аналитических функций — Fade
Полиномиальная аппроксимация и обычное разложение функций в ряд Тейлора нередко дают слишком большую погрешность. Уменьшение ее возможно при представлении аппроксимирующей функции в виде отношения двух полиномов разной степени. В подпакете Fade определены две функции для рациональной аппроксимации Паде:
- Pade[f, {x,x0,m,k}] — возвращает выражение для аппроксимации Паде функции f(x) в окрестностях точки х0 в виде отношения двух полиномов степеней m и k;
- EconomizedRationalApproximation [f, {х, {xmin, xmax}, m, k} ] —возвращает выражение для осуществления экономичной рациональной аппроксимации функции f(x) в интервале {xmin, xmax} в виде отношения двух полиномов степеней m и k.
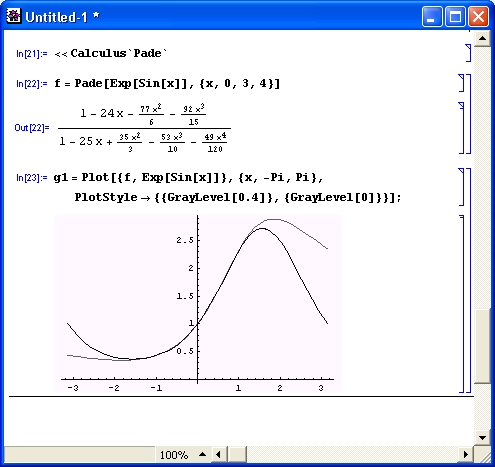
Аппроксимация Паде является расширением полиномиальной аппроксимации, обеспечивающим повышенную точность представления функции. На рис. 11.2 представлен пример выполнения аппроксимации Паде с построением графика исходной функции (темная линия) и аппроксимирующей функции (более светлая линия).
Рис. 11.2. Пример, осуществления аппроксимации Паде
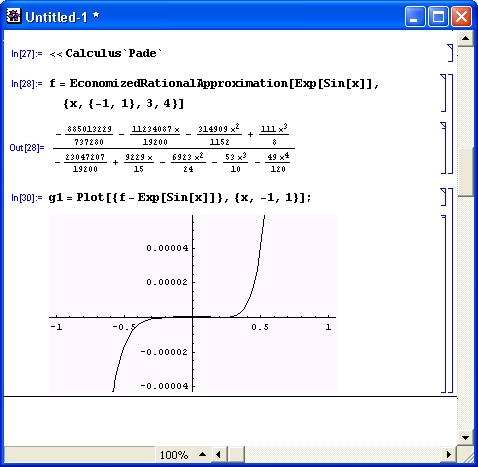
Пример осуществления экономичной рациональной аппроксимации показан на рис. 11.3. Здесь также дана визуализация аппроксимации в виде наложенных друг на друга графиков исходной и аппроксимирующей функций.
Рис. 11.3. Пример осуществления экономичной рациональной аппроксимации
Экономичная рациональная аппроксимация обычно позволяет получить приемлемую погрешность при меньшей степени полиномов числителя и знаменателя аппроксимирующей функции. В ограниченной области {xmin, xmax} эта аппроксимация нередко позволяет получить погрешность менее сотых долей процента (рис. 11.4). На этом рисунке показан график погрешности в виде разности между значениями аппроксимирующей и аппроксимируемой функций.
Рис. 11.4. Пример осуществления экономичной рациональной аппроксимации с построением графика погрешности
Несмотря на обширные возможности выбора средств аппроксимации, все же надо отметить, что они уступают таковым у конкурента системы Mathematica — Maple V R4/R5, где функций для осуществления аппроксимации больше.
Векторный анализ —VectorAnalysis
Подпакет VectorAnalysis содержит множество функций, используемых при выполнении векторного анализа. Здесь надо иметь в виду, что речь идет не о векторах как представителях одномерных массивов, которые рассматривались ранее. В данном случае вектор — это направленный отрезок прямой в пространстве, заданном той или иной системой координат.
Системы координат и их преобразования
Заметная часть функций подпакета VectorAnalysis относится к заданию и преобразованию координат:
- Coordinates [ ] — возвращает имена переменных текущей системы координат;
- Coordinates [coordsys] — возвращает имена переменных системы координат coordsys;
- SetCoordinates [coordsys] — устанавливает систему координат coordsys с текущими переменными;
- Coordinates [coordsys, {vars}] — устанавливает систему координат coordsys с переменными, заданными списком {vars }.
Ниже даны названия систем координат и соответствующие им представления.
| Наименование | Представление |
| Прямоугольные | Cartesian [х, у, z] |
| Цилиндрические | Cylindrical [r, theta, z] |
| Сферические | Spherical [r, theta, phi] |
| Параболические цилиндрические | ParabolicCylindrical [u, v, z] |
| Параболические | Paraboloidal [u, v, phi] |
| Эллиптические цилиндрические | EllipticCylindrical [u, v, z, a] |
| Вытянутые сфероидальные | ProlateSpheroidal [xi, eta, phi, a] |
| Сплющенные сфероидальные | OblateSpheroidal [xi, eta, phi, a] |
| Биполярные | Bipolar[u, v, z, a] |
| Бисферические | Bispherical [u, v, phi, a] |
| Тороидальные | Toroidal [u, v, phi, a] |
| Конические | Conical [lambda, mu, nu, a, b] |
| Конфокальные эллипсоидальные | ConfocalEllipsoidal [lambda, rnu, nu, a, b, c] |
| Конфокальные параболические | ConfocalParaboloidal [lambda, mu, nu, a, bj |
Например, параболическую систему координат можно задать следующим образом:
SetCoordinates[Paraboloidal[x, у, z] ]
Paraboloidal [x, у, z]
{CoordinateSystem, Coordinates[]}
{Paraboloidal, {x, y, z}}
Ряд функций служит для контроля и установки параметров систем координат:
- CoordinateRanges [ ] — возвращает пределы изменения переменных текущей координатной системы;
- Parameters [ ] — возвращает параметры текущей координатной системы;
- ParametersRanges [ ] — возвращает пределы изменения параметров текущей координатной системы;
- CoordinateRanges [coordsys] — возвращает пределы изменения переменных координатной системы coordsys;
- Parameters [coordsys] — возвращает параметры координатной системы coordsys;
- ParametersRanges [coordsys] — возвращает пределы изменения параметров координатной системы coordsys;
- SetCoordinates [coordsys, {vars,param} ] — устанавливает параметры текущей координатной системы как параметры coordsys с переменными vars и параметрами param.
Ниже представлены примеры применения этих функций:
CoordinateRanges[]
{0<Х<бесконечности,0<Y<бесконечность,-л<Z<=л}
Parameters[]
{}
ParameterRanges[ ]
Coordinates[Conical], CoordinateRanges[Conical]
{{Llanibda, Мmu, Nnu}, {-бесконечность< Llambda< бесконечность, l< Mmu2 < 4, Nnu2< 1}}
Parameters[Bipolar],ParameterRanges[Bipolar]
{{1}, 0< #1<бесконечность}
Для преобразования координат служат следующие функции:
- CoordinatesToCartesian [pt] — преобразование текущих координат в декартовы;
- CoordinatesToCartesian [pt, coordsys] — преобразование координат coordsys в декартовы;
- CoordinatesFromCartesian [pt] — преобразование из декартовых координат в текущие;
- CoordinatesFromCartesian [pt, coordsys] — преобразование из декартовых координат в координаты coordsys.
Эти примеры демонстрируют преобразования координат:
CoordinatesToCartesian[{I, Pi/3, Pi/3}, Spherical]
CoordinatesToCartesian [u, v, phi}, Bipolar]
CoordinatesFromCartesian [ {x, y, z} , Bipolar]
{-2Im[ArcCoth[x+ Iy]] , 2Re[ArcCoth[x+ Iy] ] , z}
Функции векторного анализа
Помимо функций для задания и преобразования систем координат подпакет Vector An a lysis содержит ряд функций собственно векторного анализа:
- DotProduct [vl, v2] — возвращает скалярное произведение векторов vl и v2, заданных в текущей системе координат;
- CrossProduct [vl,v2] — возвращает векторное произведение векторов vl и v2, заданных в текущей системе координат;
- ScalarTripleProduct [vl, v2, v3 ] — возвращает тройное скалярное произведение для векторов vl, v2 и v3, заданных в текущей системе координат;
- DotProduct [vl, vl, coordsys ] — возвращает скалярное произведение векторов vl и v2, заданных в системе координат coordsys;
- CrossProduct [vl, v2, coordsys] — возвращает векторное произведение векторов vl и v2, заданных в системе координат coordsys.
Примеры выполнения этих операций представлены ниже:
SetCoordinates[ParabolicCylindrical[ ]]
ParabolicCylindrical[Uu, W, Zz]
DotProduct[{1.2, 1.1, 0}, {5.4, -2, 1.2}]
-12.8093
CrossProduct[{1.2, 1.1, 0}, {5.4, -2, 1.2}]
{-1.78157, 0.0774597, -17.8476}
ScalarTripleProduct[{1, 0, 1}, {1, 1, 0}, {0, 1, 1}, Cartesian]
2
Для вычисления производной дуги служат функции:
- ArcLengthFactor [ { fx, f у, f z}, t] — дает дифференциал длины дуги, заданной параметрически с параметром t в текущей системе координат;
- ArcLengthFactor [ {fx, f у, fz}, t, coordsys] — дает дифференциал длины дуги, заданной параметрически с параметром t в системе координат coordsys
Примеры вычисления дифференциалов и длин дуг с помощью этих функций:
param = {Cos[t], Sin[t], t}
{Cos[t], Sin[t], t}
ArcLengthFactor[ param, t, Cartesian] //Simplify
корень из 2
f[x_, y_, z_] := x^2 y^2 z
Integrate[ f[param] ArcLengthFactor[
param, t, Cartesian], {t, 0, 2 Pi}] // Simplify
Ряд функций служит для создания матрицы Якоби (матрицы частных производных) и вычисления относящихся к ней понятий:
- JacobianMatrix [ ] — возвращает матрицу Якоби, определенную в текущих координатах;
- JacobianMatrix [pt] — возвращает матрицу Якоби в точке pt и в текущих координатах;
- JacobianMatrix [coordsys] — возвращает матрицу Якоби, определеннук в системе координат coordsys;
- JacobianMatrix [pt, coordsys] — возвращает матрицу Якоби в точке pt, определенную в системе координат coordsys;
- JacobianDeterminant [], JacobianDeterminant [pt] и т. д. — вычисление детерминанта матрицы Якоби при указанных выше определениях;
- ScaleFactor [ ], ScaleFactor [pt] и т. д. — вычисление масштабного фактора при указанных выше определениях.
Применение этих функций поясняют следующие примеры:
JacobianMatrix[Cartesian[x, у, z]]
{{1, 0, 0}, {0, 1, 0}, {0, 0, 1}}
JacobianMatrix[Spherical[r, t, p] ]
{{Cos[p] Sin[t] , rCos[p] Cos[t] ,-rSin[p] Sin[t]},
{Sin[p] Sin[t] , rCos[t] Sin[p] , rCos[p] Sin[t]},
{Cos[t] , -rSin[t], 0}}
JacobianDeterminant[Spherical[r, t, p] ]
r^2Sin[t]
Integrate[r^2 JacobianDeterminant[ Spherical[r, theta, phi]],
{r, 0, 2}, {theta, 0, Pi}, {phi, -Pi, Pi}]
128n/5
Следующие функции определяют ряд характеристик векторного поля:
- Div[f] — возвращает дивергенцию векторного поля f в текущей системе координат;
- Curl [f ] — возвращает вихрь (ротор) векторного поля f в текущей системе координат;
- Grad[f ] — возвращает градиент векторного поля f в текущей системе координат;
- Laplasian [f] — возвращает лапласиан векторного поля f в текущей системе координат;
- Вiharmonic [f] — возвращает лапласиан лапласиана векторного поля f в текущей системе координат;
- Div [f, coordsys], Curl [f, coordsys] и т. д. — указанные выше функции в системе координат coordsys.
Приведем примеры использования этих функций:
Laplacian[x*y^2*z^3,ProlateSpheroidal[х, у, z]]
(Csc[y] Csch[x] (y2z3Cosh[x] Sin [у] +
2xyz3Cos[y] Sirih[x] +2xz3Sin[y] Sinh[x] +
6xy2zCsc[y] Csch[x] (Sin[y]2+ Sinh[x]2))) /
(Sin[y]2+Sinh[x]2)
Grad[x^2 y^3 z^4,ProlateSpheroidal[x, у, z]]
Вариационные методы —VariationalMethods
Подпакет VariationaLMethods содержит функции для реализации вариационных методов. Напомним, что вариационные методы заменяют минимизацию функционала, заданного на некотором бесконечномерном линейном пространстве, задачами его минимизации на последовательности конечномерных подпространств. Функционал в системе Mathematica задается следующим образом:
F=
f[u[x], u'(x),x]dx
В данный подпакет включены следующие функции:
- VariationalD [f, u [х] , х] — дает первую вариационную производную для функционала f одной переменной х;
- VariationalD [f, u [х, у,...] , {х, у,...} ] — дает первую вариационную производную для функционала ряда переменных;
- VariationalD [f, {u [х, у,...], v [х, у],...}, {х, у,...} ] — дает список первых вариационных производных для функционала ряда переменных;
- EulerEquations [f, u [х] , х] — дает равенство Эйлера при f с одной переменной;
- EulerEquations [f, u [х, у,...], {х, у,...} ] — дает равенство Эйлера при f с рядом переменных;
- EulerEquations [f, {u [х, у,...] , v [х, у,...],...}, {х, у,...} ] — дает список с равенствами Эйлера при f с рядом переменных;
- Firstlntegral [ f, u [х] , х] — дает первый интеграл с f, определенной для одной переменной х;
- Firstlntegral [f, {u [х, у,...] ,v [х, у,...],...}, {х, у,...} ] — дает первый интеграл при f с рядом переменных;
- Firstlntegral[u] — дает первый интеграл, ассоциированный с переменной и.
Применение данных функций поясняют следующие примеры:
<<Calculus `VariationalMethods`
VariationalD[y[x] Sin[l+y'[x]], y[x], x]
-Cost 1 +У [x]] y'[x] + Sin[l + y'[x]] d+y[x] y'[x])
EulerEquations[ m1^2 theta1[t]^2/2+m g 1 Cos[theta[t]], theta[t], t]
-Im(gSin[theta[t]] + 1 theta''[ t]) == 0
Firstlntegrals[m(r'[t]^2+r[t]^2 phi'[t]^2)/ 2-U[r], r[t],phi[t], t]
{Firstlntegral[phi] ->-mr[ t]2 phi' [ t] , Firstlntegral[t] -> 1/2 (2U[r] + m (r[t]2phi'[t]2 + r^t]2)) }
Помимо указанных функций подпакет содержит функцию VariationalBound для представления границ и значений функционала. Ввиду громоздкости записи параметров этой функции ограничимся примерами ее применения:
VariationalBound[(-u[r] D[r^2 u'[r],r]/r^2-2u[r]^2/r)r^2,
u[r]^2 r^2,u[r], r,0,Infinity,(a-r)E^(-b r),a,b]
{-0.25, (a-> 2., b-> 0.5}}
VariationalBound[-u[x,у](D[u[x,y],x,2]+
D[u[x,y],y,2]) -2u[x,y],u[x,y],x,-a,a,y,-a,a,
(x^2-a^2)(y^2-a^2)(al+a2(x^2+y^2)),al,a2]
С полными возможностями этой функции можно ознакомиться по справочной базе данных (раздел Add-ons).
gl11-1.jpg
gl11-2.jpg
gl11-3.jpg

gl11-4.jpg
4. Пакет дискретной математики DiscreteMath
Пакет дискретной математики DiscreteMath
Пакет DiscreteMath задает набор функций дискретной математики. Это прежде всего функции комбинаторики и работы с графами (более 230 функций). Мы вынуждены рассмотреть их только выборочно.
Комбинаторика и ее функции — Combinatorica и CombinatorialFunctions
Несколько функций комбинаторики (Factorial, Factorial2, Binomial, Multinomial, Pochhammer и Fibonacci) могут использоваться без загрузки пакетов расширения. Рисунок 11.5 демонстрирует работу подпакета Combinatorial-Functions (функции комбинаторики). Определения функций этого пакета есть в справочной базе данных.
Рис. 11.5. Примеры работы с подпакетом функций комбинаторики
Подпакет Combinatorica задает определение ряда функций комбинаторики и теории графов. Ниже представлены имена функций комбинаторики.
| Функции перестановок и сочетаний | |
| Backtrack | BinarySearch |
| Binary Subsets | DerangementQ |
| Derangements | Distinct Permutations |
| EquivalenceClasses | EquivalenceRelationQ |
| Equivalences | Eulerian |
| FromCycles | FromlnversionVector |
| GrayCode | HeapSort |
| Heapify | HideCycles |
| Index | InversePermutation |
| Inversions | InvolutionQ |
| Josephus | Ksubsets |
| Lexicographic Permutations | LexicographicSubsets |
| MinimumChangePermutations | MultiplicationTable |
| NextKSubset | Next Permutation |
| NextSubset | NthPermutation |
| NthSubset | NumberOf Derangements |
| NumberOf Involutions | NumberOf Permu tat ion sByCycles |
| PermutationGroupQ | PermutationQ |
| Permute | Polya |
| RandomHeap | RandomKSubset |
| RandomPermutation | RandomPermutationl |
| RandomPermutation2 | RandomSubset |
| RankPermutation | RankSubset |
| RevealCycles | Runs |
| SamenessRelation | SelectionSort |
| SignaturePermutation | StirlingFirst |
| StirlingSecond | Strings |
| Subsets | ToCycles |
| ToInversionVector | TransitiveQ |
Следует отметить, что ввиду обилия функций даже в справочной системе даны примеры лишь для избранных функций. Для ознакомления с назначением конкретной функции достаточно исполнить команду ?Имя_функции, например:
<<DiscreteMath`Combinatorica`
?Permute
Permute[l, p] permutes list 1 according to permutation p.
?KSubsets
KSubsets[l, k] gives all subsets of set 1 containing exactly k
elements, ordered lexicographically.
KSubsets[{l, 2, 3, 4, 5}, 2]
{{1, 2}, {1, 3), {1, 4}, {1, 5}, {2, 3), {2, 4}, {2, 5}, {3, 4}, {3, 5}, (4, 5}}
<< DiscreteMath`Combinatorica`
MinimumChangePermutations[{1,2,3}]
{{1, 2, 3}, {2, 1, 3}, {3, 1, 2}, {1, 3, 2}, {2, 3, 1}, {3, 2, 1}}
Map[RankPermutation, Permutations[{1,2,3,4}]]
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23}
InversePermutation[{4,8,5,2,1,3,7,6}]
(5, 4, 6, 1, 3, 8, 7, 2}
Polya[Table[ RotateRight[Range[8],i], {i,8}], m]
1/8 (4m+2m2 +m4 +m8)
Table[NthSubset[n,a,b,c,d], {n,0,15}]
{{}, {a}, {b}, {a, b}, {c}, {a, c}, {b, c}, {a, b, c}, {d}, (a, d}, {b, d}, {a, b, d}, {c, d}, {a, c, d}, {b, c, d}, {a, b, c, d}}
Вторая группа функций комбинаторики представлена следующими функциями.
| Функции разделения, композиции и картин Янга | |
| CatalanNumber | Compositions |
| ConstructTableau | DeleteFromTableau |
| DurfeeSquare | EncroachingListSet |
| FerrersDiagram | FirstLexicographicTableau |
| . Insert IntoTableau | LastLexicographicTableau |
| Longest IncreasingSubsequence | NextComposition |
| Next Part it ion | NextTableau |
| NumberOf Compos it ions | NumberOf Partitions |
| NumberOf Tableaux | PartitionQ |
| Partitions | RandomComposition |
| RandomPartition | RandomTableau |
| TableauClasses | TableauQ |
| TableauxToPermutation | Tableaux |
| TransposePartition | TransposeTableau |
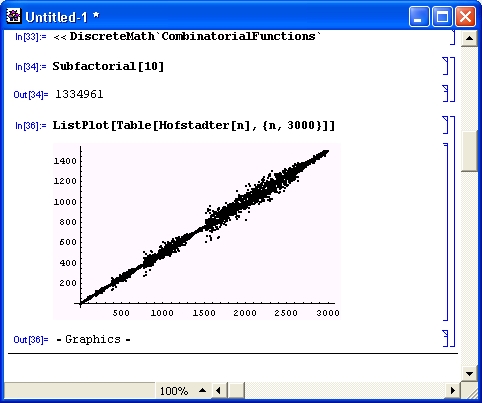
Ha рис. 11.6 показано несколько примеров работы с некоторыми из этих функций.
Рис. 11.6. Примеры работы с функциями разделения, композиции и картин Янга
Этих примеров достаточно, чтобы заинтересованный читатель по их образцу и подобию изучил свойства и возможности нужных ему функций комбинаторики.
Mathematica имеет самые обширные возможности решения задач, связанных с графами. Задание графов и манипуляции с ними также включены в пакет комбинаторики. Они представлены четырьмя группами функций.
| Представление графов | ||
| AddEdge | AddVertex | Breadth'FirstTraversal |
| ChangeEdges | ChangeVertices | CircularVertices |
| CompleteQ | Contract | DeleteEdge |
| DeieteVertex | DepthFirstTr aversal | Diameter |
| DilateVertices | Distribution | Eccentricity |
| Edges | EmptyQ | FromAd j acencyLists |
| FromOrderedPairs | FromUnorderedPairs | GraphCenter |
| GraphComplement | InduceSubgraph | M |
| MakeSimple | MakeUndirected | Normal! zeVerticesPointsAndLines |
| Pseudograph | RadialEmbedding | Radius |
| RankGraph | RankedEmbedding | ReadGraph |
| RemoveSelf Loops | RootedEmbedding | RotateVertices |
| ShakeGraph | ShowGraph | ShowLabe 1 edGr aph |
| SimpleQ | Spectrum | SpringErrbedding |
| ToAdjacencyLists | ToOrderedPairs | ToUnorderedPairs |
| TranslateVertices | UndirectedQ | UnweightedQ |
| Vertices | WriteGraph | |
Одной из самых важных функций этой группы является функция ShowGraph (показать граф). Она обеспечивает визуальное представление графа, заданного аргументом функции. Покажем работу избранных функций этой группы на нескольких примерах.
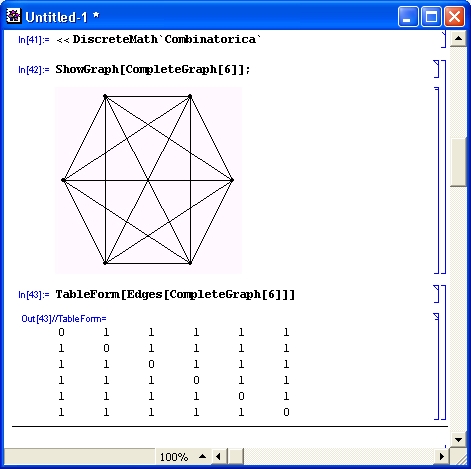
На рис. 11.7 показано построение полного графа и его таблицы. Параметром графа является число 6, характеризующее число узловых точек графа, соединенных друг с другом.
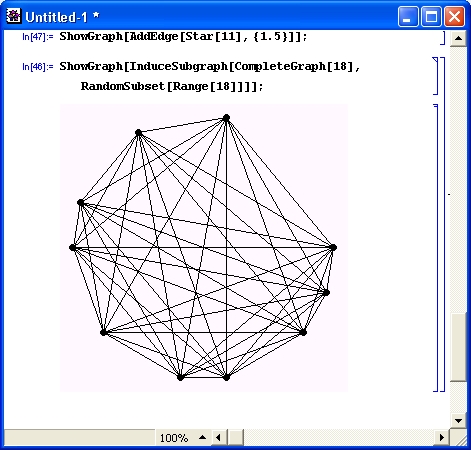
Изменяя значение параметра графа, можно получить множество других графов. На рис. 11.8 показан вид двух разных графов. Верхний граф — многолучевая звезда с добавленным отрезком, полученная с помощью функции AddEdge. Первый аргумент задает исходный граф (в нашем случае — звезду с 11 узлами), а второй — соединяемые отрезком прямой точки. Нижний рисунок иллюстрирует построение подграфа.
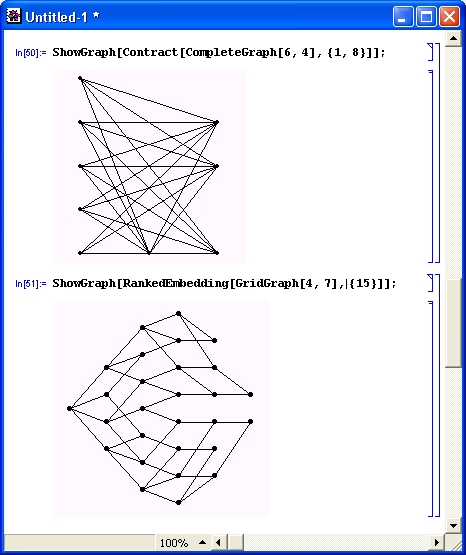
Еще пара графов представлена на рис. 11.9. Этот рисунок иллюстрирует применение функций Contract и GridGraph. Последняя из них строит сеточный граф.
Рис. 11.7. Пример построения полного графа и его таблицы
Рис. 11.8. Построение графа звезды и подграфа
Рис. 11.9. Примеры построения графов с помощью функций Contractn GridGraph
Приведенный выше набор функций позволяет строить практически любые виды графов и обеспечивает высокую степень их визуализации.
| Создание графов | ||
| CartesianProduct | CirculantGraph | CodeToLabeledTree |
| CompleteGraph | Cycle | DegreeSequence |
| EmptyGraph | ExactRandomGraph | ExpandGraph |
| Functional-Graph | GraphDif ference | Graphlnter section |
| GraphJoin | GraphPower | GraphProduct |
| GraphSum | GraphUnion | GraphicQ |
| GridGraph | Hypercube | IncidenceMatrix |
| IntervalGraph | LabeledTreeToCode | LineGraph |
| MakeGraph | NthPair | Path |
| RandomGraph | RandomTree | RandomVertices |
| RealizeDegreeSequence | RegularGraph | RegularQ |
| Turan | Wheel | - |
Рисунок 11.10 показывает применение функций GraphUnion (верхний график) и GraphProduct (нижний график).
Рис. 11.10. Создание графов с помощью функций GraphUnion и GraphProduct С действием других функций нетрудно ознакомиться самостоятельно.
| Свойства графов | ||
| ArticulationVertices | Automorphisms | Bi Connected Components |
| BiconnectedQ | BipartiteQ | Bridges |
| ChromaticNumber | Chromatic Polynomial | CliqueQ |
| Connected Components | ConnectedQ | DeBruijnSequence |
| DeleteCycle | EdgeChromatic Number | EdgeColoring |
| EdgeConnectivity | Element | EulerianCycle |
| EulerianQ | ExtractCycles | FindCycle |
| Girth | GraphPower | HamiltonianCycle |
| HamiltonianQ | Harary | HasseDiagram |
| IdenticalQ | Independent SetQ | IsomorphicQ |
| Isomorphism | IsomorphismQ | MaximumClique |
| Maximum lndependentSet | Minimum VertexCover | OrientGraph |
| PartialOrderQ | PerfectQ | SelfComplementaryQ |
| StronglyConnected Components | TopologicalSort | TransitiveClosure |
| TransitiveReduction | TravelingSalesman | TravelingSalesman Bounds |
| TreeQ | Trianglelnequality | TwoColoring |
| VertexColoring | VertexConnectivity | VertexCoverQ |
| WeaklyConnected Components | ||
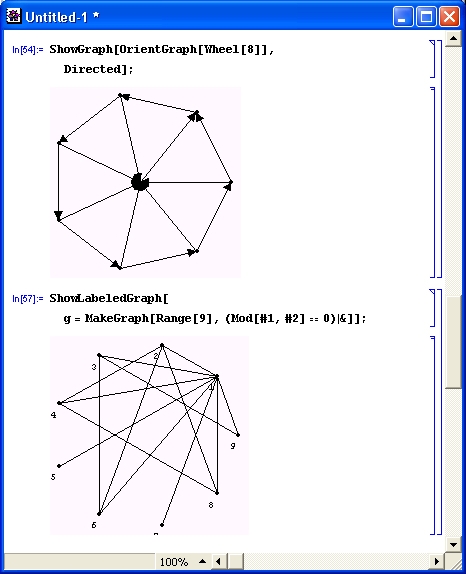
Рисунок 11.11 (сверху) показывает применение функции OrientGraph для построения ориентированного графа, который представляется стрелками. Там же (снизу) показано применение функции ShowLabeledGraph для построения графа с маркированными числами вершинами. Напомним, что функция ShowGraph позволяет наблюдать графы без маркировки вершин.
Рис. 11.11. Построение графов — ориентированного (сверху) и с маркированными вершинами (снизу)
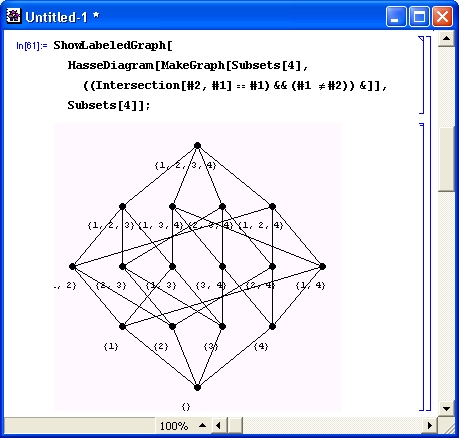
Построение широко используемой в теории графов диаграммы Хассе (Hasse) иллюстрирует рис. 11.12.
| Алгоритмическая теория графов | ||
| AllPairsShor test Path | BipartiteMatchin | Cofactor |
| Dijkstra | FindSet | GraphPower |
| InitializeUnionFind | Maxima IMatching | MaximumAntichain |
| MaximumSpanningTree | MinimumChainPartition | MinimumSpanningTree |
| NetworkFlowEdges | Networks' low | NumberOfSpanningTrees |
| PathConditionGraph | PlanarQ | Shortest PathSpanningTree |
| ShortestPath | StableMarriage | UnionSet |
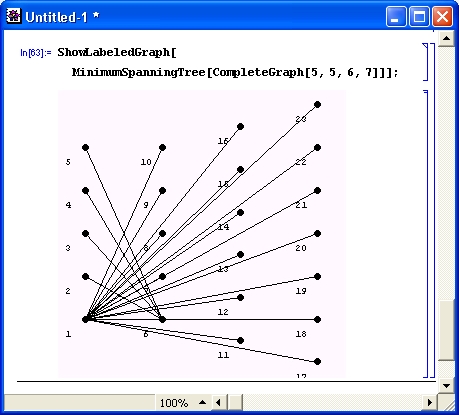
Рисунок 11.13 показывает действие функции MinimumSpanningTree с выводом графа с метками узловых точек.
Риc. 11.12. Построение диаграммы Хассе
Риc. 11.13. Пример применения функции MinimumSpanningTree
В целом следует отметить, что набор функций в области создания, визуализации и теории графов весьма представителен, так что специалисты в области графов могут найти в этом наборе как типовые, так и уникальные средства.
Функции вычислительной геометрии — ComputationalGeometry
В подпакете ComputationalGeometry заданы следующие функции, относящиеся к геометрическим поверхностям:
- ConvexHull [ { {xl, yl...}, {х2, у2,...},...] — вычисляет выпуклость оболочки в точках плоскости;
- DelaunayTriangulation[ {{xl,yl...}, {х2, у2,...},...] — вычисляет триангуляцию Делоне (разбивку на выпуклые треугольники) в точках плоскости;
- DelaunayTriangulationQ [ {{xl, yl...}, {х2, у2,...},...}, trival] — тестирует триангуляцию Делоне в точках плоскости; ,
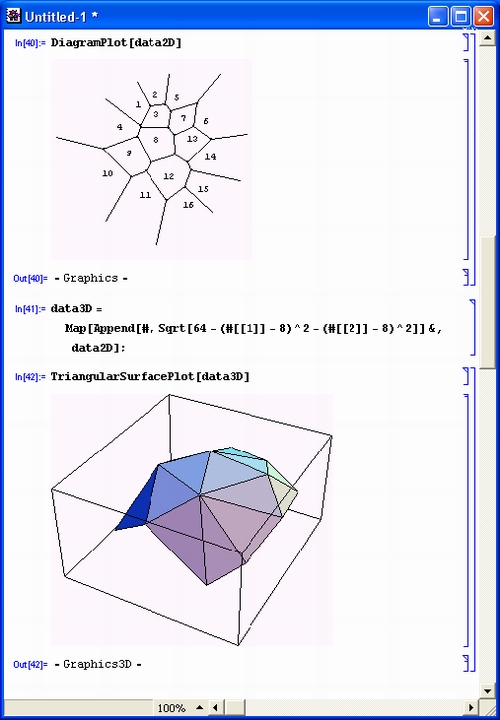
- DiagramPlot [ {{xl, yl...}, {х2, у2,...},...] — построение диаграммы по заданным точкам (после списка параметров возможны спецификации в виде списков diagvert, diagval);
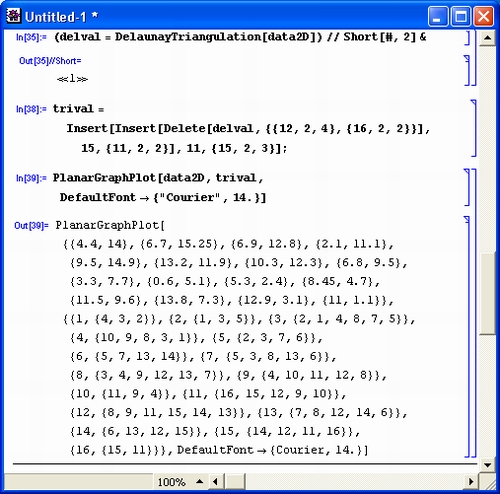
- PlanarGraphPlot [{ {xl, yl...}, {x2, y2,...},...] — построение планарного графа по заданным точкам (после списка параметров возможна спецификация в виде списка indexlist или vals);
- TriangularSurfacePlot [ {{xl,yl, zl}, {x2,y2, z2 },...] — строит поверхность из треугольников по заданным точкам;
- VoronoiDiagramm[ {{xl, yl...}, {х2, у2,...},...] — вычисляет данные для построения диаграммы Вороного.
Примеры применения этих функций приведены ниже:
<<DiscreteMath`ComputationalGeometry`
ConvexHull[{{0,2}, {1,1}, {0,0}, {2,0}, {1,2}}]
{4, 5, 1, 3}
delval = (DelaunayTriangulation[{{l,2J, {0,3}, {1,1}}]) // Short[#,2]&
{{1, {2, 3}}, {2, {3, 1}}, {3, {1, 2}}}
VoronoiDiagram[{{l,2}, {0,3}, {1,1}}]
{{{-0.50000000000000, 1.5000000000000},
Ray [{- 0.50000000000000, 1.5000000000000},
{1.5000000000000, 3.5000000000000}],
Ray [ {- 0.50000000000000, 1.5000000000000},
{2.0000000000000,1.50000000000000}],
Ray[ {- 0.50000000000000, 1.5000000000000},
{-2.5000000000000, 0.50000000000000} ]},
{{1, {1, 3, 2}}, {2, {1, 2, 4}}, {3, {1, 4, 3}}}}
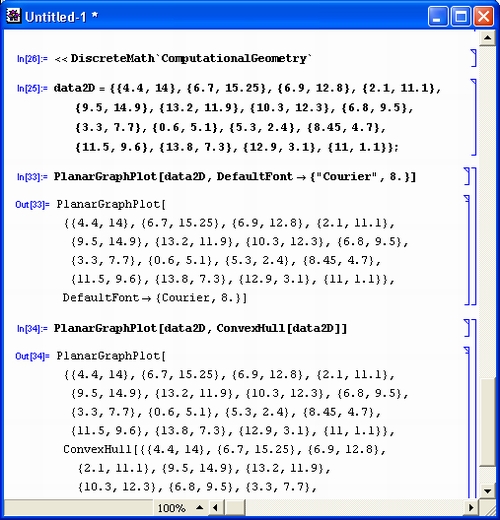
Рисунок 11.14 показывает задание на плоскости массива точек data2D, построение планарного графа и его выпуклой огибающей с помощью функции Convex-Hull.
Рис. 11.14. Пример построения планарного графа и его выпуклой огибающей Выполнение триангуляции Делоне иллюстрирует рис. 11.15.
Рис. 11.15. Выполнение триангуляции Делоне
Наконец, на рис. 11.16 показаны результаты действия еще двух функций — построение диаграммы и триангуляция в пространстве.
Рис. 11.16. Построение диаграммы (сверху) и триангуляция в пространстве (снизу)
Дискретные функции единичного скачка и импульса — KroneckerDelta
В подпакете KroneckerDelta системы Mathematica 3 заданы дискретные функции единичного скачка и единичного импульса:
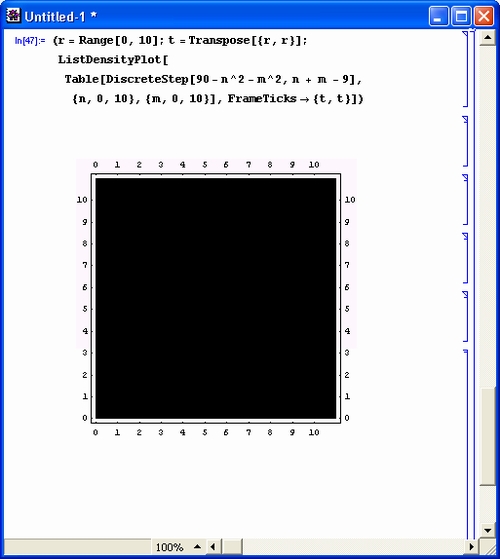
- DiscreteStep [n] — возвращает единичный скачок при целом n=0;
- DiscreteStep [n1, n2,...] — функция многомерного единичного скачка;
- KroneckerDelta [n] — возвращает 1 при целом n=0 и 0 во всех других случаях;
- KroneckerDelta [n1, n2,...] — многомерная функция Кронекера.
Примеры использования этих функций в одномерном варианте представлены ниже:
<<DiscreteMath` KroneckerDelta`
Table[DiscreteStep[n], {n, -3, 3}]
{0, 0, 0, 1, 1, 1, 1}
Table[DiscreteStep[n], {n, -3, 3, 1/2}]
{0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1}
Table[KroneckerDelta[n], {n, -2, 2, 1/2}]
{0, 0, 0, 0, 1, 0, 0, 0, 0}
Sum[KroneckerDelta[n— a]f[n], {n, -Infinity, Infinity}]
f[a]
Sum[( (KroneckerDelta[n]— KroneckerDelta[n-1]) -
(KroneckerDelta[n-1]— KroneckerDelta[n-2]) ) f[n], {n, -Infinity, Infinity}]
f[0]-2f[l] +f[2]
Рисунок 11.17 иллюстрирует применение функции единичного скачка в двумерном случае.
Рис. 11.17. Пример применения функции скачка в двумерном случае
В системе Mathematica 4 функция KroneckerDelta стала встроенной. В данный подпакет входят еще две функции:
- SimplifyDiscreteStep [ехрr] — упрощение выражения ехрг с функциями дискретного скачка;
- SimplifyKroneckerDelta [ехрг] — упрощение выражения ехрг с дельта-функцией Кронекера.
Действие этих функций демонстрируют следующие примеры:
DiscreteStep[n - 1] (KroneckerDelta[n - 2] + DiscreteStep[n, m] DiscreteStep[m - 1]) // SimplifyDiscreteStep
DiscreteStep[-1+m]
DiscreteStep[-l+m] + KroneckerDelta[-2+n]
(f[n] + KroneckerDelta[n]) DiscreteStep[n-l] // SimplifyKroneckerDelta
DiscreteStep [ -1 + n] f [ n]
Дискретные перестановки — Permutations
В подпакете Permutations определен ряд функций дискретных перестановок:
- RandomPermutation [n] — случайные перестановки из n элементов;
- Ordering [list] — дает перестановки в установленном списком list порядке;
- ToCycles [perm] — дает циклическую декомпозицию для списка list;
- FromCycles [ {cicl, cic2,...}] — возвращает перестановки из циклических декомпозиций cic1, cic2, ...;
- PermutationQ [list] — возвращает True, если список list представляет перестановки, и False в ином случае.
Работа функций поясняется следующими примерами:
<<DiscreteMath`Permutations`
RandomPermutation[16]
{16, 12, 11, 5, 3, 4, 9, 14, 2, 8, 15, I, 13, 7, 10, 6}
ToCycles[%]
{{16, 6, 4, 5, 3, 11, 15, 10, 8, 14, 7, 9, 2, 12, 1}, {13}}
FromCycles[%]
{16, 12, 11, 5, 3, 4, 9, 14, 2, 8, 15, 1, 13, 7, 10, 6}
Ordering[%]
{12, 9, 5, 6, 4, 16, 14, 10, 7, 15, 3, 2, 13, 8, 11, 1}
Решение рекуррентных разностных уравнений — RSolve
Для решения рекуррентных разностных уравнений в подпакет RSolve введены следующие функции:
- RSolve [eqn, a [n] , n] — решает рекуррентное уравнение для а [n];
- RSolve [eqn, a, n] — решает рекуррентное уравнение для функции а;
- RSolvet {eqnl, eqn2,...}, {al, a2,...},n] — решает систему рекуррентных уравнений, представленных списками.
Ниже представлены примеры применения данных функций:
<<DiscreteMath` RSolve`
RSolve[a[n+l] == 2 a[n], a[n], n]
{{a[n] -> 2nC[l]}}
RSolve[a[n] == a[n-l] + a[n-2], a[0] == a[l] == 1, a[n], n]
RSolve[ a[0] == a[l] == 2,
(n+1) (n+2) a[n+2]- 2 (n+1) a[n+l]- 3 a[n] == 0, a[n], n]
Подпакет Tree содержит функции создания и применения древовидных структур, именуемых деревьями. Вот эти функции:
- MakeTree [list] — создает дерево по информации, представленной в списке list;
- TreeFind [tree, x] — возвращает позицию наименьшего элемента, превосходящего х в списке list, представляющем дерево.
Действие этих функций поясняют следующие примеры:
<<DiscreteMath` Tree`
MakeTree[{el, e2, е3, е4}]
{{e2, 2), {{el, 1}, {}, {}}, {{e3, 3}, {}, {{e4, 4}, {}, {}}}}
tree = MakeTree[{8.5, 1.2, 9.1, 3.4, 5., 7.6 ,6.4}]
{{6.4, 4}, {{3.4, 2}, {{1.2, 1}, {}, {}}, {{5., 3}, {}, {}}},
{{8.5, 6}, {{7.6, 5}, {}, {}}, {{9.1, 7}, {},{}}}}
TreeFind[tree, 1.2]
1 . .
TreeFind[tree, 1]
0
Для визуализации деревьев служат следующие функции:
- TreePlot [tree] — строит график дерева tree;
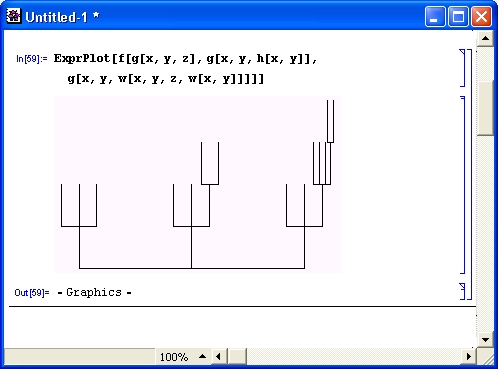
- ExprPlot [expr] — строит график, представляющий ехрг в виде дерева.
Примеры построения графиков деревьев представлены на рис. 11.18. Верхнп; график построен по данным дерева tree, определенного в приведенных выи: примерах, а нижний — по данным случайного дерева.
Построение графиков деревьев по выражению ехрг с помощью функции ExprPlot демонстрирует рис. 11.19.
Рис. 11.18. Примеры визуализации деревьев
Рис. 11.19 . Построение графиков деревьев с помощью функции ExprPlot
gl11-10.jpg

gl11-11.jpg
gl11-12.jpg
gl11-13.jpg
gl11-14.jpg
gl11-15.jpg
gl11-16.jpg
gl11-17.jpg
gl11-18.jpg

gl11-19.jpg
gl11-5.jpg
gl11-6.jpg

gl11-7.jpg
gl11-8.jpg
gl11-9.jpg
5. Геометрические расчеты — пакет Geometry
Геометрические расчеты — пакет Geometry
В этом разделе описан пакет Geometry, содержащий ряд функций, полезных при выполнении геометрических расчетов. В основном это функции, относящиеся к построению регулярных полигонов на плоскости и полиэдров в пространстве. Кроме того, в пакете есть функции, задающие вращение фигур на плоскости и в пространстве.
Характеристики регулярных полигонов и полиэдров — Polytopes
Подпакет Polytopes содержит ряд функций для регулярных полигонов (многоугольников):
- NumberOfVertices [р] — число вершин углов полигона;
- NumberOfEdges [p] — число сторон полигона;
- NumberOf Faces [p] — число граней полигона;
- Vertices [р] — список координат вершин углов полигона;
- Area [р] — площадь полигона при длине каждой стороны, равной 1;
- InscribeciRadius [р]— радиус вписанной в полигон окружности;
- CircumscribedRadius [р] — радиус описывающей полигон окружности.
В этих функциях наименование полигона р может быть следующим (в скобках дано число сторон):
Digon (2)
Triangle (3)
Square (4)
Pentagon (5)
Hexagon (6)
Heptagon (7)
Octagon (8)
Nonagon (9)
Decagon (10,)
Undecagon (11)
Dodecagon (12)
На рис. 11.20 показаны примеры применения некоторых из этих функций и построение крупными точками вершин полигона — Пентагона (пятиугольника).
Для объемных фигур — полиэдров — имеются следующие функции:
- NumberOfVertices [р] — число вершин углов полиэдра;
- NumberOfEdges [р] — число сторон полиэдра;
- NumberOf Faces [р] — число граней полиэдра;
- Vertices [p] — список координат вершин углов полиэдра;
- Area [p] — площадь полиэдра при длине каждой стороны, равной 1;
- InscribedRadius [р] — радиус вписанной в полиэдр окружности;
- CircumscribedRadius [р] — радиус окружности, описывающей полиэдр;
- Volume [p] — объем полиэдра;
- Dual[p] — дуальный полиэдр;
- Schlafli[p] — символ полиэдра.
Рис. 11.20. Примеры работы с функциями полигонов
Здесь наименование полиэдра может быть следующим:
Tetrahedron (4)
Cube (6)
Octahedron (8)
Didecahedron (12)
Icosahedron (20)
Примеры применения функций полиэдров представлены ниже:
Volume[Octahedron]
(Корень из 2) /3
Vertices [Octahedron]
{{0, 0, 1.41421}, {1.41421, 0, 0}, {0, 1.41421, 0},
{0, 0, -1.41421}, {-1.41421, 0, 0}, {0, -1.41421, 0}}
Dual [Octahedron]
Cube
InscribedRadius [Octahedron]
1/(Корень из 6)
GircumscribedRadius [Octahedron]
1/(Корень из 2)
Вращение фигур на плоскости и в пространстве — Rotations
Для задания поворота плоских фигур на заданный угол в подпакете Rotations заданы следующие функции:
- RotationMatrix2D[theta] — дает матрицу для поворота на угол theta в двух измерениях;
- Rotate2D [vec, theta] — поворачивает вектор vec по часовой стрелке на угол theta;
- Rotate2D[vec,theta,{x,y}] — поворачивает вектор vec по часовой стрелке на угол theta относительно точки с координатами {х, у}.
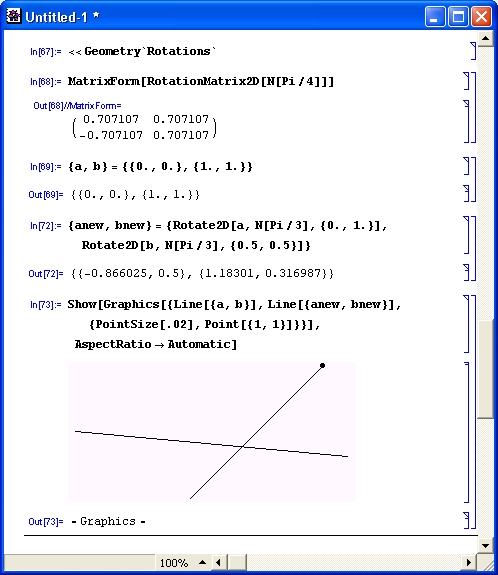
Рисунок 11.21 иллюстрирует работу с этими функциями.
Рис. 11.21. Работа с функциями поворота
Аналогичные функции существуют и для поворота трехмерных фигур:
- RotationMatrix3D [psi, theta,phi] — дает матрицу поворота на заданные углы в трехмерном пространстве;
- Rotate3D [vec, psi, theta, phi] — поворачивает вектор vec на заданные углы в трехмерном пространстве;
- Rotate3D [vec, psi, theta, phi,{x,y,z}]— поворачивает вектор vec на заданные углы в трехмерном пространстве относительно точки с координатами {х,у, z}.
Приведем пример вычисления матрицы трехмерного поворота:
RotationMatrix3D[Pi, Pi/2, Pi/6]
{{-(Корень из 3)/2,0,1/2 }},{1/2,0,(Корень из 3)/2},{ 0,1,0,}}
gl11-20.jpg

gl11-21.jpg
6. Линейная алгебра — пакет LinearAlgebra
Линейная алгебра— пакет LinearAlgebra
Пакет расширения LinearAlgebra добавляет ряд новых функций, полезных при решении сложных задач линейной алгебры.
Декомпозиция Холесского — Cholesky
Подпакет Cholesky содержит единственную функцию HoleskyDecomposition [m], которая вычисляет декомпозицию (факторизацию, разложение) Холесского для симметричной положительно определенной матрицы т.
Примеры выполнения декомпозиции Холесского даны ниже:
<<LinearAlgebra`Cholesky`
hil = Tablet l/(i + j - 1) , {i, 1, 4}, {j, 1, 4}]
Eigenvalues[ N[hil] ]
{1.50021, 0.169141, 0.00673827, 0.0000967023}
u = CholeskyDecomposition[hil]
MatrixForm[Transpose[u] . u]
Метод исключения Гаусса — GaussianElimination
Следующие функции обеспечивают реализацию метода исключения Гаусса при решении линейного уравнения вида А-x =b:
- LUFactor [m] — возвращает LU-декомпозицию матрицы m;
- LUSolve [lu, b] — решает систему линейных уравнений с матрицей коэффициентов lu и вектором свободных членов b методом исключения переменных Гаусса;
- LU [a, pivots] — создает объект, используемый в LUSolve. Применение этих функций поясняют примеры, показанные ниже:
<<LinearAlgebra`GaussianElimination`
MatrixForm[a = {{1, 2, 3}, {4, 5, 6}, {-1, 5, -5}}]
lu = LUFactor[a]
b = {10, -3, 12}
{10, -3, 12}
LUSolve[lu, b]
Метод исключения Гаусса является хорошо апробированным методом решения систем линейных уравнений, что делает реализацию описанных функций полезным дополнением к встроенным функциям линейной алгебры.
Операции с матрицами — MatrixManipulation
Подпакет MatrixManipulation добавляет к матричным функциям ядра системы Ма-thematica ряд новых функций. Начнем с функций объединения матриц:
- AppendColumns [ml,m2,...] — объединяет по столбцам матрицы ml,m2,...;
- AppendRows [ml,m2,...] — объединяет по строкам матрицы ml,m2,...;
- BlockMatrix [blocks] — объединяет по строкам и столбцам блоки blocks, создавая новую матрицу.
Данные операции с матрицами иллюстрируют следующие примеры:
<< LinearAlgebra`MatrixManipulation`
a = {{a11, a12}, {a21, a22}}; MatrixFormfa]
b = {{b11, b12}, {b21, b22}}; MatrixForm[b]
MatrixForm[AppendColumns[a, b] ]
AppendRows[a, b] //MatrixForm
BlockMatrix[{{a, b}, {b, {{0, 0}, {0, 0}}}}] //MatrixForm
Следующая группа функций вставляет или удаляет столбцы или строки матриц:
- TakeRows [mat, n] — вставляет в матрицу mat n-ю строку;
- TakeRows [mat, -n] — удаляет из матрицы mat п-ю строку;
- TakeRows [mat, {m,n} ] — вставляет в матрицу mat строки от m до n;
- TakeColumns [mat, n] — вставляет в матрицу mat п-й столбец;
- TakeColumns [mat, -n] — удаляет из матрицы mat п-й столбец;
- TakeColumns [mat, {m, n} ] — вставляет в матрицу mat столбцы от m до п.
Действие функции иллюстрируется следующими примерами:
mat = Array[m, 3, 4]; MatrixForm[mat]
m[l, 1] m[l, 2] m[l, 3] m[l, 4]
m[2, 1] m[2, 2] m[2, 3] m[2, 4]
m[3, 1] m[3, 2] m[3, 3] m[3, 4]
TakeRows[mat, -2] //MatrixForm
m[2, 1] m[2, 2] m[2, 3] m[2, 4]
m[3, 1] m[3, 2] m[3, 3] m[3, 4]
TakeColumns[mat, {2,3}] //MatrixForm
m[l, 2] m[l, 3] )
m[2, 2] m[2, 3]
m[3, 2] m[3, 3]
TakeMatrix[mat, {2, 3}, {3, 4}] //MatrixForm
m[2, 3] m[2, 4]
m[3, 3] m[3, 4]
SubMatrix[mat, {2, 3}, {2, 2}] //MatrixForm
m[2, 3] m[2, 4]
m[3, 3] m[3, 4]
Следующая группа функций служит для задания матриц специального вида:
- UpperDiagonalMatrix [f, n] — формирует наддиагональную матрицу размером пхп;
- LowerDiagonalMatrix [f, n] — формирует поддиагональную матрицу размером пхп;
- ZeroMatrix [n] — формирует квадратную нулевую матрицу размером пхп;
- ZeroMatrix [m, n] — формирует нулевую матрицу размером тхп;
- HilbertMatrix [n] — формирует квадратную матрицу Гильберта размером пхп;
- HilbertMatrix [m, n] — формирует матрицу Гильберта размером тхп;
- HankelMatrix [n] — формирует квадратную матрицу Ганкеля размером пхп;
- HankelMatrix [m, n] — формирует матрицу Ганкеля размером тхп.
Примеры задания матриц разного типа приведены ниже:
UpperDiagonalMatrix[f, 3] //MatrixForm
LowerDiagonalMatrix[#1 + #2 &, 4] //MatrixForm
HilbertMatrix[2, 4] //MatrixForm
HankelMatrix[{w, x, y, z}] //MatrixForm
Наконец, в подпакет входит еще одна функция, LinearEquationsToMatri-ces [eqns, vars], которая из записи линейного уравнения eqns с переменными vars формирует расширенную матрицу, содержащую матрицу коэффициентов левой части уравнения и вектор свободных членов.
Пример применения данной функции:
LinearEquationsToMatrices[
а[1,1]*х + а[1,2]*у == с[1],
а[2,1]*х + а[2,2]*у == с[2], х, у]
{{{{{a11, a12), {а21, а22}}[1, 1],
{{a11, a12), {a21, а22}}[1, 2]}, {{{a11, a12}, {a21, a22}}[2, 1],
{{a11, a12), {a21, a22}} [2, 2]}}, {c[l],c[2]}}
Ортогонализация и нормализация — Ortogonalization
В подпакете ортогонализации Ortogonalization имеются следующие функции:
- GramSchmidt [ {vl, v2,...} ] — создает ортогональное множество на основе списка векторов v1, v2, ...;
- Normalize [vect] — возвращает нормированный вектор vect;
- Projection [vectl, vect2] — дает ортогональную проекцию вектора vl на вектор v2.
В этих функциях после аргументов допустимы опции InnerProduct->exprn Normalized->False (отказ от нормировки). Примеры работы с функциями ортогонализации представлены ниже:
<<LinearAlgebra`Orthogonalization`
{wl, w2, w3} = GramSchmidt[ {{1,3,2}, {2,4,3}, {2,4,6}}]
{ wl . w2, w2 . w3, wl . w3, wl . wl, w2 . w2, w3 . w3}
{0, 0, 0, 1, 1, 1}
GramSchmidt[{1, x, x^2, x^3, x^4}, InnerProduct -> (Integrate[#l #2,{x,-l,l}]&)] //Simplify
Normalize[LegendreP[2,x], InnerProduct ->(Integrate[#l #2,{x,-l,l}]&)]
{wl, w2} = GramSchmidt[{{3,4,3}, {2,3,6}}, Normalized -> False]
{wl . wl, wl . w2}
{34, 0}
Решение линейных уравнений с трехдиагональной матрицей —Tridiagonal
При решении линейных уравнений часто встречаются матрицы особой формы — трехдиагональные. Подпакет Tridiagonal имеет функцию для решения линейных уравнений с такой матрицей:
- TridiagonalSolve [a,b, с, г] — решение системы линейных уравнений с трехдиагональной матрицей m. х==г (диагонали представлены векторами а, b и с, вектор свободных членов — г).
Пример применения данной функции:
<<LinearAlgebra` Tridiagonal`
{а, b, с} = {{1, 2, 3}, {4, 5, б, 7}, {10, 9, 8}}
{{1, 2, 3}, {4, 5, 6, 7}, {10, 9, 8}}
m = Table[Switch[ j-i, -1, a[[j]], 0, b[[jj], 1, c[[j-l]], _, 0], {i, 4}, {j, 4}]//MatrixForm
TridiagonalSolve[a, b, c, {8, 3, 4, 5}

7. Расширение в теории чисел — пакет NumberTheory
Расширение в теории чисел
Мы уже описывали уникальные возможности систем Mathematica 3/4 в области обработки чисел и численных вычислений. Эти возможности существенно расширяет пакет NumberTheory, содержащий функции, реализующие алгоритмы теории чисел. Данный раздел посвящен знакомству с этим пакетом.
Цепные дроби — ContinuedFractions
Следующие функции подпакста ContinuedFractions служат для представления чисел в виде цепных дробей или для формирования цепной дроби из списков:
- ContinuedFraction [х] — возвращает цепную дробь для рационального числа х;
- ContinuedFraction [х, n] — возвращает цепную дробь для числа х с числом членов п;
- ContinuedFractionForm [{а0, al,...}] — создает цепную дробь из списка {a0,al,...};
- Normal [ContinuedFractionForm[ {а0, al,...}]] — представление в нормальной форме.
Примеры разложения чисел на цепные дроби:
<<NumberTheory`
ContinuedFractionss ContinuedFraction[123/1234]//ContinuedFractionForm
ContinuedFraction[Sqrt[5], 10]//ContinuedFractionForm 2,
ContinuedFraction[GoldenRatio, 6 ] //ContinuedFractionForm
Table[ Normal[ContinuedFractionForm[Table[1, {n}]]], {n, 9}]
%- N[GoldenRatio]
{-0.618034, 0.381966, -0.118034, 0.0486327,
-0.018034, 0.00696601, -0.00264937, 0.00101363,-0.00038693}
В подпакете имеются также следующие функции:
- ToPeriodicForm[x] — дает десятичное представление для рациональнЪго числа 0 < х < 1;
- ToPeriodicForm [х, b] — дает представление рационального числа х числом с основанием b;
- PeriodicForm[ {а0,...}, {am,...}] — дает периодическую форму представления списков;
- PeriodicForm[ {а0,...}, {am,...},b] — дает периодическую форму представления списков с основанием b;
- Normal [ PeriodicForm [{а0,...}, {am,...}]] — преобразование в нормальную форму;
- Normal [PeriodicForm[ {а0,...}, {am,...} ,b] ] — преобразование в нормальную форму с основанием b.
Ниже представлены примеры применения этих функций:
ToPeriodicForm[ 1/50 ]
0.02
ToPeriodicForm[ 1/23 ]
0.0434782608695652173913
PeriodicForm[1,2,3,4]
0.1234
RealDigits[ N[ 1/23, 25 ] ]
{{4, 3, 4, 7, 8, 2, 6,
0, 8, 6, 9, 5, 6, 5, 2, 1, 7, 3, 9, 1, 3, 0, 4, 3, 5},
-1}
ToPeriodicForm[ 1/20, 2 ]
0.000011 ToPeriodicForm[ 1/127 ]
0.007874015748631496062992l2598425l968503937
Normal[%]
1/127
В системе Mathematica 4 функция ContinuedFraction стала встроенной. Имеется также встроенная функция FromContinuedFraction [list], которая строит цепную дробь по элементам списка list.
Улучшенное разложение на простые множители — FactorlntegerECM
Алгоритм разложения чисел на простые множители, реализованный в ядре Mathematiica 3, способен за 3 часа (на рабочих станциях) разлагать числа, имеющие до 18 цифр. Улучшенный алгоритм в подпакете FactorlntegerECM позволяет увеличить максимальное число цифр до 40. Реализуется разложение следующей функцией:
- FactorIntegerECM[n] — возвращает один из делителей числа п. Возможны опции FactorSize->q, CurveNumber->b и CurveCountLimit->c.
Примеры применения этой функции:
<<NumberTheory`FactorlntegerECM`
FactorIntegerECM[123456789]
34227
3*5*7*9
945
FactorlntegerECM[945]
189
Функции теории чисел — NumberTheory Functions
В подпакете NumberTheoryFunctions имеется ряд функций, относящихся к теории чисел:
- SquareFreeQ[n] — дает True, если п не имеет квадратичного фактора, и False в ином случае;
- NextPrime [n] — дает наименьшее простое число, превосходящее п;
- ChineseRemainderTheorem[listl, Iist2.] — дает наименьшее неотрицательное целое г, такое что Mod [r, Iist2] ==list1;
- SqrtMod [d, n] — дает квадратный корень из (d mod п) для нечетного n;
- PrimitiveRoot [n] — дает примитивный корень п;
- QuadraticRepresentation [d, n] — дает решение {х,у} для уравнения х 2 + (d у) 2 ==п для нечетного п и положительного d;
- ClassList[d] — дает список неэквивалентных квадратичных форм дискриминанта d для отрицательного и свободного от квадратов целого d вида 4n+1;
- ClassNumber [d] — дает список неэквивалентных квадратичных форм дискриминанта d;
- SumOf Squares [d, n] — дает число представлений целого числа п в виде суммы d квадратов;
- SumOf SquaresRepresentations [d, n] — дает список представлений целого числа п в виде суммы d квадратов, игнорируя порядок и знаки.
Примеры применения данных функций приведены ниже:
<<NumberTheory`NumberTheoryFunctions`
SquareFreeQ[2*3*5*7]
True SquareFreeQ[50]
False
NextPrime[1000000]
1000003
ChineseRemainderTheorem[{0, 1, 2}, {4, 9,
244
ChineseRemainderTheorem[Range[16], Prime[Range[16]]]
20037783573808880093
SqrtMod[3, 11]
5
SqrtMod[2, 10^64 +57]
876504467496681643735926111996
54610040103361197677707490912
2865
PrimitiveRoot[7]
3
QuadraticRepresentation[l, 13]
{3,. 2}
ClassList[-19]
{{1, 1, 5}}
ClassNumber[-10099]
25
SumOfSquaresRepresentations[3, 100]
{{0, 0, 10}, (0, 6, 8}}
Работа с простыми числами-PrimeQ
В подпакете PrimeQ в дополнение к функции ядра PrimeQ [n] имеется ряд функций для работы с простыми числами:
- ProvablePrimeQ [n] — возвращает True, если п проверено на простоту, и False в ином случае;
- PrimeQCertif icate [n] — возвращает сертификат о том, что n— простое или композитное число;
- ProvablePrimeQ [n, Certif icate->True] — возвращает сертификат, который может использоваться для проверки чисел на простоту;
- PrimeQCertif icateCheck [check, n] — проверяет, удостоверяет ли сертификат check простоту или композитность п.
Следующие примеры показывают работу с простыми числами:
<<NumberTheory` PrimeQ`
PrimeQ[127]
True
ProvablePrimeQ[127]
True
PrimeQCertificate[127]
{127, 3, {2, {3, 2, {2}.}, {7, 3, {2, {3, 2, {2}}}}}}
ProvablePrimeQ[127, Certificate->True]
(True, {127, 3, {2, {3, 2, {2}}, {7, 3, {2, {3, 2, {2}}}}}}}
PrimeQCertificate[3511, SmallPrime -> 1000]
{{CertificatePrime -> 3511,
CertificatePoint->PointEC[2, 2467, 1447, 2135, 3511], Certif icateK-> 32, Certif icateM -> 3424,
CertificateNextPrime -*107, CertificateDiscriminant -> -7},
107, 2, {2, {53, 2, {2, {13, 2, {2, {3, 2, {2}}}}}}}}
Вычисление примитивных элементов — Primitive Element
Подпакет PrimitiveElement содержит всего одну функцию для вычисления примитивных элементов множественного алгебраического выражения:
- PrimitiveElement [z, {а1„а2,...} ] — возвращает список {b, { f1, f2,...}}, где b — примитивный элемент расширения рациональных алгебраических чисел al, а2,... и f1, f 2,... — полином переменной z, представляющей al, a2, ... как термы примитивного элемента.
Ее действие видно из следующего примера:
<<NumberTheory`PrimitiveElement`
PrimitiveElement[z, {Sqrt[2], Sqrt[3]}]
RootReduce[%[[2]] /. z -> %[[1]]]
Создание рядов Рамануджанат-Дирихле — Ramanujan
В подпакете Ramanujan определены следующие функции:
- RamanujanTau [n] — n-й коэффициент ряда Рамануджана т-Дирйхле (т n );
- RamanujanTauGeneratingFunction [z] — производящая функция ряда Рамануджана т-Дирихле;
- RamanujanTauDirichletSeries [s] — ряд Рамануджана т-Дирихле f(s);
- RamanujanTauTheta [t] — функция Рамануджана т-Дирихле o(t)
- RamanujanTauZ [t] — функция Рамануджана т-Дирихле z(t).
Это довольно редкие функции, представляющие интерес для специалистов в теории чисел. Достаточно подробные их определения даны в справочной базе данных. Ограничимся приведением примеров их использования:
<<NumberTheory`Ramanujan`
RamanujanTau[5]
4830
Sum[RamanujanTau[n] z^n, {n, 5}]
z - 24 z2 + 252 z3 - 1472 z4 + 4830 z5
RamanujanTauGeneratingFunction[. 1]
0.00610209
RamanuJanTauGeneratingFunction[.99]
4.10287803703 x -1673
RamanujanTauDirichletSeries[6 + 9.221]
0.00040309-0.002390131
z = RamanujanTauZ[9.22]
0.00242388
theta = RamanujanTauTheta[9.22]
1.40372043366323 z Exp[-I theta]
0.00040309 - 0.00239013 I
Рационализация чисел — Rationalize
Подпакет Rationalize расширяет возможности представления чисел в рациональном виде. Он содержит определения следующих функций:
- ProjectiveRationalize [ {х0, xl,..., хn} ] — возвращает список целых чисел, дающих рациональные представления для чисел заданного списка;
- ProjectiveRationalize [ {х0, xl,..., хn} ,ргес] — возвращает список целых чисел, дающих рациональные представления с погрешностью не более 10- рreк
- Af f ineRationalize [ {х0, xl,..., хn} ] — возвращает список рациональных приближений для чисел заданного списка;
- Aff ineRationalize [ {х0, xl,..., xn} ,prec] — возвращает список рациональных приближений для чисел заданного списка, вычисленных с погрешностью не более 10- ргес .
Встроенная в ядро функция Rationalize дает рациональное представление для одиночных вещественных чисел. Приведенные функции выполняют рационализацию для списков чисел. Примеры их применения представлены ниже:
<<NumberTheory` Rationalize`
Rationalize[N[3 Pi], 6]/ Rationalize[N[11 Pi], 6]
9/35
ProjectiveRationalize[{N[3 Pi], N[11 Pi]}]
{3, 11}
AffineRationalize[{N[3 Pi], N[11 Pi]}, 6]
{1065/113, 3905/113 }
Нахождение полинома, дающего заданный корень — Recognize
Подпакет Recognize содержит определение одноименной с ним функции в двух формах:
- Recognize [x,n,t] — находит полином переменной t степени, большей п, такой, что х является его корнем;
- Recognize [х, n, t, k] — находит полином переменной t степени, большей п, такой, что х является его корнем, и со штрафным весовым коэффициентом k, предназначенным для подавления генерации полиномов высших степеней.
Действие этой функции поясняют следующие примеры:
<<NumberTheory`Recognize`
NSolve[2 x^3- x + 5 == 0]
{{x->-1.4797}, {x-> 0.739852-1.068711}-,
{x->0.739852+ 1.068711}}
sol = First[x /. %]
-1.4797
Recognize[sol, 3, t]
5-t+2t3
Recognize[sol, 2, t]
-225599 - 1464961 + 4032 t2
Recognize[N[Sqrt[3^(2/5)]], 5, t]
-3+t5
Recognize[N[Sqrt[3A(2/5)]], 5, t, 10]
-14625 + 11193 t + 328 t2 + 8813 + t4
Подпакет SiegelTheta содержит еще одну редкую функцию:
- SiegelTheta [z, s] — возвращает значение тета-функции Зигеля Q(Z, s).
Примеры вычисления этой функции даны ниже:
<< NumberTheory` SiegelTheta`
SiegelTheta[{1+1,2+1}, {2+1,-1+41}, {1.2, 2.3+.3I}]
0.973715-0.0002970481
Sum[E^(Pi I {tl,t2}.{ {1+1,2+1}, {2+1, -1+41} }.{tl,,t2} +
2 Pi I {tl,t2}.{l.2,2.3+.31}), {tl,-10,10>, {t2,-10,10}]
0.973715 - 0.000297048 I
В заключительной части этого примера дано вычисление тета-функции Зигеля по ее исходному определению.
8. Численные расчеты — пакет NumericalMath
Численные расчеты — пакет NumericalMath
Пакет расширения NumericalMath содержит множество полезных функций для тех, кто имеет дело с численными расчетами. В их числе функции для выполнения высокоточных аппроксимаций рациональными функциями, численного интегрирования и дифференцирования, вычисления пределов функций, решения уравнений, разложения в ряд и т. д. Ниже описано подавляющее большинство функций этого расширения. Исключены лишь отдельные функции, представляющие ограниченный интерес и несложные для самостоятельного изучения (в подпаке-mах Butcher, Microscope и ComputerArithmetic).
Аппроксимация аналитических функций — Approximations
Подпакет Approximations содержит ряд функций для улучшенной рациональной аппроксимации аналитических функций. Для рациональной интерполяции и аппроксимации функций по заданным значениям абсцисс служит следующая функция:
- Rationallnterpolation [f, {x,m, k}, {x 1 , x 2 , ...,.x m+k+1 } ] — возвращает аппроксимирующее функцию f выражение в виде отношения полиномов а степенью полинома числителя m и знаменателя k в абсциссах, заданных списком {x l ,x 2 ,...,x m+jt+1 }.
Пример применения этой функции:
<<NumericalMath `Approximations`
ril = Rationallnterpolation[ Exp[x], {х, 2, 4}, {0, 1/3, 2/3, 1, 4/3, 5/3, 2}]
Построим график погрешности аппроксимации, то есть график разности функ ии ril и Ехр [х] — он представлен на рис. 11.22.
Нетрудно заметить, что если в центральной части области аппроксимации погрешность мала (менее 5-10- 7 ), то у правого края она резко возрастает.
Представленная функция может использоваться и в иной форме:
Rationallnterpolation[f,{х, m, k},{x, xmin, xmax}]
Рис. 11.22. График погрешности рациональной аппроксимации экспоненциальной функции
В данном случае выбор абсцисс осуществляется автоматически в интервале от xmin до mах. В отличие от первого случая, когда абсциссы могли быть расположены неравномерно, в данном случае расположение их будет равномерным. Приведем пример аппроксимации функции синуса в интервале от n до n:
ri2 = RationalInterpolation[Sin[x],{x,3,4},{x,-Pi,Pi}]
Интересно оценить погрешность аппроксимации. Для этого достаточно построить график разности аппроксимирующей и аппроксимируемой функций. Это построение представлено на рис. 11.23. Любопытно, что хотя максимальная погрешность и значительна, резких выбросов погрешности в данном случае нет.
Рис. 11.23. График погрешности аппроксимации синусоидальной функции
При рациональной аппроксимации можно задать опции WorkingPrecision и Bias со значениями по умолчанию $MachinePrecision и 0 соответственно. Опция Bias обеспечивает автоматическую расстановку узлов интерполяции. При Bias->0 обеспечивается симметрирование выбросов погрешности, дающее наименьшее ее значение в пиках. Ниже приведен пример интерполяции (аппроксимации) экспоненциальной функции в интервале изменения х от 0 до 2:
ri3 = RationalInterpolation[Exp[x],{x,2,4},{x,0,2},Bias->.25]
Построение графика погрешности (рис. 11.24) показывает, что правильным выбором центра интерполяции можно существенно уменьшить ее погрешность. Теперь большая погрешность наблюдается в левой части графика. Однако резкого выброса погрешности в данном случае нет.
Рис. 11.24. Погрешность аппроксимации экспоненты при выборе опции Bias->.25
Из приведенных примеров ясно, что рациональная аппроксимация способна дать существенное уменьшение погрешности при некотором оптимальном расположении узлов аппроксимации и выравнивании погрешностей по абсолютной величине в точках минимумов и максимумов кривой погрешности. Это лежит в основе так называемой минимаксной аппроксимации. Она реализуется следующей функцией:
- MiniMaxApproximation[f,{x,{xmin,xmax},m,k}] — возвращает рациональную функцию минимаксной аппроксимации f при степени полиномов числителя и знаменателя {m, k} ив интервале изменения х от xmin до xmax:
- MiniMaxApproximation [f, approx, {x, {xmin, xmax} ,m, k} ] —возвращает рациональную функцию минимаксной аппроксимации f при степени полиномов числителя и знаменателя {m, k} ив интервале изменения х от xmin до xmax с возможностью выбора метода аппроксимации approx.
Эта аппроксимация использует итерационный алгоритм вычислений. Они начинаются с первого шага, на котором используется функция Rational Interpolation. Затем аппроксимация последовательно улучшается применением алгоритма Ремеза, лежащего в основе этого вида аппроксимации.
Функция MiniMaxApproximation возвращает два списка — первый с координатами абсцисс, при которых наблюдается максимальная погрешность, второй содержит рациональную функцию аппроксимации. Ниже представлен пример аппроксимации экспоненциальной функции:
mmlist = MiniMaxApproximation[Ехр[х], {х, {0, 2}, 2, 4}]
Выделим формулу аппроксимации:
mmfunc = mmlist[[2, 1]]
Теперь можно построить график погрешности аппроксимации (рис. 11.25).
Рис. 11.25. График погрешности при минимаксной аппроксимации экспоненциальной функции
Следует отметить, что малость абсолютной ошибки для ряда функций (например, тригонометрических) может приводить к большим относительным погрешностям в точках, где функции имеют нулевые значения. Это может привести к отказу от выполнения аппроксимации вследствие исчерпания числа итераций (опция Maxlterations по умолчанию имеет значение 20). Такой случай наблюдается, например, при исполнении следующей команды:
MiniMaxApproximation[Cos[x], {х, {1, 2}, 2, 4}]
Делением функции на (x-Pi/2) можно исключить эту ситуацию:
MiniMaxApproximation[Cos[x]/(x-Pi/2),{*,{1!,2},2,4}] [[2,1]]
График погрешности для этого примера представлен на рис. 11.26. Обратите внимание на то, что в этом примере погрешность аппроксимации не превышает (б...7)-10- 10 .
В приложении дан список функций общей рациональной интерполяции (аппроксимации) для аналитических зависимостей, заданных параметрически. Примеры применения этого довольно редкого вида аппроксимации можно найти в справочной базе данных системы Mathematica. Там же можно найти дополнительные соображения по уменьшению погрешности аппроксимации.
Рис. 11.26. График погрешности при минимаксной аппроксимации функции косинуса
Нули функций Бесселя — BesselZeros
В подпакете BesselZeros определены функции, дающие список аргументов функций Бесселя в их первых п нулевых точках: BesselJZeros [mu, n], Bessel-YZeros[mu,n], BesselJPrimeZeros[mu,n], BesselYPrimeZeros[mu,n] и др. Ввиду редкого использования функций этого класса ограничимся парой примеров их применения:
<<NumericalMath`BesselZeros`
BesselJZeros[0, 5]
{2.40483, 5.52008, 8.65373, 11.7915, 14.9309}
BesselJYJYZeros[2, 6/5, 3, WorkingPrecision -> 20]
{15.806622444176579073, 31.46556009153683, 47.1570167108650315}
Поиск корней уравнений с интерполяцией — InterpolateRoot
Подпакет InterpolateRoot дает средства для ускоренного и более точного поиска корней уравнений по сравнению с соответствующими функциями ядра. Достигается это за счет применения интерполяции функции, корни которой ищутся. Под-пакет задает функцию InterpolateRoot [f, {х, a, b} ], которая находит корень функции f в интервале х от а до b. Вместо функции f можно задавать уравнение eqn. Возможны опции AccuracyGoal->Automatic, Maxlterations->15, WorkingPrecision->$MachinePrecision и ShowProgress->False (указаны принятые по умолчанию значения).
Примеры применения данной функции (n — число итераций):
<<NumericalMath` InterpolateRoot`
n = 0; FindRoot[n++; Exp[x] == 2, {x, 0, 1},
WorkingPrecision -> 100, AccuracyGoal -> 95]
{x->
0.693147180559945309417232121458176568075500134360255 2541206800094933936219696947156058633269964186876}
n
17
n = 0; f[x_] := (n++; Exp[x]-2) /; NumberQ[x]
InterpolateRoot[f[x], {x, 0, 1), WorkingPrecision -> 100,
AccuracyGoal -> 95]; n 10
InterpolateRoot[Exp[x] ==2, {x, 0, 1},ShowProgress -> True,
WorkingPrecision -> 40]
{0, 0.58197670686932642439}
{21, 0, -0.12246396352039524100}
{1, 0.7019353037882764014443370764853594873432}
{21, 20, 0.0130121629575404389120930392554}
{3,0.6932065772065263165289985793736618546663}
{21, 20, 0.000062480788747713548804773113708}
{6, 0.6931471932603933841618726058237307884661}
{21, 20, 1.26443483693584888038460396742xHT8}
{12, 0.693147180559945119457822446
95590259222308309027205042483074}
{40, 20, -1.89953767048152086910014102216x 10-16}
{24, 0.6931471805599453094172321214
5786257157118117337249076750141}
Реализация интервальных методов —IntervalRoots
Иногда важно не найти приближенное значение корня, а уточнить интервал, в котором он находится. В подпакете IntervalRoots для этого используется ряд известных методов, реализованных следующими функциями:
- IntervalBisection [f ,x, int, eps] — находит корень функции f(x) путем уточнения исходного интервала int с заданной погрешностью eps методом половинного деления;
- IntervalSecant [f ,x, int, eps] — находит корень функции f(x) путем уточнения исходного интервала int с заданной погрешностью eps методом секущей;
- IntervalNewton [ f, x, int, eps ] — находит корень функции/(x) путем уточнения исходного интервала int с заданной погрешностью eps методом Ньютона (касательной).
Во всех функциях можно опциями задать максимальное число рекурсий (Max-Recursion) и погрешность (WorkingPrecision). Примеры применения этих функций даны ниже:
<<NumericalMath`IntervalRoots`
IntervalBisection[Sin[x], x, Interval[{2., 8.}], .1]
Interval[{3.125, 3.218750000000001}, {6.218750000000003, 6.312500000000006}]
IntervalBisection[Sin[x], x, Interval[{2., 8.}], .01]
Interval[{3.125, 3.17188}, {6.26563, 6.3125}]
IntervalBisection[Sin[x], x, Interval[{2., 8.}], .01, MaxRecursion -> 10]
Interval[{3.13672, 3.14258}, {6.27734, 6.2832}]
IntervalSecant[Sin[x], x, Interval[{2., 8.}], .01]
Interval[{3.14159, 3.1416}, {6.28316, 6.28321}]
IntervalSecant[Sin[x], x, Interval[{2., 8.}], .01]
Interval[{3.14159, 3.1416}, {6.28316, 6.28321}]
IntervalBisection[Sin[x], x,
Interval[{2, 8}], .1, WorkingPrecision -> Infinity]
Табличное численное интегрирование — Listlntegrate
Встроенная в ядро функция NIntegrate вычисляет определенные интегралы при известной подынтегральной функции. Однако нередко, например при экспериментах, такая функция задается таблицей или списком значений. В подпакете List-Integrate имеются функции для решения этой задачи — табличного интегрирования:
- Listlntegrate [ {yl, y2,..., yn} ,h] — возвращает численное значение интеграла для функции, заданной списком ординат yi при заданном шаге h по х;
- Listlntegrate [ {yl, y2,..., yn}, h, k] — возвращает численное значение интеграла для функции, заданной списком ординат yi при заданном шаге h по х, используя k точек каждого подинтервала;
- Listlntegrate [ {{xl, yl}, {х2, у2 },..., {хп, уп}}, k] — возвращает численное значение интеграла для функции, заданной списком координат {х.., у.}. используя k точек для каждого подынтервала.
Примеры применения данной функции:
<<NumericalMath`Listlntegrate`
data = Tablet n^2, {n, 0, 7}]
{0, 1, 4, 9, 16, 25, 36, 49}
ListIntegrate[data, 1]
343/3
Listlntegrate[{{0,0},{1,1},{2,4},{5,25},{7,49}},2] 241/2
При проведении интегрирования для данных, заданных таблично, можно использовать интерполяцию:
арр = Listlnterpolation[data,{{0,7}}] Integrate[app[x],{x,0,7}]
343/3
Integrate[Interpolation[{{0,0},{1,1},{2,4}, {5,25}, {7,49}},
InterpolationOrder->l][x],{x,0,7}]
241/2
Численное вычисление пределов — NLimit
В подпакете N limit определена функция
Nlimit[expr,х->х0]
для численного вычисления пределов выражений ехрг (см. примеры ниже):
<<NumericalMath` NLimit`
NLimit[Zeta[s] - l/(s-l), s->l]
0.577216
N[EulerGamma]
0.577216
С помощью команды Options [NLimit] можно просмотреть опции, которые используются функцией NLimit по умолчанию. В этом подпакете задано также вычисление бесконечных сумм Эйлера EulerSum[f, { i, imin, Infinity} ]. Например:
EulerSum[(-l)^k/(2k + 1) , {k, 0, Infinity}]
0.785398
EulerSumt(-1)^k/(2k +1), {k, 0, Infinity},
WorkingPrecision->40, Terms->30, ExtraTerms->30]
0.78539816339744830961566084579130322540
%- N[Pi/4, 40]
-2.857249565x 10-29
Имеется также функция вычисления производной в численном виде:
- ND [ f, х, хО] — вычисляет первую производную f(x) в точке х0;
- ND[f, {x,n} ,х0] — вычисляет п-ю производную f(X) в точке х0. Пример вычисления производной:
ND[Exp[Sin[x]], х, 2]
-1.03312
Options[ND]
{WorkingPrecision-> 16, Scale-> 1, Terms-> 7, Method-> EulerSum]
В некоторых случаях вычисления могут быть ошибочными. Тогда следует использовать опции — особенно опцию выбора метода Method. Помимо метода по умолчанию (EulerSum) можно использовать NIntegrate (метод интегрирования по формуле Коши).
Численное вычисление остатка — N Residue
В подпакете NResidue имеется функция вычисления остатка NResidue [expr, {x, x0} ] в точке х=х0:
<<NumericalMath` NResidue`
NResidue[1/z, {z, 0}]
1. + 6.35614x 10-18 I
Residue[f, {z, 1.7}]
0
NResidue[f, {z, 1.7}]
0.259067 - 1.9353xl0-17I
l/((z+.2+.5 I)(z+.2-.5 I)) /. z -> 1.7
0.259067 + 0. I
Options[NResidue]
Обратите внимание на возможные опции для этой функции в последнем примере.
Численное разложение в ряд — NSeries
Подпакет NSeries вводит функцию NSeries [f, {x,xO,n}], которая дает численный ряд, аппроксимирующий функцию f(x) в окрестности точки х = х 0 , включая термы от (х -х 0 ) -n до (х - х 0 ) п .
Примеры применения данной функции:
<<NumericalMath`NSeries`
NSeries[Sin[х], {х, -2, 2}]
Rationalize[Chop[%]]
Rationalize[Chop[NSeries[Log[x], {x, 1, 5}, Radius -> 1/8]]]
Rationalize[Chop[NSeries[Exp[x], {x, 0, 5},
WorkingPrecision -> 40, Radius -> 1/8]]]
Rationalize[Chop[NSeries[Exp[x], {x, 0, 5}, Radius -> 4]]]
Chop[NSeries[Zeta[s], {s, 1, 3}]]
Вычисление коэффициентов формулы интегрирования Ньютона—Котесса — NewtonCotes
Функция NIntegrate, имеющаяся в ядре системы Mathematica, реализует метод интегрирования Гаусса—Кронрода. Еще одним известным методом интегрирования является метод Ньютона—Котесса, сводящий интегрирование к вычислению взвешенных ординат функции в равномерно расположенных точках оси абсцисс. Для реализации метода используются следующие функции:
- NewtonCotesWeights [n, a, b] — возвращает список весовых коэффициентов и абсцисс узловых точек {wi, xi} для квадратуры Ньютона—Котесса на интервале от а до b;
- NewtonCotesError [n, f, a, b] — возвращает погрешность формулы Ньютона—Котесса для заданной функции f.
Примеры применения этих функций представлены ниже:
<<NumericalMath` NewtonCotes`
NewtonCotesWeights[5, 0, 10]
NewtonCotesError[5, f, 0, 10]
NewtonCotesError[5, f, a, a+h]
NewtonCotesWeights[5, -0, 10, QuadratureType -> Open]
NewtonCotesError[5, f, 0, 10, QuadratureType -> Open]
Обратите внимание на то, что приведенные формулы готовят данные для численного интегрирования методом Ньютона—Котесса, но не выполняют самого интегрирования.
В этом уроке мы научились:
- Пользоваться алгебраическими функциями пакета Algebra.
- Применять вычислительные функции пакета Calculus.
- Работать с функциями дискретной математики из пакета DiscreteMath.
- Производить геометрические расчеты с помощью пакета Geometry.
- Выполнять алгебраические вычисления с помощью пакета LinearAlgebra.
- Пользоваться расширенными функциями теории чисел из пакета NumberTheory.
- Осуществлять численные расчеты с помощью пакета NumericalMath.
gl11-22.jpg
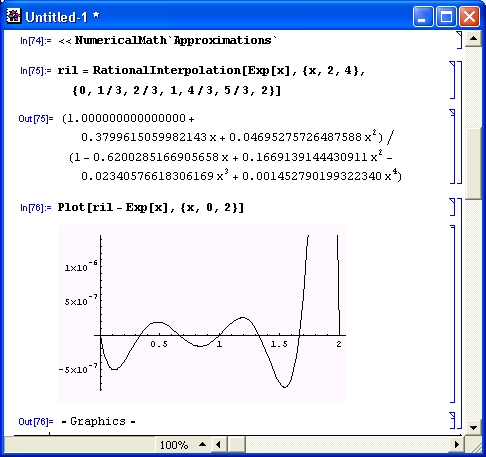
gl11-23.jpg
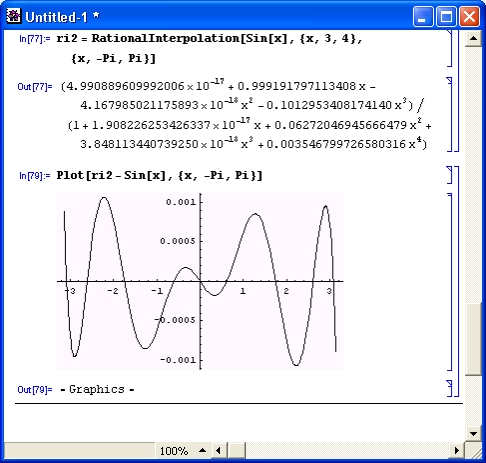
gl11-24.jpg
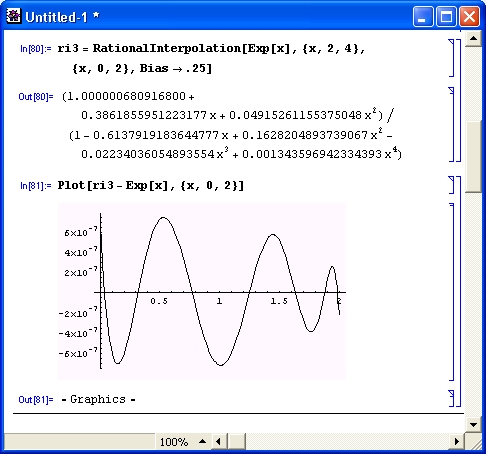
gl11-25.jpg
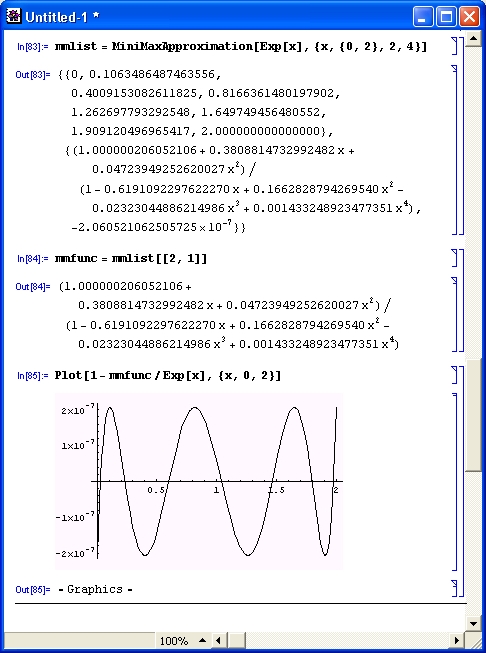
gl11-26.jpg