Урок 7. Работа с периферийными устройствами
Урок 7. Работа с периферийными устройствами
1. Работа с периферийными устройствами
Работа с периферийными устройствами
- Функции ввода/вывода
- Работа со строками
- Потоки и файлы
- Запись определений
- Системные функции
Если пользователь использует систему Mathematica для выполнения чисто математических расчетов, то он может ничего не знать о подавляющем большинстве описанных в этом уроке функций. Их основное назначение — незаметная поддержка работы с периферийными устройствами ввода/вывода. Однако все функции этого урока открыты для опытных пользователей, стремящихся использовать систему в составе программных комплексов. Здесь рассматривается только часть функций для работы с периферийными устройствами — даны те из них, которые используются достаточно часто. Многие функции этой группы перечислены в приложении.
Ввод/вывод в системе Mathematica организован с помощью интерфейсного процессора (FrontEnd) настолько естественно, что у большинства пользователей едва ли появится искушение изменять формы ввода/вывода по сравнению с установленными по умолчанию. Тем не менее, это возможно с помощью обширного набора команд, имеющихся в меню системы.
Более того, система предоставляет пользователю обширные возможности по организации ввода/вывода и различных форм диалога с помощью соответствующих функций, команд, директив и опций. Эти средства входят в язык программирования систем Mathematica и нередко используются для подготовки серьезных документов (например, обучающих и тестирующих программ), а также для создания пакетов расширения.
Прежде всего отметим функции ввода/вывода, позволяющие организовать диалог с системой в стиле, подобном тому, что используется при программировании на Бейсике. Основные функции для этого следующие:
- Input [ ] — останавливает работу системы и возвращает значение выражения, которое будет введено в появившемся диалоговом окне (служит для организации диалогового ввода);
- Input [ "prompt" ] — то же, что и предыдущая функция, но с выводом в диалоговое окно комментария prompt;
- InputString [ ] — выполняет интерактивное чтение в символьную строку;
- InputString [ "prompt" ] — то же, но с выводом в диалоговое окно комментария prompt;
- StylePrint [ехрr] — создает в текущем документе новую ячейку со стилем по умолчанию и заносит в нее выражение ехрг;
- StylePrint[expr,"style"] — создает в текущем документе новую ячейку со стилем style и заносит в нее выражение ехрr;
- Print [expr] — выводит на экран дисплея значение выражения ехрг; совместно с Input может использоваться для организации диалога;
- Print ["prompt", expr] — выводит на экран дисплея текстовый комментарий, указанный в кавычках, и следом — значение выражения ехрr.
Этих функций достаточно для организации простейшего диалога с программой.
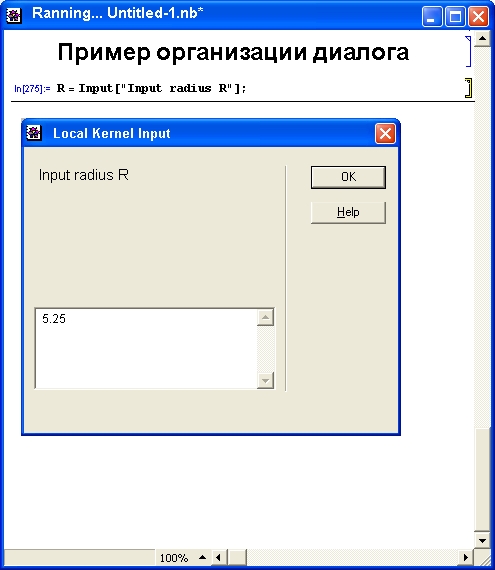
На рис. 7.1 показан простейший пример организации диалога в стиле, принятом в языке Бейсик. В данном случае вычисляется длина окружности с запросом радиуса R.
Рис. 7.1. Пример организации диалога
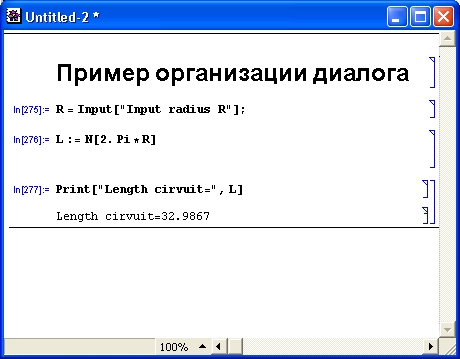
При вычислении документа, приведенного на рис. 7.1, вначале исполняется функция Input. Это ведет к появлению диалогового окна в центре экрана — на рис. 7.1 оно несколько смещено вниз, чтобы не загораживать содержимое ячейки документа. В окне виден запрос, который указан в кавычках как параметр функции Input. После ввода нужного значения (в нашем примере это радиус окружности) и нажатия клавиши Enter или щелчка на кнопке ОК диалогового окна функция Input возвращает введенное значение, и оно присваивается переменной Р.. После этого функция Print выводит на экран вычисленное значение длины окружности с кратким комментарием (рис. 7.2).
Рис. 7.2. Документ рис. 7.1 по окончании диалога
Разумеется, для данного примера нет никакого смысла организовывать диалог в такой форме, поскольку однократное вычисление длины окружности проще задать прямо в тексте документа без запроса радиуса — просто указав R = 10. Однако при составлении сложных программ, например ориентированных на многократные вычисления с различными данными по скрытым формулам, такая возможность организации диалога очень полезна. Ее можно использовать и при составлении обучающих программ на базе системы Mathematica.
К сожалению, комментарий, отображаемый в окне функции ввода Input, возможен только на английском языке — при вводе символов кириллицы вместо обычных надписей выводятся коды (в то же время функция Print исправно выводит комментарии на русском языке). Это связано с выбором для данного окна шрифта, не содержащего символов кириллицы.
gl7-1.jpg
gl7-2.jpg
2. Функции задания формата вывода
Функции задания формата вывода
Далее отметим функции, меняющие формат представления выражений. Все они имеют в своем названии слово Form (форма). Таких функций довольно много, и их полный список вы найдете в приложении. Отметим лишь несколько наиболее часто используемых функций этого рода:
- AccountingForm [ехрг] — выполняет вывод всех чисел, содержащихся в выражении ехрr, в бухгалтерской форме представления;
- CForm[expr] — выполняет вывод expr в форме, принятой для языка С;
- EngineeringForm [expr ] — дает вывод, представляя все вещественные числа в выражении expr в инженерной форме (это означает, что порядок чисел равен нулю или кратен трем);
- FortranForm[expr] — выводит expr в форме, принятой для языка Фортран;
- FullForm [expr] — выводит полную форму выражения expr без использования специального синтаксиса;
- InputForm[expr] — выводит expr во входной форме;
- NumberForm[expr, n] — выполняет вывод expr с вещественными числами, представленными с точностью до n цифр;
- OutputForm [expr] — выполняет вывод expr в стандартной выходной форме системы Mathematica;
- ScientificForm [expr] — выполняет вывод, представляя все вещественные числа в выражении expr в научном формате;
- TeXFormfexpr] — выводит expr в форме, принятой для языка ТеХ, ориентированного на верстку текстов с математическими формулами;
- TextForm[expr] — выполняет вывод expr в обычном текстовом формате;
- TreeForm [expr] — выполняет вывод expr с показом разных уровней выражения.
В большинстве своем действие этих функций вполне очевидно. Если это не так, то смело экспериментируйте с ними. Следующие примеры дают представление об использовании различных форм вывода в системе.
| Ввод (In) | Вывод (Out) |
| Accounting [30*10^15] | Accounting [30000000000000000] |
| BaseForm [55434, 16] | d88a 16 |
| CForm[x ^ 2+3*x+x] | 4*x + Power (x, 2) |
| ColumnForm [ { а , b , с ) ] | a b с |
| EngineeringForm[N[12*10 A 29] ] | 1.2xl0 30 |
| Format [Exp [x ^ 2 ] /а] | e x 2 /a |
| FortranForm[Exp[x] ^ 2/а] | E**(2*x)/a |
| HoldForm[Exp[x] ^ 2/а] | e 2x /a |
| NumberForm[N[Exp[2]] ,15] | 7.38905609893065 |
| OutputForm [Exp [x]^2/a] | e 2x /a |
| TeXForm[Exp [x]^2/a] | \frac{e^{2\,x}}{a} |
| Scientif icForm[12*10 ^ 5] | 1200000 |
Приведем еще несколько примеров использования различных форм вывода (здесь содержимое ячеек вывода дано под содержимым ячеек ввода):
FullForm[Exp[x]^2/а]
Times[Power[a, -1, Power[E, Times[2, х]]]
TreeForm[Exp[x]^2/а]
Times[ , ] Power[a, -1] Power[E, | ]
Times[2, x]
PaddedForm[(х^З+2*х^2+3*х-1)/ (x-1) ,3]
(2 3 -l+3x+2x +x)/(-1 + x)
PrecedenceForm[12*b/c,5]
a + 12 b/c
SequenceForm[Exp[x]^2/a]
E^2 x/a
TableForm[{{"x","y"},{l,2},{3,4},{5,6}}]
x у
1 2
3 4
5 6
Prefix[f[x^2]]
2
f@ (x )
Unevaluated[Exp[х^(a/b)]/x/a]
a/b
Exp[x ] Unevaluated[Exp[x^a/b]/x a]
3. Удаление введенных в ходе сессии определений
Удаление введенных в ходе сессии определений
Мы уже не раз отмечали возможность уничтожения введенных в ходе сессии определений. Приведем в систематизированной форме функции, используемые для этого:
- Clear [symbol1, symbol2,...] — стирает значения и определения для указанных символов (идентификаторов);
- Clear ["pattern1", "pattern2",...] — стирает значения и определения для всех символов, чьи имена подходят под любой из указанных строковых шаблонов;
- ClearAll [symboll, symbo!2,...] — стирает все значения, определения, атрибуты, сообщения и значения, принятые по умолчанию, связанные с указанными символами;
- ClearAll ["patternl", "pattern2",...] — стирает все символы, чьи имена буквально подходят к одному из указанных строковых образцов;
- ClearAttributes [s, attr] — удаляет attr из списка атрибутов символа s.
Применение большинства этих функций полезно разработчику серьезных приложений для систем Mathematica, например новых пакетов расширений и применений системы. В то же врем-я, для большинства пользователей вполне достаточно возможностей, предоставляемых системой по умолчанию — средств диалога с ее оболочкой и функций Input и Print.
Хотя Mathematica ориентирована на математические приложения, в ней достаточно полно представлены функции для работы со строками (strings). Они могут потребоваться как для организации вывода текстовых сообщений (например надписей на графиках), так и для организации текстового диалога при разработке пакетов расширений и приложений системы. К тому же надо постоянно помнить, что Mathematica — система символьной математики, так что символьным преобразованиям, как сугубо математическим, так и общепринятым, в ней, естественно, уделено много внимания.
Многие функции для работы со строками выполняют общепринятые преобразования, имеющиеся в большинстве языков программирования высокого уровня. Строкой является произвольная цепочка символов, заключенная в кавычки, например "String". Ниже представлены некоторые функции для работы со строками:
- StringByteCount ["string"] — возвращает полное число байтов, используемых для хранения символов в строке "string";
- StringDrop ["string", {m, n}] — возвращает строку "string", удалив в ней символы от m до п;
- StringJoin["sl", "s2",...] или StringJoin [ { "s1", "s2",...}]-формирует строку, содержащую конкатенацию (объединение) указанных строк "s1";
- Stringlnsert ["string1", "string2",M] — вставляет строку "string2" в строку "string1", начиная с позиции М от начала этой строки (при отри-, цательном М позиция отсчитывается от конца указанной строки);
- StringLength ["string" ] — возвращает число символов в строке;
- StringReplace["string", "s1 -> "spl"] или StringReplace["string", {"s1" -> "spl", "s2" -> "sp2",...}] — замещает "s1" на "spi" всякий раз, когда они появляются как подстроки "string";
- StringReverse ["string"] — меняет порядок символов в строке "string" на противоположный;
- StringPosition["string", "sub"] — возвращает список с позициями строки "sub" в строке "string" (дополнительные формы см. в справочной системе);
- StringTake ["string", n] — возвращает строку, состоящую из первых п символов строки "string";
- StringTake ["string", -n] — возвращает последние п символов из строки "string";
- StringTake ["string", {n}] — возвращает n-й символ в строке "string";
- StringTake ["string", {m, n}] — возвращает строку из символов, расположенных в позициях от m до п строки "string".
Эти функции хорошо известны программистам, работающим с современными языками программирования. Большое число дополнительных функций для работы со строками можно найти в приложении. Обилие таких функций в языке программирования системы Mathematica указывает на его универсальный характер и обширные возможности в решении даже на первый взгляд далеких от математики задач. Ниже приведены примеры действия ряда функций работы со строками.
| Ввод (In) | Вывод (Out) |
| StringByteCount [ "Hello ! " ] | 6 |
| StringDrop ["Hello my friend!", 6] | my friend! |
| StringDrop ["Hello my friend! ", -10] | Hello |
| StringDrop ["Hello my friend! ", {7}] | Hello у friend! |
| StringDrop [ "Hello my friend ! " , { 6 , 8 } ] | Hello friend! |
| Stringlnsert ["Hello friend!"," my", 6] | Hello my friend! |
| StringJoin ["Hello"," my "]<>"friend!" | Hello my friend! |
| StringLength [ "Hello" ] | 5 |
| StringPosition[ "Hello my friend! ", "e"] | {{2, 2}, {13, 13}} |
| StringReplace["Hilo" , "i"->"el"] | Hello |
| StringReverse [ "Hello ! " ] | !olleH |
| StringTakef "Hello my friend!", 6] | Hello |
| StringTake[ "Hello my friend!", -8] | friend! |
| StringTake [ "Hello my friend ! " , { 7 , 9 } ] | my |
Отметим еще несколько функций, относящихся к работе с символами и строками:
- FromCharacterCode [n] — возвращает строку, состоящую из одного символа с кодом n;
- FromCharacterCode [ {n1, n2,...}] — возвращает строку, состоящую из последовательности символов с кодами ni;
- Characters ["string"] — возвращает список целочисленных кодов, соответствующих символам строки "string";
- ToLowerCase ["string"] — производит строку, в которой все буквы преобразованы в нижний регистр;
- ToString [expr] — возвращает строку, соответствующую форме вывода выражения ехрг. Опции устанавливают ширину линии, тип формата и т. д.;
- ToUpperCase [ "string" ] — вырабатывает строку, в которой все буквы преобразованы в верхний регистр;
- Unique [ ] — создает новый символ с именем в форме $nnn (nnn — уникальный порядковый номер);
- Unique [х] — создает новый символ с именем в форме x$nnn (nnn — уникальный порядковый номер);
- Unique [ {х, у,...}]— создает список новых символов с уникальными именами;
- Unique [ "ххх" ] — создает новый символ с именем в форме xxxnnn (nnn — уникальный порядковый номер);
- Unique [name, {attrl, attr2,...}] — создает символ с указанными атрибутами attri;
- UpperCaseQ [string] — возвращает True, если все символы строки string являются прописными буквами (верхнего регистра), иначе возвращает False.
Примеры, приведенные ниже, показывают работу с этими функциями.
| Ввод (In) | Вывод (Out) |
| ToCharacterCode [ "Hello ! " ] | {72,101,108,108,111,33} |
| FromCharacterCode [ {72 , 101 , 108 , 108 , 111 , 33} ] | Hello! |
| ToExpression [ "2+3*4 " ] | 14 |
| ToLowerCase [ "HeLLo ! " ] | hello! |
| ToUpperCase [ "Hello" ] | HELLO |
| Ввод (In) | Вывод (Out) |
| x:=ToString[2+3*4] | |
| X | 14 |
| Unique [ ] | $1 |
| Unique [xyz] | xyz$2 |
| Unique [xyz] | xyz$3 |
| UpperCaseQ [ "Hello" ] | False |
| UpperCaseQ [ "HELLO" ] | True |
4. Потоки и файлы
Потоки и файлы
Система Mathematica имеет развитые средства для работы с потоками (streams) и файлами (files). Под потоком подразумевается непрерывная последовательность данных, циркулирующих внутри компьютера. Обмен потоками происходит практически непрерывно, например, при вводе поток ввода поступает от клавиатуры в компьютер, при печати поток данных поступает от компьютера в принтер через порт принтера и т. д.
Файлом является упорядоченная структура данных, имеющая имя и хранящаяся на каком-либо носителе, чаще всего на магнитном диске. Файлы могут иметь различные форматы и различный тип доступа к хранимой на них информации. Наиболее распространенные в системе Mathematica файлы документов являются файлами с последовательным доступом и имеют текстовый формат.
Последовательный доступ означает, что информация из открытого файла может быть считана строго последовательно от его начала до конца, отмеченного специальной меткой. Это напоминает считывание с магнитофонной кассеты. Текстовый формат означает, что все данные записаны в виде ASCII-кодов. Следовательно, прочесть такой файл можно с помощью любого текстового редактора, работающего с текстами в виде ASCII-кодов.
Потоки и файлы имеют много общего: имена, определенную структуру, необходимость открытия перед использованием и закрытия после использования. Однако если с файлами пользователь сталкивается уже в начале работы с системой (нужно вызвать файл с демонстрационным документом или сохранить его, а затем вызвать другой файл), то с понятием потока при работе с системой сталкиваться практически не приходится, хотя помимо нашей воли потоки данных постоянно текут между компьютером и его периферийным оборудованием.
Прежде чем рассматривать весьма обширные возможности системы по работе с файлами в целом, отметим упрощенный прием вызова файла с помощью двойного символа «<<»:
<<filename
Эта команда считывает файл с указанным именем filename и заносит в память компьютера содержащиеся в нем определения. Имя файла надо указывать полностью, то есть вместе с расширением. Исключением является случай, когда файл находится в основном каталоге системы. Эта команда эквивалентна функции
Get["filename", key]
Для записи объекта (переменной, массива, списка и т. д.) в файл служат упрощенные команды:
- expr >> filename — передает значение ехрг в файл с заданным именем;
- ехрг >>> filename — добавляет ехрг в конец файла с заданным именем.
Указанные команды по существу есть укороченные (и потому более удобные) формы следующих функций:
- Get ["filename", "key"] — читает файл, который закодирован функцией Encode с использованием ключа "key";
- GetContext [ "context' " ] — загружает файл с заданным контекстом;
- Put[exprl, expr2, ..., "filename"] — записывает последовательность выражений expri в файл с именем filename;
- PutAppend[expr1, expr2, ..., "filename"] — присоединяет последовательность выражений expri к файлу с именем filename.
Еще одна упрощенная функция — ! ! filename — выводит содержимое файла с заданным именем.
Следующие примеры показывают запись списка в файл C:\ma.vat, его считывание, затем добавление в файл еще одного списка и контроль контекста файла:
{{l,2,3},{4,5,6},{a,b,c}}>>C:\ma.val
<<С: \ma. val
{{1, 2, 3}, {4, 5, б), {а, b, с}} {d,e,f}>>>C: \ma.val
<<С: \та. val
{d, e, f}
!!С:\mа.val
1, 2, 3, 4, 5, б, а, b, с d, e, f
Такая форма вызова особенно удобна для вызова файлов пакетов расширений и применений системы. Имя файла указывается по правилам, принятым в MS-DOS. Файлы пакетов применений имеют расширение .т. Мы уже приводили примеры использования определений, содержащихся в файлах пакетов расширения системы.
Имеется еще ряд функций для работы с файлами:
- ReadList ["filename" ] — читает все оставшиеся в файле "filename" выражения и возвращает их в виде списка;
- ReadList ["filename", type] — читает из файла "filename" объекты указанного типа type до конца файла. Возвращает список считанных объектов;
- ReadList ["filename", {typel, type2,...}] — читает объекты указанных типов type1 до конца файла filename;
- ReadList [ "filename", types, n] — читает только первые п объектов указанных типов types из файла filename;
- Save ["filename", x1, x2,...] — создает файл с заданным именем filename, содержащий значения переменных x1, х2, ...;
- ! command — исполняет заданную команду операционной системы.
Допустим, что в любом текстовом редакторе создан файл с полным именем C:\datas.txt в ASCII-формате, содержащий просто шесть чисел с разделительными пробелами, размещенные в двух строках и представляющие массив 2x3 элемента:
1 11.2 34.5
2. 3.4 56
Тогда о структуре файла можно судить, используя команду
!!С:\datas.txt
1 1.2 34.5 2. 3.4 56.
Нетрудно заметить, что структура файла соответствует структуре массива. Однако считывание файла командой «name дает следующий результат:
<<С: \datas. txt
380.8
Результат представляет вычисленное выражение второй строки файла. Считывание функцией ReadList без дополнительного аргумента также дает ошибочный результат:
ReadList["С:\datas.txt"]
{41.4, 380.8}
Нетрудно подметить, что функция восприняла каждую строку содержимого файла как результат перемножения трех чисел (пробел на языке Mathematica означает умножение). С дополнительным параметром Number все числа считываются верно:
ReadList["С:\datas.txt", Number]
{1, 1.2, 34.5, 2., 3.4, 56.}
Однако мы получили одномерный список — данные просто считываются построчно. Применение дополнительного параметра в виде {Number, Number} дает следующий результат:
ReadList["С:.txt", {Number, Number}]
{{1, 1.2), {34.5, 2.}, {3.4, 56.}}
Правильный результат можно получить, используя опцию RecordList->True: .
ReadList["C:.txt",Number,RecordLists-XTrue]
{{1, 1.2, 34.5), {2., 3.4, 56.}}
Для загрузки файлов пакетов расширений (Add-On) используются функции, позволяющие задать контекст файлов (подробнее о контекстах речь пойдет в уроке 10):
- Needs ["context' ", "filename"] — загружает файл, если указанный контекст отсутствует в списке загруженных;
- Needs [ "context s " ] — загружает файл, имя которого определяется с помощью функции ContextToFilename [ "context ч " ], если указанный контекст отсутствует в списке загруженных.
Загрузка файлов с указанием их контекстов позволяет избежать конфликтов между разными пакетами расширения, используемыми одновременно (см. более подробно урок 10).
5. Использование файлов других языков программирования
Использование файлов других языков программирования
Из функций для работы с файлами особо надо отметить следующую функцию-директиву:
- Splice [ "file .mx" ] — вставляет в файлы на других языках программирования вычисленные выражения системы Mathematica, которые должны быть записаны в скобках вида <* и *>;
- Splice ["infile", "outfile"] — читает файл infile, интерпретирует фрагменты, содержащиеся между скобками <* и *>, и записывает результат в файл outfile.
Эта возможность особенно существенна при использовании программ на языках программирования С (расширение .me), Fortran (расширение .mf) и ТеХ (расширение .mtex), для форматов которых Mathematica имеет средства конвертирования выражений (CForm, FortranForm и TexForm соответственно). Таким образом, имеется возможность экспорта выражений системы Mathematica в программы, составленные на этих языках.
Поясним применение функции-директивы Splice. Пусть имеется экспортированная программа на языке С, которая должна рассчитывать численное значение некоторого интеграла, и мы хотим получить формулу для этого интеграла средствами системы Mathematica. Допустим, она представлена файлом demo.me. Его можно просмотреть следующим образом:
!!demo.me
#include "mdefs.h"
double f(x)
double x;
{
double y;
у = <* Integrate[Sin[x]^5, x] *> ;
return (2*y- 1) ;
}
После исполнения функции Splice ["demo.me"] программа будет записана в файл demo.с, в котором выражение в скобках <*...*> заменено вычисленным значением интеграла (в форме CForm). Файл при этом будет выглядеть так:
!!demo.с
#include "mdefs.h" double f(x) double x;
{
double y;
у = -5*Cos(x)/8 + 5*Cos(3*x)/48- Cos(5*x)/80 ;
return (2*y- 1) ;
}
Из простых функций, обеспечивающих создание файлов с заданными определениями, надо отметить также функцию Save:
Save ["filename", symb1, symb2,...]
Она добавляет определения символов symbi к файлу filename (возможны упрощенные формы Save).
Приведем пример ее использования:
f[x_] = Sin[x] + y
у+ Sin[x]
у=а
а
Save["demol",f]
!!demol
f[x_] = у + Sin[x]
у = а
6. Другие функции для работы с файлами
Другие функции для работы с файлами
В целом средства системы Mathematica обеспечивают возможности работы с различными файлами, присущие MS-DOS, без выхода из среды системы. Относящиеся к этой группе функции даны в приложении. Для этих функций характерно, что в момент выполнения они не дают видимого эффекта. К таким функциям относятся функции копирования директорий и файлов, смены их имен, удаления и т. д. Они хорошо известны пользователям MS-DOS и могут выполняться из среды Mathematica.
Рассматривая обширный список файловых и поточных операций, можно поневоле сделать вывод об их избыточности. Но здесь действует простое правило: не хочешь применять эти функции — не применяй! Они рассчитаны на пользователя, всерьез занимающегося стыковкой систем Mathematica с другими программными системами.
Важное место занимают функции, дающие информацию о директориях, файлах и потоках. К ним относятся следующие функции:
- Directory [ ] — возвращает текущий рабочий каталог;
- DirectoryStack [ ] — возвращает содержимое стека каталогов, которое представляет последовательность используемых в текущем сеансе каталогов;
- $Display— возвращает список файлов и каналов (pipes— канал или абстрактный файл), используемый функцией вывода $DisplayFunction по умолчанию;
- FileByteCount ["filename"] — возвращает количество байтов в файле;
- FileDate ["filename"] — возвращает дату и время последней модификации файла в виде списка;
- Filelnformation ["filename"] — возвращает информацию о файле;
- FileNames [ ] — приводит список всех файлов в текущем рабочем каталоге;
- FileNames [" form" ] — перечисляет все файлы в текущем рабочем каталоге, чьи имена совпадают с шаблоном form;
- FileNames [{ "forml", "form2",...} ] — перечисляет все файлы, чьи имена соответствуют любому из шаблонов formi;
- FileNames [forms, {"dirl", "dir2",...} ] — перечисляет файлы с именами, соответствующими шаблонам forms, в любом из указанных каталогов diri;
- FileType ["filename"] — возвращает тип файла: File, Directory или None (если указанного файла не существует);
- $HomeDirectory — дает имя «домашней» директории пользователя;
- $Output — дает список файлов и каналов, в которые направляется стандартный вывод системы Mathematica;
- ParentDirectory [ ] — возвращает имя родительского каталога для текущего рабочего каталога;
- ParentDirectory ["dir"] — возвращает имя родительского каталога для каталога dir;
- $ Path — дает список каталогов для просмотра при попытке поиска внешнего файла;
- StreamPosition [stream] — возвращает целое число, которое указывает позицию текущей точки в открытом потоке stream;
- Streams [ ] — возвращает список всех потоков, открытых в данный момент;
- Streams ["name" ] — перечисляет только потоки с указанным именем name.
Приведенные ниже примеры иллюстрируют использование большинства из этих достаточно простых функций:
Directory[]
C:\PROGRAM FILES\WOLFRAM RESEARCH\MATHEMATICA\4.0
DirectoryStack[]
{} / $Display
stdout
FileByteCount["C:.val"]
46
FileDatef'C: .val"]
{1999, 8, 3, 16, 4, 44}
FileInformation["C:.val"]
{File->C:\ma.val, FileType->File, Date -> 3142685084, ByteCount ->46}
Filenames[]
{Examples, FILES, MATHEMATICA.EXE,
MATH.EXE, MATHINSTALLER.EXE, MATHKERNEL.EXE}
FileType["C:.val"]
File HomeDirectory[]
c:\ $0utput
{OutputStream[stdout, 1]}
ParentDirectory[]
С: \m3 Streams[]
{OutputStream[stdout, 1],
OutputStream[stderr, 2]}
Высказанное выше соображение об избыточности набора операций вполне применимо и для этих функций.
Для управления системой в процессе вычислений служат системные директивы и функции. Некоторые из них широко используются при программировании решения прикладных задач, другие служат в основном для контроля над системой.
Имена многих, вспомогательных с точки зрения конечного пользователя, системных функций начинаются с символа $. Ниже описаны основные системные функции.
Ряд системных функций служит для получения информации о времени и текущей дате:
- AbsoluteTime[ ] — возвращает полное количество секунд, прошедших с момента 1 января 1900 г.;
- $CreationDate — возвращает дату и время создания используемой версии системного ядра Mathematical
- Date [ ] — возвращает текущее значение даты и времени в виде {год, месяц, день, час, минута, секунда};
- FromDate [date] — превращает дату date вида {год, месяц, день, час, минута, секунда} в число секунд, прошедших с 1 января 1900 г.;
- TimeUsedt ] — возвращает полное количество секунд процессорного времени, использованного на данный момент в текущем сеансе Mathematical
- $TimeUnit — возвращает минимальный временной интервал в секундах, который можно зарегистрировать в вашей компьютерной системе;
- TimeZone [ ] — возвращает часовой пояс, установленный для вашей компьютерной системы;
- Timing [ехрг] — вычисляет ехрг и возвращает список, состоящий из значения затраченного времени и результата вычислений;
- ToDate [time] — преобразует абсолютное время в секундах, прошедшее с 1 января 1900 г., в дату вида {год, месяц, день, час, минута, секунда}.
Следующие примеры иллюстрируют применение некоторых из этих функций.
| Ввод (In) | Вывод (Out) |
| AbsoluteTime [ ] | 2967708137 |
| Date[] | {2000, 7, 16,11, 23, 8} |
| FromDate [ {2000 ,7,15,4,51,30}] | 3172625490 |
| SessionTime[] | 8171.1 |
| TimeUsedf] | 69.57 |
Их действие вполне очевидно и не требует комментариев.
7. Общесистемные функции
Общесистемные функции
Ниже представлены функции общесистемного характера:
- $Aborted — возвращает сообщение о прекращении вычислений при их прерывании функцией Abort [ ];
- AbortProtect [ехрг] — вычисляет ехрг, запоминая все попытки прерывания, но не выполняя их до тех пор, пока не будет завершено вычисление либо пока не будет вызвана процедура CheckAbort;
- Accuracy [x] — указывает число цифр в числе х после десятичной точки, которое используется при вычислениях;
- ByteCount [expr] — возвращает число байт, которое используется для представления выражения ехрг;
- Environment [ "var" ] — возвращает значение переменной окружения операционной системы с именем "var";
- $ Line — глобальная переменная, указывающая номер текущей строки ввода;
- $MachineEpsilon — возвращает машинную точность представления — наименьшее число, которое, будучи прибавленным к 1.0, даст результат, отличный от 1.0;
- $MachineID — строка, которая возвращает, если возможно, уникальный код идентификации применяемого компьютера;
- $MachineName — строка, возвращающая имя, которое присвоено используемому компьютеру, если такое имя определено;
- $MachinePrecision — возвращает количество десятичных знаков точности представления чисел;
- $MachineType — строка, возвращающая общий тип компьютера, на котором запущена система Mathematical
- $MinMachineNumber — наибольшее машинно-представимое число, которое может применять данная компьютерная система;
- $MaxNumber — возвращает наибольшее из представимых в системе Mathe-matica чисел;
- $MinMachineNumber — наименьшее положительное машинно-представимое число, которое может применять данная компьютерная система;
- $MinNumber — возвращает наименьшее (положительное) представимое в системе Mathematica число;
- $OperatingSystem — строка, дающая тип операционной системы, под управлением которой работает Mathematica;
- Pause [n] — выдерживает паузу не менее п секунд;
- $ReleaseNumber — целое число, которое дает младший номер версии ядра данной системы Mathematica;
- $Remote — имеет значение True, если Mathematica применяется в дистанционном режиме или с программным препроцессором, иначе — значение False;
- $SessionID — уникальный номер, который присвоен данному сеансу системы Mathematica;
- SessionTime[ ] — возвращает полное число секунд реального времени, прошедшего с момента начала вашего сеанса работы в системе Mathematica; -
- $System — представляет собой строку с указанием типа используемой компьютерной системы;
- $Version — символьная строка, которая представляет используемую версию системы Mathematica;
- $VersionNumber — вещественное число, которое дает полный номер текущей версии системного ядра Mathematica.
Ниже приведены примеры использования ряда общесистемных функций.
| Ввод (In) | Вывод (Out) |
| Accuracy [12. 34] | 15 |
| ByteCount [Exp [x] A 2/a] | 120 |
| $Version | 4.0 for Microsoft Windows (April 21, 1999) |
| $ System | Microsoft Windows |
| $Path | {C:\Program FilesXCommon Files\Mathematica\ 4.0\Kernel, C:\Program FilesXCommon Files\ Mathematical . 0\AddOns\Autoload, ... } |
| $OperatingSystem | Windows 9 5 |
| $MachineEpsilon | 2.22045xl0 -16 |
| $MaxMachineNumber | 1.79769xl0 308 |
| $MinMachineNumber | 2.22507x10 -308 |
| $MachinePrecision | 16 |
| $Packages | {Global 4 , System 4 } |
Приведенные примеры показывают, что благодаря системным функциям можно извлечь достаточно полную информацию о текущих параметрах системы и использовать ее для создания специальных алгоритмов вычислений (например, для генерации последовательности псевдослучайных чисел со случайной базой, заданной системным временем) или организации развитого диалога с системой.
В этом уроке мы научились:
- Использовать функции ввода/вывода.
- Работать со строками.
- Использовать функции потоков и файлов.
- Использовать файлы других языков программирования.
- Работать с системными функциями.

