2. Ортогональные многочлены
Ортогональные многочлены
Одними из широко распространенных специальных функций являются ортогональные многочлены (полиномы). Mathematica имеет следующие функции, возвращающие значения ортогональных многочленов:
- ChebyshevT [n, х] — полином Чебышева п-й степени первого рода;
- CyebyshevU [n, x] — полином Чебышева п-йстепени второго рода;
- HermiteH[n, х] — полином Эрмита п-йстепени;
- JacobiP[n, a, b, х] — полином Якоби п-й степени;
- 'GegenbauerC [n, m, х] — полином Гегенбауэра;
- LaguerreL[n, х] — полином Лагерра n-й степени;
- LaguerreL[n, а, х] — обобщенный полином Лагерра п-й степени;
- LegendreP [n, х] — полином Лежандра n-й степени;
- LegendreP [n, m, x] — присоединенный полином Лежандра;
- LegendreQ [n, z] — функция Лежандра второго рода n-го порядка;
- LegendreQ [n, m, z] — присоединенная функция Лежандра второго рода.
LegendreType — опция для функций LegendreP и LegendreQ; она указывает выборы разрывов кривой для функций Лежандра на комплексной плоскости.
Все ортогональные полиномы имеют простые рекуррентные представления. Поэтому приведенные выше функции вычисляются по ним довольно быстро и точно. Они находят широкое применение в технике интерполяции и аппроксимации функций.
Следующие примеры иллюстрируют работу с ортогональными многочленами.
| Ввод (In) | Вывод (Out) |
| ChebyshevT [ 8, х] | 1 - 32 x 2 + 160 x 4 - 256 x 6 + 128 x 8 |
| ChebyshevT [5, 0.2] | 0.84512 |
| ChebyshevU [3,0. 15] | -0.573 |
| HermiteH[4,3] | 876 |
| JacobiP[3,l,2,0.2] | -0.256 |
| GegenbauerC [ 3 , 1 , x] | -4 x + 8 x 3 |
| N [LaguerreL [3,x]] | 0.166667 (6. -18. x+ 9. x 2 - 1. X 3 ) |
| LegendreP [ 5 , x ] | 15 x /6-35 x 3 /4+63 x 5 /8 |
| LegendreQ[2,0.2] | -0.389202 |
Важно отметить, что при указании конкретного значения параметра п и символьном значении параметра х функции этой группы возвращают присущие им представления через степенные многочлены с соответствующими коэффициентами.
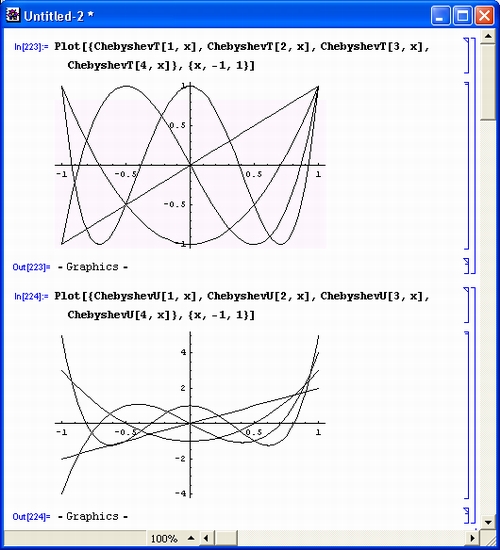
На рис. 6.1 показаны графики ортогональных полиномов Чебышева ChebyshevT и ChebyshevU. Для этих полиномов характерно изменение от -1 до +1 при \х\<1, причем при высоком порядке полиномов графики функций имеют колебательный характер.
Рис. 6.1. Графики ортогональных полиномов Чебышева ChebyshevT (сверху) и ChebyshevU (снизу)
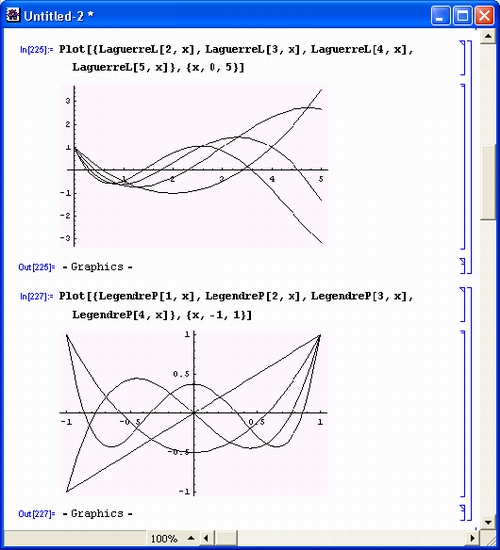
Графики функций полиномов Лагерра LaguerreL и Лежандра LegendreP показаны на рис. 6.2. Они дают представление о поведении этих функций.
Рис. 6.2. Графики ортогональных полиномов Лагерра LaguerreL и Лежандра LegendreP (снизу)
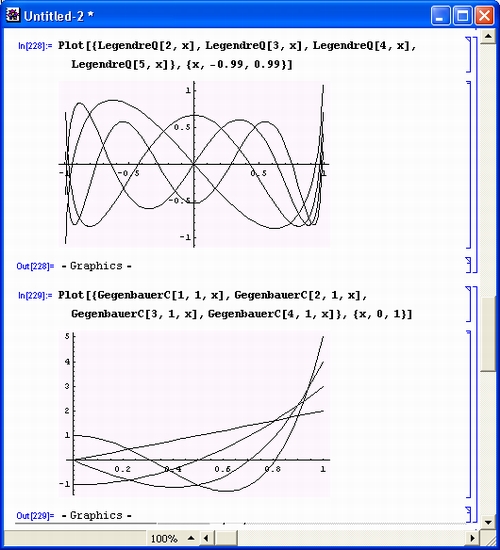
На рис. 6.3 представлены графики полиномов Лежандра LegendreQ.
Рис. 6.3. Графики функций Лежандра LegendreQ (сверху) и полиномов Гегенбауэра GegenbauerC (снизу)
gl6-1.jpg
gl6-2.jpg
gl6-3.jpg