Вычисление производных

 

К числу наиболее часто используемых математических операций принадлежит вычисление производных функций как в аналитической, так и в символьной форме. Для этого используются следующие функции:

• D [ f, х ] — возвращает частную производную функции f по переменной х;
• D [f, {х, n}]— возвращает частную производную n-го порядка по х;
• D[f, xl, х2,...] — возвращает смешанную производную;
• Dt[f, х] — возвращает обобщенную производную функции f по переменной х;
• Dt [ f ] — возвращает полный дифференциал f.

Название функции из одной буквы — это явно исключение из правил. Оно выбрано осознанно, в силу массовости этой операции.

Для функции D существует опция NonConstants, которая позволяет задать список объектов, находящихся в неявной зависимости от переменных дифференцирования. По умолчанию этот список пустой. Для функции Dt имеется опция Constants, которая, наоборот, указывает символы, которые являются константами (по умолчанию их список также пуст). На практике применять данные опции приходится редко.

Существует еще одна функция, Derivative [nl, n2,...] [f ], — основная (общая) форма представления функции, полученной в результате nl-кратного дифференцирования функции f по первому аргументу, п2-кратного — по второму аргументу и т. д.

К примеру, Derivative [2] [х*у] возвращает (ху)", a Derivative [2, 3] [х*у] — соответственно, (ху) ^(2.3)

Следующие примеры показывают применение функции D для вычисления производной в аналитическом виде:

• Производная тригонометрической функции:
  

  D[x*Sin[x],x]

xCos[x] + Sin[x]

• Производная экспоненциальной функции:
  

  D[Exp[x/b],x]

  ex/b/b

• Производная логарифмической функции:
  

  D[Log[3*x/4],x]

  1/x

• Производная степенного многочлена:
  

  D[а*х^2+b*х+с,х]

  b+ 2ах

• Пятая производная от х ⁿ :
  

  D[х^n,{х,5}]

  (-4 + n) (-3+n) (-2+n) (-1+n)nх ^-5+n

• Производная функции двух переменных:
  

  D[(x^m)*y^n,x,y]

  mnx ^-1+m y ^-1+n

• Производная функции Бесселя:
  

  D[BesselJ[2,x] ,x]

  1/2 (BesselJ[l, х] -BesselJ[3, x] )

• Производная ортогонального полинома Чебышева:
  

  D[ChebyshevT[4,x],x]

  -16x + 32x3

Следующие примеры иллюстрируют вычисление производных от первого до третьего порядка включительно для функции f [ х ], заданной пользователем.

Ввод (In)	Вывод (Out)
f[x] :=х/(1+х ^ 2)
D[f[x],{x,l}]	-2x 2 /(1+x 2 ) 2 +1/(1+x 2 )
D[%,x]	-8x 3 /(1+x 2 ) 3 +6x/(1+x 2 ) 2
D[f[x],{x,2}]	-8x 3 /(1+x 2 ) 3 +6x/(1+x 2 ) 2
D[D[D[f[x],x],x],x]	-48x 4 /(1+x 2 ) 4 +48x 2 /(1+x 2 ) 3-6/(1+x 2 ) 2
D[f[x],{x,3}]	-48x 4 /(1+x 2 ) 4 +48x 2 /(1+x 2 ) 3-6/(1+x 2 ) 2

Из предпоследнего примера видно, что для вычисления высших производных возможно последовательное применение функции D.

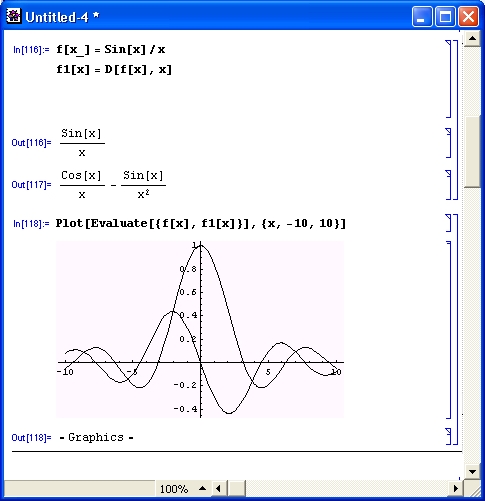
На рис. 4.1 показано построение графика функции Sin [x] /х, заданной как функция пользователя, и ее производной с помощью функции Plot.

Рис. 4.1. График функции Sin[x]/x и ее производной

В целом средства для символьного вычисления производных, имеющиеся в ядре системы Mathematica, охватывают практически все важные типы математических выражений. Они могут включать в себя как элементарные, так и специальные математические функции, что выгодно отличает систему Mathematica от некоторых простых систем символьной математики, таких как Derive.

Использование функции Dt демонстрируют примеры, приведенные ниже.

Ввод (In)	Вывод (Out)
Dt[x*n,x]	x n (n/x +Dt[n, x] Log[x] )
Dt[x*Sin[x] ,x]	xCos[x] + Sin[x]
Dt[Exp[x/b],x]	e x/b /b(1/b-xDt[b, x]/b 2 )
Dt[a*x ^ 2+b*x+c,x]	b+ 2 ax + x 2 Dt[a, x] + xDt[b, x] + Dt[c, x]
Dt[x*n,{x,2}]	x n (n/x+Dt[n, x] Log[x] ) + x n (-n/x 2 2Dt[n, x] +Dt[n, {x/2}]Log[x])
Dt[Log[3*x/4],x]	1/x
Dt[BesselJ[2,x] ,x]	1/2(BesselJ[l, x] -BesselJ[3, x] )
Dt[ChebyshevT[4,x] ,x]	-16x + 32x 3

Обратите внимание на то, что порой результаты для одного и того же дифференцируемого выражения у функций D и Dt заметно различаются. Это вполне закономерно вытекает из различных определений данных функций.