5. Работа со списками и массивами
Работа со списками и массивами
Списки относятся к данным множественного типа. Они имеют большое значение при обработке массивов данных и служат основой для создания векторов и матриц. В этом разделе мы познакомимся со свойствами списков, их созданием (генерацией) и использованием.
Часто математические или иные объекты содержат множество данных, которые желательно объединять под общим именем. Например, под объектом с именем М можно подразумевать квадратную матрицу размером 10x10 с общим числом элементов, равным 100. Человека с именем Victor, например, можно характеризовать целым списком разных данных — символьными фамилией, именем и отчеством, целочисленным годом рождения, вещественным ростом, объемом груди и т. д.
Для объединения данных могут использоваться списки (list). Mathematica имеет обширные возможности работы с объектами-списками, содержащими не только однотипные, но и разнотипные элементы. В частности, элементами списков могут быть числа, константы, переменные, выражения и даже сами списки. Списки используются для конструирования более частных типов данных — массивов, матриц и векторов [87].
На языке данной системы список — это совокупность произвольных данных, указанных в фигурных скобках, например: {1, 4, 2, 7, 9} или {а, Ь, с, d, e, sin[x], ln[y], "string"}
Возможно задание списков в списке, например, так:
{{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}
Такой список представляет матрицу
1 2 3
4 5 6
7 8 9
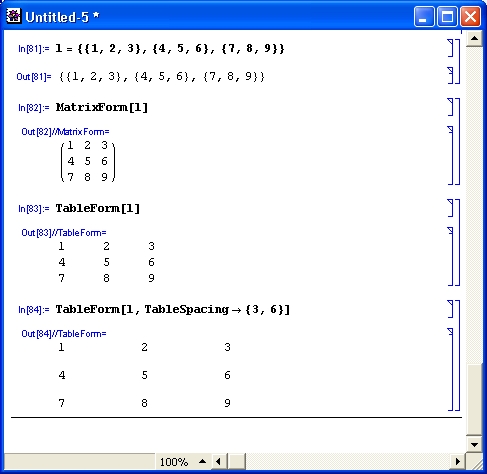
Однако, чтобы вывести список в такой матричной форме, надо использовать после списка выражение //MatrixForm (рис. 3.7).
Рис. 3.7. Примеры задания и вывода матрицы
На рис. 3.7 показан еще один способ задания списка или матрицы — с помощью функции List:
- List [a, b, с,...] — создает список {а, b,, с,...};
- List [ {а,b, с,...}, {d,e, f,...}, {i, k, 1,...} ] — создает список — матрицу { {a,b, с,...}, {d,e, f,...}, {i, k, 1,...} }.
Списки можно составлять, непосредственно задавая объекты в соответствии с описанным синтаксисом. Однако можно и генерировать некоторые виды списков, таких как таблицы. Списки могут быть объектами присваивания переменным, например
V:={1, 2, 3, 4, 5}
Списки характеризуются размером, который представляет собой произведение числа элементов списков по каждому направлению (размерности). Например, одномерный список является вектором и характеризуется числом элементов по единственному направлению. При этом вектор может быть вектором-строкой или вектором-столбцом. Двумерный список представляет матрицу, имеющую m строк и n столбцов. Ее размер равен mxn. Если m=n, то матрица называется квадратной. Трехмерный список можно представить в виде параллелепипеда, содержащего mxnxp элементов. Списки большей размерности трудно наглядно представить, но они вполне возможны. Напомним, что имена векторов и матриц в данной книге обозначены жирными символами, например, V для вектора и М для матрицы.
Для генерации списков с элементами, являющимися вещественными и целыми числами или даже целыми выражениями, часто используется функция Table, создающая таблицу-список:
- Table [expr, {imax} ] — генерирует список, содержащий imax экземпляров выражения ехрг;
- Table [expr, {i, imax} ] — генерирует список значений ехрг при 1, изменяющемся от 1 до imax;
- Table [expr, {i, imin, imax}] — генерирует список значений ехрг при i, изменяющемся от imin до imax;
- Table [expr, {i, imin, imax, di} ] — использует шаг приращения i, равный di;
- Table[expr, {i, imin, imax}, {j, jmin, jmax},...] —возвращает вложенный список. Самым внешним является список по переменной i.
Ниже приводятся примеры использования функции Table (первая строка каждого примера — ввод, следующая — вывод).
| Пример | Комментарий |
| Table[i*j,{i,l,3},{j,l,3}] {{1, 2, 3), [2, 4, 6}, {3, 6, 9}} | Генерация матрицы размером |
|
Table[N[Exp[i]], {1,0, 2,0.5}] {1., 1.64872, 2.71828, 4.48169, 7.38906}
| Генерация пяти значений Е ^ 1 численном виде |
|
Table[Exp[i],{i,l,5}] {е, е 2 , е 3 , е 4 , е 5 }
| Генерация пяти значений Е ^ i (i=l, 2, 3,4 и 5) |
|
Table[Exp[i],{5}] {е i , е i , е i , е i , е i }
| Генерация пяти значений Е ^i |
Применяется также функция Range, которая предназначена для создания так называемых числовых списков, значения которых равномерно распределены в некотором заданном диапазоне:
- Range [imax] — генерирует список числовых элементов {1, 2, ..., imax};
- Range [imin, imax] — генерирует список числовых элементов {imin, ...,
- Range [imin, imax, di] — генерирует список числовых элементов от imin до imax с шагом di.
Примеры использования функции Range.
| Пример | Комментарий |
| Range [5] {1, 2, 3, 4, 5} | Генерация пяти целых чисел |
Range[0,2,0.5] {0, 0.5, 1.,1.5, 2.}
| Генерация чисел пяти вещественных |
Для выделения элементов списка list используются двойные квадратные скобки:
- list [ [i] ] — выделяет i-й элемент списка;
- list [ [ { i, j , --.}]] — выделяет i-й, j-й и т. д. элементы списка.
Ниже приведены примеры выделения элементов списков.
| Пример | Комментарий |
| 11:={1,2,3,4,5) | Задание исходного списка 11 |
| 11[[3]] | Выделение третьего элемента |
| 3 | |
| 11[[{1,2,5}]] | Выделение первого, второго и пятого элементов |
| (1, 2, 5} | |
| 12={{1,2,3},{4,5,6}} | Задание сдвоенного (двумерного) списка |
| {{1, 2, 3}, {4, 5, 6}} | |
| TableForm[12] | Вывод сдвоенного списка в табличной форме |
| 1 2 3 | |
| 4 5 6 | |
| L2[[2,3]] | Выделение элемента сдвоенного списка |
| 6 |
Для выделения заданного z'-ro элемента списка list используется также функция Part [list, i]. При i>0 отсчет номеров элементов идет с начала списка, а при i<0 — с его конца. Это правило поясняют следующие примеры:
L:={l,2,3,a,b,c}
{Part[L,2],Part[L,5],Part[L,6]}
{2, b, с}
{Part[L,-2],Part[L,-5],Part[L,2]}
{b, 2, 2}
Функция Part может использоваться для выбора заданного элемента выражения из списка. В этом случае вместо i надо указать три числа — номер выражения как элемента списка, уровень выражения и порядковый номер извлекаемого из
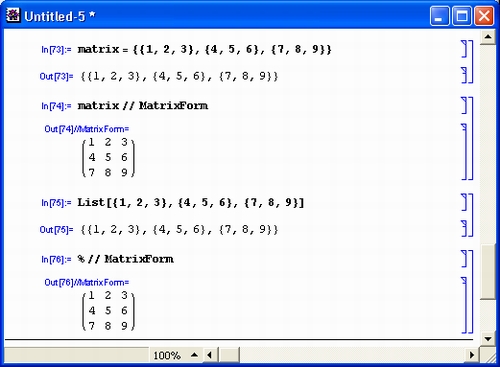
выражения объекта. Показанные на рис. 3.8 примеры иллюстрируют работу со списком, последним (четвертым) элементом которого является математическое выражение.
Рис. 3.8. Примеры выделения элементов выражения
Обратите внимание на то, что в последнем примере неверно задан уровень выражения — использованное выражение имеет только один (первый) уровень. Поэтому задание второго уровня вызывает появление сообщения об ошибке.
Функция Select используется для выделения элементов списка, удовлетворяющих заданному критерию:
- Select [list, crit] — выбирает все элементы ei списка list, для которых функция критерия crit [ei] имеет значение True;
- Select [list, crit, n] — выбирает первые п элементов, для которых critfei] есть True.
Ниже представлены примеры применения этой функции:
Select[{1,а,2,b,3,c},NumberQ]
{1, 2, 3}
Select[{l,a,2,b,3,c),NumberQ,2]
{1, 2}
Select[{l,a,2,b,3,c},PrimeQ]
{2, 3}
Для вывода элементов списка используются следующие функции:
- MatrixFormflist] — выводит список в форме массива (матрицы);
- TableForm [list] — выполняет вывод элементов списка list в виде таблицы.
С этими функциями используются следующие опции:
- TableAlignments — указывает, каким образом должно выравниваться содержимое списка в каждой размерности (слева, по центру или справа);
- TableDepth — устанавливает максимальное количество уровней, выводимых в табличном или матричном формате;
- TableDirections — указывает, как следует располагать последовательные (соседние) размерности — в виде строк или столбцов;
- TableHeadings — задает подписи (labels) для каждой размерности таблицы или матрицы;
- TableSpacing — устанавливает количество пробелов, которое следует оставлять между соседними строками или столбцами.
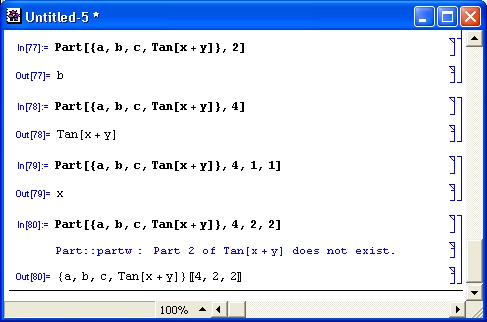
Обратите внимание на то, что эти опции используются как для функции TableForm, так и для функции MatrixForm, используемой для вывода матриц. Вообще, векторы и матрицы являются разновидностью списков. На рис. 3.9 поясняется использование функций MatrixForm и TableForm на примере вывода списка.
Рис. 3.9. Примеры вывода списка в матричной и табличной формах
Дополнительные возможности функции TableForm демонстрирует рис. 3.10. Здесь особенно полезно отметить возможность выравнивания данных в таблицах по левому и правому краям, а также по середине.
В большинстве случаев опции для функций MatrixForm и TableForm не используются. Точнее, они установлены по умолчанию. Проверить, какие опции использованы, можно, например, следующим образом:
Options[MatrixForm]
{TableAlignments -> Automatic, TableDepth-> со, TableDirections -> Column,
TableHeadings->None, TableSpacing-> Automatic}
Options[TableForm]
{TableAlignments -> Automatic, TableDepth ->бесконечность, TableDirections -> Column,
TableHeadings -» None, TableSpacing-> Automatic}
Рис. 3.10. Примеры вывода списка в табличной форме
Вывод можно сделать такой — Mathematica обладает обширными возможностями по части выделения элементов списков и представления списков на экране дисплея и в распечатках документов.
Функции выявления структуры списков
Списки относятся к данным сложной структуры. Поэтому при работе с ними возникает необходимость контроля за структурой, иначе применение списков может привести к грубым ошибкам, как явным, сопровождаемым выдачей сообщения об ошибке, так и неявным. Последние могут привести к серьезным просчетам.
Для выявления структуры списков используется ряд функций:
- Count [list, pattern] — возвращает количество элементов в списке list, которые соответствуют образцу pattern;
- Dimensions [list] — возвращает список размеров списка по каждой размерности;
- FreeQ [list, form] — возвращает True, если список list не содержит form;
- Length [list] — возвращает число элементов одномерного списка list или число размерностей в случае многомерного списка;
- MatrixQ [list ] — проверяет, является ли список матрицей, и дает True, если это так, и False в противном случае;
- MemberQ [list, form] — проверяет, есть ли form в списке, и возвращает True, если это так, и False в противном случае;
- Position [list, form] — возвращает номер позиции form в списке;
- TensorRank[list] — находит ранг списка, если он является тензором;
- VectorQ [list] — проверяет, является ли список вектором, и дает True, если это так, и False в противном случае.
Функции с буквой Q в конце имени являются тестирующими и возвращают логические значения True или False. Остальные функции возвращают численные значения соответствующего параметра списка.
Ниже даны примеры использования этих функций.
| Ввод (In) | Вывод(Out) |
| 11={1,2,3,4,1}; | |
| Length [11] | 5 |
| Dimensions [11] | {5} |
| MatrixQ [11] | False |
| TensorRank [ 11 ] | 1 |
| MemberQ[ll,l] | True |
| Count[ll,l] | 2 |
| FreeQ [11, 5] | True |
| Position [11,1] | {{1},{5}} |
| VectorQ [11] | True |
| M={{1, 2,3}, {4, 5, 6}} | |
| Length [M] | 2 |
| Dimensions [M] | {2,3} |
Система предоставляет пользователю свободу действий, производимых по результатам анализа структуры списков.
Списки можно представить в виде особой структуры данных — стека. Стек — это структура данных, напоминающая стопку тарелок в шкафу. При этом тарелки играют роль данных. Очередную тарелку можно положить только сверху (на вершину стека). На дне стека лежит первая помещенная в него тарелка. Стек подчиняется следующему правилу: последнее введенное значение извлекается первым, а первое введенное значение извлекается последним. Стек относится к системам хранения данных динамического типа, его размеры непрерывно меняются по ходу вычислений. Стек может быть пустым, если из него извлечены все данные.
Система Mathematica предоставляет широкие возможности для операций со стеками:
- Drop [list, n] — возвращает список list, из которого удалены первые п элементов;
- Drop [list, -n] — возвращает список list с отброшенными последними п элементами;
- Drop [list, {n}] — возвращает список list без n-го элемента;
- Drop [list, {m, n}] — возвращает список list с отброшенными элементами от m-го до п-го;
- Fold[f, x, list] — возвращает последний элемент из FoldList [f,x, list];
- Last [list] — возвращает последний элемент списка list;
- Rest [list] — возвращает список с уничтоженным первым элементом;
- Take [list, n] — возвращает первые п элементов списка list;
- Take [list, -n] — возвращает последние п элементов списка list;
- Take [list, {m, n}] — возвращает элементы списка с порядковыми номерами от m до п.
Следующие примеры поясняют работу со стеком.
| Ввод (In) | Вывод(Out) | |||||||
| Drop[{l | ,2 | ,3 | ,4 | ,5}, | 2] | {3, | 4, | 5} |
| Drop [ { 1 | ,2 | ,3 | ,4 | ,5}, | -2] | {1, | 2, | 3} |
| Drop [ { a | ,b | ,c | ,d | ,e>, | {2,4}] | (a, | e} | |
| Last[{l | ,2 | ,3 | ,4 | ,5}] | 5 | |||
| Rest[{l | ,2 | ,3 | ,4 | ,5}] | {2, | 3, | 4, 5} | |
| Take[{l | ,2 | ,3 | ,4 | ,5}, | 2] | (1, | 2} | |
| Take [ { 1 | ,2 | ,a | ,b | ,c}, | -2] | {b, | c} | |
| Take [ { 1 | ,2 | ,3 | ,4 | ,5}, | {2,4}] | {2, | 3, | 4} |
Тривиальная процедура общения со стеком (ввести/вывести данные) ограничивает возможности стековых операций. Из житейского опыта мы знаем, что, проявив настойчивость, можно вставить тарелку и в середину стопки. Mathematica предоставляет ряд расширенных возможностей для работы со списками, выходящих за рамки обычных стековых операций.
Так, например, для расширения списка путем включения в него новых элементов используются следующие функции:
- Append [list, element] — добавляет элемент в конец списка;
- PreoendTlist.element1 — добавляет элемент в начало списка:
- Insert [list, element, n] — вставляет элемент в позицию п (отсчет пози-ций.ведется с начала списка, а если число п отрицательное — то с конца). Данной функцией можно включать элемент в несколько позиций, указав каждую в фигурных скобках, взяв все перечисление в еще одни фигурные скобки и использовав его вместо п. При этом надо учитывать, что все позиции включаемых элементов определяются одновременно до начала расширения списка.
Следующие примеры иллюстрируют применение этих функций.
| Ввод (In) | Вывод(Out) | ||||
| 1={1,2,3} | (1, | 2, | 3} | ||
| Append[l,e] | (1, | 2, | 3, | e} | |
| Prepend[l,e] | {e, | 1, | 2, | 3} | |
| Insert[l,e,2] | {1, | e, | 2, | 3} | |
| L={1, 2, 3, 4 | , 5} | {1, | 2, | 3, | 4, 5} |
| Insert [L, e, | -5] | (1, | e, | 2, | 3, 4, 5} |
| Insert [L, e, | {{1},{5}}] | (e, | 1, | 2, | 3, 4, e, 5} |
Обратите внимание на то, что в данном случае элементы списка — числа, тогда как вставляемый элемент имеет символьное значение е.
Следует отметить, что описанные для стека функции Drop и Rest позволяют удалить из списка последний или первый элемент. Функция Delete [list, i] позволяет удалить из списка произвольный i-й элемент. Если i>0, то отсчет удаленного элемента идет с начала списка, а если i<0 — с конца:
L:={1,2,3,4,5}
{Delete[L,l],Delete[L,3],Delete[L,5]}
{{2, 3, 4, 5}, {1, 2, 4, 5}, {1, 2, 3, 4}}
{Delete[L,-2],Delete[L,-5]}
{{1, 2, 3, 5}, (2, 3, 4, 5}}
Delete[{l,2,3,{a,b,c},4,5},2]
{1, 3, {a, b, c}, 4, 5}
Если элементом списка является список, то он фигурирует как один элемент. Можно, однако, удалить избранный элемент из элемента списка, указав в фигурных скобках вместо i номер элемента списка во внешнем списке и номер удаляемого элемента во внутреннем списке. Это иллюстрируют следующие примеры:
Delete[(1,2,3,{а,Ь,с},4,5},{4,3}]
{1, 2, 3, {а, b}, 4, 5}
Delete[{1,2,3,{а, b, с},4,5},{4,1}]
{1, 2, 3, {b, с}, 4, 5}
Наконец, с помощью функции Delete можно удалить несколько элементов списка, указав каждый из них в фигурных скобках и оформив это указание также в фигурных скобках:
Delete [ {1,2,3, {a, b, c} , 4, 5}, {{2}, {4} ,{ 5}}]
{1, 3, 5}
Следует иметь в виду, что некоторые функции удаляют в списках определенные элементы. Этот вопрос будет рассмотрен ниже.
Изменение порядка расположения элементов в списке
Помимо добавления в список новых данных имеется возможность изменения порядка расположения элементов в списке. Она реализуется следующими операциями:
- Flatten [list] — выравнивает (превращает в одномерный) список по всем его уровням;
- Flatten [list, n] — выравнивает список по п его уровням;
- Flatten [list, n, h] — выравнивает выражения с заголовком h no n уровням;
- FlattenAt [list, n] — выравнивает подсписок, если он оказывается п-м элементом списка list. Если n отрицательно, позиция отсчитывается с конца;
- Sort [list] — сортирует элементы списка list в каноническом порядке;
- Sort[list,p] — сортирует согласно функции упорядочения р;
- Reverse [list] — возвращает список с обратным порядком расположения элементов;
- RotateLeft [list] — возвращает список после однократного поворота влево;
- RotateLeft [list, n] — возвращает список после n-кратного поворота влево;
- RotateRight [list] — возвращает список после однократного поворота вправо;
- RotateRight [list, n] — возвращает список после n-кратного поворота вправо;
- Transpose [list] — осуществляет транспозицию (смену строк и столбцов) для двумерного списка;
- Transpose [list, п] — осуществляет транспозицию n-мерного списка. Ниже приведен ряд примеров на использование этих функций.
| Ввод (In) | Вывод (Out) |
| 13={{1,2,3},{4,5,6},{7,8,9}}; | {1,2,3,4,5,6,7,8,9} |
| Flatten [13] | |
| FlattenAt[13,l] | {1,2,3,{4,5,6},{7,8,9}} |
| Sort[{l,5,3,4,2}] | {1,2,3,4,5} |
| Reverse[{l,2,3,4}] | {4,3,2,1} |
| RotateLeft[ {1,2,3,4,5}, 2] | {3,4,5,1,2} |
| RotateRight[{l,2,3,4,5} ,2] | {4,5,1,2,3} |
| 12={{a,b},{c,d}}; | |
| TableForm[12] | a b c d |
| TableFormf Transpose [12] ] | a c d b |
Изменение порядка расположения элементов в списке полезно при реализации некоторых алгоритмов. К примеру, сортировка списка ускоряет выполнение статистических расчетов и уменьшает их погрешности.
Комбинирование списков и работа с множествами
Иногда возникает необходимость комбинирования нескольких списков. Для этого используются следующие функции:
- Complement [list, listl, list2, ...] — возвращает список list с элементами, которые не содержатся ни в одном из списков listl, Iist2, ...;
- Intersection [listl, list2,...] (пересечение множеств) —возвращает упорядоченный список элементов, общих для всех списков listi;
- Join[list1, list2,... ] — объединяет списки в единую цепочку (выполняет конкатенацию). Join может применяться к любому множеству выражений, имеющих один заголовок;
- Union [listl, Iist2, ...] (объединение множеств) — удаляет повторяющиеся элементы списков и возвращает отсортированный список всех различающихся между собой элементов, принадлежащих любому из данных списков listi. Функция обеспечивает теоретико-множественное объединение списков;
- Union [list] — возвращает отсортированный вариант списка list, из которого удалены все повторяющиеся элементы.
Приведенные ниже примеры иллюстрируют применение функций комбинирования списков.
| Ввод (In) | Вывод (Out) | |
| Complement! {1, 2, 3,4, 5}, {1, а, 2}, {b, с, 5}] | {3, | 4} |
| 11={1,2,3,4,5}; | ||
| 12={а,b,3,4,с}; | ||
| Intersection [11 , 12] | {3, | 4} |
| Join [11, 12] | (1, | 2, 3, 4, 5, a, b, 3, 4, c} |
| Union[{l,2,4,3,2,7,3,5}] | {1, | 2, 3, 4, 5, 7}. |
| Union[{3,2},{!,4}] | (1, | 2, 3, 4} |
| Union[{a,b,c,a},{l,d,3}] | {1, | 3, a, b, c, d} |
Комбинирование списков позволяет создавать сложные структуры данных из более простых структур. Это может быть полезно при построении очередей, деревьев и иных структурных построений. Кроме того, приведенные функции обеспечивают основные операции со множествами. Функцию Union удобно использовать при решении нелинейных и алгебраических уравнений для удаления повторяющихся решений.
Ряд других функций этого урока перечислен в приложении. В целом можно сделать вывод, что обилие функций работы со списками позволяет решать практически любые задачи, в основе которых лежат манипуляции со списками, стеками и другими родственными типами данных.
gl3-10.jpg

gl3-7.jpg
gl3-8.jpg
gl3-9.jpg