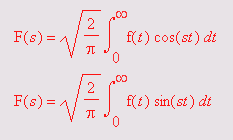Урок 14. Математические пакеты
1. Назначение пакетов расширения и обращение к ним
Урок 14.
Математические пакеты
Как уже отмечалось, некоторые функции системы Maple помимо их нахождения в ядре могут быть расположены в стандартной библиотеке и в пакетах, входящих в поставку системы. Это значит, что их не надо приобретать дополнительно, однако перед использованием таких функций надо загрузить их или отдельно, или вместе с целым пакетом, если большинство его функций представляет интерес для пользователя.
2. Обзор пакетов
Обзор пакетов
В этом уроке дается выборочная информация о функциях, содержащихся в пакетах. Напоминаем, что список пакетов можно получить, используя команду:
>?packages
Этот список приведен ниже:
- DEtools — решение дифференциальных уравнений;
- Domains — создание областей определений в вычислениях;
- GF — поля Галуа;
- Gausslnt — работа с целыми числами Гаусса;
- Groebner — вычисления в базисе Гробнера;
- LREtools — манипуляции с линейными рекуррентными отношениями;
- LinearAlgebra — линейная алгебра;
- Matlab — интеграция с MATLAB;
- Ore_algebra — основные вычисления в алгебре линейных операторов;
- PDEtools — решение дифференциальных уравнений в частных производных;
- Spread — работа с таблицами;
- algcurves — работа с алгебраическими кривыми;
- codegen — генерация кодов;
- combinat — функции комбинаторики;
- combstruct — структуры комбинаторики;
- context — контекстно-зависимые меню;
- diffalg — дифференциальная алгебра;
- difforms — дифференциальные формы;
- finance — финансовые расчеты;
- genfunc — рациональные функции;
- geom3d — трехмерная геометрия Евклида;
- geometry — евклидова геометрия;
- group — представление бесконечных групп;
- inttrans — интегральные преобразования;
- liesymm — симметрия Ли;
- linalg — линейная алгебра и структуры данных массивов;
- networks — графы;
- numapprox — численная аппроксимация;
- numtheory — теория чисел;
- orthopoly — ортогональные полиномы;
- padic — Пи-адические числа;
- plots — расширения графики;
- plottools — создание дополнительных графических объектов; >
- polytools — действия с полиномами;
- powseries — формальные степенные ряды;
- process — мультипроцессы (для операционной системы Unix);
- simplex — линейная оптимизация (симплекс-метод); '
- stats — статистика;
- student — функции в помощь студентам;
- sumtools — определенные и неопределенные суммы;
- tensor — тензоры и теория относительности.
Как следует из просмотра этого обширного списка, пакеты Maple 7 охватывают многие крупные разделы математики и существенно дополняют возможности системы, предоставляемые средствами ее ядра. Пакеты расширения пишутся на Maple-языке программирования, поэтому они могут легко модернизироваться и пополняться. Этим, в частности, объясняется тот факт, что набор пакетов расширения в Maple 7 существенно пополнен по сравнению с предшествующими реализациями системы.
3. Новые пакеты Maple 7
Новые пакеты Maple 7
Система Maple 7 пополнилась рядом новых пакетов:
- CurveFutting — приближение кривых;
- ExternalCalling — внешние вычисления;
- LinearFunctionalSystem — линейные функциональные системы;
- MathML — поддержка средств языка MathML 2.0;
- OrthogonalSeries — серии с ортогональными полиномами;
- PolynomialTools — работа с полиномами.
Из этих пакетов надо особо выделить пакет приближения кривых. Он содержит наиболее важные функции для приближения кривых, которые до сих пор были разбросаны по ряду пакетов. В конце данного урока содержится описание пакета CurveFitting. Там же имеется описание другого нового и полезного пакета — PolynomialTools.
4. Получение информации о конкретном пакете
Получение информации о конкретном пакете
С помощью команды:
>?name_package;
можно получить информацию о любом пакете расширения и найти список входящих в него функций. Названия пакетов были приведены выше.
Для обращения к функциям того или иного пакета используется его полная загрузка командой:
>with(package):[:]
Знак : блокирует вывод списка функций пакета а знак ; указывает вывести этот список.
Если вам необходима какая-то одна функция пакета или небольшая их часть, то не стоит загружать пакет целиком. Это может привести к избыточным затратам памяти компьютера и даже нарушить нормальную работу некоторых функций — следует помнить, что нередко пакеты переопределяют некоторые функции ядра. Для загрузки избранных функций используется команда with в форме
>with(package. fl. f2. ...):
или
>with(package, [fl. f2. ...]):
При этом загружаются функции fl, f2, ... из пакета с именем packages.
Может показаться, что было бы лучше иметь все функции в ядре. Однако создание ядра, реализующего все функции системы (в версии Maple 7 их около 3000), неразумно. Такое ядро занимало бы много места в памяти, имело большое время загрузки и затрудняло бы поиск конкретных нужных функций.
Поэтому ядро Maple 7 содержит определенный (и довольно обширный) минимум хорошо апробированных функций, а большинство других функций размещается в стандартной библиотеке и пакетах. Они готовятся на Maple-языке программирования и могут легко модернизироваться. К тому же пакеты могут модифицироваться (что не очень желательно) или дополняться (что приветствуется) пользователями. Некоторой платой за это является необходимость вызова того или иного пакета или функции перед их применением.
В этом разделе описана структура пакетов Maple 7, имеющих математическую направленность. Ограниченный объем книги и огромное число функций в пакетах не позволяют остановиться даже на описании синтаксических правил применения всех функций этих пакетов. Очевидно, что в этом нет и особого смысла — подавляющее большинство функций представляет малый интерес для конкретного пользователя. Те же, кто ими интересуются, могут легко восполнить пробелы в их описании с помощью справочной системы. Однако в описании состава каждого пакета в данном уроке упомянуты имена всех без исключения его функций. Это позволяет оценить полноту того или иного пакета и без труда вызвать справочные страницы для любой функции. Описание функций пакетов в уроке дано выборочно, при этом предпочтение отдавалось тем функциям, которые используются в массовых математических и научно-технических расчетах и представляют интерес для достаточно широкого круга читателей. Полезно отметить, что большинство функций имеет вполне понятные имена, отражающие их суть и назначение. К примеру, назначение функций animate или даже textplot в пакете plots или Diff, Int и Limit в пакете student понятны, пожалуй, всем. Но и в гораздо более специализированных пакетах имена входящих в них функций в значительной мере знакомы специалистам, поскольку почти всегда ассоциируются с общепринятыми названиями тех или иных специализированных функций или с их комбинациями.
5. Пакеты функций комбинаторики
Пакеты функций комбинаторики
Функции комбинаторики достаточно известны из обычного курса математики. При вызове пакета выводится (если вывод не заблокирован двоеточием) список его функций:
> with(combinat);
Warning, the protected name Chi has been redefined and unprotected
[Chi,bell, binomialcartprod, character, choose, composition, conjpart, decodepart, encodepart,fibonacci,firstpart, graycode, inttovec, lastpart, multinomial, nextpart, numbcomb, numbcomp, numbpart, numbperm, partition, permute, powerset, prevpart, randcomb, randpart, randperm, Stirling], stirling2, subsets, vectoint]
Ввиду важности функций комбинаторики приведем их полные определения:
- Chi(x) — гиперболический косинусный интеграл;
- bell(n) —возвращает число ехр(ехр(х)-1) =sum(ben(n)/n!*x^n, n=0..infinity), причем для вычислении используется рекуррентное соотношение bell(n+1) = (bell(n)+1)^n;
- binomial (n, r) — возвращает биноминальные коэффициенты, причем, если n и r — целые числа, удовлетворяющие условию 0 <= r<= n, то функция возвращает C(n.r)=n!/(r!(n-r)!), а в общем случае С(n, r) = limit(GAMMA(N+D/ GAMMA(R+l)/GAMMA(N-R-t-l),R=r,N=n);
- composition(n, k) — возвращает списки композиций для целых неотрицательных n и k;
- fibonacci(n) — возвращает числа Фибоначчи, вычисляемые по рекуррентной формуле F(n) =F(n - 1) +F(n - 2), где F(0) =0 и F(1) =1;
- fibonacci(n, х) — возвращает значение полинома Фибоначчи F(n, x) =-х F(n - 1,x) + F(n - 2, х), где F(0,x) = 0 и F(l,x) = 1, при этом F(n) = F(n, 1);
- firstpart(n) — возвращает первую часть каноническей последовательности ряда;
- nextpart(l) — возвращает следующую часть канонической последовательности ряда;
- lastpart(n) — возвращает последнюю часть канонической последовательности ряда;
- prevpart(1) — возвращает предыдущую часть канонической последовательности ряда;
- conjpart(l) — возвращает объединенный раздел в канонической последовательности ряда;
- graycode(n) — возвращает список кодов Грея для габитовых чисел;
- multinomial (n, kl, k2, .... km) — возвращает мультиномиальные коэффициенты;
- numbcomb(n) и numbcomb(n. m) — возвращает число комбинаций;
- numbcomp(n, k) — возвращает число композиций;
- numbpart(n) — возвращает список всех возможных сумм, дающих п;
- permute(n) и permute(n, r) — возвращает numbperm(n, r) = nops(permute(n. r));
- powerset(s) — возвращает степень множества в множестве s;
- randcomb(n, m) — возвращает случайную комбинацию;
- randpart(n) — возвращает случайную часть;
- randperm(n) — возвращает случайную композицию;
- stirling(n, m) — возвращает число Стирлинга первого рода;
- stirling2(n, m) — возвращает число Стирлинга второго рода;
- subsets(L) — задает итерационную процедуру над степенями множества или списка L;
- vectoint(l) — возвращает индекс вектора канонического упорядочения 1;
- inttovec(m, n) — возвращает вектор канонического упорядочения для неотрицательных целых чисел тип.
Ниже даны примеры применения некоторых из этих функций:
> choose(4,3);
[[1,2,3],[1,2,4],[1,3,4],[2,3,4]]
> choose([a,a,b,c].3):
[[a,a,b],[a,a,c],[atb,c]]
> composition(3,2):
{[2,1],[1,2]}
> decodepart(4,2);
[1,1,2]
> fibonacci(l0);
55
> seq(fibonacci(1),i-l..l2):
1,1,2,3,5,8,13,21,34,55,89,144
> partition(5);
[[1,1,1,1,1], [1,1,1,2], [1,2,2], [1,1,3], [2,3], [1,4], [5]]
> firstpart(3):
[1,1,1]
> nextpart(%);
[1,2]
> prevpart(%);
[1,1,1]
> 1astpart(3):
[3]
> conjpart(%):
[1,1,1]
> multinomial(8,2,3,3);
560
> numbcomp(8,5):
35
> nuropart(3);
numpart(3)
> numbperm(4);
24
> numbperm([a,b]):
2
> numbperm({a,b,c},2);
6
> permute(3,2);
[[l,-2],[l,3],[2,l],[2,3],[3,l],[3,2]]
> permute([a,a,b],2):
[[a,a],[a,b],(b,a]]
> powerset([a,a,b]):
[[],[а],[b],[а,Ь],[а,а],[а,а,b-]]
> randcomb([a,b,c,d],3):
[a,c,d]
> randcomb([a,b,c,d],3);
[a,b,d]
> randpart(l0);
[2,8]
> randpart(l0):
[10]
> stirling(10,5);
-269325
> stirling2(10,5):
42525
> S:=subsets({l,2}):
> while not S[finished] do S[nextva1ue]() od:
{ }
{1}
{2}
{1,2}
> vectoint([l,0,0]);
1
> inttovec(6,3);
[1,0,1]
Читателю, желающему использовать данный пакет, рекомендуется внимательно ознакомиться с этими простыми примерами и просмотреть примеры из справочной базы данных для имеющихся в пакете функций.
6. Пакет combstruct
Пакет combstruct
Еще девять функций, относящихся к структурам комбинаторики, содержит пакет combstruct:
> with(combstruct):
[allstructs, count, draw,finished, gfeqns, gfseries, gfsolve, iterstritcts, nextstruct]
Эти функции служат для создания случайно однородных объектов, принадлежащих заданному комбинаторному классу. Ограничимся приведением примеров применения этих функций:
> alltructs(Subset({one,two}));
{{ },{one, two}, {two}, {one}}
> anstructs(Permutation([x,y,z]),size=2):
[[x,y],[x,z],[y,x],[y,z],[z,x],[z,y]]
> count(Subset({l,2,3}));
8
> draw(Combiination(5),size=4);
{1,3,4,5}
> count(Permutation([a,a,b])): .
3
> 1t :=iterstructs(Permutation([a,a,b]),size=2);
it := table([finished = false, nextvalue = (pmc() ... endproc )])
> draw(Partition(9));
[2,2,2,3]
> allstructs(Composition(3), size=2):
[[2,l],[l,2]]
Для более полного знакомства с этими специфическими функциями обратитесь к справочной системе.
7. Пакет финансово-экономических функций finance
Пакет финансово-экономических функций finance
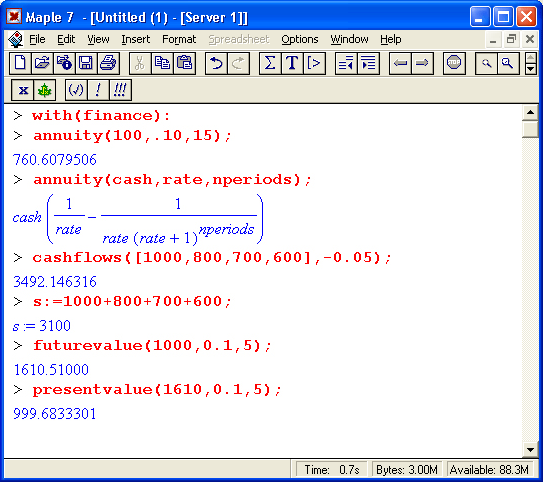
Пакет финансово-экономических расчетов открывается командой:
> with(finance)
[amortization, annuity, blackscholes, cashflows, effectiverate,futurevalue, growingannuity, growingperpetuity, levelcoupon, perpetuity, presentvalue, yieldtomaturity]
Этот пакет представлен рядом указанных выше функций в двух формах:
function(args)
finance[function](args).
Благодаря правилам задания аргументов можно реализовать практически все известные финансово-экономические расчеты, такие как амортизация, накопления и платежи по вкладам и т. д. В свете задач рыночной экономики эти функции полезны для приверженцев решения всего на свете без выхода из оболочки Maple. Все же надо отметить, что малозаметные тонкости в определении финансово-экономических функций затрудняют их применение. Есть множество специальных финансово-экономических пакетов, например «Бухгалтерия 1C», которые лучше подходят для наших экономических реалий, чем «заумный» и прозападный Maple 7.
Полный перечень функций можно найти в справке по этому пакету. Ограничимся упоминанием нескольких наиболее характерных функций, связанных с использованием вкладов:
- annuity(cash,rate,nperiods) — вычисление суммы, находящейся на вкладе с начальным значением cash, процентом начисления rate и числом периодов nperiods;
- cashflows(flows,rate) — вычисление общей суммы вклада по списку вложений flows и проценту обесценивания денег rate;
- futurevalue(amount, rate, nperiods) — вычисление будущего значения вклада при начальном вложении amount, проценте начисления rate и числе периодов nperiods;
- presentvalue(amount, rate, nperiods) — вычисление начального вклада для получения суммы в amount при проценте начислений rate и числе вкладов nperiods.
Примеры применения этих функций даны ниже:
Поскольку формулы и обозначения в финансово-экономических расчетах в различной литературе порою заметно различаются (особенно сильны различия между нашей и западной литературой), это может создать серьезные ошибки при вычислениях. К примеру, в формулах Maple на самом деле используются не проценты начислений или обесценивания вкладов, а соответствующие им относительные единицы, например 10% соответствует 0,1.. В нашей литературе проценты обычно задаются в явном виде, то есть rate = 10 при 10%. Надо следить и за знаком величины rate, поскольку она может трактоваться как процент начислений или процент обесценивания денег по вкладам, что соответствует различным ее знакам.
Расчеты такого рода для Maple 7 относятся к достаточно простым, так что даже начинающий пользователь может составить свои функции для таких расчетов по вполне понятным ему и апробированным формулам. Надо отметить, однако, что, используя символьное задание параметров функций, легко получить вывод именно тех формул, которые использует система Maple, и сравнить их со своими формулами. В случае совпадения применение функций Maple возможно и предпочтительно.
ПРИМЕЧАНИЕ
В целом применение Maple 7 как системы с символьной и точной арифметикой весьма предпочтительно в финансово-экономических и статистических расчетах, поскольку обеспечивает принципиально повышенную точность и устойчивость таких расчетов.
1.gif
8. Пакет ортогональных многочленов orthopoly
Пакет ортогональных многочленов orthopoly
Ортогональные многочлены (полиномы) находят самое широкое применение в различных математических расчетах. В частности, они широко используются в алгоритмах интерполяции, экстраполяции и аппроксимации различных функциональных зависимостей. В пакете orthopoly задано в функци:
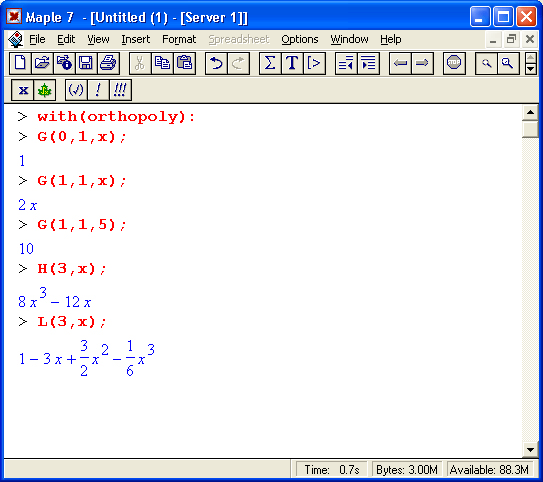
> with(orthopoly);
[G,H,L,P,T,U]
Однобуквенные имена этих функций отождествляются с первой буквой в наименовании ортогональных полиномов. Вопреки принятым в Maple 7 правилам, большие буквы в названиях этих полиномов не указывают на инертность данных функций — все они являются немедленно вычисляемыми. В данном разделе функции этого пакета будут полностью описаны. Отметим определения указанных функций:
- G(n,a,x) — полином Гегенбауэра (из семейства ультрасферических полиномов);
- Н(n,х) — полином Эрмита;
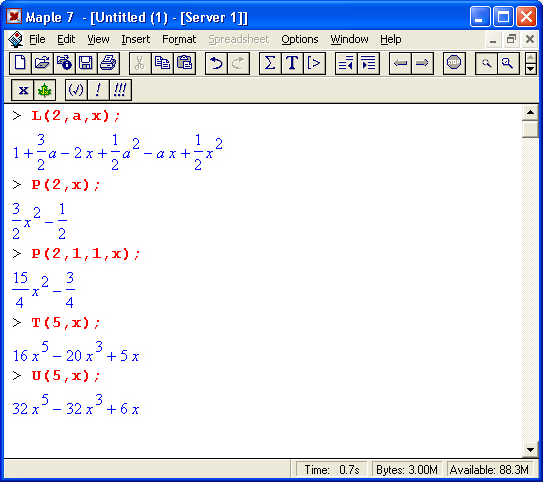
- L(n,x) — полином Лагерра;
- L(n,а,х) — обобщенный полином Лагерра;
- Р(n,х) — полином Лежандра;
- P(n,a,b,x) — полином Якоби;
- Т(n,х) — обобщенный полином Чебышева первого рода;
- U(n,x) — обобщенный полином Чебышева второго рода.
Свойства ортогональных многочленов хорошо известны. Все они характеризуются целочисленным порядком n, аргументом х и иногда дополнительными параметрами а и b. Существуют простые рекуррентные формулы, позволяющие найти полином n-го порядка по значению полинома (n - 1)-го порядка. Эти формулы и используются для вычисления полиномов высшего порядка. Ниже представлены примеры вычисления ортогональных полиномов:
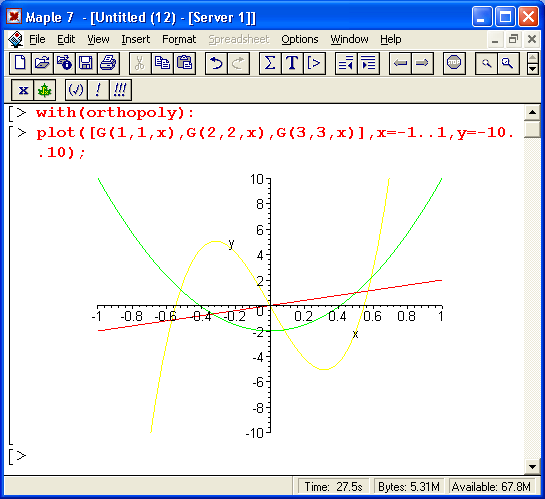
Представляет интерес построение графиков ортогональных многочленов. На рис. 14.1 построены графики ряда многочленов Гегенбауэра и Эрмита.
Рис. 14.1. Графики ортогональных многочленов Гегенбауэра и Эрмита
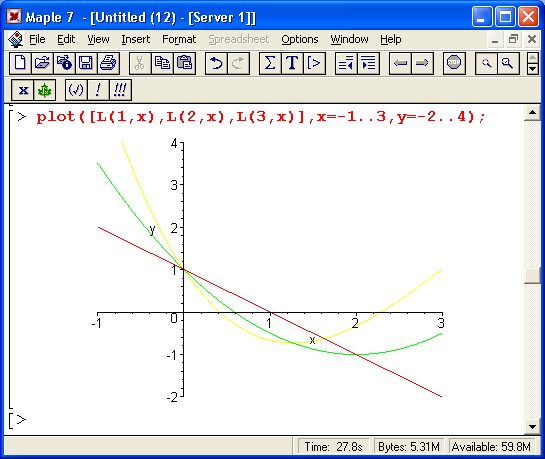
На рис. 14.2 построены графики ортогональных многочленов Лагерра и Лежандра.
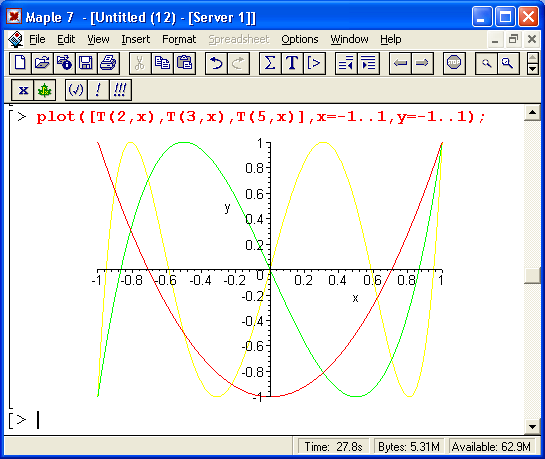
Наконец, на рис. 14.3 даны графики ортогональных многочленов Чебышева Т(n, х) и U(n, х).
Приведенные графики дают начальное представление о поведении ортогональных многочленов.
Рис. 14.2. Графики ортогональных многочленов Лагерра и Лежандра
Рис. 14.3. Графики ортогональных многочленов Чебышева
К примеру, многочлены Чебышева имеют минимальное отклонение от оси абсцисс в заданном интервале изменениях. Это их свойство объясняет полезное применение таких многочленов при решении задач аппроксимации функций. Можно порекомендовать читателю по их образу и подобию построить графики ортогональных многочленов при других значениях параметра и и диапазонах изменения аргумента х.
В отличие от ряда элементарных функций ортогональные многочлены определены только для действительного аргументах. При комплексном аргументе просто повторяется исходное выражение с многочленом:
> eva1f(U(2,2+3*I))):
Р(2,2 + 3I)
> evalf(sqrt(2+3*I)));
1.674149228+ .8959774761I
Ортогональные многочлены неопределены также и для дробного показателя n. Впрочем, надо отметить, что такие многочлены на практике используются крайне редко.
2.gif
3.gif
40.gif
42.gif
44.gif
9. Пакет для работы с суммами sumtools
Пакет для работы с суммами sumtools
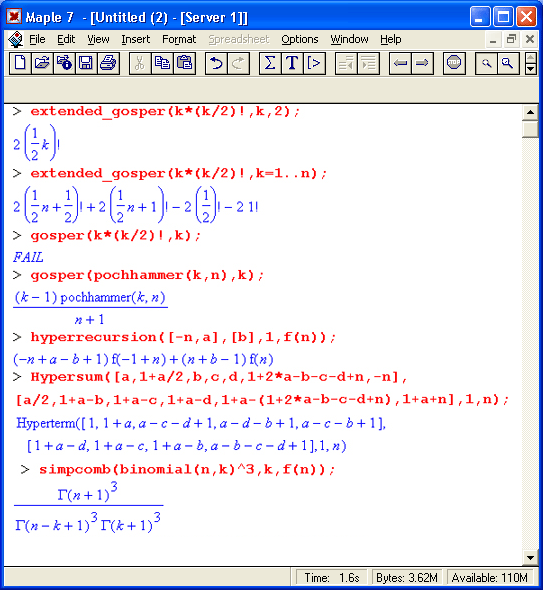
Этот инструментальный пакет предназначен для работы со специальными суммами. Он содержит указанные ниже функции:
> with(suintools);
[Hypersum, Sumtohyper, extended_gosper, gosper, hyperrecursion, hypersum, hyperterm, simpcomb, sumrecursion, sumtohyper]
Назначение функций данного пакета перечислено ниже:
- hypersum(U, L, z, n) и Hypersum(U, L, z, n) — вычисление гиперсумм;
- sumtohyper(f, k) и Sumtohyper(f, k) — преобразование сумм в гиперсуммы;
- extended_gosper(f, k), extended_gosper(f, k=m..n) и extended_gosper(f, k, j) — реализация расширенного алгоритма Госпера;
- gosper(f, k) и gosper(f, k=m..n) — реализация алгоритма Госпера;
- hyperrecursion(U, L, z, s(n)) — реализация гиперрекурсионного алгоритма;
- hyperterm(U, L, z, k) и Hyperterm(U, L,z, k) — ввод гипергеометрического терма.
10. Работа с пакетом sumtools
7.gif

8.gif
11. Пакет реализации степенных разложений powseries
Пакет реализации степенных разложений powseries
Степенные разложения часто используются в математических расчетах для приближенного представления разнообразных функций и обеспечения единообразия такого представления. В пакете powseries сосредоточены расширенные средства по реализации таких разложений. Они представлены 22 функциями:
> with(powseries);
[compose, evalpow, inverse, multconst, multiply, negative, pawadd, powcos, powcreate, powdijff, powexp, powint, powlog, powpoly, powsin, powsolve, powsqrt, quotient, reversion, subtract, template, tpsform ]
Ниже представлено определение этих функций:
- compose(а,b) — объединяет ряды а и b;
- evalpow(expr) — вычисляет выражение ехрr и возвращает его в виде ряда;
- inverse(р) — инвертирует ряд р;
- mu1tconst(p,const) — умножает ряд р на константу const; ,
- multiply(a,b) — умножает ряд а на ряд b;
- negative(p) — возвращает аддитивный, обратный по отношению к р ряд;
- powadd(a,b,...) — складывает ряды а, b, ...;
- powcreate(expr) — создает ряд для выражения ехрr;
- powpoly(pol ,var) — создает ряд для полинома pol по переменной van;
- powsolve(sys) — создает ряд для решения дифференциальных уравнений sys;
- quotient(a,b) — возвращает частное для а и b в виде ряда;
- reversion(a) — дает обратное к композиции разложение ряда а;
- subtract(а,b) — дает разность рядов а и b.
В выражении ехрr могут использоваться операторы +, -, *, / и ^. С ними могут комбинироваться встроенные функции и функции пользователя, например /(g). Кроме того, могут использоваться следующие функции:
|
Powexp |
powi nv |
powlog |
powneg |
powrev |
|
Powdiff |
powi nt |
powquo |
powsub |
powcos |
|
Powtan |
powsec |
powcsc |
powcot |
powsinh |
|
Powcosh |
powtanh |
powsech |
powcsch |
powcot h. |
|
Powsqrt |
powadd |
multiply |
12. Примеры применения пакета powseries
Примеры применения пакета powseries
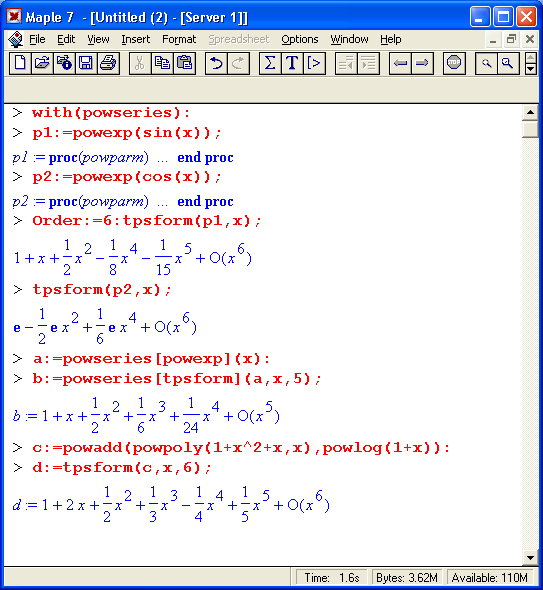
Назначение большинства этих функций очевидно из их названий — они возвращают соответствующую функцию (указанную после слова pow в имени) в виде разложения в ряд или полинома. Например, powexp раскладывает выражения с экспоненциальными функциями в ряд.
Получаемые функциями ряды представляются в специальном формате. Поэтому для их применения в обычном виде необходимо использовать функцию tpsform в следующих видах:
- tpsform(p, var, order) — преобразует ряд р в обычную форму с заданием порядка order;
- tpsform(p, var) — преобразует ряд р в обычную форму с порядком, заданным переменной Order.
Здесь р — имя степенного ряда, var.— переменная, относительно которой записан ряд, order — порядок ряда. Если параметр order не указан, используется значение глобальной переменной Order. Ниже даны примеры, иллюстрирующие технику работы со степенными разложениями:
Применение функций этого пакета достаточно просто и прозрачно, так что заинтересованный читатель может сам опробовать на примерах работу тех функций, которые не были использованы в приведенных примерах.
9.gif
13. Пакет числовой аппроксимации numapprox
Пакет числовой аппроксимации numapprox
Этот пакет содержит небольшое число безусловно очень важных функций:
> with(numapprox);
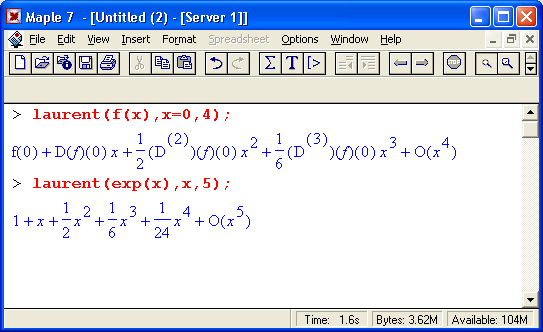
[chebdeg, chebmult, chebpade, chebsort, chebyshev, confracform, hermite_pade, hornerform, infnorm, laurent, minimax, pade, remez]
В их числе функции интерполяции и аппроксимации полиномами Чебышева, рядом Тейлора, отношением полиномов (Паде-аппроксимация) и др. Все они широко применяются не только в фундаментальной математике, но и при решении многих прикладных задач. Рассмотрим их, начиная с функций аппроксимации аналитических зависимостей.
14. Разложение функции в ряд Лорана
10.gif
15. Паде-аппроксимация аналитических функций
Паде-аппроксимация аналитических функций
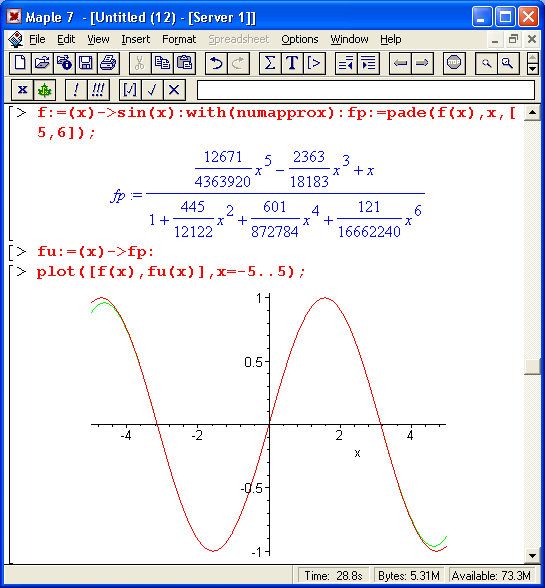
Для аппроксимации аналитических функций одной из лучших является Паде-аппроксимация, при которой заданная функция приближается отношением двух полиномов. Для осуществления такой аппроксимации используется функция pade:
pade(f. x=a, [m.n])
pade(f.,х, [m.n])
Здесь f — аналитическое выражение или функция, х — переменная, относительно которой записывается аппроксимирующая функция, а — координата точки, относительно которой выполняется аппроксимация, m, n — максимальные степени полиномов числителя и знаменателя. Технику аппроксимации Паде поясняет рис. 14.4.
На рис. 14.4 представлена аппроксимация синусоидальной функции, а также построены графики этой функции и аппроксимирующей функции. Под ними дан также график абсолютной погрешности для этого вида аппроксимации. Нетрудно заметить, что уже в интервале [-л, я] погрешность резко возрастает на концах интервала аппроксимации.
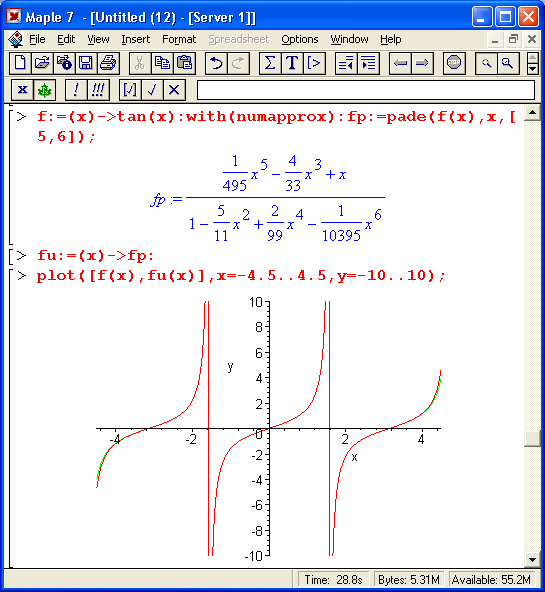
Важным достоинством Паде-аппроксимации является возможность довольно точного приближения разрывных функций. Это связано с тем, что нули знаменателя у аппроксимирующего выражения способны приближать разрывы функций, если на заданном интервале аппроксимации число разрывов конечно. На рис. 14.5 представлен пример Паде-аппроксимации функции tan(x) в интервале от -4,5 до 4,5, включающем два разрыва функции.
Как видно из рис. 14.5, расхождение между функцией тангенса и ее аппроксимирующей функцией едва заметно лишь на краях интервала аппроксимации. Оба разрыва прекрасно приближаются аппроксимирующей функцией. Такой характер аппроксимации подтверждается и графиком погрешности, которая лишь на концах интервала аппроксимации [-4,0, 4,0] достигает значений 0,01 (около 1%).
Рис. 14.4. Аппроксимация Паде для синусоидальной функции
Рис. 14.5. Аппроксимация Паде для разрывной функции тангенса
46.gif
48.gif
16. Паде-аппроксимация с полиномами Чебышева
Паде-аппроксимация с полиномами Чебышева
Для многих аналитических зависимостей хорошие результаты дает аппроксимация полиномами Чебышева. В общем случае применяется Паде-аппроксимация отношением таких полиномов. Она реализуется функциями chebpade:
chebpade(f, x=a..b, [m.n])
chebpade(f., x, [m.n])
chebpade(f, a..b, [m,n])
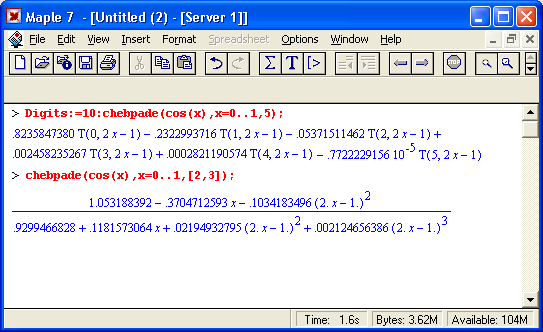
Здесь а..b задает отрезок аппроксимации, тип— максимальные степени числителя и знаменателя полиномов Чебышева. Приведенный ниже пример показывает аппроксимацию Паде полиномами Чебышева для функции f=cos(x):
11.gif
17. Наилучшая минимаксная аппроксимация
Наилучшая минимаксная аппроксимация
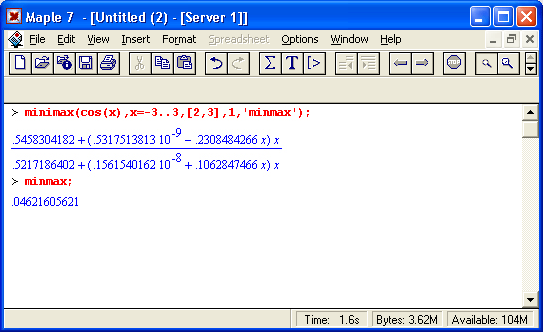
Минимаксная аппроксимация отличается от Паде-аппроксимации минимизацией максимальной абсолютной погрешности во всем интервале аппроксимации. Она использует алгоритм Ремеза (см. ниже) и реализуется следующей функцией:
mimmax(f, x=a..b, [m.n], w, 'maxerror')
minimax(f, a..b, [m,n], w, 'maxerror')
Здесь помимо уже отмеченных параметров w — процедура или выражение, maxerror — переменная, которой приписывается значение miniraax-нормы. Ниже дан пример аппроксимации функции cos(x) в интервале [-3, 3]:
12.gif
18. Наилучшая минимаксная аппроксимация по алгоритму Ремеза
Наилучшая минимаксная аппроксимация по алгоритму Ремеза
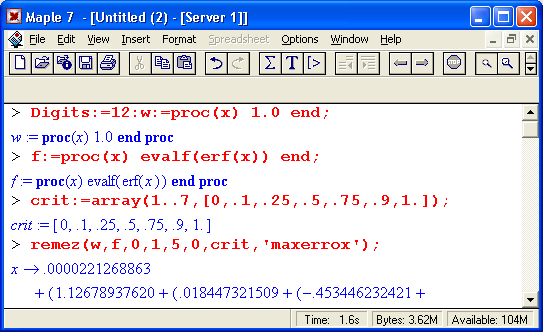
Для получения наилучшей полиномиальной аппроксимации используется алгоритм Ремеза, который реализует следующая функция:
remez(w, f, a, b, m, n,_crit, 'maxerror')
Здесь w — процедура, представляющая функцию w(x) > 0 в интервале [a, b], f — процедура, представляющая аппроксимируемую функцию а и b — числа,' задающие интервал аппроксимации fa,b], m и n — степени числителя и знаменателя аппроксимирующей функции, crit — массив, индексированный от 1 до m + n + 2 и представляющий набор оценок в критических точках (то есть точек максимума/минимума кривых погрешности), mахеrrоr — имя переменной, которой присваивается минимаксная норма w abs(f -r).
Следующий пример иллюстрирует применение данной функции для аппроксимации функции erf(x):
13.gif
19. Другие функции пакета
Другие функции пакета
Отметим назначение других функций пакета numapprox:
- chebdeg(p) — возвращает степень полинома Чебышева р;
- chebmult(p, q) — умножение полиномов Чебышева р и q;
- chebsort(e) — сортирует элементы ряда Чебышева;
- confracform(r) — преобразует рациональное выражение г в цепную дробь;
- confracform(r, х) — преобразует рациональное выражение г в цепную дробь с независимой переменной х;
- hornerform(r) — преобразует рациональное выражение г в форму Горнера;
- hornerform(r, х) — преобразует рациональное выражение г в форму Горнера с независимой переменной х;
- infnorm(f, x=a...b, 'xmax') — возвращает L-бесконечную норму функции на отрезкех [а, b];
- infnorm(f, a...b, 'xmax') — возвращает L-бесконечную норму функции на отрезке [а, b].
Действие этих функций очевидно, и читатель может самостоятельно опробовать их в работе.
20. Пакет интегральных преобразований inttrans
Пакет интегральных преобразований inttrans
Это один из пакетов, наиболее важных для общематематических и научно-технических приложений. Он содержит небольшой набор функций:
> with(inttrans):
[addtable,fourier,fouriercos,fouriersin, hankel, hilbert, invfourier, invhilbert, invldplace, invmellin, laplace, mellin, savetable]
Однако эти функции охватывают такие практические важные области математики, как ряды Фурье, прямые и обратные преобразования Лапласа и Фурье и ряд других интегральных преобразований. Ниже они обсуждены более подробно.
В предшествующих реализациях системы Maple функции прямого и обратного Z-преобразований также входили в пакет inttrans, однако в Maple 6 и 7 они перенесены в ядро системы.
21. Прямое и обратное преобразования Лапласа
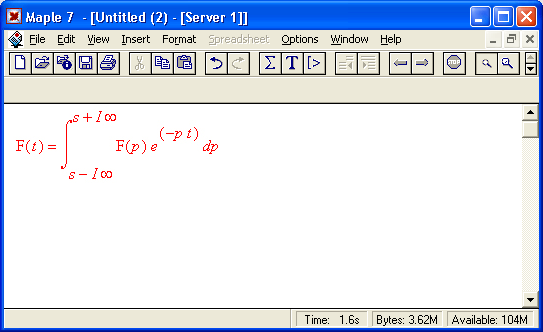
Прямое и обратное преобразования Лапласа
Прямое преобразование Лапсаса заключается в переводе некоторой функции времени f(t) в операторную форму F(p). Это преобразование означает вычисление интеграла
Для осуществления прямого преобразования Лапласа Maple 7 имеет функцию
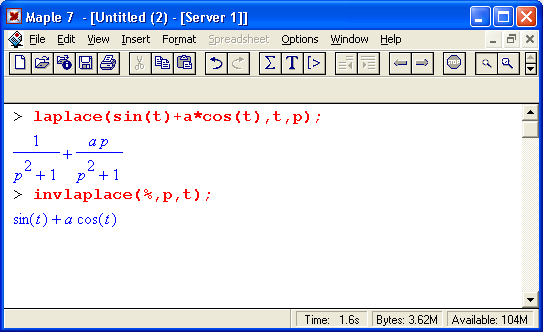
laplace(expr,t,p)
Здесь ехрr— преобразуемое выражение, t — переменная, относительно которой записано ехрr, и р — переменная, относительно которой записывается результат преобразования.
Обратное преобразование Лапласа означает переход от функции F(p) к функции (t) с помощью формулы
Для вычисления этого интеграла служит функция:
invlaplace(expr,p, t)
где ехрr — выражение относительно переменной р, t — переменная, относительно которой записывается результирующая зависимость. Оба преобразования широко применяются в практике научно-технических вычислений и отражают суть операторного метода. При этом прямое преобразование создает изображение а обратное —оригинал функции. Ниже приведены примеры применения прямого и обратного преобразований Лапласа:
Нетрудно заметить, что в данном случае последовательное применение прямого, а затем обратного преобразования восстанавливает исходную функцию sin(t) + acos(t).
14.gif

15.gif
16.gif
22. Прямое и обратное преобразования Фурье
Прямое и обратное преобразования Фурье
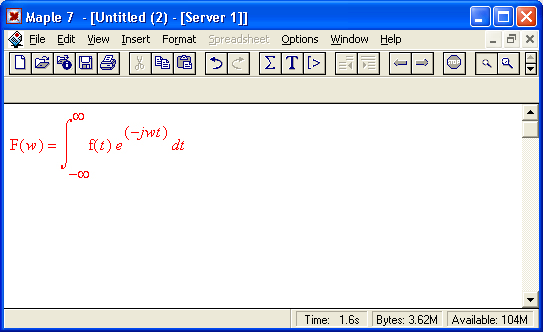
Прямое преобразование Фурье преобразует функцию времени f(t) в функцию частот и заключается в вычислении следующей интегральной функции:
Оно реализуется следующей функцией пакета интегральных преобразований inttrans:
fourier(expr,t,w)
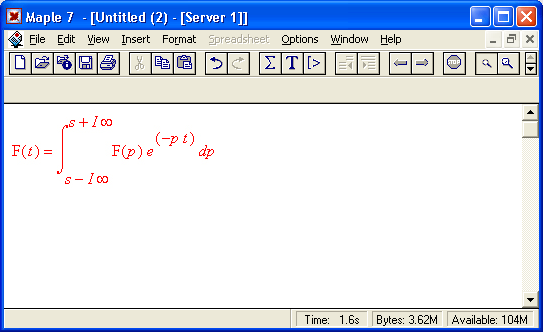
Здесь ехрr — выражение (уравнение или множество), t — переменная, от которой зависит ехрr, и w — переменная, относительно которой записывается результирующая функция. Обратное преобразование Фурье задается вычислением интеграла:
Оно фактически переводит представление сигнала из частотной области во временную. Примеры применения преобразования Фурье представлены ниже:
Обратите внимание на то, что даже в простом первом примере применение обратного преобразования Фурье вслед за прямым не привело к буквальному восстановлению исходной функции sin(t). Потребовалась: команда simplify, чтобы перевести результат в виде представления синуса через экспоненциальные функции к обычному виду sin(t).
17.gif
18.gif
19.gif

23. Вычисление косинусного и синусного интегралов Фурье
Вычисление косинусного и синусного интегралов Фурье
Разложение функции f(t) в ряд Фурье требует вычисления интегралов следующего вида:
Они получили название косинусного и синусного интегралов Фурье и фактически задают вычисление коэффициентов ряда Фурье, в который может быть разложена функция ./(t). Для вычисления этих интегралов в пакете используются следующие функции:
fouriercos(expr,t,s)
fouriersln(expr,t,s)
Поскольку формат задания этих функций вполне очевиден, ограничимся примерами их применения:
50.gif
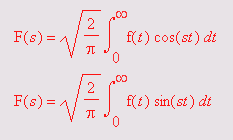
51.gif

24. Интегральное преобразование Ханкеля
Интегральное преобразование Ханкеля
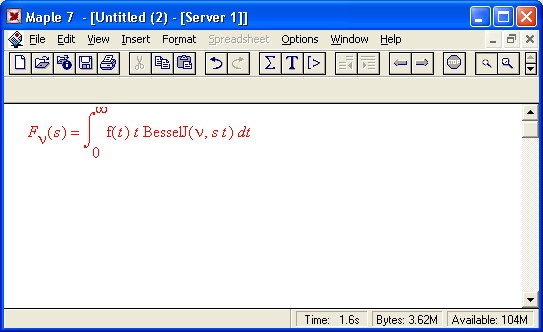
Интегральное преобразование Ханкеля задается следующим выражением:
и выполняется функцией:
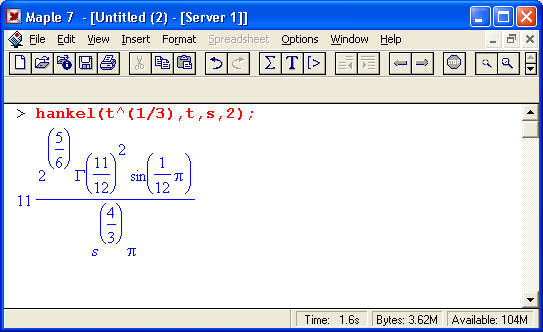
hankel(expr, t, s, nu)
Здесь ехрr — выражение, равенство (или множество, или список с выражениями/равенствами), t — переменная в ехрr, преобразуемая в параметр преобразования s, nu— порядок преобразования. Следующий пример демонстрирует применение функции Ханкеля:
20.gif
21.gif
25. Прямое и обратное преобразования Гильберта
Прямое и обратное преобразования Гильберта
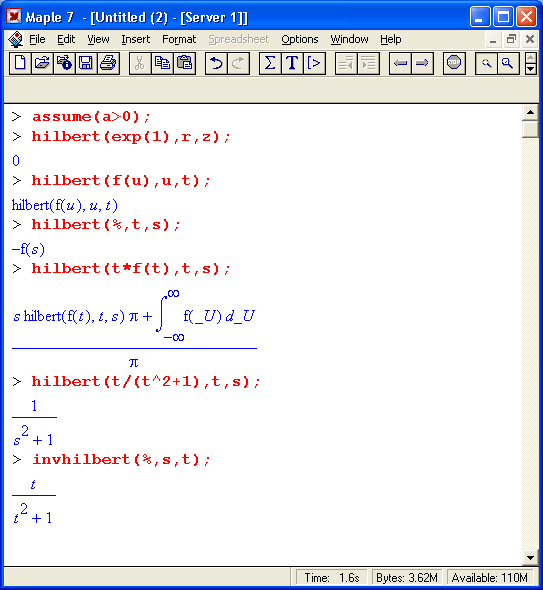
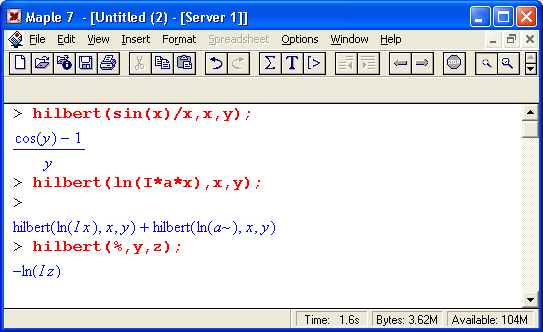
Прямое преобразование Гильберта задается следующим выражением:
и превращает функцию f(t) в F(s).
Обратное преобразование Гильберта означает нахождение f(f) по заданной F(s).
Эти преобразования выполняются функциями:
hilbert(expr, t, s)
invhilbert(expr, t,s)
где назначение параметров очевидно.
Приведенные ниже примеры иллюстрируют выполнение этих преобразований:
Как видно из этих примеров, обратное преобразование Гильберта, осуществленное над результатом прямого преобразования, не восстанавливает функцию f(t) буквально.
22.gif

23.gif
24.gif
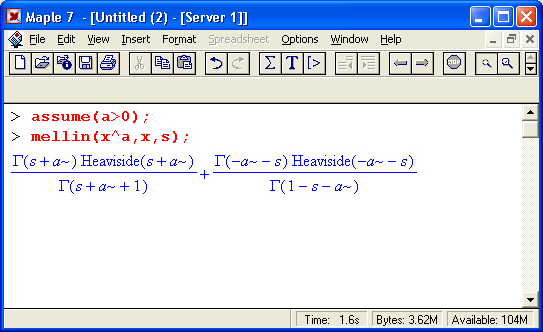
26. Интегральное преобразование Меллина
25.gif
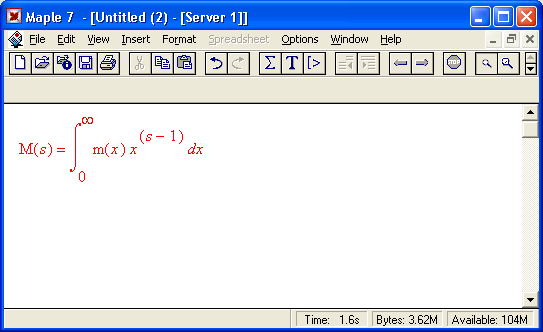
26.gif
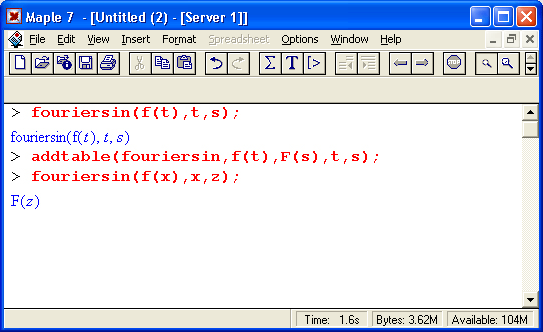
27. Функция addtable
Функция addtable
Как видно из приведенных примеров, не всегда интегральные преобразования дают результат в явном виде. Получить его позволяет вспомогательная функция:
addtable(tname,patt,ехрr,t,s)
где tname — наименование преобразования, для которого образец patt должен быть добавлен к таблице поиска. Остальные параметры очевидны.
Следующие примеры поясняют применение этой функции:
27.gif
28. Пакет приближения кривых CurveFittirrg
Пакет приближения кривых CurveFitting.
Общая характеристика пакета CurveFitting
Новый пакет приближения кривых CurveFitting весьма полезен тем, кто занимается столь распространенной задачей, как приближение кривых. Он содержит ряд функций:
> with(CurveFitting);
Доступ к функциям пакета возможен с помощью конструкций:
CurveFitting[function](arguments)
function(arguments)
Число функций пакета невелико и все они описаны ниже.
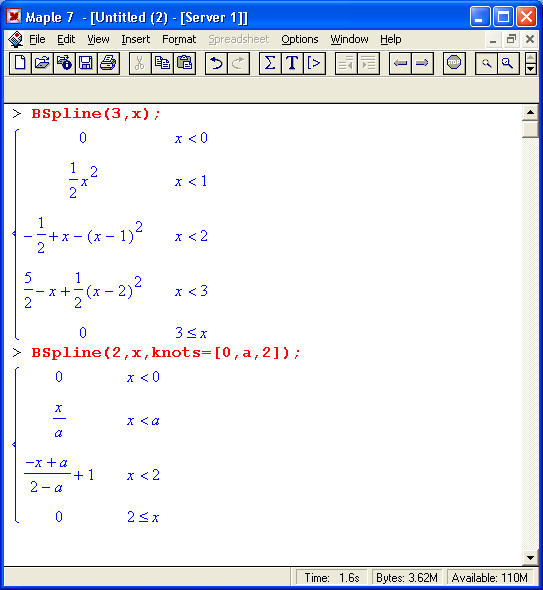
29. Функция вычисления В-сплайнов Bspline.
Функция вычисления В-сплайнов Bspline
Функция BSpline(k, v, opt) служит для вычисления В-сплайнов. Она имеет следующие параметры: k — порядок сплайна (целое число), v— имя и opt — параметр в виде knots=knotlist, где knotlist — спискок из k+1 элементов алгебраического типа. Используя функцию CurveFitting[BSplineCurve], можно строить кривые В-сплайнов. Примеры применения этой функции представлены ниже:
Как нетрудно заметить из этих примеров, функция Bspline возвращает результат в виде кусочных функций типа piecewise.
28.gif
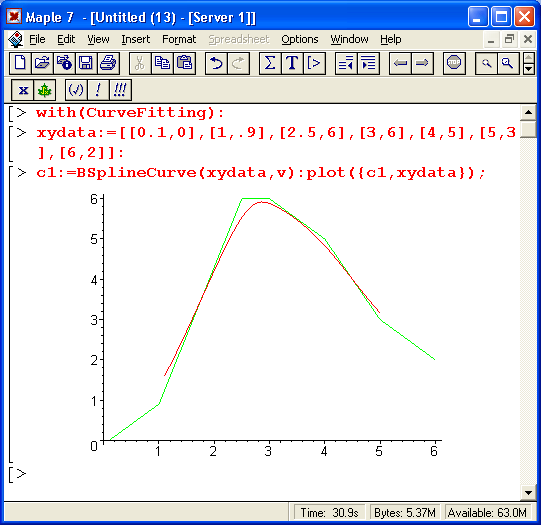
30. Функция построения В-сплайновых кривых BsplineCurve
Функция построения В-сплайновых кривых BsplineCurve
Функция BsplineCurve служит для построения кривых в B-cплайнов. Она Может использоваться в формах:
BSpl1neCurve(xydata, v, opts)
BSpllneCurve (xdata, ydata, v, opts)
Здесь:
xydata — список, массив или матрица точек в форме [[xl.ylj, [х2,у2],..., [хn,уn]];
xdata — список, массив или вектор значений независимой переменной [xl,x2,... ,хn];
ydata — список, массив или вектор значений зависимой переменной в форме [у1,у2,...,уn];
v — имя независимой переменной;
opts — необязательный параметр в форме одного или более выражений вида order=k или knots=knot1ist.
Примеры применения функции BSplineCurve с порядком, заданным по умолчанию, и с третьим порядком (кубический В-сплайн) представлены на рис. 14.6.
Рис. 14.6. Применение функции BSplineCurve
Следует отметить, что при малом, числе точек аппроксимация В-сплайнами дает невысокую точность, что и видно из рис. 14.6
52.gif
31. Функция реализации метода наименьших квадратов LeastSquares
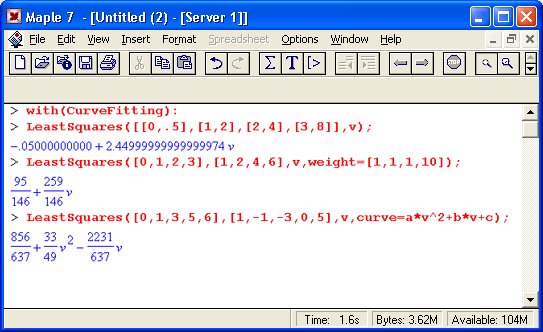
Функция реализации метода наименьших квадратов LeastSquares
Функция LeastSquares служит для реализации аппроксимации по методу наименьших квадратов:
LeastSquares (xydata, v, opts)
LeastSquares(xdata, ydata, v.,opts)
Все входящие в нее параметры были определены выше (см. параметры функции BSplineCurve). Параметр opts задается в форме выражений weight=wlist, curve=f или params=pset.
Следующие примеры иллюстрируют применение функции LeastSquares:
29.gif
32. Функция полиномиальной аппроксимации Polynomiallnterpolation
Функция полиномиальной аппроксимации PolynomialInterpolation
Функция PolynomialInterpolation реализует полиномиальную интерполяцию и может использоваться в виде:
Polynomiallnterpolation (xydata, v)
Polynomiallnterpolation(xdata, ydata, v)
Параметры функции были определены выше. Параметр v может быть как именем, так и численным значением. Примеры применения функции представлены ниже:
30.gif

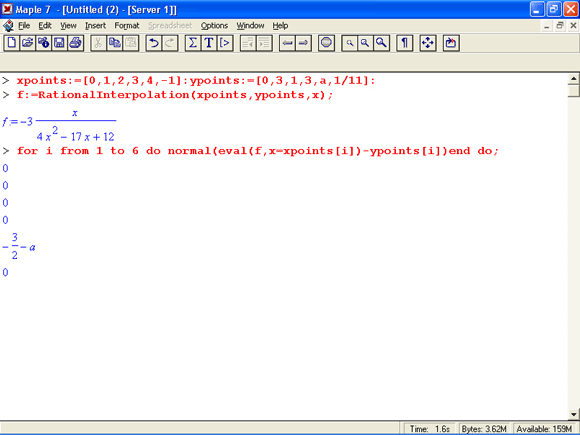
33. Функция рациональной аппроксимации Racionallnterpotation
Функция рациональной аппроксимации RacionalInterpolation
Функция рациональной интерполяции задается в Виде:
Rational Interpolation (xydata, z, opts)
RationalInterpolation(xdata, ydata, z, opts)
где необязательный параметр opts задается выражениями methochmethodtype или degrees=[dl,d2]. Функция возвращает результат в виде отношения двух полиномов. Параметр methodtype может иметь значения 4lookaround или subresultant, задающие учет или пропуск сингулярных точек.
Пример применения функции Rational Interpolation (загрузка пакета опущена, но предполагается):
31.gif
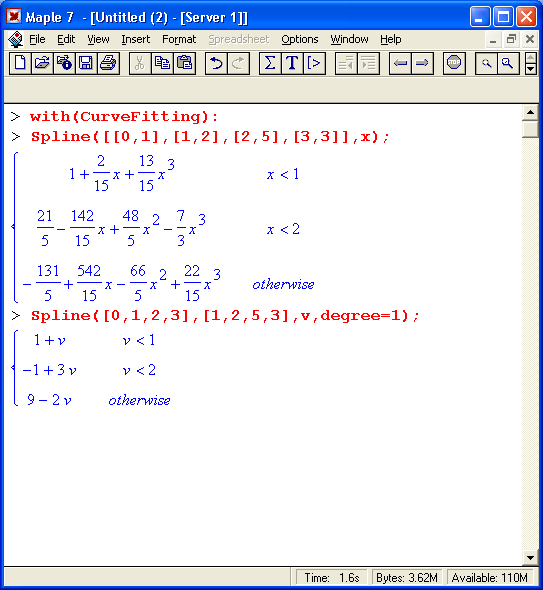
34. Функция вычисления обычных сплайнов Spline
32.gif
35. Функция аппроксимации непрерывными дробями Thielelnterpolation
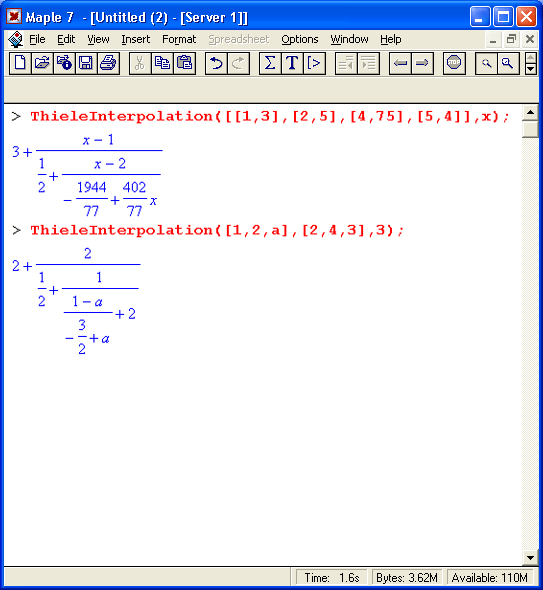
Функция аппроксимации непрерывными дробями ThieleInterpolation
Функция ThieleInterpolation осуществляет интерполяцию на основе непрерывных дробей (Thiele's-интерполяцию). Она задается в виде:
Thielelnterpolation (xydata, v)
Thielelnterpolation(xdata, ydata, v)
Примеры применения данной функции представлены ниже:
33.gif
36. Пакет для работы с полиномами PolynomialTools
Пакет для работы с полиномами PolynomialTools
Обзор возможностей пакета PolynomialTools
Пакет для работы с полиномами PolynomialTools предназначен для выполнения ряда специальных операций с полиномами или создания полиномов с заданными свойствами. Этот пакет имеет небольшое число функций:
> with(PolynomialTools):
[IsSelfReciprocal, MinimalPolynomial, PDEToPolynomial, PolynomialToPDE, Shorten, Shorter, Sort, Split, Splits, Translate]
В пакет входят функции расщепления, сортировки и преобразования полиномов (в том числе в дифференциальные уравнения и наоборот) и др.
37. Функции для работы с полиномами
Функции для работы с полиномами
Рассмотрим несколько функций пакета PolynomialTools общего характера. Примеры применения этой функции представлены ниже:
ПРИМЕЧАНИЕ
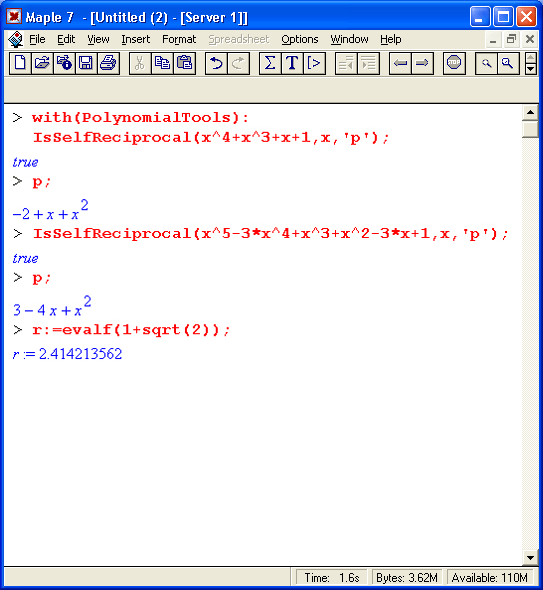
Функция IsSelfReciprocat(a, х, 'р') проверяет полином а(х) на условие coeff(a,x,k) =coeff(a,x,d-k) для всех k = 0. .d, где d = degree(a; х) — порядок полинома. Если это условие выполняется, то возвращается логическое значение true, иначе — false. Если порядок d четный и если задан третий аргумент р, то р будет представлять полином Р порядка d/2, такой, что x^(1/2)*P(x+l/x) = а. При нечетном d полином а будет взаимообратным, что подразумевает деление на х+1. В этом случае; если р указано, результат вычисляется в форме а/(х+1).
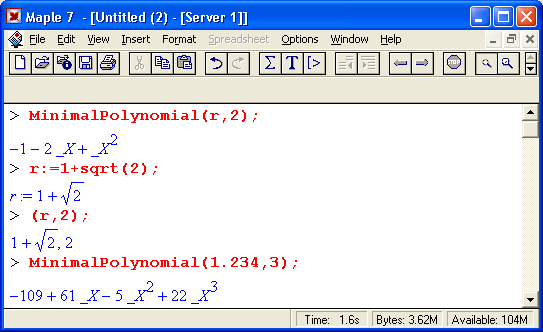
Функция MinimalPolynomial (r, n, асе) возвращает полином минимальной степени не превышающей n, имеющий корень г. Необязательный аргумент асе задает погрешность приближения. Функция MinimalPolynomia(r, n) использует решетчатый алгоритм и находит полином степени п (или менее) с наименьшими целыми коэффициентами. Корень г может быть действительным или комплексным. Результат зависит от значения переменной окружения Digits. По умолчанию асе задано как 10*(Digits-2). Примеры применения данной функции:
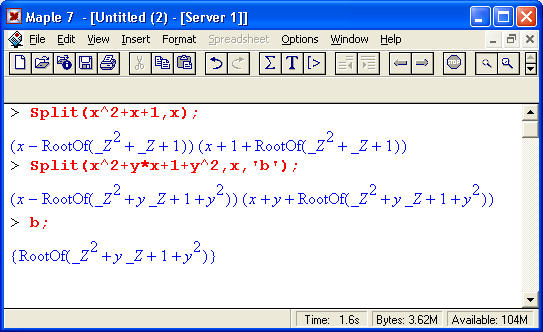
Функция Split(a, х, b) служит для расщепления полинома а с независимой переменной х. Параметр b — необязательный. Функция Split(a, х) осуществляет комплексную факторизацию инвариантного полинома а по х. Если третий аргумент b задан, он представляет множество элементов {tl,... ,tm}, таких что полином а расщепляется над K=Q(tl,... ,tm), где Q означает поле рациональных чисел. Примеры:
В пакете определена еще одна подобная функция Splits, с которой можно познакомиться по справке на нее.
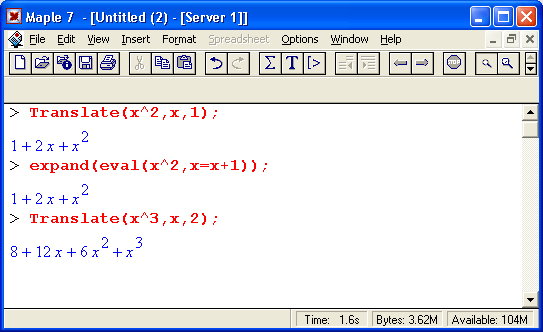
Функция Translate(a, х, х0) преобразует полином а(х) с подстановкой х - х + х0, где x0 — константа. Примеры применения этой функции даны ниже:
34.gif
35.gif
36.gif
37.gif
38. Функции сортировки полиномов
Функции сортировки полиномов
Для сортировки полиномов предназначены следующие три функции:
Shorter(f, g, х)
Sort(v, х)
Shorten(f, x)
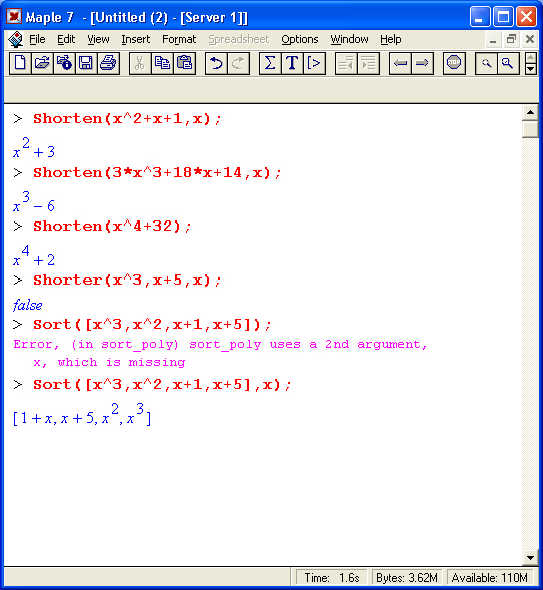
Здесь f и g полиномы, v — список полиномов их — независимая переменная. Функции отличаются характером сортировки.
Функция Shorter определяет полином f как более короткий, чем g, по следующим признакам: меньшая длина, меньшее имя независимой переменной х, не дробный и меньшая степень других переменных. Функция Sort сортирует лист полиномов х по признакам, определяемым Shorter. Функция Shorten использует преобразования Мебиуса. Многочисленные детали ее применения можно найти в справке по данной функции. Примеры применения функций сортировки:
38.gif
39. Функции преобразования полиномов в РОЕ и обратно
Функции преобразования полиномов в РDЕ и обратно
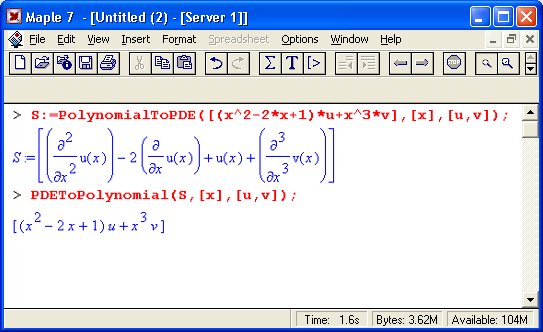
Функция PolynomialToPDE(polys, vars, depvars) преобразует полиномы polys пo независимым переменным vans в дифференциальные уравнения с частными производными (PDE). Другая функция PDEToPolynomia(pdes, vans, depvars) осуществляет обратное преобразование.
Следующие примеры иллюстрируют применение этих функций:
39.gif
40. Что нового мы узнали?
Что нового мы узнали?
В этом уроке мы научились:
- Обращаться к пакетам расширения.
- Пользоваться функциями пакетов комбинаторики.
- Применять пакет финансово-экономических функций.
- Использовать ортогональные многочлены из пакета orthpoly.
- Работать с суммами пакета sumtools.
- Применять степенные разложения пакета powerseries.
- Работать с пакетом численной аппроксимации numapprox.
- Использовать интегральные преобразования пакета inttrans.
- Осуществлять приближение кривых с помощью пакета CurveFitting.
- Использовать пакет работы с полиномами PolynomialTools.